Unobtrusive Detection of Mild Cognitive Impairment in Older Adults Through Home Monitoring

Abstract

The early detection of dementias such as Alzheimer’s disease can in some cases reverse, stop or slow cognitive decline and in general greatly reduce the burden of care. This is of increasing significance as demographic studies are warning of an aging population in North America and worldwide. Various smart homes and systems have been developed to detect cognitive decline through continuous monitoring of high risk individuals. However, the majority of these smart homes and systems use a number of predefined heuristics to detect changes in cognition, which has been demonstrated to focus on the idiosyncratic nuances of the individual subjects and thus does not generalize. In this paper, we address this problem by building generalized linear models of home activity of subjects monitored using unobtrusive sensing technologies. We use inhomogenous Poisson processes to model the presence of subjects within different rooms throughout the day. We employ an information theoretic approach to compare the activity distributions learned, and we observe significant statistical differences between the cognitively intact and impaired subjects. Using a simple thresholding approach, we were able to detect mild cognitive impairment in older adults with an average area under the ROC curve of 0.716 and an average area under the precision-recall curve of 0.706 using distributions estimated over time windows of 12 weeks.

I. INTRODUCTION

Alzheimer’s disease is reported as the fifth-leading cause of death for people aged 65 and older in North America [1] [2]. Currently, reports show that one in nine Americans, and one in eleven Canadians, aged 65 and older have Alzheimer’s disease [3], and according to data from the Chicago Health and Aging Project (CHAP), an estimated 700,000 people in the United States aged 65 and older will die with Alzheimer’s in 2014 [4]. What is more concerning is that as the “baby boomer” generation ages, both the proportion and number of older adults with dementia is projected to increase dramatically, thus greatly increasing the burden on the health-care infrastructure.

The contemporary detection process, in the form of traditional doctor visits, has resulted in a high under-recognition rate of dementia since many of the subtle clues are difficult to spot. Some studies reported that in more that 50% of the detected cases, it was the family members who served as the source of primary recognition and not the family doctors [5]. Accordingly, with the changing demographic, early detection of the cognitive decline that precedes dementia becomes imperative. For subjects with remediable causes such as medication complications or nutritional deficiencies, early detection of cognitive decline renders timely intervention, possibly increasing the chances of reversing the condition. For subjects with irreversible conditions, early detection of cognitive decline still provides them and their families with an opportunity to proactively plan for their future by seeking the appropriate interventions that can maintain their quality of life and daily functioning, and reduce any emotional stress or behavioral symptoms such as depression, apathy, wandering, sleep disturbances, agitation, and aggression [6].

Mild cognitive impairment (MCI) is a condition in which an individual has measurable changes in thinking abilities that are noticeable to the person affected and to family members, but are still mild to impact the individual’s ability to carry out activities of daily living. Although not all subjects with MCI progress to develop Alzheimer’s or other dementias, the proposed criteria and guidelines for diagnosis of Alzheimer’s disease published in 2011 suggest that in many cases, MCI is actually an early stage of Alzheimer’s or another dementia [7]. Therefore, detecting MCI serves the objective of detecting cognitive decline early enough for subjects to seek diagnosis and possible intervention and treatment.

Recent studies have shown that early changes in motor capabilities precede and may be indicative of a cognitive impairment [8], and that subjects with MCI exhibit a more variable and less consistent pattern of activity throughout the day [9]. Also, changes in walking speed and home activity have been found in other studies to be good measures for differentiating older adults with MCI and to be good predictors of progression to dementia [10]. Accordingly, and with the advancement in technology and the proliferation of smart systems, a good alternative to the traditional clinical paradigm is to bring assessment into the daily activity of a person in their home environment via unobtrusive sensors and smart systems. In this paper, we propose developing statistical models of subjects’ general activity in their homes by modeling the distribution of their presence in each room as independent inhomogenous Poisson processes. Intuitively, we postulate that there is a statistical difference in the distribution of presence in each room between cognitively intact and impaired subjects. The work of this paper is built upon a preliminary version of our proposed approach [11].

This paper is organized as follows: Section II summarizes related work, lists research questions, and presents contributions. Section III describes the inclusion criteria for subject recruitment, the data acquired, and the labeling protocol implemented. Section IV presents our proposed approach in building generalized linear models of home activity. Section V presents and discusses results obtained. Section VI addresses the limitations of the current work and proposes potential future work. Finally, Section VII concludes the paper.

II. Related Work

Many smart systems have been developed to monitor the health and well-being of older adults and support their independence such as the Microsoft’s EasyLiving project [12], the GATOR Tech Smart House [13], the AWARE home at Georgia Tech [14], the MavHome Project at the University of Texas at Arlington [15], and the GE QuietCare System [16], and other works that have attempted to detect early changes in health using unobtrusive sensors [17] [18]. However, all results reported by the majority of these system were based on data acquired in a laboratory environment and not in a real world setting. In addition, these systems monitor the general health of the inhabitants and are not designed to specifically detect cognitive changes.

In one study by the Center for Advanced Studies in Adaptive Systems (CASAS), Dawadi et al. implemented a machine learning approach to discriminate cognitively impaired older adults from their cognitively intact counterparts based on their ability to complete a ‘Day Out Task’ that consisted of a number of interwoven Instrumental Activities of Daily Living (IADL). However, the results reported were again based on subjects carrying out the task in a laboratory environment and not in a real world setting. An approach that would be more reflective of the subjects’ actual performance would be to continuously monitor the subjects’ ability to complete the task over several trials, perhaps in their homes since this would capture their true performance.

The ORegon Centre for Aging and TECHnology (ORCATECH) employed unobtrusive sensing technologies in the homes of at least 300 cognitively healthy older adults for an average period of 3 years, resulting in a large database of sensor data and clinical data. In their latest work, Dodge et al. presented trajectories of home-based daily walking speeds and their variability of recruited subjects and compared the resulting trajectories between the cognitively intact subjects and those with non-amnestic mild cognitive impairment (naMCI). [19]. Participating older adults with naMCI were characterized by a slowing of walking speed and exhibited the highest and lowest variability in their walking speeds in comparison with their cognitively intact counterparts.

Building on the work by ORCATECH, Akl et al. used a subset of the data to explore the feasibility of autonomously discriminating older adults with MCI from their cognitively intact counterparts using a number of predefined measures associated with the subjects’ walking speed and general activity in their homes [20]. Different window sizes were used to extract features from the predefined measures which were then used to train and test two machine learning algorithms, namely support vector machines and random forests. Using the measures associated with the subjects’ home activity, we demonstrated that such an approach of using predefined measures tends to focus on idiosyncratic nuances of the individual subjects and therefore could potentially generalize poorly to new subjects. Consequently, using a set of predefined measures associated with the subjects’ home activity only to detect MCI in older adults resulted in an unsatisfactory performance which motivated us to seek an approach that generalizes better to new subjects.

Generalized linear models (GLMs) are commonly used in computational neuroscience to characterize the functional relationship between external sensory stimuli and neural spike trains. GLMs are a generalization of standard linear regression models that can handle any of the predictive distributions belonging to the exponential family such as Gaussian, Bernoulli, Poisson, and others. Although single neuron spiking data could be potentially modeled as a homogeneous Poisson process, where a scalar rate parameter is used to estimate the probability of spiking, several studies have demonstrated that the assumption of homogeneity is unrealistic and the inhomogenous Poisson process is a superior model [21]. Paninski investigated the definition of the rate parameter as a non-linear warping to a linear weighting of the inputs and the use of maximum likelihood to estimate the parameters of the GLM [22]. Pillow et al. extended the model developed by Paninski and demonstrated that the model of individual neuron spiking activity was significantly improved by including coupling filters that capture dependencies on spiking in other neurons [23]. GLMs have proven to be a useful tool for exploratory data analysis in computational neuroscience, and analysis of the model parameters fit to spiking data has helped develop a stronger understanding of neural spiking behavior. Our work is similarly motivated and uses an analogous formulation to explore the following research questions:

1. Can we build statistical models of the subjects’ general activity in their homes using an approach that is robust to the idiosyncratic nuances of the individual subjects?

2. What measures of difference can be used to reveal statistical differences between models pertaining to cognitively intact and cognitively impaired subjects?

3. How does this approach compare to other methods in detecting mild cognitive impairment (MCI) in older adults?

By collaborating with ORCATECH, we were able to answer these questions using sensor and clinical data pertaining to 68 subjects collected over an average period of 3 years via unobtrusive sensing technologies installed in the subjects’ homes. This paper makes the following contributions:

1. We demonstrate that subjects’ home activity can be well-modeled as independent inhomogeneous Poisson processes.

2. We show how the resulting GLMs of the subjects’ inhome activity provide intuitive statistical analysis and the ability to visualize a subject’s pattern of activity, a feature that is very challenging to obtain with models built using a number of predefined measures.

3. We take an information theoretic approach and use the KL-divergence measure to demonstrate an existing statistical difference between activity models pertaining to cognitively intact and impaired subjects.

4. By using a simple thresholding approach of the KL-divergence measure, we were able to detect mild cognitive impairment in older adults with average areas under the ROC curve and the precision-recall curve of 0.716 and 0.706, respectively, using distributions estimated over sliding time windows of 12 weeks.

III. DATA ACQUISITION & LABELING

Data acquisition was completed by ORCATECH who recruited subjects and deployed sensing technologies in their homes for continuous unobtrusive monitoring for an average period of 3 years.

A. Participants and Data Acquisition

Participants were recruited from the Portland, Oregon, metropolitan area. The inclusion criteria included:

1. aged 70 years or older;

2. living independently in a larger than one-room “studio” apartment;

3. cognitively healthy (Clinical Dementia Rating (CDR) score < 0.5; Mini-Mental State Examination (MMSE) score > 24); and,

4. in average health for age (well-controlled chronic diseases and comorbidities or none at all).

Data were acquired by installing sensing technologies in the homes of the recruited subjects. Subjects’ homes ranged from simple one-bedroom apartments with one entry/exit door to houses with as many as 5 bedrooms, a garage, a laundry room, and more than one entry/exit doors. In order to detect movement and general activity, passive infra-red motion sensors were installed in rooms frequently visited by the participating subjects. All sensor firings were sent wirelessly to a transceiver, where they were time stamped, and then stored in a SQL database. For full details on data acquisition and speed calculation, the reader is referred to [24] [25].

In addition to the sensing technologies, recruited subjects were requested to complete a weekly online questionnaire, where the subjects reported any visitors during the week, days spent away from the home, any change in health or medication, admittance to ER, and a number of other queries. These questionnaires were extensively helpful in the cleaning process. Since we are dealing with homes with single occupants, the cleaning process involved discarding days on which subjects had their in-home annual assessments, days on which subjects had any visitors over, days which subjects spent away from the home, days spent in ER, days on which subjects had maintenance people over, or days on which people reported health problems that limited their activity, and days on which sensors failed to fire due to a dead battery or other malfunction.

B. Labeling of Data

Participants were assessed in-home at baseline, and during annual in-home visits by research personnel who administered a standardized battery of tests, including the Mini-Mental State Examination (MMSE) and the Clinical Dementia Rating (CDR). CDR served as our ground truth and was used to determine if subjects were cognitively impaired or intact. A score of 0 on the CDR scale indicated cognitive intactness whereas a score of 0.5 on the CDR scale indicated mild cognitive impairment (MCI). Since subjects were assessed annually, data labels fell into three categories:

1. cognitively intact: “CIN”,

2. transitioning to MCI: “TR”, and

3. experiencing MCI: “MCI”.

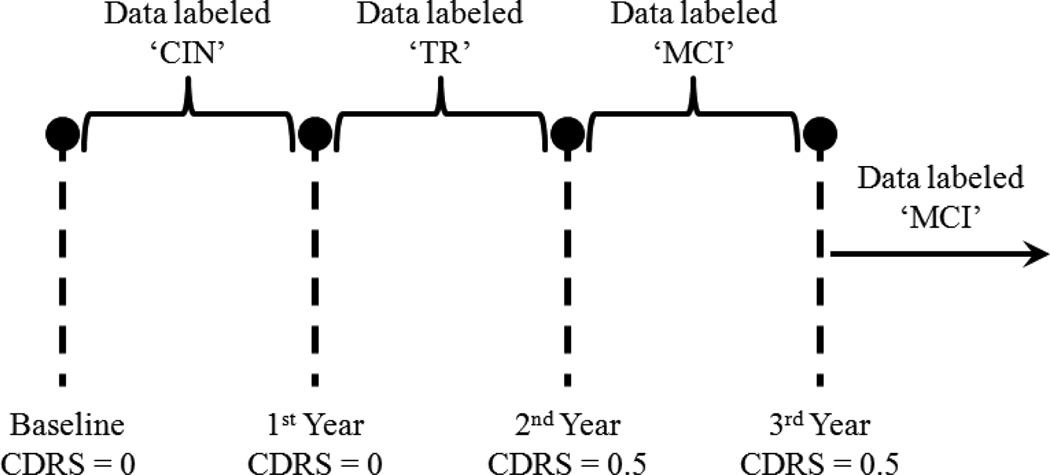
The labeling protocol that we implemented is summarized in the example depicted by Fig. 1, which represents a subject who was monitored for at least 3 years and was administered three annual assessments besides baseline. The subject scored 0 on CDR scale at baseline, but scored 0.5 on the 2nd and 3rd year assessments. Therefore, the data from baseline up to the 1st year assessment were assigned the label “CIN” and the data from the 2nd year assessment onward were assigned the label “MCI”. The data between the 1st year and the 2nd year assessments were assigned the label “TR” for transitioning to MCI. This is because the conversion to cognitive impairment is not an instantaneous event but a gradual process. Accordingly, the subject’s cognitive status would be in flux between years 1 and 2 and would not belong to either cognitive intactness or MCI.

Fig. 1.

Example of a subject who scored 0.5 on CDR scale on the 2nd year assessment onward.

IV. PROBLEM SETUP

In this section, we represent variables by lower case letters, e.g. u, vectors by bold lower case letters, e.g. u, and matrices by bold upper case letters, e.g. U.

Suppose a database consists of N subjects, each subject residing in a living unit with M rooms, and we are interested in estimating the probability of a subject being present in room r within a fixed time interval throughout the day, where 1≤ r ≤ M. Accordingly, the problem can be well-modeled as a Poission process, because a Poisson distribution models the number of occurrences of an event in a fixed period of time. In our case, the event is ‘being present in a room.’ By defining a variable, y_r, that captures the number of times a subject visits room r, the probability of the subject being present in room r can be given by

$$p(y_r)=\frac{{\mathrm{e}}^{-\lambda }{\lambda }^{y_r}}{y_r!}$$ (1)

where λ is the Poisson distribution parameter. However, after analyzing the parameter λ for all subjects, it was found that λ associated with each room was not constant and varied each day for all subjects. Furthermore, note that λ would most likely vary throughout the day too, as the presence in each room is highly time dependent. Therefore, an inhomogenous Poisson process would serve as a better model.

To estimate the distribution parameter of the the inhomogeneous Poisson process, we propose the following approach. We start by dividing the day into K intervals and define a λ_i for each interval where 1≤ i ≤ K. Therefore, a day represented by a matrix X would look like the following:

$$\mathbf{X}=[{\mathit{x}}^{(1)},{\mathit{x}}^{(2)},\dots ,{\mathit{x}}^{(i)},\dots ,{\mathit{x}}^{(K)}]$$ (2)

where,

$${\mathit{x}}^{(i)}=x_j\mathit{\text{ for }}1\le j\le Ks.t.\{\begin{array}{cc}\hfill x_j=1\hfill & \hfill i=j\hfill \\ \hfill x_j=0\hfill & \hfill i\ne j.\hfill \end{array}$$ (3)

In other words, X takes the form of an identity matrix of size K × K, where each column represents a time interval, and each interval is associated with a λ_i. The reason why we choose to binarize the day instead of treating it as a continuous variable is, in the case of the continuous variable, the probability of a person being in a room can either increase or decrease linearly throughout the day, which does not reflect a realistic situation. For example, we do not expect the likelihood of a subject to be in a room to only increase throughout the day and reach a maximum at the end of the day. On the other hand, we would expect the likelihood of a subject to be in the kitchen, for example, to be high at lunch time but to be low before and after that. Binarizing the data in the form shown in (2) and (3) takes care of this non-linearity in the likelihood throughout the day.

For a subject who was monitored for 900 days for example, the subject’s input space consists of a total number of Z = (900 × K) vectors for each of the M rooms, and each vector has a corresponding label y_r indicating the number of times the subject visits room r during the corresponding time interval. The problem can then be formulated as estimating the probability of the subject being present in room r given a time interval x⁽ⁱ⁾ as an input. To estimate this probability, the λ_ri’s corresponding to each interval for room r need to be found, denoted by the vector λ_r. Given a data set of Z time intervals along with the corresponding labels represented by the vector ${\mathit{y}}_r={\{y_r^{(s)}\}}_{s=1}^Z$, the goal is to find λ_r that maximizes the likelihood function L(λ_r),

$$L({\mathit{\lambda }}_r)=p({\mathit{y}}_r|\mathbf{X};{\mathit{\lambda }}_r)=\prod _{s=1}^Z\frac{{\mathrm{e}}^{-{\lambda }_{rs}}{{\lambda }_{rs}}^{y_r^{(s)}}}{y_r^{(s)}!}.$$ (4)

However, maximizing (4) is equivalent to maximizing its log. Therefore,

$$\ell ({\mathit{\lambda }}_r)=\text{log}(L({\mathit{\lambda }}_r))=\text{log}\prod _{s=1}^Z\frac{{\mathrm{e}}^{-{\lambda }_{rs}}{{\lambda }_{rs}}^{y_r^{(s)}}}{y_r^{(s)}!}=\sum _{s=1}^Z\text{log}\frac{{\mathrm{e}}^{-{\lambda }_{rs}}{{\lambda }_{rs}}^{y_r^{(s)}}}{y_r^{(s)}!}=\sum _{s=1}^Z-{\lambda }_{rs}+y_r^{(s)}\text{log}{\lambda }_{rs}-\text{log}(y_r^{(s)}!).$$ (5)

According to the work by Paninski in [22], to estimate λ_r originating from an inhomogenous Poisson process, λ_r should be defined as a function that is monotonic, grows at least linearly, decays exponentially, and has a derivative. λ_r of the form exp (X^Tw_r) meets these constraints, where w_r is a K × 1 vector of weights. The problem of estimating λ_r becomes equivalent to estimating the weight vector w_r. Substituting the definition of λ_rs = e^x(s)T w_r into (5),

$$\ell ({\mathit{w}}_r)=-\sum _{s=1}^Z{\mathrm{e}}^{{\mathit{x}}^{{(s)}^T}{\mathit{w}}_r}+\sum _{s=1}^Z{y}_r^{(s)}{\mathit{x}}^{{(s)}^T}{\mathit{w}}_r-\sum _{s=1}^Z\text{log}(y_r^{(s)}!).$$ (6)

Maximizing (6) is equivalent to minimizing the negative of it, i.e., minimizing

$$\ell \prime ({\mathit{w}}_r)=-\ell ({\mathit{w}}_r)=\sum _{s=1}^Z{\mathrm{e}}^{{\mathit{x}}^{{(s)}^T}{\mathit{w}}_r}-\sum _{s=1}^Z{y}_r^{(s)}{\mathit{x}}^{{(s)}^T}{\mathit{w}}_r+\sum _{s=1}^Z\text{log}(y_r^{(s)}!)$$ (7)

whose derivative is given by

$$\frac{d\ell \prime ({\mathit{w}}_r)}{w_{rj}}=\sum _{s=1}^Z{x}_j^{(s)}{\mathrm{e}}^{{\mathit{x}}^{{(s)}^T}{\mathit{w}}_r}-\sum _{s=1}^Z{y}_r^{(s)}{x}_j^{(s)}.$$ (8)

Once w_r is found, λ_r is computed as λ_r = e^w_r. For a subject residing in a living unit with M rooms, who transitioned to MCI during the study, (3 × M)λ vectors would be estimated, one for each stage of cognition. So all the data corresponding to the period for which the subject was cognitively intact would be used to estimate one set of Mλ vectors, one for each room. Similarly, all the data corresponding to the period for the which the subject was transitioning to MCI would be used to estimate another set of Mλ vectors. Finally, all the data corresponding to the period for which the subject was experiencing MCI would be used to estimate the third set of Mλ vectors. The probability that the subject is present in room r during time interval x⁽ⁱ⁾ of the day is then estimated as,

$$p^c(y=1|{\mathit{x}}^{(i)})={\mathrm{e}}^{-{\lambda }_{ri}^c}{\lambda }_{ri}^c$$ (9)

where c simply indicates the cognitive status of the subject, i.e. c = {“CIN”, “TR”, “MCI”}.

V. RESULTS & DISCUSSION

Of the 68 subjects, 7 were males and 2 transitioned to MCI during the monitoring period. The remaining 61 subjects were females, 13 of which transitioned to MCI during the monitoring period.

A. Activity Distributions

Given that sensing technologies were deployed into the homes of the participating subjects, in order to standardize the comparison across subjects, we based our analysis on the subjects’ activity in four rooms: the main bedroom, the main bathroom, the kitchen, and the living room. Accordingly, for each subject we estimated four Poisson distributions (λ_bdr, λ_br, λ_k, and λ_lr) for each stage of cognition (cognitive intactness, transitioning, and MCI). As we have established in our preliminary work [11], the smoothness portrayed by distributions estimated using 30-minute intervals was satisfactory and therefore, we present results based on K = 48 intervals.

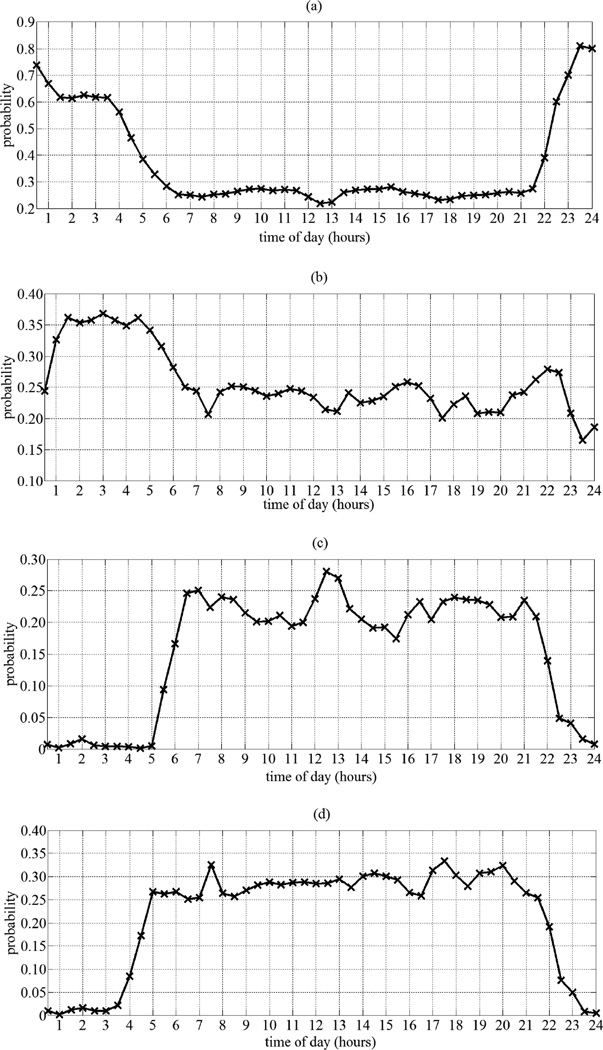
Fig. 2 depicts the estimated distributions pertaining to a female subject, residing in a one-bedroom apartment, and who remained cognitively intact for the entire period of monitoring. These distributions were created by calculating the probability defined in (9) for each interval defined in (2) and (3) for K = 48 using the estimated λ vectors. Because the motion sensors utilized in this study were passive infra-red sensors, they do not detect passive activity such as sound sleeping, recuperating, or reading. Accordingly, although we have set out to estimate the probability of a subject being present in a room at different time intervals throughout the day, Fig. 2 instead shows the probability of the sensing technologies firing in response to the subject’s activity in each room.

Fig. 2.

Estimated home activity distributions pertaining to a female subject residing in a one-bedroom apartment. a) Bedroom distribution. b) Bathroom distribution. c) Kitchen distribution. d) Living room distribution.

Interestingly, using our approach we were able to visualize and elicit patterns of activity specific to each subject, a feature that is very difficult to have using models extracted from a number of predefined measures. According to Fig. 2, night time activity, especially between 10PM and 6AM, is dominated by the bedroom with frequent trips to the bathroom during the night between 1:30AM and 6AM. The subject is most likely to wake up at 6AM before she proceeds to the kitchen and living room area to prepare breakfast. Occasionally, she seems to wake up before 6AM and rest in the living room for sometime before proceeding to the kitchen to prepare her breakfast. From the kitchen distribution, we are able to identify two distinct peaks that mostly likely correspond to breakfast, between 6AM and 7AM, and to lunch, between 12PM and 1PM. The subject usually has dinner between 5:30PM and 7:30PM. In addition, it seems that the subject frequently visits the kitchen for a late night snack or drink between 9PM and 10PM. Generally, the subject goes to bed shortly after 10PM.

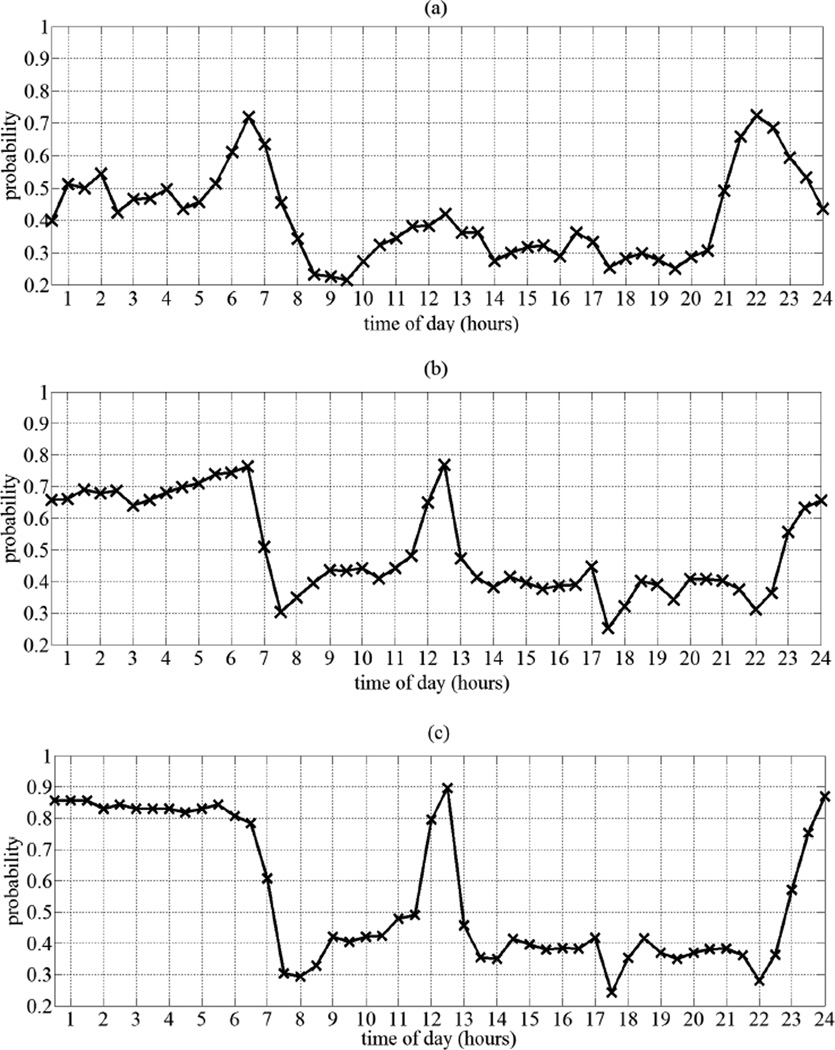
Furthermore, by comparing subjects’ activity distributions while cognitively intact to their distributions as they start transitioning to MCI and when experiencing MCI, we were able to extract important differences among the three distributions. One main observation was the distributions pertaining to the cognitive intactness stage were smoother than the distributions pertaining to the transitioning and the MCI stages. Another important observation was that we were able to extract an important activity-related MCI symptom, namely disturbed sleep patterns from many subjects who transitioned to MCI. In Fig. 3, for example, we show the bedroom distributions for a subject who transitioned to MCI during the monitoring period. As stated earlier, because the motion sensors utilized in this study were passive infra-red sensors, then sound deep sleep would not be detected by these sensors despite the presence of the subject in the bedroom. This explains the low probability from 11PM – 6AM when the subject was cognitively intact. However, as the subject started transitioning to MCI, the probability of being present in the bedroom from 11PM – 6AM increased, and increased the most when the subject was experiencing MCI. This increase in probability of presence was potentially due to movements and activity related to disturbed sleep patterns, which have been proven to be associated with MCI [26].

Fig. 3.

a) Bedroom distribution for a subject when cognitively intact. b) Bedroom distribution for the same subject when transitioning to MCI. c) Bedroom distribution for the same subject when suffering from MCI.

B. KL-divergence Measure

In order to quantify the statistical difference between the distributions of the subjects when cognitively intact, when transitioning to MCI, and when suffering from MCI, we took an information theoretic approach by computing the Kullback–Leibler (KL)-divergence, which is a measure of difference, between the estimated distributions [27]. For example, the KL-divergence of an activity distribution pertaining to a subject when in a certain cognitive status, denoted by q, from the activity distribution pertaining to the same subject when in a different or the same cognitive status, denoted by p, is computed as,

$$D_{KL}(\mathit{p},\mathit{q})=\sum _i^K\mathit{p}(i)\text{ln}\frac{\mathit{p}(i)}{\mathit{q}(i)}$$ (10)

where i and K, as defined in (2) and (3), are the interval number and the number of intervals per day, respectively. A KL-divergence of 0 implies that the two probability distributions are identical. The higher the KL-divergence the greater the difference between the two probability distributions. In this work, we used a normalized version of the KL-divergence, defined as,

$$D_{KL}^{\mathit{\text{norm}}}(\mathit{p},\mathit{q})=1-\text{exp }(-D_{KL}(\mathit{p},\mathit{q})).$$ (11)

This normalization limits the values of the KL-divergence to be between 0 and 1.

For the 15 subjects who transitioned to MCI during the monitoring period, we used (11) to compute the normalized KL-divergences between their room distributions when they were cognitively intact and when they were transitioning to MCI, to compute the normalized KL-divergences between their room distributions when they were cognitively intact and when they were experiencing MCI, and to compute the normalized KL-divergences between their room distributions when they were transitioning to MCI and when they were experiencing MCI.

According to our formulation, cognitive changes occur in the following order: cognitive intactness (“CIN”) → transitioning to MCI (“TR”) → having MCI (“MCI”). Because the KL-divergence is asymmetric, the KL-divergences were computed as the divergence of the distributions pertaining to a cognitive status from the distributions pertaining to the preceding cognitive status. For example, the KL-divergences between the “CIN” and the “TR” distributions were computed as the KL-divergences of the “TR” distributions from the “CIN” distributions. Similarly, the KL-divergences between the “CIN” and the “MCI” distributions were computed as the KL-divergences of the “MCI” distributions from the “CIN” distributions. Finally, the KL-divergences between the “TR” and the “MCI” distributions were computed as the KL-divergences of the “MCI” distributions from the “TR” distributions.

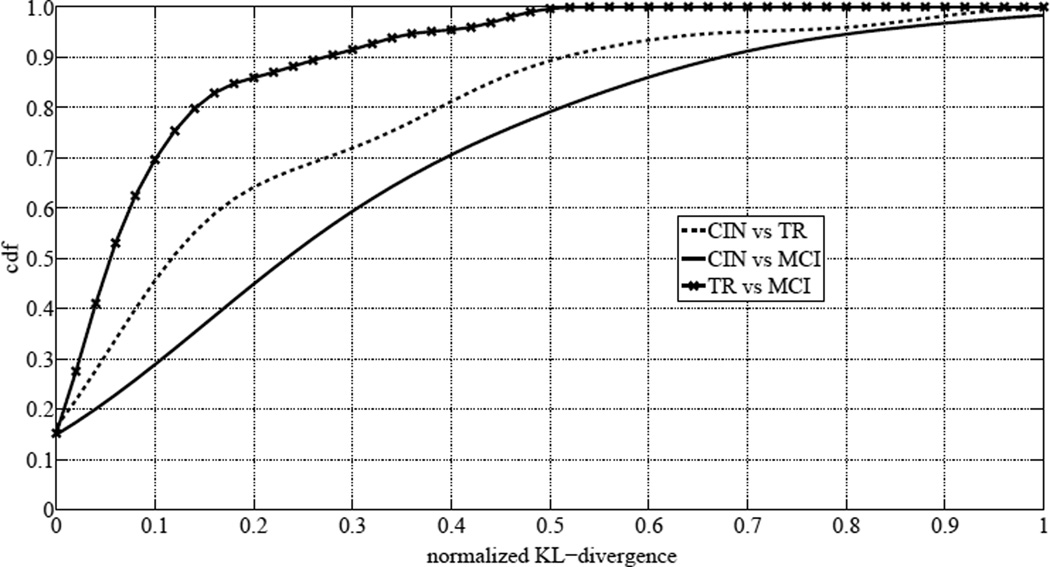
The computed normalized KL-divergences were then used to estimate the cumulative distribution function (cdf) of the normalized KL-divergences of the “TR” distributions from the “CIN” distributions, to estimate the cdf of the normalized KL-divergences of the “MCI” distributions from the “CIN” distributions, and to estimate the cdf of the normalized KL-divergences of the “MCI” distributions from the “TR” distributions, for all rooms. The estimated cdfs are shown in Fig. 4. An increasing average of normalized KL-divergence is portrayed as we move from cognitive intactness to MCI. This supports our hypothesis that activity distributions of subjects when having MCI are different from their activity distributions when cognitively intact. A very interesting observation is that 50% of the subjects have a normalized KL-divergence of their “MCI” distributions from their “TR” distributions of 0.05 or less. Only 20% of the subjects have a normalized KL-divergence of their “MCI” distributions from their “TR” distributions that is between 0.1 and 0.5. This means that the majority of the subjects, when transitioning to MCI, exhibited behaviors and patterns closer to their “MCI” patterns than to their “CIN” patterns.

Fig. 4.

Cumulative distribution function of normalized KL-divergences between CIN and TR distributions, CIN and MCI distributions, and TR and MCI distributions for all rooms.

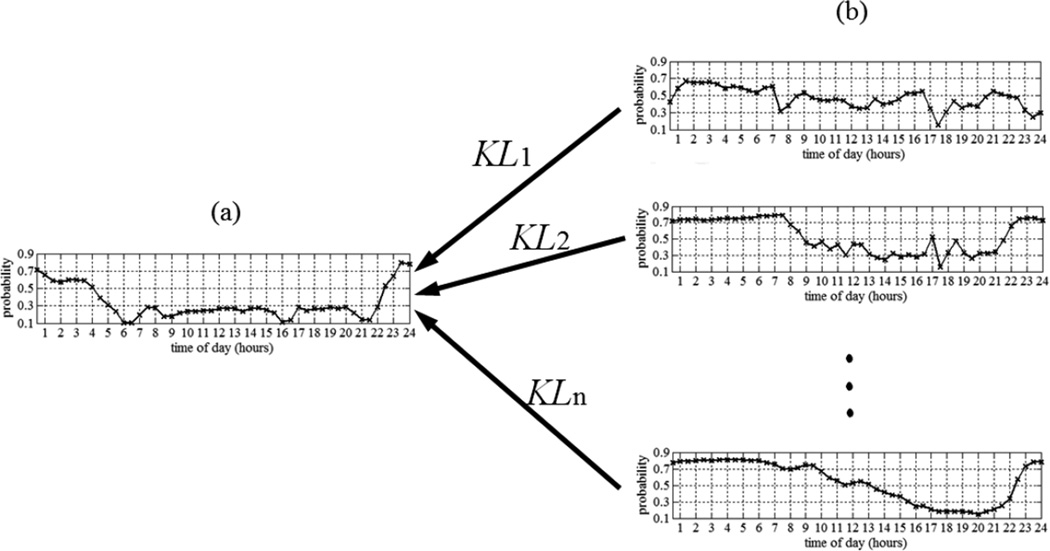
In order to investigate this finding, for the 15 subjects who transitioned to MCI, we used all the “CIN” data to estimate the subjects’ distributions for the same aforementioned four rooms. These distributions served as our reference distributions. Then a sliding time window of size ω weeks was defined and used to estimate the rooms’ distributions using a subset of the data. Then each of the distributions estimated using the sliding window was compared to the reference distribution by computing the normalized KL-divergence, defined in (11), of the distribution, estimated using the sliding window, from the reference distribution. The result was a trajectory of n normalized KL-divergences, where n is the number of slides it took the time window to span the entire period of monitoring for a particular subject. n was different for different subjects since subjects were monitored for different periods. Fig. 5 depicts the process for one room. Fig. 5a) shows the room’s reference distribution that was estimated using all the “CIN” data. Fig. 5b) shows the distributions that were estimated using a sliding time window of size ω weeks as it slid through the “CIN” data, the “TR” data, and the “MCI” data.

Fig. 5.

a) Room reference distribution. b) Distributions estimated using sliding window of size ω weeks as it slid through the “CIN” data, the “TR” data, and the “MCI” data. The result is a trajectory of n normalized KL-divergences, where n is the number of slides it took the time window to span the entire period of monitoring for a particular subject.

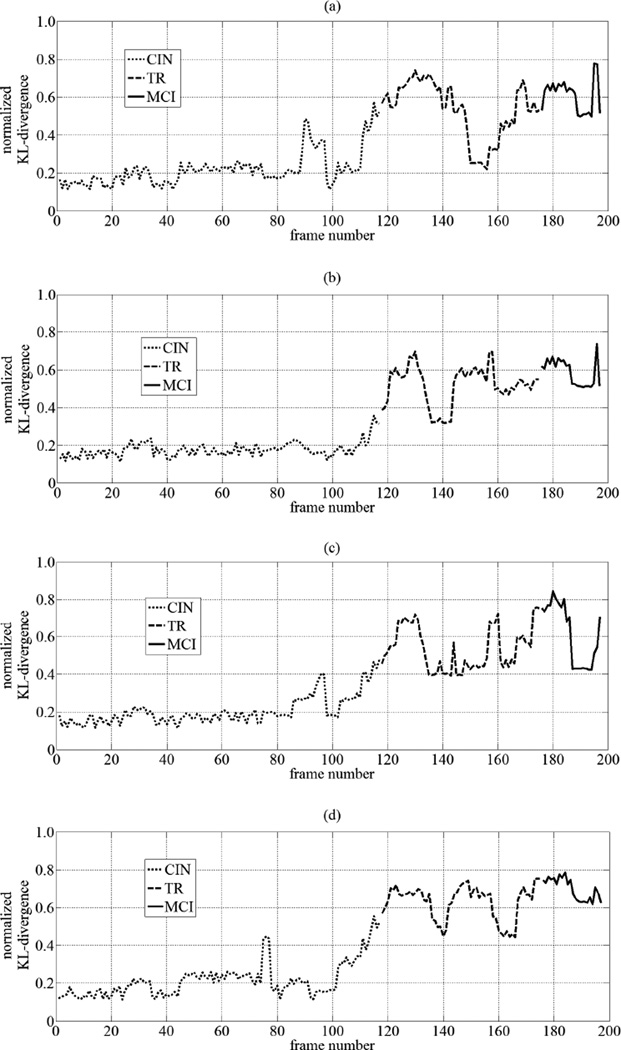
The hypothesis was that normalized KL-divergence would start increasing as the time window started sliding over the “TR” and the “MCI” data. Fig. 6 shows the trajectories of normalized KL-divergences for a subject who confirmed our hypothesis with respect to all four rooms, for whom n = 197. The dotted lines represent the “CIN” normalized KL-divergences of the distributions, estimated using the time window as it slid over the “CIN” data, from the reference distribution, the dashed lines represent the “TR” normalized KL-divergences of the distributions, estimated using the time window as it slid over the “TR” data, from the reference distribution, and the solid lines represent the “MCI” normalized KL-divergences of the distributions, estimated using the time window as it slid over the “MCI” data, from the reference distribution. According to Fig. 6, the “CIN” normalized KL-divergences fluctuated between 0.1 and 0.2. However, as the time window started sliding over the “TR” and the “MCI” data, the normalized KL-divergences increased to reach approximately 0.8 for all four rooms. Not all subjects showed the same pattern for all four rooms, but our hypothesis was confirmed for at least one room for the majority of the subjects.

Fig. 6.

Example of trajectories of normalized KL-divergences of sliding window distributions from reference distributions for a) Bedroom b) Bathroom c) Kitchen d) Living room

What was more interesting was that for the majority of the subjects, the KL-divergences started increasing significantly several months prior to the start of the transitioning period. The trajectories in Fig. 6 are a clear example of this observation. This most likely explains why the majority of the subjects had very small normalized KL-divergences of their “MCI” distributions from their “TR” distributions. Yet, these subjects still scored 0 on the CDR scale, indicating that they were still cognitively intact, and it was not until the following year that they were diagnosed as having MCI by scoring 0.5 on the CDR scale. This delay in detecting MCI in the participating subjects could be very well attributed to the inherent shortcoming of episodic cognitive assessments and examinations in that they depend on a snapshot observation of cognitive function and assume that observations recorded during the assessment represent the person’s typical state of cognition for relatively long periods of time prior to the assessment. Evidently, this was not the case here for the majority of the subjects neither before the annual assessment nor after the assessment. This finding reinforces the need for an alternative approach in which assessment is brought into the daily activity of a person in their home environment.

C. Detecting MCI

After demonstrating significant statistical difference in the activity distributions of the majority of the subjects when cognitively intact and when suffering from MCI, we were interested in comparing the performance of this approach to the recently published work [20] in detecting MCI in older adults. We formulated a classification problem, composed of two classes: “cognitively intact” which consisted of the “CIN” data, and the “experiencing MCI” which consisted of the “TR” and the “MCI” data.

The approach of calculating normalized KL-divergences of distributions, estimated using a sliding window of size ω weeks, from the reference distributions was repeated for all 68 subjects. By thresholding the resulting trajectories of normalized KL-divergences, we generated two curves: the ROC curve by plotting sensitivity versus (1 - specificity) and the precision-recall curve by plotting precision versus recall. A normalized KL-divergence that was below the threshold was classified as “cognitively intact” and a normalized KL-divergence that was above the threshold was classified as “experiencing MCI”. The area under the ROC curve was denoted as AUC_SS, and the area under the precision-recall curve was denoted as AUC_PR.

Table I presents a summary of the areas under the curves obtained using a window size ω = 12 weeks. Average areas under the ROC curve and the precision-recall curve of 0.716 and 0.706, respectively were obtained. We were able to identify three main sources of error. The first main source of error was the innate erroneous labeling of the data. The normalized KL-divergences prior to the start of the transitioning period were labeled as belonging to the “cognitively intact” class when they clearly belonged to the “experiencing MCI” class. The second main source of error was, for several subjects who transitioned to MCI during the monitoring period, no increasing “TR” and “MCI” normalized KL-divergences were detected for all the rooms especially the bathroom. This explains why the areas under the curves corresponding to the bathroom were the smallest. Finally, the third main source of error was, for three of the subjects who transitioned to MCI during the monitoring period, no increasing “TR” and “MCI” normalized KL-divergences were detected at all for any of the rooms. This could be associated with the subjects most likely suffering from amnestic MCI only, where it was only the memory skills of the subjects that were compromised while their thinking and executive functioning skills were still intact. This source of error is a consequence of the inherent shortcoming of the CDR assessment as its definition of MCI lacks a distinction of the two types of MCI: amnestic MCI (a-MCI) and nonamnestic MCI (na-MCI).

TABLE I.

Areas under curves generated by thresholding of normalized KL-divergences of distributions, estimated using as sliding window of size ω = 12 weeks, from reference distributions compared to areas under curves obtained in approach using a set of predefined heuristics associated with in-home activity [20].

Approaches	Area Under	Room				Average	Window Size
	Curve	Bedroom	Bathroom	Kitchen	Living Room		(ω) weeks
Our Approach	AUCSS	0.717	0.687	0.714	0.745	0.716	12
	AUCPR	0.689	0.652	0.726	0.757	0.706
Approach in [20]	AUCSS	-	-	-	-	0.40	12
	AUCPR	-	-	-	-	0.26
Approach in [20]	AUCSS	-	-	-	-	0.57	24
	AUCPR	-	-	-	-	0.43

Despite these sources of error, our approach significantly outperformed the best performance reported using our previous approach that utilized a set of predefined measures [20]. The best scores reported in [20] using predefined measures pertaining to in-home activity only were AUC_SS = 0.57 and AUC_PR = 0.43 using ω = 24 weeks. In other words, with only half the size of the window frame, we were able to outperform the best performance reported in [20]. Also, note that with our proposed approach we are able to learn about the cognitive capacity of the older adult based on their activity distributions in individual rooms, which is advantageous over the other approach of detecting MCI using a predefined set of heuristics. Overall, with this proposed approach, we were able to increase the area under the ROC curve by 31% and the area under the precision-recall curve by 44% for ω = 12 weeks when compared to the performance in [20].

VI. FUTURE WORK

For future work, we believe it is important to experiment with a different ground truth and to compare the results. In order to address the shortcoming with CDR’s definition of MCI, mainly lacking a distinction of the two types of MCI, neuropsychological assessments can serve as a potential alternative. With neuropsychological assessments we are able to determine the type of MCI and thus have deeper insight and better understanding of the differences between the activity distributions when subjects are cognitively intact and suffering from MCI.

Another direction for future work is to devise an online approach to automatically detect MCI in older adults using changes in their activity distributions. We anticipate that the most efficient way to approach this problem is to do change point detection similar to the work published by Adams and MacKay [28]. In essence, we want to detect when substantial changes in the model parameters occur for each older adult. In order to successfully accomplish this, it is necessary to determine the best window size needed to build the baseline distribution for each older adult for each room in their living unit. Furthermore, we need to determine how much change in the model parameters would warrant a significant change in cognition and based on which the individual at hand would be referred to a memory clinic for a comprehensive cognitive assessment to confirm any cognitive impairment.

One limitation of this work is the small population size of older adults and of older adults who transitioned to MCI during the monitoring period. We believe it is very important to test our proposed approach on a larger population size in order to corroborate these results and confirm their validity.

VII. CONCLUSION

In conclusion, we proposed and presented an alternative approach to that of existing studies on smart systems developed to monitor cognitive decline. Using the sensor and clinical data pertaining to 68 subjects, 15 of which transitioned to MCI during the monitoring period, we demonstrated that the subjects’ home activity could be well-modeled as independent inhomogeneous Poisson processes. Using this approach, we were able to visualize and elicit patterns of activity specific to each subject, a feature that is very difficult to have using other works where a number of predefined measures is used. This answered our first research question.

In order to quantify any statistical differences between activity distributions pertaining to subjects when cognitively intact and when transitioning to MCI or when experiencing MCI, we took an information theoretic approach and used the KL-divergence to demonstrate statistical differences between the distributions corresponding to the different states of cognition. This answered our second research question.

Finally, by using a simple thresholding approach of trajectories of normalized KL-divergences, we were able to detect mild cognitive impairment in older adults with average areas under the ROC curve and the precision-recall curve of 0.716 and 0.706, respectively, using distributions estimated using a sliding time window of 12 weeks. Our proposed approach outperformed other works where a number of predefined measures associated with the subjects general activity was used to detect MCI. This answered our third research question.