Stretch-Activated Current Can Promote or Suppress Cardiac Alternans Depending on Voltage-Calcium Interaction

Abstract

Cardiac alternans has been linked to the onset of ventricular fibrillation and ventricular tachycardia, leading to life-threatening arrhythmias. Here, we investigated the effects of stretch-activated currents (I_SAC) on alternans using a physiologically detailed model of the ventricular myocyte. We found that increasing I_SAC suppresses alternans if the voltage-Ca coupling is positive or the alternans is voltage driven. However, for electromechanically discordant alternans, which occurs when the alternans is Ca driven with negative voltage-Ca coupling, increasing I_SAC promotes Ca alternans. In addition, if action potential duration-Ca transients show quasiperiodicity, we observe a biphasic effect of I_SAC, i.e., suppressing quasiperiodic oscillation at small stretch but promoting electromechanically discordant alternans at larger stretch. Our results demonstrate how I_SAC interacts with coupled voltage-Ca dynamical systems with respect to alternans.

Introduction

The cardiac action potential (AP) controls the mechanical activity of the heart via excitation-contraction coupling (1). Conversely, mechanical effects can modulate cardiac electrical activity in complex ways via mechanoelectric feedback (MEF) (2). It has been shown that a depolarizing stretch-activated current (I_SAC) through stretch-activated ion channels is evoked by the deformation of a cardiomyocyte (3, 4), which affects its electrophysiological properties and excitation processes. Physiologically, I_SAC has been implicated in arrhythmias due to abnormal electric activity associated with increased pressure or hemodynamic volume loading of the ventricles, as observed in diseases such as hypertension, aortic valve disease, and congestive heart failure (5). On the other hand, the AP duration (APD) and Ca transient alternans have also been linked to the onset of ventricular fibrillation and ventricular tachycardia, leading to life-threatening arrhythmias (6). Experimentally, electromechanical alternans can be either concordant (long/short APD corresponds to a large/small Ca transient on alternate beats) or discordant (long/short APD corresponds to a small/large Ca transient). Our previous studies have shown that these phenomena depend on the underlying instability mechanisms (voltage driven or Ca driven) and bidirectional coupling between voltage and Ca cycling (7). The arrhythmogenic effects of alternans are of great interest, but the physiological influence of stretch-activated channels (SACs) on them is unknown. In this study, we aimed to determine how SAC activation caused by an active mechanical stretch along the longitudinal axis alters cardiac alternans.

Materials and Methods

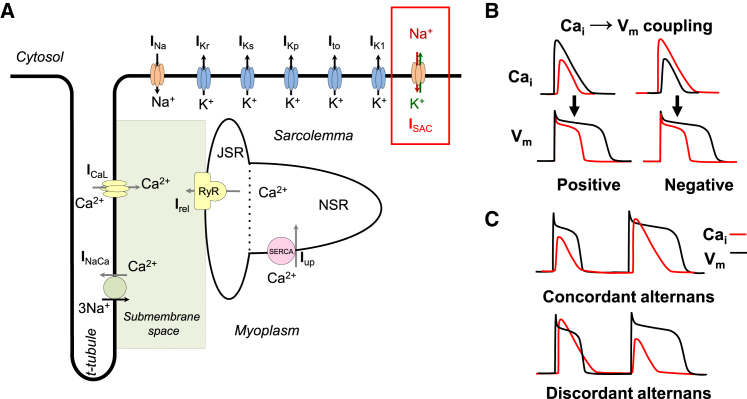
We studied the effects of SACs on the coupled dynamical systems of voltage-Ca in positive coupling (a larger Ca transient prolongs APD) and negative coupling (a larger Ca transient shortens the APD). For this purpose, we used the physiologically detailed AP and intracellular Ca cycling model of Shiferaw et al. (7) (Fig. 1 A). This model exhibits three distinct dynamical modes due to the underlying instability mechanisms and the coupling between voltage and Ca cycling: 1) concordant alternans with a long/short APD corresponding to a large/small calcium transient on alternate beats (Fig. 1, B and C), 2) discordant alternans with a long/short APD corresponding to a small/large calcium transient (Fig. 1, B and C), and 3) quasiperiodic oscillation of the APD and Ca transient. The details of the model are provided in our previous study (7). We extended this model by incorporating SACs (Fig. 1 A, red box) and a five-state model of myofilament contraction as described in (8). We performed simulations with constant length (isometric contraction) or constant applied force (isotonic contraction). We first investigated the influence of I_SAC on the AP by applying a constant stretch to a single cell (the isometric case). The cell was electrically stimulated with a pacing cycle length (PCL) of 300 ms. Then, we compared the results with those obtained from simulations in the isotonic condition. All programs were written in C++ and the fourth-order Runge-Kutta method was used to solve ordinary differential equations with a time step of 0.05 ms.

Figure 1.

(A) Schematic representation of the computational model. (B) Illustration of positive and negative Ca_i→V_m coupling. Positive (negative) coupling refers to the case in which a large Ca_i transient at a given beat tends to prolong (shorten) the APD of that beat. (C) Illustration of concordant and discordant alternans during steady-state pacing. To see this figure in color, go online.

Results and Discussion

Mechanical stimulation activates a variety of ion channels in cardiac myocytes, including stretch-activated, nonselective cation channels and mechanosensitive potassium channels (2). The response of cells to mechanical deformation depends on the way the cells are being distorted. Zeng et al. (4) reported that SACs conduct both K⁺ and Na⁺ in rat cardiac myocytes, but they did not observe a specific Ca²⁺ channel activity during longitudinal stretch. However, an increased Na⁺ influx can raise [Ca²⁺]_i via sodium-calcium exchange (NCX). Youm et al. (9) stated that although a stretch of cardiac myocytes also activates the K⁺-selective TREK and swelling-activated chloride channels, the mode of stretch activation of these channels is different from a stretch along the longitudinal axis. They also reported that these channels can be activated by applying a negative pressure to the membrane patch and perfusing a hypoosmotic solution to the cell, respectively.

To investigate the effects of I_SAC, we first imposed the cell length and performed simulations at constant stretch along the longitudinal axis (isometric). All stretch was defined relative to the resting cell length. However, in experiments, SACs are usually recorded at the length at which maximum active tension is generated. For example, Zeng et al. (4) showed that the current-voltage (I-V) relationship normalized to cell capacitance is nearly linear, with a reversal potential around −6 mV in Tyrode solution, and when cells are stretched by 5 μm, equivalent to a ∼3% strain. Consequently, an intermediate current for lesser strain needs to be estimated. In accordance with several reports showing that the change in mechanosensitive current I_SAC is linear with both sarcomere length (SL) and strain (10, 11, 12), we used the following mathematical model of I_SAC:

$$I_{SAC}=G_{SAC}\frac{\left(\lambda -1\right)}{\left({\lambda }_{\text{max}}-1\right)}\left(V_m-E_{SAC}\right),$$ (1)

where G_SAC is the whole-cell conductance. Here, we choose G_SAC = 15 pS/pF. E_SAC is the reversal potential, and several values have been reported. We first set E_SAC = –10 mV (10, 13) and later vary E_SAC to investigate the effect of the reversal potential. V_m is the membrane potential. We introduce λ as the normalized SL (λ > 1) and λ_max as the maximal stretch (λ_max = 1.1) in accordance with previous studies (14, 15). An up to 10% change in SL seems realistic for changes in ventricular filling. The electrophysiologic effects of a longitudinal stretch generated by increased preload, afterload, or acute static mechanical stretch can be explained by SAC current where the cells undergo such strains.

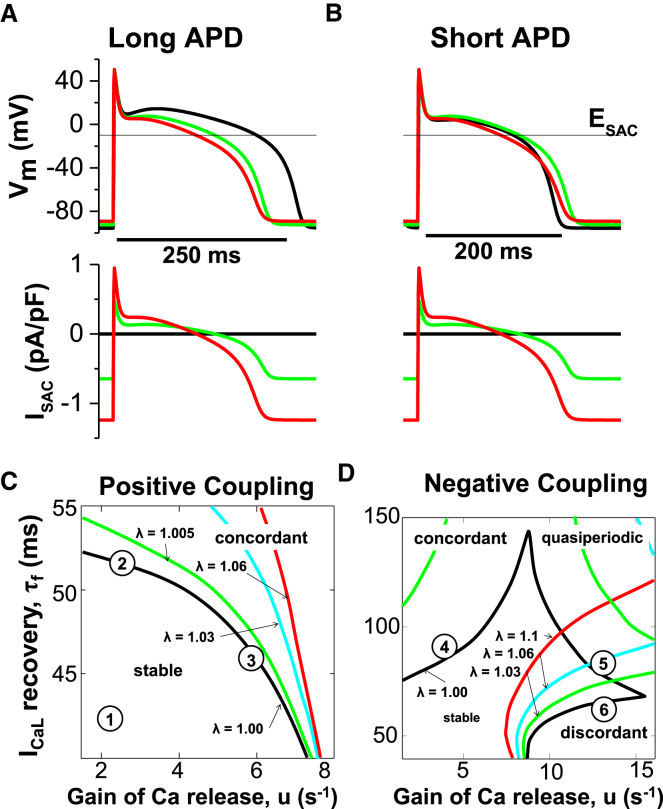
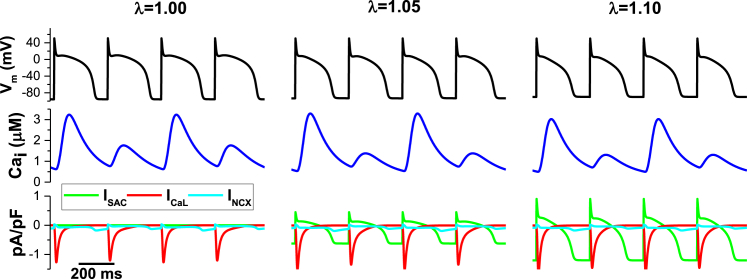
Experimentally, it has been observed that a mechanical stretch of isolated cardiomyocytes can give rise to changes in the AP configuration and to pacemaker-like afterdepolarizations (16, 17). The addition of I_SAC in the model (Fig. 1 A) shows a small depolarization of resting V_m (Fig. 2, A and B) and changes in the voltage-Ca dynamics. During the plateau phase of the AP, I_SAC is an outward current due to the reversal potential of I_SAC (−10 mV) and therefore a lowered plateau V_m and shortened APD (Fig. 2 A). At V_m below −10 mV, I_SAC becomes inward, so as repolarization proceeds, I_SAC slows the rate of late repolarization but there is still a net shortening of the APD. At a shorter baseline APD (Fig. 2 B), these same effects of I_SAC produce a shortened plateau but crossover during phase 3 repolarization, resulting in a small prolongation of APD₉₀ (Fig. 2 B).

Figure 2.

(A and B) Tracings of APs for long APD (A) and short APD (B) at a PCL of 300 ms with no SACs (black) and I_SAC with stretch λ = 1.05 (blue) and λ = 1.10 (red). I_SAC traces are shown at the bottom. Note the similarity of the traces I_SAC and V_m. E_SAC is the reversal potential of I_SAC. (C) Stability boundaries for positive coupling (black line, without I_SAC; green, cyan, and red lines, with increased stretch). Positive coupling means that a larger Ca lengthens the APD; μ and τ_f are two instability parameters that promote Ca and voltage alternans, respectively. (D) Stability boundaries for negative coupling (black line, without I_SAC; green, cyan, and red, with increased stretch). Negative coupling means that a larger Ca shortens the APD; μ and τ_f are two instability parameters that promote Ca and voltage alternans, respectively. To see this figure in color, go online.

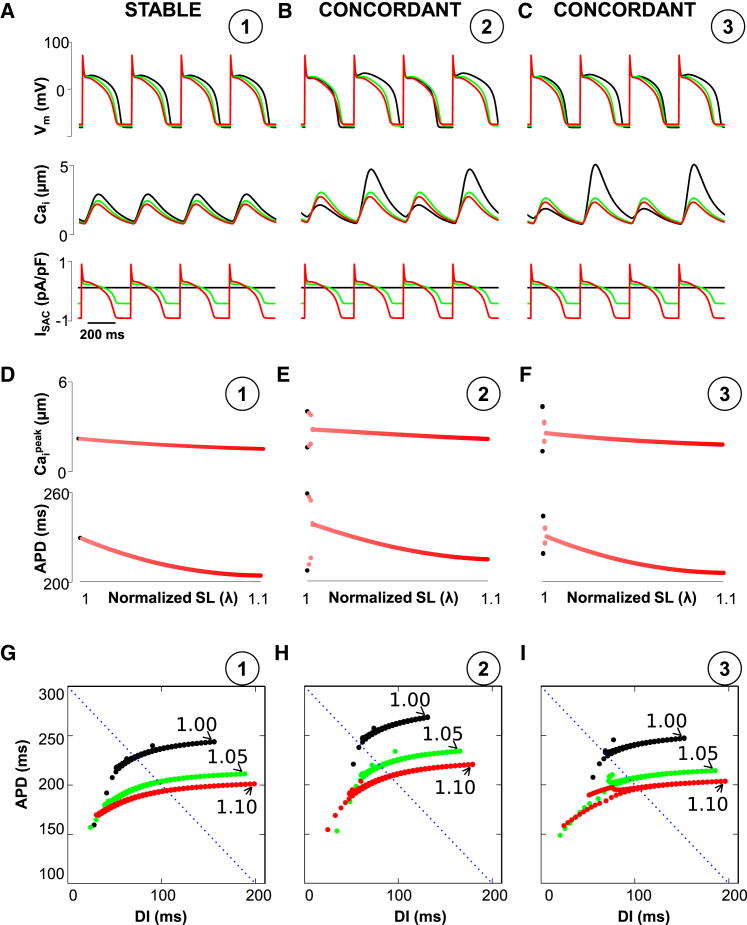
We studied the dynamics of the AP and the intracellular Ca transient under various dynamical regime combinations of voltage/Ca-driven and positive/negative coupling (using the same parameters as in (7)) and by varying the stretch. In the absence of stretch, the formation of alternans depends on two instability parameters, u (gain of Ca release) and τ_f (recovery time constant of the L-type Ca channel), which respectively promote Ca and voltage instabilities. We controlled the coupling between voltage and Ca cycling by varying the strength of the Ca-dependent inactivation of I_CaL (γ in the Ca-dependent inactivation gate f_Ca (see Eq. 9 in (7)). In our simulations, γ = 0.7 and 1.5 for positive and negative coupling, respectively. We chose six points defined in the parameter space of (u, τ_f), which are labeled 1–6 in Fig. 2, C and D. In the case of positive coupling, point 1 in Fig. 2 C is stable (meaning no alternans, as shown in Fig. 3, A and D). Point 2 in Fig. 2 C corresponds to voltage-driven concordant alternans (Fig. 3, B and E) and point 3 in Fig. 2 C corresponds to Ca-driven concordant alternans (Fig. 3, C and F). We observe that an increase of SACs abolishes concordant alternans for all points of interest (stable and both concordant points) independently of the stretch intensity.

Figure 3.

(A–C) Representative curves with no SACs (black) and I_SAC with stretch λ = 1.05 (blue) and λ = 1.10 (red) for positive coupling (circled numbers are the same as in Fig. 2C). (D–F) Evolution of APD and Ca_i^peak during an increase of stretch from λ = 1.0 to λ_max = 1.10. (G–I) Dynamic APD restitution curves. APD_n+1 plotted versus DI_n = PCL-APD_n. Dotted lines show PCL = 300 ms. To see this figure in color, go online.

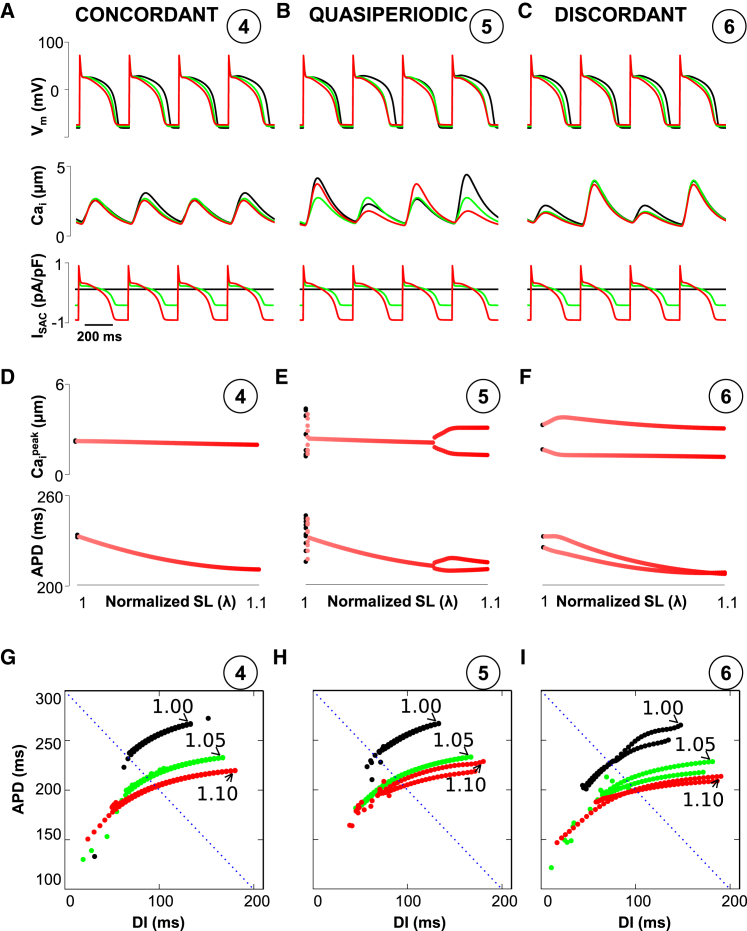
In the case of negative coupling, I_SAC suppresses voltage-driven concordant alternans (Fig. 4, A and D; point 4 in Fig. 2 D). However, I_SAC promotes Ca-driven discordant alternans (Fig. 4, C and F; point 6 in Fig. 2 D) (but reduces the amplitude when λ > 1.02). When the voltage and Ca are equally unstable (point 5 in Fig. 2 D), the APs and Ca transients show a more complex transition from quasiperiodic to stable (no alternans) for stretch levels in the range of λ = 1.0–1.06, and to discordant alternans for stretch levels of >1.06 (Fig. 4, B and E).

Figure 4.

(A–C) Representative curves with no SACs (black) and I_SAC stretch λ = 1.05 (blue) and λ = 1.10 (red) for negative coupling (circled numbers are the same as in Fig. 2D). (D–F) Evolution of APD and Ca_i^peak during an increase of stretch from λ = 1 to λ_max = 1.10. (G–I) Dynamic APD restitution curves. APD_n+1 plotted versus DI_n = PCL-APD_n. Dotted lines show PCL = 300 ms. To see this figure in color, go online.

When both the V_m dynamics and Ca dynamics become unstable, intuitively we would expect the coupled dynamics to become more unstable. This is true when the coupling is positive. When the coupling is negative, unstable V_m plus unstable Ca stabilizes the whole system (see Ref. (7)). Conversely, when V_m is stabilized by I_SAC in this case, the whole system becomes unstable. This phenomenon is independent of the details of the current-channel interactions. As long as I_SAC shallows APD restitution and stabilizes the V_m dynamics, the whole system will become unstable and electromechanically discordant alternans will appear.

To test this hypothesis, we measured the APD restitution curves using a dynamic pacing protocol. Our results show that increasing I_SAC makes the APD restitution curves shallower, which is consistent with observations by Hu et al. (18). This shifts to the left the onset of alternans if the V_m-Ca coupling is positive (Fig. 3, G–I) or if the alternans is voltage driven for negative coupling (Fig. 4 G). For the electromechanically discordant alternans, shallower APD restitution does not suppress (or even promote) Ca alternans (Fig. 4 I). Moreover, if the APD-Ca transient shows quasiperiodicity (Fig. 4, B, E, and H), shallower APD restitution due to stretch suppresses alternans first. Then, further stretch promotes electromechanically discordant alternans. These results are in agreement with Fig. 2, C and D, in which the changes in phase diagrams based on I_SAC provide the same picture.

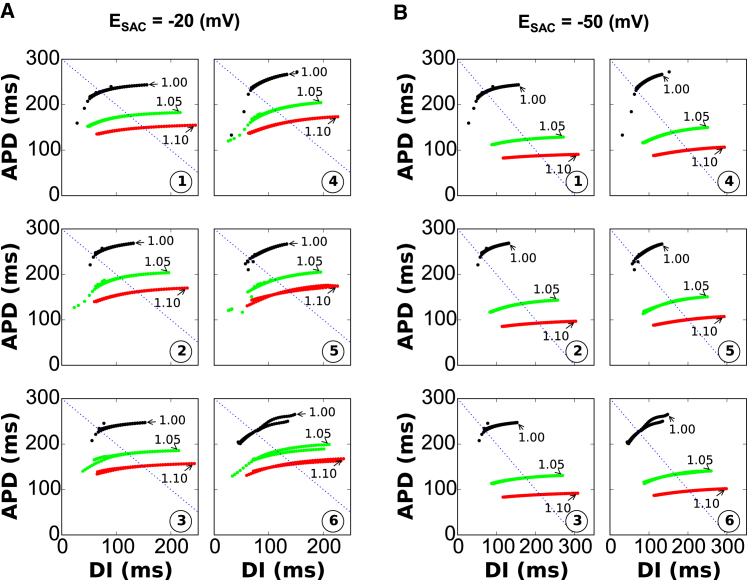
So far, we have focused our analysis on SACs nonspecific for monovalent cations to investigate the effects of SACs via stretching along the longitudinal axis in the model. However, some experimental studies have shown that stretch of cardiac myocytes also activates the K⁺-selective TREK and swelling-activated chloride channels (9). Therefore, we verified that our predictions are not altered by different reversal potential values (E_SAC = −20 and −50 mV) on the dynamic APD restitution curves as shown in Fig. 5, A and B, respectively, which is a relevant range for chloride channels. In both cases, the APD restitution curves became shallower. We think that more purely Na⁺-, Ca²⁺-, or K⁺-selective channels (with E_rev higher than +50 or lower than −80 mV) are less interesting in the context of alternans because they will either prolong or shorten all APDs regardless of the alternans phase.

Figure 5.

(A and B) Dynamic APD restitution curves for resting potentials E_SAC = −20 mV (A) and −50 mV (B). APD_n+1 plotted versus DI_n = PCL-APD_n. To see this figure in color, go online.

Fig. 6 shows the I_CaL, Ca, I_NCX relationship with I_SAC during discordant alternans (point 6, Fig. 2 D). In this case, the alternans is calcium driven and an increase of the stretch results in persistence of the discordant state. One can interpret this result by looking at the transition phase in Fig. 2 D, where the changes in the boundary under an increase of the stretch leave point 6 in the same discordant state. Interestingly, the addition of I_SAC during the AP produces a shortened plateau (Fig. 4 C) and APD while preserving the difference in Ca_i^peak (Fig. 4 F).

Figure 6.

Relationship among I_CaL (red), Ca_i (blue), I_NCX (cyan), and I_SAC (green) during discordant alternans for stretch λ = 1.0, 1.05, and 1.10. To see this figure in color, go online.

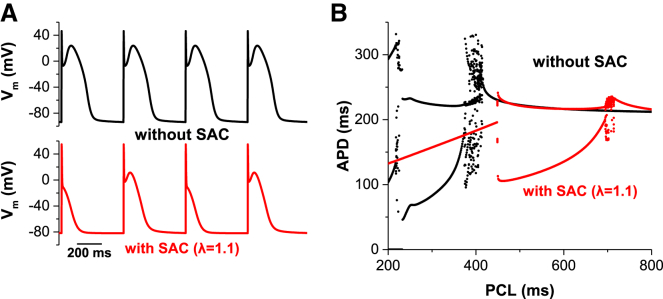
The time course of I_SAC is similar to that of I_to and the fibroblast current. Previous studies (19, 20) reported that these currents promote dome alternans. This type of alternans does not require fast pacing. Fig. 7 shows that SACs also promote the formation of dome alternans at slow heart rates.

Figure 7.

Dome alternans due to I_SAC. (A) SACs promote dome alternans at slow heart rates. (B) Bifurcation diagrams, APD versus PCL. With SACs (λ = 1.1), dome alternans was observed between 691 ms and 449 ms. APs were periodic when PCL was <449 ms. To see this figure in color, go online.

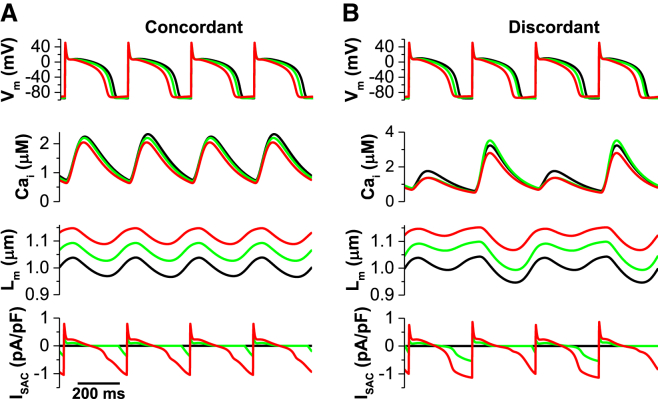
Fig. 8 shows the effects of SACs under isotonic conditions in which a constant force was applied (F_m = 0.87 mN/mm²) for points 4 (Fig. 8 A) and 6 of Fig. 2 D (Fig. 8 B), respectively). Compared with the isometric case, electromechanically discordant alternans is promoted when SACs are activated during isotonic contractions (Fig. 8 B) and concordant alternans is suppressed similarly. In addition, the contractility (L_m) is decreased when the stretch is increased and the shape of I_SAC depends on the actual length of the cell.

Figure 8.

Effects of SACs in isotonic conditions. SACs have qualitatively the same effects in isometric and isotonic conditions. (A) SACs suppress concordant alternans. From the top: voltage versus time, [Ca]_i versus time, sarcomere length L_m versus time, and I_SAC versus time. (B) SACs promote discordant alternans. Note that in this simulation, since changes in the Ca²⁺ transient due to a change in the affinity of troponin for Ca²⁺ binding had little effect (8), we did not include them in the model. To see this figure in color, go online.

Although SACs have long been viewed as important contributors to ventricular arrhythmogenesis, experimental data regarding the mechanisms by which they contribute to arrhythmia are not readily available. This is especially the case at the whole-heart level, where SACs could play an important role in the development of cardiac pathologies when preload is elevated during volume loading, stretch-induced arrhythmias, sudden (acute) aortic valve regurgitation, or aortic stenosis. It has also been shown that some cardiac drugs that act on mechanotransduction pathways, such as the SAC blocker Gd³⁺, can substantially reduce the onset of stretch-induced arrhythmias. Moreover, electromechanically discordant alternans and quasiperiodicity are relatively rare chance occurrences, and there is no reliable procedure to induce these phenomena. Therefore, mathematical modeling can provide valuable mechanistic insights into mechanoelectric coupling via SACs on alternans. We also believe that mathematical modeling and computer simulations can help experimentalists identify and understand these phenomena, which may have been overlooked in the absence of an interpretive framework.

Conclusions

In this study, we have shown that depending on the conditions, MEF can promote or suppress cardiac alternans. Our results provide new, to our knowledge, insights into how SACs can interact with the coupled dynamical systems of voltage-Ca.

Author Contributions

All of the authors participated in designing the project, performing the research, and writing the manuscript. S.G. and D.S. performed the numerical simulations.

Editor: Randall Rasmusson.