The Slow Mobility of the ParA Partitioning Protein Underlies Its Steady-State Patterning in Caulobacter

Abstract

In bacteria, ParABS systems mediate intracellular transport of various cargos, including chromosomal regions in Caulobacter crescentus. Transport of the ParB/parS partition complex requires the DNA-binding activity of ParA, which transiently tethers the partition complex during translocation. In C. crescentus, the directionality of the transport is set up by a gradient of ParA whose concentration gradually increases from one end of the cell (old pole) to the other (new pole). Importantly, this ParA gradient is already observed before DNA replication and segregation are initiated when the partition complex is anchored at the old pole. How such micron-scale ParA pattern is established and maintained before the initiation of chromosome segregation has not been experimentally established. Although the stimulation of ParA ATPase activity by the localized ParB/parS partition complex is thought to be involved, this activity alone cannot quantitatively describe the ParA pattern observed inside cells. Instead, our experimental and theoretical study shows that the missing key component for achieving the experimentally observed steady-state ParA patterning is the slow mobility of ParA dimers (D ∼10⁻³μm²/s) due to intermittent DNA binding. Our model recapitulates the entire steady-state ParA distribution observed experimentally, including the shape of the gradient as well as ParA accumulation at the location of the partition complex. Stochastic simulations suggest that cell-to-cell variability in ParA pattern is due to the low ParA copy number in C. crescentus cells. The model also accounts for an apparent exclusion of ParA from regions with small spacing between partition complexes observed in filamentous cells. Collectively, our work demonstrates that in addition to its function in mediating transport, the conserved DNA-binding property of ParA has a critical function before DNA segregation by setting up a ParA pattern required for transport directionality.

Introduction

Chromosome segregation is required for faithful propagation of genetic information to future generations. For DNA partitioning, bacteria often rely on ParABS systems. These systems consist of ParA, a deviant Walker-type ATPase, and ParB, a protein that binds to parS DNA sites and the surrounding DNA to form a nucleoprotein partition complex (PC). ParA cycles through different biochemical states: 1) upon ATP binding, ParA forms dimers, which associate with DNA nonspecifically; 2) the ParB–rich PC stimulates ATP hydrolysis of ParA dimers, resulting in ParA monomerization and DNA dissociation; and 3) nucleotide exchange reinitiates the cycle (1, 2). Previously, using Caulobacter crescentus as a model bacterium, we provided evidence for a “DNA-relay” model in which iterations of this simple biochemical cycle, coupled with the inherent elastic dynamics of the chromosome, result in segregation of a duplicated ParB-rich PC along a ParA gradient (3).

A critical but still mechanistically unresolved aspect of chromosomal segregation is the initial establishment of a stable ParA gradient inside cells (4, 5, 6, 7), which was only phenomenologically described (i.e., assumed) in our previous mathematical model (3). For plasmid-encoded ParABS systems, it has been proposed that localized ParB stimulation of ParA ATPase activity, coupled with 1) uniform redistribution of ParA on the nucleoid due to a time delay in ParA rebinding to the DNA and 2) diffusion of the ParB-coated cargo generates a propagating ParA wave (1, 8). This idea was suggested from in vitro experiments with ParB-coated beads and plasmid clusters (9, 10, 11, 12). However, in C. crescentus cells, a stable ParA gradient is established and maintained well before the initiation of chromosome replication and segregation (4, 5, 7) when the ParB-rich PC is fixed to the cell pole (13, 14). Thus, in this case, the ParA gradient can apparently form without any motion of the ParB cargo. This raises the question whether localized ParB stimulation of ParA ATPase activity followed by uniform redistribution of ParA binding to the DNA is sufficient to create the steady-state ParA pattern observed in cells. In this study, we set out to quantitatively determine the minimal factors required for the steady-state ParA patterning using experiments and modeling.

Materials and Methods

Strains and culture conditions

Strains used in this study are described in Table S1 in the Supporting Material. Strain CJW4487 was generated by sequentially transducing CJW3040 with bacteriophage ΦCR30 lysates prepared from CJW2642 and CJW763 using a previously described protocol (15). C. crescentus strains were grown at 30°C in the defined minimal M2G medium (0.87 g/L Na₂HPO₄, 0.54 g/L KH₂PO₄, 0.50 g/L NH₄Cl, 0.2% (w/v) glucose, 0.5 mM MgSO₄, 0.5 mM CaCl₂, 0.01 mM FeSO₄) unless otherwise stated. Because none of the C. crescentus strains used in this study contained replicative plasmids, antibiotics were omitted when cells were grown for the purpose of imaging. For all experiments, cells were harvested from exponentially growing cultures. When needed, cell populations were synchronized as described previously (16). To induce the synthesis of fluorescent ParB protein fusions from the xylose-inducible promoter (pXyl), cells were grown in the presence of 0.03% xylose for 60–75 min. CJW4487 was grown in the presence of 0.03% xylose to constitutively induce the synthesis of ftsZ from pXyl. All Escherichia coli (E. coli) strains were grown in M9 medium (0.87 g/L Na₂HPO₄, 0.54 g/L KH₂PO₄, 0.50 g/L NH₄Cl, 0.5 mM MgSO₄, 0.5 mM CaCl₂, 0.01 mM FeSO₄) supplemented with either 0.2% (w/v) glycerol (M9Glycerol) or glucose (M9Glucose).

Wide-field fluorescence imaging and image processing

C. crescentus and E. coli cells were spotted on 1–2% agarose pads containing M2G medium and M9Glucose, respectively, for all microscopy experiments. Images were acquired using an Eclipse Ti-U microscope (Nikon, Tokyo, Japan) with an Orca-ER camera (Hamamatsu Photonics, Hamamatsu City, Japan) and phase-contrast objective Plan Apochromat 100×/1.40 NA (Carl Zeiss, Oberkochen, Germany) at room temperature. Images were acquired with either MetaMorph software (Molecular Devices, Sunnyvale, CA) or NIS-Elements (Nikon, Tokyo, Japan) and processed with MATLAB (The MathWorks, Natick, MA). Cell outlines, segmentation, and fluorescence quantification were achieved using Oufti (17), a second-generation version of the MicrobeTracker software (18). Identification of PC positions along the long cell axis was done using peakFinder, an accessory tool in MicrobeTracker.

Analysis of ParA-YFP fluorescence profile in swarmer and filamentous C. crescentus cells

C. crescentus CJW3367 swarmer cells (G1 phase) were imaged immediately following synchronization. To induce the formation of filamentous cells, exponentially growing CJW4487 cells were pelleted, resuspended, and washed with M2G (lacking the xylose inducer for ftsZ expression) twice. Cells resuspended in M2G were then grown at 30°C for 4 h and the culture was maintained in exponential phase by dilution when necessary. Cells were spotted on an agarose pad, covered with a cover slip, and sealed and incubated at 30°C for at least another 2 h before imaging. The positions of parS sites were obtained by determining the peak positions of ParB-CFP or MipZ-CFP (which is a marker for parS) using the peakFinder function in MicrobeTracker. ParA-YFP signals and the distances between parS sites were calculated from these datasets using MATLAB. To obtain the averaged ParA fluorescence profile in swarmer cells, only cells with one fluorescently labeled parS focus (i.e., before PC segregation) was used for analysis. Cell pole assignment was based on the position of parS, which is localized to the old cell pole (position = 0 in relative cell coordinates), and then individual ParA profiles were generated by normalizing ParA-YFP fluorescence from each cell segment by the segmental area. The individual ParA profiles were then averaged across the population.

FRAP experiments

For fluorescence recovery after photobleaching (FRAP) experiments, E. coli cells (CJW3354, CJW3355, and CJW3604) were grown in M9Glycerol supplemented with chloramphenicol (20 μg/mL) at 30°C to OD₆₀₀ < 0.3. The expression of C. crescentus ParA-CFP was induced by addition of 200 μM of isopropyl β-D-1-thiogalactopyranoside (IPTG) for 2 h. To stop induction, cells were washed into M9Glucose and grown for another 2 to 2.5 h at 30°C. Then, cells were spotted on 2% agarose + M9Glucose pads. In a subset of experiments, M9Glucose medium was supplemented with cephalexin (15 μg/mL) or nalidixic acid (3 μg/mL) for all steps after induction. For FRAP experiments in C. crescentus, filamentous CJW4487 cells were generated as described above. All FRAP experiments were carried out at room temperature.

FRAP analysis

The mobility of ParA was estimated from the FRAP measurements as an apparent diffusion coefficient using a single-component one-dimensional (1D) diffusion model described previously (19). Briefly, experimental kymographs (ParA signal at the cell coordinate, x versus time, t) were constructed for each cell and fitted by the numerical solution of the corresponding diffusion equation for each measured cell individually. Since wild-type ParA and mutant ParA_D44A are mostly associated with the chromosome, only regions of interest corresponding to the chromosome (identified manually or automatically by custom-made script in MATLAB) were used in the FRAP analysis. For mutant ParA_R195E, which is delocalized throughout the entire cytoplasm, the region of interest corresponded to the entire cell length except for the polar regions (≈10 pixels from the cell poles).

Theoretical model of ParA pattern formation

ParA dimer distribution within cells with 1 PC

We consider ParA patterning as a 1D problem (x is a cell coordinate along the long axis) with following parameters: l, the cell length; D, the diffusion coefficient of DNA-bound ParA dimers; and k_h, the rate of hydrolysis (which dictates the residence time of ParA dimers at the PC). In this model, ParB (partition complex) is located at x = 0, when ParA dimer reaches x = 0, it resides there for a characteristic time of τ = 1/k_h. After ATP hydrolysis, ParA redimerizes and then become competent for DNA binding. Because we are focusing on the distribution of ParA dimers, the model does not consider ParA monomers or the mechanism of dimerization explicitly; instead we assume that the dimer rebinds DNA at a random position x (with uniform probability) following hydrolysis. This approach is valid as long as ParA diffuses freely as monomer or dimer before DNA rebinding long enough to result in a uniform distribution. The latter is supported by in vitro studies with plasmid P1 ParA that showed that there is a slow conformational change between dimerization and DNA binding (9), allowing sufficient time for ParA dimers to sample the entire cytoplasm before associating with the nucleoid.

This model leads to the following reaction-diffusion equation:

$$\frac{\partial A\left(x,t\right)}{\partial t}=DA{\left(x,t\right)}^{″}+\frac{R_h}{l},$$ (1)

where A(x) is the 1D-concentration of ParA dimers and R_h is the rate of hydrolysis as described by R_h = k_h a₀, where k_h and a₀ are the reaction constant of hydrolysis and the amount of PC-bound ParA dimers, respectively.

At steady state,

$$\frac{\partial A\left(x,t\right)}{\partial t}=0=DA{\left(x\right)}^{″}+\frac{R_h}{l}.$$ (2)

We consider a steady-state case with no in- or out-flux of ParA at the cell boundaries. This leads to the following boundary conditions:

• 1)at the new pole (x = l): the boundary is reflective (i.e., no flux beyond the cell)

$$\frac{\partial A\left(x=l\right)}{\partial x}=0;$$

and

• 2)at the old pole (x = 0), increase of ParA dimer concentration by diffusive flux is balanced by the disappearance of ParA dimers due to the ParB-stimulated ATP hydrolysis,

$$D\frac{\partial A\left(x=l\right)}{\partial x}=-R_h.$$

Equation 2 has the following analytical solution:

$$A\left(x\right)=\frac{\gamma }{D}lx-\frac{\gamma }{2D}{x}^2,$$ (3a)

where $\gamma =\left(k_h/l\right)a_0$.

The fraction of ParA dimers bound to the PC is calculated by the direct integration of the Eq. 3a as follows:

$$\frac{a_0}{a_{tot}}=\frac{1}{1+\frac{k_h{l}^2}{3D}},$$ (3b)

where a_tot is the total amount of ParA dimers per cell. Similarly, the fraction of ParA dimers bound to DNA is the following:

$$\frac{a_{tot}-a_0}{a_{tot}}=\frac{1}{1+\frac{3D}{k_h{l}^2}}.$$ (3c)

Together, Eqs. 3a–c describe the steady-state distribution of Par dimers inside the cell with one PC.

ParA dimers distribution within cells with 2 PC

If there are two PCs in the cell, one at the old pole (x = 0), and the other at the new pole (x = l), we need to solve Eq. 2 with symmetric boundary conditions.

In this case, the diffusive flux of ParA dimers to the new and old poles is balanced by the disappearance of dimers due to localized ATP hydrolysis at these two locations, with cumulative rate of hydrolysis R_h, resulting in the following symmetric boundary conditions:

$$D\frac{\partial A\left(x=0,l\right)}{\partial x}=-\frac{R_h}{2}.$$

These boundary conditions lead to the following symmetric solution of Eq. 2:

$$A\left(x\right)=\frac{\gamma }{2D}x\left(l-x\right),$$ (4a)

where, as before, $\gamma =\left(k_h/l\right)a_0$; however, note that a₀ is the total amount of PC-bound ParA (i.e., at both poles). Simple integration of Eq. 4a gives the following fraction of PC-bound ParA dimers:

$$\frac{a_0}{a_{tot}}=\frac{1}{1+\frac{k_h{l}^2}{12D}},$$ (4b)

and the following fraction of DNA-bound ParA dimers:

$$\frac{a_{tot}-a_0}{a_{tot}}=\frac{1}{1+\frac{12D}{k_h{l}^2}}.$$ (4c)

Distribution of ParA dimers within cells with multiple PCs

The equations from the previous section can be expanded to describe the distribution of ParA in a filamentous cell with n PCs. To do so, we introduced an additional variable: l: l = l₁ + l₂ + … + l_n, where l_i is a distance between neighboring PCs. Applying this definition, Eq. 4 describes the following distribution of ParA in the regions between any two neighboring PCs as DNA-bound ParA dimers cannot diffuse beyond PC:

$$A\left(x\right)=\frac{\gamma }{2D}{l}_{i}x-\frac{\gamma }{2D}{x}^2,$$ (5a)

with $\gamma =\left(k_h/l\right)a_0$, where a₀ is the total amount of PC-bound ParA (i.e., at all PCs). A₀ is given by the following:

$$\frac{a_0}{a_{tot}}=\frac{1}{1+\frac{k_h}{12Dl}\sum l_i^3}.$$ (5b)

The amount of ParA between any two neighboring PCs in such cell, a_i, can be calculated by the direct integration of Eq. 5a as follows:

$$a_i=\frac{1}{6}\frac{\alpha }{2D}{l}_i^3.$$ (5c)

To generate Fig. 4, A and B, positions of a given number of PCs inside the cell of a given length were chosen randomly and the amount of ParA in-between adjacent PCs was calculated using Eq. 5c. These procedures were repeated 200 times to simulate the distribution of ParA in 200 virtual filamentous cells.

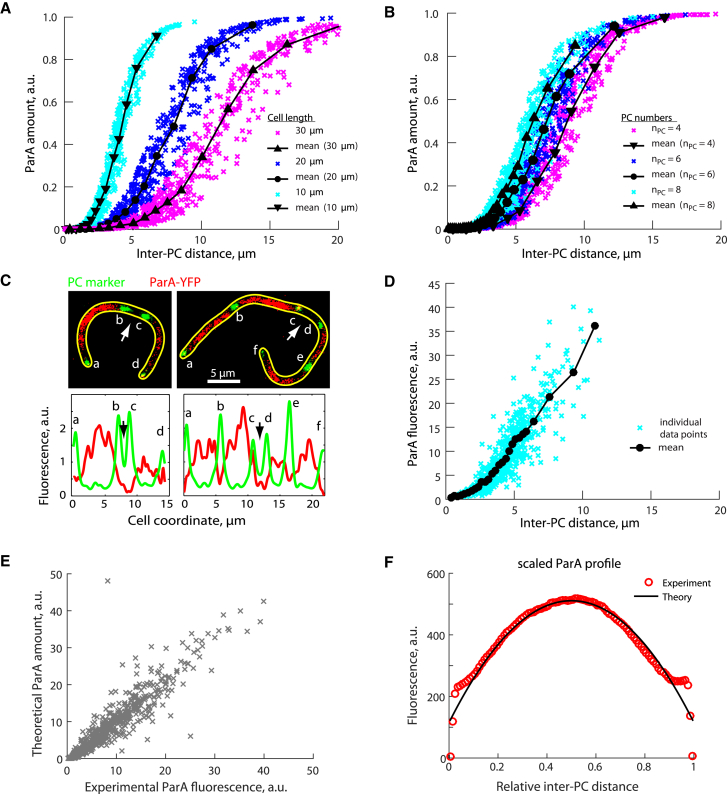
Figure 4.

Exclusion of ParA from regions with small spacing between PCs. (A) For any given cell length and number of PCs, 200 random combinations of PC positions within the cell were generated and the amount of ParA was calculated using Eq. 5 for each inter-PC interval (D = 5 × 10⁻³μm²/s and k_h = 0.03 s⁻¹). Results are shown for cells containing six PCs of different cell lengths (10, 20, and 30 μm). An example of a theoretical distribution of ParA in a filamentous cell with six PCs is shown in Fig. S3. (B) Results are shown for cells as in (A) except that cell length was fixed to 20 μm and the number of PC (n_PC) was four, six, or eight. (C) Top, fluorescent images (overlay) show ParA-YFP (red) and PCs (MipZ-CFP, green) in two representative filamentous C. crescentus cells (CJW4487). Arrows point to small inter-PC regions exhibiting low ParA-YFP fluorescence. Bottom, corresponding fluorescence profiles are provided. (D) Integrated ParA-YFP fluorescence signal within each inter-PC interval in FtsZ-depleted C. crescentus cells (n = 588, strain CJW4487) as a function of the corresponding inter-PC distance is provided. (E) Comparison between experimental and theoretical amounts of ParA for each inter-PC interval is provided. Each point corresponds to the measured ParA fluorescence signal shown in (D) and the theoretical ParA amount for the same inter-PC interval. The theoretical value for each interval was determined using Eq. 5a (D = 5 × 10⁻³μm²/s, k_h = 0.03 s⁻¹, and the cell length and the inter-PC distance corresponding to the experimental counterpart). (F) Scaled average ParA profiles measured experimentally (open circles) and described theoretically by Eq. 5d (black line) are provided. Before averaging, each profile was scaled by normalizing the ParA-YFP profile in each inter-PC region to the total ParA-YFP fluorescence per cell and by resampling the experimental data into 50 points in relative coordinates (i.e., 0 and 1 are the start and end of the interval, respectively).

Equation 5a also can be rewritten as the following:

$$A\left(x\right)=\beta l_i^2\xi \left(1-\xi \right),$$ (5d)

where ξ is a relative coordinate in the given inter-PC interval, i.e., ξ = x/l_i and β = γ/2D. Equation 5d describes the shape of a steady-state profile of ParA dimers. In real cells, ParA signal is the sum of signal from the ParA dimers and from the monomeric ParA whose profile is uniform due to fast diffusion in the cytoplasm. Therefore, we used the following:

$$A\left(x\right)=\beta l_i^2\xi \left(1-\xi \right)+c,$$ (5e)

where c is a constant to fit the average scaled experimental ParA profile in Fig. 4 F.

Stochastic simulations

A 1D stochastic model was built using MATLAB to simulate the formation of ParA gradient in a 1.8 μm “cell” containing 100 ParA dimers to match the experimentally determined values (3). The simulation began with a homogenous distribution of ParA dimers along the long cell axis. Each ParA dimer underwent random walk. The displacement, dx, at each time step, dt, was specified by a random number drawn from a Gaussian distribution with zero mean <dx> = 0 and variance <dx²> = 2 D dt. The binding of ParA dimers to the PC was assumed to be diffusion-limited. When ParA dimers entered the “PC zone” (a 40 nm region centered at 50 nm from the old pole), they became PC-bound. The dwell time of ParA dimers in the PC-bound state was exponentially distributed as dictated by the maximal ATPase rate k_h, with the mean time τ = 1/k_h. Upon dissociation, we assumed that ParA instantaneously reform dimers and rebind the chromosome with uniform probability along the long cell axis. Unless specified otherwise, the default parameters for this simulation were k_h = 0.05 s⁻¹, D = 5 × 10⁻³ μm²/s, and dt = 0.001 s. Because we are interested in the steady-state pattern of ParA, we neglected DNA fluctuations. The results of 500 simulations were averaged to generate the averaged ParA distribution profiles in Fig. 2 B.

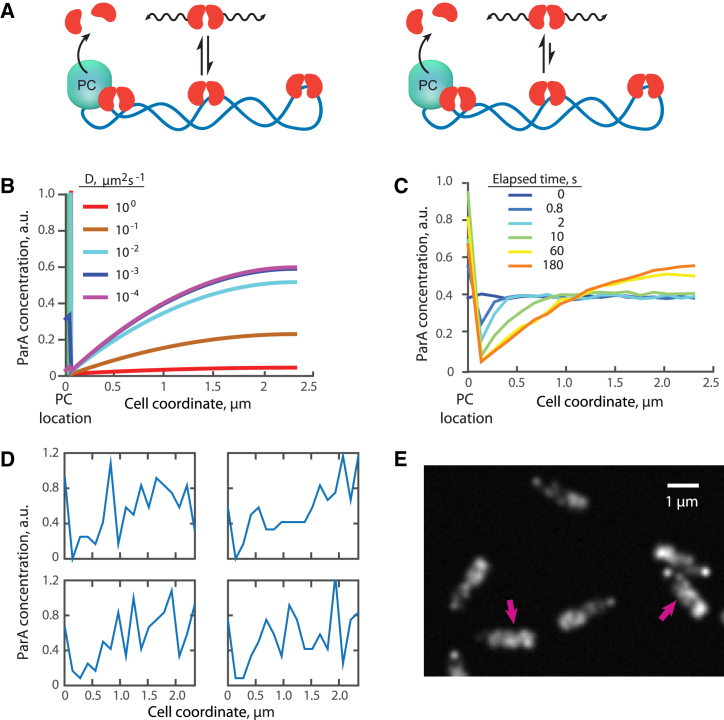
Figure 2.

Theoretical distributions of ParA dimers. (A) “Localized ATP-hydrolysis with reversible DNA binding” model for ParA distribution in the cell is provided. In this model, ParA dimers bind DNA reversibly, with ParA capable of dissociating from DNA independently of ATP hydrolysis. In this model, unbound ParA dimers diffuse quickly along the long cell axis but become temporarily immobile when they are bound to the DNA. Similar to Fig. 1A, ParA dimers that reach the PC localized at the old cell pole become associated with the PC with the residence time determined by the ATP hydrolysis rate, and then rebind DNA at random locations. Two scenarios of reversible DNA-binding were considered in our model: left, spontaneous dissociation from the DNA occurs frequently, resulting in a medium-range apparent diffusion of ParA dimers; right, spontaneous dissociation from the DNA occurs infrequently, resulting in a slow apparent diffusion of ParA dimers. (B) Steady-state distribution of ParA dimers with varying apparent diffusion coefficients according to the analytical solution (Eq. 3a) of the model in Fig. 2A is provided. (C) Time evolution of ParA dimer distribution in a stochastic 1D simulation of the model is provided. At the beginning of each simulation, 100 ParA dimers were distributed randomly (with uniform probability) along the cell coordinate. Each ParA dimer was then allowed to diffuse (D = 5 × 10⁻³μm²/s), interact with ParB (for a period of time governed by τ = 1/k_h = 20 s) and to redistribute uniformly within the cell. ParA profiles are shown at selected time points averaged more than 500 simulations. (D) Four representative examples of ParA profiles at the end of the individual simulations (t = 600 s) are provided. (E) Simulated image of ParA dimer distribution in single virtual cells is shown. About 100 ParA dimers were stochastically placed within each virtual cell (a rectangular 0.6 × 2.3 μm box) using an analytical model (Eq. 3a with D = 5 × 10⁻³μm²/s and k_h = 0.05 s⁻¹) as the probability distribution. The resulting image was generating by rendering each ParA dimer as a point-spread function (approximated by Gaussian with a width of ∼200 nm).

Results and Discussion

Localized ATP hydrolysis is not sufficient to describe the observed ParA pattern

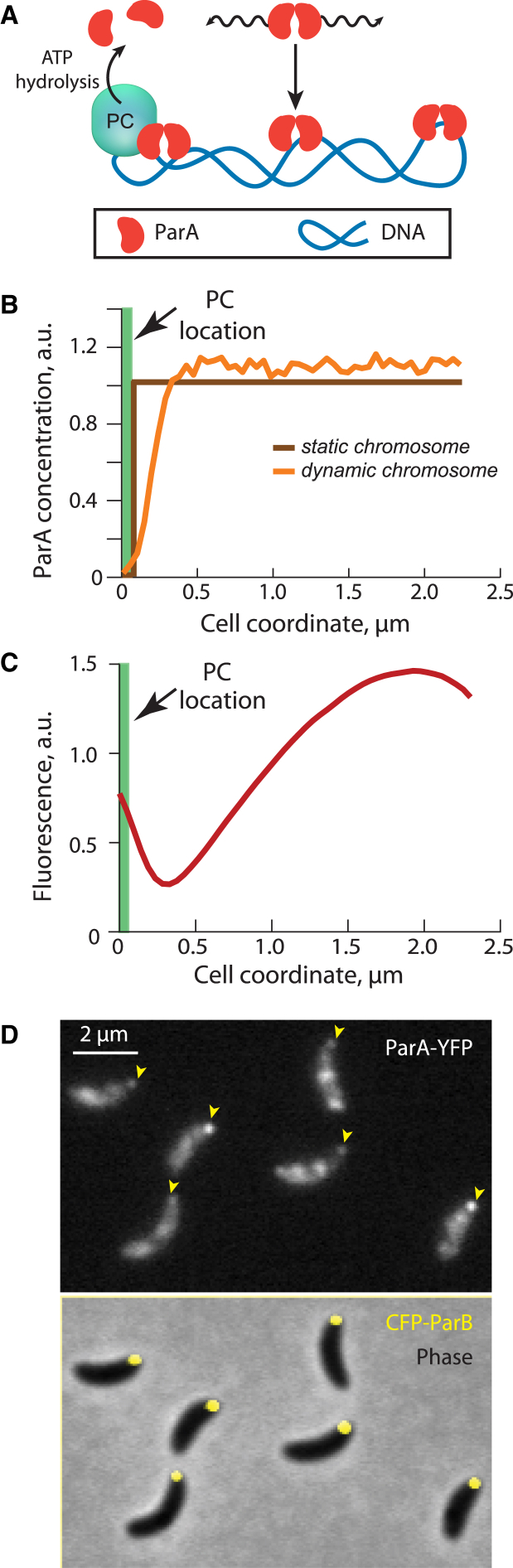
In C. crescentus, ParA already displays an asymmetric distribution across the cell in the swarmer cell stage, i.e., before chromosome replication and segregation have initiated (4, 5, 7). At this cell cycle stage, the ParB-rich PC is immobilized at the old cell pole via a direct interaction between ParB and the polar PopZ matrix (13, 14). Theoretical analysis showed that localized stimulation of ParA ATPase activity at the PC location generates the expected local depletion of ParA distribution at the PC location (Fig. 1 A). In this first analysis, we considered that ParA dimers can dissociate from the DNA only as a result of ParB-stimulated ATP hydrolysis (Fig. 1 B). Since DNA-bound ParA dimers are thought to wiggle around an equilibrium position due to the elastic dynamics of the underlying DNA (3), we also performed simulations that include these elastic dynamics. This resulted in a small expansion of a ParA depletion zone near the PC location (Fig. 1 B) because the DNA fluctuations expand the region of DNA-bound ParA dimers that can reach the PC. However, with or without elastic dynamics, the ParA depletion is only local. This is in striking contrast to the micron-range ParA gradient observed before segregation (4, 5, 7). As shown in Fig. 1 C, the average distribution of a natively expressed ParA-YFP fusion in synchronized C. crescentus swarmer cells (n = 261) exhibits a characteristic shape along the cell length, with a noticeable accumulation at the old pole where the PC is located and importantly, a smooth gradient with decreasing slope toward the new pole. Although there is evidence for interaction between ParA and the polar PopZ matrix (4, 20, 21), the accumulation of ParA near the old pole is most likely due to an interaction of ParA with the ParB-rich PC. This is because the polar ParA signal is physically separated from that of the PopZ matrix (Fig. S1 A, peak offset ≈ 120 nm), whereas it almost perfectly overlaps with that of the ParB-rich PC (Fig. S1 B), which is known to be adjacent to the PopZ matrix (14, 21).

Figure 1.

Subcellular distribution of ParA before DNA replication and segregation. (A) Schematic representation of the “localized ATP-hydrolysis” model for ParA distribution in the cell is shown. In this model, ParA dimers bind DNA nonspecifically and irreversibly. If they are within the reach of the ParB-rich PC that is localized at the old cell pole, they associate with the PC with the residence time determined by the ATP hydrolysis rate. This is followed by rebinding of ParA dimers to DNA at random locations to reflect the fast diffusion of ParA monomers throughout the cell before their redimerization and rebinding. (B) Steady-state distributions of ParA are provided for the localized ATP-hydrolysis model. The brown curve shows the theoretical distribution of ParA considering a static chromosome. The orange curve represents the steady-state distribution of ParA obtained from 500 simulations that take into consideration the fluctuating elastic dynamics of the chromosome that are observed experimentally (3). (C) Experimental distribution of ParA before DNA replication and segregation shown by the normalized ParA-YFP fluorescence in CJW3367 swarmer cells (n = 261) is provided. For each cell, a fluorescence signal from cell segments (1 pixel wide) was divided by the area of segments and quantified along cell length, from PC position to the new cell pole (defined as 5 pixels away from the tip of the cell outline). After subtraction of the lowest profile value, individual cell profiles were normalized (to total area under the profile) and then averaged over all cells. (D) Top, micrograph of ParA-YFP signal in synchronized C. crescentus swarmer cells (CJW3367) is provided. Bottom, overlay of phase contrast image and CFP-ParB signal in the same cells is provided. Arrowheads indicate the old pole of each cell, which was identified by the location of CFP-ParB-labeled PC.

We noted that at the single-cell level, there was a large variability in ParA-YFP distribution (Fig. 1 D). The distribution of ParA-YFP along the cell length was patchy, with varying degrees of both asymmetry and accumulation at the old pole where PC (labeled with CFP-ParB) is located. Ideally, a mechanistic model of ParA patterning should be able to account for not only the average distribution (Fig. 1 C) but also the cell-to-cell variability (Fig. 1 D).

Slow apparent diffusion of ParA dimers underlies ParA subcellular distribution at the population and single-cell levels

We considered the possibility that the ParA pattern is determined by the diffusive properties of the ParA dimers. Our initial model (Fig. 1 B) did not consider dissociation of ParA dimers from the DNA independently of ParB-stimulated ATP hydrolysis (i.e., without ParB interaction). However, in vitro experiments with ParA derived from E. coli P1 plasmid showed that ParA dimers bound to a DNA carpet are able to dissociate from the carpet in an ATP hydrolysis-independent manner (12).

Therefore, we hypothesized that reversibility of the DNA-binding step (Fig. 2 A) plays a role in ParA patterning inside cells. If ParA’s DNA-binding step is reversible, it would imply that, when dissociated, ParA dimers would be free to diffuse, but this diffusion would be slowed down by intermittent rebinding to the DNA. In this scenario, the apparent diffusion coefficient D of the ParA dimers would thus be dependent on the ratio between the DNA-binding and DNA-unbinding rates of ParA dimers. If unbinding from the DNA is fast, this would result in relatively high mobility of ParA dimers (Fig. 2 A, left). Conversely, if unbinding is slow relative to DNA binding, this would lead to slow mobility of ParA dimers (Fig. 2 A, right). Since diffusion combined with a local “sink” can generate protein gradients (22, 23), we hypothesized that ParA gradient formation stems from the interaction of diffusible ParA dimers with a “ParB sink” localized at the old pole. To explore this hypothesis, we considered an analytical model in which ParA dimers diffuse until they interact with localized ParB, followed by a random redistribution of ParA dimers. This random redistribution reflects ParB-induced monomerization of ParA (due to activation of ATPase activity), followed by fast diffusion of ParA monomers throughout the cytoplasm before redimerization. This mathematical model is similar to a model recently used to describe plasmid partitioning (24), although the previous study did not explore how the diffusive and DNA-binding properties of ParA relate to its pattern inside cells.

To examine what ParA patterns can be achieved through our model, we fixed the ParB-induced ATP hydrolysis rate to the experimentally measured value, 0.05 s⁻¹ (3), while varying the diffusion coefficient of ParA dimers. The analytical solution (Materials and Methods, Eq. 3), which describes the average behavior of the system, shows that D values ranging between 10⁻² to 10⁻⁴ μm²/s can account for the formation of significant micrometer-scale ParA concentration gradients as well as for the accumulation of ParA at the old pole (Fig. 2 B). Such range implies that dissociation of ParA dimers from the DNA is very slow compare with their DNA association (Fig. 2 A, right). ParA accumulation at the old pole is primarily due to an interaction with ParB that locally captures ParA dimers before their redistribution upon ParB-stimulated ATP hydrolysis. Although this creates a nanometer-scale depletion of ParA around the PC, a diffusing flux of ParA dimers toward the PC generates the micrometer-scale gradient distribution of ParA along the cell length. Note that the experimental profile (Fig. 1 C) reflects the distribution of ParA concentration convolved with a point-spread function (due to optical diffraction), thus leading to a shift in the minimum compared with the theoretical profile (Fig. 2 B).

To examine if the model can also explain the variability in ParA profile at the single-cell level, we performed stochastic 1D simulations of our model using the experimentally determined number of ∼100 ParA dimers per cell (3). The simulations started with a localized spot of ParB at the old pole and a uniform distribution of ParA dimers throughout the cell. The apparent diffusion coefficient of ParA dimers was arbitrarily set to 5 × 10⁻³ μm²/s. By averaging 500 simulations, we found that the uniform distribution of ParA dimers evolves into a steady-state profile (Fig. 2 C; Movie S1), consistent with the results from the analytical solution (Fig. 2 B). But, at the single-simulation level (i.e., at the single-cell level), the ParA profiles were noisy (Fig. 2 D), indicating that the low number of ParA dimers per cell obscures the underlying steady-state distribution. To compare with experiments, we simulated two-dimensional (2D) images of virtual rectangular cells by using ∼100 ParA dimers (to reflect the experimental value (3)) and by drawing their distribution from the analytical model. In the 2D-simulated images (Fig. 2 E), the ParA signal appeared slightly crisper than in real cells (Fig. 1 D). This is likely because the simulations do not consider at least three cellular aspects that would blur the ParA signal: 1) ParA-YFP monomers contribute to cytoplasmic signal, 2) real cells are in 3D, and 3) DNA-bound ParA dimers “wiggle” around equilibrium position (3). Despite these caveats, the simulated images (Fig. 2 E) displayed the cell-to-cell variability in ParA signal along the cell length and the ParA accumulation at the old cell pole that are characteristic of real cells (Fig. 1 D).

It is interesting to note that the low abundance of ParA results in a patchy pattern that by eye may appear as a “helix” (Fig. 2 E, arrows), even though the underlying protein distribution is not helical. Given the prevalence of proteins in low (less than a few hundreds) copy number in bacteria (25, 26, 27), our results suggest that caution should be taken when single-cell images are interpreted.

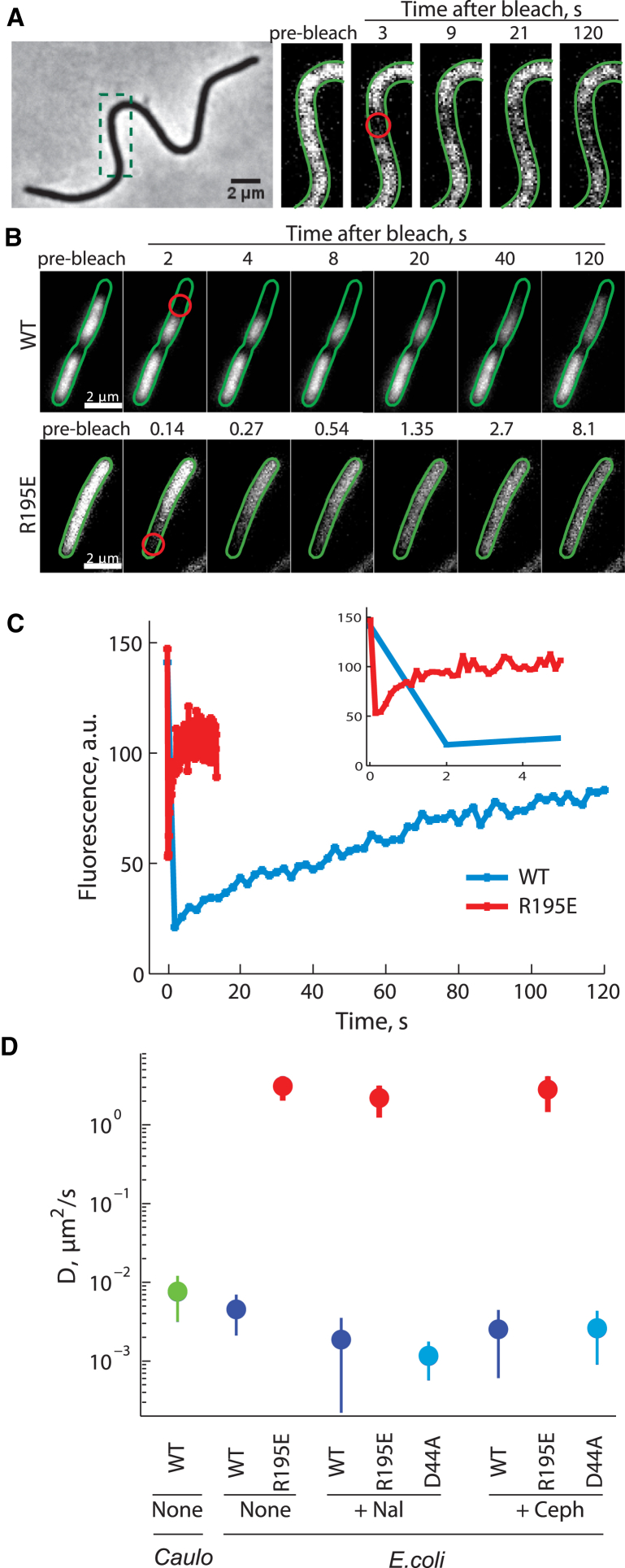
ParA dimers display a low apparent mobility that depends on DNA binding

To determine whether the diffusion coefficient of ParA in vivo falls within the 10⁻² to 10⁻⁴ μm²/s range indicated by the model, we performed FRAP experiments in cells natively producing ParA-YFP. The small size of swarmer cells, together with the low abundance of ParA, prevented us from performing FRAP experiments in these cells, as most of the ParA-YFP fluorescence was lost during the initial “bleach” step. It is common to circumvent these complications by using filamentous cells in which division is blocked (19, 28). Therefore, we performed FRAP experiments in filamentous C. crescentus cells in which the cell division protein FtsZ was depleted (Fig. 3 A). FRAP measurements in these cells showed that recovery was very slow, taking minutes to occur (Fig. 3 A). We calculated an apparent diffusion constant D of ∼8 × 10⁻³ μm²/s, which according to the mathematical model (Fig. 2 B) would be sufficient for producing a gradient. Furthermore, this D value may be an overestimation since the presence of ParB in the cells can increase ParA-YFP fluorescence recovery by stimulating ParA monomerization.

Figure 3.

Estimation of the ParA diffusion coefficient in vivo by FRAP. (A) Example of a filamentous, parA-yfp-expressing C. crescentus cell at selected time points during a FRAP experiment is shown. Filamentous CJW4487 cells were generated by growing cells in M2G medium for more than 5 h to deplete FtsZ before FRAP microscopy experiments. The red open circle indicates the bleached spot. (B) Example of ParA-CFP distribution at selected time points during the FRAP experiment in E. coli cells expressing wild-type ParA-CFP (top, strain CJW3354) or DNA-binding deficient ParA_R195E-CFP (bottom, strain CJW3355) is provided. The red open circles indicate the bleached spots. Note the difference in timescale for fluorescence recovery between wild-type and mutant ParA proteins. (C) Recovery curves for the fluorescence of wild-type ParA-CFP (blue) and ParA_R195E-CFP (red) in the respective bleached spots for images shown in (B). The inset shows a shorter timescale. (D) Plot summarizing the mean diffusion coefficients (solid circles) and the associated standard deviations (vertical lines) is provided for each ParA variant in E. coli or in FtsZ-depleted C. crescentus (Caulo). E. coli cells were treated with either nothing (None), nalidixic acid (+Nal), or cephalexin (+Ceph) before FRAP experiments.

To alleviate any possibility of interference from ParB, PopZ, and the polarity factor TipN (which can interact with ParA), we repeated the FRAP experiments in E. coli, as these proteins are absent in E. coli. When expressed in E. coli, C. crescentus ParA-YFP localizes to nucleoids (4, 21) as expected for DNA-bound ParA-ATP dimers. Fluorescence recovery at the bleached sites was also very slow (Fig. 3, B and C), giving D = 5 × 10⁻³ μm²/s (Figs. 3 D and S2). This indicates that the apparent diffusion coefficient of ParA dimers in vivo is compatible with robust gradient formation (Fig. 2).

According to the model, spontaneous (ATP-hydrolysis independent) binding/unbinding to DNA underlies the observed mobility of ParA. Consequently, perturbations in DNA-binding properties of ParA should change the mobility of ParA, whereas alteration in the ATP-hydrolysis rate should have no significant effect. Consistent with this prediction, bleached spots in E. coli cells expressing the dimerization-proficient but DNA-binding defective mutant ParA_R195E-YFP recovered fluorescence within seconds (Fig. 3, B and C), yielding D value of 3 μm²/s (Fig. 3 D). Thus, when ParA dimers cannot bind DNA, their mobility increases by two to three orders of magnitude (Fig. 3 D) and becomes similar to what is expected for freely diffusing proteins of similar size (28, 29). We obtained similar results when cells were treated with the cell division inhibitor cephalexin or the gyrase inhibitor nalidixic acid (Fig. 3 D). These drug treatments facilitated FRAP analysis by increasing the size of the cytoplasm (cephalexin) or by increasing the size of both the nucleoid and cytoplasm (nalidixic acid). We therefore concluded that DNA binding plays a key role in slowing down ParA mobility in vivo. The mobility of the ATP hydrolysis-defective mutant ParA_D44A-YFP in E. coli was only slightly slower compared with that of wild-type ParA-YFP (Fig. 3 D), suggesting that the basal (i.e., ParB-independent) ATPase activity of ParA only has a small contribution to the rate of ParA release from the DNA. This is consistent with our previous finding that C. crescentus ParA is a weak ATPase (k = 0.002 s⁻¹) in vitro (3).

Altogether, these FRAP results support the model in which ParA dimers display slow mobility, which originates from their slow dissociation from DNA and their fast rebinding to DNA nearby.

The ParA pattern is dependent on the number and distribution of ParB-rich partition complexes

The mathematical model for ParA patterning makes a nonintuitive prediction about the relationship between ParA distribution and the distance separating adjacent PCs for cells with multiple PCs. Equation 5c (see Materials and Methods) shows that the amount of ParA between adjacent PCs depends on not only the inter-PC distance but also the positions of the nonadjacent PCs and the length of the cell (see Fig. 4, A and B, for examples). Importantly, regardless of the specific values for these variables, the theory predicts that ParA will preferentially accumulate in regions where the PCs are separated by the longest distances. This results in depletion of ParA in regions with smaller inter-PC distances, even if these regions are micron-long (Fig. 4, A and B).

To test this prediction, we measured ParA-YFP distribution between PCs in filamentous FtsZ-depleted cells. In these cells, chromosome replication and segregation continue to occur as the cell elongates, resulting in multiple PCs separated by variable distances. A CFP fusion to MipZ, a protein that associates with ParB (30), was used as a marker to identify the position of ParB-rich PCs. Consistent with the theoretical prediction, ParA-YFP fluorescence was conspicuously missing from smaller inter-PC intervals (Fig. 4 C, arrow) and displayed a nonlinear relationship with inter-PC distances (Fig. 4 D). Deviations from the average curve likely reflect the cell-to-cell variability in PC positions and cell lengths. To compare theory and experiments, we therefore calculated theoretical ParA distributions using Eq. 5c and the experimental values of cell lengths and PC positions. Theoretical and experimental values were in quantitative agreement (Fig. 4 E). Moreover, theory and experiments showed excellent agreement on the averaged shape of ParA distribution between adjacent PCs (Fig. 4 F).

Conclusions

Stable protein gradients, which are important means of subcellular organization, can be achieved by various reaction-diffusion mechanisms (31, 32, 33, 34). One way to establish a protein gradient involves a “localized source,” diffusion, and a “distributed sink” (uniform inactivation). Examples in eukaryotic cells include gradients of mitotic spindle regulators Ran GTPase, Aurora B, and stathmins around chromatin during mitosis (35). In bacteria, slow diffusion combined with a local source and a distributed sink underlie gradients of MipZ (an inhibitor of cytokinetic ring assembly in C. crescentus) (36) and IscA (a virulence protein of Shigella flexneri) (37). Interestingly, in the mechanism we proposed for the stable formation of the ParA gradient, the concept is flipped: instead of a “localized source” and a “distributed sink,” the mechanism is based on a “localized sink” and a “distributed source.” The ParB-rich PC at the old pole acts as a localized sink by disrupting DNA binding of ParA while the uniform redistribution of ParA dimers over the nucleoid acts as a distributed source.

Another crucial component of the mechanism for gradient formation is the slow mobility of ParA dimers. It originates from the reversible interaction of ParA dimers with the DNA, with the (ATPase-independent) dissociation rate being very slow relative to the binding rate (Fig. 2 A, right). Thus, our work identifies a second role for the conserved DNA-binding property of ParA. We previously showed that the ParA-DNA interaction is critical for generating a translocation force during PC segregation through a DNA-relay mechanism (3). This interaction promotes the tethering of PC to the DNA through ParA, allowing the PC to harness the intrinsic elastic dynamics of the chromosome as a driving force to create motion. Now, we show that the DNA-binding property of ParA is also critical for the establishment of a stable gradient of ParA across the cell, which sets up the translocation directionality well before DNA replication and segregation are initiated. These findings reinforce the idea that the ParABS system is a closed (self-contained) biochemical system that encodes for complex self-organizing behaviors (38). Such behaviors could be modified with auxiliary factors to integrate the DNA partitioning function with the progression of the cell cycle (4, 7, 20, 21). The design principle of the ParABS system is simple, and therefore could be adapted or directly applied to generate spatially regulated signals in synthetic biology.

Author Contributions

H.C.L., I.V.S., and C.J.-W. conceived the project, designed the experiments, and analyzed the data. H.C.L. and I.V.S. performed the experiments. H.C.L. and I.V.S. performed stochastic simulations. I.V.S. developed the analytical model. H.C.L., I.V.S., and C.J.-W. wrote the article.

Editor: Zemer Gitai

Supporting Citation

Reference (39) appears in the Supporting Material.