Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2016 Jun 13;2(6):409–415. doi: 10.1021/acscentsci.6b00095

First-Principles Monte Carlo Simulations of Reaction Equilibria in Compressed Vapors

Evgenii O Fetisov †, I-Feng William Kuo ‡, Chris Knight ⊥, Joost VandeVondele §, Troy Van Voorhis ∥, J Ilja Siepmann †,#,*
PMCID: PMC4919768  PMID: 27413785

Abstract

graphic file with name oc-2016-00095f_0004.jpg

Predictive modeling of reaction equilibria presents one of the grand challenges in the field of molecular simulation. Difficulties in the study of such systems arise from the need (i) to accurately model both strong, short-ranged interactions leading to the formation of chemical bonds and weak interactions arising from the environment, and (ii) to sample the range of time scales involving frequent molecular collisions, slow diffusion, and infrequent reactive events. Here we present a novel reactive first-principles Monte Carlo (RxFPMC) approach that allows for investigation of reaction equilibria without the need to prespecify a set of chemical reactions and their ideal-gas equilibrium constants. We apply RxFPMC to investigate a nitrogen/oxygen mixture at T = 3000 K and p = 30 GPa, i.e., conditions that are present in atmospheric lightning strikes and explosions. The RxFPMC simulations show that the solvation environment leads to a significantly enhanced NO concentration that reaches a maximum when oxygen is present in slight excess. In addition, the RxFPMC simulations indicate the formation of NO2 and N2O in mole fractions approaching 1%, whereas N3 and O3 are not observed. The equilibrium distributions obtained from the RxFPMC simulations agree well with those from a thermochemical computer code parametrized to experimental data.

Short abstract

Advanced Monte Carlo sampling strategies in conjunction with Kohn−Sham density functional theory enable the prediction of reaction equilibria for nitrogen/oxygen mixtures without the need for predetermined reaction steps.

Introduction

Studying the behavior of complex chemical systems undergoing various multiphase reaction equilibria is of crucial importance in both chemistry and chemical engineering. Fundamental understanding of system composition and properties is critical for optimization and design of new processes involving chemical reactions. However, accurate experimental measurements of reaction equilibria can be challenging for extreme conditions (temperature and pressure), hazardous compounds, or nanoconfinement. These challenges necessitate development and improvement of predictive modeling techniques for such reactive systems.

Existing computational approaches to study reaction equilibria can be grouped into two general categories: static electronic structure calculations and trajectory-based approaches.1 Electronic structure calculations with their accurate energetics are usually the method of choice, but difficulties arise from the treatment of solvation environments (limited to continuum solvation models or inclusion of a few explicit solvent molecules) and computation of molecular partition functions when multiple conformations make significant contributions. In the group of trajectory-based methods, there are three approaches. Molecular dynamics (MD) methods can be used in conjunction with a first-principles description or a reactive force field to represent inter- and intramolecular interactions. The main drawback of MD methods is that reactive processes along with transfer between phases are usually associated with relatively high free energy barriers, and, hence, the rates are often beyond accessible time scales. Although reactive force fields2,3 allow one to access longer time scales than first-principles MD approaches, the former often require explicit parametrization for new systems to be studied.4 Reactive Monte Carlo (RxMC) approaches5 can overcome the kinetic limitations through the introduction of special RxMC moves that attempt the direct conversion of molecular species. However, RxMC has two major drawbacks: (i) a set of chemical reactions has to be prespecified and formation of chemical compounds is limited to those appearing in the reaction set, and (ii) the ratios of molecular partition functions need to be known for all chemical reactions, but may not always be available or applicable in condensed phases. Thermochemical kinetics simulations evolve the system based on rates of chemical reactions that have to be provided as input parameters and treat the environment via macroscopic equation-of-state approaches.

In this work, we present the reactive first-principles Monte Carlo (RxFPMC) method that combines concepts from MD and RxMC approaches. The main idea is simple but conceptually novel in the field of MC simulations. Every molecule in the system is viewed as an aggregate of individual atoms and not as a single entity, and all MC moves are performed on atoms or aggregates of atoms. That is a viewpoint also taken by MD using a first-principles description or reactive force fields. In RxFPMC, reactive events are sampled by special MC moves involving the exchange of atoms between aggregates (i.e., molecules) or the transfer of an atom from one aggregate to another. As a first application, we chose a mixture containing dioxygen (O2), dinitrogen (N2), and other NxOy species. This system is an attractive test case because, in addition to the main reaction of nitric oxide formation (N2 + O2 ⇄ 2 NO), further oxidation reactions (e.g., 2 NO + O2 ⇄ 2 NO2) can take place, particularly for oxygen-rich mixtures. The N:O mixture is especially important in atmospheric chemistry where NO formation happens during lightning storms,6 industrial chemistry,7 combustion8,9 and rocketry10 sciences, and astrochemistry.11 The new RxFPMC framework provides a consistent approach to predict and understand the behavior of chemically reactive systems in highly nonideal environments.

Reactive First-Principles Monte Carlo Methodology

To provide perspective on the RxFPMC method, we start this section with a brief description of the RxMC method introduced in the early 1990s in three flavors by Shaw,12 Smith and Triska,13 and Johnson et al.14 The main idea behind RxMC simulations is to introduce a new reactive move in addition to conventional MC moves (e.g, translations and rotations of molecules). During such a reactive move, reactant molecules are artificially converted into products or vice versa according to stoichiometry; i.e., the number of molecules can change through insertion/deletion of the respective molecules. The acceptance rate for such an RxMC move is as follows:5

graphic file with name oc-2016-00095f_m001.jpg 1

where ξ is the reaction direction (+1 and −1 for forward and backward reaction, respectively); p0, V, and ν are the standard pressure, system volume, and the total change in the number of molecules during the reaction step, respectively; K is the standard-pressure ideal-gas equilibrium constant; ΔU is the change in the potential energy caused by the move; s, Ni*, and νi are the number of molecules participating in the reaction, the number of molecules of type i prior to the reactive move, and the stoichiometric coefficient for this molecule type, respectively. Equation 1 requires K as an input parameter, and its value is obtained using either known ideal-gas chemical potentials for each molecule type (e.g., from JANAF tables15) or using statistical mechanics to calculate ideal-gas molecular partition functions.16 The reliance on ideal-gas K values for prespecified reactions leads to the limitations mentioned previously.

The RxFPMC methodology views a reactive system as a collection of independent atoms (or nuclei) that can aggregate to form molecules. To describe the energetics, we choose Kohn–Sham density functional theory (KS-DFT) due to its robustness and speed.17 However, switching from a molecular to an atomic description changes the types of degrees of freedom; i.e., rotational and vibrational degrees of freedom for molecules are converted into translational degrees of freedom for atoms. Associated with this switch, the types of MC moves that can be applied to the system change from a case where translational, rotational, and conformational moves are applied on molecules and volume changes involve scaling of center-of-mass coordinates to one where, in the simplest form, translational moves are only applied to atoms and volume changes involve scaling of atomic coordinates. Similarly, the calculation of the pressure switches from molecular virial (only intermolecular forces between molecules) to atomic virial. Thus, a set of test simulations is performed to validate that molecular and atomic representations yield indeed the same answer for prototypical systems where all atoms belong to molecules. Results for this test are described in the next section.

The main challenge for RxFPMC is to find a set of MC moves that can efficiently sample the aforementioned clustering events which, in turn, are chemical reactions. Over the years, various MC algorithms have been developed for strongly aggregating systems, including algorithms that translate or rotate all particles belonging to a cluster together as a group18 and that sample evaporization/condensation events (i.e., a particle is removed or added to a cluster)19 and even the transfer of a particle from one cluster to another.20 While these algorithms were developed to deal with strongly associating molecules, they can be also applied to individual atoms ensuring good statistical sampling. Another useful MC move is an identity exchange of two (or more) different chemical atoms. If the exchanged atoms belong to two different molecules, then the result is a chemical reaction involving two reactant and two product species. If the exchanged atoms belong to the same molecule, then the result is an isomerization. Using configurational-bias Monte Carlo approaches,21 it is also possible to adjust atomic distances (i.e., bond lengths and bend angles) during such an exchange move or to even carry out an identity exchange involving different numbers of atoms (e.g., an H atom could be exchanged with a CH3 group).22 As will be shown in the next section, unbiased N:O atom exchange moves and translations of individual atoms are sufficient for the NO system investigated here.

It is clear that RxFPMC overcomes the limitations of the RxMC method mentioned above. First, RxFPMC does not require one to specify a set of allowed reactions due to the atomic nature of the system and sampling of atomic aggregates is constrained only by the Boltzmann weights of system configurations. Second, the RxFPMC methodology does not rely on ideal-gas intramolecular partition functions that may lead to systematic errors for highly nonideal environments where the environment modifies the molecular partition functions (e.g., via the formation of a hydrogen bond or strong adsorption to a substrate). However, it needs to be emphasized that RxFPMC is designed to circumvent the kinetic limitations characteristic to MD simulations, and, hence, RxFPMC provides only the equilibrium distribution of reactants and products. In addition, the present implementation samples from the classical system partition function because including nuclear quantum effects via path integral approaches would significantly add to the expense. In contrast, RxMC can utilize quantum molecular partition functions (at least for molecules with limited conformational flexibility).

Results and Discussion

In order to demonstrate that MC sampling in an atomic representation yields consistent results with a molecular representation, we investigate three types of related systems containing (system A) Nmolec diatomic molecules with harmonic bonds, (system B) Natom= 2Nmolec atoms where each atom interacts only with its nearest neighbor through a harmonic potential, and (system C) Natom= 2Nmolec atoms where each atom interacts only with another specific atom in the system (not necessarily its nearest neighbor) through a harmonic potential. In addition, each system is probed either as an ideal gas (only harmonic bond potentials for the diatomic and no intermolecular interactions) or as liquid phase of dinitrogen (with additional Lennard-Jones interactions23). For system A, the simulations involve translational moves applied to molecules, rotational moves around the center of mass, conformational moves changing the bond length, and volume moves with scaling of center of mass positions. For systems B and C, only translational moves for individual atoms and volume moves with scaling of atomic positions are used. The number of particles used within the acceptance rule for volume changes is set to Nmolec for system A and to Natom for systems B and C. As can be seen from the numerical data provided in Table 1, these simulations yield molar volumes and internal energies that are statistically indistinguishable for systems A, B, and C and independent of the initial volume used. The small increase in the internal energy of the ideal gas from RT/2 is due to rovibrational coupling.

Table 1. Equilibrium Molar Volumes and Molar Internal Energies for an Ideal Diatomic Gas at T = 273.15 K and p = 1 bar and for Liquid Dinitrogen at T = 73.15 K and p = 10 bara.

      ⟨V⟩p/RT
 ⟨U⟩/RT
  N Vinitial p/RT System A System B System C System A System B System C
IG 100 0.057 1.0004 0.9986 1.0005 0.511 0.501 0.512
  100 7.16 0.9995 0.9995 1.0016 0.501 0.512 0.511
N2 1000 0.0007 0.00161 0.00172 0.00163 –2.133 –2.154 –2.154
  1000 0.099 0.00153 0.00162 0.00162 –2.154 –2.164 –2.135
Open in a new tab
a

The subscripts denote the 95% confidence intervals. The parameters for the harmonic potential are kf = 83 kJ mol–1 Å–2 and r0 = 1.1 Å.

Switching to the reactive NO system, we first address whether the RxFPMC method with the selected set of MC moves (atom identity exchanges, atom translations, and volume exchanges) can reach equilibrium distributions of species (independent of initial composition) and whether RxFPMC allows for faster sampling than FPMD. In order to answer these questions, we track the evolution of the molar fraction of NO molecules, xNO, as a function of runtime (or number of MC cycles or MD steps). To this extent, we investigate three system compositions for a 192-atom system (N:O ratios of 1:1, 2:1, and 5:1) with initial configurations that contain either only N2 and O2 molecules or only NO and N2 molecules. These initial configurations are taken from a nonreactive Monte Carlo simulation (i.e., using a molecular representation). In the RxFPMC approach (and, of course, also in FPMD), molecules are simply aggregates of atoms, and we use a distance cutoff at 1.6 Å to determine whether any two atoms belong to the same molecule (see Supporting Information for data validating this cutoff criterion).

The evolutions of xNO for the 12 different runs are illustrated in Figure 1. It is evident that the RxFPMC simulations rapidly converge to equilibrium xNO values (with the highest ⟨xNO⟩ for the N:O ratio of 1:1) irrespective of the initial speciation of the system. For all three N:O ratios, equilibrium is reached within about 25 MC cycles (equivalent to a total of 3500 CPU hours running on 192 cores of Intel Haswell E5-2680v3 processors; i.e., each MC move takes on average 14 s of wallclock time). It needs to be emphasized that the relatively similar bond lengths for N2, O2, and NO (see below) enable a fairly high acceptance rate for the atom identity exchanges (about 10–15%). In contrast, the six 60 ps FPMD trajectories do not yield a single reactive event even at the rather extreme conditions used here (T = 3000 K). Because of the high temperature, the FPMD simulations are carried out with a time step of 0.25 fs (i.e., each time step takes about 6 s of wallclock time). The reason for the wallclock time per MC move being longer than that per MD time step is that the MC moves can lead to more significant changes of the configuration and, hence, require more SCF steps for convergence. Similar observations regarding the number of SCF steps have been made previously for nonreactive first-principles MC simulations.24,25 It should also be noted that other recent FPMD studies utilized either a strong electric field26 or a virtual piston27 to initiate reactive events.

Figure 1.

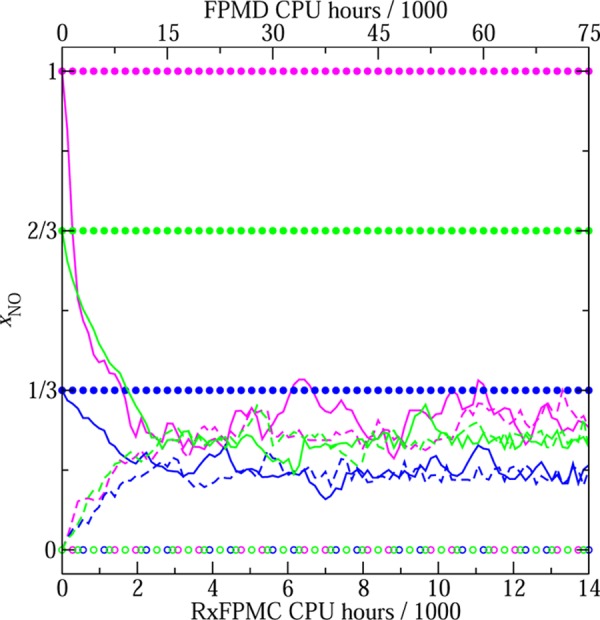
Figure 1

Open in a new tab

Evolution of instantaneous values for the molar fraction of nitric oxide with runtime. The magenta, green, and blue colors denote 192-atom systems with N:O ratios of 1:1, 2:1, and 5:1, respectively. Each RxFPMC simulation consists of 100 MC cycles (taking a total of 14 000 CPU hours, see x-axis scale at bottom), and each FPMD simulation covers 60 ps (taking a total of 75000 CPU hours, see x-axis scale at top). The solid lines and filled circles correspond to RxFPMC and FPMD trajectories, respectively, that started with all oxygen atoms being present in the form of NO molecules and the excess nitrogen atoms in the form of N2 molecules. The dashed lines and open circles correspond to RxFPMC and FPMD trajectories, respectively, that started with all atoms being present in the form of N2 and O2 molecules.

The NO formation reaction is endothermic by about 180 kJ/mol and, at normal conditions, the equilibrium is shifted very much to the reactant side. In Figure 2, the equilibrium xNO values obtained with various approaches are compared (numerical values are provided in Table S1). Using ideal-gas molecular partition functions16 for the N2 + O2 ⇄ 2 NO reaction yields xNO values ranging from 4.1% to 5.7% for N:O ratios of 5:1 and 1:1 that, by construction, are symmetric with respect to the oxygen content, xO, and the N:O ratio. In contrast, when intermolecular interactions are taken into account with various approximations (Cheetah using an equation-of-state approach,28,29 RxMC using a force field, and RxFPMC using KS-DFT), then the equilibrium xNO values are found to be about a factor of 5 larger than the ideal gas data. This very substantial increase is caused by substantially stronger NO–NO interactions compared to O2–O2 and N2–N2 interactions.30 The stronger NO–NO interactions are due to NO’s permanent dipole (μ = 0.16 D)31 and higher polarizability,32 whereas N2 and O2 possess only permanent quadrupole moments. On average, the force-field based RxMC simulations of Smith and Triska13 yield the smallest enhancement of xNO, whereas the Cheetah thermochemical code28,29 yields the largest enhancement.

Figure 2.

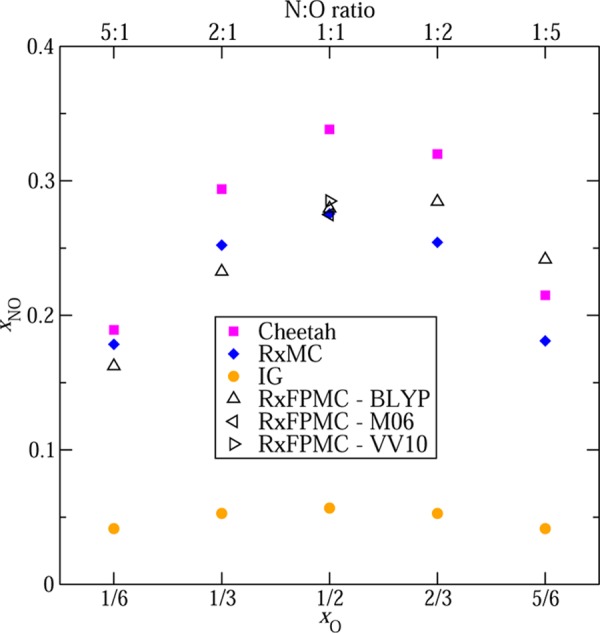
Figure 2

Open in a new tab

Equilibrium molar fractions of nitric oxide versus the oxygen content in the system. Magenta squares, blue diamonds, and orange circles denote predictions using the Cheetah thermochemical code,28 the force-field based RxMC data of Smith and Triska,13 and ratios of ideal-gas molecular partition functions, respectively. The up, left, and right triangles denote RxFPMC data obtained with the BLYP-D3, M06, and rVV10 functionals. Statistical errors are smaller than the symbol size.

The other important feature is that the RxFPMC simulations and the Cheetah predictions exhibit significantly asymmetric xNO values with a larger enhancement for higher oxygen content or smaller N:O ratio. For example, the xNO values at a 1:5 N:O ratio are larger than those at a 5:1 ratio by factors of 1.5 and 1.14 for RxFPMC and Cheetah, respectively, whereas this factor is only 1.01 for RxMC. For the RxFPMC simulations, the enhancement factors with respect to the ideal-gas values are monotonically increasing and are 3.9, 4.4, 4.9, 5.4, and 5.8 for N:O ratios of 5:1, 2:1, 1:1, 1:2, and 1:5, respectively. This asymmetric enhancement will be discussed further below.

For the 1:1 N:O ratio, RxFPMC simulations are carried out using the BLYP-D3, M06, and rVV10 functionals. Agreement between the three functionals is very good with xNO values of 0.285 ± 0.003 (rVV10), 0.279 ± 0.002 (BLYP-D3), and 0.275 ± 0.003 (M06). This order is also consistent with the reaction energies obtained for isolated molecules that are +179.8, +181.2, and +184.8 kJ/mol, respectively. These values obtained with the pseudopotential approach of CP2K are in good agreement with those obtained from all-electron calculations (see Table S2).

One approximation used for the RxFPMC simulations (but not for the RxMC and Cheetah data) is that nuclear quantum effects are neglected in the sampling. To assess the significance of this approximation, the ideal-gas equilibrium constant is calculated using either a quantum-mechanical or a classical-mechanical description of the vibrational partition function. It is found that using the classical description decreases xNO by a factor of less than 1.01 (because the zero-point energies slightly favor NO formation). That is, the neglect of nuclear quantum effects causes a shift that is approximately similar to the statistical error of the RxFPMC simulations. It certainly helps that the NO system does not contain any hydrogen atoms and is studied at high temperature.

The molar fractions of the three diatomic species are compared in Figure 3. The data for RxMC,13 Cheetah,28 and RxFPMC simulations are in very good agreement with the expected shift in population from N2 being the major species (with 0.736 ≤ xN2 ≤ 0.746) at the 5:1 N:O ratio to O2 being the major species (with 0.705 ≤ xO2 ≤ 0.743) at the 1:5 N:O ratio. As an aside, this shift in population away from N2 with the shortest bond length (see below) is also reflected in a decrease of the specific density from a value of 1194 ± 1 kg/m3 for the mixture with the 5:1 N:O ratio to 1078 ± 1 kg/m3 for the mixture with the 1:5 N:O ratio.

Figure 3.

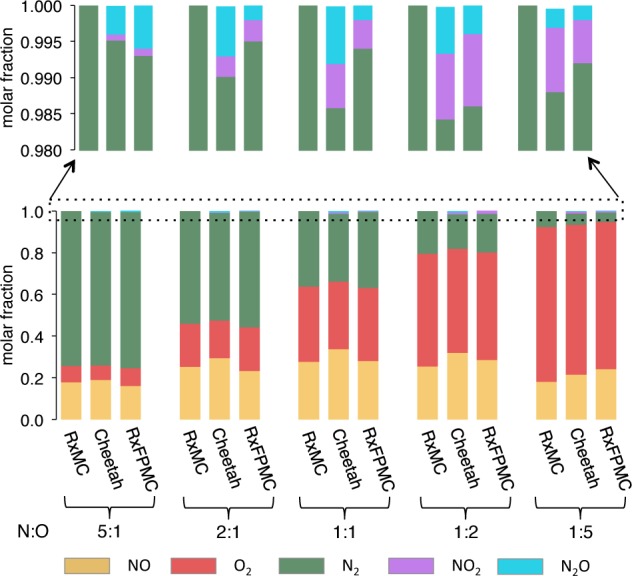
Figure 3

Open in a new tab

Equilibrium molar fractions for NO, O2, N2, NO2, and N2O obtained from RxMC,13 Cheetah,28 and RxFPMC(BLYP-D3) simulations. The upper part provides a magnified view of the molar fractions of the two triatomic species.

Most importantly, the cluster analysis of the RxFPMC simulations also yields small, but statistically significant molar fractions for the NO2 and N2O triatomic molecules (see Figure 3 and Table S1). The RxFPMC simulations do not show dissociation into atoms nor formation of homoatomic O3 and N3 species or species with four or more atoms. The presence of triatomic species demonstrates that the RxFPMC simulations with the current move set are indeed capable of generating new molecules, whereas the RxMC simulations are limited to only those species appearing in the reaction set (i.e., only the diatomic molecules for the NO system). Since we do not detect significant fractions of atomic species, the formation/destruction of the triatomic molecules involves mostly groups of six atoms that rearrange from three diatomics to two triatomics.

The Cheetah simulations also yield NO2 and N2O as the only nondiatomic species that are present in molar fractions greater than 2 × 10–4, but much better statistics for the thermochemical code allow for detection of O3, O, and N species. With the exception of the oxygen-rich system (N:O ratio of 1:5), where the xO3 value exceeds 10–4, all of these minor species are found individually only in molar fractions smaller than 10–4 in the Cheetah simulations. Averaging over the five compositions, the RxFPMC simulations yield a total molar fraction for the two major triatomic species of 0.008 compared to a value of 0.011 for the Cheetah simulations. The RxFPMC and Cheetah simulations also yield about five times more N2O than NO2 for the nitrogen-rich system with the N:O ratio of 5:1, and about three times more NO2 than N2O for the oxygen-rich system with the N:O ratio of 1:5. With regard to the two isomers possible for the triatomic species, the RxFPMC simulations yield only the N–N–O isomer for N2O, and the N–O–O isomer constitutes less than 5% of the NO2 molecules; i.e., almost all are present as the O–N–O isomer. The data for the BLYP-D3, M06, and rVV10 functionals are in agreement with respect to the fraction of triatomic molecules and their isomers for the 1:1 N:O mixture (see Table S1).

Overall, the agreement with the Cheetah data is very encouraging. The present simulations of reactive equilibria are carried out at high temperature and pressure where repulsive, first-order electrostatic, and induction interactions between molecular species are more important than dispersive interactions. Furthermore, the focus is on equilibrium distributions and not on reaction rates where sampling of transition states would be important. These factors may mask deficiencies of the KS-DFT and also explain the good agreement for data obtained with different functionals, whereas vapor–liquid equilibria are known to be very sensitive to details of the electronic structure calculations.33

To provide an explanation of the asymmetric molar fraction for NO observed in the RxFPMC simulations (see Figure 2), we turn our attention to microscopic-level information that can be obtained only from the RxFPMC simulations but not from an equation-of-state based approach. Data for the average bond lengths of the diatomic molecules are presented in Figure 4. Compared to isolated molecules, the environment provided by the highly compressed gas phase leads to a shortening of the NO bond length by about 3%, whereas the O2 bond is lengthened by about 2%. As expected, the effect on the N2 triple bond is very small. Taking bond length as a proxy for bond strength, the compressed-vapor environment leads to a stabilization of the NO radical, whereas O2 is destabilized. This finding supports higher xNO values for the oxygen-rich mixtures (N:O ratios of 1:2 and 1:5) than for the corresponding nitrogen-rich mixtures. It is also consistent with the observation that xO2 for the 1:5 N:O mixture is somewhat smaller (by a factor of 1.06) than xN2 for the 5:1 N:O mixture. It should also be noted that the extent of the lengthening of the O2 bond is found to decrease slightly with increasing oxygen content.

Figure 4.

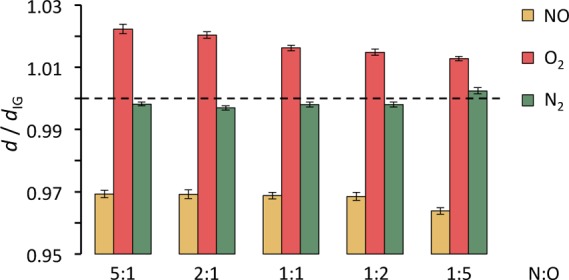
Figure 4

Open in a new tab

Ratios between average bond lengths of the diatomic molecules in the bulk phase and for an isolated molecule at T = 3000 K for the five compositions studied with the BLYP-D3 functional.

From an analysis of the various radial distribution functions and the corresponding number integrals another structural feature emerges that supports the higher molar fraction of NO in oxygen-rich environments. Combining data from various number integrals, the local molar fraction enhancement can be computed that provides information on preferential solvation. For the NO system, we find such an enhancement for the solvation of NO molecules by O2 molecules (see Figure 5). That is, the local surrounding of an NO molecule is occupied on average by significantly more O2 molecules than one would expect from the bulk composition and random mixing. As for other systems,34 this relative enhancement is largest for the O2-poor mixture, i.e., the 5:1 N:O mixture with xO2 = 0.085. The enrichment is greatly diminished for the 1:5 N:O mixture with xO2 = 0.705 because sufficient O2 molecules are present to provide NO’s preferred solvation environment. This local microheterogeneity also supports the higher xNO values for the oxygen-rich mixtures when NO can be stabilized by solvation with O2.

Figure 5.

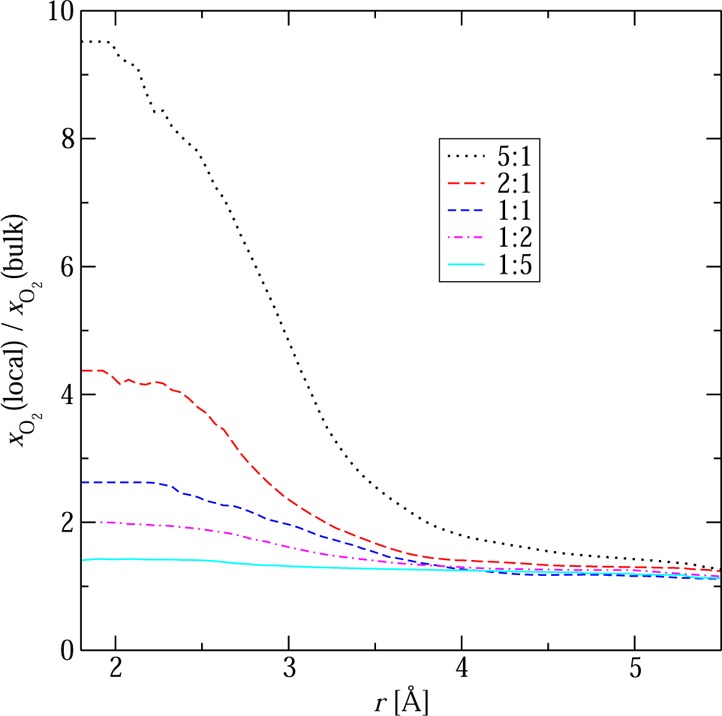
Figure 5

Open in a new tab

Local enhancement for O2 molecules surrounding NO molecules calculated for the systems with the five N:O ratios studied using RxFPMC and the BLYP-D3 functional.

In conclusion, a new first-principles Monte Carlo approach for simulating reactive equilibria is introduced that does not rely on any set of prespecified reactions nor on ideal-gas equilibrium constants that hamper conventional RxMC simulations. Using a first-principles description of the system’s energetics allows one to view molecules as being formed by the strong aggregation of atoms. Special Monte Carlo moves can then be used to efficiently sample the distribution of atoms over molecular species, thereby overcoming the kinetic limitations of first-principles MD simulations. Application of the RxFPMC method to nitrogen/oxygen mixtures in the highly compressed vapor phase region shows significant enhancement of NO molecules. Structural analysis demonstrates stabilization of NO and destabilization of O2 molecules and preferential solvation of NO by O2. These structural features support an asymmetry in the species distributions and a maximum in the NO concentration when oxygen is present in slight excess. This study illustrates the promise of using RxFPMC to investigate reaction equilibria in highly nonideal environments.

Computational Details

The RxFPMC simulations are performed with the CP2K simulation package35 which solves the KS-DFT equations with the Gaussian plane wave method as implemented in the Quickstep module.36 Most of the simulations use the BLYP functional37,38 with the third-generation Grimme dispersion correction (D3)39 along with a triple-ζ, double polarization basis set,40 GTH pseudopotentials,41,42 and a plane wave cutoff at 600 Ry. For one state point, additional simulations with the M0643 and rVV1044,45 functionals are carried out to assess the accuracy of the predictions. For the compressed vapor phase, only system sizes and atomic compositions are considered that lead to an even number of electrons and the spin multiplicity of the entire system is restricted to 1, but employing spin-polarized (unrestricted) KS-DFT. Constraining the overall spin multiplicity to 1 is a reasonable assumption for bulk systems; i.e., there are enough molecules in the system to allow the individual molecules to adjust their spin state as needed. Two triplet O2 molecules that are sufficiently far apart constitute a singlet system; there will be two spin up electrons on one molecule and two spin down electrons on the other. Similarly, two NO molecules can adopt the spin state as needed, i.e., both spin up or spin down when the two NO molecules are formed from the reaction of a triplet O2 molecule and a singlet N2 molecule. Snapshots illustrating the local spin densities for the 2:1 and 1:2 N:O systems are shown in Figure S2. All N2 molecules are found to be singlets without appreciable local spin density, whereas the other species exhibit significant local spin density, e.g., triplet O2 molecules.

System sizes consisting of 96 and 192 atoms are used to confirm that the RxFPMC approach converges to equilibrium compositions irrespective of the starting compositions (see Figure 1). Increasing the system size from 96 to 192 atoms may lessen the constraint on speciation caused by setting the overall spin multiplicity to 1, but increases the average computer time per MC cycle (where one MC cycle consists of Natom randomly selected moves) by a factor of about 14. Since the species distributions obtained from the initial simulations for 96- and 192-atoms systems are statistically indistinguishable (see Table S1), subsequent simulations exploring different ratios of nitrogen to oxygen atoms (N:O = 5:1, 2:1, 1:1, 1:2, and 1:5) are carried out using the smaller system size in the NpT ensemble (Natom = 96, p = 30 GPa, and T = 3000 K). Equilibration periods run for at least 100 MC cycles, followed by at least 150 MC cycles of production. The MC move probabilities are adjusted to yield one accepted volume and one accepted N:O atom identity exchange move per cycle, and the remainder is distributed between O and N translational moves according to the atomic composition. The maximum displacement applied for the volume moves is set to yield an acceptance rate of about 20%; for example, 13 and 20 Å3 are used for the 1:1 N:O systems with 96 and 192 particles, respectively (corresponding to about 0.7 and 0.5% of the total volume, respectively). The N:O atom exchange moves yield an acceptance rate of about 10–15%. The maximum displacements for the translational moves are adjusted to yield acceptance rates of about 30% and are about 0.35 and 0.45 Å for nitrogen and oxygen atoms, respectively. To gather satisfactory statistics, 32 independent simulations are carried out at each composition for the 96-atom system. These are used to estimate the 95% confidence interval for the calculated properties.

Acknowledgments

This work was supported by the National Science Foundation through Grant CHE-1265849. Part of this work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. Additional computer resources were provided by the Minnesota Supercomputing Institute at the University of Minnesota.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.6b00095.

  • Details on the procedure for identifying molecules, reaction energies, snapshots of configurations illustrating the local spin density, and numerical values for the data shown in Figures 2, 3, and 4 (PDF)

The authors declare no competing financial interest.

Supplementary Material

oc6b00095_si_001.pdf (5.7MB, pdf)

References

  1. Santiso E. E.; Gubbins K. E. Multi-Scale Molecular Modeling of Chemical Reactivity. Mol. Simul. 2004, 30, 699–748. 10.1080/08927020412331294878. [DOI] [Google Scholar]
  2. Liang T.; Shin Y. K.; Cheng Y.-T.; Yilmaz D. E.; Vishnu K. G.; Verners O.; Zou C.; Phillpot S. R.; Sinnott S. B.; van Duin A. C. T. Reactive Potentials for Advanced Atomistic Simulations. Annu. Rev. Mater. Res. 2013, 43, 109–129. 10.1146/annurev-matsci-071312-121610. [DOI] [Google Scholar]
  3. Brenner D. W.; Shenderova O. A.; Harrison J. A.; Stuart S. J.; Ni B.; Sinnott S. B. A Second-generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydrocarbons. J. Phys.: Condens. Matter 2002, 14, 783–802. 10.1088/0953-8984/14/4/312. [DOI] [Google Scholar]
  4. Farah K.; Müller-Plathe F.; Böhm M. C. Classical Reactive Molecular Dynamics Implementations: State of the Art. ChemPhysChem 2012, 13, 1127–1151. 10.1002/cphc.201100681. [DOI] [PubMed] [Google Scholar]
  5. Turner C. H.; Brennan J. K.; Lísal M.; Smith W. R.; Johnson J. K.; Gubbins K. E. Simulation of Chemical Reaction Equilibria by the Reaction Ensemble Monte Carlo Method: A Review. Mol. Simul. 2008, 34, 119–146. 10.1080/08927020801986564. [DOI] [Google Scholar]
  6. Leigh G. J.The World’s Greatest Fix: A History of Nitrogen and Agriculture; Oxford University Press: New York, 2004. [Google Scholar]
  7. Fisher K.; Newton W. E.. Nitrogen Fixation at the Millennium; Elsevier: Amsterdam, 2002. [Google Scholar]
  8. Tomeczek J.; Gradoń B. The Role of Nitrous Oxide in the Mechanism of Thermal Nitric Oxide Formation within Flame Temperature Range. Combust. Sci. Technol. 1997, 125, 159–180. 10.1080/00102209708935658. [DOI] [Google Scholar]
  9. Goldman N.; Bastea S. Nitrogen Oxides as a Chemistry Trap in Detonating Oxygen-rich Materials. J. Phys. Chem. A 2014, 118, 2897–2903. 10.1021/jp501455z. [DOI] [PubMed] [Google Scholar]
  10. Seshadri D. N.; Viswanath D. S.; Kuloor N. R. Thermodynamic Properties of the System N2O4⇄2NO2⇄2NO + O2. AIChE J. 1970, 16, 420–425. 10.1002/aic.690160319. [DOI] [Google Scholar]
  11. Quintana-Lacaci G.; Agundez M.; Cernicharo J.; Bujarrabal V.; Sanchez Contreras C. S.; Castro-Carrizo A.; Alcolea J. Detection of Circumstellar Nitric Oxide. Enhanced Nitrogen Abundance in IRC + 10420. Astron. Astrophys. 2013, 560, L2. 10.1051/0004-6361/201322728. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Shaw M. S. Monte Carlo Simulation of Equilibrium Chemical Composition of Molecular Fluid Mixtures in the NatomsPT Ensemble. J. Chem. Phys. 1991, 94, 7550–7553. 10.1063/1.460188. [DOI] [Google Scholar]
  13. Smith W. R.; Triska B. The Reaction Ensemble Method for the Computer Simulation of Chemical and Phase Equilibria. I. Theory and Basic Examples. J. Chem. Phys. 1994, 100, 3019–3027. 10.1063/1.466443. [DOI] [Google Scholar]
  14. Johnson J. K.; Panagiotopoulos A. Z.; Gubbins K. E. Reactive Canonical Monte Carlo. Mol. Phys. 1994, 81, 717–733. 10.1080/00268979400100481. [DOI] [Google Scholar]
  15. Chase M. W. J.NIST-JANAF Thermochemical Tables; Journal of Physical and Chemical Reference Data Monographs; American Institute of Physics: New York, 1998. [Google Scholar]
  16. McQuarie D. A.Statistical Mechanics; Harper & Row: New York, 1976. [Google Scholar]
  17. Jones R. O. Density Functional Theory: Its Origins, Rise to Prominence, and Future. Rev. Mod. Phys. 2015, 87, 897–923. 10.1103/RevModPhys.87.897. [DOI] [Google Scholar]
  18. Frenkel D., Smit B.. Understanding Molecular Simulation, Second Edition: From Algorithms to Applications (Computational Science), 2nd ed.; Academic Press: Cambridge, 2001. [Google Scholar]
  19. Chen B.; Siepmann J. I. A Novel Monte Carlo Algorithm for Simulating Strongly Associating Fluids: Applications to Water, Hydrogen Fluoride, and Acetic Acid. J. Phys. Chem. B 2000, 104, 8725–8734. 10.1021/jp001952u. [DOI] [Google Scholar]
  20. Chen B.; Siepmann J. I. Improving the Efficiency of the Aggregation-Volume-bias Monte Carlo Algorithm. J. Phys. Chem. B 2001, 105, 11275–11282. 10.1021/jp012209k. [DOI] [Google Scholar]
  21. Martin M. G.; Siepmann J. I. Novel Configurational-bias Monte Carlo Method for Branched Molecules. Transferable Potentials for Phase Equilibria. 2. United-atom Description of Branched Alkanes. J. Phys. Chem. B 1999, 103, 4508–4517. 10.1021/jp984742e. [DOI] [Google Scholar]
  22. Siepmann J. I.; McDonald I. R. Monte Carlo Simulations of Mixed Monolayers. Mol. Phys. 1992, 75, 255–259. 10.1080/00268979200100201. [DOI] [Google Scholar]
  23. Bouanich J.-P. Site-site Lennard-Jones Potential Parameters for N2, O2, H2, CO and CO2. J. Quant. Spectrosc. Radiat. Transfer 1992, 47, 243–250. 10.1016/0022-4073(92)90142-Q. [DOI] [Google Scholar]
  24. Kuo I.-F. W.; Mundy C. J.; McGrath M. J.; Siepmann J. I.; VandeVondele J.; Sprik M.; Hutter J.; Chen B.; Klein M. L.; Mohamed F.; Krack M.; Parrinello M. Liquid Water from First Principles: Investigation of Different Sampling Approaches. J. Phys. Chem. B 2004, 108, 12990–12998. 10.1021/jp047788i. [DOI] [Google Scholar]
  25. McGrath M. J.; Siepmann J. I.; Kuo I.-F. W.; Mundy C. J.; VandeVondele J.; Hutter J.; Mohamed F.; Krack M. Simulating Fluid Phase Equilibria of Water from First Principles. J. Phys. Chem. A 2006, 110, 640–646. 10.1021/jp0535947. [DOI] [PubMed] [Google Scholar]
  26. Saitta A. M.; Saija F. Miller Experiments in Atomistic Computer Simulations. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 13768–13773. 10.1073/pnas.1402894111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wang L.-P.; Titov A.; McGibbon R.; Liu F.; Pande V. S.; Martínez T. J. Discovering Chemistry with an ab initio Nanoreactor. Nat. Chem. 2014, 6, 1044–1048. 10.1038/nchem.2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Bastea S.; Fried L. E. Exp-6 Polar Thermodynamics of Dense Supercritical Water. J. Chem. Phys. 2008, 128, 174502. 10.1063/1.2913055. [DOI] [PubMed] [Google Scholar]
  29. Bastea S.; Fried L. E.. Chemical Equilibrium Detonation. In Shock Wave Science and Technology Reference Library, Vol. 6; Zhang F., Ed.; Springer: Berlin, 2012; pp 1–31. [Google Scholar]
  30. Schott G. L.; Shaw M. S.; Johnson J. D. Shocked States from Initially Liquid Oxygen-Nitrogen Systems. J. Chem. Phys. 1985, 82, 4264–4275. 10.1063/1.448817. [DOI] [Google Scholar]
  31. Gijsbertsen A.; Siu W.; Kling M. F.; Johnsson P.; Jansen P.; Stolte S.; Vrakking M. J. J. Direct Determination of the Sign of the NO Dipole Moment. Phys. Rev. Lett. 2007, 99, 213003. 10.1103/PhysRevLett.99.213003. [DOI] [PubMed] [Google Scholar]
  32. Zen A.; Trout B. L.; Guidoni L. Properties of Reactive Oxygen Species by Quantum Monte Carlo. J. Chem. Phys. 2014, 141, 014305. 10.1063/1.4885144. [DOI] [PubMed] [Google Scholar]
  33. McGrath M. J.; Siepmann J. I.; Kuo I.-F. W.; Mundy C. J. Vapor-liquid Equilibria of Water from First Principles: Comparison of Density Functionals and Basis Sets. Mol. Phys. 2006, 104, 3619–3626. 10.1080/00268970601014781. [DOI] [Google Scholar]
  34. Chen B.; Potoff J. J.; Siepmann J. I. Monte Carlo Calculations for Alcohols and Their Mixtures with Alkanes. Transferable Potentials for Phase Equilibria. 5. United-atom Description of Primary, Secondary and Tertiary Alcohols. J. Phys. Chem. B 2001, 105, 3093–3104. 10.1021/jp003882x. [DOI] [Google Scholar]
  35. Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  36. VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. QUICKSTEP: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
  37. Becke A. D. Density-functional Exchange-energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  38. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  39. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  40. VandeVondele J.; Hutter J. Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases. J. Chem. Phys. 2007, 127, 114105. 10.1063/1.2770708. [DOI] [PubMed] [Google Scholar]
  41. Goedecker S.; Teter M.; Hutter J. Separable Dual-space Gaussian Pseudopotentials. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 1703–1710. 10.1103/PhysRevB.54.1703. [DOI] [PubMed] [Google Scholar]
  42. Hartwigsen C.; Goedecker S.; Hutter J. Relativistic Separable Dual-space Gaussian Pseudopotentials from H to Rn. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 3641–3662. 10.1103/PhysRevB.58.3641. [DOI] [PubMed] [Google Scholar]
  43. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  44. Vydrov O. A.; Van Voorhis T. Implementation and Assessment of a Simple Nonlocal van der Waals Density Functional. J. Chem. Phys. 2010, 132, 164113. 10.1063/1.3398840. [DOI] [PubMed] [Google Scholar]
  45. Sabatini R.; Gorni T.; de Gironcoli S. Nonlocal van der Waals Density Functional Made Simple and Efficient. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 041108. 10.1103/PhysRevB.87.041108. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc6b00095_si_001.pdf (5.7MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES