Control of timing, rate and bursts of hippocampal place cells by dendritic and somatic inhibition

Abstract

A consortium of inhibitory neurons control the firing patterns of pyramidal cells, but their specific roles in the behaving animal are largely unknown. We performed simultaneous physiological recordings and optogenetic silencing of either perisomatic (parvalbumin (PV) expressing) or dendrite-targeting (somatostatin (SOM) expressing) interneurons in hippocampal area CA1 of head-fixed mice actively moving a treadmill belt rich with visual-tactile stimuli. Silencing of either PV or SOM interneurons increased the firing rates of pyramidal cells selectively in their place fields, with PV and SOM interneurons having their largest effect during the rising and decaying parts of the place field, respectively. SOM interneuron silencing powerfully increased burst firing without altering the theta phase of spikes. In contrast, PV interneuron silencing had no effect on burst firing, but instead shifted the spikes’ theta phase toward the trough of theta. These findings indicate that perisomatic and dendritic inhibition have distinct roles in controlling the rate, burst and timing of hippocampal pyramidal cells.

Computation in the brain relies on dynamic interactions between excitatory and inhibitory circuits^1–4. Appropriately timed inhibition exerted on specific somatodendritic compartments of principal cells is needed not only to balance excitation, but also for the selective filtering of synaptic excitation, timing of spike output, gain control, governing burst firing and synaptic plasticity, and, at the network level, coordination of cell assemblies through maintenance of oscillations and synchrony^1,3,5–10. A large diversity of inhibitory interneurons are available for such tasks, but the division of labor among them and their specific contributions are poorly understood.

In the hippocampus, interneurons are known to be involved in several network activity patterns and rhythms that support hippocampal functions, such as spatial navigation and the storage and recall of episodic information^11,12. During exploration, ‘place cell’ activity is the characteristic network pattern of the hippocampus. Place cells encode information through several means such as firing rate, pattern of discharge and spike timing. Increases in firing rate occur when the animal visits their respective place field. In the place field, pyramidal neurons alternate between two distinct modes of discharge: single spikes and bursts of spikes¹³. Finally, spikes are temporally organized in theta oscillations, such that neurons with place fields located behind the animal in its running path discharge on the descending phase of theta and neurons with place fields located in front of the animal discharge on the ascending phase^14–20. The mechanisms proposed for the control of spike rate, pattern and timing of CA1 place cells range from a complete inheritance from upstream neurons to a dominant role for somatic or dendritic inhibition^{12,14,21–29}. As changes in rate and theta phase tend to occur together as the animal crosses the place fields, several models infer that both aspects originate from related mechanisms^21–23, whereas other findings suggest independent implementations^18,30. Models supporting either of these views involve inhibitory mechanisms, mediated by either perisomatic interneurons or dendrite-targeting interneurons^21–29.

Recent work has begun to explore the firing pattern correlates of anatomically identified interneuron types during theta oscillations and other network patterns in anesthetized animals^2,5. However, a full understanding of their domain-specific functions requires the selective manipulation of each neuron type in appropriate behavioral contexts. To address the contribution of perisomatic and dendrite-targeting inhibitory interneurons to the firing patterns of pyramidal cells, we used a combination of large-scale unit recording, optogenetic methods³¹ and foraging behavior on a treadmill apparatus, which enabled us to selectively and focally silence either parvalbumin (PV)- or somatostatin (SOM)-expressing interneurons during place cell activity. Our findings show distinct roles for perisomatic and dendritic inhibition in controlling rate, burst and theta cycle timing of place cell activity.

RESULTS

Place cell sequences during stationary treadmill running

To generate sequential activation of hippocampal neurons, we trained mice to run head-fixed^26,32 on a treadmill equipped with a 1.7-m-long belt rich in visual and tactile cues (Fig. 1a, Supplementary Fig. 1a and Supplementary Movie 1). The belt was moved actively by the mouse and provided continuously changing local cues while environmental cues remained stationary. A water-sucrose reward was delivered on every trial (complete belt rotation) at the same position of the belt. Both the running speed and the number of trials increased over training days, reaching an asymptotic level by approximately day 6 (Fig. 1b,c).

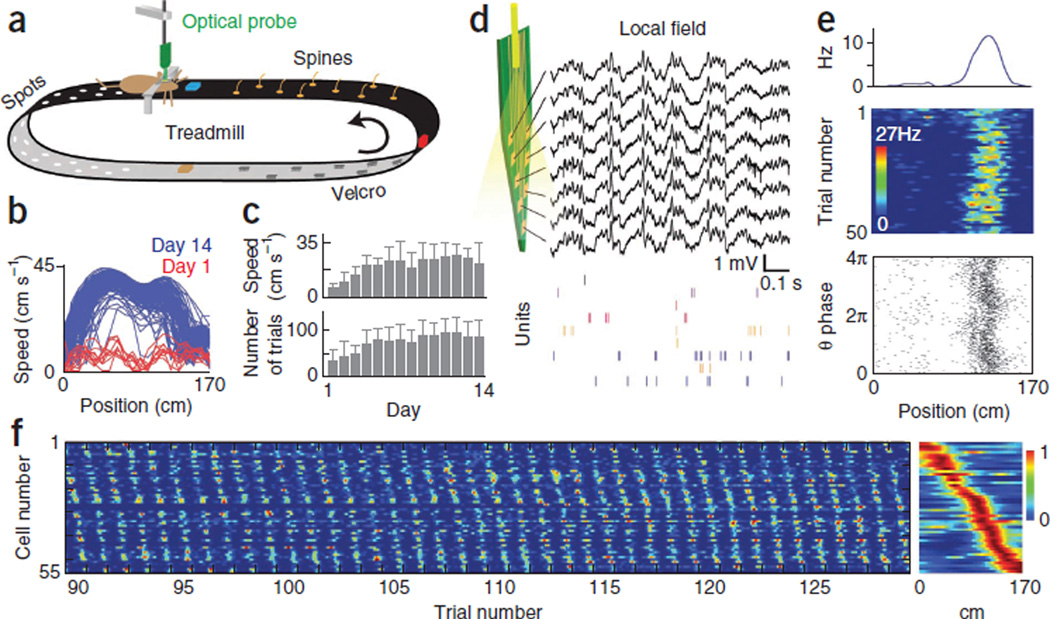
Figure 1.

Self movement–controlled local stimuli generate hippocampal cell sequences. (a) Experimental setup for optical probe recording in head-fixed mice during treadmill running. Visual and tactile stimuli of the belt are illustrated. Three reflector cubes placed at equal intervals (blue, red and orange colors are only for illustration purposes) triggered photo-beam sensors for the control of water reward delivery and laser stimulation. (b) Running speed as a function of belt position during the first and last days of training in a mouse. Each line is a single trial. Sucrose-water reward was delivered on every trial at position 0. (c) Average speed between the 57- and 113-cm positions and number of trials completed after 30 min (mean ± s.d. of three mice). (d) Wide-band (1 Hz to 5 kHz) recording of electrical activity on a single shank of the optical probe. Color ticks indicate spikes of isolated CA1 pyramidal cells. (e) Place field of a single neuron. Mean firing rate, single trials and spike theta phase as a function of belt position. (f) Activity of 55 place cells recorded simultaneously. Each row is one neuron normalized firing rate. Successive trials are concatenated (only trials 90–130 are shown) and the cells are ordered according to their place field position. Right, average of 131 trials.

After approximately 2 weeks of training, we performed recordings from the CA1 hippocampal pyramidal layer using an eight-shank silicon probe. The local field potential (LFP) showed prominent theta oscillations and theta phase-modulated gamma oscillations during running (Fig. 1d)³³. Single pyramidal neurons fired clusters of spikes at specific locations of the belt, which repeated reliably over successive trials (Fig. 1e). In these firing fields, the theta phase of spikes shifted forward (phase precession¹¹) (Fig. 1e). Individual pyramidal cells fired at different positions on the self-controlled treadmill so that the firing fields of the population evenly covered the entire belt (Fig. 1f). These findings indicate that active movement–generated changes of local cues are sufficient to generate sequences of hippocampal pyramidal cell activity with many of the physiological characteristics of place cells^11,34. For this reason, we shall refer to these cells and their activity as place cells and place fields.

Silencing of soma- and dendrite-targeting interneurons

To transiently silence interneurons mediating perisomatic and dendritic inhibition⁶, we virally expressed (adeno-associated virus, AAV) a Cre recombinase–dependent construct containing the NpHReGFP fusion protein (halorhodopsin) in the CA1 region of the dorsal hippocampus of mice expressing Cre recombinase under the control of the promoter for either the parvalbumin gene (PV-Cre mice) or the somatostatin gene (SOM-Cre mice)³¹. Histological examination and in vitro experiments showed that a large fraction of PV-containing and SOM-containing cells in the dorsal CA1 region expressed high levels of halorhodopsin (n = 13 PV-Cre mice, n = 20 SOM-Cre mice; Fig. 2a and Supplementary Figs. 2–4)¹. The basic biophysical properties of the virus-infected and non-infected neurons from PV-Cre and Som-Cre mice, respectively, were similar and the quantity of interneurons was unaltered by halorhodopsin expression (Supplementary Figs. 2–4). To allow for simultaneous recording of single-unit activity and focal inactivation of halorhodopsin-expressing neurons, we equipped four adjacent shanks of the silicon probe with micrometer-scale light guides (Supplementary Fig. 1b,c)³¹.

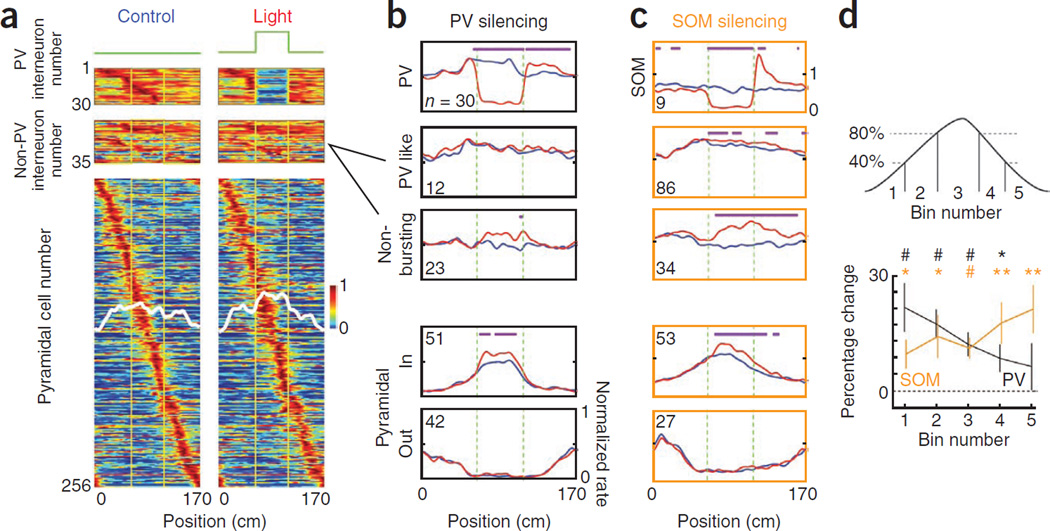
Figure 2.

Light-assisted silencing of PV and SOM neurons. (a) Specific halorhodopsin expression in hippocampal interneurons. Top, low-magnification images of halorhodopsin-GFP in PV and SOM interneurons following viral injection. Bottom, higher magnification of the boxed areas. Ori, stratum oriens; pyr, pyramidal layer; rad, stratum radiatum; lm, stratum lacunosummoleculare. (b) Peristimulus histograms of simultaneously monitored neuronal responses to 1-s-long light pulses (50 pulses, 7-s interpulse interval), aligned to their respective recording shanks in a PV-Cre mouse. (c) Higher magnification of the boxed peristimulus histograms in b. (d) Percent decrease and increase of firing rates of PV cells (black, 69 cells) and other non-PV neurons (white, 722 cells), respectively, shown separately for each shank (mean ± s.d. of all neurons recorded from 11 sessions in 5 mice). Note that the largest effect occurred on the shanks carrying optical fibers. On shanks located further away from the stimulated volume, the magnitude of changes was decreased and the number of detectable PV neurons was reduced (n = 1 and 0 on the seventh and eighth shanks, respectively). (e) Normalized activity of simultaneously recorded PV interneurons and pyramidal cells during alternate light and light-off (control) trials. (f) Example PV interneuron and pyramidal cell firing patterns. Each line is a single trial. The color scale is the same as that used in e. Right, session average firing rates of the two cells (averages of the 50 trials). The blue line indicates control trials and the red line indicates light trials. Magenta dots indicate significant rate differences in different pixels (P < 0.05, rank test, 1,000 shuffles, see Online Methods).

For testing local physiological changes without affecting the patterns of activity in the entire hippocampus, a focal light stimulation confined to the volume of neurons monitored by the recording electrodes is desired. To test the volume of tissue affected by the light stimulation, we delivered 1-s pulses of light (561 nm, ~1 mW at the tip of the shanks) 50 times every 7 s in 11 recording sessions from five PV-Cre mice (Fig. 2b–d). The magnitude of both suppression and enhancement of spiking decreased with distance from the illuminated shanks, indicating that the light stimulation was relatively focal³¹ (Fig. 2b,d).

To examine the consequences of interneuron silencing on place cell activity, we delivered light on alternate trials (Fig. 2e,f) during the same 57-cm segment of the belt (see Fig. 1a), that is, in the steady run portion of the travel (Fig. 1b). To ensure that the analysis of place cell activity is performed during steady running, we included in the analyses only trials in which the mice ran this segment in <3 s. The number of ‘light off’ (control) and ‘light on’ trials meeting this criterion ranged from 18 to 75 (45.6 ± 16.6, mean ± s.d.) and from 18 to 79 (45.9 ± 17.9), respectively. We isolated a total of 1,678 cells from four PV-Cre mice (n = 852 neurons in 8 sessions) and six SOM-Cre mice (n = 826 neurons in 9 sessions).

Identification of putative neuron types

Prior to analyzing the effect of interneuron silencing on place cells, we classified the recorded neurons into putative cell types (Figs. 3 and 4 and Supplementary Figs. 5–7). Halorhodopsin-expressing PV and SOM interneurons were significantly suppressed by light in most pixels of the stimulated segment (P < 0.05; Fig. 4a–c and Supplementary Fig. 5). An average of 4.6 (range, 2 to 7) PV neurons were identified per session. Only nine SOM neurons were identified by light, likely because the recordings were made mostly in the pyramidal layer, whereas most SOM cell bodies are located in the stratum oriens¹. We classified the remaining neurons into three groups by their spike-burst magnitude and refractory period (Supplementary Fig. 5): PV-like neurons that had similar physiological characteristics as identified PV neurons (Supplementary Figs. 5–7), non-bursting neurons (putative ‘other’ interneurons) and pyramidal neurons. Pyramidal neurons included virtually all cells that were identified as presynaptic excitatory cells (Supplementary Fig. 6) and had defined place fields (Fig. 4a and Supplementary Fig. 7). PV and PV-like neurons had short refractory periods, high firing rates and fired on most parts of the belt (Supplementary Figs. 5–7). In addition, they accounted for most of the neurons excited by the putative pyramidal cells (40% of PV neurons were monosynaptically excited, versus 4% of non-bursting and 0.5% of pyramidal cells; Supplementary Fig. 6). SOM and non-bursting neurons showed heterogeneous firing patterns in terms of firing rates, refractoriness and bursting (Supplementary Figs. 5–7).

Figure 3.

Firing activity of different cell types during SWRs and theta oscillations. (a) Left, population average of peri-ripple histograms for PV (n = 23), SOM (n = 8), PV like (n = 89), non-bursting (n = 80) and pyramidal cells (n = 707). Right, distribution of ripple modulation index in the five cell groups. Higher positive indexes indicate larger increases in firing rate during ripples, whereas larger negative indexes indicate larger decreases in firing rate during ripples. The bimodal behavior of SOM neurons indicates that they represent a mixture of oriens-lacunosum moleculare (ripple activated) and bistratified (ripple suppressed) interneurons². (b) Left, population average of theta phase histograms for PV (n = 30 cells, 30,369 spikes), SOM (n = 9 cells, 7,078 spikes), PV like (n = 98 cells, 116,616 spikes), non-bursting (n = 56 cells, 16,306 spikes) and pyramidal cells (n = 356 cells, 38,623 spikes) during control trials. Right, distribution of mean theta phases.

Figure 4.

Light-induced changes in firing patterns. (a) Normalized activity of PV interneurons, non-PV interneurons (PV-like interneurons and non-bursting cells) and pyramidal cells during control (left) and light (right) trials in PV-Cre mice (Supplementary Figs. 5–8). Each line is the average of control or light trials for a single neuron. The cells are ordered according to the position of their place field. Vertical yellow lines delimit the light-stimulated segment of the belt. White lines indicate group average. (b) Population averages of firing rates for each neuron group during control (blue) and light (red) trials in PV-Cre mice. Numbers in each panel indicate the number of cells included in each average. Pyramidal neurons whose place fields completely covered the stimulated area (in) or that had no overlap with the stimulated area (out) are shown separately. Magenta dots indicate significant rate differences in different pixels (P < 0.05, two-tail paired t test). (c) Data are presented as in b for neurons in SOM-Cre mice. (d) Top, binning of the place fields. Bottom, percent rate increase in each bin (mean ± s.e.m.) in PV-Cre and SOM-Cre mice. The percent rate increase was first computed for individual neuron in each place field bin overlapping with the stimulated area of the belt and then the average increase of the neuron population was computed for each bin (*P < 0.05, **P < 0.005, ^#P < 0.0005, unpaired t test).

Given that histologically identified interneurons were previously categorized by theta phase preference and sharp wave ripples^2,5,7 (SWRs), we also examined these physiological features. During periods of immobility, theta oscillations disappeared and were replaced by SWRs. For three recording sessions from one PV-Cre mouse and eight sessions from six SOM mice, the recordings were extended to include long periods of immobility with SWR events. We detected 29–933 SWRs per session by applying a threshold to the bandpass-filtered (120–170 Hz) LFP trace and correcting by visual inspection. The majority of PV and PV-like interneurons formed a relatively homogeneous group that fired robustly and maximally during SWRs, as in the rat^5,7 (Fig. 3a and Supplementary Fig. 8). In contrast, SOM and non-bursting neurons showed heterogeneous firing patterns, either being suppressed or excited during SWRs. This bimodality may reflect the presence of two subpopulations with distinct SWR preference (oriens-lacunosum moleculare and bistratified interneurons)². Individual pyramidal cells were either strongly recruited or strongly suppressed during SWRs, with a minority that were not influenced by SWRs at all⁷.

Most of the PV and PV-like neurons fired preferentially before the trough of the theta wave, whereas all of the SOM neurons were phaselocked to the ascending phase of the cycle (Fig. 3b)². Members of the non-bursting group fired at various phases, but avoided the peak of theta. Pyramidal cells had the widest range of phase preference⁷. As these observations were made on limited datasets, appropriate population pattern classification will require more extensive studies.

Interleaved gain control of firing rates

We first examined the effect of light stimulation on the firing rate of pyramidal cells. To compare the effect of light stimulation inside and outside of the place fields, we separately computed the average firing fields of neurons depending on whether their place fields were inside or outside of the stimulated segment. For both PV and SOM interneuron silencing, we observed significant increases in firing rate only in the place fields (P < 0.05; Fig. 4b,c), suggesting that the absence of firing outside of the place field is mainly a result of a lack of excitatory drive rather than an enhanced inhibition.

Next, we examined the effect of light on different parts of the place fields. We divided each field into five spatial bins and computed the percent change in firing rate between control and light trials for each bin located in the stimulated segment of the belt. Only bins containing at least 20 spikes during control trials were considered to ensure a reliable statistical significance of the percent change estimate. We then computed the average percent change across the neuron population for each bin (Fig. 4d). We found that the effect of PV and SOM neuron silencing exhibited opposite trends, as the influence of PV interneurons was progressively reduced, whereas that of SOM interneurons gradually increased in the place fields. Together, these data indicate that the two classes of interneurons do not contribute to the ‘bell shape’ appearance of place fields, but instead coordinate to produce an interleaved gain control on firing activity in the place fields.

Control of burst firing by dendritic inhibition

Hippocampal pyramidal cells fire both single spikes and spike bursts¹³ (Fig. 5a), and these different firing modes have somewhat different theta phase preference³⁵. Previous intracellular work has suggested that generation of spike bursts involves either dendritic^36–38 or somatic³⁹ mechanisms. In vitro experiments manipulating dendritic inhibition favor dendrites as the source of spike bursts^37,40. We defined spike bursts in pyramidal cells as events with more than two spikes with <9-ms interspike intervals^13,41.

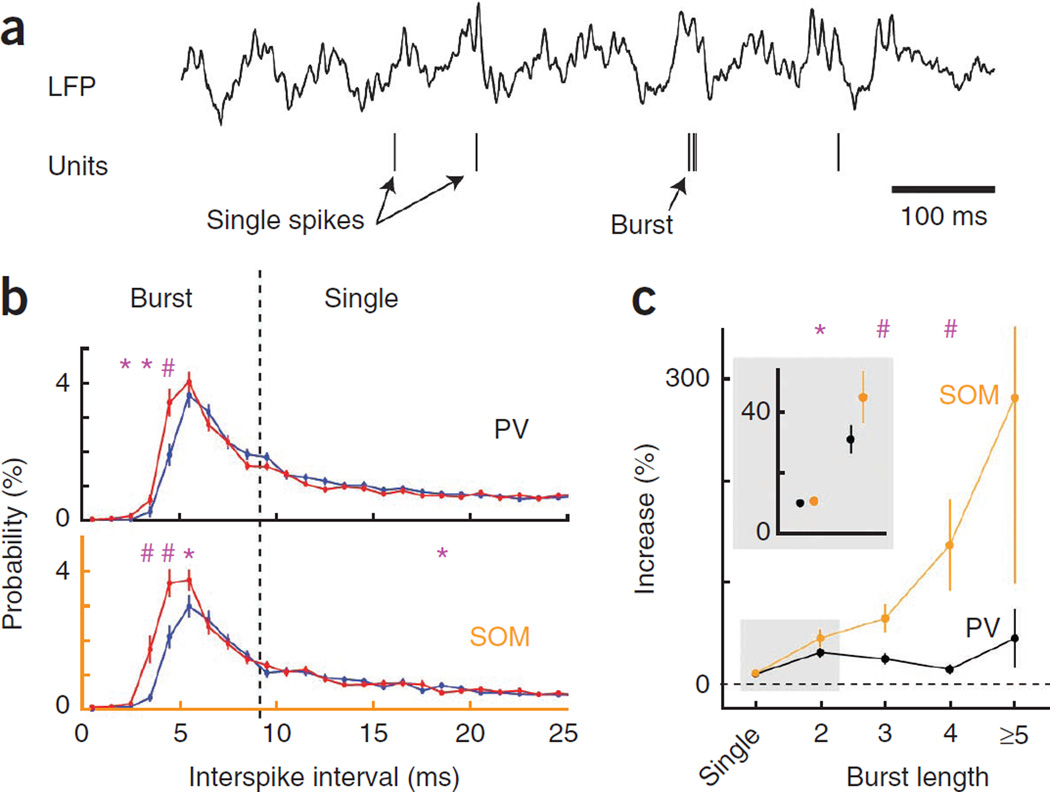
Figure 5.

SOM interneurons control spike bursts in pyramidal cells. (a) LFP and unit activity of one pyramidal cell example, illustrating single spikes and burst discharge. (b) Average (mean ± s.e.m.) probability distribution of interspike intervals of pyramidal neurons. Control (blue) and light (red) histograms include 20,514 and 23,557 spikes for PV-Cre mice (123 cells) and 16,336 and 19,680 spikes for SOM-Cre mice (98 cells) (comparison between control and light, *P < 0.05, ^#P < 0.0005; two-tail paired t test). (c) Relative increase (mean ± s.e.m.) of occurrence for different burst lengths (comparison between PV-Cre and SOM-Cre mice, *P < 0.05, ^#P < 0.0005; unpaired t test).

Silencing SOM interneurons during treadmill running greatly increased the probability of pyramidal cell burst firing, particularly promoting the discharge of longer bursts (percent increase ranging from 45% for spike doublets to 280% for bursts of ≥5 spikes; Fig. 5b,c and Supplementary Fig. 9). In contrast, silencing PV interneurons produced a much more modest effect on spike bursts, except for spike doublets (30% increase). Thus, these results indicate that dendritic inhibition by SOM interneurons, but not somatic inhibition, are critical for controlling spike burst firing during active exploration, extending previous in vitro observations^37,40.

Control of spike theta phase by somatic inhibition

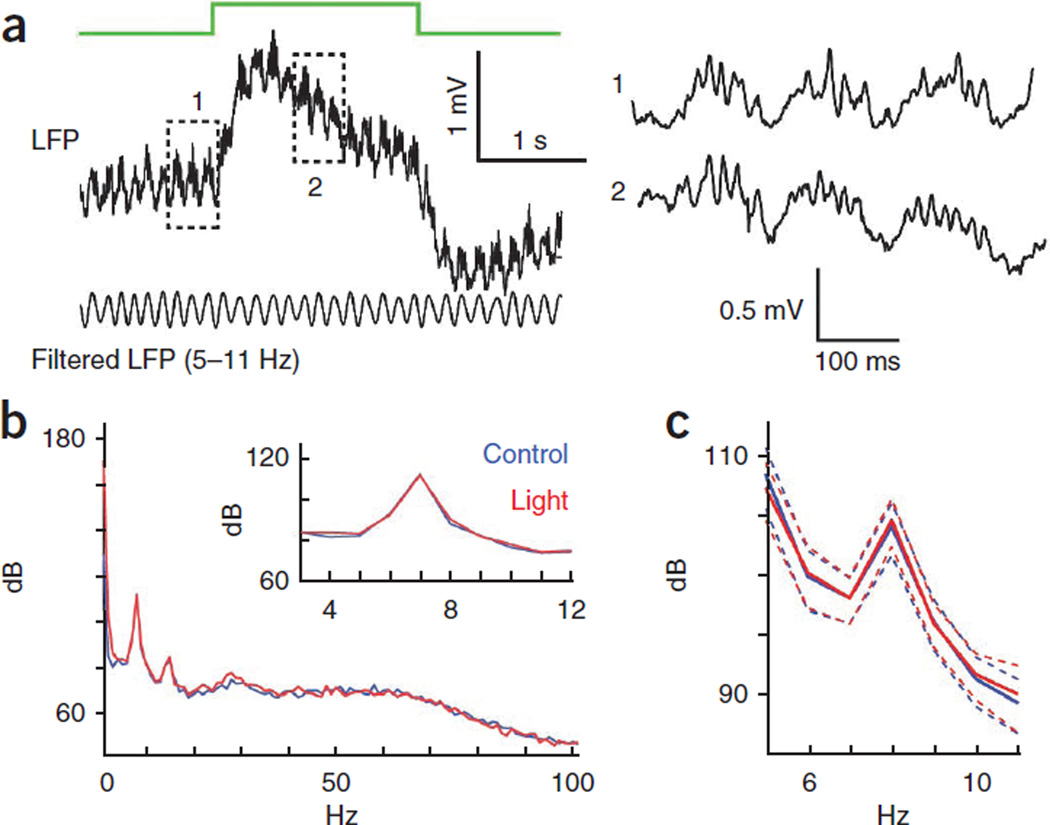
Given that the mean firing rates of place cells were elevated to a similar degree by both perisomatic and dendritic disinhibition, we asked whether these two forms of inhibition have similar effects on place cell spike timing. We first investigated the effects of light stimulation on the LFP. The light stimulation did not affect the LFP theta (5–11 Hz) activity (Fig. 6), which was likely a result of volume conduction of the field from surrounding unaffected areas and/or the focal perturbation of inhibition.

Figure 6.

Theta oscillations are not affected by focal disinhibition. (a) Wide-band LFP segment during light stimulation (green line) and theta band–filtered trace (bottom). Right, three theta cycles during lights off and light on conditions. (b) Power spectra calculated separately for control and light trials of a representative recording session in a PV-Cre mouse. Inset, zoom on theta band. (c) Average power spectra of all sessions from PV-Cre mice. Dash lines indicate standard error (n = 8 sessions, P > 0.05, two-tail paired t test).

Next, we determined the spike-theta phase relationship of single neurons using two complementary measures: the spike phase histogram and the mean theta phase of the spikes⁴². For pyramidal cells, we calculated these measures for each place field bin separately (Fig. 7a). Place cells whose firing rates were increased significantly by light (affected group) and pyramidal neurons that were not affected (unaffected group) were analyzed independently (Fig. 7b). We found no significant effect on spike phase during the silencing of SOM interneurons (P > 0.05). In contrast, we observed a significant phase shift in several bins of the affected group during the silencing of PV interneurons. In these cells, light stimulation heavily altered the spike theta-phase relationship profile as it induced a forward phase shift at the beginning of the field and a backward shift in the center and outbound regions (Fig. 7b and Supplementary Fig. 10). Together, perisomatic disinhibition caused the spikes to be gathered toward the trough of theta, reducing the phase difference between the onset and the peak of the place fields by more than half (from 244° to 107°; Fig. 7c). These data indicate that perisomatic inhibition is far more effective at regulating spike timing than dendritic inhibition, even though their silencing produced the same level of disinhibition.

Figure 7.

Within-theta timing of spikes is regulated by PV interneurons. (a) Left, place field of an example pyramidal cell from a PV-Cre mouse and spike theta phase as a function of belt position during control (blue) and light (red) trials. Right, theta phase histogram of spikes in bin 4 of the place field (control, n = 60 spikes, 18 trials; light, n = 69 spikes, 18 trials). The arrow indicates the direction of phase shift during PV disinhibition. (b) Comparison of rate and theta phase shift of spikes in PV-Cre and SOM-Cre mice, shown separately for rate-affected (upward arrow) and non-affected subgroups (O). Top, subgroup mean firing rates during control and light trials (PV, 78 non-affected cells, 69 rate-affected cells; SOM, 59 non-affected cells, 51 rate-affected cells). Magenta dots indicate significant rate differences in different pixels (P < 0.05, two-tail paired t test). Bottom, subgroup mean phase shifts (±s.e.m.). P values for bins with significant phase shifts are indicated (see Online Methods). (c) Mean theta phases (± s.e.m.) during control and light trials for PV (n = 30), SOM (n = 9), PV-like (n = 12 and 86 in PV-Cre and SOM-Cre mice respectively), non-bursting (n = 23 and 33 in PV-Cre and SOM-Cre mice, respectively) and pyramidal cells (from PV-Cre mice, same cell numbers as in b). Orange shading indicates data from SOM-Cre mice. Pyramidal neurons in PV-Cre mice with no rate change to light (O) and with significant increases (upward arrow) to light are shown separately. Note the late-to-early phase advancement of spikes across the bins of the field and the significant phase shifts in the rate affected group. Right, average theta phase histograms for PV and SOM interneurons and in bins of place field for the rate affected pyramidal cells (control, n = 5,872 spikes; light, 8,276 spikes; see also Supplementary Fig. 9).

DISCUSSION

We found that the rate, timing and burst firing of pyramidal neuron activity are controlled cooperatively by PV interneuron–mediated perisomatic and SOM interneuron–mediated dendritic inhibitory mechanisms. Both types of inhibition influenced the discharge rate inside of, but not outside of, the place fields, indicating that neither somatic nor dendritic (SOM) inhibition is critical for adjusting the spatial scale of place field. In the place field, the strength of somatic and dendritic inhibition evolved in an interleaved manner, with the strongest PV interneuron– and SOM interneuron–mediated inhibitory effects being present at the beginning and end of the place field, respectively. This pattern fits in vitro data reporting a gradual shift of inhibition from somatic to dendritic sites when CA1 pyramidal cells are repetitively activated at theta frequency⁴³, and may be explained by short-term plasticity at the excitatory and/or inhibitory synapses^43,44. The complementary control of PV and SOM inhibition of place cell firing can also account for the in vivo observation that spike phase variability in the decaying part of place field is considerably larger than that in the rising part^16,17.

Dendritic inhibition was most effective at controlling the burst discharge of pyramidal cells, and this effect likely reflects an enhanced ability of dendritic inhibition to regulate dendritic plateau potential generation^36–38. As burst firing is particularly effective at promoting synaptic plasticity and downstream excitation^38,45, this finding suggests that dendritic inhibition is critical for selecting the CA1 inputs to be strengthened and the CA1 outputs to be most effectively transmitted to downstream areas. Thus, dendritic inhibition is potentially an important component of the input comparison type of computation hypothesized to be performed in area CA1 (refs. 38,46).

Notably, suppression of dendritic inhibition did not affect the spike phase preference of pyramidal cell firing even though SOM interneurons showed a strong theta-phase firing preference. On the other hand, local suppression of perisomatic inhibition resulted in firing rate elevations that co-occurred with shifts of spike phase preference. Thus, spike rate and theta phase were either coupled or independently controlled depending on the somatodendritic origin of disinhibition. It therefore appears that perisomatic inhibition possesses a unique ability to regulate spike phase preference and it will be important to determine in the future the exact cellular/network level mechanisms involved. At this point, however, the data are consistent with the following scheme. As PV interneurons provide a theta phase-locked perisomatic inhibition that integrates with depolarizing excitatory input from the dendrites^21,24,26, silencing of perisomatic inhibition increases the level of soma/axonal depolarization near the trough of theta, advancing spike phase at the start of the field and delaying spike phase at later locations. The spike phase precession that remains after PV interneuron silencing could be the result of an incomplete silencing or, more likely, indicates that additional mechanisms are involved. These include phase advance of incoming excitation and/or influence from other types of interneurons^1,24. In this scheme, under normal conditions, dendritic inhibition decreases the amount of excitatory depolarizing current reaching the soma/axon by removing excitation at the site of input and, perhaps more importantly, by limiting regenerative dendritic activity⁴⁰. During dendritic disinhibition, the increase in firing rate is, in part, a result of the conversion of single spikes into bursts of multiple action potentials. However, the timing of the additional spikes is maintained, as the perisomatic inhibition responsible for regulating spike phase is still intact.

Previous work has shown that perisomatic and dendritic inhibitory cells are differentially targeted by subcortical neuromodulators and other extrahippocampal afferents^30,33, and this was suggested to provide flexible substrates for context- and behavioral state–dependent reconfiguration of the hippocampal network during learning⁴⁷. Our results extend this knowledge by demonstrating that dendritic or perisomatic inhibitory circuits differentially regulate hippocampal output modes critical for spatial navigation and memory mechanisms⁴⁸. Given that these features are fundamental elements of cortical networks, it is likely that the distinct mechanisms of rate, burst and phase control described here are also in place in other cortical structures.

ONLINE METHODS

All experiments were conducted in accordance with institutional regulations (Institutional Animal Care and Use Committees of the Howard Hughes Medical Institute, Janelia Farm Research Center and Rutgers University).

Virus preparation and injection

The NpHReGFP fusion protein was cloned into an adeno-associated viral cassette containing the mouse synapsin promoter, a woodchuck post-transcriptional regulatory element (WPRE), SV40 polyadenylation sequence, and two inverted terminal repeats. rAAV-FLEX-rev-NpHReGFP⁴⁹ was assembled using a modified helper-free system (Stratagene) as a serotype 2/7 (rep/cap genes) AAV, and harvested and purified over sequential cesium chloride gradients as previously described⁵⁰.

The virus was injected into the dorsal hippocampal CA1 region of Pvalbcre⁵¹ (PV-Cre) transgenic mice (hybrid C57BL/6-129/SV, 3–5 weeks old, Jackson Laboratory) at three sites: 2.2, 2.4 and 2.7 mm posterior from bregma, and 2.1 mm from midline. We injected 10–20 nl of virus every 150 µm from 1.55 mm to 0.95 mm below pia. The pipette was held at 0.95 mm for 3 min before being completely retracted from the brain. Sst-cre⁴⁰ mice (SOM-Cre, hybrid C57BL/6-129/SV, 4–7 weeks old) were injected at one site 2.0 mm posterior from bregma and 1.6 mm from the midline, with 40–50 nl of virus injected 1.15 and 1.05 mm below the pia.

In vitro electrophysiology

PV-Cre mice were injected with Cre-dependent eNpHR-sfGFP (n = 8) or with Cre-dependent tdTomato AAV (n = 5) into the CA1 region of the dorsal hippocampus. SOM-Cre mice were injected with Cre-dependent eNpHR-sfGFP (n = 6) or crossed with tdTomato Cre reporter mice (B6;129S6-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J from Jackson Laboratory). SOM-Cre × Cre reporter mice (n = 7) were injected with rAAV-FLEX-ChR2-sfGFP. The animals were deeply anaesthetized and decapitated 2–5 weeks after the injection and coronal slices (350–400 µm) from the dorsal part of the hippocampus were prepared. Cells were visualized using epifluorescence microscopes equipped with Dodt gradient contrast or differential interference contrast (DIC) under infrared illumination and a water immersion lens (40× with 0.8 NA). Experiments were performed at physiological temperature (32–35 °C) in artificial cerebrospinal fluid containing 125 mM NaCl, 2.5–3 mM KCl, 25 mM NaHCO₃, 1.25 mM NaH₂PO₄, 1.3–2 mM CaCl₂, 1 mM MgCl₂, 0–1 mM ascorbate, 0–3 mM pyruvate and 20–25 mM glucose, and saturated with 95% O₂ and 5% CO₂. Whole-cell current-clamp recordings from interneurons and pyramidal neurons, located in the injected area, were performed using a patch-clamp amplifier in the active ‘bridge’ mode, filtered at 1–3 kHz and digitized at 50 kHz. Recording electrodes were filled with an internal solution containing either 120 mM potassium gluconate, 6 mM KCl, 10 mM HEPES, 4 mM NaCl, 8 mM Mg₂ATP, 0.6 mM Tris₂GTP, 28 mM phosphocreatine and 0.1 mM Alexa 594, pH = 7.25, or 134 mM potassium gluconate, 6 mM KCl, 10 mM HEPES, 4 mM NaCl, 4 mM Mg₂ATP, 0.3 mM Mg₂GTP, 14 mM phosphocreatine and 0.1 mM Alexa 594, pH = 7.25. Interneurons expressing eNpHR-sfGFP or tdTomato were identified under two-photon microscopy and were subsequently patched under Dodt gradient contrast or DIC. For eNpHR activation, a yellow light (EXFO Excit 120 arc lamp, 582/20 nm excitation band pass filter, 0.5–1 mW at prep) was delivered using full-field epi-fluorescence path of the microscope.

Anatomy

PV-Cre mice were injected unilaterally in the CA1 region of the dorsal hippocampus with Cre-dependent eNpHR-sfGFP AAV. Animals were anesthetized and perfused transcardially with 4% paraformaldehyde in phosphate buffer, 14, 23 and 32 days after viral infection (n = 2 animals in each age group). We cut 60-µm-thick coronal sections using a vibratome. Sections were blocked in 5% normal goat serum (NGS, vol/vol) and 0.1% Triton X-100 (vol/vol). Slices were then incubated for 48 h at 4 °C in 5% NGS, 0.1% Triton X-100 and primary antibody (Rb-α-PV polyclonal, 1:300). After Tris-buffered saline washes, sections were then incubated with Alexa Fluor(r) 633 conjugated donkey antibody to rabbit (1:200). After washes, the sections were mounted and coverslipped on slides in Vectashield mounting medium. Confocal stack images (21–30 slices, 1-µm optical thickness) from the CA1 region of the injected and the contralateral control hippocampi were acquired (20× objective, 0.5 NA). Number of eNpHR-sfGFP and PV-immunopositive cell bodies was counted on stack images. To quantify co-localization, we identified individual NpHR-sfGFP–labeled interneurons and subsequently scored for PV immunoreactivity. To avoid cross-talks between samples, we collected scans from each sample in multiple track mode.

Preparation for in vivo experiment

During a first surgery under isofluorane anesthesia, five male PV-Cre and six SOM-Cre mice were injected with Cre-dependent eNpHR-sfGFP AAV in the dorsal hippocampus (left hemisphere) as described above. To prepare mice for chronic recordings in the treadmill, two small watch-screws were driven into the bone above the cerebellum to serve as reference and ground electrodes. A custom-fabricated platinum head-plate with a window opening above the left hippocampus was cemented to the skull with dental acrylic.

Behavioral training

After a post-surgery recovery period of 7 d, the mice were water restricted to 1 ml d⁻¹ of water and trained for 2 weeks (40-min sessions per day) to run on the treadmill with their head fixed (the head plate clamped to a holder device³²). Sucrose-in-water (10%) rewards were delivered every trial at the same position of the belt via a licking port (Supplementary Movie 1). After behavioral learning reached an asymptote, the animals completed 64 to 124 trials in the first 30 min of the sessions. The quantity of sucrose-in-water drank in the treadmill was measured after each session, and additional water was provided in order that the mice drank a total amount of 1 ml d⁻¹.

Recording procedures

We previously described the preparation of micrometer-scale fibers and construction of silicon optrodes³¹. Recordings were performed 3–6 weeks after the virus injection. On recording days, the mice were initially anesthetized with isofluorane and their heads were fixed in the treadmill. On the first day of recording, the hole used for the virus injection was enlarged and the dura was removed (on subsequent days, the hole was simply cleaned with saline). The optical probe was fixed to a micromanipulator and lowered into the brain. The hole was then sealed with liquid agar (1.5%) applied at near body temperature. Aluminum foil was folded around the entire optical probe assembly, which both served as a Faraday cage and prevented the mice from seeing the light emitted by the optical fibers. After reaching the CA1 pyramidal layer with the probe, mice were allowed to recover completely from the anesthesia. Recording sessions typically lasted for 90 min, during which the animal’s behavior alternated between periods of running and immobility. After each recording session, the probe was removed and the hole was filled with a mixture of bone wax and paraffin oil, and covered with silicon sealant (WPI, Kwik-sil). Each mouse was recorded for a maximum of three sessions (one session per day).

Light stimulation

A DPSS laser (561 nm, 100 mW, Crystalaser) controlled by transistor-transistor logic was used for halorhodopsin activation. To adjust the intensity of the laser, we placed a neutral density filter wheel in front of the beam. An optical probe with four optical fibers was used (Supplementary Fig. 1b), thus, the laser beam was first split with beam splitters (ThorLabs #CM1-BS1) and diverted by reflecting mirrors (ThorLabs #CM1-P01) into four separate fiber ports (ThorLabs #PAF-X-7-A). Long single-mode optical fibers connected the fiber ports to the probe fibers.

Behavior control and data acquisition

The valve for reward delivery, the light beam sensors and the laser control circuit were connected to a computer board (National Instruments #NI PCI-6221) and controlled by custom-made LabView (National Instruments) and Python programs. Neurophysiological signals were acquired continuously at 32.552 kHz on a 128-channel DigiLynx system (Neuralynx). The wideband signals were digitally high-pass filtered (0.8–5 kHz) offline for spike detection or low-pass filtered (0–500 Hz) and down sampled to 1.252 kHz for LFPs. Spike sorting was performed semi-automatically, using KlustaKwik (http://osiris.rutgers.edu/frontmid/indexmid.html), followed by manual adjustment of the clusters⁵². Additional data analysis was done using custom Matlab routines.

Single neuron firing field implementation

The length of the belt was divided into 100 pixels. For each pixel, the number of spikes discharged in the pixel was divided by the time the animal spent in the pixel to generate a vector of firing rates. The firing rate vector was smoothed by convolving it with a Gaussian function (6 pixels (10 cm) half-width).

Significance of changes in firing rate for single neuron

The rate difference (Δf) between control and light trials was calculated for each pixel. The same measure was repeated 1,000 times for different shuffles of control and light trials (Δf_s1:1000). The P value in each pixel was determined from the rank of Δf in the Δf_s1:1000 distribution. For a given pixel, if less than 50 values from Δf_s1:1000 were lower (higher) than Δf, that is, the P value was less than 0.05 (50/1,000), then the firing rate decrease (increase) was deemed significant.

Burst probability and burst index

Bursts were defined as groups of spikes with interspike intervals <9 ms. Threshold values of 6 and 12 ms were also tested. In a first analysis, the number of bursts N_B and single spikes N_S occurring in the stimulated portion of the belt was counted for each cells (control and light trials separately). The burst probability was calculated using the following equation: Burst probability = N_B/(N_B + N_S). The change in burst probability (Supplementary Fig. 9b) was the difference between the burst probability during light and control trials.

In a second analysis, the number of bursts composed of two, three, four and more than four spikes were counted separately. Either the percent change (N_light − N_control)/N_control (Fig. 5c and Supplementary Fig. 9c) or the probability (Supplementary Fig. 9d) of each burst length was measured.

We also defined a burst index that captured the propensity of neurons to discharge in bursts. This measure was used for cell-type identification (see below). The amplitude of the burst was estimated from the spike auto-correlogram (1-ms bin size) by subtracting the mean value between 40 and 50 ms (baseline) from the peak measured between 0 and 10 ms. Positive burst amplitudes were normalized to the peak and negative amplitudes were normalized to the baseline to obtain indexes ranging from −1 to 1.

Binning of place fields

The control trials (no-light condition) were used to determine five bins of the place field. For each place field, we detected the pixel of the beginning, 40% cross-points, 80% cross-points and end (Fig. 3c). The estimation of beginning and end of place fields was not always equivocal as a result of the occasional presence of multiple place fields. To correct for multiple place fields, we first smoothed the firing field vector by averaging over moving windows of size equal to the place field half-width at 66% of peak amplitude. The first local (smoothed) minima on both sides of the place field peak were detected on the smoothed pixels. Next, the real minima were identified on the unsmoothed pixels, in the vicinity of the smoothed minima.

The bins were defined as the intervals between these consecutively detected pixel positions, as shown in Figure 3c. Only bins in the stimulated segment of the belt were used in the analysis. When a bin overlapped partially with the stimulated segment, the bin was truncated to the overlapping fraction only. The same bin positions were used for the light trials.

Local field power spectrum

The LFP epochs during the stimulated segment of the belt were selected, and the power spectrum over 0 to 100 Hz was computed for each trial. Power spectra of control and light trials were averaged separately. The significance of differences between control and light trials was estimated the same way as for the firing fields. The difference (Δpwr) between control and light trials was calculated for each frequency. The same measure was repeated 1,000 times for different shuffles of control and light trials (Δpwr_s1:1000). The P value for each frequency was determined from the rank of Δpwr in the Δpwr_s1:1000 distribution. For a given frequency, if less than 50 values from Δpwr_s1:1000 were lower (higher) than Δpwr, the P value was less than 0.05 (50/1,000) and the power decrease (increase) was deemed significant by the light stimulation.

None of the eight recording sessions in the PV-Cre mice showed significant power difference in the theta band (5–15 Hz), and only one of the nine sessions in SOM-Cre mice showed a significant increase of theta on a few channels. A likely explanation for the lack of difference is volume conduction of theta signal from the surrounded, non-affected, tissue⁵³.

Theta phase of spikes

The LFP was band-pass filtered in the theta range (5–11 Hz). A vector of instantaneous phase was derived using the Hilbert transform. The theta phase of each spike was interpolated from the vector of instantaneous phase.

Theta phase histograms

The theta cycle was divided into 16 equal phase bins. The phase histogram of the spikes was computed for each individual neuron. Each phase histogram was smoothed by convolving a Gaussian function (four bins half width). For the population average in Figure 4c, histograms of each neuron, for both control and light trials, were first normalized to the peak value of the control trials. For pyramidal neurons, the theta phase histograms were computed in each bin of place field. For other cell types, all spikes during the stimulated segment of the belt were used.

Mean theta phase

For the determination of phase precession of spikes¹⁴, we examined the mean phases of place field bins for two reasons. First, light stimulation was delivered only in the middle segment of the belt (57 to 113 cm) where the running speed was most constant. Although spikes of many neurons could have been affected by the light stimulation in this segment, several of them had only part of their place fields represented making difficult the use of standard phase slope methods^{14,16,17,22,23,35}. Second, our preliminary analysis of phase precession showed that despite the reliable rate-position relationship, spike phase-position relationship was much ‘noisier’ in the mouse compared to rat (confirming previous observations by Mayank Mehta, personal communication). The binning method provided clearer phase values compared with the ‘traditional’ display of all spikes (Fig. 1e).

To calculate the mean theta phase of single neurons, each spike was expressed as a unitary vector in polar coordinates with direction its theta phase, and all spike vectors were summed. The mean theta phase of a cell was the angle of the resultant vector sum. In mathematical terms (equation 2.9 from ref. 54),

$$\text{Let }a={\sum }_i\text{cos}{\theta }_i\text{ and}b={\sum }_i\text{sin}\theta$$ (1)

with θ as the theta phase and i as the spike index.

$$\text{If }a\ge 0\text{and}b\ge 0\hspace{1em}\overline{\theta }=\text{arctan}(b/a)$$

$$\text{If }a<0\hspace{1em}\overline{\theta }=\text{arctan}(b/a)+\pi$$ (2)

$$\text{If }a>0\text{and}b<0\hspace{1em}\overline{\theta }=\text{arctan}(b/a)+2\pi$$

where θ̄ is the mean theta phase.

After the calculation of each neuron’s mean theta phase, either the population distribution (Fig. 3b) or the population mean (Fig. 3b and 7c) were computed. The same method as described above was used to compute the population mean, using each neuron’s mean theta phase as unitary vectors. The circular standard errors were calculated (equation 4.21 of ref. 54).

$$\text{Let }d=(1-q)/(2p^2)\text{ where }q={\sum }_i\text{cos}(2({\theta }_i-\overline{\theta }))/n\text{and }P={\sum }_i\text{cos}({\theta }_i-\overline{\theta })/n$$

then the circular standard error (cSE) is

$$\mathrm{c}\mathrm{S}\mathrm{E}=\sqrt{\frac{d}{n}}$$ (3)

To test the significance of theta phase changes caused by the light stimulation, we tested the hypothesis of common means between the control and light trials phases (equations 8.4 and 5.3.4 from ref. 54).

Neuron type identification and characterization

Several parameters were measured to identify and characterize the different neuronal types (Supplementary Figs. 5–8). PV and SOM interneurons could be identified by the robust suppression of their firing rates by the light stimulation (Supplementary Fig. 5a,c). The physiological characteristics that were found to most effectively differentiate PV interneurons from other cell types were the cell’s refractory period and bursting property (Supplementary Fig. 5b,d). Three relatively distinct clusters were tentatively assigned to pyramidal cells, PV interneurons and non-busting neurons (Supplementary Fig. 5d). The PV interneuron group included the light-suppressed PV interneurons and other unaffected cells (PV like), including presumably PV interneurons that were not infected by the AAV virus. The separation of these three groups was further supported by information obtained from monosynaptic interactions between neuron pairs⁵⁵. Neuron pairs with cross-correlograms showing sharp and significantly large bins in monosynaptic latency (<3 ms) were identified⁵⁶. Reference (putative presynaptic) neurons were designated as excitatory and the referred (postsynaptic) neuron was designated as excited⁵³ (Supplementary Fig. 6a). Projecting these identified excitatory and excited neurons onto the three clusters placed the majority of excitatory neurons in the pyramidal cell cluster and the excited neurons in the PV neuron cluster (Supplementary Fig. 6b). Combinations of other features, such as spike duration, spike asymmetry⁵⁷ (Supplementary Fig. 7a,c), mean firing rate and spatial coverage (Supplementary Fig. 7b,d) showed consistent differences between groups, but with less clear distinction.

Refractory period

We measured each neurons refractory period on the spike autocorrelogram implemented with 1-ms bin. First, the instantaneous derivative from 0 ms to the time of the peak of the auto-correlogram was computed and the s.d. of the derivative values was estimated. The refractory period was defined as the first time bin for which the instantaneous derivative exceeded one s.d.

Mean firing rate

The mean firing rate of individual neurons was calculated in consecutive 60-s bins across the recording session. The mean firing rates reported in Supplementary Figure 7d are from the bins with the highest mean rate.

Spatial coverage

We defined a spatial coverage index that captured the profile of firing activity across the belt. The position pixels were sorted in decreasing magnitude order and the cumulative sum was computed across the pixels. To obtain the spatial coverage index, the number of pixels for the cumulative sum to reach 75% of the sum of all pixels was divided by 75 (75% of the total number of pixels). Index values close to 1 indicated that the neurons firing activities were uniform along the belt, whereas values closer to 0 indicated firing activity concentrated in a small portion of the belt, that is, in place fields.