Multi-site Study of Diffusion Metric Variability: Characterizing the Effects of Site, Vendor, Field Strength, and Echo Time using the Histogram Distance

Abstract

MRI-based multi-site trials now routinely include some form of diffusion-weighted imaging (DWI) in their protocol. These studies can include data originating from scanners built by different vendors, each with their own set of unique protocol restrictions, including restrictions on the number of available gradient directions, whether an externally-generated list of gradient directions can be used, and restrictions on the echo time (TE). One challenge of multi-site studies is to create a common imaging protocol that will result in a reliable and accurate set of diffusion metrics. The present study describes the effect of site, scanner vendor, field strength, and TE on two common metrics: the first moment of the diffusion tensor field (mean diffusivity, MD), and the fractional anisotropy (FA). We have shown in earlier work that ROI metrics and the mean of MD and FA histograms are not sufficiently sensitive for use in site characterization. Here we use the distance between whole brain histograms of FA and MD to investigate within- and between-site effects. We concluded that the variability of DTI metrics due to site, vendor, field strength, and echo time could influence the results in multi-center trials and that histogram distance is sensitive metrics for each of these variables.

1. INTRODUCTION

One common step in the beginning of a multi-site imaging study is “site qualification” in which a site scans one or more subjects using a protocol harmonized across site. The data is then processed and compared to that from other sites in some manner to determine whether the site's scans are within acceptable limits as determined either by a gold standard set of scans or by normative data provided by the scans from the other sites in the study. What is then needed is a method to determine whether a set of scans are acceptable or not. This is especially critical for imaging types in which quantitative metrics are used for analysis, e.g. diffusion-weighted imaging (DWI). In addition, it would be useful if such a method could be used to understand whether differences in factors such as site, vendor, field strength, and echo time result in unacceptable data variability. We propose here the idea of distance between histograms as a method sensitive enough to show changes in the above factors and one that is relatively easy to implement. In this work, we explore the sensitivity of different distance metrics from a variety of metric families and apply them to data from healthy control subjects.

Histogram analyses has been performed on derived data maps in MRI-based diffusion experiments. However, even when histograms have been created from whole-organ imaging data, only the histogram mean and possibly the peak height were measured. Changes in those quantities were sometimes measured after intervention or treatment. We list several examples that span the range of common analyses. Kang et al.¹, used differences in ADC histogram percentile values of tumor volume data to attempt to determine glioma grade and to evaluate the diagnostic performance of ADC maps at two different b-values. Pope et al.^2,3 has fit the ADC histogram post-treatment to a bimodal distribution and analyzed the mean ADC for each component. Nusbaum et al.⁴ created ADC whole-brain histograms of different types of MS patients and noted the increase in mean ADC_av of controls and different categories of patients using shifts in peak location and peak height. Rovaris et al.⁵ looked at normal-aging subjects and created whole brain histograms of ADC and FA and analyzed both the mean value and peak height versus age. Several studies have gone beyond ‘peak-position’ analysis of histogram data. For example, Yankeelov et al.⁶, in a study that created dynamic contrast enhancement and ADC maps in a study of breast cancer, created ADC histograms and looked for statistically significant changes in individual bin frequency between pre- and post-treatment histograms. Finally, Tozer et al.⁷ used principal-component (PC) and linear-discriminant (LD) analysis on T1 and ADC histograms from multiple sclerosis patients and compared PC- and LD-derived metrics to the standard peak height and location metrics.

In this study, we hypothesized that since histograms of common DWI metrics were non-Gaussian, analysis of the mean/median/peak height were not as sensitive to subtle shifts in the histogram brought about either by tissues structural changes or by differences in site- and protocol-related factors such as the ones mentioned above. We therefore collected DTI data at five sites representing three vendors and calculated the histogram distance between these data sets based on several families of distance metrics to see if any were sensitive enough to reflect differences that arose from site, scanner vendor, field strength and TE values. We also investigated the variability of data when the number of diffusion-sensitizing gradient directions was varied. The goals of this study were:

• 1)to establish the variability of FA and MD histograms and to determine whether they depend upon vendor, site, field strength or TE.
• 2)to establish a ‘calibration’ method for DTI, based on histogram distance metrics, that can be used in longitudinal studies that include hardware and software upgrades. The data acquired through this method could identify scanner issues brought on by the upgrades or simply by hardware failure. A wide range of metrics are investigated to determine whether there is a characterization advantage between single- or multi-bin metrics and whether the computational cost of more complex metrics results in greater sensitivity.

2. METHODS

2.1 Subjects

Five normal, locally-recruited subjects were scanned at each site. Number of female subjects and age range for each site were: Massachusetts General Hospital (3 female, 24 yr ± 3), UC-Irvine (3 female, 32 ± 8 yr), Duke (1 female, 39 ± 9 yr), and Johns Hopkins School of Medicine (5 females, 36 ± 10 yr), and UT Southwestern Medical Center, Dallas (3 female, 32 ± 5). The studies were approved by the local Institutional Review Board of each site.

2.2 Imaging

All scanners had field strengths of 3.0T, except for a single Philips 1.5T scanner. Three scanner vendors were represented: Siemens (2 sites – Massachusetts General Hospital, UC-Irvine), GE (1 site - Duke), and Philips (2 sites – Johns Hopkins School of Medicine, UT Southwestern Medical Center, Dallas, 1.5T).

Ten diffusion-weighted imaging (DWI) scans were performed on each subject during a scan session. Each scan consisted of 30 isotropic diffusion-weighted directions (DWD) and 5 b=0 scans. The Jones30⁸ set of diffusion-weighted directions was chosen because each vendor uses different sets of gradient directions. Each 30 b>0 / 5 b=0 set was defined to be one “scan-time unit” (STU) (Landman et al.⁹ call this grouping a “scan time equivalent (STE)”); we choose a different nomenclature to emphasize the use of 1 STU as the unit of data used to calculate the tensor metrics). The pulse sequence used was a spin-echo Stejskal-Tanner sequence with echo-planar readout. No compensation for the eddy currents generated by the diffusion gradients was provided by the sequence because not all sites had access to a doubly-refocused DWI pulse sequence. The sequences chosen were the standard vendor supplied sequences. Other protocol parameters include: b-value of 1000 s/mm², 2.5 mm³ isotropic voxels, acquisition matrix size: 96 × 96, full k-space coverage, FOV: 240 × 240 mm, slice thickness: 2.5 mm, number of slices: 25, parallel imaging: SENSE (p = 2) for Philips, GRAPPA for Siemens and ASSET for GE, 1 signal average for each volume. TR/TE (ms) values were: Siemens = 4000/98 (MGH), 3800/98 (UCI); GE = 5200/69.8 and 4000/99.5 (Duke); Philips = 4000/101.2 (Dallas), 4000/100.0 (JHU). The achievable TR/TE is dictated by the achievable duty cycle of the scanner and the maximum gradient strength; the variations seen here were not expected to affect the results. Each scan was roughly 2.5 min (except for the short TE sequence on the GE scanner) so the entire protocol could be completed easily in less than a half an hour.

2.3 Tensor Calculation

In this study, data sets with different numbers of STU were achieved by concatenating a sequentially increasing number of data sets before processing, i.e., data set 1 (STU=1), data set 1 and 2 (STU=2), et cetera. Each frame within the concatenated data set was registered to the first b=0 frame using a 12 degree-of-freedom registration code (FLIRT, FSL, University of Oxford). Tensors and the tensor metrics FA and MD were calculated using in-house code written in C. Noise and skull voxels were removed from the image before metric processing using a combination of Brain Extraction Tool (FSL, University of Oxford) and in-house code written in IDL (ITT-VIS, Boulder, CO, USA).

In addition, subsampling of the number of gradient directions within each data set was performed to investigate its effect on the resulting FA and MD maps. Subsampling of the gradient directions was performed by in-house code written in Matlab (Mathworks, Natick, MA, USA) using the Jones30 data as the set from which to select the smaller number of samples. Samples were made of 15, 10, and 6 directions by choosing the directions in the Jones30 set that most closely corresponded with separations that would be obtained using an electrostatic model. The same Matlab code created the whole brain histograms.

3. DATA ANALYSIS

3.1 Contrasts

The data from the three different vendors (Siemens, GE, and Philips), two field strengths (Philips 1.5T and 3.0T), and two different echo times (TE = 69.8 ms and 99.5 ms, for the GE site both at 3.0T) comparisons could be made that measured the effect of site, vendor (at the same field strength and TE, different sites), field strengths (same vendor and TE, different sites), and TE (same vendor, site, and field strength). The full set of 11 contrasts are listed in Table 1.

Table 1.

Table of contrasts designed into this study. The contrasts are site, vendor, field strength and echo time (TE). “GEL” and GES” stand for the long and short TE values, resp ectively, acquired from the GE scanner. Sites are labeled by number or field strength if applicable, e.g., “SM1” refers to the first Siemens site and “PH3.0” refers to the Philips 3.0T scanner.

Site(s)	Vendor(s)	Field Strength (T)	TE (ms)	Comparison
SM1/ SM2	Siemens	3.0	98	site
PH3.0 / PH1.5	Philips	3.0 / 1.5	100.0 / 101.2	site, field strength
GES / GEL	GE	3.0	69.8 / 99.5	TE
SM1 / GEL SM2 / GEL	Siemens / GE	3.0	98 /99.5	site, vendor
PH3.0 / GEL	Philips / GE	3.0	99.5	site, vendor
SM1 / PH3.0 SM2 / PH3.0	Siemens / Philips	3.0	98 / 100.0	site, vendor
GES/ PH3.0	Philips / GE	3.0	69.8 / 101.2	site, vendor, TE
GES/ SM1 GES/ PH3.0	Siemens / GE	3.0	69.8 / 98 69.8 / 100.0	site, vendor, TE
SM1 / PH1.5 SM2 / PH1.5	Siemens / Philips	3.0 / 1.5	98 / 101.2 98 / 101.2	site, vendor, field strength
GES/ PH1.5	Philips / GE	3.0 / 1.5	69.8 / 101.2 ms	site, vendor, field strength
GEL/ PH1.5	Philips / GE	3.0 / 1.5	99.5 /101.2	site, vendor, field strength

3.2 Experimental Histogram Distance Analysis

Whole-brain histograms of brain FA/MD voxel values were calculated using 0.01 / 0.00005 mm²/s-wide bins over the ranges [0.0+, 1.0] / [0.0+, 0.004 mm²/s]. In the ranges, ‘+’ denotes that histograms did not include those voxels with a value of zero, i.e., the background. Analysis was performed on histograms normalized by the total number of voxels in the brain mask.

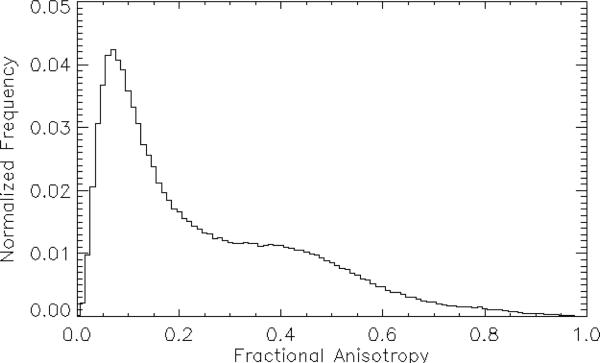
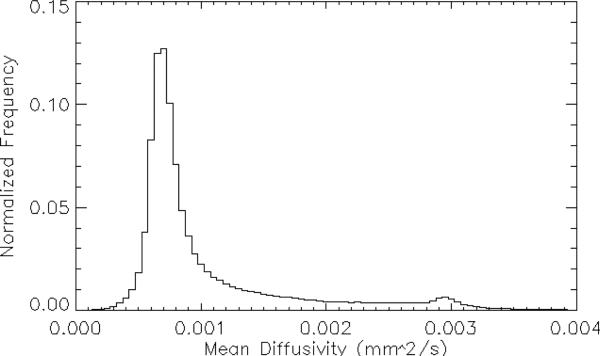
Representative normalized FA and MD histogram is shown in Figs. 1 and 2 respectively. Note that neither distribution is normal, thus defying easy characterization by the simple parameterizations of mean, median, and standard deviation. In fact, the shapes of these histograms are much closer to log-normal distributions, i.e., a distribution in which the natural logarithm of the parameter values is distributed normally. Given this, direct modeling of these distributions with an eye towards distribution fitting and using the resulting model parameters as indicators of histogram (dis)similarity seems prohibitively complicated. We therefore seek to use the entire histogram as a “parameter” and look for differences in this parameter to compare the variability between sites and conditions. Since different histogram distance metrics are more or less sensitive to histogram shape, extent, offset et cetera, we therefore investigate different families of distances, looking for metrics that are able to reflect differences between MD and FA maps arising from the variables investigated here. We proceed as follows: we use the Jones30 histograms as the ‘gold standard’ and directly calculate a set of histogram distance metrics for the subsamples⁹ (PE15, PE10, PE6) between the: 1) data sets for each site-specific subject, 2) Jones30 sets from subjects at the same site, and 3) Jones30 sets for the relevant contrasts in Table 1. In this way we can probe both intra-subject and inter-subject contrasts, as well as the contrasts mentioned above.

Figure 1.

Representative histogram of the distribution of fractional anisotropy (FA) values from the entire brain. Note that the distribution is non-Gaussian.

Figure 2.

Representative histogram of the distribution of mean diffusivity (MD) values from the entire brain. Note that the distribution is non-Gaussian.

3.3 Simulations to Determine Critical Values

While histogram distance metrics can easily be calculated within subject, between subjects, and between sites, there is no analytical way to determine the statistical significance for the resulting distance values. Lampariello¹⁰, with access to ‘gold standard’ control samples, was able to use a histogram similarity metric to set bounds on its variability within the control samples and this information was then applied to non-control samples. In human brain DWI there are no easily obtainable ‘gold standards’ or phantoms that can be used in this fashion. Therefore, we adopt the tack suggested by the work of Bernas et al.¹¹, namely to use to Monte-Carlo methods to generate a set of histograms based on samples drawn from random subpopulations of a predetermined shape. Distance metrics can then be calculated from sequential pairs of these histograms. The results of these comparisons will be a set of distance values that themselves form a distribution. From these metric distributions one can determine cutoff values for each metric for chosen percentiles (e.g., 95%). The significance of experimentally-determined distance metric values can then be determined using the calculated cutoff values. This method was employed using both log-normal and normal distributions of varying widths and number of elements. The reason for using both distributions was to determine how much the cutoff values depended upon the exact shape of the chosen distribution. If it was found that both gave similar cutoff values, then we can be reasonably confident in applying the d_c values to our experimentally measured histograms. In this process, the width of the distributions as well as the number of elements were varied to create families of d_c curves of either constant variance while the number of elements was varied or vice versa. These families of curves could them be used to determine the correct d_c for a given data set or to explore the range of cutoff value variation as discussed below.

A Monte Carlo algorithm, written in IDL, was used to calculate the randomly-populated histograms. The normal distribution was generated using

$$Y_N(\mu ,\sigma ,i)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{{(1-\mu )}^2}{2{\sigma }^2}}$$ (1)

and then normalized by dividing the number of elements in each bin by the total number of elements. Here μ is the distribution mean, σ is the standard deviation, and i is the index of the histogram bin. The log-normal distribution was generated using the Metropolis-Hastings¹² algorithm and implemented using in-house code written in IDL according to

$$Y_{LN}(\mu ,\sigma ,i)=\frac{1}{i\sigma \sqrt{2\pi }}{e}^{\frac{{(\ln \left(i\right)-\mu )}^2}{2{\sigma }^2}}$$ (2)

A random seed value was set and samples from the required distribution were generated. A single random seed was used to generate the random samples from the normal distribution and was continued for all of the histogram elements. The IDL random number generator is that of Park et al.¹³ with the addition of a Bays-Durham shuffle to remove low-order serial correlations.

In order to determine cutoff values for experimental histograms, simulations were undertaken using both distributions of varying standard deviations. Curves of metric cutoff values versus histogram variance were determined by first generating 351 histograms. Calculating the distance of each to all of the others resulted in a total of 61245 histogram distances for each metric. Using the resulting distribution of these distance metric values, the 95th percentile value was determined for each metric and used as a cutoff value, d_c. This process was repeated for 18 normal distribution variance values and 12 values evenly spaced in the log for the log-normal distribution. In addition, 9 different number of histogram elements, N, in the range [10,000, 90,000] were calculated. This gives a family of curves of d_c versus N, with each curve having a specific distribution variance. In this way, one can determine the appropriate variance for a given experiment and read off of the curve the applicable d_c value that can then be used to determine the statistical significance of the calculated histogram distance for the experimental data. Threshold values used in this analysis were determined by estimating the variance of the empirical FA and MD distributions and interpolating the threshold value from the set of values found from the simulations. Since the experimental distributions are strictly neither normal nor log-normal, the threshold values used here must be considered estimates, but we have found that the thresholds are fairly insensitive to the exact variance chosen in the range of variances encountered here and the changes are also smooth (no discontinuous jumps). Therefore, while the thresholds used in this paper are not calculated for the exact or average variance of the measured histograms they are generally correct and useful.

3.4 Histogram Distance Selection

In the field of pattern recognition many distance metrics have been proposed to measure the distance between histograms¹⁴. We investigate the efficacy of metrics from seven different families of distance measures. The families chosen here represent the two broad categories of histogram distance metrics: those that treat histograms as vectors and those that treat them as probability distribution functions (PDF). The families chosen were 1) Minkowski, 2) Fidelity, 3) Intersection, 4) Inner Product, 5) Squared L2 Norm, 6) Shannon Entropy, and 7) Earth Movers. Given that there is no a priori reason to help guide the appropriateness of metrics to this application, we chose one or more examples from each family and then evaluated their performance when applied to our data. We chose a single metric from each family to use in the final analysis, eliminating those family members that were less sensitive to small changes or were as sensitive, but possessed greater computational complexity. We assume in what follows that all histograms have been normalized to the total number of binned values. The rationale for investigating metrics other than those in the simplest Minkowski family is that other families address the insensitivity of the Minkowski metrics to small shifts between histograms. For example, if two histograms are identical, but are slightly shifted in bin number, the Minkowski metrics tend to overestimate the distance between histograms. The final set of metrics used was: Minkowski family - City Block; Fidelity family – Hellinger; Intersection family - Non-Intersection; Inner Product family – Cosine; Squared L2 norm family - Squared chi-squared; Shannon's Entropy family – Jeffreys; and Earth-Movers Family - Cha-Srihari.

4. RESULTS

4.1 Simulation of Histogram 95% Cutoff Values

Simulations were run as described above to determine the behavior of the 95% cutoff value for each metric as the distribution parameters were changed. Fig. 3 show a sample plot of the curves generated for each metric in the simulation step. Each curve represents the data for different distribution standard deviation at a given number of histogram elements ranging from 10,000 to 90,000. It can be seen that the cutoff value reaches an asymptote as the number of elements increases and also as the width of the distribution increases.

Figure 3.

Plot of the 95% cutoff values obtained by performing histogram comparisons between simulated histograms with a range of variance values and number of histogram elements. The results shown here are for the Hellinger metric and the log-normal distribution. Each set of points are for a given number of histogram elements and the labeling number in the legend is given in units of thousands of elements.

In order to ensure that multiple types of distance metrics were explored in detail as well as to reduce the number of metrics to be evaluated, we chose one metric to represent each metric family. The heuristic for the selection of the representative metric was subjective; namely we looked at the variance and range of metric values for all possible comparisons within the same site under the assumption that increased variance implies sensitivity (given that each metric value was determined from the same set of data). In addition we also eliminated all but one of the metrics that gave equivalent results within a family.

4.2 Selection of a Histogram Distance Measure From Each Family

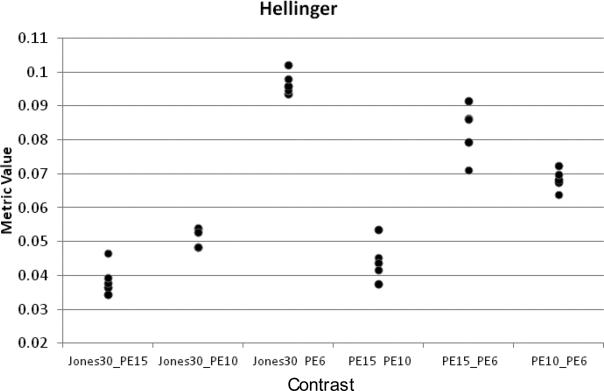
This process also allowed for the investigation of differences due to the number of gradient directions used in the calculations. Fig. 4 shows example decision data for the Hellinger metric using STU=10 FA data from the Siemens1 site for all of the combinations for a single site for the full Jones30, PE15, PE10, and PE6 gradient subsamplings. There are five points for each comparison, one for each subject. Note that the metric distances increase as the comparisons are calculated between data sets with smaller numbers of gradient directions. Also, the metric value is higher for any contrast that involves PE6, the subsampling with the least amount of data. This was true for all metrics and for the MD data as well, and shows that the histogram distance is sensitive to the number of gradient directions

Figure 4.

Plot of histogram distance for the Hellinger distance metric using the STU = 10 FA histograms on data from the SM1 site. All possible contrasts are made between the full dataset (Jones30) and each of the subsamplings, as well as between each of the subsamplings. The horizontal axis is the contrast between different gradient subsamplings and the vertical axis is the computed distance metric value. Each point represents a subject at that site (N=5). Similar plots were generated for each distance metric and site. The metrics chosen for use in the final analysis were determined from these plots on the basis of their ability to show the greatest differentiation between subjects.

4.3 Within-Site Analysis

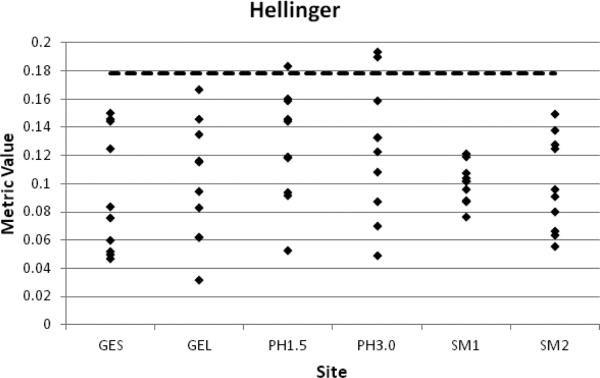
We present in Fig. 5, a representative plot of the within-site FA distance metric values using the Hellinger metric and the STU=10 data. Each of data set from each subject is compared to the remaining others for a total of 10 distances. The plots in this figure are for the full Jones30 set of gradient orientations. It is important to remember that the distance metrics are calculated from the same data set at each site, so any differences are due to the metrics themselves. We note that the difference between the data for STU=1 and STU=10 manifests itself for the most part in the range of the values and generally larger ranges are found in the STU=10. The dashed line in Fig. 9 is the 95% threshold determined from simulations described earlier.

Figure 5.

Plots of within-site, Jones30, STU=10 FA histogram distance metric values for the Hellinger metric as a representative example. Each data point represents the metric value obtained by performing the histogram comparison between each of the five subjects for a total of 10 points per site. The sites are labeled as: GE site with shorter TE value = GES, GE site with longer TE value = GEL, Philips site with 1.5T scanner = PH1.5, Philips site with 3.0T scanner = PH3.0, Siemens site 1 = SM1, Siemens site 2 = SM2. The dashed line represents the 95% cutoff value obtained from the simulations using the log-normal distribution.

Generally the metric values for each site are below the threshold for each of the metrics studied, except for the Cosine metric, which is opposite and significant differences are below the 95% line. The two sites with the largest spread in the data, for all metrics, are the two Philips sites, PH1.5 and PH3.0, though either of the GE TE data sets has equivalent variance depending upon the metric. The sites with the smallest variances were SM1 and SM2. The Hellinger, Jeffreys and the Squared Chi-squared metrics give roughly the same information; each has the same pattern of variance at each site and has the same three comparisons that fall above the threshold. In addition, the City Block and Non-intersection also give the same information. The Cha-Srihari and Cosine metrics, on the other hand, have patterns and variances that are not replicated by any other metric. These similarities and differences are generally true regardless of whether FA or MD is under consideration since they arise from the definitions of the metrics.

In summary, by a wide range of metrics, the histogram comparisons for FA within each site have low variance and this assessment is not particularly sensitive to the exact placement of the 95% threshold value. Therefore, the FA can generally be considered as reproducible within each site.

In the MD case (data not shown), there are many more metric values above the threshold for each site, and only the PH3.0 site has metric values that are all below the threshold. In addition, the ranges of the metric values for MD are on the order of twice that for FA. The sites with the largest spread in the data, for all metrics, are GES, GEL and SM2, though the PH1.5 data set has equivalent variance depending upon the metric. The sites with the smallest variances were PH3.0 and SM1.

In summary, by a wide range of metrics, the MD histogram comparisons within each site have higher variance than did FA and again, this assessment is not particularly sensitive to the exact placement of the 95% threshold value. Therefore, the MD can generally not be considered as reproducible as FA within each site. We have determined that the source of the largest variance is the amount of CSF present in the MD maps after brain extraction.

4.4 Between-Site Analysis

Again, we show here in Fig. 6 results from a single metric for the between-site FA data and look at the results of the comparisons listed in Table 1. We note that the metric values for identical scanners (SM1, SM2), are under the threshold value for all of the metrics and show the smallest variance of all the comparisons. This demonstrates that, there is no significant difference in the resulting FA histograms due to site alone. The comparisons between GES and all of the other sites and conditions have the majority of their metric values above the 95% threshold which indicates that this method is sensitive to differences due to differences in TE. Third, comparisons between FA histograms from sites that differ in field strength, but not vendor, show that roughly half of the contrasts are above the significance threshold, indicating that there is some significant effect of field strength, but the effect is less than that for TE. Interestingly, vendor contrasts shows a similar effect magnitude as field strength, though FA histograms from GE scanners (at the same TE value) are more similar to Siemens than they are to Philips. Finally, a Philips 1.5T scanner produces FA histograms with no significant differences to Siemens and GE at 3.0T. Overall, it was found that the City Block, Cosine and Hellinger metrics led to the same conclusions. The Cha-Srihari metric however, shows the same relative behavior as the other three, but the calculated threshold value is higher thereby implying few significant differences for most comparisons. It should also be noted that with a lower threshold the same general results as noted above would result.

Figure 6.

Representative plot of between-site FA histogram distance metric values for the Hellinger metrics and for the highest (STU=10) STU value and full Jones30 set of gradient orientations. Each data point represents the metric value obtained by performing the histogram comparison between each of the subjects at both sites for a total of 25 points per site.

The between-site data for MD (not shown) show the same patterns as do the FA metric values; the TE has a large effect and inter- and intra-vendor differences produce small variances in metric values, however, the calculated threshold level is too low to give the same significant results. One difference is that the difference in field strength does not create as large of a spread in the distances. Again, we trace the overall increase in metric values and variance to the inclusion of the CSF voxels.

5. CONCLUSIONS

The histogram distance method has the advantage that it produces a single value that can be compared within and between sites, a value that condenses information from the entire FA or MD histogram. However, the individual distance methods can reflect changes in the shape of the histograms, which can be important experimentally for pathologies in which there are shifts in the diffusion metric values in portions of the tissues but not others. Simulations were used to determine a statistical significance threshold and it was found that in-silico thresholds performed well for FA, but not as well for MD in which the variability of CSF-containing voxels resulted in a bias. Experimentally determined thresholds from normative data sets could be used to eliminate this issue, as could modifying the acquisition b-values to reduce the signal from CSF. The Hellinger, Jeffreys, and Squared Chi Squared metrics were found to perform the best with DWI data.