Abstract
The accuracy of electron backscatter diffraction (EBSD) and confocal Raman microscopy (CRM) for small-scale strain mapping are assessed using the multi-axial strain field surrounding a wedge indentation in Si as a test vehicle. The strain field is modeled using finite element analysis (FEA) that is adapted to the near-indentation surface profile measured by atomic force microscopy (AFM). The assessment consists of (1) direct experimental comparisons of strain and deformation and (2) comparisons in which the modeled strain field is used as an intermediate step. Direct experimental methods (1) consist of comparisons of surface elevation and gradient measured by AFM and EBSD and of Raman shifts measured and predicted by CRM and EBSD, respectively. Comparisons that utilize the combined FEA-AFM model (2) consist of predictions of distortion, strain, and rotation for comparison with EBSD measurements and predictions of Raman shift for comparison with CRM measurements. For both EBSD and CRM, convolution of measurements in depth-varying strain fields is considered. The interconnected comparisons suggest that EBSD was able to provide an accurate assessment of the wedge indentation deformation field to within the precision of the measurements, approximately 2 × 10−4 in strain. CRM was similarly precise, but was limited in accuracy to several times this value.
Keywords: EBSD, AFM, Confocal Raman Microscopy, FEA, Indentation, Strain
1. Introduction
1.1. Technical Motivation
Many advanced technologies depend on control of deformation or strain at micro- or nano-scales in order to enhance device performance. For example, strain engineering of conducting channels in semiconducting structures increases the mobility of carriers via piezoresistive effects, thereby improving the performance of microelectronic devices [1]. Strain engineering of bandgaps in optical materials determines photon absorption and emission wavelengths, thereby controlling the performance of optoelectronic devices [2]. Strain engineering of membranes and other components in microelectromechanical systems (MEMS) determines device sensitivities to pressure or electric fields, thereby affecting the ability of MEMS devices to perform as sensors or actuators [3]. Conversely, lack of strain control can lead to thermomechanically-induced or direct mechanical failure, particularly in cases in which disparate materials are brought into contact, for example in microelectronic devices [4, 5], or in which the deformations can be large, for example in MEMS devices [6].
In all cases, strain control depends on the ability to measure and map strain at the micro- or nano-scales—that is, perform quantitative strain microscopy at very small length scales. Two techniques have emerged over the past few decades capable of strain microscopy in small-scale structures formed from silicon (Si), a material pervasive in the technologies highlighted above: high resolution electron backscatter diffraction (EBSD) [7–10] and confocal Raman microscopy (CRM) [11–16]. These techniques are complementary, and both offer fine spatial resolution and great strain sensitivity. EBSD is a high-vacuum scanning electron microscope (SEM)-based technique that determines strain by cross-correlation of high resolution electron backscatter diffraction patterns (EBSPs) formed from elastically backscattered electrons. Lateral spatial resolutions of approximately 50 nm and strain resolutions of less than 10−4 are possible and experimental scan rates of about one pixel/s are common [8–10]. CRM is an ambient atmosphere Raman spectroscopy-based technique that determines strain by measuring shifts in the frequency of photons inelastically scattered by lattice phonons. Meaningful pixel spacing of approximately 70 nm and strain resolutions of 10−4 are possible and experimental scan rates are also about one pixel/s [15–19]. In both cases, the strain maps are internally calibrated relative to a reference location of known strain, usually taken to be strain free. A key requirement for advancing these microscopy techniques for strain mapping of small-scale structures is that specifications be provided for method accuracy (how closely strain values estimate the true values) and precision (how closely repeated measurements distribute about the mean strain value). Such specifications will enable comparison of measurements performed using different techniques, comparison of experimental measurements and modeling results, and predictions of device performance.
Assessments of the accuracy and precision of strain measurements performed by EBSD and CRM have been made by comparing measurements from both techniques on the same structure and by comparison with measurements or predictions from additional methods: Strain variation around a wedge indentation in a Si surface was measured by EBSD and CRM and the agreement between the two techniques shown to be very good [17], especially when the CRM excitation wavelength was small, leading to surface-localized CRM measurements, similar to those of EBSD. Surface deformation around a similar wedge indentation was measured using atomic force microscopy (AFM) and compared with the deformation inferred from EBSD and predicted by a simple indentation model; the two measurements and model were in good agreement [18]. (In some earlier studies, AFM topography measurements were correlated with CRM measurements adjacent to surface scratches and Vickers indentations in Si, but in a qualitative manner [20, 21].) CRM shifts adjacent to an imbedded tungsten (W) structure in Si were compared with shifts predicted from an opto-mechanical extension of finite element analysis (FEA) of the strain field arising from the W deposition process and thermal expansion mismatch with the Si; the measurements were in very good agreement with the predictions [19]. In a recent detailed study [22], EBSD strain measurements of silicon-germanium (SiGe) thin-film structures heteroepitaxially deposited on a Si substrate were performed. The measurements were compared with predictions from independent composition and X-ray diffraction measurements of the strain arising from the SiGe and Si lattice mismatch. For films that were coherent with the Si substrate, the EBSD strain measurements were in agreement with the predictions to within 2 × 10−4, similar to earlier studies [7, 8, 10].
Here we extend the above comparisons, applying all four of EBSD, CRM, AFM, and FEA to a single test vehicle, a wedge indentation in a Si surface similar to those considered previously [17, 18], Fig. 1(a). Application of all four techniques further refines assessments of the accuracy and precision of EBSD and CRM strain microscopy. In addition, many other extensions to the previous works are made here, including: (a) the use of a FEA model that incorporates the elastic anisotropy of Si and a semi-elliptical indentation deformation zone that is more realistic [23] than the rectangular zone [24] used previously [18]; (b) self-consistent comparison of the strain fields determined from EBSD and CRM with that of the model, using AFM to adapt the FEA model parameters; (c) greater surface localization of the CRM measurements using a smaller excitation wavelength; and, (d) explicit consideration of the effects of depth convolution on EBSD and CRM outputs. The four techniques provide different levels of information regarding deformation and strain states, and of course all four have very different input requirements in order to generate a strain map. The following section considers the input and output quantities for each technique, detailing the quantitative points of comparison, and provides a framework for the experimental and analytical results to follow.
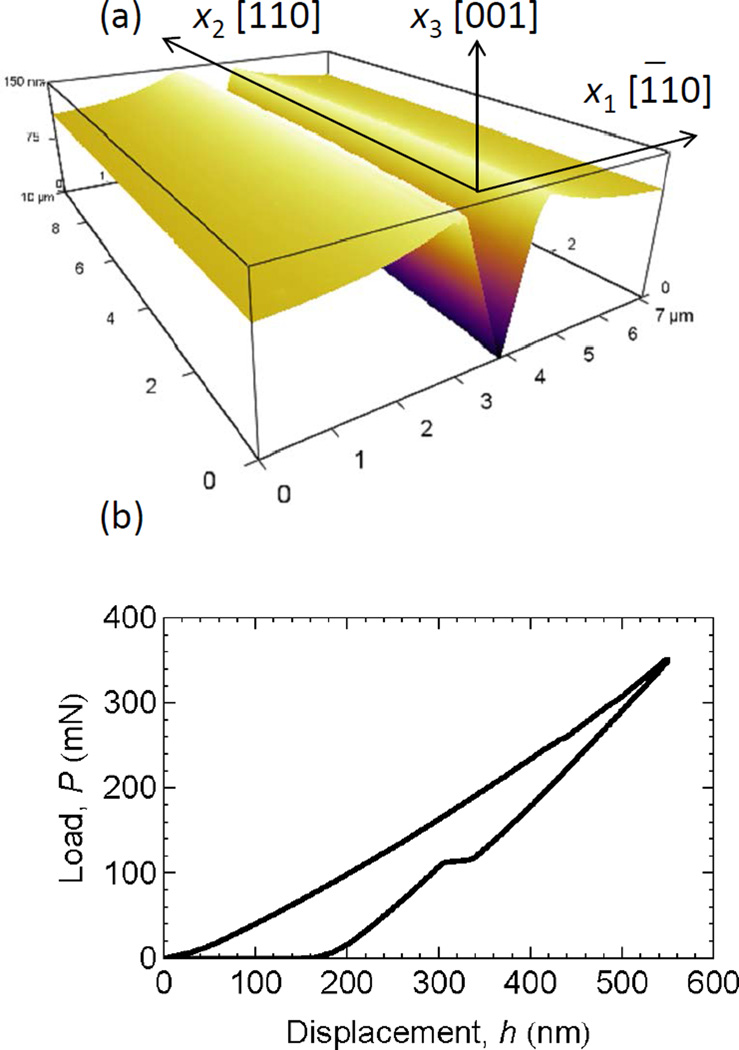
Fig. 1.
(a) SEM image of the analyzed wedge indentation and adjacent deformation field. The image is foreshortened in the vertical direction along the indentation long axis by a factor of 2.5. (b) AFM-obtained three-dimensional rendering of the residual deformation profile of the central section of the wedge indentation. The x1–x2–x3 coordinate system used is indicated. (c) The load-displacement behavior observed during indentation.
1.2. Comparison of Deformation and Strain Measurement Techniques
Wedge indentation of a Si surface generates a residual contact impression associated with a localized sub-surface irreversible deformation zone [17, 25] that includes plastically deformed and phase transformed material [26, 27]. The residual irreversible deformation zone is in a state of compression. In response to the strain mismatch between this zone and the surrounding matrix, a distributed elastic strain field [28], including a surface uplift field [18], is generated in the matrix. As the contact impression is long (here 20 µm) relative to the impression width and associated irreversible deformation zone (< 2 µm), the state of deformation is approximately plane strain in the x1–x3 plane perpendicular to the impression long axis, Fig. 1(b), with negligible deformation in the x2 direction parallel to the long axis.
FEA can provide a complete and detailed specification of the displacement field arising in the material, ui(x1, x3), once the form and nature of the irreversible deformation zone stressor are known. Two outputs of the FEA are used here for comparison with other methods: the displacement of the surface u3(x1, x3 = 0) and the elastic distortion (or displacement gradient [29]) tensor, Aij(x1, x3) = ∂ui/∂xj. The symmetric component of Aij is the six-component elastic strain tensor, εij(x1, x3) = (1/2)(∂ui/∂xj + ∂uj/∂xj), and ε22 = ε12 = ε23 = 0 is anticipated here for the x1–x3 plane-strain wedge indentation [29].
EBSD can generate the most complete experimental specification of the displacement field, providing the entire traceless elastic distortion tensor, Ãij, from measurements of shift vectors, qk, relating strained EBSPs to the reference EBSP [9]. The traceless distortion tensor, indicated by Ãij as opposed to the full distortion tensor Aij, has only eight independent components and is geometrically equivalent to the five independent deviatoric elastic strain tensor components, ε̃ij, and the three rotation tensor components, ωij, characterizing the material displacement field [29]. The trace of the distortion tensor is determined using an assumed closure relation, typically that the measurement is localized to a stress-free surface, thereby providing the missing distortion and strain tensor components. The EBSD response actually reflects an average over a depth, x3 ≈ −dEBSD, very close to the surface, where the EBSD information depth, dEBSD, depends on the SEM operating conditions, particularly accelerating voltage and sample tilt [30]. Two outputs of EBSD are used here for comparison with other experimental methods: the orientation of the surface, A31(x1, x3 ≈ 0), and the surface-localized strain, εij(x1, x3 ≈ 0). Integration of the single-argument surface-localized A31(x1) provides the surface displacement field, ∫ A31(x1)dx1 = u3(x1).
AFM provides a single component of the displacement field, the surface topography, u3(x1, x3 = 0). Differentiation of the single-argument surface-localized u3(x1) provides the local surface orientation, ∂u3(x1) / ∂x1 = A31(x1).
CRM responds to all components of the strain field averaged over a depth, x3 ≈ −dCRM, very close to the surface, where the CRM information depth, dCRM, depends on the Raman microscope operating conditions, particularly the input excitation wavelength, λi [17]. The CRM output is interpreted as a single Raman scattered wavelength, λo, expressed as a frequency in wavenumbers (cm−1) ω = 1/λi − 1/λo. At the (unstrained) reference location, this frequency is ω0 and at a measurement location, x1, the frequency is shifted to ω0 + Δω(x1). If the form of the strain field is known and relatively simple, for example, uniaxial tension, the scalar frequency shift Δω(x1) can be related to a single independent component of the strain field, for example ε11(x1, x3 ≈ 0), by a simple multiplicative factor [6, 11, 12, 20, 31]. If the strain field is complex, an opto-mechanical analysis incorporating all the components of the strain tensor, say obtained from FEA, can be used to predict the effective frequency shift arising from the various Raman scattering modes in the material [13, 19].
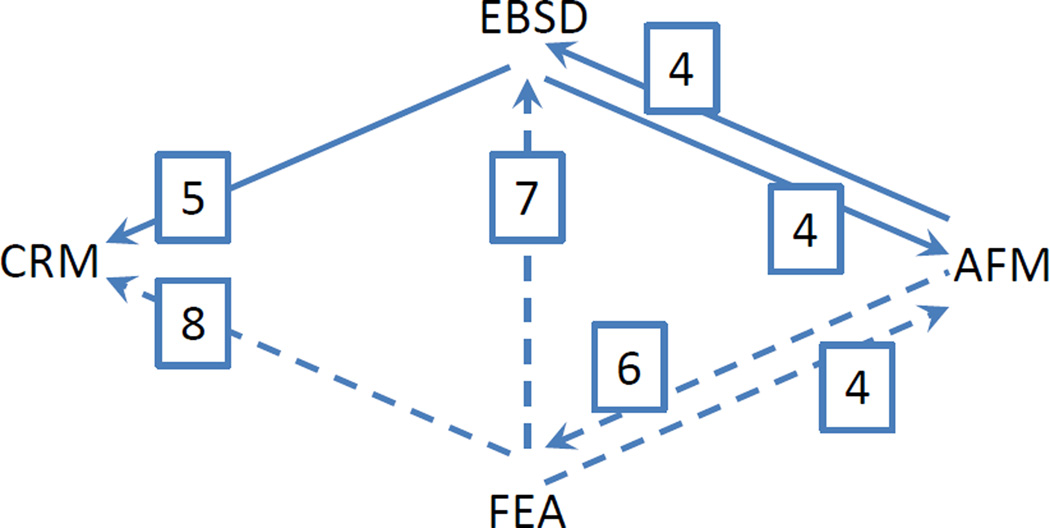
Table 1 summarizes the measured and calculated quantities for each deformation and strain measurement technique, highlighting the points of comparison. The direct output of the technique is listed and quantities calculated from it indicated by arrows. The approach taken in this work is to predict the response of one microscopy technique using another, taking advantage of these points of comparison, as illustrated in Fig. 2, which provides an outline of the paper. The predictions are divided into two parts: (i) strictly experimental (shown as the solid lines in Fig. 2) and (ii) using FEA as an intermediate step (dashed lines). In (i), AFM topography measurements are used to predict the surface orientation determined by EBSD, the EBSD orientation measurements are used to predict the topography measured by AFM, and the EBSD strain measurements are used to predict the frequency shift measured by CRM. In (ii), AFM topography measurements are used to adapt parameters defining the irreversible deformation zone in the FEA and the adapted FEA is then subsequently used to predict the strain components measured by EBSD and the frequency shifts measured by CRM. The numbers in boxes in Fig. 2 indicate the number of the Figure in this paper that will illustrate the prediction-measurement comparison.
Table 1.
Comparison of Deformation and Strain Prediction and Measurement Techniques
| Technique | Direct Output | Calculated Quantity |
|---|---|---|
| FEA |
ui (x1, x3) u3(x1, x3 = 0) |
Aij (x1, x3) = ∂ui / ∂xj → εij (x1, x3) → Δω(x1, x3) |
| EBSD | qk → Ãij (x1, x3 ≈ 0) | Closure relation →Aij (x1, x3 ≈ 0) → εij (x1, x3 ≈ 0) →∫ A31 (x1, x3 ≈ 0)dx1 = u3 (x1, x3 ≈ 0) |
| AFM | u3(x1, x3 = 0) | ∂u3 / ∂x1 = A31 (x1, x3 = 0) |
| CRM | Δω(x1, x3 ≈ 0) | Simple form of strain field → ε(x1, x3 ≈ 0) |
Fig. 2.
Diagram showing the interrelations between predictions made from the three microscopy techniques, AFM, EBSD, and CRM, and the FEA model; the directions of the arrows indicate the direction of prediction or constraint and the boxed numbers indicate the relevant figure comparing measurement with prediction. Solid connectors indicate direct experimental predictions and dashed connectors indicate model-mediated predications.
2. Experimental methods
The experimental methods are the same as those in prior studies on wedge-indented Si [17, 18]. The (001) surface of a device–grade Si wafer was indented with a wedge-shaped diamond indenter to a peak load of 350 mN. The indenter was 20 µm long with an interior angle of 140° and aligned along a [110] direction of the wafer. A single indentation is studied here from the same series of indentations considered previously, and had a residual contact impression depth and width of about 150 nm and 1.5 µm, respectively, and a maximum surface uplift adjacent to the impression of about 40 nm. The height profile of the indentation and surrounding material obtained using intermittent contact mode AFM are shown in Fig. 1(b); the uncertainty in the height profile at any location was < 0.1 nm. The load-displacement response of the considered indentation is shown in Fig. 1(c). The load-displacement response indicates residual plasticity during the indentation process, as well as more complicated behavior, such as pop-out phenomena, associated with phase transformations on unloading [23, 26, 32]. The details of the load-displacement responses and residual impression dimensions varied from indentation to indention within the series, but all exhibited the overall behavior shown in Fig. 1, and all exhibited uniform residual topography near the middle of the 20 µm long impression, suggesting plane-strain deformation at that location.
Line scans, ranging from 40 µm to 70 µm long, across the center of the indentation impression (in the x1 direction of Fig. 1(b)) were performed to obtain EBSD and CRM responses. EBSPs and Raman spectra were obtained in 500 nm or 250 nm steps in the scans, respectively. The commercial SEM operating conditions were an accelerating voltage of 20 kV, a sample current of 2 nA, and a sample tilt about the x1 axis of 70° relative to the electron beam normal. The SEM spot size was 75 nm in the x1 direction (and about 2.5 times larger in the x2 direction); adequate for the slowly-varying strain fields to be measured here. Typical acquisition time per pixel was 1 s. An EBSP obtained far from the indentation impression, at location designated xr, was chosen as the reference pattern. Cross correlations of regions of interest (ROIs) in strained EBSPs with the same ROIs in the reference EBSP were used to generate the mean shift vectors, , for the ROIs in a strained EBSP, where (i) indicates the ROI index. Measurement of as a function of the ROI location vector, , for 21 ROIs in each EBSP enabled the best-fit traceless distortion tensor Ãij(x) for the probed region to be determined as a function of probe location [9]. The assumption of plane stress at the surface was used, such that σ33 = σ13 = σ23 = 0 in the x1–x2 surface plane, providing ε33 = −(c12 / c11)ε11 at the surface. This relation enabled closure of the distortion tensor, Aij, and specification of the full strain and rotation tensors, εij and ωij respectively (cIJ are elastic stiffness matrix terms [33] using contracted notation). Note that under these conditions the deformation state at the surface is one of simultaneous plane stress in the x1–x2 plane and plane strain in the x1–x3 plane such that all shear stress and shear strain components are zero; there are only four non-zero stress and strain components, σ11, σ22, ε11, and ε33, which are related by elastic constants such that there is only one degree of freedom in the deformation field. The NIST custom CRM utilized four different laser excitations of wavelengths, 405 nm, 488 nm, 532 nm, and 633 nm, with incident beams polarized parallel to the indentation long axis and focused on the sample using a 60 × oil immersion lens with a numerical aperture of 1.4. Incident power at the sample surface was approximately 1 mW. Scattered light was collected by the same lens and a Raman spectrum at each point in the scan collected with a spectrograph. The position of the approximately 521 cm−1 Raman peak was determined for each spectrum by fitting a Pearson VII function to the data. In particular, the shift of the peak relative to that obtained at a reference point, xr, far from the indentation was determined as a function of probe location, Δω(x1). The use of the additional shorter 405 nm excitation wavelength beyond the longer three used previously [17], increased the ability of CRM to make surface-localized measurements.
The simple deformation state leads to relatively simple relations between the uncertainties in the quantities measured by EBSD and CRM and the bounds on the precision of their strain determinations. The mean shift vectors, , in EBSD could be determined here to within about 0.1 pixel within (1024 × 1024) pixel arrays, leading to about 10−4 relative uncertainty in the components of the distortion tensor, Ãij, and about 2 × 10−4 relative uncertainty in the non-zero strain components, εij [9]. The peak shifts, Δω, in CRM could be determined to within about 0.05 cm−1, which, when multiplied by the ratio of the scalar shift factor and Young’s modulus for [110] uniaxial stress in Si, (−434 MPa/cm−1)/(169 GPa) [6, 25], leads to about 1.3 × 10−4 relative uncertainty in the ε11 strain component. These uncertainties provide lower bounds on the precision with which repeated determinations of strain in the wedge indentation system can be made and thus bounds on assessments of method accuracy.
3. Analysis methods
3.1. Topography analysis
While AFM gives a direct measurement of the surface topography and thus local elevation, u3, under the conditions used here of small spot size relative to the deformation variation, EBSD measures the local elevation gradient, A31 = ∂u3 / ∂x1. The two can be compared by either differentiating the AFM-measured height profile numerically,
| (1) |
for comparison with the EBSD measurements, or by integrating the EBSD-measured elevation gradient numerically from a reference point, xr,
| (2) |
for comparison with the AFM measurements. In both cases j, k are step indices, x1 − xr = kΔx1, and Δx1 is the scan step spacing. Note that A31 is obtained directly from the EBSD measurements without need for utilization of a closure condition, but that in the second case above specification of u3(xr) is required to match the heights. For direct comparison with the FEA model, it was necessary to average the left and right sides of the measured AFM height data, u3(x1), to generate the symmetric component of the profile (asymmetric profiles have been observed previously [18, 20, 21] and are likely due to very small indenter misorientations relative to the surface). The AFM data were averaged by using the peaks in the AFM profile as the indentation edges and setting the midpoint as the origin. The left-right average of the height data was then taken, with unpaired data points at the tail ends discarded.
3.2. FEA analysis
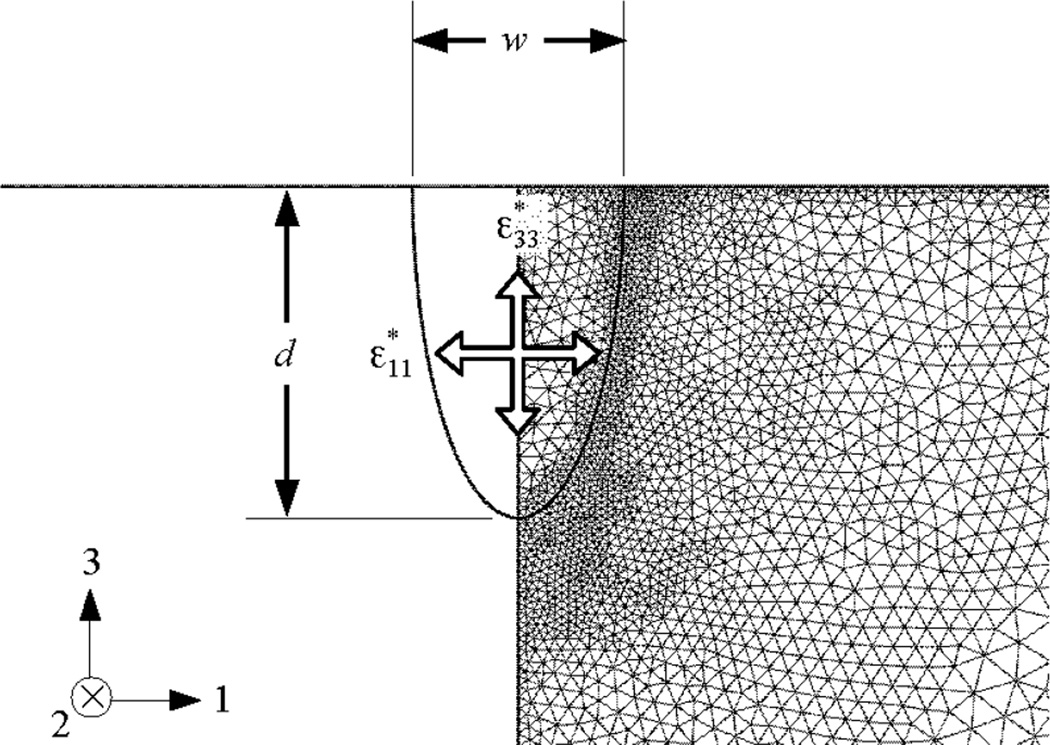
A FEA model of the wedge indentation deformation field was developed and tuned to AFM measurements of the elevation profile exterior to the residual contact impression. The modeling procedure included some approximations and simplifications that were justified in light of prior usage and the theory of the elastic deformations that were of primary interest: those measured by EBSD and CRM exterior to the irreversible deformation zone of the indentation. A diagram of the cross-section of the undeformed FEA model is shown in Fig. 3. The FEA model approximations included:
Fig. 3.
Schematic diagram of the FEA model cross section showing the semi-elliptical residually-strained deformation zone and the FEA mesh. The AFM-adapted zone depth dimension, d, and eigenstrains, and , are indicated.
Plane Strain
Fitting to the AFM profile was an iterative procedure and the use of plane-strain greatly improved the speed of numerical modeling.
Simplified Irreversible Deformation Zone
Determining the state of irreversible deformation beneath the indentation via direct modeling was intractable as the plastic deformation and phase transformations of Si have very complex constitutive relations that lead to very different irreversible deformation zone geometries and residual stress states depending on the relationship chosen and model implementation [34–40]. More importantly, as noted above and elsewhere [18, 23, 26, 32, 41], great variability (pseudo-randomness) and distinct quantitative differences are observed in the behavior and residual deformation patterns of indentations formed in Si under nominally identical conditions. Fortunately, the elastic uplift around a particular indentation is less complicated when treated phenomenologically: The uplift is overwhelmingly determined by the average irreversible strain beneath the indentation, the location of the strain-weighted centroid of the strained zone, and the requirement that the entire zone be contained beneath the residual impression. This conclusion was reached by studying the effects of varying parameters in the elastically isotropic, buried rectangular stressed-brick model [24] and through a series of preliminary, elastically anisotropic, FEA models using various zone shape sections: semi-circular, semi-elliptical, and truncated circular (tear-drop, with a wider zone beneath the surface). Ultimately, a good match with the AFM measured profile necessitated a three-fit-parameter, semi-elliptical model (Fig. 3); the zone shape is similar to that of a previous elastic simulation [23] and of most combined elastic-plastic-phase transformation models [35, 37–40] and much smaller-scale molecular dynamics simulations [42–44] (some models do exhibit tear-drop shapes [34, 36]). The half-width of the zone was taken to be the half-width of the residual impression and used as the semi-ellipse minor axis (w/2 = 0.733 µm). The semi-ellipse major axis (d), the horizontal eigenstrain , and the vertical eigenstrain were then varied to obtain the best least-squares fit to the symmetric component of the AFM measured uplift. [It was not possible to obtain a good fit to the AFM data using just one ( with d = w/2) or even two (e.g., and d) parameters.] As a final note, the physical interpretation of and is subtle. These initial strains are equivalent to the residual plastic and phase transformation strains only in the sense that they gave similar elastic fields outside the irreversible deformation zone. No additional physical interpretation should be inferred without care. [Eigenstrain or initial strain, , is defined as the strain occurring at zero stress such that the final stress is given by in contracted notation. Thermal strain is the most common example of initial strain [45].]
Symmetry
The AFM profile and EBSD and CRM measurements were slightly asymmetric, and it was cumbersome to develop an enhanced theory of indentation deformation zones to account for the asymmetry. Instead, the left and right halves of the experimental data were averaged and then compared with a symmetric model. Justification is found from the theory of elastic deformation: Outside the irreversible zone, linear elasticity is a good approximation, introducing errors that are on the order of elastic strain squared or about 10−4 for a maximum strain of 0.01. The principal of superposition (for small strains) then allows the left-right averaged fields (or symmetric part) and the left-right difference fields (or antisymmetric part) to be treated separately. The symmetry line was taken to be the center of the residual impression.
Finite element modeling was performed using 6-node quadratic triangles. Adaptive meshing was used to limit the relative error estimate for the von Mises stress to less than 0.5 %. The resulting characteristic numerical error in strain was approximately 10−4 based on comparison of the last two mesh refinements. (While von Mises stress is suitable for characterizing mesh error, no additional physical significance to its use should be inferred.) Linear anisotropic plane-strain elasticity was used with the elastic stiffness coefficients of Si as c11 = 165.8 GPa, c12 = 63.9 GPa, and c44 = 79.6 GPa [33] and the plane of deformation taken as the (110)-plane (x1–x3 plane, Fig. 1(b)). Least squares fitting was performed on the measured symmetric profile, , and the modeled elastic uplift, u3,FEA (xk; , d), to determine the mean strains, and , and the zone depth, d. The values of u3,FEA (xk) were interpolated between FEA nodes as the AFM measurement positions, xk, were not coincident with the FEA nodes. The fitting procedure took further advantage of the principal of superposition. For a given value of d, FEA was used to find separately the elastic uplifts proportional to and ,
For each value of d, the functions u(1) and u(2) were calculated via FEA, so that the eigenstrains were solved rapidly via linear least squares [46]. The optimal value of d was then found by varying the geometry of the FEA deformation zone and repeating the procedure for finding and . Thereby, a search in a three-parameter space was accomplished with only twice the calculations required for searching for one optimal parameter.
3.3. CRM analysis
The Raman spectrum of unstrained Si consists of a triply degenerate peak at a frequency of approximately 521 cm−1. Under anisotropic strain, the spectral degeneracy is split either partially or fully into shifted peaks of possibly unequal intensity, with the shifts and the intensities determined by the strain state, the Si phonon deformation potentials (the PDPs, p, q, and r that link the change in polarizability of Si to the strain), the directions and polarizations of the excitation and collected light, and the crystal orientation [11–14, 19]. Typically, the split peaks are not resolved, and a single peak is fit. The method for predicting the single peak position from knowledge of the full tensor strain field was that used previously [13, 19]: In summary, three piezo-Raman shifts and three relative intensities for the separate peaks were calculated and the shifts averaged, weighted by their relative intensities, to give a mean piezo-Raman shift, Δω. Two sets of PDPs [47, 48] were used in evaluating the mean shift from the strain field, and are given in Table 2. Both sets are commonly cited and span the range of other experimental measurements of Si PDPs [49–50]. In general, the scalar shift is not a simple function of the components of the strain tensor. However, a priori knowledge of the strain or stress state (linked by the components of cIJ) allows for considerable simplification: A common rule of thumb, as noted above for elongated stressors in the [110] x2-direction (as here, Fig. 1(b)), is that the spectrally-weighted Raman shift is related to the stress perpendicular to the elongated stressor by [14, 17, 19, 48]
| (3) |
where the mean shift is given in units of cm−1 and σ11 is expected to be the dominant stress component here. Eq. 3 is written in the format that is most useful for stress or strain mapping—a stress or strain component can be inferred from a measured scalar Raman shift. The opposite procedure will be performed here that is more useful for technique comparisons and that takes advantage of more complete knowledge of the deformation field—a scalar Raman shift will be predicted from the full strain tensor. The strain tensor will be obtained from two sources: (i) the EBSD measurements in combination with the zero normal-traction closure condition (solid line, Fig. 2) and (ii) the FEA model adapted by the AFM profile measurements (dashed line, Fig. 2). Comparisons of both of these predictions with CRM measurements is complicated when the strain field is non-uniform, in particular when subsurface strains are probed due to the finite information depths of CRM and EBSD and the resulting CRM and EBSD signals are convolutions over these depths.
Table 2.
Phonon Deformation Potentials for Raman Scattering in Si
3.4. Depth convolution analysis
Experimental measurements have finite interaction volumes, and it is important to include these effects in simulations to obtain a fair comparison with experiments and to elucidate how such volumes affect experimentally inferred quantities. Analysis of the experimental data showed that there was no effect of lateral averaging; hence here we consider only depth convolution. As will be shown, the penetrating and exiting beams such as electrons in EBSD and photons in CRM experienced different deformation states at sub-surface scattering sites, as well as suffering attenuation per unit length while entering and exiting the sample volume. For EBSD this attenuation typically leads to an average information depth, dEBSD, with the different backscattering depths contributing information that is exponentially weighted in terms of depth,
| (4) |
where (x3 − u3) takes negative values inside the sample and x3,0 ≤ x3 ≤ u3(x1), where x3,0 is the coordinate of the base of the sample. I(x3) can be interpreted as a product of the relative attenuation of the incoming electron beam and the relative attenuation of the quantum coherence of the backscattered electrons. Measured EBSPs will be created by distortions from a variety of depths and weighted by their relative intensity in the EBSP so that the measured distortion tensor at position x1, , will be the result of a weighted average of the depth-varying distortion Aij(x1, x3):
| (5) |
where “M” indicates measured distortion, and the denominator in the first term on the right side is chosen to give a total integrated weight of unity. The information depth for EBSD in Si is between 10 nm and 100 nm [30] and hence bounds were calculated corresponding to the limit dEBSD → 0 (the distortions at the surface) and a large value, dEBSD = 100 nm. Substituting FEA simulated values for Aij(x1, x3) in Eq. 5, values of were obtained for direct comparison with those measured by EBSD. The numerical integration of Eq. 5, and Eq. 6 below, is discussed in Appendix A.
Simulating depth-convolution effects on measured piezo-Raman shifts was a two-step process. First, the simulated strain components were converted to piezo-Raman shifts as outlined previously [19] and summarized above. As in the case of EBSD, the resulting piezo-Raman shift spectrum is expected to be a weighted average through the depth. As before, the centroid of the spectrum was calculated for comparison with a single fit peak. The attenuation of excitation and Raman-scattered light leads to an exponentially-weighted form essentially identical to Eq. 5,
| (6) |
with the ingoing and outgoing attenuation lengths added in parallel to give . (See Appendix A; in general, dout is greater than din because Raman scattering shifts the light to longer wavelengths that have less attenuation.) Two published sets of attenuation lengths for Si were used [52, 53] to determine the information depth and then to simulate the measured piezo-Raman shifts. Published tables were interpolated with cubic splines. The attenuation lengths from each set and the resulting information depths are reported in Table 3.
Table 3.
Information Depths for CRM in Si
| (a) | (b)Green and Keevers [53] | (b)Dash and Newman [52] | |||||
|---|---|---|---|---|---|---|---|
| λin (nm) | λout (nm) | din (nm) | dout (nm) | dCRM (nm) | din (nm) | dout (nm) | dCRM (nm) |
| 405 | 414 | 127 | 167 | 72 | 156 | 192 | 86 |
| 488 | 501 | 764 | 910 | 415 | 744 | 862 | 399 |
| 532 | 547 | 1302 | 1522 | 702 | 1184 | 1351 | 631 |
| 633 | 655 | 3125 | 3700 | 1694 | 2606 | 3067 | 1409 |
Vacuum wavelengths of excitation light, λin, and Raman scattered light, λout.
Ingoing and outgoing attenuation lengths, din and dout, and calculated information depths, dCRM.
4. Results
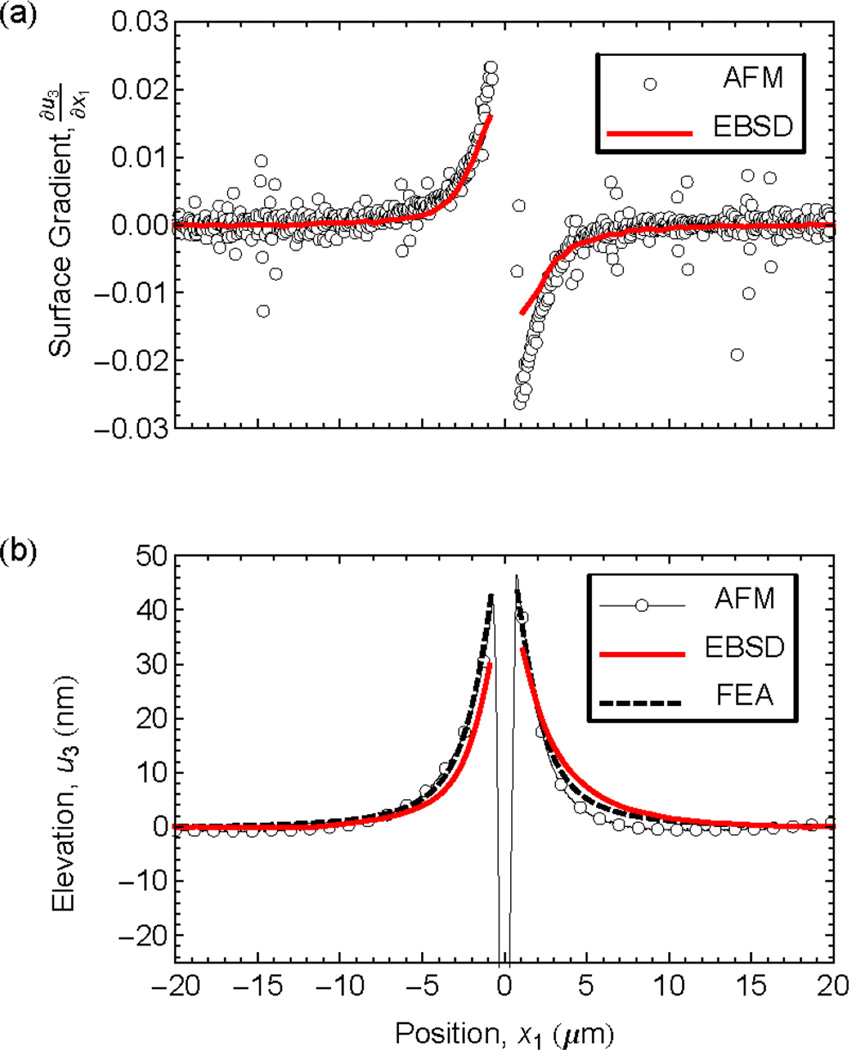
Figure 4 is a comparison of the surface gradients measured by EBSD and AFM adjacent to the indentation contact impression. The solid line is the gradient, A31(x11), measured by EBSD and the symbols are the gradient values determined numerically from the AFM measurements using Eq. 1. A common reference point of xr = −20 µm was used. There is very good agreement between the two measurements over scans of 40 µm, noting that the gradients correspond to a maximum of 0.02 rad ≈ 1.1°. The uncertainty in the EBSD gradient measurement is approximately 10−4 rad, much smaller than the line width in Fig. 4(a); the scatter in the AFM calculated gradient is about 4 × 10−3 rad. Within approximately 1 µm of the impression center (about 0.25 µm from the impression edge) the AFM gradient exceeds the EBSD gradient somewhat, at least on one side of the contact impression; it is possible that the finite depth EBSD measurements are sensing the irreversible deformation zone at these small distances from the impression center and that the values of A31 returned by the EBSD measurements do not solely reflect surface measurements as sensed by AFM.
Fig. 4.
(a) Plot of elastic elevation gradient of the Si surface across the center of the wedge indentation as measured by EBSD and calculated from AFM. (b) Plot of the elevation of the Si surface across the center of the wedge indentation as measured by AFM, calculated from EBSD, and simulated by FEA.
Figure 4(b) is a comparison of the surface heights measured by AFM and EBSD. The symbols represent the surface displacement, u3(x), measured by AFM, and the solid line is the surface height variation determined numerically from the EBSD measurements using Eq. 2. A common reference point of xr = −20 µm and u3(−20 µm) = 0 nm was used. Once again there is very good agreement between the two measurements over the scan range. The experimental scatter in the AFM height measurements is approximately 2 nm, largely arising from surface roughness, about the symbol size and not visible in Fig. 4(b); the uncertainty in the EBSD height measurements is approximately 0.03 nm per integration step, giving a possible root mean square accumulated error of (0.06 nm)(40)1/2 = 0.38 nm at the center of the scan. In this case, the EBSD measurements exhibited deviation from the AFM measurements about 5 µm from the impression center, again asymmetrically, as overestimation and underestimation of about 3 nm at points either side.
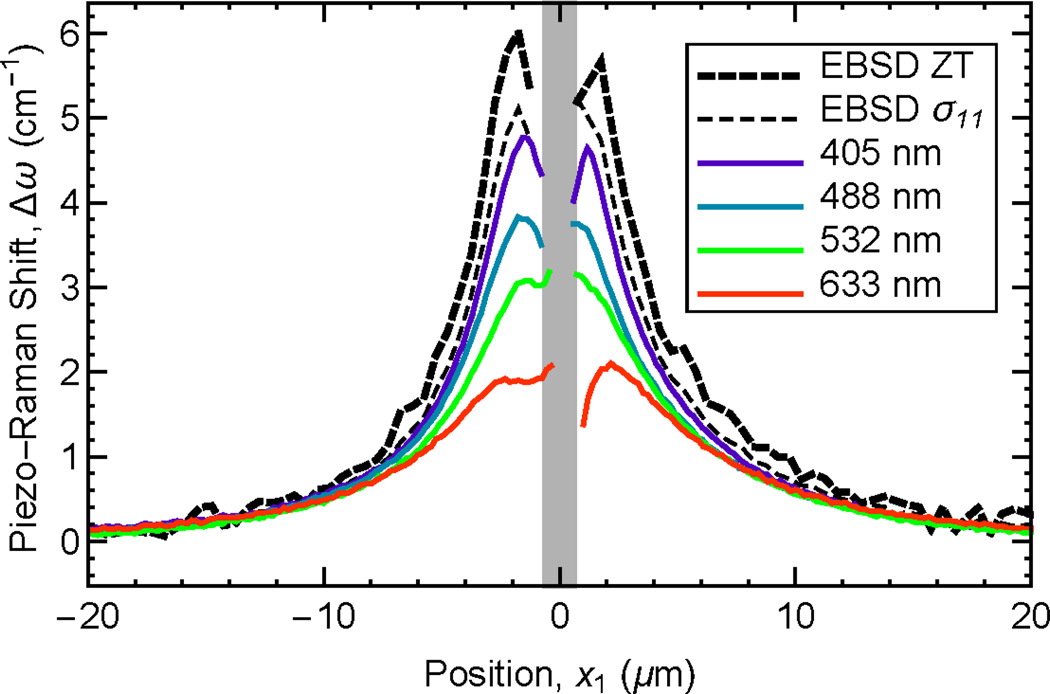
The above measurements reinforce the agreement observed earlier between AFM and EBSD measurements [18], and focus on one component of the traceless distortion tensor. Figure 5 shows a comparison of Raman shifts adjacent to the contact impression measured by CRM and predicted by EBSD, using all six components of the strain tensor obtained from EBSD measurements and the zero normal-traction closure relation. A common reference point of xr = 500 µm was used. The variations in the peak frequency shift, Δω(x1), with position in the scans are shown as the solid lines for the four CRM excitation wavelengths indicated. In all cases, Δω increases from approximately 0 at the edge of a scan to a maximum towards the center of a scan. The maximum increases with decreasing excitation wavelength, such that at the center of the scan the 633 nm excitation exhibits a peak shift of about 2 cm−1 and the 405 nm excitation about 5 cm−1. The uncertainty in the peak shift from the unstrained reference state is approximately 0.1 cm−1, about twice the line widths. The CRM responses all exhibited asymmetry about the impression center and in many cases about 2 µm from the impression exhibited a decreased shift from a maximum value. The dashed lines in Fig. 5 indicate predictions of the CRM shift from the EBSD strain measurements. The bold dashed line, labelled ZT, zero normal traction, is a prediction using the full strain tensor and the weighting method described above to generate the mean shift of the apparent single peak. The fine dashed line is a prediction using the full strain tensor and the elastic constant matrix to calculate the σ11 stress component from which the peak shift was generated from inversion of the scalar Eq. 3. Neglecting uncertainty in the PDPs (see below and Discussion) and in the elastic constants (negligible [33]) the uncertainty in the EBSD-based predictions is of order (6 × 10−4.ω0) ≈ 0.3 cm−1, about six times the line widths. Both EBSD predictions display the overall trends observed in the CRM measurements: the shifts increase significantly as the contact impression is approached and then decrease from a maximum value about 2 µm from the impression. Within experimental uncertainty, the predictions of both EBSD methods are consistent with the CRM shifts measured further than about 5 µm from the contact impression. Closer to the contact impression, the predicted shifts are slightly greater than those observed, even for the 405 nm excitation response, the weighted peak method more so than the scalar uniaxial stress method.
Fig. 5.
Plot of Raman shifts measured by CRM and calculated from EBSD across the center of the wedge indentation. Wavelengths 405 nm, 488 nm, 532 nm, and 633 nm show Raman shifts measured using increasing excitation wavelengths and increasing information depths. ZT indicates the shift predicted from EBSD using the zero normal-traction closure relation and the full strain tensor. σ11 indicates the shift predicted from EBSD using the same closure relation and the single σ11 component of the stress tensor. The gray band indicates the residual contact impression region for which no data were analyzed.
Several strong inferences can be drawn from the observations of Fig. 5 and consideration of the information depths for EBSD (between 10 nm and 100 nm [30]) and CRM (increasing from about 80 nm for 405 nm excitation to about 1550 nm for 633 nm excitation, Table 3). First, further than about 5 µm to 10 µm from the contact impression, depth convolution effects are negligible as all measurements and predictions agree; the implication is that there is negligible variation in the strain tensor over the depths sampled at these locations. Second, closer than about 5 µm from the impression center, there is a decrease in the magnitudes of the components of the strain tensor with depth, as CRM measurements with longer excitation wavelengths (and hence greater information depths) exhibit smaller peak shifts indicative of smaller average sensed strain. Third, the agreement between the CRM measurements and the “EBSD σ11” prediction suggests that this (compressive) stress component is the dominant feature of the deformation field, although the partial agreement with the full weighted tensor calculation suggests it is not the sole feature. Fourth, in agreement with previous observations [17], CRM measurements with smaller excitation wavelengths, particularly the additional 405 nm excitation used here, come closer to EBSD measurements, suggesting that the smaller information depths of the CRM measurements are approaching those of the more surface-localized EBSD measurements. These inferences are tested below by developing a FEA model of the indentation that provides full specification of the strain field beneath the surface, and enables information depth and depth convolution effects to be assessed explicitly.
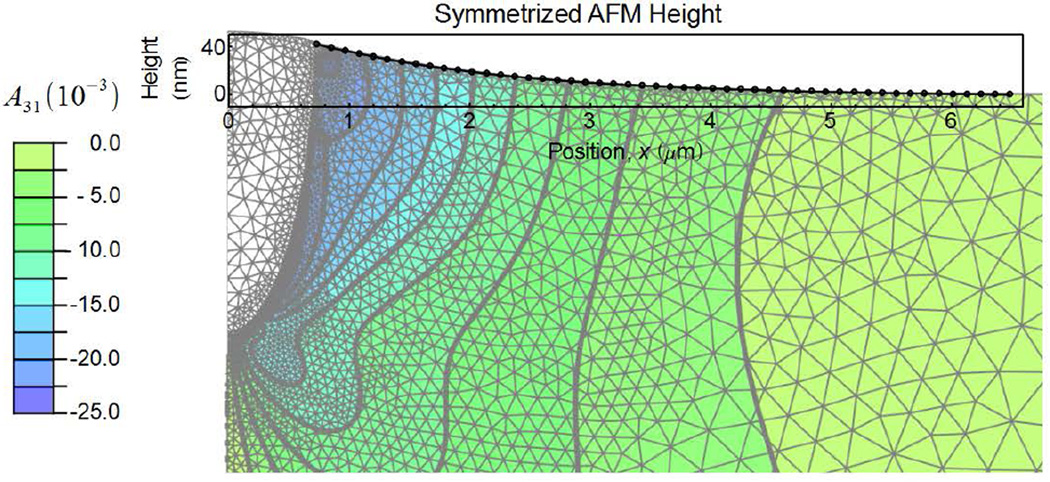
Figure 6 shows the cross section of the deformation field determined from the best-fit FEA model of the indentation; the final, deformed mesh is shown and the vertical dimension is exaggerated by a factor of 14. On the left, not shaded, is the semi-elliptical region that was pre-strained, representing the AFM-adapted irreversible deformation zone. To the right of the zone at the top of the diagram is superposed the symmetrized AFM height profile; the agreement between the best-fit FEA model and profile is evident. The zone parameters giving rise to the best fit were d = (2.38 ± 0.28) µm, , where the uncertainties represent the standard errors of the FEA fit to the AFM data. Also to the right of the zone is the deformed elastic matrix, on which shaded contours of A31(x1, x3) are drawn. The contours increase in horizontal density closer than about 5 µm to the zone and, due to deformation curvature, increase in vertical density closer than about 2 µm to the zone. It is clear from these contours that there are subsurface deformation gradients that could influence observed CRM and EBSD measurements.
Fig. 6.
A schematic diagram of the FEA model of elastic deformation adjacent to a wedge indentation, symmetric about x1 = 0. The initial semi-elliptical stressed region is shown as the white elements. The elastic region is shown as colored contours of the distortion tensor element A31=∂u3/∂x1 related to rotation about an axis perpendicular to the diagram. Vertical displacements are multiplied by 14 for visualization. The measured AFM height profile used to adapt the model is shown to identical scale as the overlayed plot.
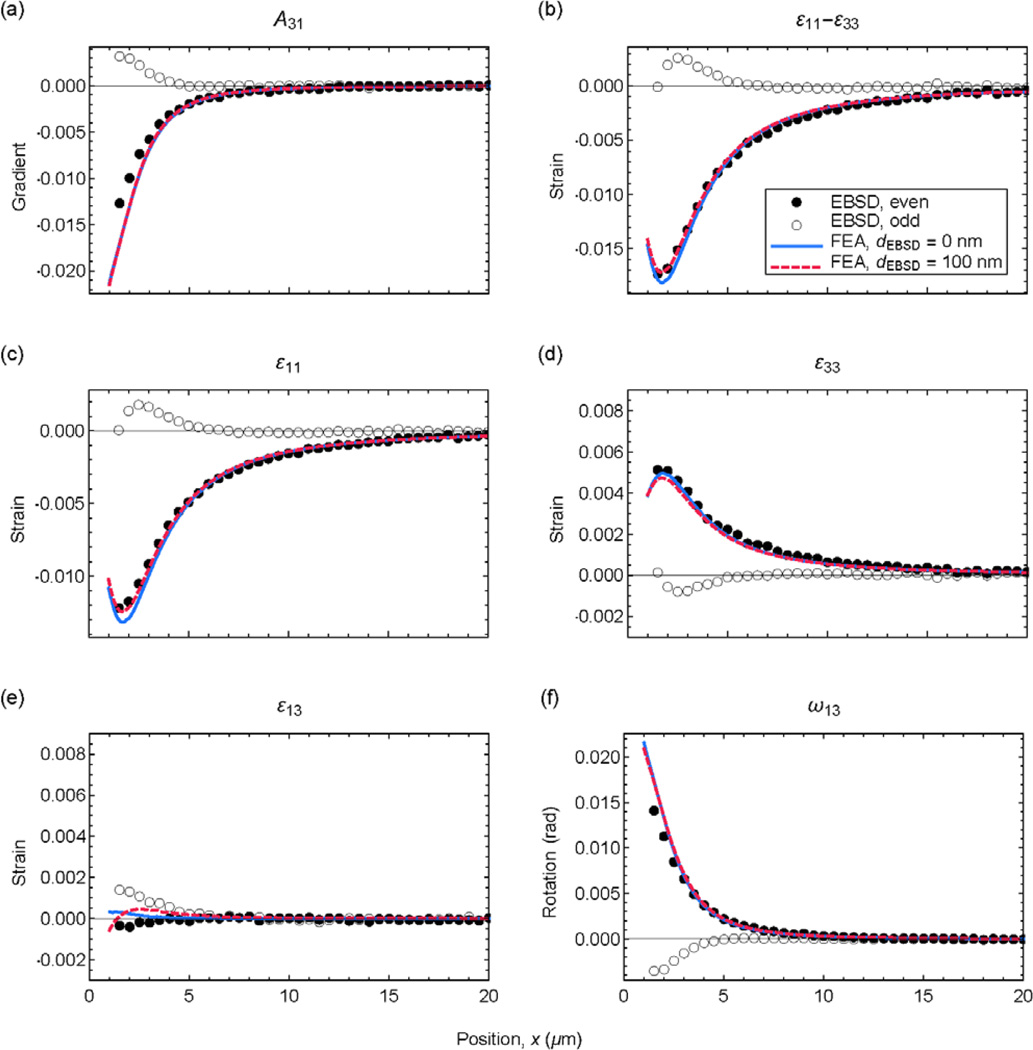
Figure 7 shows a comparison of EBSD measurements of distortion, strain, and rotation with the results from the AFM-adapted FEA model. The EBSD data were treated in the same way as the AFM data to obtain the symmetrized components: The center of the indentation was found in SEM imaging mode and the data outside the indentation left-right averaged with any unpaired points discarded. Figure 7(a) shows the EBSD-measured even (symmetric) and odd (anti-symmetric) components of A31(x1) as closed and open symbols, respectively. The odd component has appreciable amplitude only within about 5 µm of the contact impression. Also shown in Fig. 7(a) are the predictions of A31(x1) from the FEA using numerical integration of Eq. 5 and minimal (dEBSD → 0 nm) or maximum (dEBSD = 100 nm) information depths as full and dashed lines, respectively. The agreement with the experimental observations is very good, and there is very little effect of depth convolution for the bounds chosen. The related FEA (even) height response is shown in Fig. 4(b) as the dashed line; the small effects of asymmetry are again apparent. Figure 7(b) shows the even and odd components of (ε11 – ε33)(x1) from EBSD and the depth-weighted FEA predictions using the same scheme as Fig. 7(a). Once again there is very good agreement between the two, including the small reversal in strain about 2 µm from the indentation center. Implementing a closure relation enables the EBSD measured (ε11 – ε33) to be separated (noting that the FEA model provides them explicitly) and comparison of the two components is shown in Figs. 7(c) and (d), respectively. Apart from the agreement between the model and prediction, including the small strain reversal, the results are consistent with a dominant σ11 uniaxial compressive stress field with large and negative ε11 associated with in-plane longitudinal contraction and smaller and positive ε33 associated with out-of-plane Poisson expansion (note the change in scales between Figs. 7(c) and (d)). Finally, the symmetric and anti-symmetric off-diagonal components of the distortion tensor, the shear strain, ε13 = (A13 + A31)/2, and the rotation, ω13 = (A13 − A31)/2, also show agreement between the EBSD measurements and the FEA predictions, Figs. 7(e) and (f), respectively.
Fig. 7.
Plots of strains, gradients, and rotations measured by EBSD (symbols) adjacent to the wedge indentation compared with values simulated by FEA (lines): dEBSD = 0 nm indicates surface values, dEBSD = 100 nm indicates depth-averaged values obtained using Eq. (5).
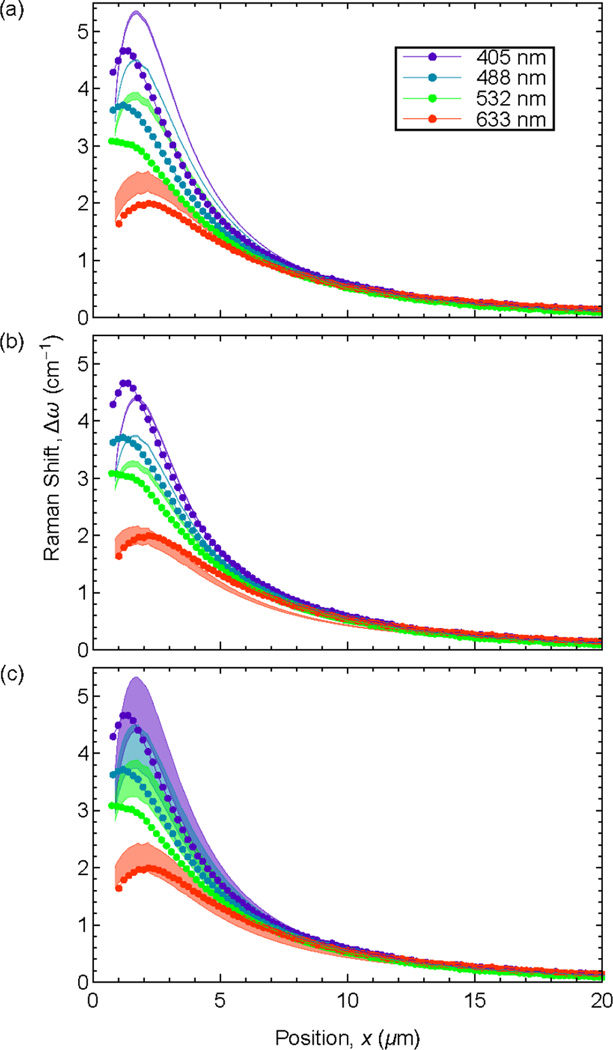
Figure 8 shows a comparison of symmetrized CRM peak shift measurements with predictions from the AFM-adapted FEA model. The CRM data were symmetrized by selecting a center point in the full scan such that the maxima in the shifts (Fig. 5) occurred at similar distances from the center and then left-right averaging was performed about this point. Such data are shown as the symbols in Fig. 8. The bands in Fig. 8 represent predictions of the piezo-Raman shift from the AFM-adapted FEA model using the full strain tensor opto-mechanical analysis and combinations of published attenuation lengths and PDPs. Figures 8(a) and (b) demonstrate the effect of optical attenuation length on predicted piezo-Raman shift in a depth varying strain field. Different sets of PDPs (Table 2) are used in each of (a)[48] and (b)[47]. The upper edges of the uncertainty bands in Figs. 8(a) and (b) represent predictions using the shorter of the information depths and the lower edges represent predictions using the longer of the information depths. More than 10 µm from the indentation, the edges overlap implying that there is negligible vertical strain gradient at that location and that differences in information depth for a given excitation wavelength do not matter. Closer to the indentation, the uncertainty bands expand, more so for the longer excitation wavelengths. This expansion represents two factors: (i) the longer excitation wavelength measurements have larger information depths and therefore differences in estimated information depth will lead to greater divergences in predicted piezo-Raman bounds for depth varying strain fields; and (ii) the differences in the published attenuation lengths and subsequently calculated information depths are greater for the longer excitation wavelengths (Table 3). The combination of these two factors leads to a factor of 40 % difference in the piezo-Raman shift prediction bounds close to the indentation for the longest (red) excitation wavelength, in spite of the fact that the relative information depth difference is only 10 % to 20 %.
Fig. 8.
Plot of Raman shifts measured by CRM (symbols) adjacent to the wedge indentation compared with values simulated by FEA and opto-mechanical analysis (bands). The effects of selection of information depths (Table 3) are shown in (a) using PDPs from [47] and (b) using PDPs from [48]. The effects of selection of PDPs and information depths (Tables 2 and 3) are shown in (c).
Figures 8(a) and (b) show that there is very good quantitative agreement between the CRM shift measurements and the FEA-AFM predictions at positions further than about 7 µm (about five times the contact impression width) from the impression center. Closer to the impression the measured and predicted shifts are in qualitative agreement, including the large increases in shift approaching the impression and small shift reversals about 2 µm from the impression center, analogous to that observed in the EBSD-measured strain components. However, in this region, the predicted bounds in (a) consistently overestimate the measurements and the bounds in (b) mostly underestimate the measurements, a consequence of two different sets of PDPs, with those in (a) of greater magnitude than those in (b). Figure 8(c) demonstrates the effects of PDP range in piezo-Raman shift prediction. The bands in Fig. 8(c) represent the extremes of prediction using the two sets of PDPs and the two information depths. The predicted bounds for the various excitation wavelengths now overlap and encompass almost all the experimental observations over the full scan range. However, the maximum width of the bounds for all excitation wavelengths is about 0.7 cm−1 compared with maximum observed shifts of 2 cm−1 to 4.5 cm−1.
5. Discussion and Conclusions
As summarized in Fig. 2, the results presented here provide an interconnected and comprehensive study of the accuracy of two quantitative strain microscopy techniques, EBSD and CRM. That is, the results enable an assessment of the abilities of EBSD and CRM to generate strain maps that are representative of the true strain values, measured by independent means. Three aspects of the study were crucial in enabling this assessment: First, a single test structure was used, a linear wedge indentation in single crystal Si, which exhibited relatively simple deformation, strain, and stress fields, thereby minimizing ambiguities in interpretation. Second, FEA was used to model the test structure and provide complete specification of the form of the deformation, strain, and stress fields for direct and complete comparison with the EBSD and CRM measurements. Third, and critical, a third microscopy technique, AFM, was used to provide an independent and absolute measure of the scale of deformation of the test structure. In assessing accuracy, an independent measure of overall scale of deformation was needed; using the AFM data was an essential step that prevented circularity in the analysis or reliance on the very method to be tested as in input parameter.
The elastic deformation field of the wedge indentation was modeled far more rigorously than the previous study [18]. In particular, anisotropic elasticity was used in the FEA simulation and the full strain tensor calculated for a more complete analysis. The cross-section of the indentation irreversible deformation zone was taken as a more realistic semi-ellipse and the scale and eigenstrains of the zone made consistent with the AFM-measured surface topography. The outputs from the model for EBSD and CRM responses treated information depths explicitly. It is thus possible to take the FEA-AFM output as the best representation of the deformation state of the material adjacent to the wedge indentation to which other measurements should be compared.
Thus, in terms of quantitative microscopy and metrology considerations, the agreement between the individual components of the distortion, strain, and rotation tensors determined by EBSD with those predicted by FEA-AFM, Fig. 7, imply that EBSD measurements, at least as implemented here, provide an accurate measure of deformation. The greatest deviations between the EBSD measurements and the FEA-AFM predictions are of order 10−3, and then only for a few measurements directly adjacent to the indentation contact impression where strain gradients are greatest and there is the greatest possibility of the measurements sampling irreversibly-deformed material. For the majority of the positions sampled the EBSD measurements agree with the FEA-AFM predictions to within the precision of the measurements, ≈ 2 × 10−4. This assessment of the accuracy of EBSD strain measurements is in agreement with earlier measurements on SiGe films, which exhibited a far simpler strain state of homogeneous tetragonal distortion [7, 8, 10, 22].
There is very good qualitative agreement between the features observed in the CRM shift measurements and the FEA-AFM predictions over the full scan range, Figs. 8(a) and 8(b): Both the measured and predicted shifts are positive, suggesting a predominantly compressive strain field. Far from the contact impression, the shifts are small, decrease slowly with distance from the contact impression, and have no dependence on excitation wavelength, suggesting small strains that have very little depth dependence and that vary slowly with lateral position; the shifts increase significantly as the impression is approached, more so for the shorter wavelength excitations, suggesting large strains with both large lateral and depth gradients; adjacent to the impression there is a small shift reversal, more so for the shorter excitation wavelengths, suggesting a surface-localized strain decrease. For the shortest excitation wavelengths, the range of predicted shifts arising from the range of information depths (Table 2) is comparable to the precision of the shift measurements, about 0.05 cm−1. The implication is that CRM measurements provide a method for precise measurements of relative deformation if the nature of the deformation field is known. For example, the increase in shift from about 1 cm−1 to about 4 cm−1 for the surface-localized 405 nm excitation measurements at 7 µm and 2 µm, respectively, in the scans of Fig. 8 can be interpreted as a simple 4-fold increase in both ε11 and ε33 as these are the only non-zero strain tensor components at the surface and ε11/ε33 is a constant (see Section 2). In other cases in which the form of the strain tensor is unknown, and there is perhaps convolution of measurements over an information depth, relative shift measurements can provide information on the relative magnitudes of the entire strain tensor, for example between two different indentations measured by 633 nm excitation 5 µm from the impression centers.
The current limitations on the accuracy of CRM deformation measurements, that is, in the specification of the numerical values of ε11 and ε33 in the example above, are shown in Fig. 8(c). The predicted shift bands encompassed the experimental measurements only when the range of PDP values (Table 3) was taken into account. At its greatest, the range is about 0.7 cm−1 on a shift of about 4.5 cm−1. Taken as an uncertainty, this range suggests that accuracy of CRM measurements is about ±7.5 % of the inferred stress or strain value. A similar assessment of accuracy was made by Srikar et al. [6], based on CRM measurements of the stress variation in a MEMS-scale bent beam. The stress state was relatively simple; linear variation in uniaxial stress across the depth of the beam, allowing Eq. 3 to be used. Using PDPs [48, 49] similar to those here, differences in stress inferred from CRM measurements were shown to be systematically 10 % greater than predictions from FEA and beam theory, both adapted by the imposed deflection of the beam.
The implication of the above CRM observations is that the loss of accuracy of CRM-inferred stress and strain states likely arises from inaccuracy of the PDPs. The PDPs used here [47, 48] were determined under uniaxial compression conditions and have not been fully tested for general stress states. In some cases, simplified hydrostatic, plane stress, or uniaxial stress states have been assumed for Si adjacent to microelectronic structures fabricated on Si surfaces. Qualitative comparisons of measured CRM shifts with those anticipated from the assumed stress states were made [11, 12, 20]. In other cases, a uniaxial stress state was assumed, such that Eq. 3 pertains, and quantitative CRM shift comparisons made with FEA or analytical predictions [7, 14] or EBSD measurements [17]. CRM shifts resulting from general multi-axial stress states adjacent to microelectronic structures formed on or in single-crystal Si [13, 19] or in polysilicon MEMS structures [31] have been quantitatively compared with predictions from FEA models, but the FEA models were not adapted to an orthogonal experimental measurement. The limited numbers of comparisons and the lack of agreement noted here between strain states inferred from CRM observations and those determined by FEA-AFM and EBSD suggests that specification of the accuracy of strain microscopy by CRM is yet to be achieved. Such strain accuracy requires measurements of the Si PDPs under conditions similar to those used in strain mapping. In particular, the effects of large numerical apertures in back-scattered imaging, in which the incident and scattered radiation contain large components of electric field parallel to the microscope optical axis [20], need to be considered. Although the PDPs are most conveniently measured under uniaxial stress states, final assessment of PDP accuracy for stress and strain mapping requires measurements under controlled multi-axial stress states, including consideration of depth convolution effects.
From a materials science perspective, the combined FEA-AFM method implemented here provided insight into the nature of the irreversible deformation zone beneath the wedge indentation, in particular the geometry and eigenstrains. This approach is similar to a previous study [54], in which FEA and AFM were combined in study of Rockwell indentation profiles on metal surfaces to infer material properties, in particular yield stress and work-hardening rate. As noted above, these inferred quantities need to be interpreted with some care, they are only representative in that they are consistent with the measured profiles, but the combined FEA-AFM approach clearly provides a method for determining material properties. The quantitative microscopy methods demonstrated here provide a means of validating this approach through measurement of quantities, here distortion and strain, not directly used in establishing FEA and AFM self-consistency. Hence, limited EBSD or CRM measurements could be used to validate a FEA-AFM methodology on one indentation or one material, such that the methodology could then be extended to others with confidence in the accuracy of the material property determination.
Finally, from a component engineering perspective, both EBSD and CRM would appear to have sufficient strain measurement precision, ≈ 2 × 10−4, to measure strains engineered in microelectronic and optoelectronic devices, ≈ 10−2 [1, 2] but may struggle with the strains deliberately engineered or arising from thermomechanical effects, ≈ 10−3 or less, in MEMS devices [3, 6] or in microelectronic interconnection or packaging structures [4, 5]. The accuracy demonstrated here for EBSD enables not just comparison of measurements performed using different techniques and with modeling results, but also enables predictions of device performance. CRM will not achieve the spatial resolution of EBSD but it is an ambient atmosphere technique that is simpler to implement, especially on larger samples, and can more rapidly provide information on strain if the form of the stress field is known. Hence, there are strong driving forces to increase the accuracy of CRM so as to enable similar comparisons and predictions.
Appendix A: Depth Convolution Analyses
A.1. Numerical integration of FEA simulation results
Calculation of Eqs. 5 and 6 must be implemented in an efficient manner that takes into account, and advantage of, the characteristics of the distortions simulated via FEA. The exponential convolution kernel (Eq. 4) is analytic and well behaved, but the distortion components are piecewise linear (derivatives of quadratic forms) with no guarantee of continuity at element boundaries. For simplicity of notation in this Appendix, x1 is represented as x and x3 is represented as z. Each part of the integral over an individual linear segment was solved analytically in terms of z and the function value f (z) = Aij (z) or f (z) = Δω(z) at the endpoints. The total integral was then the sum of these piecewise integrals. For segment k with endpoint values and the partial integral is
and the resulting simulated value of f(x) is
A.2. CRM weighting function and information depth
The CRM weighting function is exponential as the ingoing and outgoing light is attenuated at a constant rate determined by the material attenuation length for the particular wavelength of light. Light traveling to a depth u3 − z will be attenuated by a factor, e[u3(x)−z]/din. Backscattered and wavelength-shifted light will traverse the same distance while exiting the Si and suffer additional attenuation by a factor e[u3(x)−z]/dout. The total attenuation will be the product that simplifies to the single exponential
Other attenuation effects such as scattering efficiencies are assumed to be independent of strain and z-coordinate so that the relative intensities are well-characterized by the exponential factor. The piezo-Raman contribution is neglected when calculating λout and dout because the piezo-Raman shift is a small part of the total Raman shift, a few cm−1 contrasted with 520.9 cm−1.
References
- 1.Lee ML, Fitzgerald EA, Bulsara MT, Currie MT, Lochtefeld A. J. Appl. Phys. 2005;97:011101. [Google Scholar]
- 2.Hwang JS, Gokarna A, Cho Y-H, Son JK, Lee SN, Sakong T, Paek HS, Nam OH, Park Y, Park SH. J. Appl. Phys. 2007;102:013508. [Google Scholar]
- 3.Marzencki M, Defosseux M, Basrour S. J. Microelectromech. Syst. 2009;18:1444. [Google Scholar]
- 4.Nakabayashi M, Ohyama H, Simoen E, Ikegami M, Claeys C, Kobayashi K, Yoneoka M, Miyahara K. Thin Solid Films. 2002;406:195. [Google Scholar]
- 5.Suhir E. J. Electron. Packag. 2003;125:261. [Google Scholar]
- 6.Srikar VT, Swan AK, Unlu MS, Goldberg BB, Spearing SM. J. Microelectromech. Syst. 2003;12:779. [Google Scholar]
- 7.Troost KZ, van der Sluis P, Gravesteijn DJ. Appl. Phys. Lett. 1993;62:1110. [Google Scholar]
- 8.Wilkinson AJ. Ultramicroscopy. 1996;62:237. doi: 10.1016/0304-3991(95)00152-2. [DOI] [PubMed] [Google Scholar]; Wilkinson AJ. Mater. Sci. Technol. 1997;13:79. [Google Scholar]
- 9.Wilkinson AJ, Meaden G, Dingley DJ. Ultramicroscopy. 2006;106:307. doi: 10.1016/j.ultramic.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 10.Villert S, Maurice C, Wyon C, Fortunier R. J. Microsc. 2009;223:290. doi: 10.1111/j.1365-2818.2009.03120.x. [DOI] [PubMed] [Google Scholar]
- 11.De Wolf I, Vanhellemont J, Romano-Rodriguez A, Norstrom H, Maes HE. J. Appl. Phys. 1992;71:898. [Google Scholar]
- 12.De Wolf I, Maes HE, Jones SK. J. Appl. Phys. 1996;79:7148. [Google Scholar]
- 13.Ma Q, Chiras S, Clarke DR, Suo Z. J. Appl. Phys. 1995;78:1614. [Google Scholar]
- 14.Senez V, Armigliato A, De Wolf I, Carnevale G, Balboni R, Frabboni S, Benedetti A. J. Appl. Phys. 2003;94:5574. [Google Scholar]
- 15.Starman LA, Lott JA, Amer MS, Cowan WD, Busbee JD. Sens. Actuat. A. 2003;104:107. [Google Scholar]
- 16.Beechem T, Graham S, Kearney SP, Phinney LM, Serrano JR. Rev. Sci. Instrum. 2007;78:061301. doi: 10.1063/1.2738946. [DOI] [PubMed] [Google Scholar]
- 17.Vaudin MD, Gerbig YB, Stranick SJ, Cook RF. Appl. Phys. Lett. 2008;93:193116. [Google Scholar]
- 18.Vaudin MD, Stan G, Gerbig YB, Cook RF. Ultramicroscopy. 2011;111:1206. doi: 10.1016/j.ultramic.2011.01.039. [DOI] [PubMed] [Google Scholar]
- 19.Koseski RP, Osborn WA, Stranick SJ, DelRio FW, Vaudin MD, Dao T, Adams VH, Cook RF. J. Appl. Phys. 2011;110:073517. [Google Scholar]
- 20.Bonera E, Fanciulli M, Batchelder DN. J. Appl. Phys. 2003;94:2729. [Google Scholar]
- 21.Schmidt U, Ibach W, Müller K, Weishaupt K, Hollricher O. Vibrational Spectroscopy. 2006;42:93. [Google Scholar]
- 22.Vaudin MD, Osborn WA, Friedman LH, Gorham JM, Vartanian V, Cook RF. Ultramicroscopy. 2015;148:94. doi: 10.1016/j.ultramic.2014.09.007. [DOI] [PubMed] [Google Scholar]
- 23.Bradby JE, Williams JS, Wong-Leung J, Swain MV, Munroe P. J. Mater. Res. 2001;16:1500. [Google Scholar]
- 24.Davies JH. J. Appl. Mech. 2003;70:655. [Google Scholar]
- 25.Cook RF. J. Mater. Sci. 2006;41:841. [Google Scholar]
- 26.Domnich V, Gogotsi Y. Rev. Adv. Mater. Sci. 2002;3:1. [Google Scholar]
- 27.Gerbig YB, Michaels CA, Forster AM, Cook RF. Phys. Rev. B. 2012;85:104102. [Google Scholar]
- 28.Lawn BR, Cook RF. J. Mater. Sci. 2012;47:1. [Google Scholar]
- 29.Mase WE. Continuum Mechanics. New York: McGraw-Hill; 1970. [Google Scholar]
- 30.Winkelmann A, Savat-Pujol F, Werner WSM. Micros. Microanal. 2013;19:738. [Google Scholar]
- 31.Myers GA, Hazra SS, de Boer MP, Michaels CA, Stranick SJ, Koseski RP, Cook RF, DelRio FW. Appl. Phys. Letters. 2014;104:191908. [Google Scholar]
- 32.Gerbig YB, Stranick SJ, Morris DJ, Vaudin MD, Cook RF. J. Mater. Res. 2009;24:1172. [Google Scholar]
- 33.McSkimin HJ, Andreatch P. J. Appl. Phys. 1964;35:2161. [Google Scholar]
- 34.Zhang L, Mahdi M. J. Mater. Sci. 1996;31:5671–5676. [Google Scholar]
- 35.Yoshino M, Aoki T, Chandrasekaran N, Shirakashi T, Komanduri R. Int. J. Mechanical Sci. 2001;43:313–333. [Google Scholar]
- 36.Galanov BA, Domnich V, Gogotsi Y. Exp. Mechanics. 2003;43:303–308. [Google Scholar]
- 37.Vodenitcharova T, Zhang LC. Int. J. Solids Structures. 2003;40:2989–2998. [Google Scholar]
- 38.Vodenitcharova T, Zhang LC. Int. J. Solids Structures. 2004;41:5411–5424. [Google Scholar]
- 39.Kiriyama T, Harada H, Yan J. Semicond. Sci. Technol. 2009;25:025014. [Google Scholar]
- 40.Budnitzki M, Kuna M. Int. J. Solids Structures. 2012;49:1316–1324. [Google Scholar]
- 41.Domnich V, Gogotsi Y, Dub S. Appl. Phys. Lett. 2000;76:2214. [Google Scholar]
- 42.Cheong WCD, Zhang LC. Nanotechnology. 2000;11:173. [Google Scholar]
- 43.Kim DE, Oh SI. Nanotechnology. 2006;17:2259–2265. [Google Scholar]
- 44.Kim DE, Oh SI. J. Appl. Phys. 2008;104:013502. [Google Scholar]
- 45.Zienkiewicz OC, Taylor RL. The Finite Element Method: The Basis. Vol. 1. Woburn: Butterworth-Heinemann; 2002. [Google Scholar]
- 46.Barlow RJ. Statistics: A Guide to the Use of Statistical Methods in the Physical Sciences. Chichester: John Wiley & Sons; 1989. [Google Scholar]
- 47.Anastassakis E, Pinczuk A, Burstein E, Pollak FH, Cardona M. Solid State Communications. 1970;8:133. [Google Scholar]
- 48.Anastassakis E, Cantarero A, Cardona M. Phys. Rev. B. 1990;41:7529. doi: 10.1103/physrevb.41.7529. [DOI] [PubMed] [Google Scholar]
- 49.Chandrasekhar M, Renucci JB, Cardona M. Phys. Rev. B. 1978;17:1623. [Google Scholar]
- 50.Anastassakis E, Liarokopis E. J. Appl. Phys. 1987;62:3346. [Google Scholar]
- 51.Peng C-Y, Huang C-F, Fu Y-C, Yang Y-H, Lai C-Y, Chang S-T, Liu CW. J. Appl. Phys. 2009;105:083537. [Google Scholar]
- 52.Dash WC, Newman R. Phys. Rev. 1955;99:1151. [Google Scholar]
- 53.Green MA, Keevers MJ. Progress in Photovoltaics: Research and Applications. 1995;3:189. [Google Scholar]
- 54.Schmaling B, Hartmaier A. J. Mater. Res. 2012;27:2167. [Google Scholar]