Noninvasive Measurements of Glycogen in Perfused Mouse Livers Using Chemical Exchange Saturation Transfer NMR and Comparison to ¹³C NMR Spectroscopy

Abstract

Liver glycogen represents an important physiological form of energy storage. It plays a key role in the regulation of blood glucose concentrations, and dysregulations in hepatic glycogen metabolism are linked to many diseases including diabetes and insulin resistance. In this work, we develop, optimize, and validate a noninvasive protocol to measure glycogen levels in isolated perfused mouse livers using chemical exchange saturation transfer (CEST) NMR spectroscopy. Model glycogen solutions were used to determine optimal saturation pulse parameters which were then applied to intact perfused mouse livers of varying glycogen content. Glycogen measurements from serially acquired CEST Z-spectra of livers were compared with measurements from interleaved natural abundance ¹³C NMR spectra. Experimental data revealed that CEST-based glycogen measurements were highly correlated with ¹³C NMR glycogen spectra. Monte Carlo simulations were then used to investigate the inherent (i.e., signal-to-noise-based) errors in the quantification of glycogen with each technique. This revealed that CEST was intrinsically more precise than ¹³C NMR, although in practice may be prone to other errors induced by variations in experimental conditions. We also observed that the CEST signal from glycogen in liver was significantly less than that observed from identical amounts in solution. Our results demonstrate that CEST provides an accurate, precise, and readily accessible method to noninvasively measure liver glycogen levels and their changes. Furthermore, this technique can be used to map glycogen distributions via conventional proton magnetic resonance imaging, a capability universally available on clinical and preclinical magnetic resonance imaging (MRI) scanners vs ¹³C detection, which is limited to a small fraction of clinical-scale MRI scanners.

Liver glycogen represents an important physiological form of energy storage. In the postprandial state, the liver takes up approximately one-third of the ingested glucose,¹ the majority of which it stores as glycogen. In the fasted state or in periods of hypoglycemia, the liver shifts to glycogen breakdown and glucose release in order to maintain appropriate levels of glycemia, thereby providing sufficient glucose to other tissues. These states of glucose uptake or release are controlled in a reciprocal manner in part by the hormones insulin and glucagon, primarily via modifications of the activities of the glycogen synthesizing and degrading enzymes. As such, liver glycogen metabolism plays a central role in whole body glucose homeostasis, and its dysregulation is linked to many diseases including diabetes.²⁻⁵

While blood glucose levels can be easily measured and used as diagnostic biomarker, accurate noninvasive measurements of tissue glycogen concentrations are inherently challenging, but of considerable interest for basic scientific and clinical applications. As glycogen is confined to intracellular locations, robust measurements of liver glycogen content have been problematic. The biochemical assay of glycogen following a tissue biopsy is the oldest measurement method, but its invasive nature, along with the potential for regional variation within the liver,⁶ has limited the clinical utility of this approach. The ability to measure glycogen noninvasively in liver and muscle with ¹³C NMR spectroscopy was demonstrated approximately 25 years ago.^7,8 Numerous subsequent studies in type I and type II diabetic patients yielded valuable insights into the dysregulation of both muscle and liver glycogen metabolism in the diabetic state (e.g., refs (9 and 10)). Despite these advances, in vivo ¹³C NMR spectroscopy still remains handicapped by its inherently low signal-to-noise ratio (SNR) due to the low natural abundance and the low gyromagnetic ratio of the ¹³C nucleus, as well as the cost of the often required ¹³C labeled isotopes. Furthermore, the vast majority of clinical magnetic resonance imaging (MRI) scanners lack ¹³C detection capability, and clinical adaptation of this technology will likely remain within the research community only.

Recently, a novel MRI method for detection of tissue glycogen was reported¹¹ based on sensing the chemical exchange of glycogen hydroxyl protons with tissue water. This general method is relatively straightforward to implement on current MRI imaging systems, because only proton detection is required (e.g., refs (12 and 13)). However, whether it can reliably measure physiological concentrations of glycogen and what other factors affect its accuracy have not been established. In this paper, we report experiments using perfused livers that evaluate the proposition that chemical exchange saturation transfer (CEST)-based measurements are able to reliably quantify glycogen levels with high sensitivity.

Proton-based CEST approaches benefit from increased SNR compared to ¹³C NMR spectroscopy and also from the wide availability of ¹H MR hardware. The use of CEST-based approaches to detect other −OH and −NH containing metabolites has been recently reported for glycosaminoglycans,¹⁴ creatine,¹⁵ glutamate,¹⁶ glucose,¹⁷ and 2-deoxy-glucose.^18,19 Despite the demonstration of proof of concept for detection of these metabolites, the optimization, calibration, and quantification (including glycogen) in the tissue of interest using CEST has, for the most part, not yet been reported. Furthermore, in the initial report of CEST-based detection of glycogen,¹¹ there appeared to be a nonlinear and saturating relationship between the amount of glycogen and the CEST signal measured in phantoms over the expected physiological range, calling into question the utility of this approach for measurements of physiological levels of tissue glycogen. Therefore, the goal of this study was to measure the relationship between total liver glycogen (as measured with ¹³C NMR) and the CEST MR signal and to demonstrate that appropriate CEST methods can provide reliable and accurate measurement of liver glycogen. Specifically, our aims were (1) to optimize the acquisition parameters for CEST detection of glycogen over the expected physiological range in phantoms, (2) to use these parameters to perform measurements of perfused liver glycogen with CEST, and (3) to correlate these measurements with those obtained with ¹³C NMR and to investigate the inherent errors in each of these techniques.

Methods

CEST Background

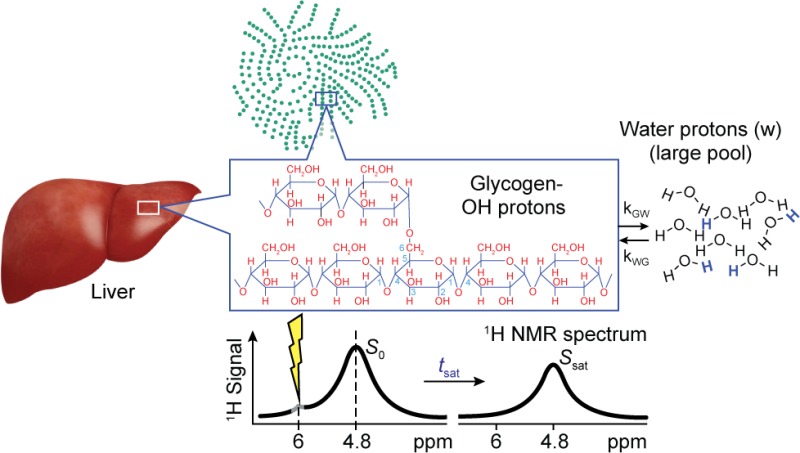
The basis of CEST detection of glycogen hydroxyl protons is shown schematically in Figure 1 where the ¹H NMR signal from a relatively small solute pool (glycogen in this case) with exchangeable protons (Figure 1a) can be indirectly detected via saturation with NMR pulses, transfer of these saturated protons to the hydroxyl functional groups to water, and subsequent measurement of the attenuation of the water ¹H NMR signal (Figure 1b). The series of water peaks acquired at varied frequency offsets (ω) of the saturation pulse is typically called a “Z-spectrum” (Figure 1c) and is used to calculate the magnetization transfer ratio asymmetry (MTR_asym) (Figure 1d) as

1

Here, S represents the water signal observed at a saturation offset ω from the water resonance, and S₀ is the water signal observed at a saturation offset far (>20 ppm) from the water resonance. (Note that we have adopted the standard convention in CEST studies of defining the water resonance to be 0 ppm.) Most reported measures of CEST are based on this MTR_asym parameter; though for some choices of the saturation parameters, there may be factors other than exchange that influence measured values of MTR_asym.

Figure 1.

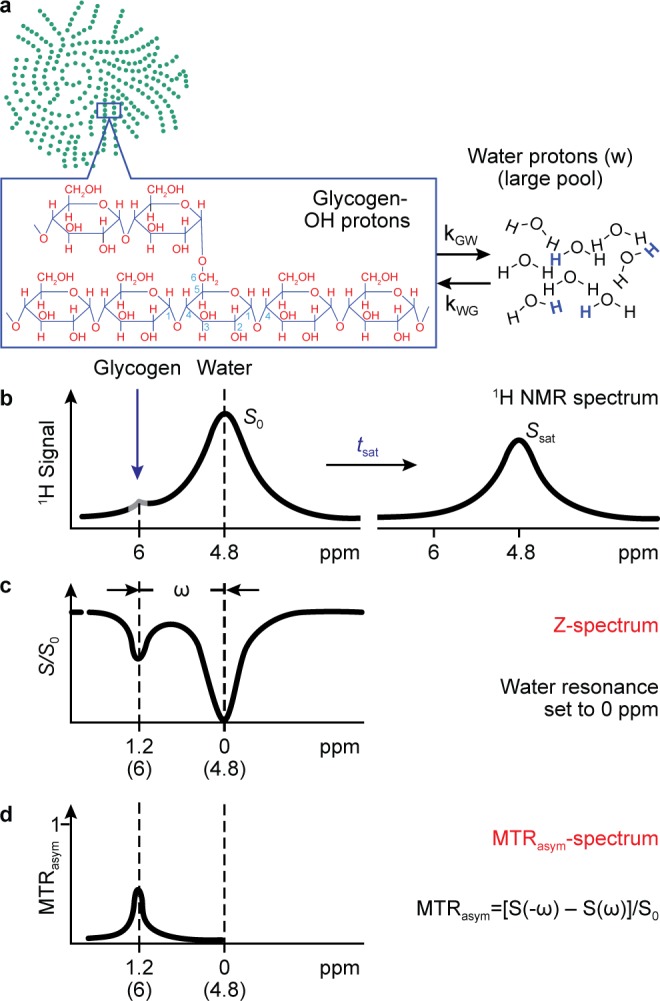
Schematic of CEST phenomena and measurements. (a) Small glycogen pool exchanging hydroxyl protons with a large water pool. (b) Idealized ¹H NMR spectrum showing location of RF irradiation and subsequent reduction in water NMR signal. (c) Plot of normalized signal intensity versus frequency offset of RF irradiation. (d) MTR_asym plot showing asymmetry in the region corresponding to the NMR resonance of the exchangeable glycogen hydroxyl protons. Note that, in c and d, the ppm axis has been adjusted so that the water resonance is at 0 ppm, as often is the convention in CEST studies. (Adapted with permission from ref (25). Copyright 2011 John Wiley & Sons.)

NMR Acquisitions

All studies were performed on a Bruker 500 MHz (11.7 T) vertical bore NMR spectrometer using XWin-NMR 3.2 and a 20 mm TXO probe with ¹³C/³¹P on the inner coil and ¹H/²H on the outer coil with a custom fabricated 20 mm NMR tube. Magnetic field lock was provided by a small (∼0.5 mL) separate sealed tube of D₂O placed inside the 20 mm NMR tube. Natural abundance ¹³C NMR acquisitions were performed using a 15° square pulse, ¹H broadband decoupling, an interpulse delay of 560 ms, and 1600 averages (22 min acquisition time). CEST NMR acquisitions were performed using 32 nonuniformly spaced frequency offsets as follows: ±9, ±8.5, ±8, ±6, ±4, ±2.5, ±2, ±1.75, ±1.5, ±1.25, ±1, ±0.75, ±0.5, ±0.25, ±0.1, 0, and 40 ppm from water. These were chosen to facilitate Lorentzian modeling of the Z-spectrum as described later in the Data Analysis protocol. Saturation pulse power and time for perfused liver studies were optimized using phantom studies (described below) and were 4 μT and 0.5 s. The total repetition time of the sequence was 30 s, which yielded a total scan time of 20 min.

Phantom Studies

Glycogen (oyster, Sigma-Aldrich P/N #G8751) was dissolved in a Krebs-Henseleit buffer supplemented with 0.25% bovine serum albumin, 0.1 mM palmitate, 0.5 mM glutamate, 0.5 mM glutamine, and 2 mM ATP (final pH = 7.4). As the maximum expected concentration of liver glycogen is approximately 400 μmol/g and the maximum expected mouse liver size for these studies was 2 g, phantoms were constructed with up to 800 μmoles of glycogen, measured as glucose equivalents, in the sensitive volume of the NMR probe. CEST spectra were acquired with varying saturation pulse powers and times in order to investigate which combination of parameters yielded a linear relationship between total glycogen and the numerically integrated CEST MTR_asym area under the curve (AUC), with maximal dynamic range. It should be noted that these phantom studies were performed only to determine the optimal saturation pulse parameters and were not used to calibrate the glycogen CEST signal. This is because tissue glycogen will likely have different structural (chain length, branching, protein binding) and relaxation characteristics compared to glycogen in solution.

Perfused Liver Studies

The animals were studied under the purview of an Institutional Animal Care and Use Committee, and all applicable regulations and laws pertaining to the use of laboratory animals were followed. The perfused liver procedure has been published in detail elsewhere²⁰ and is summarized briefly here. C57/BL6 mice (3–6 months old) were fed either normal chow or a high fructose diet (Research Diets Inc. #124908i) for 4–7 days to elevate liver glycogen.²¹ Mice were anesthetized (Nembutal IP, 50 mg/kg) during the dark cycle. Following a laparotomy, the portal vein was exposed and cannulated, and the liver was excised and perfused with a preoxygenated Krebs-Henseleit bicarbonate buffered solution. The liver was then placed into a custom 20 mm NMR tube, and the entire assembly was placed inside the NMR spectrometer. ³¹P NMR spectroscopy was initially performed to assess liver viability via ATP and Pi levels. Following manual shimming adjustments (typical water ¹H line width = 30–50 Hz) and centering of the water frequency, baseline ¹³C NMR and CEST Z-spectra were acquired and followed by the addition of glucagon (100 pM) to the perfusate to stimulate glycogenolysis and thereby provide a range of liver glycogen values to be measured in a single study. Interleaved ¹³C NMR and CEST acquisitions were then performed until liver glycogen reached a level near the ¹³C NMR detection limit, estimated to be ∼50 μmoles. This protocol is shown in Figure 2. A total of 13 perfused liver studies were performed, with each study yielding 1–4 separate glycogen measurements (determined by the starting glycogen content, glycogen breakdown rate, and LOQ).

Figure 2.

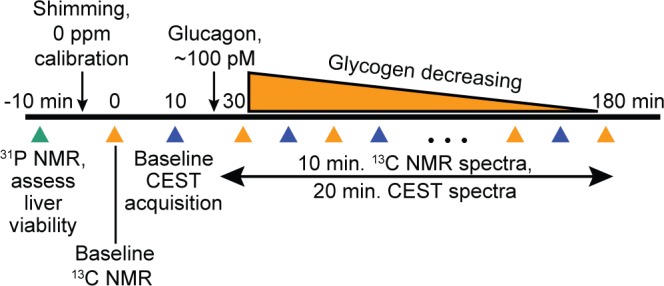
Protocol for measurement of total perfused liver glycogen content using ¹³C NMR and CEST. Glucagon administration was used as a tool to stimulate glycogen breakdown and efficiently generate a range of liver glycogen values over the course of a single study.

Data Analysis

¹³C NMR spectra of glycogen were analyzed with peak fitting programs written in Matlab. Briefly, the glycogen NMR resonances were each fit to a Lorentzian line shape model, the parameters of which were optimized using a least-squares minimization routine. Each modeled resonance was then integrated analytically and the sum of the areas was converted to an absolute amount of glycogen by comparison with a standard curve of glycogen phantoms acquired under identical conditions.

For the CEST acquisitions, all data analysis was performed using Matlab functions. Z-spectra were calculated by first numerically integrating each magnitude ¹H NMR spectrum between +2 and −2 ppm from the water resonance (to avoid the lipid ¹H NMR signal) from each saturation frequency offset. These integrals were then normalized to the corresponding integral of the ¹H NMR signal acquired with a 40 ppm frequency offset to form the Z-spectrum.

For this particular application, the Z-spectrum can be considered as the sum of the CEST contribution and the direct water saturation (DWS) contribution. Starting from the two-site model of chemical exchange and incorporating the weak saturation pulse (WSP) approximation,²² it can be shown that the DWS component of the Z-spectrum is theoretically inverted Lorentzian in shape. Accordingly, experimental Z-spectra were fit over the nonglycogen signal containing regions with an inverted Lorentzian model given by

2

where L₀ is a small DC offset parameter, h is the height, ω₀ is the center frequency, and LW is the line width at 50% peak height. This fit was performed over the nonglycogen signal containing regions of the Z-spectrum using the following subset of saturation frequency offsets: ± 9, ±8.5, ±8, ±0.1, 0, −0.25, −0.5, −0.75, −1, −1.25, −1.5, and −1.75 ppm from water.²³ The glycogen MTR_asym function was then calculated as the difference between the modeled DWS spectrum and the experimental Z-spectrum, i.e.,

3

and this glycogen MTR_asym curve was numerically integrated to yield the final measure of glycogen CEST signal. While this Lorentzian fitting procedure may be subject to small errors due to the potential inclusion of NOE effects in the region used to fit the DWS portion of the Z-spectrum, it should be noted that the direct calculation of the MTR_asym (eq 1) would suffer from the same shortcoming. Furthermore, we observed that this procedure proved superior to the direct calculation of the MTR_asym as it allowed for any slight deviations of the 0 ppm offset to be incorporated into the model and corrected for.

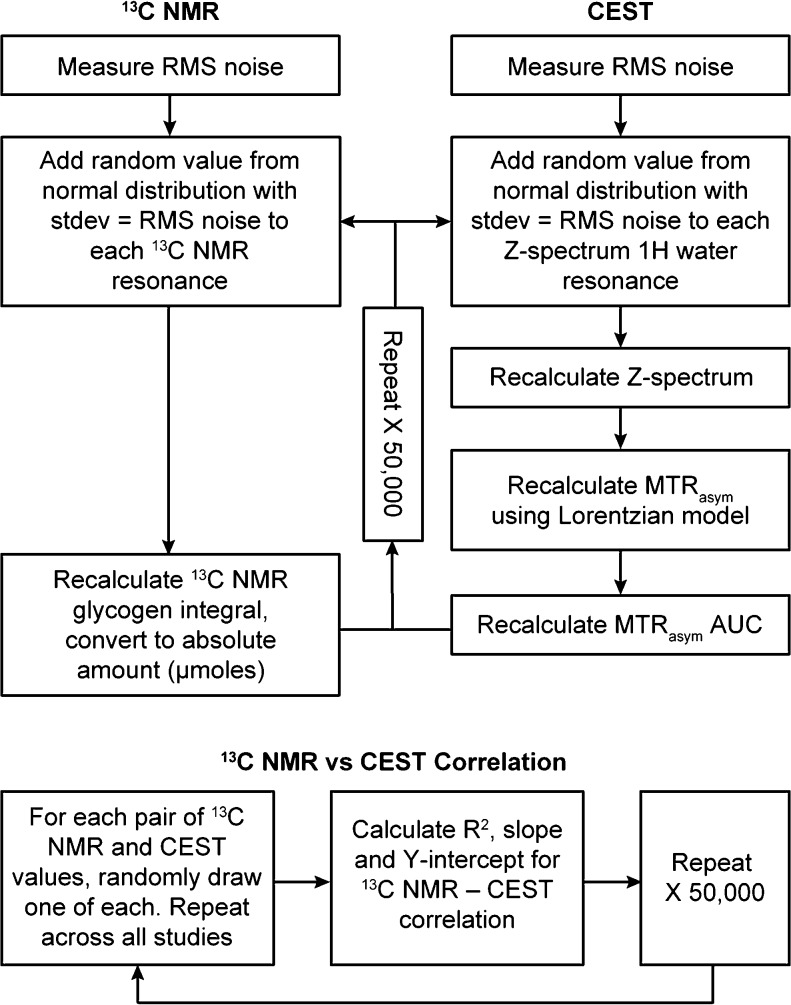
Monte Carlo Error Simulations

As each liver started with a different glycogen level, the calculation of error estimates with repeated measures was not feasible. As an alternative, we used Monte Carlo simulations based on the SNR of the ¹³C and ¹H spectra to generate standard deviations for each ¹³C NMR and CEST measurement, respectively. For the ¹³C NMR errors, a normal distribution with a mean of zero and standard deviation equal to the root-mean-square (RMS) noise of the ¹³C NMR spectrum was created, and random values from this distribution were added to each resonance integral value. The total sum of the areas of the glycogen NMR peaks was then recalculated, and this procedure was repeated 50 000 times to generate a distribution of ¹³C NMR signal areas. The standard deviation of this distribution was used as the horizontal error bar in the plot of ¹³C NMR determined glycogen versus CEST MTR_asym AUC. For the CEST errors, a normal distribution with a mean of zero and a standard deviation equal to the RMS noise of the ¹H NMR spectra in the Z-spectrum was created and random values from this distribution were added to each resonance in the Z-spectrum. The integral of each resonance in the new Z-spectrum was then recalculated, and this new Z-spectrum was fit with an inverted Lorentzian model, from which the MTR_asym AUC could be recalculated as described in the Data Analysis section above. This process was repeated 50 000 times to generate a distribution of MTR_asym AUC values, and the standard deviation of this distribution was used as the vertical error bar in the plot of ¹³C NMR determined glycogen versus CEST MTR_asym AUC.

The correlation between ¹³C NMR determined glycogen and CEST MTR_asym AUC was then investigated by randomly choosing pairs of ¹³C NMR determined glycogen values and CEST MTR_asym AUC values from each distribution for all perfused liver studies, performing a linear regression, and repeating for all 50 000 values in the respective distributions. In this way, distributions for the R², slope, and Y-intercept values characterizing this correlation could be formed and the standard deviation of each was used as an estimate of the error in each of these parameters. This error simulation protocol is shown schematically in Figure 3.

Figure 3.

Schematic showing the simulation protocol used to generate estimates of the inherent errors in the ¹³C NMR and CEST measurements of perfused liver glycogen and also in the correlation between the two measurement methods.

Results and Discussion

Phantom Studies

We first used simple liver tissue-mimicking phantoms to optimize the performance of CEST over the expected physiological range of liver glycogen levels. Figure 4a shows sample Z-spectra (B₁ = 4 μT, 0.5 s) and MTR_asym curves for total phantom glycogen amounts of 0, 200, 400, and 800 μmoles of glucose equivalents. Figure 4b shows a plot of total phantom glycogen versus CEST MTR_asym total AUC for a B₁ = 4 μT saturation pulse with saturation times of 0.25, 0.5, 1, and 2 s. The 0.5 s pulse was defined as optimal based on the observation that it yielded the maximum dynamic range while maintaining a high degree of linearity (R² = 0.96). Studies with lower B₁ values and/or longer saturation times were also performed but, as expected from other reports, resulted in either a reduced dynamic range or a nonlinear relationship. As described in Methods, these phantom studies were performed only to determine the optimal saturation pulse parameters for glycogen and were not used to calibrate the glycogen CEST signal due to expected differences in structural and relaxation characteristics compared to glycogen in tissue.

Figure 4.

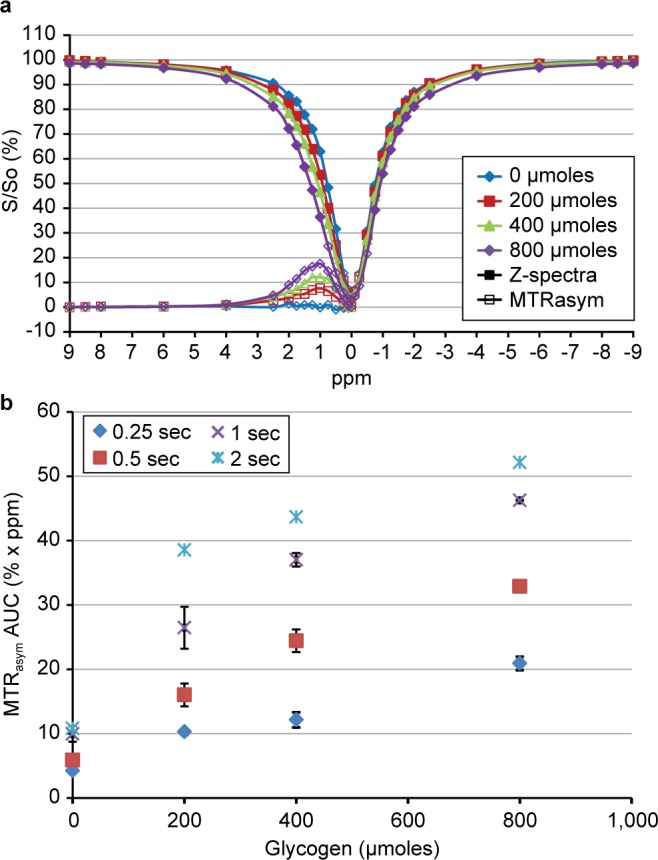
Data from phantom studies showing (a) a sample set of Z-spectra (closed plot symbols) and MTR_asym curves (open plot symbols) for increasing total glycogen amounts for B₁ = 4 μT, 0.5 s, and (b) the relationship between total glycogen and MTR_asym AUC (mean ± SEM, n = 2) for increasing saturation pulse lengths with B₁ = 4 μT.

Our RF-pulse parameters and MTR_asym values were similar to those reported in many other biomolecule CEST studies. We also separately studied the CEST MR signal from glucose in similarly prepared phantoms (data not shown) and found that the CEST signal was approximately 2-fold greater, consistent with the fact that free glucose has 5 exchangeable −OH groups, while the glucosyl units in glycogen have 2–3 exchangeable −OH groups depending on branching within the glycogen molecule.

Perfused Liver Studies

We then performed perfused liver studies using lean C57/Bl6 mice, which were fasted, fed normal chow, or fed a high fructose diet to generate a range of liver glycogen levels. Studies were performed using interleaved natural abundance ¹³C NMR and CEST acquisitions as shown in the protocol in Figure 2. After initial ¹³C NMR and CEST acquisitions, a 100 pM dose of glucagon was added to the perfusion system. Figure 5a,b shows raw ¹³C NMR and CEST data, respectively, acquired in a selected perfused liver experiment. Here, we can see that the 100 pM dose of glucagon stimulated glycogenolysis and served to generate a range of liver glycogen values in a single study. However, since glucagon will also cause glucose release from the liver and since glucose −OH protons have also been shown to have a CEST signal,^11,17 there was likely to be additional CEST signal following glucagon administration. To account for this, data from all the perfused liver studies were separated into two groups, those acquired before glucagon addition and those acquired after glucagon addition.

Figure 5.

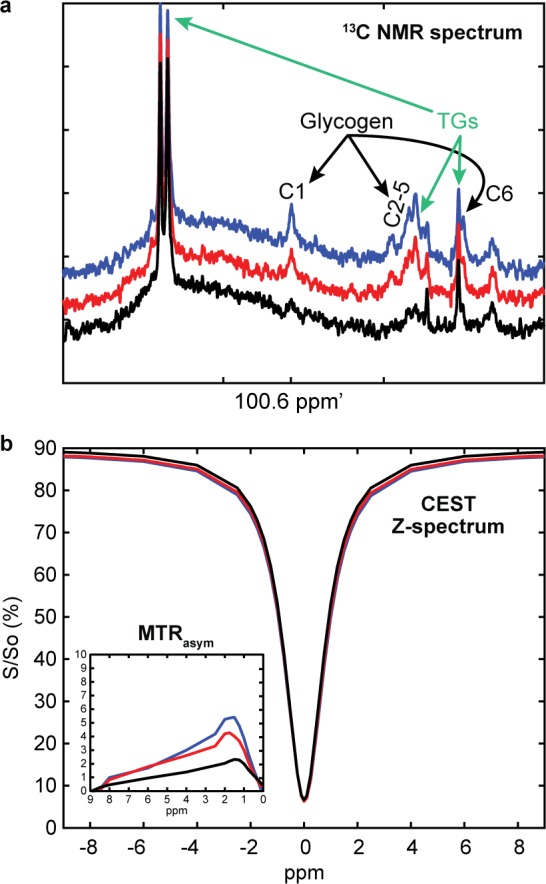
Raw ¹³C NMR (a) and CEST data with MTR_asym inset (b) from a sample perfused liver study for T = baseline (blue), 60 min postglucagon (red), and 120 min postglucagon (black).

We also investigated which region of the MTR_asym curve would be optimal to use for correlation with the ¹³C NMR data by comparing the R² value for the correlation between ¹³C NMR determined glycogen and CEST MTR_asym AUC as different regions of the MTR_asym curve were incorporated into the AUC calculation. Figure 6 shows the dependence of this R² value on which region of the MTR_asym curve was integrated (for fixed integration range of +2 ppm). Here, we see that the region that produced the maximum R² value is 0.5–2.5 ppm which is consistent with the glycogen −OHs being reported to resonate at approximately 1.2 ppm downfield from water.¹¹

Figure 6.

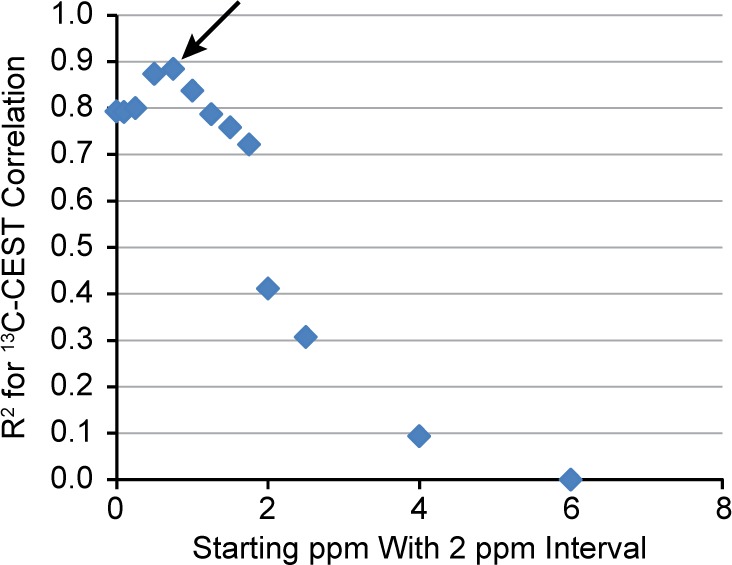
R² value for the ¹³C NMR–CEST correlation as a function of which region of the MTR_asym curve was used for integration. The x-axis represents the beginning of the integration region, and a 2 ppm interval was used. Note that the maximum R² value occurs at approximately 0.5 ppm (arrow) suggesting that the optimal range of the MTR_asym curve to use for integration is 0.5–2.5 ppm. Data shown is for the group of measurements made after glucagon was administered to the perfused livers; however, the data from the preglucagon measurement is similar.

Figure 7 shows a plot of ¹³C NMR determined glycogen versus CEST MTR_asym AUC_0.5–2.5 for data acquired before (blue) and after (red) glucagon. The R² values were 0.88 ± 0.054 and 0.87 ± 0.040; the slope values were 0.0091 ± 0.00078 and 0.0082 ± 0.00064, and the Y-intercept values were −0.50 ± 0.38 and 2.4 ± 0.21, respectively (mean ± SD). Error bars for the data points in Figure 7 as well as for the standard deviations for the correlation parameters were determined by Monte Carlo simulations (see Methods). We observed a strong linear relationship between ¹³C NMR determined glycogen and CEST MTR_asym AUC_0.5–2.5 both before and after glucagon treatment. The slope of the relationship was similar in both groups as evidenced by the overlapping standard deviations. This slope value can be used in future studies as a calibration factor between CEST MTR_asym AUC_0.5–2.5 and total perfused liver glycogen. The fact that the Y-intercept is within two standard deviations of zero (i.e., not statistically different from zero) in the data obtained before glucagon addition demonstrates that there are few competing endogenous CEST metabolites in this spectral region of the liver. The increased Y-intercept value observed after glucagon addition is attributed to glucose release from the liver adding an additional CEST signal during this period of the experiment.

Figure 7.

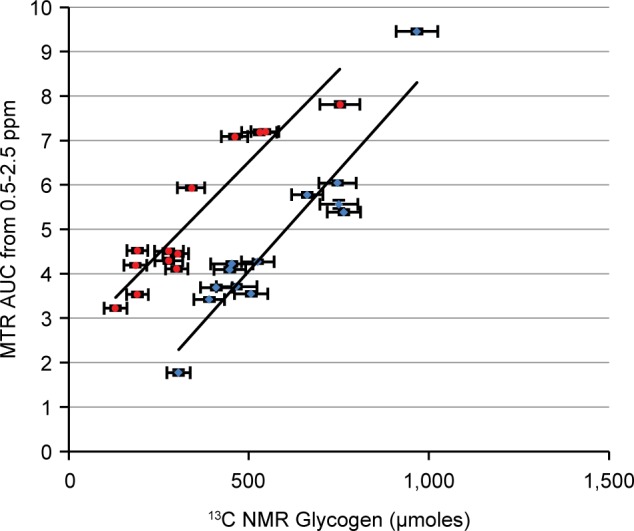
Correlation of CEST vs ¹³C NMR determined total glycogen in perfused livers under baseline conditions (blue) and following glucagon addition (red). Note that the slopes in the two plots appear to be similar while the Y-intercept is higher in the red group due to the release of glucose stimulated by glucagon.

Interestingly, this glucose CEST signal is much higher than would have been predicted on the basis of the expected perfusate glucose concentration of approximately 1 mM in the NMR tube (determined by the perfusion flow rate and observed glycogen breakdown rate) and differences in numbers of exchangeable −OH groups between glucose and glycogen. We noted that, while the linear relationship between total glycogen and CEST MTR_asym that was observed in phantoms was preserved in the perfused liver studies, the overall magnitude of the MTR_asym signal was reduced approximately by a factor of 4 in the perfused liver studies. Factors which could account for this are the lower water relaxation (T_1w) values in liver compared to the phantom solutions, differences in the molecular architecture of glycogen (e.g., branching patterns, number of tiers) in liver compared to that in phantom solutions (oyster glycogen), and also the protein-bound nature of glycogen in tissue.²⁴ The latter could reduce the CEST effect either directly by removing exchangeable glycogen −OH groups or by altering the relaxation properties of the glycogen −OH groups. This observation of reduced glycogen CEST signal in liver has two significant implications in the design of in vivo studies using CEST-based measurements of tissue glycogen. First, glycogen phantom solutions cannot be used to calibrate in vivo tissue glycogen measurements as is often done with the NMR detection of other metabolites/biomolecules. Second, the competing CEST signal from glucose represents a much larger potential hurdle than originally anticipated in the translation of this measurement to an in vivo setting (where glucose is always present in the liver). For example, a typical range of values for liver glycogen is 100–400 mM, while circulating glucose is generally near 5 mM. However, the 4-fold reduction of glycogen signal in liver we observed combined with the approximate 2-fold reduction in exchangeable protons in glycogen suggests that, in vivo, the glucose CEST signal can range from 10% to 40% of the glycogen CEST signal. As such, care must be taken to maintain glucose as constant as possible throughout an in vivo study to allow for specific detection of changes in the glycogen CEST signal. This implies that the use of CEST to measure absolute changes in liver glycogen in vivo would likely perform optimally with a glucose clamp protocol. It should be noted, however, that these studies were performed at 11.7 T which is much higher than most clinical MRI scanners. As such, it is possible that, at lower fields where relaxation times are generally shorter, the amount of competing glucose CEST signal may be different.

Relative Precision of CEST

The error bars for the plot shown in Figure 7, along with the errors reported for the R², slope, and Y-intercept values, were determined by Monte Carlo simulations (see Methods) based on the respective SNR of the ¹³C NMR glycogen spectra and ¹H NMR Z-spectra. These error values allow us to estimate and compare the relative precision inherent to each approach. Defining the relative precision as the ratio of the dynamic range to the average error for each technique, we estimate values of 10:1 and 80:1 for ¹³C NMR and CEST MTR_asym AUC, respectively, implying that CEST is inherently ∼8-fold more precise than natural abundance ¹³C NMR. It is important to realize, however, that this calculation is based solely on the SNR of the original ¹H and ¹³C spectra, and it is likely that other experimental factors such as variations in shimming quality and variations in B₁ pulse power from experiment to experiment could reduce the precision of the CEST measurement. As a preliminary assessment of this, we studied a 40 mM glycogen phantom (prepared as described in Methods) and measured the CEST MTR_asym under the following three conditions: (1) optimal shimming (¹H line width = 40 Hz) with B₁ = 4 μT, (2) suboptimal shimming (¹H line width = 50 Hz) with B₁ = 4 μT, and (3) optimal shimming with B₁ = 3.6 μT (i.e., a 10% error in the B₁ pulse). We found that case (2) produced an error in the CEST MTR_asym of ∼5% while case (3) produced an error of ∼10%. Both of these errors are larger than the SNR-based errors estimated by the Monte Carlo simulations (∼1–2%), demonstrating that variations in experimental parameters are likely to be the dominant source of error in CEST measurements of liver glycogen. In contrast, we routinely observe that errors in ¹³C NMR measurements of glycogen are relatively insensitive to small variations in shimming and other experimental parameters and are dominated mostly by the inherently low SNR of the ¹³C nucleus.

Conclusion

In summary, we have implemented and optimized an experimental protocol in which ¹H CEST NMR was used to accurately and noninvasively measure liver glycogen over the normal physiological range in perfused livers. The CEST data were calibrated by reference to ¹³C NMR spectroscopic data and under appropriate experimental conditions varied in direct proportion to the ¹³C NMR measurement. Using Monte Carlo simulations, we found that inherent errors in glycogen CEST measurements were small and likely to be less important than errors caused by variations in experimental conditions. We found that the CEST signal from glycogen in liver was significantly less than that observed from identical amounts in solution. As a consequence of this, we assert that (1) phantom solutions cannot be used to calibrate in vivo or whole tissue glycogen measurements and (2) free glucose, despite its lower physiological concentration, could still significantly interfere with glycogen CEST measurements.

Our findings open the door for accurate and reliable measurements of tissue glycogen in vivo, assuming that suitable experimental protocols are chosen to keep circulating glucose levels constant. The validated CEST method offers the advantage of using conventional proton MRI scanners and proton detection, which is widely available. Therefore, CEST-based sensing has a strong potential for future clinical translation, which can be used as a tool to noninvasively report glycogen levels. Furthermore, unlike ¹³C detection inherently limited by low SNR, CEST-based imaging methods already demonstrated in vivo could additionally report on the distribution and heterogeneity of in vivo glycogen.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.