Phasing for medical sequencing using rare variants and large haplotype reference panels

Abstract

Motivation: There is growing recognition that estimating haplotypes from high coverage sequencing of single samples in clinical settings is an important problem. At the same time very large datasets consisting of tens and hundreds of thousands of high-coverage sequenced samples will soon be available. We describe a method that takes advantage of these huge human genetic variation resources and rare variant sharing patterns to estimate haplotypes on single sequenced samples. Sharing rare variants between two individuals is more likely to arise from a recent common ancestor and, hence, also more likely to indicate similar shared haplotypes over a substantial flanking region of sequence.

Results: Our method exploits this idea to select a small set of highly informative copying states within a Hidden Markov Model (HMM) phasing algorithm. Using rare variants in this way allows us to avoid iterative MCMC methods to infer haplotypes. Compared to other approaches that do not explicitly use rare variants we obtain significant gains in phasing accuracy, less variation over phasing runs and improvements in speed. For example, using a reference panel of 7420 haplotypes from the UK10K project, we are able to reduce switch error rates by up to 50% when phasing samples sequenced at high-coverage. In addition, a single step rephasing of the UK10K panel, using rare variant information, has a downstream impact on phasing performance. These results represent a proof of concept that rare variant sharing patterns can be utilized to phase large high-coverage sequencing studies such as the 100 000 Genomes Project dataset.

Availability and implementation: A webserver that includes an implementation of this new method and allows phasing of high-coverage clinical samples is available at https://phasingserver.stats.ox.ac.uk/.

Contact: marchini@stats.ox.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Information about the haplotypes underlying diploid genotypes is central to pipelines for a wide range of genetic analyses. Standard examples include inference of human demographic history (1000 Genomes Project Consortium et al., 2012; Hellenthal et al., 2014), detection of signatures of selection (Sabeti et al., 2002) and imputation of untyped genetic variation (Li et al., 2010; Marchini and Howie, 2010). Estimation of haplotypes from genotype data, known as phasing, is typically treated as a problem of computational statistical inference for which there is an extensive literature (Browning and Yu, 2009; Delaneau et al., 2012, 2013b; Li et al., 2010; Stephens et al., 2001; Scheet and Stephens, 2006). Typically, these methods estimate phase for a number of samples together, often augmented by a reference panel of previously estimated haplotypes. They operate by exploiting patterns of linkage disequilibrium (LD) between SNPs and local haplotype sharing between individuals which arise from the processes which generated the data. Consequently, accuracy improves as sample size increases.

Increasingly, however, there is a need for accurate phasing of small or even single samples of sequenced genotypes. This springs from a growing recognition that haplotype information is essential in medical genetics and personal genomics for reasons ranging from assessing the phase of potentially disease-causing recessive mutations (compound heterozygosity) (Fong et al., 2010; Lupski et al., 2010; McLaughlin et al., 2010; Roach et al., 2010; Zschocke, 2008), to prediction of the drug response profiles of patients in order to improve dosing and reduce the extent of adverse reactions (Drysdale et al., 2000). In this setting, the phasing of rarer variants assumes greater importance (Tewhey et al., 2011). This poses an additional challenge for existing computational methods as it is not possible to gain accuracy through joint phasing of a large number of similarly sequenced samples. Therefore, an alternative approach is needed.

One approach to this problem is through direct, experimental phasing which aims to resolve haploptypes as part of the data generation process (Snyder et al., 2015). Dense methods phase all heterozygous sites in blocks up to several mega-bases in length; sparse direct methods provide phase information for a subset of variants across much longer physical distances, but leave many individual variants unphased. To resolve haplotypes over long regions, either blocks covered by dense methods must be overlapped, or computational, population-based inference is required either to link blocks together or to assign phase probabilistically to the many variants left unresolved by sparse methods (Kuleshov et al., 2014; Selvaraj et al., 2013). Inevitably, the accuracy of the probabilistically assigned phase is worse for rarer variants. Moreover, such methods are currently expensive and often labour-intensive.

In this paper, we propose a computational approach to phase small numbers of samples. Our main focus is on samples sequenced at high coverage, so that SNP genotypes can be called without using LD, and for which many rare variants will have been detected. To phase small numbers of samples we take advantage of very large haplotype reference panels that are ever increasing in size and diversity by explicitly using patterns of rare variant sharing between each sample and the reference panel.

For the purposes of describing our new method, we refer to it in this paper as SHAPEITR. It is based on SHAPEIT2 (Delaneau et al., 2013b) which has been shown to be an accurate phasing method for more common heterozygotes, such as those assayed on commercially available genotyping arrays. However, we demonstrate that SHAPEITR can achieve significantly greater accuracy when phasing single samples which include many rare heterozygotes.

SHAPEITR is based on the same underlying HMM as SHAPEIT2 and hence also exploits patterns of LD and local haplotype sharing between individuals. However, it is able both to compensate for the sparse information contained in only a small number of unphased samples and simultaneously to improve the quality of phasing of rarer heterozygotes by exploiting a combination of two things: the rich phase information that is contained in patterns of rare variant sharing between samples and the growing size of haplotype reference panels.

Considerable effort is currently being expended on creating ever larger reference panels. The first reference panel of high-quality estimated haplotypes was provided by The International HapMap Consortium (The International HapMap Consortium, 2005), and consisted of 270 samples from 3 populations at 3.1 million SNPs. This has recently been superseded in both size, variant coverage and diversity by data released by the 1000 Genomes Project (1000GP) (1000 Genomes Project Consortium et al., 2012), the final Phase 3 release consisting of 2504 samples from 26 populations at more than 84 million sites. The UK10K Project (The UK10K Consortium, 2015) has recently sequenced 3781 whole genomes at low depth (average 6.7×). Both the UK10K cohort and the 1000GP have, in turn, very recently been incorporated into a new, much larger panel by the (HRC) Haplotype Reference Consortium (http://www.haplotype-reference-consortium.org). This panel combines 32488 individuals from 20 different cohorts genotyped at 39139 470 SNPs all of which have an estimated minor allele count of at least 5. Future versions of the HRC resource will grow in size and diversity. The 100000 Genomes Project http://www.genomicsengland.co.uk will construct an even larger panel using high coverage sequencing.

As reference panels become larger, the probability of finding a shared stretch of identical sequence between samples increases. We exploit this, but identify putative tracts of sharing in a computationally efficient way by searching for sharing of rare variants. This relies on the simple idea that sharing of such rare variants between two individuals is more likely to arise from a recent common ancestor and, hence, also more likely to indicate longer stretches of similar shared haplotypes. Conceptually our approach is related to that of (Mathieson and McVean, 2014) who identify shared haplotypes based on the sharing of rare variants (doubletons) between individuals. While they use properties of these haplotypes to infer the ages of rare variants, we use rare variant sharing to help infer the haplotypes, specifically via careful choice of conditioning states for an HMM-based phaser. Since we assume that genotypes have been obtained from high-coverage sequencing we also use phase information from reads that span multiple heterozygous sites to gain extra performance (Delaneau et al., 2013a).

2 Methods

To describe our method, we use the following notation: ${\mathit{G}}_i$ denotes a vector of genotypes for the i^th of U unphased individuals at L markers and ${\mathit{H}}^U$ is a set of estimated haplotypes underlying these genotypes; $\mathit{H}$ denotes a set of M reference haplotypes for N individuals and ${\mathit{H}}^{*}$ denotes a subset of $\mathit{H}$ of size K.

A common approach to phasing employs a HMM in which compatible haplotypes underlying each ${\mathit{G}}_i$ are modelled as an imperfect mosaic of haplotypes in ${\mathit{H}}^{*}$ (Scheet and Stephens, 2006). We call these the copying states. Typically, the composition of ${\mathit{H}}^{*}$ varies as we move along the genome. In principle, it could change from one site to the next; in practise the region to be phased is divided into windows of specified size and the same ${\mathit{H}}^{*}$ corresponds to all sites within a window.

When U is large, estimation is done iteratively. Updated estimates of the haplotypes, ${\mathit{H}}^{U_i}$, for the i^th unphased individual are sampled from an HMM in which ${\mathit{H}}^{*}$ is chosen from a set which combines $\mathit{H}$ with ${\mathit{H}}_{\mathrm{\hspace{0.17em}}i}^U$, the current haplotype estimates of all other unphased individuals. The logic behind this approach is that, while imperfect, the estimated haplotypes, ${\mathit{H}}_{\mathrm{\backslash }i}^U$, still contain information useful for phasing ${\mathit{G}}_i$. However, we consider a setting in which U = 1 and so ${\mathit{H}}^{*}$ is chosen simply from $\mathit{H}$. Even if we wished to phase more than a single sample, there is some existing evidence in the literature that when N is much greater than U, little accuracy is usually sacrificed by selecting ${\mathit{H}}^{*}$ only from $\mathit{H}$ (Delaneau et al., 2013b). Nevertheless, we do not wish to completely exclude the idea that incorporating information from ${\mathit{H}}_{\mathrm{/}i}^U$ could be beneficial, and we return to this point in the discussion.

By choosing $K\ll 2N$ we control computational cost, but sacrifice potentially useful information. To mitigate this effect one would like to choose, in each window, a set ${\mathit{H}}^{*}$ comprising the K most informative haplotypes for phasing in that window. Genealogical intuition suggests that one should seek to identify K haplotypes that reside nearest in the genealogical tree to the haplotypes of the individual being updated. However, the structure of the underlying genealogical tree is usually unknown. Therefore, a tractable measure of similarity is required which approximates genealogical distance. This idea underpins the approach used by SHAPEIT2 (Delaneau et al., 2013b) which derives originally from IMPUTE2 (Howie et al., 2009). It also underpins our new approach, SHAPEITR.

To phase single samples using a reference panel, there are two options within SHAPEIT2. In the first approach, (-nomcmc option) the haplotype reference panel is collapsed into a compact graph structure that encodes local haplotype sharing. An initial estimate of the sample’s haplotypes are then obtained using an HMM model that conditions on the haplotypes in this compact graph. We often refer to this as using the SHAPEIT1 model, as the compact graph structure was developed in SHAPEIT1 (Delaneau et al., 2012). These initial estimates are then used to construct ${\mathit{H}}^{*}$ by choosing the K closest haplotypes (in terms of Hamming distance) in $\mathit{H}$ in each window along a chromosome. A final estimate of the haplotypes is then obtained by re-running the HMM on these K haplotypes in each window. The second approach, uses MCMC to iteratively update the haplotypes of the single sample. At each iteration the current haplotype estimates are used to re-estimate the K closest haplotypes in terms of Hamming distance. Due the iterative nature of this approach the method takes longer to run. This approach has been shown to work very well in phasing common sites but can be less accurate in phasing in the vicinity of rarer variants (Delaneau et al., 2013a).

In contrast, our approach exploits the information inherent in rare variants to improve phasing across the allele frequency spectrum. We use rare variants to determine HMM copying states once at the start of the method, and this allows us to avoid using MCMC to estimate haplotypes.

2.1 Using rare variant sharing to determine HMM copying states

Our method of choosing copying states is based on the premise that the sharing of a rare allele by two haplotypes at a given site is a strong indicator of proximity on the genealogical tree: sharing of rare alleles is most likely to arise from a recent common ancestor. The rarer the allele, the more recent the common ancestry is likely to be and, hence, the more likely that the two surrounding haplotypes will be identical by descent (IBD) over a significant interval. An analysis of the 1000 Genomes Project data showed that f₂ variants (variants present twice in the whole sample) typically lie on long shared haplotypes, with a median of ∼0.1 Mb. When searching in a reference panel for individuals that share a rare allele in sample to be phased, we would expect to find an individual with an increasingly longer shared tract when the reference panel increases in size. This occurs since the chance of the reference panel including a sample with a close genealogical relationship increases with increasing panel size. For example, at some point the reference panel will become large enough to contain relatives such as siblings, parents, children and cousins, which are highly likely to share extensive tracts of sequence. Given this intuition, it is natural to select ${\mathit{H}}^{*}$ based on the K haplotypes in $\mathit{H}$ that share the rarest alleles with ${\mathit{G}}_i$ within a window. This is the core of our approach.

Since the population frequency of alleles is unknown we approximate population frequencies by frequencies in the panel. Consequently, our approach derives two benefits from the trend for panels of increasing size: not only are more rare alleles likely to be represented, but the distribution of their counts in the panel will more closely approximate their population frequencies. In addition, our approach also becomes relatively more efficient as panels grow: the computation of allele frequencies need only be performed once.

One noteworthy difference between our new SHAPEITR rare variant selection method and the -nomcmc option in SHAPEIT2 is that SHAPEITR does not depend on any initial estimate of haplotypes consistent with ${\mathit{G}}_i$. We expected that this might lead to less variation in accuracy over different runs of the algorithm, and empirically we observe this (see Section 2).

One way of understanding both the SHAPEITR approach and that of SHAPEIT2 is by comparison to the long range phasing (LRP) method of Kong et al. (Kong et al., 2008). Their method uses rule-based techniques to phase putative unrelateds by identifying ‘surrogate parents’ in local regions of the genome who are informative about the phase of the individual due to shared segments of sequence. In other words, in each region of the genome the method searches for close relatives, with recent shared ancestry, that can help with phasing. However, the method is only applicable when a large enough proportion of the population has been assayed (Kong et al. estimate 10% of a population is needed). SHAPEIT2 is predominantly designed for phasing in smaller sample sizes typically of GWAS and population genetic studies, in which there is only a low probability of being able to find surrogate parents. So a larger set of haplotypes (or ‘surrogate family’) is used as the basis for inferring the phase of each sample, with this set of haplotypes being updated iteratively in a Gibbs sampling algorithm. Our rare variant selection approach can be seen as interpolating between LRP and SHAPEIT2 in the specific case where a large reference panel of haplotypes is available. We use rare variants to better identify the set of close relatives with recent shared ancestry to the sample being phased.

2.2 Algorithm details

We assume that we have already read the following into memory: a panel of reference haplotypes, $\mathit{H}$ in the form of an $L\times 2N$ matrix where consecutive pairs of columns correspond to pairs of haplotypes for the same individual; a list of L genotypes, $\mathit{G}$, for the sample to be phased; and a precomputed list, $\mathit{C}$, of L allele counts at the L sites common to $\mathit{G}$ and $\mathit{H}$. We further assume that we have specified a window size, W, and a number of copying states, K, to find for each window. Our algorithm consists of two steps. First, we construct the set of rare variant sharing patterns between G and H. Secondly, we use this set of sharing information to choose sets of copying states within each window.

Figure 1 consists of a small example of a set of 80 reference haplotypes in a window of 40 SNPs, together with single sample to be phased. The figure caption describes the algorithm for choosing the copying states as applied to this small example. We provided pseudo-code in the Supplementary Material with fine details of the method.

Fig. 1.

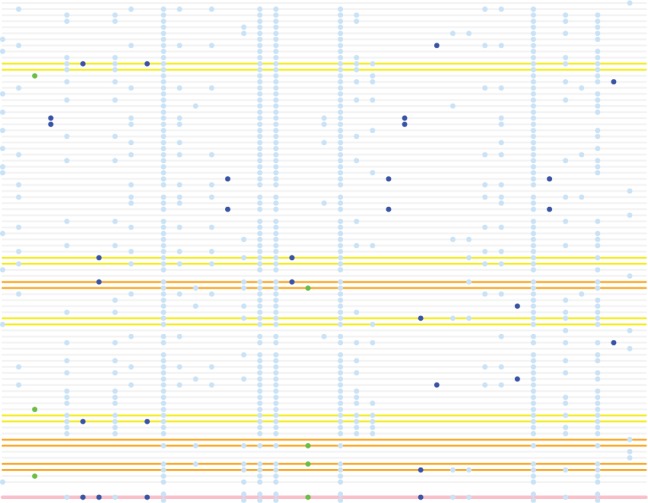
Example of copying state selection. A reference panel of 80 haplotypes in a window of 40 SNPs is represented by horizontal grey lines with non-reference alleles shown as coloured circles. An unphased individual is shown beneath the reference panel (pink line). Alleles at SNPs with a minor allele count (MAC) in the panel of 2 and 3 are coloured dark blue and green respectively. Haplotypes selected due to sharing of alleles with MAC = 2 sites are highlighted in yellow. Haplotypes selected due to sharing of alleles with MAC = 3 sites are highlighted in orange. In total 14 haplotypes are selected using MAC = 2 and MAC = 3 sites. The haplotype selection process proceeds in a similar fashion utilizing MAC >3 sites until K haplotypes are selected

The algorithm begins by generating a set of window boundaries, $\mathit{B}$. This is done simply by choosing a random site within the region to be phased as a seed boundary. Further boundaries are placed by moving outwards from this seed in steps of size W until the end of the region is reached. Typically this can mean that the windows at either end are somewhat narrower than W. However, choosing windows randomly in this way avoids any risk of bias that might result from always starting at one end.

When the window boundaries are chosen, we scan through $\mathit{G}$. When we find an alt. allele that is also a minor allele, if it is also present in the reference panel, we store the position and the number of occurrences of that allele as a pair in a dictionary. Henceforth, we refer to the number of occurrences of a specific allele at a site as the count of that allele at that site. Sites is a list of such dictionaries, one for each window. Armed with this information, we accumulate the indices of the copying state haplotypes for each window in a list, CopyStates, by finding the set of reference haplotypes that match at each allele count, m, starting with the lowest. We do this until we have found K such states for the window or until we have considered all sites. The algorithm is described in Algorithm 1 in the Supplementary Material.

The second step of choosing sets of copying states within each window is described in Algorithm 2 in the Supplementary Material. Although, conceptually straight-forward we highlight two points. Firstly, we add copying states to the list in order of the allele count of the sites at which they match with $\mathit{G}$. Consequently, as the allele count on which we perform the matching increases there will typically come a point when the next set of matching haplotypes will exceed the number we still require. In this case, we simply choose a random subset sufficient to result in a set of size K.

The second point is more subtle. Instead of choosing K independent haplotypes, we choose to select haplotypes in pairs corresponding to reference panel individuals. The idea here is simple: we look for matches at rare alleles, but the phasing of the panel haplotypes themselves would be harder at those sites. Consequently, we expect a proportion of switch errors in the vicinity these sites, each of which will split a potentially highly informative haplotype across the pair. For example, in Figure 1, haplotypes selected due to sharing of alleles with MAC = 2 are highlighted in yellow. By choosing individuals rather than haplotypes when we find a match, we attempt to avoid losing this information.

2.3 Validation haplotypes

To assess phasing accuracy we created a validation set of haplotypes from high-coverage (∼130×) Illumina sequencing data on a mother-father-child of European ancestry which had previously been subject to processing and quality control (Delaneau et al., 2013a). After removing all sites not shared with our reference panel, as well as sites that were heterozygous in all three family members (as these could not be phased unambiguously), we applied simple rules of Mendelian inheritance to phase the resulting set of 202 447 bi-allelic sites for both trio parents.

Using the genotypes derived from our ground-truth haplotypes, we performed experiments to assess the performance of SHAPEITR using SHAPEIT2 as a benchmark. All experiments consisted of phasing runs on the whole of chromosome 20.

2.4 Reference panel

To test the method, we used an existing reference panel derived from the UK10K Cohorts project. This set of 3781 whole genomes has been sequenced at low coverage (average 6.7×) and aims to characterize genetic variation down to 0.1% minor allele frequency in the British population. Initially, BEAGLE (Browning and Yu, 2009) was used to call genotypes and haplotypes. However, re-phasing using SHAPEIT2 has been found to produce significantly higher quality haplotypes in terms of downstream imputation performance (Huang et al., 2014). A set of 26 probable twin pairs were identified by high levels of concordance at a set of 1000 randomly selected bi-allelic sites across the genome. We removed one of each twin pair and filtered sites using VCFtools (v0.1.12b) (Danecek et al., 2011) to create a reference panel for chromosome 20 in the format required by SHAPEIT2. This consisted of a set of 523 913 phased, bi-allelic sites for 3755 individuals.

2.5 Measuring performance

Phasing performance was assessed by the switch error rate. As both algorithms incorporate a stochastic element, we repeated all experiments twenty times and report switch error rates averaged over these runs.

For both algorithms, the region to be phased is divided into windows of specified length. Within each window, a set of K copying states are selected from the reference panel haplotypes. For unphased genotypes derived from sequencing data, SHAPEIT2 has previously been found to give good performance with a window size of 0.5 Mb (Delaneau et al., 2013b) (Supplementary Fig. S3). Therefore we used this window size for all experiments. In contrast, there is a clear trade-off involved in choosing K: as K increases we expect increased accuracy but greater runtime. We compare the sensitivity of both methods to this choice using K = 400 and K = 800.

We also expected that the performance of SHAPEITR would be sensitive to the minimum allele frequency, in the population, of sites used for selecting copying states. We explored the effect of varying the minimum allele count used for selecting copying states between 1 and 20.

SHAPEIT2 is able to improve the phasing accuracy of rare variants by incorporating information from sequencing reads that span multiple heterozygous sites (Delaneau et al., 2013a). SHAPEITR can also use such phase-informative reads (PIRs) to complement the information provided by rare variants. We investigated the utility of this combination using PIRs extracted from the BAM files for the mother-father-child trio using the extractPIRs tool available from the SHAPEIT2 website.

2.6 Using rare variants to rephase UK10K panel

An obvious avenue for development of our rare variant selection method is to phase large sets of genotypes sequenced at high coverage such as those planned by the 100 000 Genomes Project www.genomicsengland.co.uk. As a proof of principle, we performed a simple rephasing of the UK10K panel using SHAPEITR. Using a window size of 0.5 Mb and setting K = 400, we rephased every UK10K sample, using all other samples as a reference panel. Copying states were selected for each individual based on sharing of rare variants with all other panel individuals. Our hypothesis was that even a single pass through the data in this way would already lead to some improvement. We tested this hypothesis by using the rephased panel to phase the trio parents.

2.7 A phasing server

We have created a phasing server that allows clinical samples sequenced at high coverage to be phased against the HRC reference panel or the UK10K reference panels https://phasingserver.stats.ox.ac.uk/. Users can upload their samples, with or without additional phase information from reads, and select a reference panel to be used when phasing. Initially, we have allocated a 16 core server for this purpose and access is restricted to bona fide researchers who wish to phase a small number of clinical samples.

3 Results

Figure 2 compares the performance of SHAPEITR with that of SHAPEIT2. SHAPEIT2 was run both with and without the use of MCMC. In addition, we ran all three methods with and without the use of PIRs. We also ran SHAPEITR using the rephased UK10K panel. Switch error rates are averages across the two trio parents. We use box plots to indicate the variability across the 20 different runs.

Fig. 2.

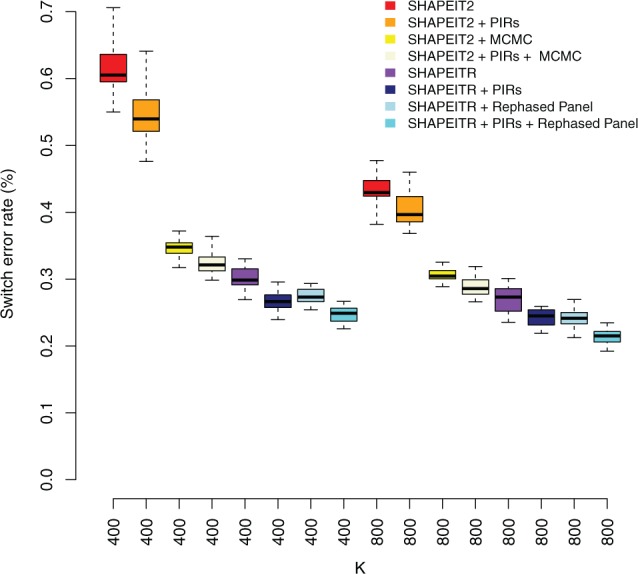
Comparison of switch error rates for trio parents. The box-plot compares the empirical distribution of switch error rates achieved by different methods in 20 different phasing runs of chromosome 20 averaged over the two trio parents. Two different numbers of copying states were used: $K\in \left\{400,800\right\}$ for a single, fixed window size of 0.5 Mb. Methods compared are SHAPTEITR and SHAPTEIT2 with and without use of MCMC. We also applied SHAPEITR using the rephased UK10K panel. All methods were run with and without use of PIRs

SHAPEITR is non-iterative and does not use MCMC. Compared to the non-iterative -nomcmc version of SHAPEIT2, SHAPEITR is considerably more accurate at both K = 400 and K = 800, by 50.8 and 37.6% respectively. In addition, there is much less variability between runs when using SHAPEITR. Typically, only one phasing run is performed so stability across runs is a desirable result.

SHAPEITR also outperforms SHAPEIT2 when using MCMC by 13.0% and 11.6% for K = 400 and K = 800 respectively. This is a significant observation since it speaks to the value of using rare variants to determine copying states in HMM phasing algorithms. By using rare variants we can fix copying states once in advance of running the HMM and completely avoid using MCMC. The resulting method is not only more accurate but, for the results presented here, avoids over an order of magnitude of compute time for the HMM calculations. We used a total of 35 MCMC iterations (the default settings for SHAPEIT2). Averaged over both trio parents and 20 runs, the times taken by these iterations for chromosome 20 were 200.8 and 439.2 s for K = 400 and K = 800 respectively. In contrast, the times taken by SHAPEITR for performing the equivalent computations were 44.3 and 53.7 s.

Rephasing every individual in the UK10K panel using SHAPEITR and then using this panel to help phase the trio parents results in a further increase in accuracy (11.0% at K = 800) when compared to the use of the original UK10K panel. For chromosome 20, this took 15.1 h using 12 CPU cores.

Finally, Figure 2 also indicates that a further improvement in accuracy is obtained in phasing the trio parents by using PIRs.

We investigated how accuracy depends upon reference panel size by repeating the experiments using both half and one quarter of the original UK10K panel. The results are shown in Supplementary Figures S1–S4, and show that reducing reference panel size leads to a reduction in phasing accuracy.

3.1 Properties of using rare variants for state selection

The method of copying state selection used by SHAPEITR is based on the premise that alleles shared between a reference haplotype and an unphased genotype are more phase-informative when they are more rare. Figure 3a supports this presumption. As the minimum allele count used for selecting copying states in SHAPEITR (solid lines) is increased from 1 to 20, it is evident that the improvement in accuracy from using SHAPEITR is steadily eroded. Performance does remain better than SHAPEIT2 without using MCMC which reflects a much better initial choice of copying states. However, the results for K = 400 indicate that, when SHAPEIT2 uses MCMC iterations to update this choice, copying states chosen based on sharing of rare alleles with a minor allele count of ∼6 or greater are already no more informative of phase than the Hamming distance metric employed by SHAPEIT2. As expected, performance for K = 800 is more robust to loss of information from the lowest frequency alleles; typically the number of sites used by our algorithm for copy state selection is greater for larger K. While, on average, the sites corresponding to higher frequency alleles are less informative, their greater number (for K = 800) gives greater coverage within the window.

Fig. 3.

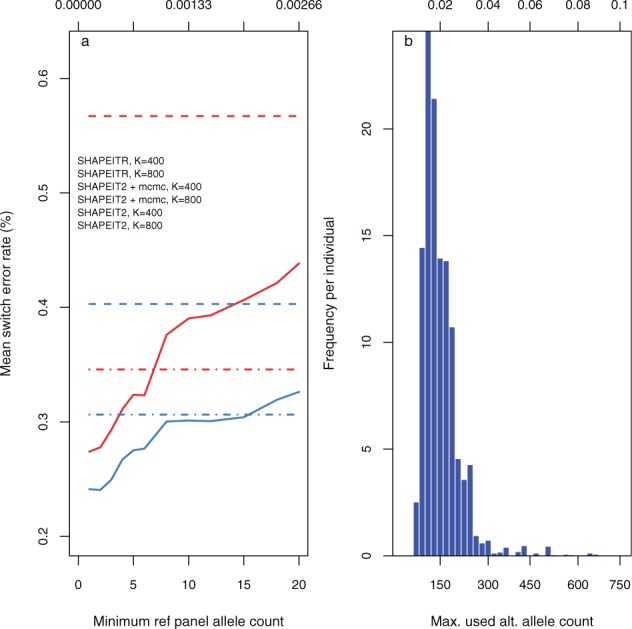
Properties of using rare variants for state selection. (a) Effect on switch error rate of varying the minimum minor allele count used for selecting individuals from whom to copy in SHAPEITR. Horizontal axes: minimum minor allele count (bottom) and corresponding frequency in panel (top) used for selection. Solid lines: mean switch error rates for SHAPEITR; dashed (and dashdot) lines: mean switch error rates for SHAPEIT2 with (and without) MCMC. Colours indicate whether $K=400$ (red) or $K=800$ (blue) copying states were used. In both cases, errors refer to phasing the whole of chromosome 20 and were averaged over both trio parents and 20 runs. (b) Distribution of maximum allele counts used for matching in a single window when choosing K = 400 copying states. Horizontal axis: maximum minor allele count (bottom) and corresponding frequency in the reference panel (top) of a site used for matching. Vertical axis: frequency averaged over both trio parents and 20 different runs. Each bar represents a bin of width $\simeq 0.0027$ corresponding to an allele count of 20

While Figure 3a indicates that performance is strongly influenced by the rarest shared alleles, selection is typically extended to consider sharing at sites further up the frequency spectrum in order to select a full complement of copying states within a window. Figure 3b shows how the maximum frequency of the minor alleles used for selection in a window are distributed when using K = 400. The mean of this distribution is $\simeq 0.0177$ corresponding to an allele count in the panel of $\simeq 133$. While most of the mass of these distributions (90%) lies at minor allele frequencies below 0.027, there is a tail.

The tail is simply explained: we have observed that panel haplotypes which share a rare allele with an unphased individual, also often share several slightly less rare alleles. As we wish to find a number of unique haplotypes as copying states, this often forces the search to proceed further up the allele frequency spectrum than the cumulative sum of allele counts at the sites considered. In such cases, it is likely that the haplotypes that share several rarer variants with the unphased sample carry almost all of the phase information. A second factor is the random placement of window boundaries which occasionally resulted in a window which contained very few rare variants.

4 Discussion

We have shown that large haplotype reference panels can be exploited for phasing of single samples. We have done this by using the sharing of rare alleles between unphased genotypes and individuals in the reference panel to inform the selection of copying states for an HMM-based phasing algorithm. This can already be potentially useful in many contexts in medical genetics, where genotypes have been obtained via high-coverage sequencing.

One important feature of our method is that the selection of copying states depends only on the unphased genotypes. In any iterative extension, this means that the selection of states need be done only once. For existing methods which update copying states at each iteration based on matching of estimated haplotypes, this selection step becomes a computational bottleneck when the number of unphased samples is very large ($>15\hspace{0.17em}000$) and necessitates additional approximations (O’Connell et al. 2015, manuscript submitted). The general principle of using rare variants to pre-calculate which samples are potentially informative for phase offers a potentially more accurate and computationally more tractable approach.

We would expect the benefits of an iterative application of our method to be especially evident in the phasing of whole-genome sequencing data on large cohorts of individuals such as the 100 000 samples being collected as part of the Genomics England project. The high-coverage sequencing and large sample size will uncover a high number of very rare variants. An accurately phased set of haplotypes will be important for downstream analyses such as genotype imputation and demographic inference. We are working towards extending our method for application to such datasets.

Our method relies on access to a large haplotype reference panel. The haplotype reference panels such as those produced by the Genomics England project and the Haplotype Reference Consortium will not be publicly available as has been the case with projects such as HapMap and the 1000 Genomes Project, due to the way in which the study individuals have consented for data release. To address these restrictions we have developed a phasing server that allows clinical samples sequenced at high coverage to be phased against the HRC reference panel or the UK10K reference panels https://phasingserver.stats.ox.ac.uk/.

The method is primarily designed for application to high coverage sequencing data where SNP genotypes can be called very accurately and without using LD. The method could in principle be applied to low-coverage sequencing data, but genotype calling without LD from such data will produce incorrect genotypes, which would affect downstream phasing accuracy.

As we have described it, this approach does not permit the phasing of sites that are polymorphic in the unphased sample, but not represented in the reference panel. One possibility for phasing such sites is to use PIRs (Delaneau et al., 2013a). Our method complements this approach and, as we have shown, can be combined with it. However, in settings where we have a number of unphased samples which perhaps share some rare variants not represented in a reference panel, it would make sense to pool the unphased samples with the reference panel before selecting copying states and then to apply an iterative updating scheme. We are working towards extending our method to do this.

Funding

J.M acknowledges support from the ERC (Grant no. 617306).). W.K acknowledges support from the Wellcome Trust (Grant no. WT097307).

Conflict of Interest: none declared.