FRAGSION: ultra-fast protein fragment library generation by IOHMM sampling

Abstract

Motivation: Speed, accuracy and robustness of building protein fragment library have important implications in de novo protein structure prediction since fragment-based methods are one of the most successful approaches in template-free modeling (FM). Majority of the existing fragment detection methods rely on database-driven search strategies to identify candidate fragments, which are inherently time-consuming and often hinder the possibility to locate longer fragments due to the limited sizes of databases. Also, it is difficult to alleviate the effect of noisy sequence-based predicted features such as secondary structures on the quality of fragment.

Results: Here, we present FRAGSION, a database-free method to efficiently generate protein fragment library by sampling from an Input–Output Hidden Markov Model. FRAGSION offers some unique features compared to existing approaches in that it (i) is lightning-fast, consuming only few seconds of CPU time to generate fragment library for a protein of typical length (300 residues); (ii) can generate dynamic-size fragments of any length (even for the whole protein sequence) and (iii) offers ways to handle noise in predicted secondary structure during fragment sampling. On a FM dataset from the most recent Critical Assessment of Structure Prediction, we demonstrate that FGRAGSION provides advantages over the state-of-the-art fragment picking protocol of ROSETTA suite by speeding up computation by several orders of magnitude while achieving comparable performance in fragment quality.

Availability and implementation: Source code and executable versions of FRAGSION for Linux and MacOS is freely available to non-commercial users at http://sysbio.rnet.missouri.edu/FRAGSION/. It is bundled with a manual and example data.

Contact: chengji@missouri.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Fragment library is one of the key components of widely used fragment-based protein structure prediction methods (Kolodny and Levitt, 2003; Simons et al., 1997), where complete models of the target structures are generated by combining fragments from the library. Therefore, improving speed, accuracy and robustness of fragment library generation have direct impact on the performance of these methods. Several approaches have been introduced over the last decade for fragment detection ranging from exhaustive search to more sophisticated profile hidden Markov models (HMM) based comparison (Kalev and Habeck, 2011). These methods require a template database against which segment of the target sequence is matched in order to identify suitable fragments. Due to large size of the template database that includes all representative structures from the Protein Data Bank (PDB) (Berman et al., 2000), the search is often slow. Moreover, the incomplete coverage of PDB makes it difficult to map a reasonably large fragment for the target protein. Recent developments in fragment selection using probabilistic models (Boomsma et al., 2008; Hamelryck et al., 2006) have shown promising directions to overcome the size and diversity restriction of database-driven approaches by sampling local structure from a generative model. Here, we extend their scope by (i) sampling fragments of protein backbone in full-atomic detail rather than using a coarse-grained representation or assuming ideality in backbone planarity and (ii) allowing robustness against noise in sequence-based predicted information like secondary structure. The resulting application, FRAGSION, has been compared to the popular database-driven fragment assignment protocol of ROSETTA (Gront et al., 2011) on template-free modeling (FM) targets from 11th edition of Critical Assessment of Structure Prediction (CASP11) experiment. The results show that FRAGSION (i) provides slightly better coverage than ROSETTA at the expense of minor loss in precision and (ii) computationally much more efficient than ROSETTA.

2 Methods

FRAGSION is implemented on top of our recently-developed Input–Output Hidden Markov Model (IOHMM) (Bhattacharya and Cheng, 2015) tested in the CASP11. In each slice of the IOHMM, a discrete input node A represents eight groups of residues showing distinct structural behavior (Gly, Pro, Ile/Val, other general residues and each of these groups preceding Pro) selected from twenty standard residue types, while the discrete emission node S denotes the three-state secondary structure types (Helix, Strand and Coil). We model backbone torsion angles pairs ϕ and ψ using mixtures of bivariate von Mises distributions (Mardia et al., 2007) and ω dihedral angle of the peptide bonds using mixtures of univariate von Mises distributions (Mardia and Jupp, 2009). A description of the model, training and model selection is provided in the Supplementary Information. The output emission nodes can be flagged as observed or hidden for a specific sequence position. This enables us to deal with noise in the sequence-derived predicted secondary structure by flagging secondary structure as observed only in residue positions for confident prediction and leaving the rest as hidden. Furthermore, using a probabilistic model makes it possible to sample potentially unlimited sequence of angles accessible to proteins for any given stretch of sequence.

3 Results

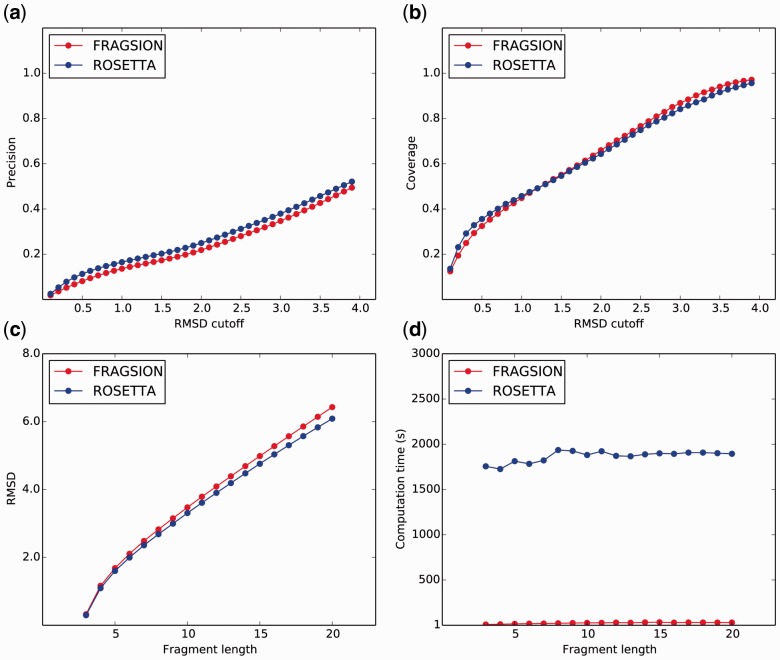
We assessed the performance of FRAGSION using 30 CASP11 FM domains (Supplementary Information) by simulating in a blind de novo protein structure prediction scenario. First, we obtained sequences of the target proteins from CASP11 and executed PSIPRED (Jones, 1999) to predict secondary structure using a non-redundant (NR) protein sequence database curated before CASP11. The sequence and predicted secondary structures were then used to generate 200 fragments for each sequence position with variable fragment lengths ranging from 3-mer to 20-mer. The experimental structures of target domains were then downloaded from CASP11 and the residues that were not present in experimental structures were discarded from fragment libraries. Finally, we assessed the quality of fragment library by superimposing each fragment in the library on to the experimental structure. We used two commonly used metrics to measure accuracy of fragment library: (i) precision (the proportion of good fragments in the libraries): number of good fragments divided by total number of fragments in a library and (ii) coverage (the proportion of protein residues represented by a good fragment): number of residues represented by at least one good fragment divided by number of residues of the target. We also executed ROSETTA’s fragment picker application (Version 3.5) with the same input to generate fragment libraries using a template database created before CASP11 and after excluding all homologues fragments during ROSETTA’s fragment picking. The results show that there is only some minor difference between the performance of FRAGSION and ROSETTA over the entire dataset at various RMSD cutoffs between 0.1 and 4.0 Å (Fig. 1). FRAGSION provides slight advantage in coverage (64 versus 63%) while ROSETTA is slightly better in terms of precision (26 versus 24%). Average RMSD of fragments for different fragment lengths are also comparable (3.8 Å for FRAGSION and 3.7 Å for ROSETTA).

Fig. 1.

Comparison between FRAGSION and ROSETTA. Precision (a), coverage (b) at various RMSD cutoffs and RMSD (c), computation time (d) at different fragment lengths averaged over the dataset generated by FRAGSION (red) and ROSETTA (blue)

To investigate the effect of fragment quality on the performance of de novo protein modeling, we executed AbinitioRelax application of ROSETTA (Simons et al., 1997) to generate two model pools (each pool has 100 models) for each target using 9mer and 3mer fragments from FRAGSION and ROSETTA. The average accuracy of models generated using ROSETTA’s fragments is better than FRAGSION’s in terms of RMSD (19.980 Å for FRAGSION and 17.995 Å for ROSETTA). The most accurate models in terms of TM-score (Zhang and Skolnick, 2004) using ROSETTA’s fragments outperforms that of FRAGSION’s for all targets. Accuracy of FRAGSION’s best prediction in terms of RMSD, however, is better than ROSETTA’s for six targets. The models having the lowest ROSETTA energy generated using FRAGSION’s fragment library outperforms that of ROSETTA’s for ten targets in terms of RMSD and only for three targets in terms of TM-score. In general, the accuracy of models generated using ROSETTA’s fragments is better than FRAGSION’s. The most significant advantage of FRAGSION is, therefore, speed. Average computation time for FRAGSION takes only 24 s, more than 75 times faster than ROSETTA with average computation time exceeding 30 min. A target-by-target comparison between FRAGSION and ROSETTA is presented in the supplementary document along with analysis on the qualities of the model pools produced using fragments generated by FRAGSION and ROSETTA.

4 Conclusion

We developed an easy-to-use software tool (FRAGSION) based on an input-output hidden Markov model (IOHMM) to sample structural fragments for proteins. The model-based tool without carrying a large fragment database is light-weighted and very fast and has the performance comparable to some widely used fragment generation tool, which makes it a useful tool for template-free protein structure modeling.

Funding

This work has been supported in part by the US National Institutes of Health (NIH) grant (R01GM093123) to J.C.

Conflict of Interest: none declared.