Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue

Abstract

The ultimate promise of diffusion MRI (dMRI) models is specificity to neuronal microstructure, which may lead to distinct clinical biomarkers using noninvasive imaging. While multi-compartment models are a common approach to interpret water diffusion in the brain in vivo, the estimation of their parameters from the dMRI signal remains an unresolved problem. Practically, even when q space is highly oversampled, nonlinear fit outputs suffer from heavy bias and poor precision. So far, this has been alleviated by fixing some of the model parameters to a priori values, for improved precision at the expense of accuracy. Here we use a representative two-compartment model to show that fitting fails to determine the five model parameters from over 60 measurement points. For the first time, we identify the reasons for this poor performance. The first reason is the existence of two local minima in the parameter space for the objective function of the fitting procedure. These minima correspond to qualitatively different sets of parameters, yet they both lie within biophysically plausible ranges. We show that, at realistic signal-to-noise ratio values, choosing between the two minima based on the associated objective function values is essentially impossible. Second, there is an ensemble of very low objective function values around each of these minima in the form of a pipe. The existence of such a direction in parameter space, along which the objective function profile is very flat, explains the bias and large uncertainty in parameter estimation, and the spurious parameter correlations: in the presence of noise, the minimum can be randomly displaced by a very large amount along each pipe. Our results suggest that the biophysical interpretation of dMRI model parameters crucially depends on establishing which of the minima is closer to the biophysical reality and the size of the uncertainty associated with each parameter.

INTRODUCTION

Diffusion MRI (dMRI) is sensitive to the micrometer-scale displacement of water molecules and has therefore become an invaluable clinical diagnostic tool, particularly in neuroimaging. Empirically, the diffusion signal in brain tissue is sensitive to the density, orientation and permeability of barriers (e.g. myelin) and the presence of various cell types and organelles (e.g. cell bodies, dendrites, axons, neurofilaments and microtubules) (1). In other words, dMRI can in principle provide information about the tissue microstructure on a much smaller scale than that of the actual image resolution: micrometers versus millimeters. This technique has therefore found numerous applications in the study of processes and pathologies known to alter the microstructure of white or gray matter: brain development (2–6), aging (7,8), stroke (9,10), traumatic brain injury (11,12), multiple sclerosis (13,14), Alzheimer’s disease (15,16), etc.

There are two complementary approaches for analyzing the diffusion signal: either signal representations or tissue models, with the distinction between the two along the lines of sensitivity versus specificity.

Signal representation is a phenomenological, i.e. model independent, approach. Arguably the most popular signal representation is the cumulant expansion (17), which is a Taylor expansion of the logarithm of the signal in the powers of the diffusion weighting parameter b:

$$\text{ln}\frac{S}{S_0}=-b\sum _{i,j=1}^3{g}_i{g}_j{D}_{ij}+\frac{1}{6}{b}^2{\overline{D}}^2\sum _{i,j,k,l=1}^3{g}_i{g}_j{g}_k{g}_l{W}_{ijkl}+\dots$$ [1]

where S₀ = S(b = 0), $\overline{D}=\frac{1}{3}\mathrm{\Sigma }{D}_{ii}$ is the mean diffusivity, and g_i are the components of the unit vector g in the direction of the applied diffusion-weighting gradient. D_ij and W_ijkl are the components of the diffusion and kurtosis tensors, respectively (18,19).

While being sensitive to the underlying tissue microstructure, empirical signal representations such as diffusion tensor imaging (DTI) and diffusion kurtosis imaging (DKI) lack specificity. For example, a change in fractional anisotropy (FA) or in mean kurtosis in a white matter region can be the result of demyelination, axonal degeneration, inflammation, etc. Therefore, the complementary approach is to fit an analytical expression derived from a theoretical model to the measured dMRI signal, in search of improved specificity.

Modeling of the dMRI signal relies on distinct assumptions about tissue structure and is by construction specific to a particular tissue type, in contrast to the universally applicable series [1]. The promise of microstructural specificity has recently elevated the interest to dMRI models of neuronal tissue. In the past few years, several such models for white or gray matter have been proposed (20–28).

While each of these models has its own specific assumptions, they have many common features. The tissue is separated into two (sometimes three or more) compartments with negligible exchange between them, each weighted by a volume fraction f_i such that Σ_if_i = 1. The two principal compartments represent the intra-and extra-neurite spaces. The neurites (dendrites and axons) are modeled as long narrow cylinders. The presence of these highly anisotropic structures is a distinctive signature of neuronal tissue and of all corresponding models. The orientation distribution function (ODF) of the neurites however has been modeled in a variety of fashions, from perfectly parallel orientations (20,22,26) to an expansion in spherical harmonics up to L = 2 (24) and L = 4 (25), as well as by employing convenient functional forms with few parameters (e.g. the Watson distribution, characterized by a main orientation and a concentration parameter κ (27)).

Diffusion inside neurites is characterized by a diffusivity D_a along the neurite; for clinically relevant diffusion times (t > 50 ms), the intra-neurite perpendicular diffusivity is negligible and neurites can be modeled as “sticks” (cylinders with zero radius). The extra-neurite compartment encompasses both the extracellular matrix and cell bodies, assuming they are in fast exchange over the diffusion time t. It is usually modeled as a Gaussian anisotropic compartment, orientationally correlated with the neurite ODF, and characterized by axial and radial diffusivities D_e,‖ and D_e,⊥. When accounted for, the third, cerebrospinal fluid (CSF) compartment is modeled as Gaussian isotropic, characterized by a diffusivity D_iso = 3 µm²/ms at body temperature.

The total number of parameters that need to be estimated quickly increases with model complexity. This, in itself, is not a problem since q space is often oversampled; it is not uncommon to have N ~ 100 q-space points.

Unexpectedly, even when the number of measurements exceeds the number of neuronal tissue model parameters by an order of magnitude, parameter estimation (fitting) suffers from extremely poor precision. The typical fix to this problem is to make further simplifying assumptions in the model and set certain parameters to a priori values (27,29). Unfortunately, while making the fit more precise, fixing parameters to given values with little or no biological validation may introduce substantial bias in the remaining, estimated parameters. This approach seems to defeat the purpose of biophysical modeling: if parameters can no longer mirror the underlying biological reality, they become mere “indices”, potentially with as little specificity as the model-independent metrics of the cumulant series [1].

In this work, we examine parameter estimation in detail for a representative two-compartment model where the above issues are already manifest. We have specifically chosen this model so that it meets the following criteria simultaneously: (i) it is representative of a broad class of neuronal models mentioned above; (ii) it captures the main geometrical and biophysical features of neural tissue; and (iii) it is simple enough (with only five parameters) to allow us to uncover the fundamental issues in parameter estimation in a way that is still tractable and easy to illustrate. Because the model is fully representative of a broad class, we expect these issues to come up in models with more parameters, as it has been independently analytically confirmed in a parallel line of work (30).

The model considered here, which we previously dubbed NODDIDA (6), is a variation of NODDI (neurite orientation dispersion and density imaging) (27) with all diffusivities released (NODDI with diffusivity assessment) and the CSF compartment neglected. NODDIDA is better suited to a clinical acquisition setting than CHARMED (composite hindered and restricted model of diffusion) (21), AxCaliber (22) or ActiveAx (20): the diffusion gradients are sufficiently small and the diffusion time sufficiently long for the non-Gaussian effects in each compartment to be neglected, such as restricted diffusion across the neurite diameter. A detailed description of both NODDI and NODDIDA is provided in the next section. By examining the minimization landscape of the parameter estimation problem defined by this model, we reveal the existence of an intrinsic duality of solutions, and thereby uncover the underlying reasons for the poor precision and significant bias (unrelated to Rician noise bias) in parameter estimation.

THEORY

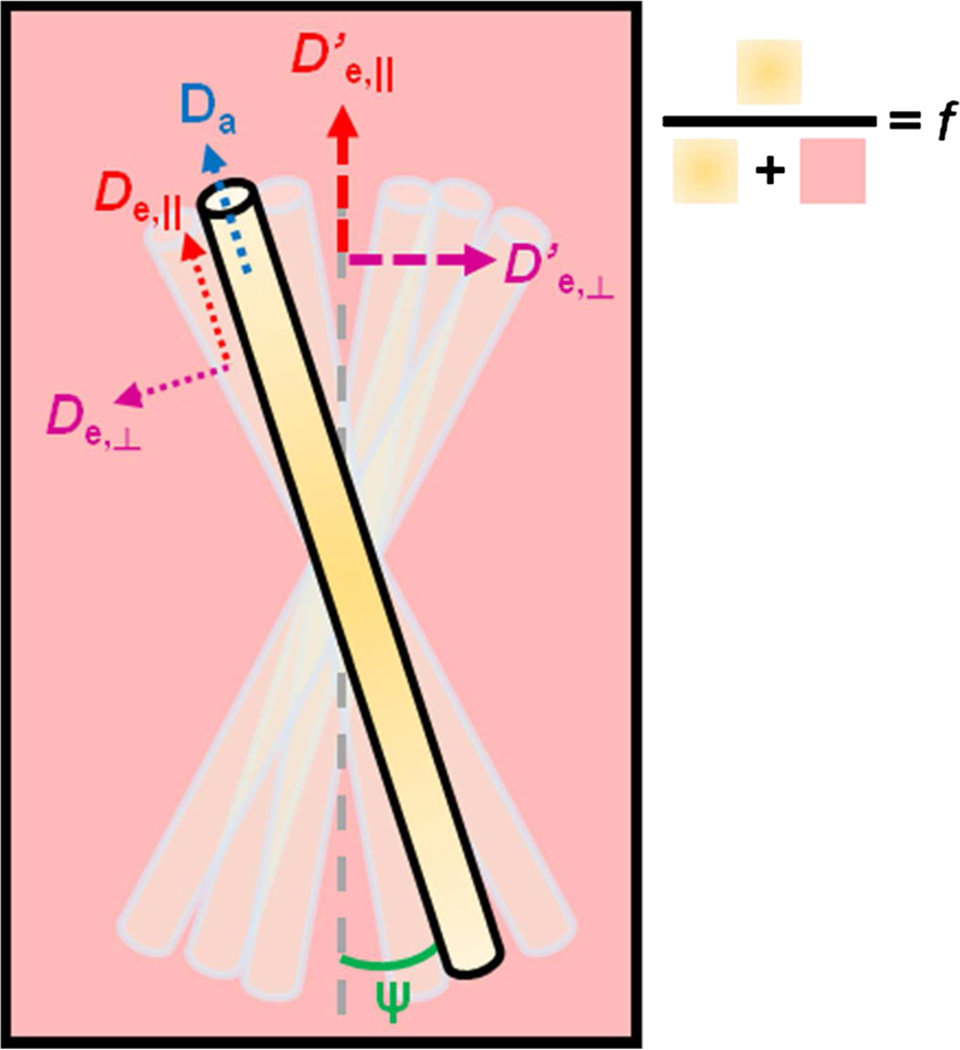
We consider the water dMRI signal to originate from two distinct compartments, restricted intra-neurite and hindered extra-neurite, and we neglect the CSF compartment for simplicity. As in NODDI, we assume neurites to be perfectly aligned locally, forming coherent domains (fiber tract segments or sub-bundles) (Fig. 1), and we model the orientation distribution of these domains by an axially symmetric Watson distribution, characterized by a concentration parameter κ. Small values of κ correspond to large fiber dispersion (e.g. gray matter) and large values of κ to highly aligned axons (e.g. white matter tracts). The model signal in the unit diffusion gradient direction g with the b-matrix bgg^T is therefore

$$S(b,\mathbf{g})/S_0=f{\int }_{{𝕊}^2}W(\mathbf{n}){\mathrm{e}}^{-b{D}_{\mathrm{a}}{(\mathbf{g}·\mathbf{n})}^2}\mathrm{d}\mathbf{n}+(1-f){\mathrm{e}}^{-b{\mathbf{g}}^{\mathrm{T}}{({\int }_{{𝕊}^2}W(\mathbf{n}){\hat{D}}_{\mathrm{e}}(\mathbf{n})\mathrm{d}\mathbf{n})}_{\mathbf{g}}}$$ [2]

where f is the intra-neurite water fraction, D_a is the intra-neurite diffusivity, D̂_e (n) = D_e,‖ nn^T + D_e,⊥ (1 − nn^T) is the local axially-symmetric extra-neurite tensor with the eigenvalues given by the axial and radial diffusivities D_e,‖ and D_e,⊥, and $W(\mathbf{n})=M{(\frac{1}{2},\frac{3}{2},\kappa )}^{-1}{\mathrm{e}}^{\kappa {(\mathbf{\mu }·\mathbf{n})}^2}$ is the Watson ODF characterized by the mean orientation μ and the concentration parameter κ around this orientation; the ODF normalization factor 1/M is given in terms of a confluent hypergeometric function. For a more intuitive measure of orientation dispersion, κ is related to the mean cosine squared, c₂, over the neurite ODF (27):

$$c_2\equiv \langle {\text{cos}}^2\psi \rangle =-\frac{1}{2\kappa }+\frac{1}{\sqrt{\pi }{\mathrm{e}}^{-\kappa }\text{erfi}(\sqrt{\kappa })\sqrt{\kappa }},\hspace{1em}\text{where}\hspace{1em}\frac{1}{3}\le c_2\le 1.$$ [3]

Figure 1.

Schematic diagram of the NODDIDA neuronal tissue model. Neurite sub-bundles have a given orientation distribution about the main bundle axis (vertical axis in the figure). The local diffusivities within each subbundle are denoted as D_a, D_e,‖ and D_e,⊥. Apparent diffusivities D’_e,‖ and D’_e,⊥ for the extra-neurite space in the whole voxel can be calculated as D’_e,‖ = D_e,‖·c₂ + D_e,⊥(1−c₂) and D’_e,⊥ = (D_e,‖(1−c₂) + D_e,⊥(1 + c₂))/2.

Assuming the main orientation μ can be obtained independently by calculating the principal eigenvector of the overall diffusion tensor, there are six parameters to be estimated in this model: f, D_a, D_e,‖, D_e,⊥, κ and S₀. The estimation of the unweighted signal amplitude S₀ is very robust and presents no practical difficulty. Fitting is a minimization procedure of an objective function F with respect to all model parameters. Effectively, the objective function to be minimized here is

$$F=\frac{1}{N}\sum _{i=1}^N{(S_i-S(b_i,{\mathbf{g}}_i))}^2$$ [4]

in a remaining five-dimensional (5D) parameter space, where N is the number of q-space measurements S_i. While different optimization criteria can be used, in this work we chose, without loss of generality, to focus on nonlinear least squares estimation. In this context, the data analyzed, whether stemming from acquisitions or simulations, will have a signal-to-noise ratio (SNR) of 5 or higher, such that Rician bias is minimal and the least squares minimization is equivalent to the maximum likelihood (31).

In NODDI, although an additional isotropic compartment is considered, which adds a parameter f_iso to the model, both local intra- and extra-neurite axial diffusivities are set equal to each other and fixed to a given value D_a = D_e,‖ = D_‖ (1.7 µm²/ms in adults and 2 µm²/ms in newborns (27,32)). Additionally, the radial diffusivity of the extra-axonal space (i.e. perpendicular to the sub-bundle) is related to other parameters via the mean-field tortuosity model (33):

$$D_{\mathrm{e},\perp }=D_{\mathrm{e},\Vert }(1-f)$$ [5]

thus constraining the model significantly. The validity of these approximations has been discussed elsewhere (6).

In this work, we focus on the possibility of characterizing the full two-compartment model with all diffusivities released, and the issues and questions that arise while finding the minimum of the function F in Equation [4].

METHODS

MATLAB scripts from the NODDI toolbox (34) were modified to suit the assumptions of NODDIDA: free independent estimation of D_a, D_e,‖ and D_e,⊥ in addition to f, κ and S₀, and no CSF compartment (f_iso = 0). The fitting procedure was also modified to use a Levenberg–Marquardt algorithm with box constraints, implemented in C and compiled for MATLAB (35). Optimization settings included the following: initial damping factor 10⁻³/stopping thresholds 10⁻¹⁷/maximum iterations 1000. The Jacobian was provided analytically. The box constraints were f ∈ [0 1]; D_a, D_e,‖, D_e,⊥ ∈ [0 4]; κ ∈ [0 64]. The upper bound on diffusivities was relaxed to 4 µm²/ms instead of 3 µm²/ms because of possible overshoot of the free diffusivity value at 37 °C due to noise, Gibbs ringing and/or CSF pulsation.

Experiment

Clinical data

Data from one healthy volunteer (67 year old female) was used to provide an initial assessment of the fitting behavior. The subject was scanned after giving informed consent as approved by our Institutional Review Board. MRI images were acquired on a 3 T Siemens system (mMR Biograph, Siemens Medical Solutions, Erlangen, Germany) with a 12-channel head coil for reception. Diffusion-weighted images were acquired with b = 0 (four averages with anterior–posterior and one average with posterior–anterior phase encoding directions), b = 1 ms/µm² (20 directions), b = 1.5 ms/µm² (20 directions) and b = 2 ms/µm² (30 directions), using a twice-refocused spin-echo echo planar imaging (EPI) sequence. Other imaging parameters were TE/TR = 96/8200 ms, FOV = 230 × 230 mm², in-plane resolution = 2.5 × 2.5mm², 50 slices, thickness = 2.5mmand no gap. Images were reconstructed using the adaptive combine algorithm.

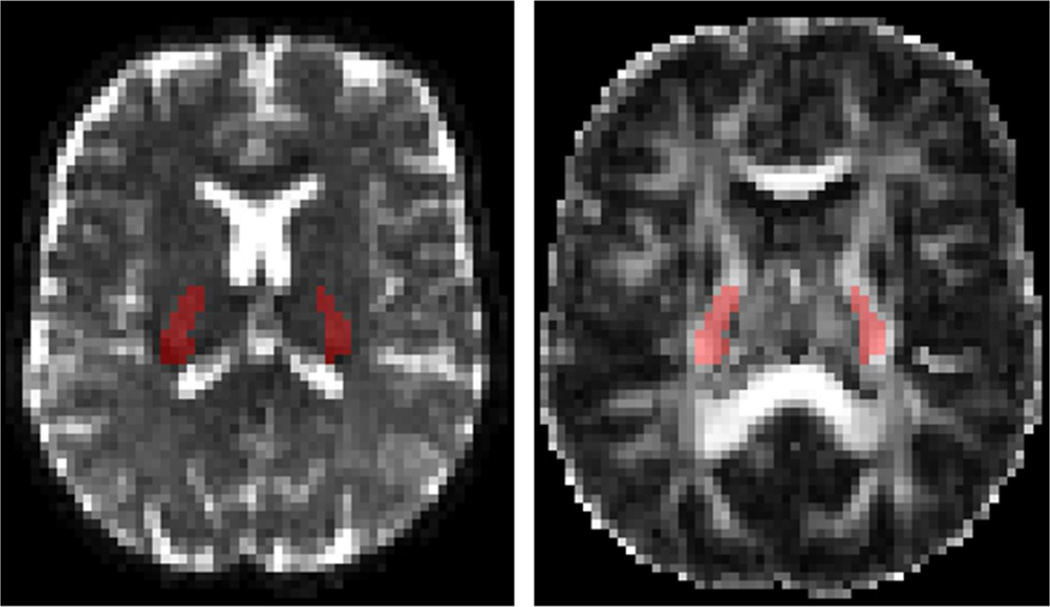
Pre-processing consisted in combined eddy-current and EPI distortion corrections with FSL’s “EDDY” (36). A parametric FA map was calculated after tensor fitting using a weighted linear least squares algorithm (37). It was used as a guide for region of interest (ROI) drawing and voxel selection. The posterior limb of the internal capsule (PLIC) was manually drawn and an additional FA threshold was applied to the ROI (FA > 0.4) (Fig. 2). The PLIC was chosen as an ROI because it represents a relatively large white matter tract and, compared with the corpus callosum, has limited Gibbs ringing artifacts (38) and CSF contamination. The latter feature also justifies neglecting the CSF compartment in the model. The mean SNR over all voxels in the PLIC and all directions at b = 2 ms/µm² was 5.3 (39), which is above the threshold for significant Rician bias (40) and justifies the use of the least squares minimization.

Figure 2.

Clinical dataset: b = 0 image (left) and FA map (right, scaled 0 – 0.8). The PLIC ROI is shown in red. Note that the entire ROI covers several axial slices, of which only one is shown here.

In a first step, Equation [2] was fit to the data from each voxel in the PLIC using a different uniformly distributed random initialization within the parameter intervals¹ 0.2 ≤ f ≤ 0.8; 0.5 ≤ D_a, D_e,‖ ≤ 3; 0.1 ≤ D_e,⊥ ≤ 2.0; 1/3 ≤ c₂ ≤ 1, with c₂ further converted into κ. In a second step, three representative voxels of interest were chosen: one in the right PLIC (FA = 0.62), one in the splenium (FA = 0.89) and one in the right thalamus (FA = 0.34). For each of the voxels, the nonlinear fit was performed for 2500 different initializations, randomly chosen from the same parameter intervals as specified above, in order to determine the dependence of the fit output on initialization.

Last, one slice in the mid-axial plane was selected. For each brain voxel in the slice, the nonlinear fit was performed with 50 different random initializations. Out of the 50 outcomes, the one associated with the lowest objective function F (Equation [4]) was retained. A parametric map illustrating the “best fit” solution in each voxel was produced.

Human Connectome Project (HCP) data

One dataset was downloaded from the WU-Minn HCP database (subject no. 100307). Briefly, the diffusion protocol consisted in 18 b = 0 images and b = 1/2/3 ms/µm² with 90 directions each. Other parameters included TE = 89.5 ms/TR = 5520 ms/FOV = 210 × 180 mm², in-plane resolution = 1.25 × 1.25 mm², 111 slices, thickness = 1.25 mm.

A parametric FA map was calculated after tensor fitting using a weighted linear least squares algorithm (37) and was used as a guide for ROI drawing and voxel selection. The PLIC was manually drawn and an additional FA threshold was applied to the ROI (FA > 0.4).

As for the clinical dataset, Equation [2] was first fit to the data from each voxel in the PLIC using a different uniformly distributed random initialization. In a second step, a representative voxel of interest was chosen in the right PLIC (FA = 0.83). The nonlinear fit was repeated for 2500 different random initializations.

Simulations

Synthetic dMRI signals were calculated based on the model described in Equation [2], with ground truth parameter values taken to be the two possible solutions (Sets A and B) found through the fitting procedure on the single PLIC voxel described above. For reference, values are collected in Table 1.

Table 1.

Two sets of possible solutions of the NODDIDA model applied to a voxel in the PLIC. The two sets have parameter values within a biologically acceptable range, while representing very different case scenarios. Set A is characterized by D_a < D_e,‖, f < 0.5 and almost no orientation dispersion. Set B is characterized by D_a > D_e,‖, f > 0.5 and some orientation dispersion. These results are further used as our two sets of ground truths in the simulations. Typical DTI/DKI tensor metrics stemming from each of these sets are provided. They are very similar to each other. M/A/RD, mean/axial/radial diffusivity; M/A/RK, mean/axial/radial kurtosis

		Set A	Set B
Input parameters	f	0.38	0.77
	Da	0.50	2.23
	De,‖	2.10	0.16
	De,⊥	0.74	1.48
	κ [c2]	64 [0.98]	4 [0.70]
Equivalent tensor metrics	FA	0.61	0.54
	MD	0.79	0.78
	AD	1.42	1.32
	RD	0.47	0.51
	MK	1.28	1.30
	AK	0.72	0.63
	RK	1.88	2.12

The simulated clinical protocol consisted in one b = 0 and two shells (b = 1 and b = 2 ms/µm²) with 30 directions each, aiming to represent a clinically feasible and widespread diffusion protocol.

An extended protocol (one b = 0, four shells – b = 1/2/5/10 ms/µm² with 30 directions each) was also simulated.

First, for both protocols, the outputs of the nonlinear fit were evaluated for both noiseless and SNR = 50 synthetic data. Although Rician noise was added to the data, the SNR level was chosen to be sufficiently high to justify the use of a least squares algorithm. Moreover, if issues are apparent in the case of a relatively high SNR (for typical dMRI data), one can only expect them to be more pronounced at lower SNR. The fitting procedure was repeated for 2500 different initializations and noise realizations. As previously, the starting point was randomly chosen from the parameter intervals 0.2 ≤ f ≤ 0.8, 0.5 ≤ D_a, D_e,‖ ≤ 3, 0.1 ≤ D_e,⊥ ≤ 2.0, 1/3 ≤ c₂ ≤ 1, with c₂ further converted into κ.

Second, for the simulated clinical protocol only, the 5D fitting landscape was evaluated in 3D sub-spaces by calculating the value of the objective function F in Equation [4] for all combinations of f = 0.2:0.01:0.8, D_a = 0.5:0.01:3.6 and κ = [2:0.1:20, 21:1:64]. The remaining parameters (D_e,‖; D_e,⊥) were fixed to combinations corresponding to either the true or the spurious minimum of each ground truth, i.e. (D_e,‖; D_e,⊥) = (2.10; 0.74) or (0.32; 0.85) for Set A, and (D_e,‖; D_e,⊥) = (0.16; 1.48) or (1.94; 0.87) for Set B. Landscapes of objective function values were calculated in the absence of noise, as well as for three different noise levels (SNR = 35/50/70).

RESULTS

Experiment

Clinical data

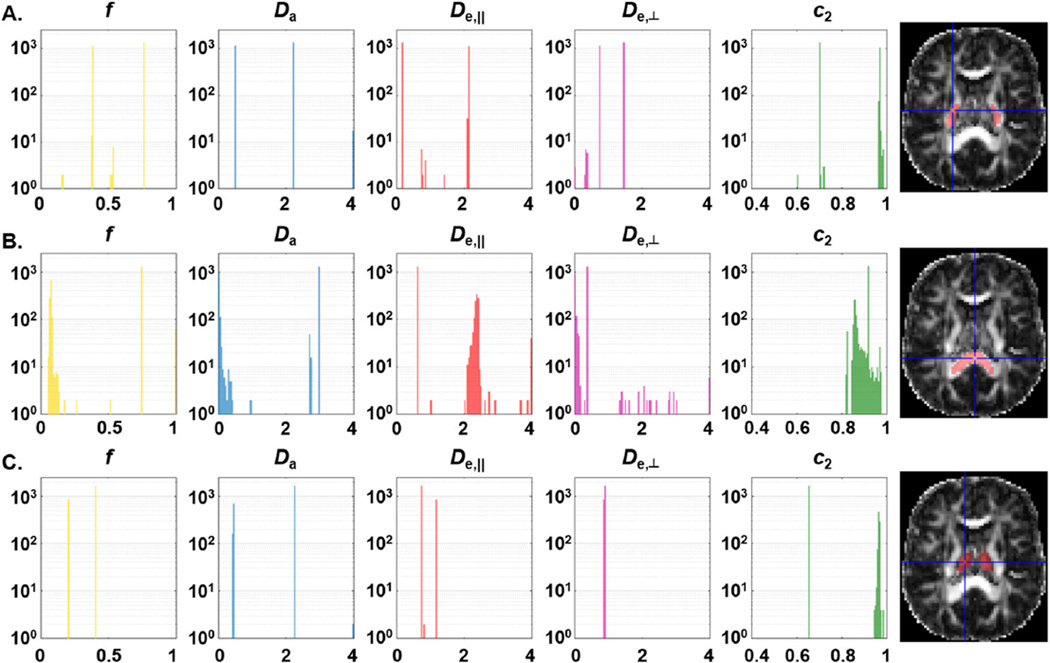
The chosen ROI included both left and right PLIC and amounted to 228 voxels. Figure 3 presents the parameter estimation results in this ROI. The histograms of estimated model parameters across the ROI are extremely broad, likely much more than could be expected from biological variability. This hints at the fact that the minimization landscape makes the fitting procedure highly sensitive to algorithm initialization and noise. Essentially, nonlinear fitting can output virtually anything. The scatter plots in Figure 3B also reveal a substantial degree of correlation between estimated parameters, in particular between f and D_a.

Figure 3.

Empirical bias and precision issues in parameter estimation on a clinical datatset, illustrated by the results of nonlinear fitting of NODDIDA in the PLIC. (A) Histograms of fitted parameter values across the ROI. The histograms are exceedingly broad and essentially non-informative. (B) Correlations between the estimated fraction f and all other model parameters: D_a, D_e,‖, D_e,⊥ and c₂. There are spurious correlations between parameters, in particular between f and D_a.

While this is the most challenging case scenario – each voxel is characterized by a different ground truth, noise realization and algorithm initialization – it represents a realistic application of the NODDIDA model in vivo. Indeed, experimental data is corrupted by noise and displays biological variability, and there is currently insufficient biological knowledge to provide the algorithm with an educated initial guess rather than a random one.

The sole impact of algorithm initialization can be visualized in Figure 4, where the fitting procedure was repeated 2500 times on the same voxels, changing only the initial guess. These histograms reveal a systematic bimodal behavior in each voxel examined. In other words, given a certain biological ground truth and noise realization, there can still be two solutions to the problem: one with D_a < D_e,‖, low f and low orientation dispersion (high value of κ or c₂), and the other with D_a > D_e,‖, high f and high orientation dispersion (low value of κ or c₂). For both sets of solutions, the parameters are within biologically acceptable ranges; hence we cannot give any preference to one over the other. For the PLIC voxel, these two solutions are identified as Set A and Set B, respectively, and the complete set of parameter values is provided in Table 1.

Figure 4.

Histograms of fit results for a single voxel, using 2500 initializations, in the PLIC (A), splenium of corpus callosum (B) and thalamus (C). The axial slices on the right show the ROI at stake in red and the exact location of the voxel at the crosshairs. The fitting procedure is dependent on the initialization and mainly leads to two very distinct solutions (see Table 1 for exact values in the PLIC). Note the logarithmic scale on the vertical axis.

The choice of solution based on goodness of fit (i.e. yielding the smallest value of the objective function F) is represented in Figure 5. Neighboring voxels belonging to a given structure can be allocated to qualitatively different solutions (i.e. in one voxel the Type A solution is selected, while in the other the Type B solution is selected) using this criterion. This indicates that the solution closest to the biophysical reality is not necessarily the one with the minimal objective function when the data is corrupted by noise.

Figure 5.

"Choice map": parametric map sketching the choice of a solution based on the best fit (minimal F) in each voxel. Voxels where the best fit yielded a solution such that D_a < D_e,‖ are in gray, while those where the best fit yielded D_a > D_e,‖ are in white. Non-brain voxels, as well as voxels where the algorithm systematically yielded unphysical results, are in black. The PLIC is outlined in red, the thalamus in green and the splenium in blue. The choice of solution based on the minimum F is inconsistent from one voxel to the next even within a given structural ROI, which would be expected to be homogeneous in that respect.

HCP data

The chosen ROI included both left and right PLIC and amounted to 884 voxels. Figure 6A presents the parameter estimation results in this ROI. The histograms of estimated model parameters across the ROI are narrower than those obtained from the clinical dataset, revealing directly a bimodal distribution. The bimodality remains present at the single-voxel level, as illustrated in Figure 6B.

Figure 6.

Empirical bias and precision issues in parameter estimation on an HCP dataset, illustrated by the results of nonlinear fitting to NODDIDA in the PLIC. The histograms of fitted parameter values across the ROI (A) are narrower than in the clinical data case, but remain relatively broad (especially axial diffusivities). The bi-modality is immediately apparent even at the ROI level, and is confirmed by single voxel fits with 2500 different initializations (B).

Simulations

Clinical protocol

As announced, the two ground truths utilized in simulations were Set A and Set B (Table 1). For each of these ground truths (identified by solid red lines), Figure 7 shows histograms of fit outputs resulting from 2500 runs.

Figure 7.

Inherent duality of solutions for a two-compartment model. Shown are histograms of fit results from 2500 random initializations and noise realizations assuming the ground truth to be Set A (top) or B (bottom). Note the logarithmic scale on the vertical axes. Red line: ground truth. Black histograms: SNR = ∞. For both sets, there is a second solution in addition to the true one found with high frequency (~40%). Blue and yellow histograms: SNR = 50. The blue or yellow color was attributed based on the value of the D_a estimate relative to the true one, to visually separate two groups of solutions. (A) The two solutions for SNR = ∞ are: ground truth (Set A, Table 1: f = 0.38/D_a = 0.50/D_e,‖ = 2.10/D_e,⊥ = 0.74/c₂ = 0.98) and spurious (f = 0.78/D_a = 2.67/D_e,‖ = 0.32/D_e,⊥ = 0.85/c₂ = 0.68). (B) The two solutions for SNR = ∞ are: ground truth (set B, Table 1: f = 0.77/D_a = 2.23/D_e,‖ = 0.16/D_e,⊥ = 1.48/c₂ = 0.70) and spurious (f = 0.42/D_a = 0.61/D_e,‖ = 1.94/D_e,⊥ = 0.87/c₂ = 0.98).

In the noiseless case (black histograms), each run had a different initialization. The bimodal behavior observed experimentally in the single voxel is reproduced, with the correct solution having a slightly higher frequency of outcomes than the incorrect one. Some other solutions exist as well, although with very low frequency and predominantly for Set A; they are most likely the result of highly unfavorable initializations.

In the realistic SNR = 50 case, each run had both a different noise realization and initialization. The distributions remain clearly bimodal (blue and yellow histograms; the color is attributed based on the value of the D_a estimate relative to the true one), with each peak now displaying some width around its mean value, due to noise.

It therefore appears that, for a given ground truth, the noiseless minimization landscape of NODDIDA contains at least two local minima. Figures 8 (ground truth Set A) and 9 (ground truth Set B) each provide 3D illustrations of two cubical projections from the full 5D minimization landscape: one containing the true (global) minimum, and the other containing the false (local) minimum, with the remaining two parameters fixed as described in the methods section.

Figure 8.

Shallow pipe-like ensemble of low objective function values in a 3D sub-space of F, Set A. Shown are 3D isosurfaces of the objective function F(f, D_a, κ) for Set A, Table 1, calculated for all combinations of f = 0.2:0.01:0.8; D_a = 0.5:0.01:3.6; κ = [2:0.1:20 21:1:64]. (Aa) F calculated with (D_e,‖; D_e,⊥) = (2.10; 0.74) and SNR = ∞, thus containing the true global minimum. (Ab) F calculated with (D_e,‖; D_e,⊥) = (0.32; 0.85) and SNR = ∞, thus containing the second local minimum of the 5D minimization problem. (Ac) The same as Aa, but SNR = 50. (Ad) The same as Ab, but SNR = 50. The theoretical minimum of F along each pipe is identified by a black bullet.

Figure 9.

Shallow pipe-like ensemble of low objective function values in a 3D sub-space of F, Set B. Shown are 3D isosurfaces of the objective function F(f, D_a, κ) for Set B, Table 1, calculated for all combinations of f = 0.2:0.01:0.8; D_a = 0.5:0.01:3.6; κ = [2:0.1:20 21:1:64]. (Ba) F calculated with (D_e,‖; D_e,⊥) = (0.16; 1.94) and SNR = ∞, thus containing the true global minimum. (Bb) F calculated with (D_e,‖; D_e,⊥) = (1.48; 0.87) and SNR = ∞, thus containing the second local minimum of the 5D minimization problem. (Bc) The same as Ba, but SNR = 50. (Bd) The same as Bb, but SNR = 50. The theoretical minimum of F along each pipe is identified by a black bullet.

In the noiseless case, the region around each of these minima appears as a narrow pipe. This topological representation, combined with the previous simulation results in the absence of noise, implies that the initialization determines into which of the two pipes the algorithm will fall, but from there on the minimum along the chosen pipe is systematically found, as confirmed by the bimodal distribution of outcomes with very narrow peaks.

On the other hand, in the finite SNR case, the landscape is dominated by random noise fluctuations. Due to the flatness (i.e. lack of contrast in the objective function) of the noise-free landscape along the direction of the pipe compared with the noise power, the estimators’ solution can be found in a large vicinity along each pipe.

This particular projection along the parameters (f, D_a, κ) high-lights the most challenging topological features of the landscape. Indeed, the parameter D_e,⊥ is the least problematic, as its values are similar between the true and the false minimum, while the projection along (f, D_e,‖, κ) shows two very distinct minima, but a very short pipe around each minimum. An example of landscape F(f, D_e,‖, κ) is provided in Supplementary Figure S1. The identification of (f, D_a, κ) as the most problematic subset of parameters is also supported by Figure 3B, which shows that the strongest spurious correlations indeed occur between f, D_a and κ. In other words, there is a 1D “quasi-flat” manifold rather than a higher-dimensional “quasi-flat” surface.

For the purpose of the landscape characterization shown in Figures 8 and 9, the objective function F was evaluated over two 3D sub-spaces delimited by f = [0.2 0.8], D_a = [0.5 3.6] and κ = [2 64], each encompassing one pipe (e.g. Fig. 8Aa and Ab). Each sub-space thus contained 61 × 311 × 225 = 4 268 475 evaluations of F. In the noiseless case, we determined, for each f, the location and value of the minimum F in the corresponding (D_a, κ) plane. Figure 10 shows the corresponding plots of F along the core of the pipe as a function of f. The values of F along the pipes for SNR = 70, 50 and 35 are also represented; they provide an indication of how the F value for the true minimum is transformed by a particular noise realization and which location along the pipe can become the minimum as a result of noise.

Figure 10.

Bias and precision issues in finding the minimum of F. Objective function values along the cores of the two pipes represented in Figure 8Aa and Ab (top row) and in Figure 9Ba and Bb (bottom row). The left column shows results for infinite and finite SNR (70/50/35). The right column shows blow-ups of the areas inside the black rectangles, showing the finite SNR curves in more detail. The minimum along each curve is identified by a bullet. In the noiseless case, the minima of the correct and the spurious pipes are very well marked. In the finite SNR cases, the F values of the two minima take values within less than 10% of each other and the minima are also much less marked, i.e. F values for neighbors along the pipe are very similar; as a result, the “false” minimum can be selected, and further, the minimum along each pipe can be substantially displaced from the theoretical one by noise – see Set A, SNR = 50 in particular. This rationalizes the broad parameter histograms from Figure 3A.

In the noiseless case, the F value of the global minimum is zero, and therefore distinguishes itself from the local minimum along the spurious pipe. However, the latter remains very well marked (F ~ 10⁻⁶) and disconnected from the global minimum, such that the algorithm can still land in the spurious minimum depending on initialization values. In the finite SNR cases, two features should be noted. First of all, the F values of the two local minima are much more similar, taking values within less than 10% of each other. In consequence, as observed experimentally (Fig. 5), even when multiple initializations are used on a single voxel to extract both minima, it is still impossible to choose the “correct” minimum based on the values of F, or, in other words, on quality of fit. Second, within each pipe, the minimum can be substantially displaced from the ground truth by noise. For example, in Set A, the minimum along the correct pipe for SNR = 50 is displaced from the true combination (f = 0.38; D_a = 0.50; κ = 64) to (f = 0.76; D_a = 2.01; κ = 3.3) for the particular noise realization illustrated here. The combination of these two features results in a nearly equal probability of outcomes for almost all parameter values within the biologically relevant range (see Fig. 3A).

Extended protocol

Figure 11 shows histograms of fit results from 2500 random initializations and noise realizations assuming ground truths Set A and Set B. With this extended protocol (b up to 10 ms/µm², see the Methods section), in the infinite SNR case, the correct minimum is systematically found and the duality is levied. The spurious minimum nonetheless reappears in a realistic SNR = 50 case, albeit with a much reduced frequency compared with the true minimum.

Figure 11.

Evolution of solution duality with an extended protocol (one b = 0, four shells—b = 1/2/5/10 ms/µm2 with 30 directions each). Shown are histograms of fit results from 2500 random initializations and noise realizations assuming the ground truth to be Set A (Aa and Ab) or B (Ba and Bb). Red line: ground truth. Aa and Ba: SNR = ∞. The correct minimum is systematically found and the duality is levied. Ab and Bb: SNR = 50. The spurious minimum reappears due to noise, although with a much lower frequency of outcomes than the correct one.

Summary of results

The existence of two distinct pipes (minima) in the parameter space, Figures 8 and 9, points to the intrinsic duality of solutions to the parameter estimation problem. This seems to be a distinctive feature of two-compartment models, as will be discussed below. This duality is the first source of bias in parameter estimation, which can be viewed as “discrete”, i.e. two physically very different sets of values are obtained – either with D_a < D_e,‖ or with D_a > D_e,‖. Due to the topology of the minimization landscape, it seems impossible to continuously travel from one minimum to another without overcoming a high barrier. Moreover, the objective function takes very similar values in the two minima such that, even if a global optimizer is used, the selection of the biologically relevant minimum is not guaranteed.

The narrow pipe-like shape of the landscape around each minimum is yet another source of bias, in this case a “continuous” one. Since the profile of F along the pipe is not symmetric (Fig. 10), noise would result in the preferential selection of a flatter part of the pipe relative to the true minimum. Additionally, sometimes another, false minimum appears along the pipe at finite SNR.

Finally, the flatness of the F profile along each pipe compared with the noise level is also a source of large uncertainty in parameter estimation, and of spurious correlations between parameters. Since noise shifts the location of the minimum along the direction of the pipe, the flatness of the F profile along the latter results in a high probability of large deviations from the ground truth. This explains why even an order-of-magnitude oversampling in q space does not seem to be enough for precise parameter estimation (cf. Fig. 3). The contrast in objective function values along the pipe is somewhat improved for higher SNR data with even more extensive q-space coverage, such as HCP datasets (Fig. 6).

DISCUSSION

In this work, we studied the feasibility of nonlinear parameter estimation of neuronal tissue in a representative two-compartment diffusion model, and revealed a highly unfavorable minimization landscape underlying strong bias and poor precision in fit outcomes. This landscape essentially precludes finding the true minimum: there are two distinct disconnected minima of the objective function, very similar in value, yet each corresponding to very different, but physically plausible, model parameter values. Additionally, each of these minima has a pipe-like ensemble of similar objective function values around it, which strongly amplifies the effect of the noise.

We underscore that, qualitatively, our results are general, since the duality of fit outcomes was highlighted in three different brain regions (Fig. 4) and on two very different datasets (Figs. 3 and 6). Moreover, the NODDIDA model is representative of the broad class of multi-compartment models of diffusion in neuronal tissue (20–27). From this standpoint, NODDIDA can be thought of as an example of a minimal model – a model complex enough to account for the main features of neural tissue, yet with a minimal number of parameters, in which the fundamental duality of solutions, as well as bias and poor precision of nonlinear fitting, already become manifest. It is characterized by the intra-neurite fraction f, the neurite axial diffusivity D_a, the extra-neurite space axial and radial local diffusivities D_e,‖ and D_e,⊥, and the concentration parameter κ of the Watson ODF. Note that the duality of solutions is already present in a model assuming perfectly aligned sticks (41), but since dispersion is non-negligible even in structures such as the corpus callosum (42) it is an important parameter to include in the model. The chosen Watson ODF shape allows for a wide range of axially symmetric dispersions (from fully aligned to fully isotropic) and can thus describe both white and gray matter. We specifically considered a simple ODF shape to demonstrate that the problem is not tied to ODF complexity. Understanding the behavior and limitations of such a minimal model is therefore essential for making progress in unbiased and precise parameter estimation. Since the fundamental issues arise already at the level of two compartments, adding a third compartment, such as CSF, would only make matters worse. The problem is likely generalizable, with an n-compartment model yielding at least n solutions, as follows from recently derived general relations between diffusion signal moments and model parameters, where the duality of solutions emerges as the two branches of a square root in a quadratic equation relating parameters to moments for the two-compartment case, and where the corresponding equation would be of a higher order for more than two compartments (30).

In what follows, we discuss the impact of noise and algorithm initialization on the fit output, the possibility of choosing between the two potential solutions based on biological insight, and the limitations of the current study. Finally, we discuss possibilities of using linear fitting approaches for extracting the model parameters.

Impact of noise and initialization

Because of the topology of the minimization landscape, the results of nonlinear fitting are highly dependent on algorithm initialization and on noise. Indeed, we have shown that, given a clinical dataset, the direct application of NODDIDA to a white matter ROI such as the PLIC yields a distribution of fit results that is essentially noninformative, as the histograms are extremely broad and span the entire range of physically acceptable parameter values. This reflects both falling into one of the two minima, and the role of the noise displacing each minimum along the pipe around it. A dataset such as provided by the HCP, with higher SNR in each diffusion-weighted image and higher number of total measurements compared with the clinical dataset, yields narrower, while still bimodal, parameter value distributions.

The repetition of the fitting procedure using 2500 different algorithm initializations on single voxels stemming from three different ROIs further yielded a bimodal distribution of fit results, reflecting the existence of two distinct minima at the voxel level, both in the range of physically plausible values. This result was further reproduced in simulations, where such bimodal distributions of fitting results were retrieved in both the absence and presence of noise. This bimodality is therefore not due to NODDIDA being potentially ill suited to the tissue ground truth, since it was observed even when the ground truth was itself based on the NODDIDA model.

The choice between two distinct solutions

Depending on the initial guess, the algorithm falls into one or the other minimum. The two possible solutions are quite distinct. One is characterized by D_a < D_e,‖ and limited orientation dispersion (high value of κ), and the other one by D_a > D_e,‖ and larger orientation dispersion (lower value of κ). The bimodality seems to be a general feature of having two compartments. Indeed, this duality of solutions has already been highlighted in Reference 41 and later in Reference 43 for a two-compartment model of perfectly aligned axons, where the parameter estimation procedure did not involve nonlinear fitting. Rather, the first two terms of the cumulant series [1] were estimated using linear matrix pseudoinversion and analytically related to the model parameters. Recently, this same duality was identified in a two-compartment model with a general ODF, defined by the decomposition into spherical harmonics up to an arbitrary order, using a similar approach (30).

We have also shown that, in a realistic SNR case, noise brings the values of the objective functions of the two minima very close to each other. The biologically relevant minimum therefore cannot be chosen based purely on quality of fit (Fig. 5). Simulations of an extended protocol with b values up to 10 ms/µm² suggest that, for such data, the correct minimum can be found with much higher probability than the spurious one, which might be one way of testing experimentally what the biologically relevant minimum is. However, experimental data at b = 10 ms/µm² with sufficient SNR is difficult to obtain in practice. It would therefore be extremely valuable to have a priori biological insight into which solution might be the true one, in order to choose the algorithm initialization accordingly.

Unfortunately, there is no consensus in the literature as to whether D_a is higher than, lower than, or equal to D_e,‖ (1,25,44,45). The current results support the hypothesis that, under the assumptions of two compartments and a Watson ODF, they are at least not similar to each other – the NODDIDA implementation would allow for this particular case scenario but it is almost never observed. In order to discard the possibility that this is an effect of over-parameterization, we ran simulations where the ground truth was set to D_a = D_e,‖ and assessed the distribution of NODDIDA outcomes (Supplementary Figure S2). In this particular scenario, the histograms are broad but unimodal around the true values, with 30% of outcomes having both axial diffusivities within 10% of their common ground truth. This confirms that, were D_a and D_e,‖ similar in reality, the histograms of NODDIDA fit outcomes on human brain data would be unimodal rather than bimodal.

As to the choice of which axial diffusivity is greater, D_a or D_e,‖, the evidence is conflicting. On the one hand, several recent works are built on the assumption that D_a < D_e,‖ (6,43), or even claim that this solution is unique (46). This inequality is also supported by recent work showing that white matter tract integrity metrics correlate as expected with the concentration of (purely intra-axonal) N-acetyl-aspartate under the assumption D_a < D_e,‖ rather than the opposite (D_a > D_e,‖) (47).

On the other hand, there is recent evidence based on isotropic diffusion weighting measurements suggesting that the other solution (D_a > D_e,‖) is the correct one (48). An argument against this solution is that it seems to output, more often than not, combinations of parameters such that D_e,‖ < D_e,⊥, which may seem counter-intuitive. However, several leads are possible to rationalize this result. First, it could be the result of a bias, due to model assumptions, such that the ground truth would be in fact closer to D_e,‖ ≈ D_e,⊥, or even D_e,‖ > D_e,⊥. We found that such a bias can for example be introduced by a small CSF fraction f_iso (i.e. a third compartment). Assuming f = 0.77, D_a = 2.23, D_e,‖ = 0.8, D_e,⊥ = 0.5, κ = 8, f_iso = 0.05 and D_iso = 3, the NODDIDA noiseless fit gives estimates of f = 0.83, D_a = 2.27, D_e,‖ = 0.67, D_e,⊥ = 0.98 and κ = 6.9. In other words, mild (5%) CSF contamination increases D_e,⊥ while bringing the estimates of D_a and D_e,‖ further away from each other, which leads to tortuosity appearing lower than unity. Second, further investigation is required in order to determine whether the ground truth D_e,‖ < D_e,⊥ could not, in fact, make biological sense. Axonal structure and packing at this level is not well known in vivo, and Monte Carlo simulations of diffusion in 3D electron tomography reconstructions have not been performed to address this specific question. Glial cell bodies and other restrictions could reduce D_e,‖ considerably relative to the free water value that one pictures from the ideal parallel cylinders’ cartoon. Having realistic axonal structures in mind, it becomes less obvious in which direction the effect of hindrance is greater. For an equal amount of heterogeneity (disorder), hindrance is expected to be much easier to achieve in one dimension (axial direction) than in two dimensions (radial plane). This is well known in the physics of localization in quantum transport (49,50). Classical considerations also support this picture: mapping diffusivity to conductivity via Einstein’s relation, the conductivity of a linear circuit is limited by the part with highest resistance; i.e., every “bottleneck” leads to hindrance in one dimension (such bottlenecks can be due to, e.g., glial cells in the extra-axonal space). In two dimensions, the effect of bottlenecks is much weaker than in one dimension (51,52). Whether the amount of disorder in the longitudinal direction is sufficient for making D_e,‖ < D_e,⊥ is currently unknown. The D_e,‖ < D_e,⊥ inequality would, nonetheless, be in contradiction with any local tortuosity model currently employed in white matter modeling (33,53–55), as well as with measurements of extracellular tortuosity of other molecules (e.g. fluorescein isothiocyanate–dextran in the spinal cord of mice (56)).

Choosing between the two solutions based on the fraction value f is also debatable, since these fractions are likely weighted by the respective T₂ values of the intra- and extra-neurite compartments, the values of which find no consensus across the community (57–60).

Moreover, diffusivities and fractions are expected to change significantly with development, aging and pathology, such that a reasonable guess in healthy adult controls might not hold for other population groups. Diffusivities are particular candidates for markers of tissue vitality. For instance, the diffusivity along the neurites drops in stroke, as inferred (61) from oscillating-gradient measurements (10), and as measured in the rat brain after eliminating the effect of extracellular water with added contrast (62). There is also evidence that, in white matter, the intra-axonal fraction increases dramatically during development due to myelination (6) and that it decreases as a result of demyelination and axonal loss (63,64).

The choice between the two minima based on the degree of fiber orientation dispersion is also uncertain at this point. There is indeed an increasing consensus that even the reputedly most coherent white matter tracts in the brain, such as the corpus callosum, present a significant amount of orientation dispersion and cannot be approximated as a collection of strictly parallel axons. Mean intra-voxel dispersion estimates for the corpus callosum were reported at 15–18° in humans (42,65) and up to 34° in rats (66), which, using the conventions in the current work, would correspond to c₂ values of 0.90–0.93 and 0.69, respectively. However, such levels of dispersion are not sufficient to disregard “Set A”-type solutions of NODDIDA, because the c₂ output value might simply be biased towards slightly higher values.

Constraining the fit using additional simplifying assumptions is tempting in order to overcome both the issue of duality of solutions and of very large fit uncertainty. However, given all the aforementioned arguments, it appears that, to date, all the assumptions typically used (e.g. D_a = D_e,‖ = 1.7 µm²/ms (27); D_a = 1.4 µm²/ms and D_e,‖ = D_e,⊥ (29)) lack biological validation and do not therefore give trustworthy solutions to the problem, particularly when studying pathology. As an example, we provide the outputs of NODDI assuming ground truths Set A and Set B, when D_‖ = D_a = D_e,‖ is fixed to a given value between 1.1 and 2.1 and D_e,⊥ = D_e,‖(1 − f) (Supplementary Figure S3). The errors on the estimated parameters can be as large as 300%. Moreover, because Set A and Set B are the two complementary possible solutions of NODDIDA, the estimates of NODDI for the two sets are nearly identical: NODDI is unable to distinguish between these two very different biological configurations (see the caption of Figure S2 for more details).

Limitations

Although the impact of the acquisition protocol was not evaluated explicitly, the HCP dataset showed that an extensive and intelligent coverage of q space improves the precision of the fit along each pipe. Simulations using the extended protocol also suggested that going to higher b values could, perhaps, levy the duality of solutions. However, as expected, SNR issues still precluded finding the correct minimum systematically. Additionally, we believe it is of interest to present the performance of a model applied to clinically achievable data, such as “two shells, 30 directions per shell”. However, dedicated acquisitions on high-performance scanners with b values up to 10 ms/µm² might provide some insight into which minimum is biologically relevant.

It should also be pointed out that the two solutions are associated with the underlying two-compartment model. Should this model be inappropriate for describing brain dMRI data, e.g. because it does not account for orientation dispersion asymmetry or for a third compartment, the biological reality might differ substantially from both solutions exhibited here. Additionally, if a third compartment were present in the underlying tissue, accounting for it in the fitting procedure might also make the biologically relevant solution more likely than the spurious one (in terms of outcome frequency from a series of minimizations with random initializations).

For ease of presentation and understanding, landscapes and profiles of objective function values were plotted in 3D, with the remaining two parameters of the model, D_e,‖ and D_e,⊥, set to the values corresponding to the minimum of each pipe for SNR = ∞. Nonetheless, simulation results in Figure 7 provide an additional indication of how the minimum is displaced due to noise in the full 5D parameter space. Moreover, we stress that the three parameters chosen, f, D_a and κ, were the ones revealing the most problematic features of the overall landscape (Figs. 8, 9 and S1).

Outlook

This study uncovers a major problem with parameter estimation, which puts into question previous multi-compartmental parameter estimation results in neuronal tissue. While not resolving this problem here, we hope that formulating a concrete question (“which solution out of the distinct two?”) can help move the field forward by stimulating dedicated measurements.

The problem is technically formulated via showing that the nonlinear fitting landscape, even for a relatively simple tissue model, is highly unfavorable. The two-compartment model considered allows for two distinct minima representing two very different realities, neither of which can be discarded based on biological evidence from the literature. This appears to be a general fundamental property of two-compartment models (30). Moreover, the objective function values associated with the two minima in a finite SNR situation are very close to each other, which discourages the “best fit” approach for selecting the biologically relevant solution out of the two, and also undermines the efficacy of the initial grid search to determine a good starting point (20,67). In other words, our work confirms that solution selection is in general very difficult; one cannot circumvent developing a thorough physical understanding and a subsequent histological validation. Although various models have not been directly compared here, our results also suggest that it is generally unreliable to base model selection purely on goodness of fit; a similar observation using a simpler model was made previously (68).

In view of the high bias and uncertainty associated with nonlinear estimation, should one lean towards a purely linear estimation? This can be accomplished by estimating model-independent parameters of the series [1] using linear pseudoinversion, which has a unique solution. The duality then re-emerges at the level of relating signal moments (or cumulants) to the model parameters (30). Fundamentally this is of course expected, since the duality is a feature of the minimization landscape that cannot be cured by linearization. Practically, however, one may hope that making numerical estimation “easy” (i.e. in a linear way), while taking care of the “difficult” (i.e. nonlinear) step of relating moments to parameters analytically, would protect the overall parameter estimation from falling into a potentially growing number of local minima in a high-dimensional parameter space generally needed to adequately describe fiber ODF in voxels with complicated orientation pattern such as fiber crossings.

CONCLUSIONS

Compared with empirical DTI/DKI metrics, brain white/gray matter models of diffusion come with the promise of improved specificity. In this work, we used a minimal two-compartment model to highlight the essential problems of the fitting landscape in the parameter space defined by such a model, namely the existence of two physically plausible and distinct pipe-like minima of the objective function. We thus uncovered two distinct sources of bias – a “discrete” bias due to falling in the wrong minimum, and a “continuous” bias due to a nonsymmetric profile of the objective function near each minimum. We also explained the reason for spurious parameter correlations and poor precision as the effect of noise shifting the minimum by a large amount along the “pipe” of low objective function values. We underlined that fixing model parameters to a priori values with no biological validation is not a viable solution. Overall, due to the aforementioned problems, parameters obtained to date from multi-compartmental models in neuronal tissue should be considered merely as “indices” and new considerations should be incorporated in their interpretation, at least until more evidence is accumulated about which of the two solutions outlined in this work is biologically more meaningful. Further efforts to improve the precision of the estimates will then still be necessary.

Abbreviations used

3D/5D

three/five dimensional

CSF

cerebrospinal fluid

DKI

diffusion kurtosis imaging

dMRI

diffusion MRI

DTI

diffusion tensor imaging

EPI

echo planar imaging

FA

fractional anisotropy

HCP

Human Connectome Project

NODDI(DA)

neurite orientation dispersion and density imaging (with diffusivity assessment)

ODF

orientation distribution function

PLIC

posterior limb of the internal capsule

ROI

region of interest

SNR

signal-to-noise ratio.