Abstract
Cardiac electrical dynamics are governed by cellular-level properties, such as action potential duration (APD) restitution and intracellular calcium (Ca) handling, and tissue-level properties, including conduction velocity restitution and cell–cell coupling. Irregular dynamics at the cellular level can lead to instabilities in cardiac tissue, including alternans, a beat-to-beat alternation in the action potential and/or the intracellular Ca transient. In this study, we incorporate a detailed single cell coupled map model of Ca cycling and bidirectional APD-Ca coupling into a spatially extended tissue model to investigate the influence of sarcoplasmic reticulum (SR) Ca uptake and release properties on alternans and conduction block. We find that an intermediate SR Ca uptake rate and larger SR Ca release resulted in the widest range of stimulus periods that promoted alternans. However, both reduced SR Ca uptake and release promote arrhythmogenic spatially and electromechanically discordant alternans, suggesting a complex interaction between SR Ca handling and alternans characteristics at the cellular and tissue level.
Keywords: calcium handling, alternans, conduction block, sarcoplasmic reticulum release, sarcoplasmic reticulum uptake, heart failure
Introduction
Sudden cardiac death is primarily caused by ventricular fibrillation, a disorganized and irregular electrical rhythm that arises as a consequence of electrical reentry and wavebreaks.1 Cardiac electrical dynamics are governed primarily at the cellular level by the interaction between action potential properties, including action potential duration (APD) restitution, and intracellular calcium (Ca) handling, and at the tissue level, by action potential propagation properties, including conduction velocity (CV) restitution and cell–cell coupling.2–8 Irregular dynamics at the cellular level can lead to instabilities in cardiac tissue, including alternans, a beat-to-beat alternation in APD and/or the intracellular Ca transient.9,10 Complex patterns in the alternations of the APD and Ca transient can arise at multiple spatial scales. In the cardiac myocyte, alternans can be electromechanically concordant (EMC), in which the long–short APD alternation accompanies a large–small alternation in the Ca transient, or electromechanically discordant (EMD), in which long–short APD alternation accompanies a small–large alternation in the Ca transient.9,11 In cardiac tissue, alternans can be spatially concordant (SC), in which the long–short alternation of the APD is in phase throughout the tissue on each beat, or spatially discordant (SD), in which tissue regions of long–short alternations are adjacent to regions of short–long alternations.9,12,13 Critically, SD APD alternans is highly arrhythmogenic, promoting a steep gradient in repolarization, which can lead to conduction block and reentry initiation.14
Coupled maps are a valuable tool for investigating the complex interactions between subcellular-, cellular-, and tissue-level cardiac dynamics. Early studies focused on the relationship between APD and preceding diastolic interval (DI), the APD restitution curve, and identified APD restitution slope as a critical parameter governing the onset of alternans.15,16 Subsequent experimental and computational work has shown that APD may depend on more than just the previous DI, referred to as short-term memory.17,18 Short-term memory effects may collectively refer to ion channel recovery dynamics, intracellular Ca cycling, and other ionic concentration changes that occur on time scales longer than a single beat.19 Coupled maps have been expanded to account for the influence of memory on APD.20–24 However, it is difficult to make mechanistic predictions using these models, since memory effects are typically collectively encompassed by one or two variables and a few parameters that govern the time scale and relative influence of memory. Although it is clear that alternans can arise at the cellular level via instabilities in both electrical and Ca signaling, experimental evidence in recent years has suggested that Ca-driven instabilities may be the primary mechanism underlying alternans formation,4,10,14 demonstrating the need to specifically account for intracellular Ca signaling, in particular sarcoplasmic reticulum (SR) Ca handling, in computational models. In 2007, Qu et al developed a detailed coupled map model, coupling APD and Ca cycling dynamics, ie, excitation–contraction coupling, including bidirectional APD–Ca coupling and SR Ca uptake and release dynamics, and investigated bifurcations that lead to cellular instabilities, including alternans and chaos.25
By incorporating coupled maps of cellular dynamics into a model of action potential wave propagation, one-dimensional cable coupled map models have been developed to investigate tissue-level properties that have shown, for example, how a steep CV restitution relationship, ie, the relationship between CV and the preceding DI, can lead to a transition from SC to SD alternans.5,12,26 This arrhythmogenic phenomenon can arise purely via restitution dynamics, in the absence of spatial heterogeneity: if APD alternans arises, via instabilities in calcium or voltage, at an upstream location in the cardiac tissue, a short DI will precede a short APD and a long DI will precede a long DI. For steep CV restitution, the shorter DI will result in slower electrical wave propagation, lengthening the DI at locations downstream. For sufficiently steep CV restitution, the lengthened DI will facilitate a long APD (via APD restitution). Similarly, the upstream long DI results in faster propagation, leading to a shorter DI at downstream locations, and thus a short APD downstream. Thus, SD alternans arises in the tissue on a beat-to-beat basis.
Cell coupling effects on repolarization have also been incorporated in one-dimensional cable coupled map models and shown to influence the onset of alternans, even for steep APD restitution.22,27 In nearly all prior studies utilizing one-dimensional cable-coupled maps, APD dynamics have been minimally defined by the APD restitution relationship, with the addition, in some studies, of a short-term memory variable. In this study, we incorporate a single cell coupled map, with detailed Ca handling and bidirectional APD-Ca coupling, into a one-dimensional cable model of cardiac tissue. It is well-established that SR Ca handling is perturbed in pathological settings, in particular in heart failure.28–34 Our analysis focuses on predicting how altered SR Ca handling leads to arrhythmogenic instabilities at the cellular level, ie, EMD alternans, and at the tissue level, ie, SD alternans.
Methods
Single cell excitation–contraction coupling map model
In this section, we describe in brief the single myocyte-coupled map, incorporating excitation–contraction coupling, previously described by Qu et al.25 and illustrated in Figure 1A. As mentioned in the “Introduction” section, APD is often assumed to be a function of the preceding DI via APD restitution.16 In this model, APD is governed by both voltage-dependent recovery kinetics and Ca-dependent processes, ie,
| (1) |
where an+1 is the APD of the (n + 1)th beat, is the peak intracellular Ca on the (n + 1)th beat, γ governs Ca–APD coupling, f(dn) is the APD restitution function (Eq. A1), dn is the DI of the nth beat, and an and dn are related by tn = an + dn, where tn is the interbeat interval (IBI) of the nth beat.
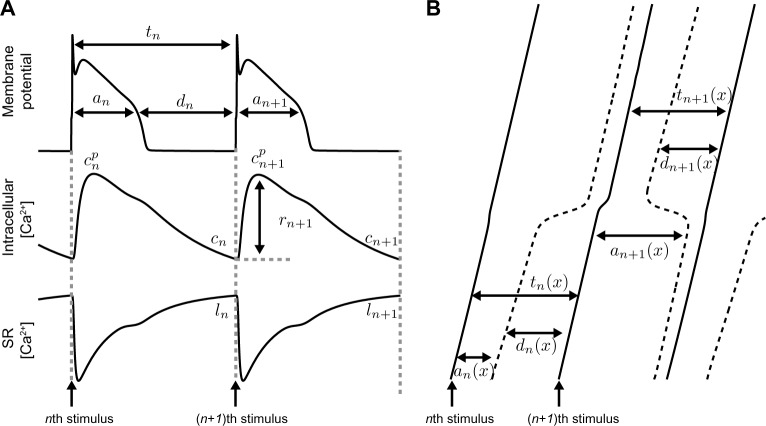
Figure 1.
Single cell and one-dimensional cable simulations. (A, top) Illustration of the APD an, DI dn, and IBI tn; (middle) peak intracellular Ca at the end of each beat (cn), SR Ca release (rn); (bottom) and SR Ca load at the end of each beat (ln). (B) Illustration of action potential wavefronts (solid) and wavebacks (dashed), propagating along a cable, denoting APD, DI, and IBI as an(x), dn(x), and tn(x), respectively, as functions of space x.
Peak intracellular Ca is given by the sum of the diastolic intracellular Ca concentration (cn) and the total SR Ca released (rn+1) during the (n + 1)th beat, ie,
| (2) |
where cn is the diastolic Ca in the cytoplasm at the end of the nth beat and is given by the difference of the total cellular Ca concentration, bn, and the SR Ca load, ln, at the end of the nth beat, ie,
| (3) |
The SR Ca load on the (n + 1)th beat (ln+1) is given by the SR Ca load on the nth beat (ln), less the SR Ca release (rn+1), and plus the SR Ca uptake (un+1), ie,
| (4) |
SR Ca release on the (n + 1)th beat is given by
| (5) |
where q(dn) relates the restitution properties of SR Ca release (Eq. A2), depending on the previous DI, g(ln) relates the dependency of SR Ca release on the current SR Ca load (Eq. A3), and λ ∈ (0,1] describes the fraction of SR Ca released. In the setting of pathological impairment, λ < 1 may occur, eg, due to reduced ryanodine receptor functional expression, open channel gating, or reduced cluster density.
SR Ca uptake via SERCA pumps on the (n + 1)th beat is given by
| (6) |
where u(tn+1) (Eq. A4) and (Eq. A5) relate the dependence of SR Ca uptake on the stimulus period and peak intracellular Ca levels, respectively, and ν is the rate of SR Ca uptake.
Finally, the total cellular Ca on the (n + 1)th beat (bn+1) is given by the total Ca on the nth beat (bn), plus the net Ca influx or efflux during the (n + 1)th beat,
| (7) |
where c(tn+1) is the steady-state intracellular Ca for stimulus period tn+1 (Eq. A6), κ is a rate of Ca accumulation, and η is the APD–Ca coupling. Total Ca increases at shorter stimulus periods. Positive or negative APD–Ca coupling results in a net Ca influx or efflux, respectively, during an alternating or chaotic state, ie, when an+1 ≠ an. Note that the dynamics of Ca concentrations, ie, bn, cn, , and ln do not account for cellular or subcellular compartment volumes nor Ca buffering, and thus are more representative of a cellular or subcellu-lar compartment Ca content. As a consequence, concentration values presented somewhat differ from typical experimental measurements. In particular, accounting for the SR–cytoplasm volume ratio would result in larger SR Ca concentrations subsequently presented. However, for comparison with prior work using the model,25 we have used the original model formulation, with Ca dynamics and concentrations presented as previously described.
Combining Eqs. 1–7, the single myocyte map model can be written succinctly as
| (8a) |
| (8b) |
| (8c) |
| (8d) |
In the single myocyte, IBI is equal to the stimulus period and assumed to be constant, ie, tn = tn+1 = T. All model equations and parameters are given in the Appendix and Table A1, respectively.
One-dimensional myocyte cable map model
We next extend the single cell-coupled map to a one-dimensional cable model that accounts for APD and CV restitution, excitation–contraction coupling, and cell–cell coupling. APD, DI, IBI, total Ca, diastolic intracellular Ca, and SR Ca load on the nth beat, given by an(x), dn(x), tn(x), bn(x), cn(x), and ln(x) as before, are now functions of spatial position x ∈ [0, L], where L = 10 cm is the cable length (Fig. 1B). If the cable is stimulated at x = 0 and action potentials on the nth beat propagate down the cable length with velocity given by the CV restitution curve, v(dn) (Eq. A7), ie, the relationship between CV and the preceding DI, then the IBI at position x is governed by the following relationship:
| (9a) |
We next augment the equation for APD in the single cell (Eq. 8a) with additional terms to account for cell coupling effects on repolarization26,27,35–39:
| (9b) |
The first spatial term, proportional to accounts for diffusion of the membrane potential during repolarization, and the second spatial term, proportional to , accounts for the asymmetry that arises due to pacing one end of the cable. Finally, Eqs. 8b–8d, which do not contain any additional coupling terms since we assume that intercellular Ca coupling is minimal, are similarly defined at each location x:
| (9c) |
| (9d) |
| (9e) |
Numerical integration
We can numerically integrate Eq. 9 by first defining spatial location xj = jΔx, where Δx = 0.1 mm (the length of a single cell), j = 0, 1,…,m and m = L/Δx. We next define the spatially discretized variables , and similarly, , , , and .
For a cable stimulated with pacing period T at x = 0, we define the initial conditions at all spatial locations, ie, , , , , for all j, by first iterating the single cell map model (Eq. 8) for 1000 beats at stimulus period T. We then define each variable as the average of the final four beats of their corresponding values in the single cell map model. We also define .
For the (n + 1)th beat, discretizing the spatial derivatives and imposing no-flux boundary conditions at x = 0 and x = L, we can write and solve Eq. 9b as a tridiagonal linear system of equations
| (10) |
where
K1 = (ξ/Ax)2 + w/(2Δx), K2 = −1–2(ξ/Δx)2, and K3 = (ξ/Δx)2−w/(2Δx). Note that we have included fictitious boundary grid points and .
We next use a forward Euler scheme to numerically integrate Eq. 9a:
| (11) |
with boundary condition imposed at x = 0 and where we have used and similarly for . Finally, we iterate Eqs. 9c–9e:
| (12) |
| (13) |
| (14) |
Results for both single myocyte and cable simulations are presented for 1000 beats. Loss of capture in the single myocyte model is defined as occurring when DI is less than 2 ms. Conduction block in the cable simulations is defined when there is a loss of capture at any spatial location. The incidence of alternans is defined as an APD alternans amplitude greater than 10 ms.
Results
Single cell excitation–contraction coupling map model
The single cell map model developed by Qu et al has a wide range of parameters. Here, we focus on two critical SR Ca properties, specifically SR Ca uptake and release, and then extend the single cell model to a spatially extended cable to explore how these properties alter the formation of alternans and conduction block.
We iterate the single cell map for 1000 beats and plot APD, peak intracellular Ca, and SR Ca as a function of the stimulus period T (Fig. 2). For SR uptake rate ν = 0.7, APD and Ca alternans are present at faster stimulus rates, between T of 265 and 320 ms, below which there is a loss of capture (Fig. 2A). Further, alternans is EMC, ie, a long APD corresponds with a large peak Ca, and vice versa. SR Ca is out of phase with the peak intracellular Ca, consistent with a high SR Ca load leading to a larger SR Ca release on the subsequent beat. For a smaller uptake rate, ν = 0.4, both the peak intracellular Ca and SR Ca load are reduced (Fig. 2B). EMC alternans is present at a longer stimulus period, while loss of capture occurs at a shorter stimulus period.
Figure 2.
Reduced SR Ca uptake can promote EMD alternans. APD, peak intracellular Ca, and SR Ca load are shown as a function of stimulus period T on even (black) and odd (red) beats, for SR Ca uptake rate v = (A) 0.7, (B) 0.4, (C) 0.28, and (D) 0.1. Other parameters: λ = 1.
For a slightly smaller uptake rate, ν = 0.28, as T decreases, EMC alternans is present at T = 295 ms. However, as T decreases further, APD and peak intracellular Ca become out of phase at T = 275 ms, such that the long APD corresponds with the small peak Ca, and vice versa, ie, EMD alternans. EMD alternans is present until the loss of capture at T = 235 ms. Reducing uptake rate further, ν = 0.1, alternans is present for T between 235 and 285 ms, EMD over the entire range of stimulus rates.
For all uptake rates, SR Ca load decreases as ν decreases and is out of phase with APD. APD and Ca alternans are present over the widest range of values for T for an SR uptake rate ν near 0.4. For ν = 0.4, SR Ca load is between 70 and 95 µM, which corresponds to the steepest region of the SR Ca release vs. SR Ca load relationship g(ln) (Fig. A1), which has been previously shown to promote Ca alternans via the following mechanism.9 At the end of nth beat, if SR Ca load is reduced slightly, the subsequent SR Ca release on the (n + 1) th beat is also reduced. As such, at the end of the (n + 1)th beat, the SR Ca load is larger (due to the prior smaller Ca release), and the subsequent SR Ca release on the (n + 2)th beat is larger, leading to a further reduction of the SR Ca load. This alternating pattern is promoted by a steep SR Ca release vs. SR Ca load relationship. As ν increases above or decreases below 0.4, the SR Ca load increases or decreases, respectively, such that the corresponding SR Ca load operates in a shallower portion of the SR Ca release relationship, and as such, alternans is promoted to a lesser extent.
Importantly, note that both the Ca–APD coupling parameter γ and the APD–Ca coupling parameter η are positive, which both promote EMC alternans. Thus, the incidence of EMD alternans in the setting of reduced SR Ca uptake is an interesting dynamical behavior (Fig. 3). If APD on the nth beat is short, the DI on this beat will be long, and the diastolic Ca at the end of the beat will be low. Thus, on the (n + 1)th beat, APD will be long, due to APD restitution (Eq. A1), and SR Ca release will be large due to SR Ca release restitution (Eq. A2). The large SR Ca release can lead to a large peak intracellular Ca (Eq. 2), such that alternans is EMC (Fig. 3A). However, when SR uptake is reduced, the SR Ca load is reduced, such that SR Ca release is also reduced, due to the steep dependence on SR Ca load (Eq. A3). Therefore, for reduced SR Ca uptake, on the (n + 1)th beat, even though the SR Ca release is relatively large (compared with the prior beat), peak intracellular Ca can still be small, due to the low diastolic Ca at the end of the prior beat, such that alternans is EMD (Fig. 3B). This situation is further promoted at shorter stimulus periods due to reduced SR Ca restitution.
Figure 3.
Mechanism underlying reduced SR Ca uptake-driven EMD alternans. Map model variables, an, cpn, rn, cn, un, and ln, are shown as a function of beat number, for SR Ca uptake rate v = (A) 0.7 and (B) 0.1. Other parameters: T = 270 ms, λ = 1.
We next investigate to what extent SR Ca release parameter λ alters the incidence of EMC and discordant alternans. For large ν = 0.7, we find that, for all values of λ, there is a transition from regimes of no alternans, EMC alternans, and loss of capture as T decreases (Fig. 4A). Decreasing λ leads to alternans and loss of capture at slightly shorter stimulus periods T. For a smaller ν = 0.4, decreasing λ leads to a more pronounced decrease in the onset of alternans, with a smaller decrease in the period for loss of capture (Fig. 4B). Critically, there is a transition from EMC to EMD alternans as λ decreases. For a slightly smaller ν = 0.28, the transition from EMC to EMD alternans occurs as λ or T decreases (Fig. 4C), while for ν = 0.1, only EMD alternans is present (Fig. 4D).
Figure 4.
Reduced SR Ca uptake and release can promote EMD alternans. Parameter regimes for no alternans, EMC alternans, EMD alternans, and loss of capture are shown as a function of stimulus period T and SR Ca release parameter λ, for SR Ca uptake rate v = (A) 0.7, (B) 0.4, (C) 0.28, and (D) 0.1.
In summary, we find in the single cell map model that reduced SR Ca uptake and release can lead to EMD alternans. In the next section, we extend our analysis to consider the spatially extended one-dimensional cable map model. We investigate whether the results of the single cell simulations extend to the tissue model and further to what extent the SR Ca properties alter electromechanical and spatial discordance and conduction block.
One-dimensional myocyte cable map model
In Figure 5, we plot APD and peak intracellular Ca as a function of spatial location on even (black) and odd (red) beats, for T = 288 ms, varying SR Ca uptake rate ν. For ν = 0.7, APD and peak Ca are SD, with a node approximately at x = 5 cm, while at essentially all spatial locations, APD and peak Ca are EMC (Fig. 5A). For smaller ν = 0.4, alternans become SC (Fig. 5B), and then transition to SD again for ν = 0.35 (Fig. 5C). For ν = 0.3, alternans remain SD but become EMD as well (Fig. 5D).
Figure 5.
Reduced SR Ca uptake promotes complex spatial and electromechanical alternans patterns. APD and peak intracellular Ca are shown as a function of spatial location on even (black) and odd (red) beats, for SR Ca uptake rate v = (A) 0.7, (B) 0.4, (C) 0.35, and (D) 0.3. Other parameters: λ = 1, T = 288 ms.
This example demonstrates the complex relationship between intracellular and SR Ca handling and APD dynamics at the cellular level and cell coupling and CV restitution at the tissue-level properties, in particular how variation in SR Ca uptake rate can alter spatial and electromechanical concordance and discordance, which we explain as follows. Decreasing ν from 0.7 to 0.4 results in a transition from SD to SC alternans (via a transition at ν ≈ 0.672). Decreasing ν decreases SR Ca uptake, and thus the SR Ca load. Reduced SR Ca load decreases both the large and small peak intracellular Ca level (via the SR Ca release vs. SR Ca load relationship), which in turn shortens the long APD (due to positive Ca–APD coupling). However, via APD restitution, the short APD is lengthened. Collectively, this results in a longer short DI, attenuating CV slowing via CV restitution, and thus promoting SC alternans via the mechanism described in the “Introduction” section. Interestingly, decreasing ν from 0.4 to 0.35 results in a transition from SC back to SD (via a transition at ν ≈ 0.358). This decrease in ν similarly results in reduced SR Ca uptake and load, peak intracellular Ca, and long APD and an increase in the short APD. However, in this example, the collective dynamics result in a shorter long DI, which promotes CV slowing via CV restitution, and thus SD alternans.
We demonstrate this complexity in another example, in which we plot APD and peak intracellular Ca as a function of spatial location, for T = 280 ms, varying SR Ca release parameter λ. For λ = 1, alternans is SC and EMC (Fig. 6A). For smaller λ = 0.5, the APD spatial pattern changes only slightly, while peak Ca decreases at all spatial locations (Fig. 6B), such that for λ = 0.36, alternans is EMD, while SC (Fig. 6C). For smaller λ = 0.3, alternans transitions to SD (Fig. 6D).
Figure 6.
Reduced SR Ca release promotes complex spatial and electromechanical alternans patterns. APD and peak intracellular Ca are shown as a function of spatial location on even (black) and odd (red) beats, for SR Ca release parameter λ = (A) 1, (B) 0.5, (C) 0.36, and (D) 0.3. Other parameters: v = 0.4, T = 280 ms.
In Figure 7, we plot the parameter regimes for spatial and electromechanical concordance and discordance for different stimulus rates T, and SR Ca uptake and release parameters ν and λ. For ν = 0.7, as in the single myocyte model, alternans is EMC, for all values of λ (Fig. 7A). Further, as T decreases, there is a transition from SC to SD alternans. There is a small difference between the onsets of alternans and conduction block stimulus period in the cable simulations (black lines), in comparison with the single cell simulations (gray lines).
Figure 7.
Reduced SR Ca uptake and release promote complex alternans patterns. Parameter regimes for no alternans, SC, SD, EMC, and EMD alternans, and conduction block are shown as a function of stimulus period T and SR Ca release parameter λ, for SR Ca uptake rate v = (A) 0.7, (B) 0.5, (C) 0.4, (D) 0.35, (E) 0.3, and (F) 0.2. The regime boundary between SC and SD alternans regimes is indicated by a thick black line, and between EMC and EMD alternans, regime is indicated by a thin black line. The parameter regimes for cable simulations are bounded by black lines. Parameter regimes are identified as SC-EMC (blue), SD-EMC (red), SC-EMD (yellow), and SD-EMD (green). The boundaries for the single cell simulation regimes are shown in gray, for comparison.
For smaller ν = 0.5, the parameter regimes are more complex (Fig. 7B). As in the single cell model, in general, as λ decreases, EMD alternans is promoted, while SD alternans is promoted at shorter values of T, such that all four possible combinations of spatial and electromechanical concordance and discordance occur for some values of λ and T. As ν decreases further to 0.4 (Fig. 7C) and 0.35 (Fig. 7D), the parameter regimes for SC and EMC alternans become smaller, such that for ν = 0.3 (Fig. 7E) and ν = 0.2 (Fig. 7F), alternans is SD and EMD for all values of T at which alternans is present. Interestingly, we note that for ν = 0.3, the single cell model predicts a parameter regime for EMC alternans, while in the cable model, alternans is EMD for all parameter values considered, demonstrating that spatial coupling promoted EMD.
We next measure how both SR Ca parameter ν and λ alter the stimulus period for alternans onset (TAlt, defined as APD alternans greater than 10 ms) and conduction block (TCB). We find that both TAlt and TCB decrease as ν decreases, and in general, TAlt and TCB decrease as λ decreases, although this dependence is weaker (Fig. 8A and B). Thus, reduced SR Ca uptake and release decrease both the onset of alternans and conduction block, which would appear to be antiarrhythmogenic. Since both the onset of alternans and conduction block are functions of ν and λ, we can define an alternans window, ie, the size of the stimulus period range for which alternans is induced, given by TAlt – TCB.40 We find that the alternans window is largest for larger λ and ν ≈ 0.55 (Fig. 8C), while the alternans window is smaller for reduced SR Ca uptake and release.
Figure 8.
Reduced SR Ca uptake and release alter alternans onset and conduction block. The stimulus period for alternans onset (A, TAlt) and conduction block (B, TCB) is shown as a function of SR Ca uptake rate v and release parameter λ. The alternans window (TAlt − TCB) is shown in C.
To further measure propensity for arrhythmias, we can divide the alternans window into windows for spatial and electromechanical concordance and discordance alternans. We measure the alternans windows for the four possible cases for spatial and electromechanical concordance and discordance (Fig. 9). The window for SC-EMC alternans is largest for larger λ and ν between 0.4 and 0.65 (Fig. 9A), while the window for SC-EMD alternans is largest for smaller λ less than 0.5 and larger ν between 0.55 and 0.65 (Fig. 9B). The parameter regime for the SD-EMC alternans window (Fig. 9C) is similar to that in panel A (ie, larger λ and ν between 0.4 and 0.65), however with the window largest for intermediate values of λ and ν. Critically, the SD-EMD alternans window is largest for smaller ν and λ (Fig. 9D).
Figure 9.
SC, EMC, SD, and EMD alternans windows. The alternans windows for (A) SC-EMC, (B) SC-EMD, (C) SD-EMC, and (D) SD-EMD are shown as a function of SR Ca uptake rate v and SR Ca release parameter λ.
Next, we investigate to what extent SR Ca handling properties influence the size of spatial and electromechanical concordant and discordant alternans windows. We first consider the influence of a steeper SR Ca release vs. SR Ca load relationship, by decreasing parameter β (Eq. A3) by a factor of 2 (dashed line in Figure A1, g(ln)). In Figure 10A, we measure the alternans windows for different values of λ and ν, for reduced β, and we find that, in general, the parameter spaces are very similar, in comparison with the baseline value for β. The SC-EMC alternans window is largest for larger λ and ν, and SD-EMD alternans windows is largest for reduced λ and ν. Consistent with prior studies,9,41 a steeper SR Ca release relationship promoted alternans and led to a much larger SC-EMC alternans window. Further, via the mechanism described in the “Single cell excitation–contraction coupling map model” section, steeper SR Ca release also promoted larger EMD alternans windows, for some values of λ and ν.
Figure 10.
SC, EMC, SD, and EMD alternans windows for steeper SR Ca release and uptake. The alternans windows for SC-EMC, SC-EMD, SD-EMC, and SD-EMD are shown as a function of SR Ca uptake rate v and SR Ca release parameter λ, for (A) a steeper SR Ca release vs. SR Ca load relationship and (B) a steeper Ca uptake vs. peak intracellular Ca relationship.
We next consider the influence of a steeper SR Ca release vs. peak intracellular Ca relationship, by decreasing parameter θ (Eq. A4) by a factor of 2 (dashed line in Figure A1, ). We find that a steeper SR Ca uptake relationship has a similar effect as that as a steeper SR Ca release relationship, in that alternans are promoted, most prominently increasing the size of the SC-EMC alternans window and to a lesser extent, promoting larger EMD alternans windows (Fig. 10B). In general, in the setting of steeper SR Ca uptake, the dependence on SR Ca release and uptake parameters, λ and ν, respectively, is similar, compared with the baseline value for θ.
Finally, we investigate to what extent key tissue properties influence the size of spatial and electromechanical concordant and discordant alter nans windows. We first consider the influence of reduced cell coupling on alternans formation. Echebarria and Karma previously derived and showed that APD coupling parameters, w and ξ, are proportional to D and , respectively, where D is the coefficient parameter governing the diffusion of the membrane potential in the standard cable equation.35 In Figure 11A, we measure the alternans windows, as above, after reducing both w and ξ by a factor of 2 and , respectively. Interestingly, reducing the cell coupling parameters has a minimal influence on the alternans windows parameter space, with approximately 11 ms being the largest difference between the alternans windows for the baseline cell coupling values in Figure 9 and reduced cell coupling in Figure 11A. In general, the SC alternans windows are slightly smaller and the SD alternans windows are slightly larger, for reducing cell coupling. However, we note that reducing w and ξ only accounts for the effects of reduced cell coupling on APD. The effects of reducing cell coupling on CV and CV restitution may further alter the size of alternans windows and will be investigated in further studies.
Figure 11.
SC, EMC, SD, and EMD alternans windows for reduced cell coupling and tissue size. The alternans windows for SC-EMC, SC-EMD, SD-EMC, and SD-EMD are shown as a function of SR Ca uptake rate v and SR Ca release parameter λ, for (A) reduced cell coupling and (B) reduced tissue size.
We finally investigate the influence of reducing the size of the cardiac tissue, by reducing the cable length L by a factor of 2 (Fig. 11B). Previous studies have shown that tissue of a sufficiently large size is needed for the formation of SD alternans, and indeed, longer cable lengths promote the formation of more nodes or phase reversals.5 We similarly find that reducing the cable length reduces the size of SD alternans windows and increases the size of SC alternans windows, with alternans window differences between the (ν, λ)–parameter spaces as large as 40 ms for some specific parameter sets. Interestingly, EMC and EMD alternans windows are not greatly influenced by tissue size, as the general shape of the parameter space maps is similar, with the exception of larger SC-EMC alternans windows for small values of ν. Thus, in general, reducing tissue size reduces the formation of SD alternans windows, consistent with previous work,5 with additional modulation by SR Ca uptake and release.
Discussion
Summary of main findings
In this study, we incorporate a detailed single cell map model of Ca cycling and bidirectional APD–Ca coupling into a spatially extended tissue model to investigate the influence of SR Ca uptake and release properties on the incidence and characteristics of alternans and conduction block. We find that an intermediate SR Ca uptake rate and larger SR Ca release resulted in the widest range of stimulus periods that promoted alternans, measured by the alternans window (Fig. 8C). However, reduced SR Ca uptake and release lead to the largest window for arrhythmogenic SD and EMD alternans (Fig. 9D).
Our findings illustrate the complex interaction between SR Ca handling, APD and CV restitution, and cell coupling, influencing the formation of alternans and electromechanical and spatial discordance at the cellular and tissue level, respectively. As illustrated in Figure 5, subtle changes in SR Ca handling can alter APD via Ca–APD coupling, which in turn alters propagation via CV restitution, and can lead to spatial discordance. In particular, our results suggest the interesting prediction that an intervention that acts to inhibit alternans onset and conduction block is, in fact, not less arrhythmogenic. By facilitating conduction at faster rhythms, ie, shorter T, reduced SR Ca uptake and release engage dynamical instabilities at the cellular level, promoting electromechanical discordance, and tissue level, promoting spatial discordance, that are not present for normal SR Ca handling. Critically, we find that normal SR Ca uptake and release play pivotal roles in preventing arrhythmias.
Further, we performed additional simulations in both the setting of a steeper SR Ca release vs. SR Ca load relationship and a steeper SR Ca uptake vs. peak intracellular Ca relationship, in order to highlight the generality of our findings (Fig. 10). Steepening both of these relationships led to larger alternans windows, in particular the window for SC-EMC alternans, and to a lesser extent, larger EMD alternans. However, importantly, we show that the general conclusions of the study did not depend on the steepness of these relationships: reduced SR Ca uptake and release promote SD and EMD alternans.
Our findings demonstrate that reduced cellular coupling during repolarization has minimal influence on EMD (Fig. 11A), suggesting that EMD is primarily governed by SR Ca handling properties. However, differences between single cell and cable map model results emphasize that tissue-level properties do play a role in governing EMD, suggesting that CV and CV restitution are also critical factors. Future work will investigate the role of CV restitution on electromechanical discordance, in conjunction with altered SR Ca handling. Finally, in agreement with prior work,5 we find that tissue size is also a critical factor governing the formation of SD alternans, while demonstrating the novel result that SR Ca handling properties modulate this relationship (Fig. 11B).
Comparison with prior results
Many prior studies have utilized one-dimensional cable-coupled map models to investigate the arrhythmogenicity of different cellular- and tissue-level properties. Fox et al previously showed that spatiotemporal heterogeneity in electrical properties promoted large APD alternans, potentially leading to conduction block.26 Conduction block was less likely in the setting of a shallow APD restitution curve, slow conduction at short DIs, and when short-term memory provided a larger contribution to APD dynamics.36 Cell–cell coupling, or electrotonic interactions, during repolarization have been shown to suppress alternans in the setting of steep APD restitution42 and the onset of SD alternans39 and, similarly, suppress incidences of conduction block.36 Henry and Rappel, confirming behavior observed in an ionic model, demonstrated a relationship between tissue size and the dynamics of conduction block.37 The aforementioned studies investigated alternans and conduction block properties in models accounting for APD and CV restitution, cell–cell coupling, and in some studies, short-term memory, but did not explicitly account for cellular Ca dynamics.
In an excellent 2005 study, Shiferaw et al investigated the coupled dynamics of the transmembrane potential and Ca cycling in both a detailed ionic model and reduced single cell coupled map, demonstrating instabilities leading to EMC and EMD alternans and quasiperiodic oscillation.11 A further reduction investigating Ca-driven alternans identified the slope of SR Ca release vs. SR Ca load and the efficiency of SR Ca uptake as two key parameters governing instabilities.9,41 Shiferaw and Karma showed that in a single cell model coupling APD and Ca, with subcellular diffusion between neighboring sarcomeres, a Turing-type symmetry breaking instability driven by Ca diffusion can lead to out-of-phase Ca alternans within a single cell.43 In the single cell map model that is used in this study,25 Qu et al showed that SR Ca uptake rate ν influenced the parameter regime for alternans and complex dynamics, particularly for ν in the range of 0.1–0.6, consistent with our findings, although this study was only performed in the setting of the Ca cycling subsystem for fixed total cellular Ca. In the map model with fully coupled APD and Ca dynamics, the authors demonstrated that negative Ca–APD coupling could lead to EMC or EMD alternans, as well as quasiperiodicity and chaos.
Recently, Skardal et al formulated a spatially extended coupled map model, incorporating APD and intracellular Ca coupling, demonstrating that for Ca-driven instabilities, large discontinuous jumps in the Ca alternans amplitude can be observed, while APD alternans vary smoothly, a phenomenon not observed for voltage-driven instabilities.44,45 While providing significant insight into alternans incidence in the setting of Ca-driven instabilities in tissue, the authors used phenomenological forms of the maps governing APD and Ca dynamics. To our knowledge, our study is the first to incorporate a detailed representation of intracellular and SR Ca cycling25 into a spatially extended coupled map model.
Physiological implications
In this study, we investigated the influence of impaired SR Ca uptake and release on cellular- and tissue-level alternans. Impaired SR Ca uptake prevents complete refilling of the SR stores, in particular at fast heart rates, promoting alternans via the mechanism described in the “Single cell excitation–contraction coupling map model” section.46,47 Many studies have demonstrated that SR Ca uptake is impaired in heart failure, a consequence of reduced expression of the SR Ca-ATPase (SERCA) pump.28,31,32,48,49 Reduced SR Ca uptake in heart failure sub sequently results in reduced SR Ca load, consistent with our findings shown in Figure 2 (bottom panels), a reduction that is also promoted by enhanced diastolic SR Ca leak,30,50 and subsequently, results in alternans onset at slower heart rates and higher arrhythmia incidence.47 Further, upregulation of the SR Ca pump, SERCA2a, via gene transfer into failing hearts has been shown to suppress the incidence of alternans and critically reduce incidence of cardiac arrhythmias,51,52 consistent with our simulation predictions as well.
Experimental evidence is less clear as to whether SR Ca release is impaired during heart failure. Protein kinase A hyperphosphorylation of ryanodine receptors during heart failure has been associated with increased open probability of the ryanodine receptors, leading to the aforementioned diastolic SR Ca leak.32 However, there is also evidence that ryanodine receptor expression is reduced in human ventricular myocytes from heart failure patients.29,33,53 Further, there is significant evidence that T-tubule structure is disorganized in heart failure, leading to so-called orphaned ryanodine receptors and slower and less synchronous Ca release throughout the cell.33,54 Thus, in the context of our present study, in which SR Ca release parameter λ governs systolic SR Ca release, we investigated the influence of impaired systolic SR Ca release, ie, λ < 1.
Overall, our simulations of impaired SR Ca release and uptake are consistent with the clinical presentation of T-wave alternans in heart failure patients. T-wave alternans, a precursor for lethal cardiac arrhythmias, is the clinical manifestation of cellular-level APD alternans and is associated with many cardiac diseases, including heart failure.55–57 Consistent with these findings, we previously demonstrated in an in vivo tissue model that a larger SD alternans window was associated with a greater incidence of spiral wave formation.40 Due to the simplicity of the coupled map model, it is not possible to directly correlate the heart failure disease state with the SR Ca uptake and release parameters that are the focus of this study. However, our results highlight the complex and highly nonlinear relationship between impaired SR Ca handling and the manifestation of arrhythmogenic EMD and SD alternans, consistent with the highly unpredictable clinical presentation of arrhythmias, in particular in heart failure patients. The unpredictable nature of arrhythmias in heart failure patients is further complicated by the fact that, as noted by Bers et al, heart failure as a disease is heterogeneous, complex, and the relative contributions of impaired SR Ca uptake and leak likely vary in different origins and stages of the disease.58 Thus, the overall qualitative conclusions of our results, ie, impaired SR Ca uptake and release promote arrhythmogenic alternans, agree with previous findings that these properties are critical factors in promoting arrhythmias in heart failure.
Limitations
The coupled map model formulation is inherently a reduction of complex subcellular-, cellular-, and tissue-level dynamics. Our model is an attempt to incorporate detailed Ca cycling into a tissue model, while still maintaining the computational efficiency of a reduced coupled map. However, the model is not without limitations. In particular, our model does not account for the detailed kinetics of the transmembrane potential and ion channel gating59,60 and neglects stochastic aspects of subcellular Ca release, such as Ca sparks and microdomain Ca fluctuations.61–64 Stochasticity may be particularly important to account for in future work, as Sato et al showed that Ca fluctuations can govern the phase of Ca alternans, which in turn may lead to the formation of SD alternans.8 Ma and Xiao showed that Ca fluctuations can alter alternans formation and lead to chaotic or disordered dynamics in a single cell-coupled map.65 It is worth noting that the use of the discrete time-coupled map model provides a significant computational savings over these more detailed continuous-time ordinary and stochastic differential equation formulations. The present study performed considered over 825,000 parameter combinations (varying λ, v, β, θ, L, w, ξ, and T), summarized in Figures 8–11, a parameter investigation that would be essentially computationally infeasible using the detailed models mentioned above. Importantly, the coupled map model simulations highlight potentially significant parameter regimes that can be investigated further in more detailed model formulations.
Further, our model is limited to a one-dimensional tissue and does not account for the complex three-dimensional architecture of cardiac tissue, in particular, heterogeneities in anatomical and functional properties.60 Finally, our study focuses on two critical SR Ca handling properties, and thus, the conclusions of our study may depend on other model parameters, such as APD and CV restitution and cell coupling properties, that may vary in settings of disease. However, these limitations do not detract from the overall conclusion that impaired SR Ca release and uptake can lead to an arrhythmogenic state, promoting instabilities at the cellular and tissue level.
Acknowledgments
The author is thankful for the support of the Turing High Performance Computing Cluster at Old Dominion University.
Appendix
Model equations
In this appendix, the full equations for APD and CV restitution and Ca cycling are given, as described in the “Methods” section, originally from the study by Qu et al.25 (unless otherwise noted), and are plotted in Figure A1. All model parameters are given in Table A1. The APD restitution function is given by
| (A1) |
The SR Ca release function that describes the restitution properties is given by
| (A2) |
and the function that describes the SR Ca load dependence is given by
| (A3) |
The SR Ca uptake function that describes the dependence on the stimulus period is given by
| (A4) |
and the function that describes the dependence on peak intracellular Ca is given by
| (A5) |
The steady-state total Ca concentration is given by
| (A6) |
The CV restitution curve, from the study by Fox et al.36, is given by
| (A7) |
Table A1.
Model parameters.
| PARAMETER | DEFINITION | UNITS | VALUE |
|---|---|---|---|
| a0 | APD restitution parameter | ms | 220 |
| d0 | APD restitution parameter | ms | 40 |
| τ0 | APD restitution parameter | ms | 30 |
| dmin | APD restitution parameter | ms | 2 |
| vmax | CV restitution parameter | mm/ms | 0.55 |
| dv | CV restitution parameter | ms | 2 |
| δ | CV restitution parameter | ms | 14 |
| σ | SR Ca release parameter | – | 0.5 |
| tq | SR Ca release parameter | ms | 80 |
| a | SR Ca release parameter | – | 0.036 |
| lc | SR Ca release parameter | µM | 93.5 |
| β | SR Ca release parameter | µM | 5* |
| λ | SR Ca release parameter | – | Varied |
| ν | SR Ca uptake parameter | – | Varied |
| ρ | SR Ca uptake parameter | – | 0.15 |
| τu | SR Ca uptake parameter | ms | 200 |
| c0 | SR Ca uptake parameter | µM | 28 |
| θ | SR Ca uptake parameter | µM | 20* |
| γ | Ca–APD coupling parameter | µM−1 | 10−3 |
| e | Ca accumulation parameter | – | 2 |
| τc | Ca accumulation parameter | ms | 300 |
| k | Ca accumulation parameter | – | 0.1 |
| η | APD–Ca coupling parameter | µM/ms | 0.1 |
| ξ | Cell coupling parameter | mm | 1* |
| w | Cell coupling parameter | mm | 0.35* |
| L | Cable length | mm | 100* |
Figure A1.
Nonlinear map model functions. The model equations, given by Eqs. A1–A7, are shown, in addition to the APD restitution slope. The dashed line in the panels showing g(ln) and correspond with decreasing the scaling parameters, β and θ, respectively, by a factor of 2.
Footnotes
ACADEMIC EDITOR: Thomas E. Vanhecke, Editor in Chief
PEER REVIEW: Five peer reviewers contributed to the peer review report. Reviewers’ reports totaled 2,389 words, excluding any confidential comments to the academic editor.
FUNDING: Author discloses no external funding sources.
COMPETING INTERESTS: Author discloses no potential conflicts of interest.
Paper subject to independent expert blind peer review. All editorial decisions made by independent academic editor. Upon submission manuscript was subject to anti-plagiarism scanning. Prior to publication all authors have given signed confirmation of agreement to article publication and compliance with all applicable ethical and legal requirements, including the accuracy of author and contributor information, disclosure of competing interests and funding sources, compliance with ethical requirements relating to human and animal study participants, and compliance with any copyright requirements of third parties. This journal is a member of the Committee on Publication Ethics (COPE).
Author Contributions
Conceived and designed the experiments: SHW. Analyzed the data: SHW. Wrote the first draft of the manuscript: SHW. Developed the structure and arguments for the paper: SHW. Made critical revisions: SHW. The author reviewed and approved of the final manuscript.
REFERENCES
- 1.Zipes DP, Wellens HJJ. Sudden cardiac death. Circulation. 1998;98:2334–51. doi: 10.1161/01.cir.98.21.2334. [DOI] [PubMed] [Google Scholar]
- 2.Cao JM, Qu Z, Kim YH, et al. Spatiotemporal heterogeneity in the induction of ventricular fibrillation by rapid pacing: importance of cardiac restitution properties. Circ Res. 1999;84:1318–31. doi: 10.1161/01.res.84.11.1318. [DOI] [PubMed] [Google Scholar]
- 3.Riccio ML, Koller ML, Gilmour RF. Electrical restitution and spatiotemporal organization during ventricular fibrillation. Circ Res. 1999;84:955–63. doi: 10.1161/01.res.84.8.955. [DOI] [PubMed] [Google Scholar]
- 4.Chudin E, Goldhaber J, Garfinkel A, Weiss J, Kogan B. Intracellular Ca2+ dynamics and the stability of ventricular tachycardia. Biophys J. 1999;77:2930–41. doi: 10.1016/S0006-3495(99)77126-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Watanabe MA, Fenton FH, Evans SJ, Hastings HM, Karma A. Mechanisms for discordant alternans. J Cardiovasc Electrophysiol. 2001;12:196–206. doi: 10.1046/j.1540-8167.2001.00196.x. [DOI] [PubMed] [Google Scholar]
- 6.Comtois P, Vinet A, Nattel S. Wave block formation in homogeneous excitable media following premature excitations: dependence on restitution relations. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72:031919. doi: 10.1103/PhysRevE.72.031919. [DOI] [PubMed] [Google Scholar]
- 7.Sato D, Shiferaw Y, Garfinkel A, Weiss JN, Qu Z, Karma A. Spatially discordant alternans in cardiac tissue: role of calcium cycling. Circ Res. 2006;99:520–7. doi: 10.1161/01.RES.0000240542.03986.e7. [DOI] [PubMed] [Google Scholar]
- 8.Sato D, Bers DM, Shiferaw Y. Formation of spatially discordant alternans due to fluctuations and diffusion of calcium. PLoS One. 2013;8:e85365. doi: 10.1371/journal.pone.0085365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weiss JN, Karma A, Shiferaw Y, Chen P-S, Garfinkel A, Qu Z. From pulsus to pulseless: the saga of cardiac alternans. Circ Res. 2006;98:1244–53. doi: 10.1161/01.RES.0000224540.97431.f0. [DOI] [PubMed] [Google Scholar]
- 10.Kanaporis G, Blatter LA. The mechanisms of calcium cycling and action potential dynamics in cardiac alternans. Circ Res. 2015;116(5):846–56. doi: 10.1161/CIRCRESAHA.116.305404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shiferaw Y, Sato D, Karma A. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71:021903. doi: 10.1103/PhysRevE.71.021903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Qu Z, Garfinkel A, Chen PS, Weiss JN. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation. 2000;102:1664–70. doi: 10.1161/01.cir.102.14.1664. [DOI] [PubMed] [Google Scholar]
- 13.Weinberg SH, Tung L. Oscillation in cycle length induces transient discordant and steady-state concordant alternans in the heart. PLoS One. 2012;7:e40477. doi: 10.1371/journal.pone.0040477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Weiss JN, Nivala M, Garfinkel A, Qu Z. Alternans and arrhythmias: from cell to heart. Circ Res. 2011;108:98–112. doi: 10.1161/CIRCRESAHA.110.223586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nolasco JB, Dahlen RW. A graphic method for the study of alternation in cardiac action potentials. J Appl Physiol. 1968;25:191–6. doi: 10.1152/jappl.1968.25.2.191. [DOI] [PubMed] [Google Scholar]
- 16.Guevara MR, Ward G, Shrier A, Glass L. Electrical alternans and period doubling bifurcations. IEEE Comp Cardiol. 1984;562:167–70. [Google Scholar]
- 17.Cram AR, Rao HM, Tolkacheva EG. Toward prediction of the local onset of alternans in the heart. Biophys J. 2011;100:868–74. doi: 10.1016/j.bpj.2011.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Visweswaran R, McIntyre SD, Ramkrishnan K, Zhao X, Tolkacheva EG. Spatiotemporal evolution and prediction of [Ca 2+] iand APD alternans in isolated rabbit hearts. J Cardiovasc Electrophysiol. 2013;24:1287–95. doi: 10.1111/jce.12200. [DOI] [PubMed] [Google Scholar]
- 19.Gilmour RF, Otani NF, Watanabe MA. Memory and complex dynamics in cardiac Purkinje fibers. Am J Physiol. 1997;272:H1826–32. doi: 10.1152/ajpheart.1997.272.4.H1826. [DOI] [PubMed] [Google Scholar]
- 20.Fox JJ, Bodenschatz E, Gilmour RF. Period-doubling instability and memory in cardiac tissue. Phys Rev Lett. 2002;89:138101. doi: 10.1103/PhysRevLett.89.138101. [DOI] [PubMed] [Google Scholar]
- 21.Tolkacheva EG, Schaeffer DG, Gauthier DJ, Krassowska W. Condition for alternans and stability of the 1:1 response pattern in a “memory” model of paced cardiac dynamics. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67:031904. doi: 10.1103/PhysRevE.67.031904. [DOI] [PubMed] [Google Scholar]
- 22.Cherry EM, Fenton FH. Suppression of alternans and conduction blocks despite steep APD restitution: electronic, memory, and conduction velocity restitution effects. Am J Physiol Heart Circ Physiol. 2004;286(6):H2332–41. doi: 10.1152/ajpheart.00747.2003. [DOI] [PubMed] [Google Scholar]
- 23.Kalb SS, Tolkacheva EG, Schaeffer DG, Gauthier DJ, Krassowska W. Restitution in mapping models with an arbitrary amount of memory. Chaos. 2005;15:023701. doi: 10.1063/1.1876912. [DOI] [PubMed] [Google Scholar]
- 24.Dvir H, Zlochiver S. The interrelations among stochastic pacing, stability, and memory in the heart. Biophys J. 2014;107:1023–34. doi: 10.1016/j.bpj.2014.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Qu Z, Shiferaw Y, Weiss JN. Nonlinear dynamics of cardiac excitation-contraction coupling: an iterated map study. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;75:011927. doi: 10.1103/PhysRevE.75.011927. [DOI] [PubMed] [Google Scholar]
- 26.Fox JJ, Riccio ML, Hua F, Bodenschatz E, Gilmour RF. Spatiotemporal transition to conduction block in canine ventricle. Circ Res. 2002;90:289–96. doi: 10.1161/hh0302.104723. [DOI] [PubMed] [Google Scholar]
- 27.Weinberg SH. Spatial discordance and phase reversals during alternate pacing in discrete-time kinematic and cardiomyocyte ionic models. Chaos. 2015;25:103119. doi: 10.1063/1.4932961. [DOI] [PubMed] [Google Scholar]
- 28.Hasenfuss G, Reinecke H, Studer R, et al. Relation between myocardial function and expression of sarcoplasmic reticulum Ca(2+)-ATPase in failing and nonfailing human myocardium. Circ Res. 1994;75:434–42. doi: 10.1161/01.res.75.3.434. [DOI] [PubMed] [Google Scholar]
- 29.Vatner DE, Sato N, Kiuchi K, Shannon RP, Vatner SF. Decrease in myocardial ryanodine receptors and altered excitation-contraction coupling early in the development of heart failure. Circulation. 1994;90:1423–30. doi: 10.1161/01.cir.90.3.1423. [DOI] [PubMed] [Google Scholar]
- 30.Shannon TR, Pogwizd SM, Bers DM. Elevated sarcoplasmic reticulum Ca2+ leak in intact ventricular myocytes from rabbits in heart failure. Circ Res. 2003;93:592–4. doi: 10.1161/01.RES.0000093399.11734.B3. [DOI] [PubMed] [Google Scholar]
- 31.Piacentino V, Weber CR, Chen X, et al. Cellular basis of abnormal calcium transients of failing human ventricular myocytes. Circ Res. 2003;92:651–8. doi: 10.1161/01.RES.0000062469.83985.9B. [DOI] [PubMed] [Google Scholar]
- 32.Wehrens XHT, Lehnart SE, Marks AR. Intracellular calcium release and cardiac disease. Annu Rev Physiol. 2005;67:69–98. doi: 10.1146/annurev.physiol.67.040403.114521. [DOI] [PubMed] [Google Scholar]
- 33.Louch WE, Hake J, Mørk HK, et al. Slow Ca2+ sparks de-synchronize Ca2+ release in failing cardiomyocytes: evidence for altered configuration of Ca2+ release units? J Mol Cell Cardiol. 2013;58:41–52. doi: 10.1016/j.yjmcc.2013.01.014. [DOI] [PubMed] [Google Scholar]
- 34.Røe ÅT, Frisk M, Louch WE. Targeting cardiomyocyte Ca2+ homeostasis in heart failure. Curr Pharm Des. 2015;21:431–48. doi: 10.2174/138161282104141204124129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Echebarria B, Karma A. Instability and spatiotemporal dynamics of alternans in paced cardiac tissue. Phys Rev Lett. 2002;88:208101. doi: 10.1103/PhysRevLett.88.208101. [DOI] [PubMed] [Google Scholar]
- 36.Fox JJ, Riccio ML, Drury P, Werthman A, Gilmour RF. Dynamic mechanism for conduction block in heart tissue. New J Phys. 2003;5(1):101. [Google Scholar]
- 37.Henry H, Rappel WJ. Dynamics of conduction blocks in a model of paced cardiac tissue. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71:051911. doi: 10.1103/PhysRevE.71.051911. [DOI] [PubMed] [Google Scholar]
- 38.Echebarria B, Karma A. Amplitude equation approach to spatiotemporal dynamics of cardiac alternans. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76:051911. doi: 10.1103/PhysRevE.76.051911. [DOI] [PubMed] [Google Scholar]
- 39.Wang S, Xie Y, Qu Z. Coupled iterated map models of action potential dynamics in a one-dimensional cable of cardiac cells. New J Phys. 2008;10:55001–24. doi: 10.1088/1367-2630/10/5/055001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Weinberg S, Malhotra N, Tung L. Vulnerable windows define susceptibility to alternans and spatial discordance. Am J Physiol Heart Circ Physiol. 2010;298:H1727–37. doi: 10.1152/ajpheart.01036.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xie L-H, Sato D, Garfinkel A, Qu Z, Weiss JN. Intracellular Ca alternans: coordinated regulation by sarcoplasmic reticulum release, uptake, and leak. Biophys J. 2008;95:3100–10. doi: 10.1529/biophysj.108.130955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cytrynbaum E, Keener JP. Stability conditions for the traveling pulse: modifying the restitution hypothesis. Chaos. 2002;12:788–99. doi: 10.1063/1.1503941. [DOI] [PubMed] [Google Scholar]
- 43.Shiferaw Y, Karma A. Turing instability mediated by voltage and calcium diffusion in paced cardiac cells. Proc Natl Acad Sci U S A. 2006;103:5670–5. doi: 10.1073/pnas.0511061103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Skardal PS, Karma A, Restrepo JG. Unidirectional pinning and hysteresis of spatially discordant alternans in cardiac tissue. Phys Rev Lett. 2012;108:108103–108105. doi: 10.1103/PhysRevLett.108.108103. [DOI] [PubMed] [Google Scholar]
- 45.Skardal PS, Karma A, Restrepo JG. Spatiotemporal dynamics of calcium-driven cardiac alternans. Phys Rev E Stat Nonlin Soft Matter Phys. 2014;89:052707. doi: 10.1103/PhysRevE.89.052707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kameyama M, Hirayama Y, Saitoh H, Maruyama M, Atarashi H, Takano T. Possible contribution of the sarcoplasmic reticulum Ca(2+) pump function to electrical and mechanical alternans. J Electrocardiol. 2003;36:125–35. doi: 10.1054/jelc.2003.50021. [DOI] [PubMed] [Google Scholar]
- 47.Edwards JN, Blatter LA. Cardiac alternans and intracellular calcium cycling. Clin Exp Pharmacol Physiol. 2014;41:524–32. doi: 10.1111/1440-1681.12231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lindner M, Erdmann E, Beuckelmann DJ. Calcium content of the sarcoplasmic reticulum in isolated ventricular myocytes from patients with terminal heart failure. J Mol Cell Cardiol. 1998;30:743–9. doi: 10.1006/jmcc.1997.0626. [DOI] [PubMed] [Google Scholar]
- 49.Hobai IA, O’Rourke B. Decreased sarcoplasmic reticulum calcium content is responsible for defective excitation-contraction coupling in canine heart failure. Circulation. 2001;103:1577–84. doi: 10.1161/01.cir.103.11.1577. [DOI] [PubMed] [Google Scholar]
- 50.Kubalova Z, Terentyev D, Viatchenko-Karpinski S, et al. Abnormal intrastore calcium signaling in chronic heart failure. Proc Natl Acad Sci U S A. 2005;102:14104–9. doi: 10.1073/pnas.0504298102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cutler MJ, Wan X, Laurita KR, Hajjar RJ, Rosenbaum DS. Targeted SER-CA2a gene expression identifies molecular mechanism and therapeutic target for arrhythmogenic cardiac alternans. Circ Arrhythm Electrophysiol. 2009;2:686–94. doi: 10.1161/CIRCEP.109.863118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cutler MJ, Wan X, Plummer BN, et al. Targeted sarcoplasmic reticulum Ca2+ ATPase 2a gene delivery to restore electrical stability in the failing heart. Circulation. 2012;126:2095–104. doi: 10.1161/CIRCULATIONAHA.111.071480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ling L-H, Khammy O, Byrne M, et al. Irregular rhythm adversely influences calcium handling in ventricular myocardium: implications for the interaction between heart failure and atrial fibrillation. Circ Heart Fail. 2012;5:786–93. doi: 10.1161/CIRCHEARTFAILURE.112.968321. [DOI] [PubMed] [Google Scholar]
- 54.Song L-S, Sobie EA, McCulle S, Lederer WJ, Balke CW, Cheng H. Orphaned ryanodine receptors in the failing heart. Proc Natl Acad Sci U S A. 2006;103:4305–10. doi: 10.1073/pnas.0509324103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation. 1999;99:1385–94. doi: 10.1161/01.cir.99.10.1385. [DOI] [PubMed] [Google Scholar]
- 56.Laurita KR, Rosenbaum DS. Cellular mechanisms of arrhythmogenic cardiac alternans. Prog Biophys Mol Biol. 2008;97:332–47. doi: 10.1016/j.pbiomolbio.2008.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Qu Z, Xie Y, Garfinkel A, Weiss JN. T-wave alternans and arrhythmogenesis in cardiac diseases. Front Physiol. 2010;1:154. doi: 10.3389/fphys.2010.00154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bers DM, Eisner DA, Valdivia HH. Sarcoplasmic reticulum Ca2+ and heart failure: roles of diastolic leak and Ca2+ transport. Circ Res. 2003;93:487–90. doi: 10.1161/01.RES.0000091871.54907.6B. [DOI] [PubMed] [Google Scholar]
- 59.Roberts BN, Yang P-C, Behrens SB, Moreno JD, Clancy CE. Computational approaches to understand cardiac electrophysiology and arrhythmias. Am J Physiol Heart Circ Physiol. 2012;303:H766–83. doi: 10.1152/ajpheart.01081.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Henriquez CS. A brief history of tissue models for cardiac electrophysiology. IEEE Trans Biomed Eng. 2014;61:1457–65. doi: 10.1109/TBME.2014.2310515. [DOI] [PubMed] [Google Scholar]
- 61.Berridge MJ. Calcium microdomains: organization and function. Cell Calcium. 2006;40:405–12. doi: 10.1016/j.ceca.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 62.Weinberg SH, Smith GD. Discrete-state stochastic models of calcium-regulated calcium influx and subspace dynamics are not well-approximated by ODEs that neglect concentration fluctuations. Comput Math Methods Med. 2012;2012:1–17. doi: 10.1155/2012/897371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Weinberg SH, Smith GD. The influence of Ca2+ buffers on free [Ca2+] fluctuations and the effective volume of Ca2+ microdomains. Biophys J. 2014;106:2693–709. doi: 10.1016/j.bpj.2014.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ji H, Li Y, Weinberg S. Calcium ion fluctuations alter channel gating in a stochastic luminal calcium release site model. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2015;99:1–1. doi: 10.1109/TCBB.2015.2498552. [DOI] [PubMed] [Google Scholar]
- 65.Ma J, Xiao D. Nonlinear dynamics of a mathematical model on action potential duration and calcium transient in paced cardiac cells. Discrete Continuous Dyn Syst Ser B. 2013;18:2377–96. [Google Scholar]