Physical basis of some membrane shaping mechanisms

Abstract

In vesicular transport pathways, membrane proteins and lipids are internalized, externalized or transported within cells, not by bulk diffusion of single molecules, but embedded in the membrane of small vesicles or thin tubules. The formation of these ‘transport carriers’ follows sequential events: membrane bending, fission from the donor compartment, transport and eventually fusion with the acceptor membrane. A similar sequence is involved during the internalization of drug or gene carriers inside cells. These membrane-shaping events are generally mediated by proteins binding to membranes. The mechanisms behind these biological processes are actively studied both in the context of cell biology and biophysics. Bin/amphiphysin/Rvs (BAR) domain proteins are ideally suited for illustrating how simple soft matter principles can account for membrane deformation by proteins. We review here some experimental methods and corresponding theoretical models to measure how these proteins affect the mechanics and the shape of membranes. In more detail, we show how an experimental method employing optical tweezers to pull a tube from a giant vesicle may give important quantitative insights into the mechanism by which proteins sense and generate membrane curvature and the mechanism of membrane scission.

This article is part of the themed issue ‘Soft interfacial materials: from fundamentals to formulation’.

1. Introduction

Lipid bilayers constitute the structural basis of cell membranes. They are quasi impermeable to most ions and molecules, which prevents the cell’s contents from escaping uncontrollably. Nevertheless, cells have to continuously exchange materials with the external world. They have to internalize ions and nutrients, to receive or emit signal molecules, and also to regulate the number of adhesion molecules and receptors they present at their surface. Specialized proteins embedded in the plasma membrane—i.e. ion channels, ion pumps, transporters—are responsible for the active internalization of ions or some small molecules. The rest of the exchange of molecules is mediated by processes called endocytosis and exocytosis, for entry and egress of material, respectively [1]. In endocytosis, cargos first bind to the cell membrane. The membrane deforms and engulfs them in a vesicle that eventually pinches off towards the cytoplasm. This vesicle then enters the endosomal pathway for a later redistribution to various parts of the cell [2]. Depending on the size and the nature of the cargo, one also distinguishes phagocytosis for the internalization of larger cargos (e.g. pathogens, particles, cells) and pinocytosis for the internalization of very small cargos or liquids. Bacteria and viruses also have to cross this barrier to invade cells [3]. Furthermore, drug or genes are delivered into the cells by way of endocytosis, typically in the form of liposomes. Importantly, for any of these mechanisms to take place, cell membranes have to undergo a series of deformations and eventually scission [4].

Lipid bilayers, and more generally cell membranes, are very interesting materials from a soft matter point of view. They are very thin lipid sheets (approx. 5 nm), but can extend laterally over much larger distances, up to hundreds of micrometres. In cells, the composition is such that membranes are fluid, which makes them much more flexible than solid elastic shells. Since the 1970s, a number of physicists coming from a mechanics or soft matter background, starting with Helfrich [5], Evans [6,7] and Canham [8], have developed elastic descriptions of lipid membranes that have been remarkably successful in explaining the physical basis of large-scale membrane behaviour. Moreover, their work has provided a very useful analytical framework for analysing and understanding the experimental data (for reviews, see e.g. [9–12]). Very early on they realized that if an asymmetry exists between the leaflets (i.e. the number of lipids is different, proteins are inserted or locally deform the membrane in an unbalanced fashion), an originally flat membrane spontaneously bends. The corresponding membrane curvature (i.e. the relaxed equilibrium curvature of the membrane in the absence of external mechanical action) was named spontaneous membrane curvature.

In cells, the sequence of membrane shaping events leading to successful endocytosis is driven by the interaction of different proteins with the membrane. Currently in biology, endocytic pathways are split into two types [13]: clathrin-mediated endocytosis (CME) and clathrin-independent endocytosis (CIE). For a long time, CME has been recognized as the canonical endocytic pathway [14,15], but in the recent years, more and more clathrin-independent routes have begun to emerge [16,17]. Clathrin proteins interact with the membrane via adaptor molecules and polymerize into a rigid coat, mediating the formation of spherical vesicles of typically 80 nm in diameter [15,18,19]. Clathrin is assisted by different proteins such as proteins containing Bin/amphiphysin/Rvs (BAR) or epsin N-terminal homology domains [20]. The final step, scission, is mediated by the GTPase dynamin that polymerizes at the neck of a clathrin bud and constricts it [21]. Actin polymerization can also assist CME, especially in conditions where the cell membrane is stretched [22]. In CIE, membrane deformation is generally achieved by proteins that do not assemble into spherical coats, but rather shape the membrane into cylindrical tubules. Many new actors and processes have been identified in the scission step of this pathway, including lectin–glycosphingolipid couples [23], glycosylphosphatidylinositol-anchored proteins and short cortical actin filaments [24]. It was also recently shown that the BAR-domain endophilin is an essential actor of this pathway [25,26]. Figure 1a illustrates CME and one CIE mechanism, highlighting the key players in these pathways.

Figure 1.

(a) Schematics of clathrin-mediated endocytosis (CME) and an example of the many mechanisms of clathrin-independent endocytosis (CIE) mediated by endophilin. (b) Structure of representative BAR proteins derived by X-ray crystallography. Each subunit is differently coloured, with the N-terminal amphipathic helices in the N-BAR protein coloured red. The orange dotted line highlights the intrinsic curvature in their structure.

The BAR-domain proteins are involved in many places in cells where they contribute to membrane deformations [27]. The characteristic structural feature of these proteins is an intrinsically curved domain with an anisotropic ‘banana’ shape that peripherally adheres to the membrane surface (figure 1b). Based on the shape of this domain, they are subdivided into (i) classical BAR, (ii) N-BAR (BAR + N-terminal amphipathic helix) which generally display highly curved BAR domains as revealed by X-ray diffraction, (iii) F-BAR, and (iv) I-BAR, whose BAR domains are generally shallower (figure 1b) [28]. In CME, F-BAR proteins bind at early stages of the bud formation when the membrane is weakly bent [29], whereas N-BARs (endophilin and amphiphysin) bind at the very late stage, just before scission, when the neck of the bud has already narrowed [30,31]. In CIE pathways involving endophilin, this protein is essential for membrane tubulation but intriguingly, it is also involved in tubule scission [26].

Members of the BAR protein family interact differently with the sign of membrane curvature. By convention, the sign of membrane curvature is chosen to be positive when the centre of curvature is on the side of the membrane opposite to that on which proteins are present; otherwise, it is negative. F-BAR, BAR and N-BAR proteins are associated with membranes with positive curvature. By contrast, I-BAR proteins bind to negatively bent membranes and are usually involved in the formation of membrane protrusions extending outside the cells. It has been shown that IRSp53 participates in the formation of filopodia—tubular extensions that cells use for sensing the external environment. In this mechanism, the I-BAR protein binds first, followed by the binding of actin adaptors and the actin filament, which promotes filopodial growth [32]. These different observations point to a relation between the amplitude of membrane curvature and that of the BAR domain bound to it. Motivated by the growing body of evidence of the role of BAR domains in membrane trafficking and protrusion formation, biophysicists have developed new models based on elastic descriptions of lipid membranes mentioned above, in vitro experiments and computer simulations. These approaches help to explain the coupling between the intrinsic shape of BAR proteins and the shape of the membrane, as well as the parameters that influence their mode of action (for a recent review with a biological perspectives, see [33]).

As endocytic proteins and especially BAR proteins have a wide range of functions and structures, we will review here recent work on these proteins from a biophysics point of view as a revealing illustration of the approaches developed to understand mechanisms underlying membrane shaping by proteins in cells.

2. Some methods for measuring membrane shaping by Bin/amphiphysin/Rvs-domain proteins

One convenient method for quantifying membrane deformation induced by proteins is to mix model membrane systems with purified proteins. This allows many important parameters to be controlled, such as protein concentration, lipid composition, surface tension and membrane geometry—parameters that cannot be controlled in vivo, in order to comprehensively describe the effect of specific proteins on membranes.

The consequences on membrane shape can be monitored directly using imaging methods at various resolutions, or indirectly by mechanical measurements coupled to theoretical models. Micrometre-sized liposomes are well suited to micromanipulation experiments and mechanical measurements. As the membrane-binding surface of the BAR domains is lined with positively charged residues, these liposomes must contain negatively charged lipids to mediate protein binding [34,35]. We list below some of the methods that are now commonly used for such measurements.

(a). Electron microscopy

Electron microscopy (EM) is the method of choice for monitoring membrane shaping by proteins. It has been extensively used to demonstrate that BAR domains are efficient membrane remodellers. A typical approach consists of incubating 50- to 100-nm-wide liposomes in the presence of a high concentration of proteins (usually higher than 1 or few micromolars). Negative staining or better yet, cryo-EM, can then be used to observe morphological changes such as tubular exvaginations or the complete conversion of vesicles into tubules in the case of BAR and N-BAR proteins [36–38], or tubular invaginations in the case of I-BAR proteins [39]. Additionally, when proteins form a regular organization on the tubules, the molecular structure of this protein coat can be resolved [34,40].

(b). Spontaneous tubulation of giant vesicles

Giant unilamellar vesicles (GUVs) are commonly used as models of quasi-flat membranes, as they are big enough (typically with a 5–50 μm diameter) to be observed by optical microscopy and they are amenable to micromanipulation. The most basic method consists of incubating GUVs (doped with fluorescent lipids) with fluorescently tagged proteins. Under appropriate conditions—usually relatively low membrane tension and high enough protein bulk concentration [33]—membrane tubulations or invaginations can be observed with confocal microscopy (see [41] for a review and [42–44] for examples on BAR proteins). However, no quantitative measurement of protein shaping can be extracted from these observations. Recently, a method has been designed in the group of Baumgart where the threshold in protein density on the membrane for spontaneous tubulation is deduced from calibrated fluorescence measurements, as a function of membrane tension, which is controlled by micropipette aspiration (figure 2a) [45]. The protein’s intrinsic curvature can be deduced from this analysis, provided that a theoretical model is developed (see below).

Figure 2.

In vitro assays to study the curvature coupling of membrane-binding proteins. (a) Immersing the micropipette-aspired GUVs into a solution of the protein. The tubulation is evident by the change in length of the aspirated part of the membrane. (b) Tube-pulling assay. The aspiration micropipette (left) controls the tension in the GUV, while the other micropipette (right) is used to inject the protein. Optical tweezers (OT) are used to trap a streptavidin-coated bead, tether it to the GUV (containing a fractionate amount of biotinylated lipids) and finally pull a tubule. Confocal microscopy measures the tubule radius (from lipid fluorescence) and the amount of bound proteins (from protein fluorescence). (c) The SLiC assay. Small liposomes of various sizes are tethered to a polyethylene-glycol surface via streptavidin–biotin bonds. Following the injection of proteins, liposome size and the amount of bound proteins are measured with fluorescence microscopy.

(c). Membrane nanotubes

In our group, we adapted the method of pulling a membrane nanotube from a GUV, a method initially designed to probe lipid membrane mechanics [46–48], to study the mechanical effects of BAR-domain and other membrane shaping proteins. A membrane nanotube can be extruded from a GUV by tethering a vesicle via streptavidin–biotin bonds to a micrometre-sized bead trapped in optical tweezers. The GUV is aspirated in a micropipette that sets the membrane tension [49,50]. With another micropipette, the fluorescently labelled proteins are injected next to the nanotube (figure 2b). Using confocal microscopy, we can measure the absolute density of proteins bound on the GUV and on the nanotube, which gives the relative enrichment of proteins on a curved membrane [42]. As detailed in the theory section below, the nanotube radius R of the bare membrane can be tuned by changing the membrane tension σ, achieved by modulating pipette aspiration. In practice, R can range between 7 and a few hundred nanometres. As the tube radius is generally below optical resolution, R can be directly deduced from the fluorescence intensity of the tube in the lipid channel after appropriate calibration using the relation between radius, force and tension R=f/4πσ [42], provided that the fluorescent lipids do not interact with the proteins and are not curvature sensitive. The force f to hold the nanotube also depends on σ, that is, . In the presence of proteins shaping membranes, R and f may change (see theory section) and the intrinsic curvature of the protein can be deduced from this analysis. This method has now been used for various proteins [51–54].

(d). Small liposomes

Another assay called SLiC (single liposome curvature) has been designed in the group of Stamou to measure the affinity of proteins for curved membranes, in particular BAR-domain proteins, but it is not adapted for measuring mechanical effects. In this assay, a few hundred small vesicles (50–500 nm in diameter) are tethered via streptavidin–biotin bonds to a polyethylene-glycol-covered surface, doped with a biotinylated polymer (figure 2c). The surface density of proteins and the size of the vesicles are individually measured with total internal reflection microscopy, allowing a measure of the curvature-induced sorting with very good precision [55]. This measure is a priori complementary to the sorting deduced from nanotube experiments, but it is possible that the geometry of the membrane might influence how anisotropic proteins (such as BAR domains) bind to the surface, ultimately affecting their sorting [56,57].

3. Proteins shaping membranes: a physical model for the nanotube assay

We present here the main points of a theoretical model that describes the physics of curved membranes with bound BAR-domain proteins. It is relevant for experiments corresponding to nanotube assays described in §2.3 where proteins interact with a membrane nanotube connected to a GUV.

The bending energy per unit area of a lipid membrane is given by the Helfrich’s elastic model: F=(1/2)κC², with κ being the membrane bending modulus and C the membrane mean curvature [5]. In the presence of proteins asymmetrically bound on one side of the bilayer inducing a spontaneous curvature C₀, Helfrich proposed that the bending energy density is reduced and becomes: F=(1/2)κ(C−C₀)². C₀ is a global ‘coarse-grained’ parameter that integrates many molecular and structural aspects of the interaction of the protein with the membrane. In addition, in this model, only isotropic mean curvature is considered and this might appear as a limitation in the future. This simple mechanical description has inspired many models over the years.

In particular, in past years, various theoretical expressions have been used to represent the free energy of proteins bound to membrane tubules [42,58,59]. We present here a generic model, in agreement with a large range of experimental data. It has been developed in [54], with similar terms to those used in a different context [60,61]. In the presence of bound proteins, the membrane energy of a tube held by an external force consists of four terms:

3.1

First, there is a phospholipid membrane bending energy, with stiffness κ that penalizes the curvature C=1/R of the tube. Second, there is an energy associated with the membrane tension σ. Note that in the presence of proteins, the tension in the tube is not the same as that in the vesicle, σ_v [54]. These two terms describe the elastic energy of a bare tube. Third, there is an energy associated with the mismatch between the local membrane curvature and the intrinsic spontaneous curvature of the protein . is a positive constant corresponding to the mismatch penalty between protein and membrane curvatures. Note that our model of protein–membrane interaction energy is very similar to that in [59,62,63]. Then, there is a mixing energy, penalizing spatial inhomogeneities that are entropically unfavourable in a two-component membrane (lipids plus proteins). The last term is the work done by the force applied on the membrane via the optically trapped bead.

Neglecting direct protein–protein interactions (valid in dilute situations) the mixing free energy f_m has the Flory–Huggins form:

3.2

where k_B is Boltzmann’s constant, T the temperature and a is the area per lipid.

If no proteins are present (i.e., ϕ=0), the radius of a lipid bilayer tube of length L is found by minimizing the energy with respect to R yielding:

3.3

Thus, controlling membrane tension allows setting the radius of a bare tubule, which in addition can be modulated by membrane composition (implicitly, bending rigidity). Similarly, the force needed to hold a tube is found by minimization with respect to L, for ϕ=0, yielding (see also [64,65])

3.4

In the presence of bound proteins, a rich variety of behaviours is expected because of the nonlinearity of equation (3.1). The third term represents the coupling between protein density and membrane curvature; it favours the enrichment of proteins in membranes with curvature close to . The fourth term limits it.

How the amount of protein depends on membrane curvature, at equilibrium (this property is generally called ‘membrane curvature-induced sorting’), is found by writing a similar energy, as in (3.1), for the near flat reservoir vesicle (R=0), and balancing the protein chemical potentials: [54]. As a result, the protein density on the tube, ϕ_t, R and f are coupled; R and f depend not only on κ and σ_v, but also on the protein density on the GUV, ϕ_v.

Generally, two different regimes are distinguished that are directly determined by the protein area fraction on the membrane reservoir ϕ_v. Note that only the bulk concentration, and not ϕ_v, is typically measured, which obscures comparisons between different experimental systems and between experiment and theory. Indeed, the quantity of proteins actually bound depends strongly on lipid composition and can also vary among vesicles in the same preparation. Thus ϕ_v must be measured for each vesicle, and along with the bare membrane mean curvature in the tube or SLiC assays, or membrane tension in the spontaneous tubulation experiments, is a key experimental control parameter. We will detail in the next section the relations between the tube radius R, the force f, and ϕ_v. We will also discuss published data on BAR-domain proteins.

According to these experiments, three main trends are observed:

• (1) At very low ϕ_v, protein enrichment on the tube (i.e. sorting) is independent of ϕ_v, it increases linearly with curvature for 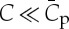, and reaches a maximum at . In other cases, the relation is more complex. Under this regime, no significant mechanical effect is expected, therefore the relations between R and f as a function of σ_v (equations (3.3) and (3.4)) are essentially unchanged.

• (2) At high ϕ_v, the magnitude of sorting weakly depends on curvature. Owing to an imposed protein scaffold on the membrane tubule, R is independent of σ_v and is of the order of . For the same reason f varies linearly with σ_v instead of with .

• (3) At intermediate densities, the two regimes are mixed.

4. Measuring the intrinsic spontaneous curvature of Bin/amphiphysin/Rvs domains

(a). At low ϕ_v: curvature-induced sorting

We focus in this section on the physics underlying the tube-pulling assay (§2.3) (figure 2b). When a low density of protein is present on the membrane reservoir (i.e. the GUV), the proteins become enriched on the tubule because of their preferred affinity for curved membrane, which can be measured with confocal microscopy (figure 3a). The sorting coefficient S is given by the ratio between the protein fraction on the tube and on the vesicle: S=ϕ_t/ϕ_v. It can be obtained from the ratio of the fluorescence intensities of the protein on the tube, , and on the GUV, I^p_v, normalized by the same ratio for the lipid fluorescence: 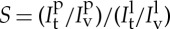. As the tube radius cannot be simply calculated from equation (3.3) in the presence of proteins, it is measured from the lipid fluorescence as 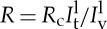, where R_c is a calibration constant deduced from measurements in the absence of proteins [42].

Figure 3.

Curvature sorting of BAR proteins. (a) A confocal image showing the enrichment of an I-BAR protein IRSp53 (labelled green) on a tube pulled from a GUV (lipids labelled purple). The proteins are encapsulated in the GUV, bound at 4% surface coverage.Scale bar, 5 μm. Image adapted from Prévost et al. [54]. Copyright © 2015 Nature Publishing Group. (b) Curvature sorting of endophilin A1 at bulk protein concentration of 1 μM. Reprinted from Zhu et al. [66]. Copyright © 2012 Elsevier. (c) Curvature sorting of I-BAR IRSp53 at different membrane surface densities of the protein, as indicated. Proteins are sorted when encapsulated (because they are negative curvature sensors) and not when they are bound on the outside of the tubule. Image adapted from Prévost et al. [54]. Copyright © 2015 Nature Publishing Group.

The relationship between the protein area fractions on the tube and on the vesicle and the tube curvature can be obtained from a balance of protein chemical potentials, yielding an implicit dependence of ϕ_t on the curvature:

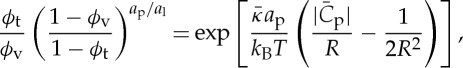4.1

where a_p and a₁ are the protein and lipid areas, respectively, defined as projections onto the plane parallel with the membrane. In the limit of very low densities, a Gaussian dependence is predicted

with a maximum for a tube curvature matching .

All tested BAR proteins so far have shown to be sorted on membrane nanotubes, e.g. N-BARs: amphiphysin 1 [42], amphiphysin 2 (BIN1) [67], endophilin A1 [66], F-BAR: syndapin 1 [52] and I-BAR: IRSp53. See figure 3b for the sorting measurement of endophilin A1. A decrease in S when increasing ϕ_v has been reported for non-vanishing protein densities on GUVs, in agreement with the model [42]. For all cases, except for the I-BAR protein IRSp53, a monotonic increase in S with C is observed (figure 3b). We predict that other proteins also display non-monotonic dependence; the peak values of S were likely not observed because the corresponding high tube curvatures could not be accessed. In the case of IRSp53, an optimal sorting at a curvature C=1/18 nm⁻¹ has been observed (figure 3c), in line with the known structure of the I-BAR domain. In this case, excellent agreement has been observed with equation (4.1) as well as the variation of S with ϕ_v [54] (figure 3c). Note that a maximum and a Gaussian dependence of S on C have also been observed for a transmembrane protein (KvAP), measuring a similar intrinsic curvature 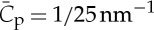[53].

Consistent with the observed monotonic increase of S with curvature, a higher intrinsic curvature was obtained for amphiphysin 1 [42] and endophilin A1 [66], although other models were used to extract in those cases. In the case of an F-BAR protein syndapin 1, S did not show a maximum, even though its structure suggests a low similarly to IRSp53 [52]. It was hypothesized that this protein may have a different conformation when bound to a tubule, which may even change with tubule radius. Moreover, the presence of loops that insert into the bilayer would also affect . The wedging effect of amphipathic helices in amphiphysin 1 could also explain why was found to be much higher than predicted from the X-ray structure and from the diameter of the scaffold. This result illustrates well that is a global parameter that integrates many molecular details associated with the protein structure, such as anisotropic two-dimensional curvatures and the terminal or lateral domain insertions.

(b). At medium ϕ_v: mechanical tube deformation

We note that whereas S described above represents a measure of the relative enrichment of the proteins on the tube and decreases with increased ϕ_v, the absolute density of proteins on the tube increases with ϕ_v. It is thus expected that R and f are increasingly affected by proteins, and deviation in equations (3.4) and (3.4) can be detected with increased ϕ_v. In the case of amphiphysin, a consistent tube constriction was observed when increasing ϕ_v at constant GUV tension, σ_v, as set by the micropipette (figure 4a) [42]. The model described in §3 also provides a non-analytical solution for the tube radius versus σ_v. It was found to fit well the data for IRSp53 [54]. At ϕ_v=1%, no mechanical effect was detected, but, when the density increased, very clear deviations in the force were observed, with a constriction of the bare tube at low tension and an expansion of the narrow tubes at high tension (figure 4b). The protein assembly on the tube thus strongly perturbs its shape. The case of low ϕ_v provides a useful analytical limit, showing how R should scale with σ_v and ϕ_v:

4.2

in agreement with the experimental results. It shows that the effective rigidity of the coated tube is higher and is given by . In addition, R depends weakly on σ_v and interestingly, is not set by . For non-vanishing σ_v, R becomes almost constant and also weakly dependant on ϕ_v: .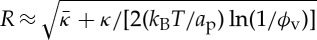

Figure 4.

(a) The steady-state radius of the tubule is progressively lower with increased bound density of the N-BAR protein amphiphysin 1. (b) I-BAR proteins impart a mechanical effect on the membrane when bound at greater than 1%, indicated by a change in tubule radius from the expected at a given membrane tension. (c) At very high bound densities, the tubule radius is fixed at any tension. Data shown for amphiphysin 1, where ‘force’and ‘fluo’ denote whether the radius was deduced, respectively, from the force or the fluorescence intensity of lipids in the tubule. (d) The effect on membrane force at high-density binding of amphiphysin 1. (a,c and d) Adapted from Sorre et al. [42]. Copyright © 2012 National Academy of Sciences, USA. (b) Adapted from Prévost et al. [54]. Copyright © 2015 Nature Publishing Group.

In the presence of proteins, a systematic drop in the force has been observed, further amplified at higher ϕ_v, consistent with the stabilization effect due to proteins accumulating on the membrane. With the same model as before, f can be derived and fits very well the data for IRSp53, with parameters consistent with other fits. By minimizing 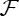with respect to L, and under the same conditions leading equation (4.2), we obtain

4.3

It predicts that the force should decrease with protein density on the GUV and should be offset by .

(c). At high ϕ_v: rigid scaffold

As shown on the case of amphiphysin 1, at a sufficiently high protein density, the tube radius does not vary any more, even if more proteins are added onto the GUV (figure 4a). Similarly, it does not vary when σ_v is changed (figure 4c). This is the hallmark for the formation of a rigid scaffold on the tube. BAR-domain proteins are able to form such a scaffold at densities much lower than surface saturation [26,42]. It results from their ability to self-assemble on membranes [68,69].

When the rigid scaffold is formed with a radius R_s, a simple expression for the force can be derived [42,70] that shows a different scaling with the vesicle tension. Indeed, a simple linear relationship now couples f to σ_v

4.4

where σ* represents the tension threshold in this geometry to spontaneously form a tube. In principle, σ* is related to [42]. Below σ*, no force is necessary to hold the tube. This scaling has been observed for the high concentrations of amphiphysin (ϕ_v>5%; figure 4d) with the corresponding scaffolding radius measured to be R_s=7 nm. This high concentration regime is technically difficult to achieve for I-BAR-domain proteins encapsulated in GUVs; thus R_s has not been measured for IRSp53.

(d). Alternative method: spontaneous tubulation

In the spontaneous tubulation method (§2.2), experiments are performed in conditions where, at a fixed membrane tension, the threshold protein density on the vesicle to get spontaneous membrane tubulation is measured. At the lowest membrane tension accessible in this assay, the threshold corresponds to about ϕ_v>7.5%, but it can reach area fractions as high as 50% for high tensions. Under this regime, protein–protein interactions cannot be neglected. In [45], the authors use a classical linear coupling between protein concentration and membrane curvature to account for the effect of proteins on the membrane and include Van der Waals interactions between proteins. By performing a linear stability analysis of a flat membrane with bound proteins, they find the following criterion for the membrane tension in order to obtain tubulation:

4.5

where a_i are fitting constants: a₁ is proportional to the protein intrinsic curvature; a₂ is inversely proportional to the energy penalty for protein density gradients and a₃ is proportional to the strength of protein–protein attraction. Thus, large a₃, which favours protein clustering, favours tubulation; by contrast, large a₂ opposes tubulation as it penalizes the protein density gradients needed to locally deform a patch of membrane. Using this approach, the authors have fit their micropipette data and measured an intrinsic curvature for endophilin , in very good agreement with the tube assay at high protein density measured by the same group [66].

Surprisingly, a very high intrinsic curvature was deduced for MIM (an I-BAR-domain protein with N-terminal amphipathic helices), measuring 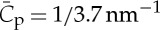. An even stronger tubulation capacity was observed for IRSp53 [71]. This observation is surprising considering that IRSp53 does not contain amphipathic helices, and are in apparent contradiction with [54]. These puzzling differences may arise from the different density regimes probed by the two methods, but still remain to be understood.

(e). At high ϕ_v: electron microscopy

In the presence of high protein concentrations (greater than 50%), the protein intrinsic spontaneous curvature can in principle be deduced from the diameter of the tubules R_s that spontaneously form out of small liposomes [72]. EM can report on the radius of the scaffold with a high resolution. The shaping capability of BAR-domain proteins has been generally first assessed with this type of method, demonstrating the large range of curvature these proteins span. Nevertheless, it is interesting to note that theoretically, there is a slight difference between R_s and 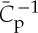, which depends on the ratio between the bare membrane bending rigidity and the elastic constant :

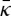4.6

For proteins with a strong coupling to curvature, we could expect 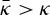, thus a scaffold radius smaller than . This effect should be considered when comparing data from mechanical measurements and from EM.

5. Studying scission with membrane nanotubes

The final step in endocytosis is a complete detachment of the endocytic vesicle from its underlying membrane, termed membrane scission. Scission is a very important biological process, as it underlies all trafficking events that involve the membrane. However, due to its highly dynamic nature, it is not understood as well as curvature-instability phenomena, such as budding or tubulation. Many proteins have been implicated in scission, most notably dynamin, which terminates CME. The model in which dynamin takes the energy from GTP-hydrolysis to constrict a tubule is very attractive as it provides an intuitive understanding of how scission may occur at the molecular level: the stability of the bilayer structure is compromised by squeezing. The actual mechanism of scission is more complicated as it involves many physical parameters, such as membrane shape, composition, tension, the arrangement of proteins, etc. Moreover, cells use more than one method to cut membranes. Pulling tubules from GUVs provides an excellent set-up to study the scission of membranes, especially in the context of endocytosis, characterized by a similar membrane geometry.

(a). Fundamental models of membrane scission

Scission produces two membrane components, each having a smaller area and a higher curvature (e.g. a planar membrane producing a vesicle in endocytosis or cutting one vesicle into two smaller ones). Therefore, scission pays the price of mean bending energy, so membranes with higher κ resist scission. Unlike budding or tubulation, scission changes the lipid interconnectivity, which gives rise to Gaussian bending energy, F_G=2πκ_Gχ, where κ_G is the Gaussian bending rigidity modulus and the genus χ=2(N_compartments−N_holes)=2 in the case of endocytosis. Therefore, more negative values of κ_G favour scission. Moreover, scission affects the enthalpic contribution because of the change in lipid–lipid interactions and also the entropy, as lipids upon scission gain a smaller diffusion space. Finally, surface and line tension affect the likelihood and timescale of scission, and whether it is favoured or disfavoured will depend on the shape of the intermediate state.

A model in which the membrane goes through a hemifusion intermediate is often used to describe scission in endocytosis, as it does not involve the opening of large pores, which would presumably leak out the vesicle material [73]. According to theoretical predictions, the total free energy of a membrane connected to a spherical vesicle—altogether adopting a catenoid shape—strongly increases as the aperture between the neck and the vesicle tightens. Once the aperture radius falls below a critical value, the membrane bilayers fuse. The energy of the separated membranes is always lower than the hemifusion energy, therefore upon fusion, scission spontaneously occurs. It was found that the critical aperture radius increases with the vesicle size, having an approximate radius of 5 nm for a 40-nm wide vesicle bud [74]. Of note, the results of this model are frequently quoted as stating that the neck radius needs to collapse to 3 nm to reach the hemifusion state. In fact, the calculations showed that for a 40-nm-wide bud the neck radius is closer to 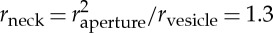 nm. This result is sensitive to the bilayer thickness, spontaneous curvature and the bending moduli of the membrane, which depend on the lipid composition and the bound protein.

Another way of rupturing membranes is by applying tension. For a pure lipid membrane, the tension at which the membrane ruptures (the so-called lysis tension) is very high (1–30 mN m⁻¹) and it largely depends on composition [75,76]. When applying a rapid tension ramp, rupture is a consequence of nucleating defects in the membrane. Apparently, a model based on experimental data predicts very small size rupture pores (approx. 1 nm width) with lifetimes of approximately 0.1 s to 10 s [75,77]. This model may be important in endocytosis where the complex protein machinery may impose significant mechanical stress locally on the membrane.

(b). Scission of pure lipid membranes

It has been shown that pure lipid membranes may be cut simply by virtue of mismatch in mechanical properties of multiple components. GUVs that undergo phase separation gain significant edge energy at the boundary of the two phases, which may induce a budding instability and even scission into two vesicles of distinct phases [78]. Analogously, triggering phase separation in tubules pulled from GUVs causes a rapid breakage at the interface of the two phases (figure 5a) [81]. According to theoretical modelling, in the absence of line tension, the radius between the phases increases almost smoothly from the phase with a higher to the phase with a lower mean bending modulus. Line tension squeezes the interface down to vanishing radius for a very high line tension. The difference in Gaussian bending rigidities of the two phases creates an instability for a non-zero neck radius [79]. Interestingly, calculations on a tubule bridging two vesicles showed that scission may take place if the minor component of a perfectly mixed binary membrane favours positive Gaussian curvature [82]. Both results demonstrate that the minimum requirements for scission is a two-component system with different elastic properties that may—but do not need to—phase separate.

Figure 5.

(a) Spontaneous scission followed by a phase separation of lipids in a tubule (evident from a difference in radius between the two phases). Scale bar, 10 μm. Reprinted from Allain et al. [79]. Copyright © 2014American Physical Society. (b) Scission of a membrane tubule induced by dynamin at the edges of the dynamin coat. Dynamin labelled green, lipids red. Time denotes after GTP injection. Scale bar, 5 μm. Reprinted from Morlot et al. [80]. Copyright © 2012 Elsevier. (c) Scission of a membrane tubule coated with endophilin A2 upon applying a pulling force. Reprinted from Renard et al. [26]. Copyright © 2015 Nature Publishing Group.

(c). Scission by dynamin

Dynamin is a relatively small GTPase that coats a membrane tubule in the form of loosely connected dimers with 13 or 14 dimers typically involved in scission [83]. This coat is relatively stiff and imposes a 10-nm radius on the tubule, independently of the mechanical tension equilibrium [21]. It is widely believed that GTP hydrolysis induces a conformational change in dynamin [84], which significantly constricts the membrane tubule and lowers the energy barrier of the hemifusion state [85–87]. In a recent work employing a tube-pulling assay, it has been shown that scission takes place at the edge of a dynamin coat (figure 5b). At this edge, there is a significant mismatch in the tubule radius and the mechanical properties of the membrane, which, together with dynamin torque, increases the elastic energy enough to reduce the energy barrier of the hemifusion state. They also found that increased membrane tension contributes to the lowering of the energy barrier [80].

(d). Scission by Bin/amphiphysin/Rvs proteins

There is an increasing amount of evidence that membrane scission can take place in the cell in a nucleotide-independent manner. In particular, endocytic proteins containing amphipathic helices (N-BARs and epsins) induce the fragmentation or the reticulation of submicrometre vesicles, where in both cases, the bilayer topology is changed [88,89]. The extent of fragmentation has been shown to directly correlate with the number of amphipathic helices per protein, indicating that shallow insertions are the destabilizing factor in promoting scission [88]. By using the tube-pulling set-up, we have shown that the N-BAR protein endophilin may mediate scission of membrane tubules, but requires an active elongation force, such as one provided by molecular motors (figure 5c). Indeed, the importance of pulling force on endophilin-mediated scission has been demonstrated in the cell in the course of CIE [26,90].

6. Conclusion and perspectives

Molecular structures of proteins obtained through X-ray diffraction give clues as to how they may interact with the membrane, and so far for BAR proteins their structure has provided very good qualitative predictions on how they affect membrane shape (a more curved BAR domain induces thinner tubules). However, a more quantitative approach is required to precisely measure the morphological and the mechanical effects BAR proteins impose on the membrane. The experimental setups that we reviewed here, and especially the assay of pulling tubules from GUVs, elucidated a rich behaviour of endocytic proteins. Strikingly, the subtle differences in protein shape or molecular structure (such as the presence of short wedging domains), together with extrinsic factors—namely, the amount of proteins on the membrane, surface tension or membrane geometry—regulate precisely how these proteins interact with one another or with the membrane. This knowledge helps us to reconstruct a sequence of events in endocytosis, from sensing curved membranes, to inducing buds, tubules or vesicles, and finally, to scission.

There are still many open questions in the biophysics of membrane remodelling. The mechanics-based methods described here, in their current form, capture the essentials of membrane shaping by BAR domains, but fail to distinguish the structural details. Puzzling differences have been reported when probing curvature sensing with SLiC and with the tube-pulling assay: the N-terminal amphipathic helices but not the BAR domains are curvature sensitive to spherical liposomes in the SLiC assay [91], whereas the tube-pulling assay demonstrates that BAR domains devoid of these helices are highly curvature sensitive to membrane nanotubes [54]. Current analytical models cannot predict a difference in binding to spherical compared with cylindrical geometry. Another discrepancy was observed in the measured spontaneous curvature: much higher spontaneous curvatures were deduced for I-BAR domains from spontaneous tubulation experiments [71] than from nanotube pulling [54]. How proteins interact at the molecular level may also be crucial in altering the analytical models that underlie these experiments. Thus, these discrepancies reveal an urgent need to develop more comprehensive theoretical models that better integrate molecular and structural details, protein–protein and protein–membrane interactions, as well as dynamical aspects.

By using electron paramagnetic resonance, it has recently been revealed that N-BAR domains differently bind spherical than cylindrical membranes [56,57]. On a spherical membrane, binding is primarily mediated by the helices while, on a membrane nanotube, the BAR domain more tightly adheres on the surface. These insights give a basis to the apparent differences between the SLiC and nanotube assays reported above. It also points to an important role for the initial shape of the membrane prior to the binding of BAR domains, which might help to better understand how CME and CIE work as they are characterized by different membrane geometries. Multiscale simulations are also extremely valuable to reveal how the BAR-domain proteins interact with membranes [92,93], assemble and organize on the surface [68,69], and eventually deform them [68,69,89,94–97]. Some recent coarse-grained and continuum theoretical models have accounted for the structural features of BAR proteins by including anisotropic curvature terms [96–99]. The next challenging step in modelling the physics underlying membrane shaping by proteins will account for the microscopic aspects of the protein–membrane and protein–protein interactions in a more careful way, especially by more correctly modelling the mean and Gaussian curvature contributions. The parameters for such a model might be calculated from a coarse-grained simulation of the protein on a membrane. New experiments and models will be invaluable in understanding how both molecular interactions and the mechanical aspects of protein activity are regulated in many membrane-reshaping phenomena in the cell.

Authors' contributions

M.S. and P.B. drafted the manuscript; A.C.J. and C.P. revised it critically for important intellectual content.

Competing interests

We have no competing interests.

Funding

M.S. was funded in part by the Chateaubriand fellowship and the France and Chicago Collaborating in the Sciences grant, and received support from the University Paris Diderot. C.P. received a PhD grant from the Université Paris Diderot and support from the Fondation pour la Recherche Médicale. P.B. is funded by Institut Curie, the Centre National de la Recherche Scientifique (CNRS), the Agence Nationale pour la Recherche (ANR-15-CE18-0016-03), and the European Research Council (Advanced grant no. 339847, MYODYN).