Coevolution between positive reciprocity, punishment, and partner switching in repeated interactions

Abstract

Cooperation based on mutual investments can occur between unrelated individuals when they are engaged in repeated interactions. Individuals then need to use a conditional strategy to deter their interaction partners from defecting. Responding to defection such that the future payoff of a defector is reduced relative to cooperating with it is called a partner control mechanism. Three main partner control mechanisms are (i) to switch from cooperation to defection when being defected (‘positive reciprocity’), (ii) to actively reduce the payoff of a defecting partner (‘punishment’), or (iii) to stop interacting and switch partner (‘partner switching’). However, such mechanisms to stabilize cooperation are often studied in isolation from each other. In order to better understand the conditions under which each partner control mechanism tends to be favoured by selection, we here analyse by way of individual-based simulations the coevolution between positive reciprocity, punishment, and partner switching. We show that random interactions in an unstructured population and a high number of rounds increase the likelihood that selection favours partner switching. In contrast, interactions localized in small groups (without genetic structure) increase the likelihood that selection favours punishment and/or positive reciprocity. This study thus highlights the importance of comparing different control mechanisms for cooperation under different conditions.

1. Introduction

Interactions where all participants gain a direct net fitness benefit, namely cooperation, are widespread in natural populations [1]. Many cases of cooperation involve investments; that is, the reduction of current personal payoff by some amount in order to increase the partner's payoff. This observation raises the question how individuals can ensure that their investments yield future benefits; that is, how they can avoid being defected by their partner over repeated bouts of interactions. When individuals engage in repeated interactions over their lifespan, the evolution of cooperation is often modelled as an iterated Prisoner's Dilemma game where individuals have to choose whether to cooperate or defect at each interaction stage. The payoffs are such that mutual cooperation yields a higher payoff than mutual defection, while to defect yields a higher payoff than to cooperate in each single round, irrespective of the partner's action, hence the dilemma. In order to deter a partner from defecting and stabilizing cooperation in a repeated game, an individual can use a conditional strategy that reduces a defecting partner's payoff relative to that of cooperating with it. We define the broad type of such a conditional response as a partner control mechanism [2].

Different types of partner control mechanisms have been proposed to stabilize cooperation in the repeated Prisoner's Dilemma game. Perhaps the most well known is positive reciprocity, where cooperative acts are reciprocated by cooperation in future interactions, whereas defection is not, thus making defection unfavourable in the long run. An often-studied strategy using positive reciprocity as a partner control mechanism is tit-for-tat (TFT), which starts by cooperating and then in subsequent rounds implements the previous action of the partner [3–5]. Although positive reciprocity is often favoured by selection in evolutionary models [3,6–8], its relevance outside humans has been questioned ([9], but see [10,11]).

Another partner control mechanism is punishment, which comes at an immediate payoff cost to the actor, but also reduces the payoff of a defector relative to cooperating [12–14]. Although punishment thus comes at a cost to the punisher, this can be overcome if punishment results in the partner being more cooperative in the long run. Punishment can be favoured by selection in evolutionary models of repeated interactions [12], and examples of punishment as a partner control mechanism can be found in natural populations (reviewed in [15]).

Still another partner control mechanism is partner switching [16–20]. By partner switching an individual can avoid being exploited by a defector by simply stopping the interaction. Although switching entails an opportunity cost because it necessitates finding a new partner, it has been shown to be favoured by selection in the iterated Prisoner's Dilemma game [18], and several examples of partner switching have been suggested in nature [21–23].

For individuals interacting in an iterated Prisoner's Dilemma game positive reciprocity, punishment, and partner switching are predicted as main partner control mechanisms capable of stabilizing cooperation [2]. However, the evolution of these three main types of partner control mechanisms for cooperation is generally investigated in isolation from each other. It thus remains unclear under which conditions selection will favour one mechanism over another. More recently, however, different partner control mechanisms have been investigated together [17,19]. In a landmark study, Izquierdo et al. [19] have shown that selection favours partner switching over TFT. However, this study has assumed that switching does not incur any costs, it excluded the strategic option to punish partners, and restricted the analysis to a population with random interactions only, which are all factors that may change which mechanism is favoured by selection. In order to predict which partner control mechanisms are likely to be observed in natural populations, it is important to consider the coevolution of positive reciprocity, partner switching, and punishment, and understand the conditions under which one partner control mechanism is favoured over the others by selection.

Here, we present an evolutionary model where we let positive reciprocity, punishment, and partner switching co-evolve when interactions are random in the population and when they occur in groups in a panmictic population (i.e. no genetic structure within groups, Haystack model of population structure [24]). The aim of this study is to identify the partner control mechanisms favoured under different conditions, and we therefore chose the Prisoner's Dilemma game as a payoff matrix for the pairwise interactions, where defection always yields a higher single round payoff, and thus selection for responding to defection is strong. We explore the role of the proximate costs and benefits of cooperation, punishment, and switching on these dynamics, as well as the role of interactions localized to groups and the duration of punishment. Our results show that, when interactions occur at random between all population members, the likelihood that partner switching is favoured by selection increases if the number of interactions in an individual's lifespan increases. However, when interactions are localized to groups, we find that punishment generally dominates in sizable groups, unless punishment efficiency is reduced. In the latter case, we do find conditions where positive reciprocity outcompetes alternative partner control mechanisms, but we were unable to identify a particular factor that would consistently favour it.

2. The model

(a). Population and lifecycle

We consider a haploid population of constant size with a total number of N = d × n adult individuals, which are subdivided into d groups of equal size n. The lifecycle is marked by the following events. First, group members interact socially with each other and accumulate payoffs. Next, each individual produces a large number of offspring proportionally to accumulated payoff, and dies. Finally, offspring disperse randomly (with probability 1/d to a given group, including the natal one) and compete randomly with exactly n individuals reaching adulthood in each group. Hence, the population is panmictic (no genetic structure will be obtained).

(b). Social interactions

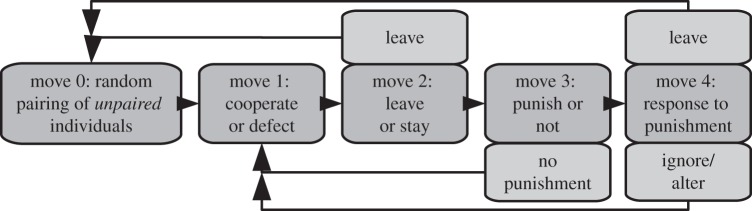
In the social interaction phase of the lifecycle, individuals play a repeated game for T rounds, whose stage game consists of a pairwise extensive-form game (see [25] for a description of different types of games). The per-round extensive-form game consists of five sequential moves where the individuals of a pair choose actions simultaneously during each move (figure 1), and where pair rematching may occur during each round, as follows.

Figure 1.

Chain of events per generation. The five moves are repeated for T rounds. After looping T times, the next generation is produced, and the parental one dies.

Move 0: random pairing. Each unpaired individual (all individuals in the first round) gets randomly paired with another unpaired individual. Individuals cannot influence this process, i.e. there is no partner choice.

Move 1: the Prisoner's Dilemma. Each individual in a pair can either cooperate (action C) or defect (action D). To cooperate means paying a payoff cost C_h to contribute a payoff benefit B_h to the partner, whereas defection has no effect on payoff.

Move 2: leaving. Each individual can either leave its partner (action L) or stay (action S) and a pairbond is broken if at least one individual leaves. A payoff cost of C₁ is paid by both individuals of a broken pair and only unbroken pairs are engaged in the forthcoming move 3 and 4, otherwise, individuals are added to a pool of individuals that will be paired in move 0 of the next round.

Move 3: punishment. Each individual in a pair can either opt to punish its partner (action P) or not punish (action N). Playing action P incurs a payoff cost C_p to self and reduces by D_p the payoff of the partner. Only punished individuals enter the next move.

Move 4: response to punishment. A punished individual has three possible (re)actions available. (i) It receives the punishment but ‘ignores’ it and does not change any future action if the pairbond is maintained (action I). (ii) The individual leaves its partner, namely it expresses action L as in move 2 with the same payoff consequences. (iii) The individual alters its behaviour (action A), which means that, if it played action D (C) in move 1, it will cooperate (defect) in the next z rounds in move 1. An individual that has switched to defection (cooperation) owing to punishment and is punished again, will again change its behaviour in move 1 for z rounds.

In addition to a fixed cost C₁ of partner switching, we also consider an alternative cost function for individuals that leave (or were left) in either move 2 or 4, where the cost depends on the number of unpaired individuals at the end of a round. For this, we consider the function

2.1

which decreases as the number i of unpaired individuals in the population increases, where a > 0 determines the maximum cost, and k > 0 the shape. Thus, we assume that if a larger number of individuals is searching for a partner, then the cost of finding a partner is reduced.

(c). Strategies

We assume that individuals use pure strategies, which deterministically specify the actions to be taken at moves 1–4 of the stage game, possibly conditionally on past actions. The strategy of an individual for the entire game is specified by a vector s = (x₁, x₂, x₃, x₄), where x_k represents the move-wise strategy the individual uses when faced with a choice at move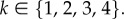

In the electronic supplementary material, table S1, we list all move-wise strategies, which are obtained as follows. We assume that the strategy for move 1 specifies an action taken when the individual first interacts with its partner, and an action taken in subsequent rounds is conditioned on what the partner did in the previous round in move 1. This move-wise strategy can thus be written as a₁a_Ca_D, where 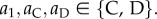Here, a₁ is the action taken the first time the two individuals in a pair interact, a_C is the action taken if the partner cooperated in the previous round, and a_D is the action taken if the partner defected in the previous round. We thus have a total of 8 (2³) move-wise strategies for move 1: {CCC, CCD, CDC, CDD, DCC, DCD, DDC, DDD}.

For move 2, the decision to leave or stay is assumed to be conditional on the action taken by the partner in move 1 of the current round. Hence, the move-wise strategy can be written as a_Ca_D, where 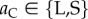(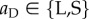) gives the action taken when the partner cooperated (defected), whereby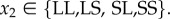

Likewise, for move 3, the decision to punish or not to punish the partner is assumed to be conditional on the action taken by the partner in move 1, so that the move-wise strategy is a_Ca_D, where 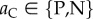(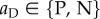) is the action taken when the partner cooperated (defected), whereby 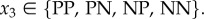Importantly though, we assume that if an individual punishes its partner in this move and the pair is not broken in the next move, then the individual expresses in move 1 of the next round the same action it expressed in this round. This is assumed to avoid individuals responding to the action of the partner both by punishing and by (possibly) changing their own action in move 1 of the following round, and thus take two conditional actions as a response to one action of its partner. Because we want to compare strategies that differ in their response to defecting individuals, we did not allow individuals that punish in the current round to take a conditional action in move 1 of the following round. Finally, the response to punishment in move 4 is simply given by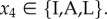

(d). Removing phenotypically indistinguishable strategies

As there are eight different alternatives for x₁, 4 for x₂ and x₃, 3 for x₄ (see electronic supplementary material, table S1), there is a total of 384 strategies. However, given the set-up of our model, many strategies in the strategy space are phenotypically indistinguishable. By phenotypically indistinguishable strategies, we mean those strategies that at no point in the game would act differently from one another, and so will be neutral in an evolutionary model. Therefore, to decrease the complexity of the model, we removed strategies from the strategy space as follows. Per set of phenotypically indistinguishable strategies, only one strategy was used. For example, consider the set of strategies with the same move-wise strategy for move 1 (e.g. x₁ = CCC) and that always leaves the partner in move 2 (x₂ = LL). Strategies from this set never reach move 3 and 4, and thus will always behave similarly, despite having different move-wise strategies for these moves. The 92 strategies that remain after removing phenotypically indistinguishable strategies are shown in the supplementary material (table S3).

(e). Pooling strategies into classes

Although there are many strategies in the model, we are mainly interested in cooperative strategies that differ in their response to defection, i.e. cooperative strategies using different partner control mechanisms. A cooperative strategy is defined as a strategy that, when paired with another cooperative strategy, will always cooperate in move 1 of the game, without punishing or leaving the partner. Within the set of cooperative strategies, we can distinguish between classes of strategies that differ in their partner control mechanism: no response (no control), conditional play in the Prisoner's Dilemma (move 1), leaving (move 2), or punishment (move 3). Each of these four classes consists of three strategies that differ only in their response to punishment (move 4). Because we are interested in comparing partner control mechanisms, when comparing frequencies of strategies, we will do so according to class, i.e. in our analysis, we will always pool the frequencies of the strategies belonging to the same class.

Here, we will give a verbal description of each of the six classes of strategies that we consider (electronic supplementary material, table S2). Each strategy of the positive reciprocity class (denoted 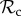) cooperates on the first interaction. It cooperates in subsequent rounds if the partner cooperated in the previous round and defects if the partner defected in the previous round, without leaving or punishing the partner. Each strategy of the partner switching class (denoted 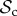) cooperates on the first round, cooperates if the partner cooperates, does not punish, but leaves as soon as the partner defects. Each strategy of the punishment class (denoted 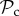) cooperates on the first round, cooperates in subsequent rounds, does not leave, but punishes a partner that defects. Each strategy of the always cooperate (denoted 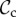) and always defect class (denoted 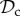) always cooperates (defects), and does not express any conditional play in move 1–3. The remaining 92 − 5 × 3 = 77 strategies will be pooled in ‘rest’.

(f). Analyses

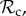
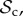
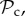
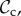
In order to analyse the model, we used individual-based simulations to track the frequencies of the six classes of strategies ( 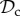, and ‘rest’) in the population over generations. Strategies are assumed to be inherited from parent to offspring with probability 1 − μ. With probability μ, the offspring mutates to another strategy taken at random among all remaining strategies. To form the next generation of offspring, we use multinomial sampling over the aggregate payoff of each strategy type of the parental generation with a baseline payoff guaranteeing there can be no negative payoff (Wright–Fisher process, [26]).

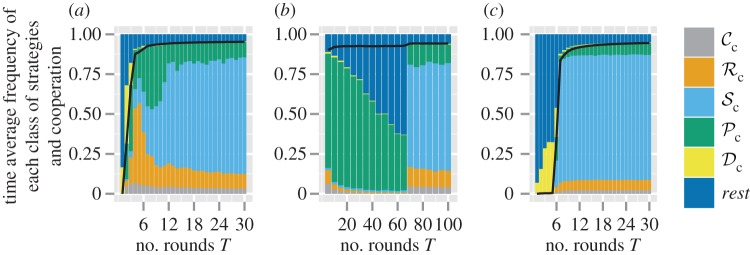
For all reported results (figures 2 and 3), we ran the simulations for 10⁶ generations and computed the time average frequency of the six classes of strategies starting with uniformly sampled initial frequencies. We also evaluated the total frequency of cooperation in the population, which we define as the average frequency over the whole population and length of the repeated game of the pairs of individuals in the population where both individuals in the pair cooperated in the Prisoner's Dilemma game.

Figure 2.

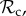
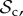
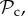
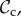
Time average frequency (over 10⁶ generations) of the frequency of cooperation (black line) and the six classes of strategies ( 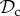, and rest) plotted as a function of the number of rounds T of the repeated game. Parameter values: B_h = 2, C_h = 1, D_p = 2, C_p = 1, z = T, μ = 0.01, d = 1, n = 10 000. Panel specific parameters: C₁ = 1 (a), C₁ = 5 (b), using equation (2.1) with a = 100, k = 0.9 (c).

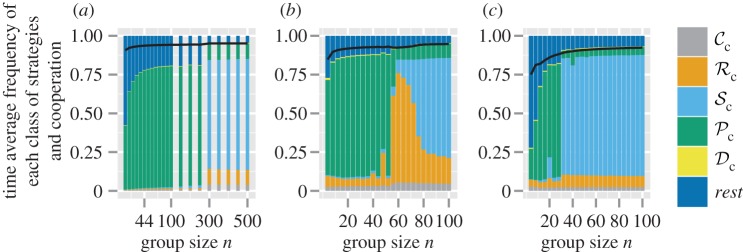
Figure 3.

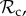
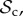
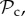
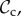
Time average frequency (over 10⁶ generations) of the frequency of cooperation (black line) and the six classes of strategies ( 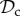, and rest) plotted as a function of group size n. Parameter values: B_h = 2, C_h = 1, D_p = 2, C_p = 1, T = 30, μ = 0.01, d = 250. Panel specific parameters: C₁ = 1, z = T (a), C₁=1, z = 5 (b), C₁ = 0, z = 5 (c).

3. Results

We first present results assuming that the population consists of a single group (d = 1, n = 10 000), so that the pairing process (move 0, figure 1) is random at the population level. We will refer to this as the well-mixed case. Then, we introduce group structure (d = 250, varying n), where the pairing process occurs at the group level but with otherwise similar parameters to show how this factor alters the relative effectiveness of each partner control mechanism.

(a). Well-mixed population

Our results are based on the following baseline parameter values: B_h = 2, C_h = 1, D_p = 2, C_p = 1, C₁ = 1, μ = 0.01, whereas we let T vary between 1 and 30 (table 1) and set z = T, so that the behavioural change after punishment lasts indefinitely. We find that the average frequency of cooperation in the population is strongly dependent on the number of rounds (T) per generation (figure 2a, black line). When the game is one shot (T = 1), conditional strategies are unable to affect payoff or behaviour in future rounds, and thus cooperation is selected against (less than 1%), which is consistent with the standard result that defection is favoured in such cases [3]. As the number of rounds is increased, the frequency of cooperation quickly increases, with more than 90% of mutual cooperation for T ≥ 6.

Table 1.

List of parameters.

parameter	meaning
Bh	benefit to the recipient of a cooperative act
Ch	cost of a cooperative act
Dp	payoff reduction for target of punishment
Cp	cost of punishment
C1	cost of switching partner
z	duration of punishment
d	number of groups
n	group size
T	number of rounds in one generation
μ	mutation rate
N	population size
a, k	used to calculate the cost of switching in equation (2.1)

Additionally, we find that the number of rounds has a strong influence on which partner control mechanism is favoured by selection. Our main results are as follows.

For 4 ≤ T ≤ 6, we find that the positive reciprocity class (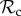) is dominant (figure 2a). Here, the number of rounds is very low, and thus the costs of punishment or partner switching in the first rounds cannot be negated in later rounds of mutual cooperation. Switching to defection to minimize payoff losses is more beneficial for the lifetime payoff and thus the 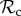class is selected for.

For intermediate T (7 ≤ T ≤ 9), we find that the punishment class (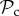) dominates (figure 2a). Although 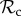and 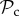strategies gain equal payoffs when paired with each other, their respective payoff gain will differ considerably when paired with a defector. An 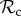strategy switches to defection when paired with a defector resulting in both players gaining the baseline payoff. A 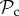strategy, however, continues to cooperate while punishing defection. If the recipient of punishment switches to play cooperate, then through several rounds of mutual cooperation, a 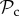strategy is likely to obtain more payoff than an 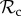strategy. This difference in payoff between 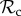and 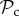when matched with defectors may thus explain why for a higher number of rounds of interaction selection will favour the 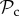class over the 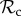class. However, not all strategies respond to punishment by altering behaviour, and thus 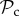strategies cannot force all individuals to cooperate. Some partnerships can therefore be very costly for these individuals as they pay double costs (cooperating and punishing).

Finally, for large T (T ≥ 10), we find that the switching class (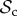) dominates the population (figure 2a). Strategies in the 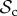class do not face the problem of prolonged costly partnerships as they will always leave uncooperative individuals. Two 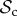strategies will therefore always manage to find each other in a well-mixed population, given enough rounds. When the number of rounds increases, 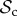strategies will have more rounds to reap the benefits of mutual cooperation once a cooperative partner has been found, and thus the 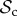class outcompetes both the 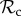and the 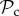class for T ≥ 10. If the cost of switching is increased to C₁ = 5, however, then the number of rounds needed for the 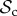class to dominate is increased to T ≥ 70 (figure 2b). In all simulations where d = 1 (single group), we find that switching is generally favoured when T is large enough. The finding that a high number of rounds favours partner switching is robust even when the cost of switching increases exponentially with fewer number of unpaired individuals (using equation (2.1), a = 100, k = 0.9, figure 2c; see the electronic supplementary material, section SM-II.2 for other parameter values).

(b). Group-structured population

We now introduce group structure (without genetic structure as dispersal is random to any group) into the population, setting the number of groups (d) to 250 while varying group size (n). Otherwise, we use the same set of parameter values as in the baseline case for the well-mixed population (B_h = 2, C_h = 1, D_p = 2, C_p = 1, C₁ = 1, μ = 0.01, figure 2a) with T = 30 and z = T. Our main aim is to determine the conditions where the 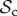class dominates in frequency.

Interestingly, switching only dominates in very large groups (n ≥ 300, figure 3a). Instead, we find that the 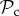class is dominant for any group size lower than 300. The 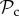class coexists in these simulations with a strategy that always defects, punishes other defectors, and alters behaviour if punished. While the 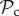individuals can force such individuals to cooperate, other strategies will either be exploited or punished.

To determine the robustness of the result that the 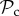class tends to dominate in a group-structured population, we relaxed the assumption of punishment altering behaviour for the lifetime of the individual (in move 4). Such a strong effect of punishment is unlikely to occur in nature, and punished individuals may attempt to defect again after several interactions. We find that the evolutionary success of punishment is strongly dependent on this parameter. If z = 5, then the 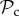class is still dominant in groups up to a size of 52 (figure 3b). In larger groups however, it is first the 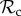class that dominates, whereas for n ≥ 76, the 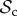class is dominant. Strikingly, if the cost of switching partner is absent as well (C₁ = 0), the 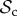class is still outcompeted by the 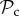class in small groups (n ≤ 28, figure 3c). This may stem from the fact that if individuals interact in small groups, a partner switcher may be rematched with the individual it left on the previous round and may end up repeatedly interacting with the same defector (despite switching every round). The 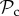class therefore still dominates in small groups, because its payoff is mostly dependent on how a defecting individual responds to punishment, but not on the composition of the group it is in. This effect largely persists in a structured population if T is small, unless the cost of punishment is doubled, in which case the 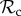class takes over (electronic supplementary material, figure S4).

(c). Sensitivity analysis

To test the robustness of the various results presented here, we have performed additional analyses testing a larger part of the parameter space adding up to at least 15 000 different parameter combinations for which we have run simulations. The results of these analyses are presented in the electronic supplementary material.

4. Discussion

Cooperative individuals can use partner control mechanisms; that is, broad types of conditional strategies to reduce the lifetime payoff of defectors relative to cooperators. Three partner control mechanisms (positive reciprocity, punishment, and partner switching) have all been shown to be able to stabilize cooperation in panmictic populations in separate models [3,20,27]. However, few studies have investigated under which conditions selection would favour one partner control mechanism over another. Here, we have addressed this issue by investigating the coevolution of these three control mechanisms in a panmictic population in which the interaction structure is either well-mixed (i.e. all individuals are potential partners) or group structured with interactions occurring only locally among a small number of individuals (with no genetic structure within groups). In most simulations, we find a polymorphism where the different classes of strategies coexist. However, it is clear that under most conditions a specific class of strategies tends to be favoured by selection over alternatives and thus dominates in this polymorphism.

Our key result for the well-mixed case is that the likelihood of partner switching being favoured by selection over positive reciprocity, punishment, and defection increases if the number of rounds of interaction is larger (figure 2 and electronic supplementary material, figures S1–S3). For a fewer number of rounds punishment and positive reciprocity tend to be favoured, but which of the two classes dominates depends on changes in various parameters, and thus no general conclusion can be reached here. When interactions are localized to the group level, punishment is relatively more favoured in small and moderately sized groups for otherwise similar parameter values as in the well-mixed interactions case, and this is for both a small and large number of rounds (electronic supplementary material, figures S4a and 3a, respectively). Positive reciprocity dominates under certain conditions in a group-structured population when punishment efficiency is reduced; for example, for a high number of rounds, intermediate group size, and a low duration of the effect of punishment (figure 3b), or for a low number of rounds and high cost of punishment (electronic supplementary material, figure S4c). We did not, however, identify a specific factor that would consistently induce positive reciprocity to dominate the other control mechanisms. In the following, we will first discuss each control mechanism separately and then evaluate how our results connect to empirical research.

(a). Switching

In our analysis, partner switching emerges as the dominant partner control mechanism when many potential partners exist and many interactions take place during an individual's lifespan, unless the cost of switching is high and the number of rounds of interaction is insufficiently large to compensate for these costs. These results make intuitive sense if one considers how the three control mechanisms respond to unconditional defectors: punishers and positive reciprocators may spend their entire life with a defecting partner, whereas partner switchers leave and will invariably end up with another cooperative individual and hence reap the benefits of cooperation as long as enough rounds are played. Izquierdo et al. [19] have already shown that partner switching is a powerful partner control mechanism stabilizing cooperation; if it is cost-free, then it dominates over positive reciprocity. Our results extend their insights by showing that switching can be favoured by selection over not only positive reciprocity, but also punishment in a well-mixed population, with the caveat that a sufficient number of rounds of interaction must take place.

Switching (when linked to cooperation) is a cognitively simple strategy that, via the exploration of partner behaviour, rejects defectors and tends to assort with cooperators. It can thus be regarded as a primitive form of partner choice. Although more active mechanisms of partner choice exist, such as using information about past behaviour of individuals or other signals of cooperative behaviour [28,29], partner switching allows individuals to respond to variation in the population in the same way. This generally tends to stabilize cooperation because, if individuals can exert some level of choice in the presence of variation of the expression of cooperation, the system of interacting individuals functions as a biological market where cooperators end up assorted with themselves [30,31].

A critical result of our model, however, is that the size of the interaction group has a clear impact on the likelihood of a partner switcher to find the right partner, and thus the evolutionary success of partner switching. Relaxing the assumption of well-mixed interaction opportunities [18,19], we find that the prevalence of partner switching diminishes the smaller the number of potential interaction partners gets. This conclusion holds even if partner switching is free of opportunity costs (figure 3c). The reason for this result is that the smaller the group the more likely it becomes that switchers can only be rematched with their defecting partner as nobody else is available. In other words, the market for interaction partners becomes increasingly restricted with decreasing numbers of potential interaction partners.

(b). Punishment

Via punishment an individual can actively attempt to change the behaviour of its partner, by paying a small payoff cost to reduce the payoff of its defecting partner, thereby making cooperation more attractive. Punishment is more favoured when the population is group structured (compared with unstructured), up to relatively large group sizes, especially if punishment results in the defecting recipient changing its behaviour to cooperation indefinitely (z = T, figure 3a). Importantly, a punisher can induce cooperative behaviour in a conditionally defecting partner but switchers cannot, which gives punishment an advantage when the number of potential partners and hence the number of unmatched cooperators is limited. For the same reason, punishment outcompetes positive reciprocity for various parameter value combinations, because within the limits of the strategy space explored in this paper, the behaviour of the partner and focal individual can be more easily aligned through punishment than through positive reciprocity. Therefore, we find in group-structured populations that selection generally favours punishment over positive reciprocity and partner switching in sizable groups (figure 3). If one of the parameters influencing punishment efficiency is changed (i.e. high cost of punishment, low payoff reduction for the recipient of punishment, or short behavioural change after being punished), then we find that alternative classes of strategies dominate (electronic supplementary material, figure S5).

(c). Positive reciprocity

The conditions where positive reciprocity is favoured over punishment and partner switching are less easily characterized. Although in group-structured populations we find that punishment dominates often in sizable groups (figure 3), when punishment efficiency is decreased, there are various conditions where positive reciprocity dominates instead (figures 3b and electronic supplementary material, S4 and S5). However, depending on the number of rounds of interaction, cost of partner switching, and other parameters, we also find conditions where the always defect class or the switching class dominates in the population (electronic supplementary material, figure S5). In sum, there is not a specific factor that would consistently increase the likelihood of positive reciprocity dominating the population.

Our analyses suggest that 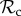strategies may often be outcompeted by other control mechanisms, because 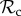individuals paired with defectors are unable to reach the cooperative outcome (both individuals play C in move 1). That is, there exists no strategy in our strategy set that would exploit unconditional cooperators, but that can also ‘identify’ the 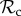strategy and cooperate with it. Such strategies would require several rounds of interaction (and thus a large memory) to identify that the partner is playing TFT. Punishment, on the other hand, is a much more direct signal (a single punishing act) to which defectors can respond. Thus, if strategy complexity is limited to one round of memory, then the 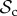and 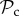class can still reach the cooperative outcome when paired with a defector, but the 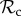class cannot. Therefore, even though the 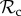class avoids being exploited by defectors by switching to play defect as well, it gains less payoff than other classes of control mechanisms and is thus frequently outcompeted. This does not necessarily mean that positive reciprocity can never be favoured. As the results show, we have found conditions where positive reciprocity dominates (figures 2a and 3b and electronic supplementary material). More importantly, however, our results show that the deterministic play and a single round of memory of our 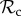class (as in the TFT strategy) causes it to often be outcompeted by classes of strategies that do manage to reach a cooperative outcome with their partners. Therefore, for positive reciprocity to evolve, it is likely necessary that strategies evolve that take into account a larger history of the interaction or play less deterministically.

(d). Connection to the empirical literature

It is still a largely unanswered question of how frequently each of the three partner control mechanisms investigated here occurs in natural populations. According to current evidence, there are very few examples for punishment [15], while there are various examples for positive reciprocity [11]. Regarding partner switching, we are aware only of clear interspecific examples where partner switching in response to defection occurs. For example, in an interspecific interaction between client and cleaner fish, it has been observed that client reef fish with access to several cleaning stations use a partner switching strategy in response to a defecting client even though they could alternatively use punishment—as clients without choice options do [22,32]. Our model is, however, limited to intraspecific interactions, and thus it remains to be investigated how much our results would be affected if interacting individuals belong to two separate gene pools. In intraspecific contexts, empirical tests of biological market theory focus on individuals actively choosing a partner prior to interactions based on a comparison of offers [33,34], rather than on leaving a partner that has defected. Investigating active choice rather than partner switching would be another interesting avenue for future research.

Our result that partner switching does not perform well in small groups (and hence for low behavioural variation) is of potential importance for empirical research on cooperation in stable groups, as is often found in primates. It has been proposed that various trades of investments in primates (e.g. grooming, tolerance, and support in agonistic encounters) are stable against defection partially because of partner switching [35]. However, it has also been argued that social bonds in primate groups are highly differentiated where individuals form long-term social bonds with particular individuals in the group [36]. In such groups, partner switching may be highly restricted. Hence, our model suggests that partner switching cannot be accepted as a default partner control mechanism in stable groups without convincing empirical evidence.

The most surprising result of our analyses is the success of punishment in sizable groups, as the evidence for this partner control mechanism in symmetric two-player interactions is rather rare [15]. One reason for its success is the assumption that any player can use punishment in a relative cost-efficient way, i.e. the cost of punishing is lower than the cost of being punished. In nature, cost efficiency is likely linked to asymmetries between players and hence asymmetric games. Fittingly, experimental evidence for punishment has been reported for asymmetric games in interspecific interactions [32,37], and the most important intraspecific context involves the ‘pay-to-stay’ concept where helpers help and show appeasement apparently to avoid aggression by dominant breeders [38]. A major problem with asymmetric strength is that it may turn a cooperation game in which punishment stabilizes cooperation into an exploitation game in which dominants coerce subordinates [12], i.e. defect while forcing the partner to cooperate. For example, only larger male cleaner wrasse punish their smaller female partners for cheating a joint client, a game akin to an iterated Prisoner's Dilemma [39,40]. To fully understand the effect of asymmetries between individuals on the relative effectiveness of punishment over other partner control mechanisms, this will need to be modelled explicitly, however. In addition, further work is needed to determine how factors such as asymmetries or relatedness between interacting individuals may change the adaptiveness of each partner control mechanism.

Data accessibility

The doi of the simulation code is: doi:10.5061/dryad.5ps58.

Authors' contributions

All authors contributed to the conceptual design and the writing of the manuscript. M.W. wrote the code and performed the analysis.

Competing interests

We have no competing interests.

Funding

This work was supported by a grant from the Swiss National Science Foundation.