Notes on the birth–death prior with fossil calibrations for Bayesian estimation of species divergence times

Abstract

Constructing a multi-dimensional prior on the times of divergence (the node ages) of species in a phylogeny is not a trivial task, in particular, if the prior density is the result of combining different sources of information such as a speciation process with fossil calibration densities. Yang & Rannala (2006 Mol. Biol. Evol. 23, 212–226. (doi:10.1093/molbev/msj024)) laid out the general approach to combine the birth–death process with arbitrary fossil-based densities to construct a prior on divergence times. They achieved this by calculating the density of node ages without calibrations conditioned on the ages of the calibrated nodes. Here, I show that the conditional density obtained by Yang & Rannala is misspecified. The misspecified density can sometimes be quite strange-looking and can lead to unintentionally informative priors on node ages without fossil calibrations. I derive the correct density and provide a few illustrative examples. Calculation of the density involves a sum over a large set of labelled histories, and so obtaining the density in a computer program seems hard at the moment. A general algorithm that may provide a way forward is given.

This article is part of the themed issue ‘Dating species divergences using rocks and clocks’.

1. Introduction

There has been much interest in using the Bayesian method to estimate the times of divergence (the node ages) of species in phylogenies [1]. However, in a Bayesian analysis, specifying the prior distribution on the ages of nodes is not a trivial task: for a phylogeny with s species, there are s – 1 node ages to be estimated, and thus a probability distribution with s – 1 dimensions needs to be constructed. Such high-dimensional priors may be hard to specify, in particular if the prior is built from different sources of information, such as when combining information from the fossil record with a speciation process (such as the birth–death process [2]).

For example, in the first Bayesian method of molecular clock dating, Thorne et al. [3] used the Yule process (a speciation process) to construct the prior on the node ages, but no attempt was made to combine the process with node-age calibrations based on the fossil record. Later, Kishino et al. [4] used a gamma density to specify the prior on the age of the phylogeny's root, and then used the Dirichlet distribution to construct the prior on the remaining node ages. They innovatively used the ages of fossils as minimum or maximum constraints on the ages of nodes (that is, by truncating the Dirichlet distribution). Thus, in Kishino et al.'s method, information from the fossil record can be used to inform the time prior throughout the phylogeny, but arbitrary fossil-based calibration densities on node ages could not be used.

Bayesian methods to construct the prior on node ages by combining a speciation process with arbitrary fossil-based distributions were developed later. For example, Drummond et al. [5] introduced one such method, although no mathematical details on how their prior is constructed were initially given. Details of prior construction were given later [6]: the prior density is constructed by simply multiplying the speciation process density with the arbitrary probability densities on nodes with fossil calibrations. This approach to construct the prior seems undesirable as it ‘does not follow the rules of probability calculus’ [6].

Yang & Rannala [2] laid out the correct approach to combine a speciation process density with arbitrary probability densities to construct the time prior. Let 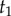be the age of the root, and let 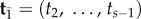be the ages of the remaining s – 2 nodes in a phylogeny of s species. Write 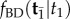for the birth–death density of node ages conditioned on the age of the root [2]. Let be a probability density (such as the gamma) describing the age of the root. A joint prior of divergence times can thus be constructed as

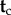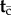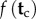Now suppose fossil calibration information is available for a subset of the node ages (other than the root), while are the node ages without fossil calibrations, such that . Write for the joint probability density that summarizes the fossil information about 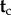. A joint time prior on all node ages that combines the birth–death process density and the fossil-based densities can be constructed as

1.1

Thus, to calculate the time prior using fossil calibrations and the birth–death process, one must calculate: (i) , (ii) 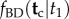and (iii) . Calculating (i) and (iii) is straightforward; however, it turns out that calculating (ii) is in general very hard. In fact, here I show that the procedure proposed by Yang & Rannala to obtain (ii) leads to a misspecified density. Thus, Yang & Rannala's resulting conditional density for node ages without calibrations, 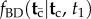, is also misspecified. The problem is moderate, in the sense that the fossil calibration densities are not affected, and estimated divergence times on the phylogeny will be appropriately constrained by the fossil calibrations specified by the user. However, the misspecified 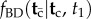density can look quite strange and sometimes can have multiple modes, and may thus lead to a multi-modal posterior distribution for the ages of nodes without fossil calibrations. Such misspecified densities may be biologically unrealistic. An example of the misspecified prior is given in figure 1.

Figure 1.

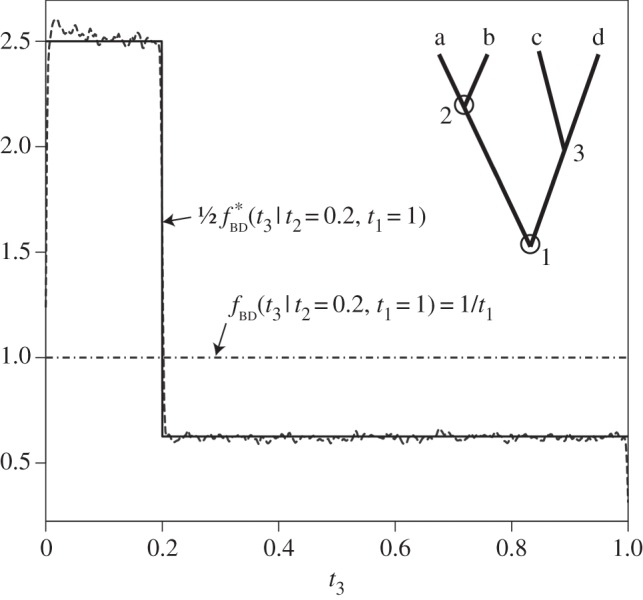
A misspecified birth–death prior with fossil calibrations. The inset tree has point fossil calibrations on the ages of nodes 1 and 2: and (white circles). The birth–death process with fossil calibrations is used to construct the prior of conditioned on the fossil ages. The correct conditional prior is 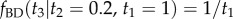(dashed-dotted line). The misspecified conditional prior, 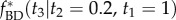, calculated under the procedure of Yang & Rannala [2] is a piecewise uniform distribution (solid line). The wiggly, dashed line shows the misspecified density sampled by MCMC using the computer program MCMCTree, which implements the misspecified prior. Because MCMCTree does not allow point calibrations, we use 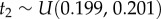and as an approximation in the MCMC analysis. This example is analysed in §5, where full details are given.

The prior of equation (1.1), using the misspecified densities, has been implemented in the computer program MCMCTree [7] for molecular clock dating of phylogenies. The program is popular and has been used, for example, to estimate node ages in phylogenies using genome-scale alignments (e.g. [8–10]). Given the popularity of MCMCTree, and given the limitations of other methods (e.g. [3–5]), it is important to obtain the correct prior density of divergence times with fossil calibrations.

Thus, the purpose of this paper is to derive, from first principles, the prior density of divergence times under the birth–death process with fossil calibrations of equation (1.1). Here, I show that calculation of the correct density in small phylogenies is straightforward, and I give a general form of the density for arbitrarily large phylogenies. Unfortunately, the density involves a sum over the set of possible labelled histories in the phylogeny (i.e. the possible orderings of node ages given the rooted tree). This set can be explosively large in phylogenies of many species, and thus application of the general form of the density is impractical. Thus, I also sketch out a more efficient tree traversal algorithm that can be used to calculate the density. A few special cases where the MCMCTree program calculates the density correctly are pointed out, and brief recommendations to construct a reasonable prior in other cases are given.

The procedure of Yang & Rannala [2] is used to construct the time prior in phylogenies of extant (or contemporaneous) species. In some cases, data for extinct species may be available (for example, molecular data for viruses sampled through time [11] or morphological data for fossil species [12]), or data about the temporal sampling frequency of fossils may also be available (e.g. [13,14]). In such cases, it is not necessary to use fossil calibration densities. The birth–death process conditioned on the extant and extinct species can then be used to construct the time prior [11,14]. Development of the time prior in the variety of cases that may arise is an exciting and fast-paced area of research. The focus of this paper is on the special case of phylogenies of extant species with fossil calibration densities [2].

2. The birth–death process with species sampling

The birth–death process with species sampling was introduced by Yang & Rannala [15] for Bayesian estimation of phylogenies. Consider estimating the tree topology and divergence times for s contemporaneous species. The ordered divergence times are , where 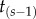is the age of the root. Under the birth–death process, the joint (prior) distribution of a labelled history π (an ordering of node ages for topology τ) and a set of ordered times conditioned on the age of the root and the s species is

2.1

(eqn 5 in [15]), where 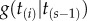is the birth–death kernel density (eqn 4 in [2]), and 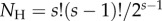is the total number of labelled histories given s species. In the birth–death process, all histories have the same probability of being sampled, and thus .

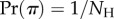For example, consider the case of four species. There are 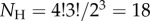labelled histories, corresponding to 15 distinct rooted tree topologies. Figure 2 lists two of the histories for one topology. Now consider the smallest time in the phylogeny, , and the age of the last common ancestor of species a and b, (we call 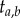a labelled time). In some labelled histories, 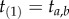, but in general this is not the case (figure 2). Clearly, 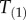and 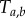are different random variables. Thus, in order to adapt the birth–death process to estimation of divergence times on fixed topologies with fossil calibrations, we need to derive the density of the labelled times, so that we can apply fossil calibrations on them.

Figure 2.

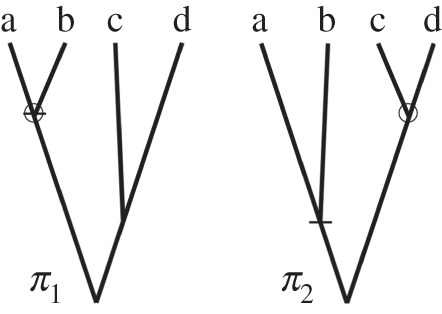
Two labelled histories for a four-species phylogeny. The labelled histories are denote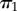d and 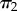, and they share the same the tree topology τ = ((a,b),(c,d)). The empty circle indicates the youngest node in the phylogeny, which has age 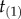, while the small horizontal bar indicates the last common ancestor of a and b, which has age .

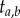For example, consider calculation of the distribution of , given topology τ (figure 2), . Half of the time, we will sample history 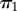(i.e. 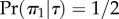), where , and thus will have the density of an order statistic of rank 1 (the minimum, [16]), and so 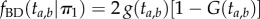, while the other half of the time, we will sample 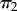and thus 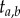will have the density of the maximum, 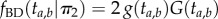. Thus, the density is

To obtain the joint density of 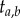and 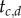given τ, note that there are 2! ways to order the two times, but ‘only’ two of those (the two labelled histories) are compatible with the tree; this leads to

This observation can be generalized to any tree of s species to obtain the joint density for the ages of the s – 2 internal nodes conditioned on the age of the root. One can then use first principles of probability theory to derive the marginal densities of the sets of nodes with fossil calibrations. This is the topic of §3.

3. Birth–death prior of times with fossil calibrations

Consider a phylogeny of s species, where the topology, τ, of the phylogeny is known. The s – 1 labelled divergence times are 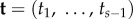, where is the age of the root. The joint prior of conditioned on the age of the root 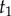and the tree topology τ is

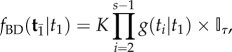3.1

where the indicator function if any node is older than its parent, and 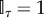if otherwise. Here K is the normalizing constant

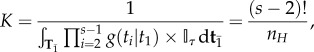3.2

where is the number of labelled histories given the rooted tree. To derive K note that there are 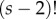ways to order the s – 2 internal node ages, but only of those are compatible with the tree topology, thus resulting in equation (3.2).

The joint time prior for all the node ages given the tree topology is then

where is the fossil-based calibration density of the root age.

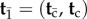Now suppose that, apart from the root, there is an additional set of nodes, , with calibration information. The set of nodes with no calibrations is , so that . The calibrated nodes have joint calibration density The time prior is then defined as

where

3.3

and

3.4

We can obtain a general expression for equation (3.4) by using the theory of order statistics. Consider a particular labelled history π given the rooted tree. Write 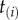for the node age with rank i. For example, for history 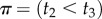in the tree of figure 1, the rank of 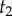is unity (because 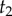is the youngest node), and so 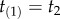and 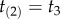. The brackets around the subscripts are used to emphasize that the variables are ordered. Let k be the number of nodes with fossil calibrations, and let 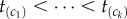, be the ranked calibrated times. The ordered node ages form a set of ordered statistics given history π. Thus, the joint density of conditioned on history π, is the joint density of the subset of order statistics, . This density is given (after suitably defining 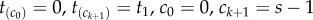) by

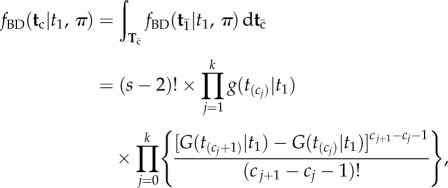3.5

([16], p. 12), where 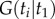is the distribution function of the birth–death kernel density, . Now note that the integration volume of equation (3.4) can be ‘sliced’ such that each slice corresponds to a particular labelled history π. Therefore, the integral of equation (3.4) can be expressed as a sum of integrals over labelled histories, i.e. over the slices (equation (3.5)). This gives

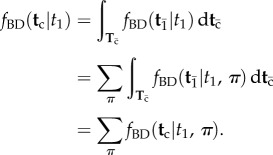3.6

Calculation of the conditional density 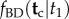by using equation (3.6) is, in general, not very practical. In trees of many species, the number of labelled histories may be so explosively large that the sum may not be computed. An algorithm to calculate equation (3.4) on a tree is given in §6.

4. Misspecification of the time prior in MCMCTree

As mentioned, the ordered times, , and the labelled times, 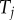, are different random variables, and so it would be inappropriate to assume that they have the same probability distribution. Yet, this is what Yang & Rannala [2] assumed when they adapted equation (2.1) to estimation of divergence times on a fixed topology. They equated the joint density of the set of labelled times (i.e. times that refer to a specific common ancestor, such as 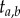) on a fixed topology, with the joint density of ordered times on a labelled history:

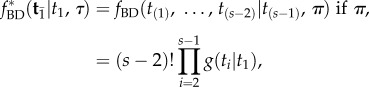4.1

thus the normalizing constant, 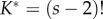, is incorrect (eqn 9 in [2], cf. equation (3.1)). They then obtained a misspecified marginal density for calibrated times by integrating the density over the ordered times:

4.2

(eqn 11 in [2], cf. equations (3.5) and (3.6)). The asterisk is used to indicate that the densities are misspecified.

The misspecified prior is implemented in the computer program MCMCTree [7], which performs Bayesian estimation of divergence times on phylogenies by MCMC sampling. Misspecification of the integration constant, K, is unimportant, given that this constant cancels out during MCMC sampling on fixed topologies. However, the use of the misspecified conditional density is a more serious problem, as it can lead to strange time priors that do not reflect the true density under the birth–death process. Note that MCMCTree does not need to calculate for all labelled histories π, it only does so for the particular labelled history being proposed during MCMC sampling. Thus, MCMCTree can perform much faster MCMC sampling using the misspecified density of equation (4.2) than how it would perform if it sampled the correct distribution (equation (3.6)).

For some special cases, the misspecified (equations (4.1) and (4.2)) and correct (equations (3.1) and (3.4)) densities give the same result. Thus, for such cases, MCMCTree (v. 4.8 at the time of writing) is guaranteed to calculate the birth–death prior with fossil calibrations correctly. The important cases are as follows:

• (1) When there is a single calibration on the age of the root, and the birth–death process is used to specify the prior on all remaining nodes. In this case, only K is miscalculated, but as mentioned, this is unimportant.

• (2) For comb phylogenies, irrespective of the configuration of the fossil calibrations. In a comb phylogeny, each node has only one other internal node as its child (the other child is a tip), and therefore there is a single labelled history compatible with the tree. Thus, in this case, equations (3.4) and (4.2) give the same result. K is also calculated correctly.

• (3) When all nodes have fossil calibrations, because in this case the conditional density 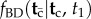does not need to be calculated.

In any other cases, the time prior needs to be examined explicitly. In §5, a couple of examples of calculation of the time prior under the correct and misspecified densities are given.

5. Some examples

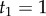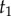Consider the four-species phylogeny of figure 1. The age of the root is , and the age of node 2 is . The age of node 3, , is unknown. We want to construct a prior density on conditioned on and 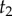using the birth–death process: (i) first we find 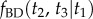; (ii) then we find 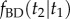and (iii) finally we find 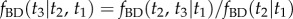. The kernel density is 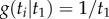(a uniform distribution between 0 and 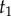) with distribution function 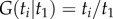. This is the limiting case when the parameters of the birth–death process are 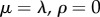[2]. Using equations (3.1) and (3.4), we obtain

The same result can be obtained by noting that 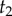and are conditionally independent on (i.e. two random variables a and b are conditionally independent on c if ).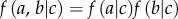

We now calculate the conditional density as currently implemented in MCMCTree, that is, by using equation (4.2)

Applying equation (3.5) to calculate gives

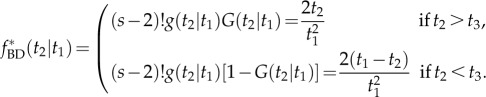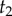The misspecified prior of conditioned on and 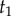is then given by

Using the fossil calibrations 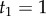and 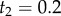, we obtain

Note the density above is not a probability density as it does not integrate to unity: (this is because is twice what it should be). Figure 1 shows the misspecified density and the correct density 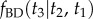. The shape of the misspecified density is confirmed numerically by MCMC sampling with MCMCTree. The shape of the misspecified density is not reasonable. Inadvertently, the user has specified an informative prior on , with half of the prior probability mass on the narrow 0–0.2 interval, while a diffuse prior over the 0–1 interval was required.

Figure 3 shows an example where the resulting misspecified conditional prior is bimodal. Nodes 1–5 in the tree have point calibrations, while the age of node 6 is unknown. Using the uniform kernel density, it is easy to see that the correct density of 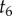conditioned on the calibrated times is simply 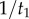. However, under the procedure of equation (4.2), the conditional density must be calculated over each one of the five labelled histories on the tree. The resulting misspecified density is thus a piecewise uniform distribution, with each segment of the distribution representing one labelled history, and with the resulting distribution having two modes (figure 3). Multi-modal time priors like this may not be biologically realistic.

Figure 3.

A misspecified, bimodal birth–death prior with fossil calibrations. The inset tree has point fossil calibrations for nodes 1–5: 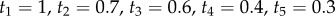(white circles). The age of node 6 is unknown. The conditional prior of under the birth–death process is 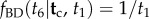(not shown). The misspecified conditional prior, (solid line), is a piecewise uniform distribution, where each segment corresponds to one of the five labelled histories compatible with the tree. The density has discontinuities located at the point fossil calibrations: 0.3, 0.4, 0.6 and 0.7. The misspecified normalizing constant is 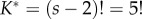The correct constant is 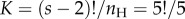. Thus, the misspecified density integrates to 5 (i.e. 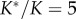). The misspecified density is confirmed by MCMC sampling using MCMCTree (dashed line) using uniform calibrations: , where c is the calibration age for node i.

6. Integrating over histories: calculating the joint density of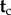

In small phylogenies (as in the four-species case), the marginal density 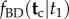can be obtained by solving the integral of equation (3.4) directly. For large phylogenies, the integral may be too cumbersome. Equation (3.6) offers an alternative, by partitioning the integral as a sum over the labelled histories, with each integral having a known form (the joint density of a subset of order statistics, equation (3.5)). However, for large phylogenies, the number of labelled histories may be too large to make computation of this sum practical. Here, I discuss a post-order tree traversal algorithm to calculate the integral that may provide a way forward.

Before laying out the algorithm, it is useful to note the following. Consider the two daughter nodes of the root. These nodes are the last ancestors of two subtrees, which we call the left and right subtrees. For example, in the tree of figure 4, species a–f form the left subtree, while species g–j form the right subtree. The times on each subtree are conditionally independent on 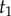, and thus the joint density of equation (3.1) can be written as

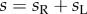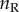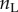where and are the number of species on the right and left subtrees, respectively (), and are the number of labelled histories on the right and left subtrees, and the products are over the node ages on the right subtree (the 's), and over the left subtree (the 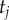s). For example, for the tree of figure 4, , , and . Conditional independence simplifies calculation of the integral of equation (3.4) as the non-calibrated node times in one subtree can be integrated out independently of the other subtree.

Figure 4.

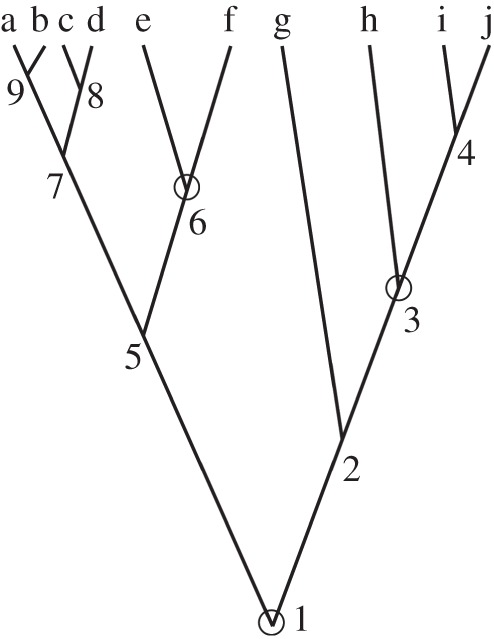
A 10-species tree with fossil calibrations. Nodes 1, 3 and 6 have fossil calibrations (white circles).

Now we can use a post-order algorithm to traverse the nodes of the 10-species phylogeny of figure 4 to integrate out the node ages without calibrations. If we start by visiting nodes on the left, then the first node age to be integrated out is . The partial integral is

The limits of integration are zero and 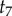because 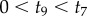. We next visit node 8, and integrate 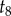out, giving

The algorithm now returns to node 7, and we integrate out

The term inside the integral is the result of integrating the two daughter node ages, and , in the previous steps. This integral is solved by recalling that 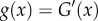. The algorithm now returns to node 5. The age of node 6 is not integrated out as it has a fossil calibration. Because node 6 has no daughter nodes, we integrate directly

Thus, because the left subtree is independent of the right subtree, and noting that 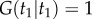, we obtain the marginal density of 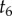(one of the calibrated times) as

Now integrating out the non-calibrated node ages ( and ) on the right subtree, we obtain the marginal density of 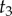(the other calibrated time) as

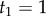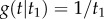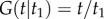For example, if we set , , and , we obtain

6.1

6.2

6.3

6.4

where are the appropriate cumulative distribution functions.

Figure 5 shows the marginal densities and distribution functions of equations (6.1)–(6.4). To confirm the accuracy of the analytical calculations, we use MCMCTree to obtain samples from the joint distribution 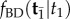(note this density is correctly calculated by MCMCTree). The sampled values of 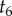and 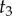can be summarized to obtain their distributions (histograms), or their sampled cumulative distributions. The sampled and analytical functions match almost perfectly (figure 5).

Figure 5.

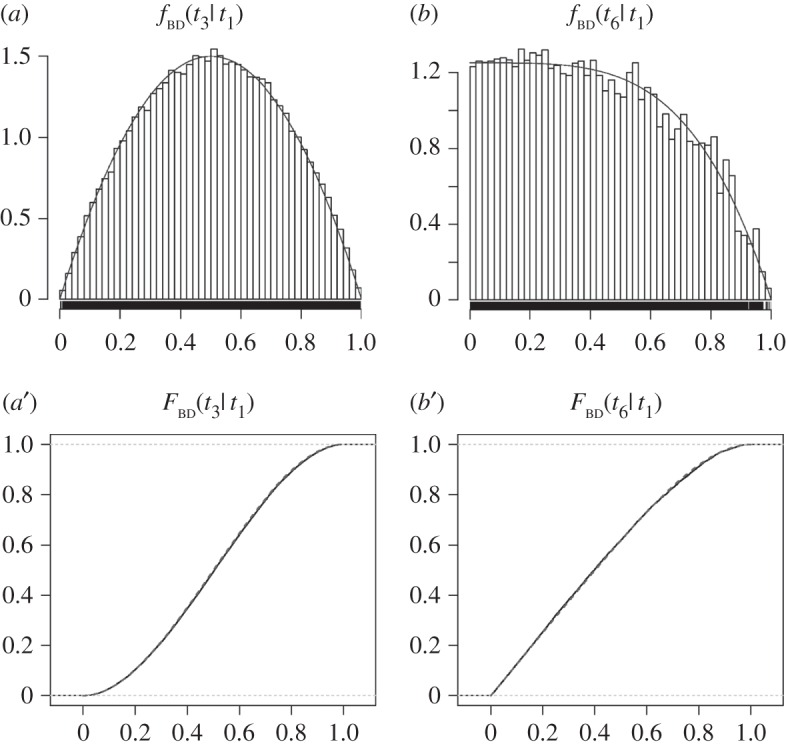
Marginal densities and distribution functions of two calibrated nodes in the 10-species phylogeny of figure 4. The marginal densities in (a), and in (b) are shown as solid lines. The corresponding sampled densities obtained with MCMCTree are shown as histograms. The cumulative distribution functions 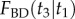in (a’), and 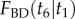in (b’) are shown as thick dashed lines. The sampled cumulative distributions obtained with MCMCTree are shown as solid lines (they overlap almost perfectly the analytical solutions). The analytic forms of the marginal densities and distribution functions are calculated according to equations (6.1)–(6.4).

7. Discussion

The tree traversing algorithm laid out in §6 can be implemented in a computer program by performing symbolic integration of the corresponding densities at the nodes of the tree. The symbolic solution to the integral can then be evaluated to perform MCMC sampling. My initial analysis suggests that all the possible integrals that can be generated have analytic solutions. However, the task of writing computer code to perform the symbolic integration may not be trivial. It may be worth exploring in detail the special case of the uniform kernel density, . A relatively simple general solution to the form of 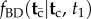could perhaps be obtained under this kernel. Alternatively, equation (3.6), which has a known form, could be implemented in the program, but this would make MCMC feasible only for small trees, or for certain special types of large trees with few labelled histories. In the meantime, the biologist interested in using MCMTree for Bayesian molecular clock dating must deal with the misspecified densities, unless the analysis can be performed under one of the three special cases laid out above.

The misspecification of the birth–death process in MCMCTree only affects the prior density of times without fossil calibrations; thus, the fossil calibration densities themselves are not affected. This means that in an analysis carried out using the misspecified density, the node ages will be adequately constrained by the fossil calibrations constructed by the user (however, note that truncation effects among fossil calibrations may affect the actual prior used, but this is entirely another issue [17]). Users of MCMCTree are advised to obtain MCMC samples from the prior (i.e. by running the program without sequence data), so that the prior can be examined. In most cases, the misspecified prior will be quite reasonable. Multi-modal or other bizarre looking priors may be obtained with MCMCTree especially if several very precise calibrations are present throughout the tree. If the user considers the resulting priors to be biologically unrealistic, then several attempts at tweaking the calibrations and recalculating the prior by MCMC may provide a way forward. This advice should also be followed when estimating divergence times using any of the plethora of computer programs now available for Bayesian clock dating (e.g. [18–21]): each program has its own idiosyncratic way of dealing with fossil calibrations, and unfortunately, it is not always possible to predict what the resulting priors will be.

Competing interests

The author declares no competing interests.

Funding

Part of this work was carried out while the author was a postdoc funded by the Biotechnology and Biological Sciences Research Council (BBSRC, UK) grant BB/J009709/1 awarded to Ziheng Yang.