Species relationships and divergence times in beeches: new insights from the inclusion of 53 young and old fossils in a birth–death clock model

Abstract

The fossilized birth–death (FBD) model can make use of information contained in multiple fossils representing the same clade, and we here apply this model to infer divergence times in beeches (genus Fagus), using 53 fossils and nuclear sequences for all nine species. We also apply FBD dating to the fern clade Osmundaceae, with about 12 living species and 36 fossils. Fagus nuclear sequences cannot be aligned with those of other Fagaceae, and we therefore use Bayes factors to choose among alternative root positions. The crown group of Fagus is dated to 53 (62–43) Ma; divergence of the sole American species to 44 (51–39) Ma and divergence between Central European F. sylvatica and Eastern Mediterranean F. orientalis to 8.7 (20–1.8) Ma, unexpectedly old. The FBD model can accommodate fossils as sampled ancestors or as extinct or unobserved lineages; however, this makes its raw output, which shows all fossils on short or long branches, problematic to interpret. We use hand-drawn depictions and a bipartition network to illustrate the uncertain placements of fossils. Inferred speciation and extinction rates imply approximately 5× higher evolutionary turnover in Fagus than in Osmundaceae, fitting a hypothesized low turnover in plants adapted to low-nutrient conditions.

This article is part of the themed issue ‘Dating species divergences using rocks and clocks’.

1. Introduction

Under the fossilized birth–death (FBD) model, molecular clocks are calibrated with all securely assignable young and old fossils of a clade, not just its oldest fossils [1]. The main strengths of the approach are fourfold. It can provide better estimates of speciation and extinction rates because the fossils add otherwise ‘unseen’ past divergence events; it may yield more reliable ages for deep nodes because both stem and crown group fossils will contribute to the estimates; it eliminates the need to specify ad hoc age distribution densities for each fossil; and it can help understand a clade's biogeography because fossils represent geographical occurrences. This last potential strength is not yet realized in current implementations, which do not use geography as part of the input data, but could become part of the priors placed on fossils in the future. The FBD model is most applicable in groups with numerous fossils, especially where the fossil record has been thoroughly revised so that fossils can be properly interpreted. The approach differs markedly from traditional dating approaches, in which only ‘oldest-cum-reliable’ fossils are used to constrain the ages of particular nodes.

Calibrated divergence-time estimation under the FBD process in the absence of character data for fossil taxa (as developed by [1,2]) has so far been used to estimate the divergence times in three clades. The first, analysed in the original paper, were the bears (Ursidae), a clade of eight species for which 24 outgroup and ingroup fossils dating from the Oligocene to the Pleistocene were used (data reanalysed in [2]). The second clade to be analysed were the royal ferns (Osmundaceae), a family of approximately 15 species (12 sequenced) for which 36 fossils were used that dated from the Late Triassic to the Pleistocene/Holocene [3]. A third analysis focused on the tetraodontiform fishes (Teleostei: Percomorphaceae), a clade of 450 species, 95 of them included, for which 36 fossils were used, dating from the mid-Cretaceous to the Pleistocene/Holocene [4]. Although the widely different branches of the tree of life addressed by these studies (Miocene bears; a mid-Cretaceous clade of fishes; Late Triassic ferns) and their different sampling proportions of extant species makes comparison difficult, it is noteworthy that two of the three studies yielded older root ages than obtained with other dating approaches, in spite of overlap in oldest calibration fossils ([1] versus [5] for the bears; [3]: comparison of root ages obtained with different approaches in table 1). One yielded a younger root age than obtained with the same fossils applied in total evidence dating in the software programs MrBayes or BEAST ([4], fig. 3). Speciation and extinction rates were only reported in the Osmundaceae study, perhaps because of the highly incomplete sampling of extant species in the fish study (although the FBD model has a parameter accounting for incomplete species sampling). As far as is known, node age estimates under the FBD model are robust to several biased sampling strategies of fossils and extant species [1].

Table 1.

Intrageneric divergence times (million years) estimated for Fagus with the FBD model, using either each fossil's oldest stratigraphic age, youngest stratigraphic age, or a random age from in between. MRCA, most recent common ancestor; the Engleriana lineage includes the East/Northeast Asian species F. engleriana and F. japonica; the Fagus lineage includes the remaining living species. Stratigraphic ages are shown in electronic supplementary material, table S3.

node	oldest stratigraphic age	random age in between	youngest stratigraphic age
MRCA of all extant species (=divergence of Engleriana and Fagus lineages)	54.8 (65.7–46.4)	52.5 (62.0–43.0)	52.4 (77.8–36.2)
divergence of F. engleriana from F. japonica	9.3 (21.2–1.9)	9.5 (20.3–1.9)	10.1 (42.1–0.6)
divergence of Pacific-North American lineage (F. grandifolia) from Fagus lineage	47.5 (54.1–42.2)	44.4 (50.8–39.1)	43.6 (58.7–35.5)
first radiation within Eurasian clade, separation into East Asian and widespread Eurasian clade	44.3 (49.8–40.2)	41.5 (46.1–37.4)	40.2 (52.9–34.9)
divergence of F. lucida from F. hayatae/F. longipetiolata	40.5 (44.1–38.1)	37.9 (41.3–35.8)	36.6 (46.5–33.9)
divergence of F. hayatae from F. longipetiolata	38.5 (40.6–37.8)	35.9 (37.9–35.3)	34.5 (41.3–33.9)
divergence of Japanese F. crenata from western Eurasian F. sylvatica s.l.	27.1 (38.0–17.8)	23.0 (34.9–13.9)	23.2 (42.9–11.7)
divergence of F. orientalis (=F. sylvatica subsp. orientalis) from C. European F. sylvatica	10.6 (21.1–2.6)	8.7 (20.0–1.8)	9.8 (34.8–0.6)

Here we apply the FBD model to estimating divergence times in the genus Fagus (Fagaceae), which is an ecologically important clade of broad-leaved deciduous trees occurring in the Northern Hemisphere. Fagus comprises nine species, six of them in East Asia, where they occur in mainland China and Taiwan (F. hayatae), the South Korean island Ulleung-do and mainland China (F. engleriana), Japan (F. crenata and F. japonica) and China (F. longipetiolata and F. lucida). Fagus sylvatica and F. orientalis occur in western Eurasia, and F. grandifolia in eastern North America from Canada to Mexico [6–8]. The fossil record suggests that beeches already existed in the Early Cenozoic in the northern Pacific Basin ([9,10]: foliage, cupules and nuts, and dispersed pollen from the Early Eocene of western North America; [11]: foliage and cupules from the Early Middle Eocene of Northeast China). By the Middle Eocene, Fagus had reached Axel Heiberg Island and western Greenland [12,13] and during the Oligocene it spread westwards to Central Asia and Europe ([14,15]: leaf, pollen, cupule and nut remains). The two molecular phylogenetic studies that sampled most species (some with multiple accessions) for plastid DNA regions and/or spacers of the nuclear ribosomal DNA ([16]: F. hayatae not sampled; [17]) resulted in largely unsupported topologies.

A parsimony analysis of morphological characters from all living and two fossil species of Fagus, and four outgroups (Castanea, Quercus, Trigonobalanus and Nothofagus) by Denk [8] weakly supported the two informal subgroups of Fagus proposed in the Ph.D. thesis of Shen [18]: Engleriana with the Asian species F. engleriana and F. japonica and Fagus with all remaining species. The outlier was the American species F. grandifolia, which shares characters with both groups. Denk & Grimm [11], using an emended morphological matrix, concluded that the ancestor of the F. engleriana/F. japonica group probably had separated from the ancestor of the remaining species by the Oligocene. They refrained from molecular-clock dating, however, instead focusing on a detailed description of the diverse fossil record.

Given the rich fossil record of beeches (some of it only recently described), we decided to apply the FBD model to a new molecular matrix (generated for this study) that includes all species to answer two questions. When did the major extant lineages of beeches diverge from each other and when did the morphologically isolated single North American species originate (diverge from surviving relatives)? And how do speciation rates, extinction rates and fossil recovery rates estimated for Fagus compare with those obtained for the Osmundaceae, a clade with a similar ratio of extant to fossil species (35 fossils and 11 sequenced species in Osmundaceae; 53 fossils and 9 extant sequenced species in Fagus)? Inferring speciation and extinction under the FBD model is of interest because its fundamentally different treatment of fossils in principle allows estimates of these rates [1], enabling comparisons among lineages. It has been suggested that low-nutrient tolerant plants, particularly ferns, tend to have slower evolutionary turnover rates than lineages that dominate mesic habitats ([19]; Osmunda is listed in table 22.1 on p 451, among other examples of ancient groups occurring in low-nutrient sites), and if this holds, one might expect beeches to have higher species turnover than do royal ferns. Note that we repeated our earlier FBD dating of Osmundaceae [3] because two fossils have since been reassigned [20].

2. Material and methods

(a). Sequencing, alignment, phylogeny estimation and finding the best root

DNA isolation, sequencing and alignment followed standard procedures. Electronic supplementary material, table S1 lists the plant material used, with species names and authors, herbarium vouchers, their place of deposition, geographical origin and GenBank accession numbers. Nuclear rDNA data (ITS1, 5.8S rDNA, ITS2) are individual-consensus sequences [17,21]. Sequences of the second LEAFY intron (LFY-i2) were newly generated using the same primers as Denk & Grimm [22]. We also screened plastid data harvested from GenBank as an additional source of information (electronic supplementary material, table S2). The data were not used because of lacking or unclear vouchers and problems with possible introgression or hybridization (e.g. intra-species divergence exceeds inter-species differentiation and near-identical or identical haplotypes are found in species from the same geographical regions, independent of whether they are close or distant relatives). These problems affected the topology for Fagus obtained by Xing et al. [23].

Maximum-likelihood (ML) tree searches and ML bootstrapping were performed using the program RAxML [24,25]. Tree searches relied on the GTR+G model (six general time reversible substitution rates, assuming gamma rate heterogeneity, with four gamma rate categories); model parameters were estimated over the duration of specified runs using three data partitions (ITS1, ITS2, LFY-i2); the essentially invariable 5.8S rDNA was excluded from analysis.

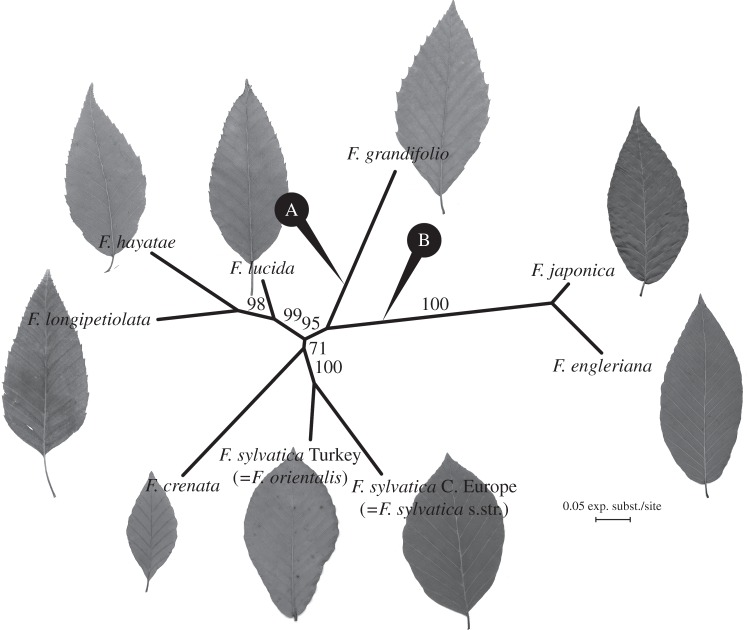
Two previous molecular studies that sampled most species placed the root between F. engleriana and all remaining species ([16]: fig. 4) or F. hayatae and all remaining species ([17]: fig. 5). Because we could not reliably align the Fagus LEAFY sequences with the few LEAFY sequences available for other Fagacae genera, we relied on rooting under a strict clock model (without fossils because absolute time is irrelevant here) and then quantifying the support for alternative root positions (shown in figure 1) using Path sampling and Bayes factors [26,27]. Both runs used a strict clock model and 10⁶ Markov Chain Monte Carlo (MCMC) iterations for 50 steps, with a 50% burnin. Upon completion of the runs, we calculated the Bayes factor by comparing the marginal likelihoods for a tree rooted on F. grandifolia (model A) with that of a tree rooted on F. japonica/F. engleriana (model B).

Figure 1.

Maximum-likelihood (ML) phylogram from nuclear ITS and LFY-i2 sequences from representatives of all species of Fagus with the alternate roots (see Material and methods). Bayes factor comparison favoured the rooting A. Numbers at branches indicate non-parametric bootstrap support under ML optimization. Characteristic leaves are shown for each species (photos: T. Denk).

(b). The fossils used and their assignment

We linked Fagus fossils to extant species based on the studies of Denk [28] and Denk & Grimm [11], with recent updates from ongoing work by Thomas Denk ([10–12,15,28–50]; K. Uemura 2015, personal communication). Electronic supplementary material, table S3 lists the 53 fossils used together with their geographical origin, locality, taxonomic/systematic affinity to modern taxa, age range, organ type, references for the fossils as well as any revised age estimates or synonyms.

The FBD model of Heath et al. [1] treats fossils as members of user-defined clades. For instance, F. protolongipetiolata is a fossil taxon virtually indistinguishable from F. longipetiolata, and we therefore defined a clade that comprises this fossil and this extant species. Conversely, Middle Eocene Fagus pollen [13] from Hareø in western Greenland, which cannot be assigned to any extant lineage, was assigned to the total clade of Fagus including its stem line. For age determination, we follow the most recent accounts on the respective fossil assemblages ([51–56]; electronic supplementary material, table S3), and the geological time scale used is that of Walker et al. [57].

(c). Fossilized birth–death process model settings

The FBD process is a diversification model derived from a serially sampled birth–death process [58]. We used the version implemented in BEAST v. 2 ([59]; including the SampledAncestors package, https://github.com/CompEvol/sampled-ancestors), with the model parameters being speciation rate (λ), extinction rate (μ), fossil recovery rate (ψ) and proportion of sampled extant species (ρ). The diversification rate d = λ − μ, the turnover rate r = μ/λ, and the probability of fossil observation prior to species extinction s = ψ/(μ + ψ). Given the strong correlation between parameters, the calculations are more efficient if one of them is fixed. In our analyses, we chose to fix ρ to 100% in the case of Fagus, as all extant species were included in the analyses, and about 72% for Osmundaceae.

For the lineage-specific variation in substitution rate, we used the uncorrelated rates model with a lognormal distribution; we set a diffuse gamma (shape 0.001, scale 1000) hyperprior for the mean (ucld.mean) of the distribution. Under the FBD model, fossil species can be ancestors or extinct sister groups, and when analysed without a morphological matrix, their placement is constrained only by assigning them to subclades or the root of the entire clade of interest. The FBD model assumes that the fossil represents a single point in time ([1], electronic supplementary material, table S3), and we therefore ran analyses with three sets of ages: (i) only the upper bounds of the fossil ages (i.e. each fossil's youngest stratigraphic stage as listed in our electronic supplementary material, table S3), (ii) only the lower bounds of the fossil ages (each fossil's oldest stratigraphic age) and (iii) a random number drawn from within each age range. We performed all analyses on a partitioned alignment, under the DNA substitution models selected under the Bayesian information criterion in jModelTest [60]. The best scoring models, also implemented in BEAST, were for the rDNA, ITS1, and ITS2 the HKY model and for the nuclear LFY gene the HKY + G model. All remaining parameters were calculated under the default prior distributions. Each analysis was run twice for 2 × 10⁷ generations, sampling every 1000th step.

Runs were evaluated using Tracer v. 1.5 to confirm that (i) each Markov chain reached stationarity, (ii) the effective sample sizes (ESS) were greater than 200 for all optimized parameters and (iii) independent runs produced converging results. The initial 25% of the MCMC samples (Bayesian-inferred topologies) in each analysis were discarded as burn-in, and the remaining samples were summarized in TreeAnnotator (part of the BEAST package) and visualized using FigTree. We also computed a bipartition network based on 10 000 MCMC samples from the end of the chain using SplitsTree 4 [61] to investigate the placement of fossils in each individual MCMC sample. A bipartition network is a form of tree consensus network [62] in which the edge lengths are proportional to the frequency of a subtending branch observed in the tree sample (invoked using the option ‘COUNT’ while calculating the consensus network in SplitsTree after reading in a tree sample; [63]).

3. Results

(a). Rooting Fagus and effects of the three treatments of fossil ages

Figure 1 shows a phylogram depiction and the statistical support of the new Fagus phylogeny obtained in this study, with the two root positions that were compared using marginal likelihoods (Path sampling). Rooting on F. grandifolia (model A) received a marginal likelihood of −3715.883069, while rooting on F. engleriana/F. japonica (model B) had a marginal likelihood of −3711.813456. The BF is calculated as BF = (B − A) × 2 = 8.139224 [64], which provides strong support for the second scenario (model B). We, therefore, concentrate on the chronogram resulting from FBD runs rooted on F. engleriana/F. japonica.

The FBD runs that used our 53 fossils, with either each fossil's oldest stratigraphic age, youngest stratigraphic age, or a random age drawn from in-between its oldest and youngest age, yielded the divergence times shown in table 1, which also shows credible intervals. For Fagus, all analyses reached convergence for all parameters with good mixing (effective sample size > 200, after 25% burn-in). The estimates for the majority of the nodes were almost identical and the maximal difference was 3–4 Ma for the two oldest nodes of the tree. In Osmundaceae, the runs that used the oldest fossil stratigraphic ages converged later than the other two runs (after 7 × 10⁶ MCMC cycles), thus we used an increased burn-in percentage. Repeated runs converged with ESS > 200 for all parameters, and the estimated divergence times were highly similar (data not shown).

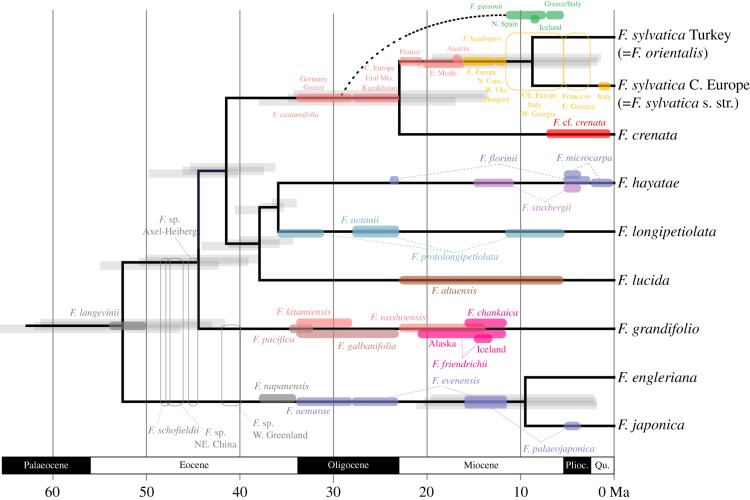
(b). A new Fagus phylogeny and evolutionary time frame

Figure 2 shows the divergence times obtained with the FBD approach when the tree was rooted on F. engleriana/F. japonica, as preferred by the Bayes factor statistics (Material and methods), and with ages randomly drawn from within the lower and upper bounds of the fossils' stratigraphic ages. It needs to be stressed that the coloured bars in the figure, which are drawn by hand, indicate the fossils' stratigraphic age range and are not prior distributions on fossil age parameters. We infer an Early Eocene age (53 (62–43) Ma) for the crown group age of Fagus. A Pacific-North American lineage, leading to the eastern North American F. grandifolia, apparently diverged from its Eurasian relatives by the Middle Eocene, with the western North American fossil F. pacifica and the Japanese F. kitamiensis the earliest representatives of the American lineage. By the Late Eocene, the Eurasian lineage subdivided further into an East Asian clade (F. lucida, F. longipetiolata + F. hayatae; including the fossil Central Asian F. altaensis) and a widespread Eurasian clade with a distribution (and more or less continuous fossil record) from western Eurasia into Japan. The disjunction between the western Eurasian (F. sylvatica) and Japanese (F. crenata) species is estimated to have occurred at the Oligocene–Miocene boundary (ca 23 Ma), 10–15 Myr after the first representatives of this clade (F. castaneifolia) reached Europe. The Miocene F. gussonii (Iceland, Mediterranean) may represent an extinct branch of this clade. Notably, all fossils of the Fagus group are younger than the reconstructed divergences.

Figure 2.

A chronogram for Fagus inferred with fossilized birth death (FBD) dating and 53 fossil taxa obtained with the randomly drawn ages from within each fossil's stratigraphic age interval (electronic supplementary material, table S3). The right-most grey bars at nodes show the highest posterior density (HPD) intervals obtained with the youngest stratigraphic ages, the left-most grey bars, the HPDs obtained with the oldest stratigraphic ages and the middle grey bars, the HPDs obtained with random fossil ages. The coloured bars and dotted lines represent the chronological distribution of the respective fossil based on the palaeobotanical studies cites in electronic supplementary material, table S3 and take into account the divergence times inferred under the FBD model; the raw BEAST2 output is shown in electronic supplementary material, figure S2. Plioc., Pliocene; Qu., Quaternary (Pleistocene, Holocene).

(c). Inferred extinction, speciation and fossil discovery rates for Fagus and Osmundaceae

The Osmundaceae chronogram is shown in electronic supplementary material, figure S1, and FBD process rates for both Fagus and Osmundaceae are given in table 2. The inferred values for the turnover rate r and the diversification rate d were similar regardless of whether the youngest bound of each fossil's stratigraphic age, the oldest bound, or a random age drawn from within each fossil's stratigraphic range was used (this was true for Fagus as well as Osmundaceae). However, the inferred probability s that a lineage's fossils were observed prior to going extinct almost doubled when fossil ages were drawn randomly from within the relevant age ranges. The estimates for s were similar for Fagus and Osmundaceae, but r and d were higher for Fagus than for Osmundaceae (table 2). With randomly drawn ages, the inferred speciation rate for Osmundaceae was 0.02 Myr and the extinction rate 0.01 (table 2) and for Fagus 0.08 and 0.06, resulting in a species turnover rate in Fagus about 5× higher than in Osmundaceae.

Table 2.

Rates of turnover, diversification and fossil ‘discovery’ prior to a lineage's extinction (Myr⁻¹) inferred with FBD applied to Fagus and Osmundaceae. Means of oldest, random, and youngest as in table 1. Turnover rate r = μ/λ; diversification rate d = λ − μ; probability of fossil observation prior to species extinction s = ψ/(μ − ψ); speciation rate λ; extinction rate μ; fossil recovery rate ψ. Meaning of oldest, random, and youngest as in table 1.

	oldest	random	youngest
Fagus
r	0.8709	0.7379	0.8423
d	0.018	0.0197	0.0198
s	0.3015	0.6154	0.3792
λ	0.1394	0.0752	0.1256
μ	0.1214	0.0555	0.1058
ψ	0.0524	0.0887	0.0646
Osmundaceae
r	0.7249	0.58380	0.6856
d	8.73 × 10−3	8.30 × 10−3	7.88 × 10−3
s	0.3932	0.5831	0.3754
λ	0.0317	0.0199	0.0251
μ	0.0230	0.0116	0.0172
ψ	0.0149	0.0163	0.0103

4. Discussion

(a). The use of fossils in the fossilized birth–death model and their depiction on fossilized birth–death-derived chronograms

We here use the BEAST2 implementation of Heath et al.'s [1] FBD dating approach. One of the differences between the original implementation of the FBD model and that in BEAST2 is that the new implementation supports partitioned analyses, an improvement that we took advantage of here (by using separate substitution models for the nuclear and plastid data). The key aspect of the FBD model is that it integrates over all fossil placements, with each fossil providing time information for the clade to which it was assigned (in principle, all 53 fossils could have been assigned to the root), but its precise placement not being an issue (therefore, no morphological data matrix for the fossils is needed). This means, however, that the raw BEAST2 output (electronic supplementary material, figures S1 and S2), which shows fossils on more or less long branches, can easily be visually misleading, as it seems to apply a particular topological position for each fossil. We used a bipartition network as an alternative means to visualize the output (electronic supplementary material, figure S3). Bipartition networks allow efficient inspection of topological alternatives [11,62,65] and help in assessing whether the fossil placements were as intended and which fossils ‘moved’ between placements, based on their ages (morphology obviously could not have played a role).

(b). A new temporal and biogeographic framework for the evolution of beeches

As inferred here, the common ancestor of F. engleriana and F. japonica had diverged from the lineage that gave rise to the remaining species by the Early Eocene. By the Middle Eocene, Fagus had extended into high latitudes as shown by pollen and foliage from Axel Heiberg and Greenland [13,66]. Among the strengths of the FBD model is that in its MCMC chain, fossils will be placed both as ancestors (on stems) and as sister species of surviving lineages, which is conceptually pleasing because we do not usually know the true situation. It is also satisfying that all fossils, not just a single known ‘oldest’ fossil, contribute to the overall root age inferred under the FBD model. The high crown group age here inferred for Fagus is thus due to all fossils, not just a few ambiguously placed oldest fossils, such as F. pacifica or F. uemurae (electronic supplementary material, table S3). For the North American F. grandifolia, its genetic distinctness (seen in the phylogram, figure 1) correlates with its inferred deep Middle Eocene divergence from the remaining species and matches the finding that ITS variants are shared among Eurasian Fagus, but not between them and F. grandifolia [17], suggesting the absence of any substantial gene flow across the Beringian and North Atlantic land bridges during the Neogene.

The closure of the Turgai Sea between Europe and East Asia in the Oligocene allowed the westward spread of the F. crenata/F. sylvatica lineage. This westward expansion of beech is documented in the fossil record by the spatial and temporal distribution of F. castaneifolia and the younger F. haidingeri fossils, the latter a putative precursor of F. sylvatica [11,28]. The Asian continental beeches in south-central China and Taiwan (F. hayatae, F. longipetiolata, F. lucida) probably had already diversified by this time (table 1), and the precursor of F. crenata, a species today restricted to Japan, may already have been geographically isolated.

The inferred Miocene age for the split between F. crenata and the Central European F. sylvatica (F. sylvatica sensu stricto) and its Turkish form F. orientalis is unexpectedly old given their similar ITS sequences. F. sylvatica/F. orientalis has a wide geographical range and shows substantial intra-genomic variation [6,7,67,68], supporting the view that there may be two or even more species. Hence, our population sampling may be insufficient, and the genetic distances in our DNA tree between the included single individuals of F. crenata, F. sylvatica and F. orientalis unrepresentative. In addition, fixation rates in the multi-copy and perhaps multi-loci [69] Fagaceae ITS region are poorly understood. For instance, the Georgian relict species Quercus pontica, a white oak, shares the ITS signature of the northern Californian relict Q. sadleriana [22], although gene flow in relatively recent times is unlikely.

(c). Turnover rates and fossil discovery rates in Osmundaceae and Fagus from the fossilized birth–death process model

In our earlier study of the royal ferns (Osmundaceae), we inferred a speciation rate (λ) of 0.03 Myr⁻¹ and an extinction rate (μ) of 0.02, indicating a relatively slow diversification and high taxonomic turnover, although all such estimates under a model of constant speciation and extinction rates are doubtful [3]. The estimated fossil recovery rate, ψ = 0.0153, modelling how many fossils (fossil lineages) have been sampled, appeared low. With the FBD model implemented in BEAST (Material and methods), we inferred speciation rates for Osmundaceae between 0.02 and 0.03 Myr⁻¹ and extinction rates of 0.01 and 0.02 (depending on which of the stratigraphic boundaries were used; table 2). The inferred probability that a lineage's fossils are observed prior to going extinct (s) almost doubled when fossil ages were drawn randomly from within the relevant stratigraphic age ranges, suggesting that a biased placement of the fossils across lineages of a given phylogeny, introduced by forcing the fossil ages to the limits of their stratigraphic ranges (youngest, oldest) decreases the inferred recovery probability of fossils.

If we accept these estimates (for clades of similar size and with similar species sampling), the species turnover rate in Fagus is approximately 5× higher than that in the royal ferns, implying that beech species tend to survive for shorter periods than do royal fern species. These different evolutionary turnovers match the suggestion of Page ([19], pp 460 and 451) that low-nutrient-adapted clades, such as Osmunda, ‘exploiting marginal conditions’, have slower turnover rates than lineages that dominate mesic habitats. While beeches realize a broad ecological niche in terms of soil chemical properties and water availability, they appear not to be competitive in very acidic soils with low-nutrient availability ([70] for F. sylvatica).

In conclusion, using a statistically well-supported phylogeny that includes all species of beeches, we provide divergence-time estimates that are based on 53 fossils, with fossil placements evaluated by Thomas Denk for this study. Besides this empirical result, our study uses Osmundaceae and Fagus as suitable ‘experimental datasets' for comparing FBD-estimated turnover rates, diversification rates, probability of fossil observation prior to species extinction, and fossil recovery rates, parameters that yet have to be estimated in many more artificial and real datasets for users to obtain a sense of their meaningfulness.

Data accessibility

DNA sequences: GenBank accessions all listed in electronic supplementary material, table S1. The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

P.K. ran FBD analyses and carried out the Bayes factor comparison; T.D. compiled the fossil data; G.W.G. carried out phylogenetic analyses and prepared all figures; S.S.R. conceived the study, funded the sequencing, and drafted the manuscript; all authors contributed to the writing and approved the submitted version.

Competing interests

We have no competing interests.

Funding

G.W.G. acknowledges funding from the Austrian Science Fund (M1751-B16) and T.D. from the Swedish Research Council (VR).