Abstract
Understanding when species diverged aids in identifying the drivers of speciation, but the end of gene flow between populations can be difficult to ascertain from genetic data. We explore the use of pairwise sequential Markovian coalescent (PSMC) modelling to infer the timing of divergence between species and populations. PSMC plots generated using artificial hybrid genomes show rapid increases in effective population size at the time when the two parent lineages diverge, and this approach has been used previously to infer divergence between human lineages. We show that, even without high coverage or phased input data, PSMC can detect the end of significant gene flow between populations by comparing the PSMC output from artificial hybrids to the output of simulations with known demographic histories. We then apply PSMC to detect divergence times among lineages within two real datasets: great apes and bears within the genus Ursus. Our results confirm most previously proposed divergence times for these lineages, and suggest that gene flow between recently diverged lineages may have been common among bears and great apes, including up to one million years of continued gene flow between chimpanzees and bonobos after the formation of the Congo River.
This article is part of the themed issue ‘Dating species divergences using rocks and clocks'.
Keywords: PSMC, great apes, bears, species divergence
1. Introduction
The assumption that lineages accumulate sequence-level changes at an approximately constant rate through time, also known as the molecular clock hypothesis, makes it possible to place estimates of evolutionary divergence on calendar and geological timescales using DNA sequence data. The molecular clock hypothesis was first proposed in the 1960s [1,2] and has been widely used across evolutionary biology. Inference of the time to most recent common ancestor (TMRCA) of two or more lineages has been used, for example, to provide insights into environmental events that may have driven evolutionary radiations [3], episodes of cross-species transmission in viruses [4] and the colonization of new habitats by a dispersing species [5].
Prior to recent advances in genome-scale sequencing, most studies incorporating a molecular clock approach estimated the TMCRA of two lineages using phylogenies inferred from one or a few loci, or ‘gene trees'. However, except for instances of post-divergence admixture, the TMRCA of a particular locus within the genome will be more ancient than the population-level divergence of the two lineages. Genome-scale data present an opportunity to unravel the divergence histories of two lineages with increased accuracy, as each of the many ‘gene trees' within the genome describes a different aspect of the ‘species tree’ [6,7].
Pairwise sequentially Markovian coalescent (PSMC) [8] and multiple sequentially Markovian coalescent (MSMC) [9] are two new computational approaches that are capable of estimating the demographic history of a lineage from genome-scale data. Both PSMC and MSMC infer fluctuations in ancestral effective population size (Ne) from either a single genome (PSMC) or from multiple genomes sampled from the same population (MSMC). PSMC and MSMC estimate ancestral population size by measuring the rate of heterozygosity across regions of the genome. Because heterozygous sites are nucleotide positions where the two parental chromosomes differ, genomic estimates of heterozygosity can be paired with the molecular clock to infer when an individual's parents shared a common ancestor. The distribution across the genome of these times to parental common ancestry, or coalescence events, can then be used to infer changes in the ancestral population size over time, as the probability of observing a coalescence event at some time in the past is inversely proportional to the ancestral population size.
In addition to inferring changes in effective population size over time, PSMC and MSMC have been used to estimate divergence times between species [8–13]. The most common approach has been to first infer PSMC plots for each species separately and then to overlay these plots. When reading the plots from the present into the past, between-species divergence is inferred to have occurred at the point in time when the trajectories of two overlain plots become identical, which presumably reflects the transition to shared population histories (e.g. the time prior to divergence). This approach has been used, for example, to estimate the timing of interspecific divergences within the great apes [11], between modern humans and Neanderthals and Denisovans [12], and between dogs and wolves [13]. This approach does not, however, account for the possibility of demographic processes other than complete divergence, such as population structure or that the two lineages might have the same effective size owing to chance [8]. The second approach, which we investigate further here, uses phased data, which has either been the X chromosomes of male individuals [8], or from multiple whole genomes drawn from high-quality human datasets [9]. These phased data are used to create artificial F1 hybrid genomes comprising one chromosome from each of the two lineages whose divergence time is to be inferred, and plots are generated from these artificial hybrid genomes. Sites along an F1 hybrid genome cannot coalesce more recently than the speciation of the two parent species. These plots therefore show a transition from an infinite population size during the time of lineage divergence to population sizes that reflect the shared ancestry period prior to divergence. Where this transition falls is interpreted as the time of divergence [8].
Although the artificial F1 hybrid approach is a potentially powerful method to learn when two lineages diverged, it is unknown to what extent this approach is suitable for organisms for which high-quality, phased genomic data are not yet available. Here, we use a combination of simulated and real data to investigate the utility of the F1-hybrid PSMC approach, hereafter hPSMC, under a variety of demographic scenarios and with low-coverage and unphased data. First, we use simulated phased and unphased data to explore the influence of (i) amount of time since divergence, (ii) post-divergence gene flow and (iii) effective population size prior to divergence on the accurate recovery of divergence time using hPSMC. We then apply hPSMC to two well studied, real datasets: great apes and bears from the genus Ursus. We compare hPSMC estimates of divergence timing within these lineages to estimates inferred using other approaches.
2. Methods
(a). Simulated data
First, we explored the influence of several demographic factors on the accuracy of divergence-time inference using hPSMC. Using the coalescent simulation program ms [14], we simulated chromosome sequences to generate four datasets: (i) phased haplotypes with no post-divergence gene flow between populations; (ii) unphased ‘haploidized’ sequences generated by randomly selecting from one of two haplotypes with no post-divergence gene flow between populations to mimic data that are typically available from short-read shotgun sequencing; (iii) unphased sequences generated from populations with a range of pre-divergence effective sizes; and (iv) phased haplotypes with varying amounts of post-divergence gene flow between populations.
We simulated the populations and DNA sequences using ms coalescent simulation [14]. For each simulation in this study, we simulated 200 Mb genomes divided into chromosomes of equal length of either 5 or 10 Mb (electronic supplementary material, tables S1 and S2). We assume a mutation rate of 1 × 10−9 mutations per site per year, a recombination rate of 1 CM Mb−1 per site per generation, and a generation time of 25 years. To create simulated phased datasets, we simulated one haploid sequence per chromosome each from two populations, both with an effective size of 10 000 individuals. The populations were simulated to diverge from an ancestral population of 10 000 individuals at time t. We then used these haploid sequences to create an artificial F1 hybrid. We converted the ms output to psmc input files (.psmcfa format) by parsing the sequences and calling a heterozygous site where the parents differ (see https://github.com/jacahill/hPSMC). Although the default settings for PSMC is to bin the genome into 100 base-pair regions [8], we reduced this binning to 10 base pairs so as to compensate for the higher expected heterozygosity in our simulated hybrid genomes. This change also allows for greater resolution at older time periods and avoids mutation saturation. To assess the influence of the evolutionary distance between populations, we created seven phased datasets where t = 100 000, 500 000, 1 million, 2 million, 3 million, 4 million or 5 million years ago (Ma). To assess the influence of post-divergence migration between populations, we created five additional datasets where post-divergence migration rates were 0.1, 1, 10, 100 or 1000 migrants per generation. For each of these five datasets, t = 1 Ma.
To create unphased datasets, we used a process called ‘haploidization’ [15], which involves selecting a single high-confidence base call at each site where reads are mapped to the reference genome. Haploidization is useful for genomic analyses of low-coverage data, as it requires only a single high-quality base call mapped to each site compared with more than 20× coverage needed for calling and phasing genotypes [16]. To generate a haploidized dataset, we simulated data using ms [14] as above, but generated two haplotypes per population. Then, for each population, we randomly selected a single allele at each site where the two simulated haplotypes differed. As with the phased data above, we created eight datasets reflecting a range of divergence times between populations from 0 to 5 Ma.
(b). Real data
We next applied hPSMC to two well-studied biological test cases where whole genome sequence data are available and for which divergence between lineages has been estimated previously: bears from the genus Ursus and great apes. We downloaded reads from the NCBI SRA for five bears—two polar bears (Ursus maritimus), one from Svalbard (SAMN01057660) [17] and another from Alaska (SAMN01057676) [17]; two brown bears (Ursus arctos SAMN03252407, SAMN02045559) [18,19], one from North America (SRA) and one from Europe; and an American black bear (Ursus americanus SAMN02045561) [18]—and for one individual from each of the five extant great ape species—human (Homo sapiens, ERP001960) [20], chimpanzee (Pan troglodytes, ERS027400) [21], bonobo (Pan paniscus, ERX012399) [21], gorilla (Gorilla gorilla, SRX339460) [22] and orangutan (Pongo pygmaeus, ERS225256) [22]. We aligned the bears to the polar bear reference genome [23,24] and the great apes to the human reference genome (hg19) [25]) using bwa 0.7.10 [26] with the BWA–MEM algorithm and default settings. We processed the files, filtered reads with map quality scores less than 30 and removed duplicate reads using Samtools v. 0.1.19 [27]. After mapping, we generated haploidized sequences as described above for each individual from base calls with minimum base quality and read mapping qualities of 30. We ran PSMC on simulated hybrids from all pairwise combinations of bears and all pairwise combinations of great apes, and estimated the divergence times between each species and between populations as described above. For all bears and great apes, we used the default PSMC settings described in the original publication of the method [8]. For bears, we assumed the polar bear generation time of 15 years [28] for all comparisons, and a mutation rate of 1 × 10−9 mutations per site per year [29]. For great apes, we used a generation time of 25 years as per the human analyses in the original publication of PSMC [8], and also estimated chimp generation time [30], with a mutation rate of 1 × 10−9 mutations per site per generation.
3. Results
(a). Simulated data
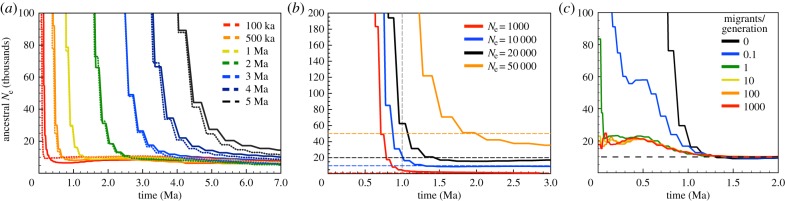
We first explored the influences of three demographic parameters—time since divergence, pre-divergence population size and post-divergence gene flow—on the ability of PSMC to infer the time of divergence between lineages. Using simulation, we created artificial F1 hybrid chromosomes to mimic both high coverage (phased) genomic datasets and lower coverage (unphased) genomic datasets, and estimated PSMC plots from these artificial hybrid chromosomes. In each resulting plot, the timing of the transition between an infinite inferred population size to a population size that reflects the shared ancestry period of the two lineages is interpreted as the time of divergence between those lineages.
First, we created artificial hybrid chromosomes from simulated populations in which the time of divergence between parent populations ranged from 100 thousand years ago (ka) to 5 Ma. Using the same divergence times, we created datasets that reflected both phased and unphased data. As expected, plots generated using phased, artificial F1 hybrid genomes (those generated from a single parental chromosome of each species or lineage) show a transition (a rapid change in inferred ancestral population size) at the simulated divergence time (figure 1a). The plots are qualitatively similar whether they are generated from phased or unphased data; however, the precise timing of transition is somewhat offset.
Figure 1.
Results of simulation experiments designed to test the accuracy of hPSMC in inferring divergence time under three varying demographic scenarios: (a) the influence of using phased (dashed lines) versus unphased (solid lines) data to infer divergence times at seven different depths of divergence; (b) the influence of pre-divergence effective population size on the ability of hPSMC to detect divergence between unphased data; (c) the influence of post-divergence migration between populations. In (b,c), divergence between populations occurs 1 Ma, and the dashed horizontal lines indicate the pre-divergence effective population size.
Using unphased data, we then generated eight additional datasets in which the divergence occurred 1 Ma, but the pre-transition effective population size ranged from 1000 to 50 000 individuals. Pre-divergence population size influences the transition time, with larger populations resulting in more ancient transitions from infinite Ne to Ne that is reflective of shared ancestry (figure 1b). This effect is also observed when the divergence occurred 100 000 years ago (data not shown), suggesting that this approach may be more likely to produce accurate estimate of divergence time when populations are small.
We next simulated datasets in which gene flow continues between the populations post-divergence. Assuming a 1 Ma divergence between lineages and pre- and post-divergence Ne of 10 000, we varied the number of migrants per generation from 0 (complete isolation) to 1000. Figure 1c shows that gene flow between populations quickly erodes the precision of hPSMC to detect divergence. At low rates of migration, a transition is observed, but it is not the typical rapid change in Ne and may be challenging to interpret in real data (figure 1c). A rate of one or more migrants per generation results in a plot of Ne that is the post-divergence sum of the populations exchanging migrants (here, 20 000), which is what would be expected in the absence of population divergence. Like phased data, post-divergence gene flow produces a much slower rate of hPSMC-inferred population size increase in haploidized datasets (electronic supplementary material, figure S18–S21). At large population sizes, haploidized data appear to be less impacted by gene flow than phased data (figure 1c and electronic supplementary material, figures S18–S21).
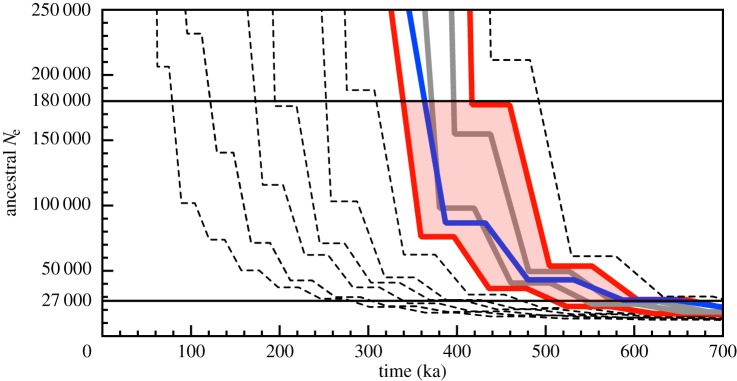
The results described in figure 1 show that population divergence can be inferred as a transition between an infinite population size to population sizes that reflect the shared ancestry of the two parent lineages. However, pinpointing the exact timing of this transition can be challenging, in particular given the demographic complexities of real data. We therefore implemented a simulation-based procedure that estimates the most likely transition time by comparing hPSMC plots estimated from analyses of simulated data generated under a range of transition times to plots estimated from the real data. This procedure assumes that, if the transition occurs more recently in a simulated dataset than it does in the real data, the time of divergence assumed in the simulation was probably more recent than the truth. Likewise, if the transition is older than that observed in the real data, then the time of divergence used in that simulation was probably older than the truth. We therefore consider the time range during which divergence is most likely to have occurred to be the narrowest range of simulated divergence times that include the real data without intersecting it (figure 2). So as to capture the portion of the hPSMC plot that is most influenced by the divergence event, we consider only the portion of the inferred hPSMC plots where the ancestral Ne is between arbitrary thresholds of 1.5 and 10 times the pre-divergence Ne. The lower bound is to avoid conflating pre-divergence increases in population size with the signal of population divergence. The upper bound is to avoid exploring parameter space in which little information is present; in instances where inferred Ne increases exponentially after population divergence, the values reported by PSMC are informed by increasingly little data and so will eventually become a greater source of error than information for very large inferred values of Ne. The cut-off values of 1.5 to 10 time pre-divergence Ne are intended as a reasonable starting point for interpretation, but may not be appropriate for all datasets.
Figure 2.
An approach to pinpoint the transition (divergence) time using simulation. Here, the hPSMC plot generated for the artificially created chimpanzee/bonobo hybrid genome (blue line) is compared with 11 simulated datasets with divergence times ranging from 0 to 500 ka. Divergence is inferred to have occurred between the simulated divergence times of 300–400 ka (red shaded region), as these are the closest simulations with transition times that do not intersect the transition time of real data. All simulations assume a pre-divergence effective population size of 18 000, which was estimated from the plot of the real data. The horizontal lines delineate the range of ancestral effective population size estimates that correspond to 1.5–10 times the pre-divergence Ne (27 000–180 000). Plots resulting from all other comparisons are provided as electronic supplementary material, figures S1–S17.
(b). Real data
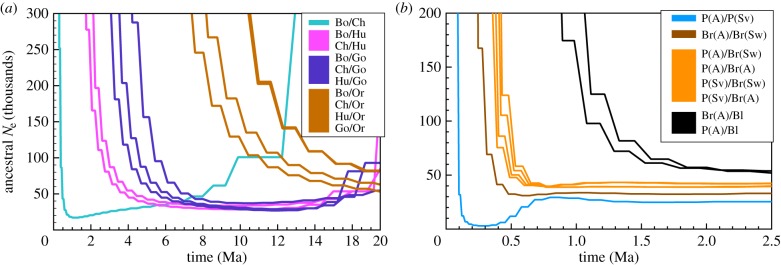
We next used hPSMC, as described above, to infer the timing of divergence between lineages of great apes and bears in the genus Ursus. For each comparison, we first generated hPSMC plots from artificial F1 hybrid genomes generated from two parent lineages (figure 3). To infer the most likely transition intervals for each pair of lineages, we then simulated populations of each pre-divergence Ne as above, where simulated populations diverged at a range of times spanning those suggested by the hPSMC plot (figure 2 and electronic supplementary material, figure S1–S17), and used these results to infer the most likely range of divergence times for each pair of lineages (table 1). For the great apes, hPSMC infers the end of gene flow between chimpanzees and bonobos to be 300–450 ka. Our results indicate that humans diverged from the common ancestor of chimpanzees and bonobos about 1.75–3.75 Ma, and that the Hominini (Homo and Pan) diverged from the lineage leading to gorillas 3.75–6.25 Ma. We find that the lineage leading to orangutans diverged from the other great apes approximately 7.5–13.0 Ma. For the bears, we infer that brown bears and polar bears diverged within the last 200 ka, and their common ancestor diverged from American black bears 500 ka–1 Ma (figure 3b). In addition to between-species divergence, we also estimate the divergence between geographically disparate polar bear populations from Svalbard and Alaska and brown bear populations from Sweden and Alaska. These intraspecific divergences are also within 200 ka, 50–150 ka for the polar bears and less than 100 ka for the brown bears.
Figure 3.
Results of hPSMC analyses of (a) five species of great apes (human, chimpanzee, bonobo, gorilla, orangutan) and (b) three species of bears in the genus Ursus (American black, brown, polar). Within the great apes (a), we observe the expected pattern of divergence in which orangutans diverge most anciently followed by gorillas and then humans, and chimpanzees and bonobos diverge most recently. Within bears (b), we also find the expected order of divergence, where the American black bear is the most ancient divergence, followed by brown bear/polar bear divergence (light brown) and brown bear/brown bear divergence (dark brown) The polar bear/polar bear divergence (blue) is inferred to have occurred very recently and may be an artefact of the small effective population size of polar bears (figure 1b).
Table 1.
Corrected estimates of the inferred divergence time between lineages using hPSMC. Estimates were corrected using the procedure described in figure 2.
| hPSMC ‘parent’ 1 lineage | hPSMC ‘parent’ 2 lineage | inferred recent bound for divergence | inferred ancient bound for divergence | pre-divergence Ne for simulations |
|---|---|---|---|---|
| bonobo | chimpanzee | 300 000 | 450 000 | 18 000 |
| bonobo | human | 2 000 000 | 3 750 000 | 40 000 |
| bonobo | gorilla | 4 000 000 | 5 250 000 | 40 000 |
| bonobo | orangutan | 8 000 000 | 10 500 000 | 80 000 |
| chimpanzee | human | 1 750 000 | 3 250 000 | 40 000 |
| chimpanzee | gorilla | 3 500 000 | 4 750 000 | 40 000 |
| chimpanzee | orangutan | 7 500 000 | 9 500 000 | 80 000 |
| human | gorilla | 5 000 000 | 6 250 000 | 40 000 |
| human | orangutan | 10 000 000 | 13 000 000 | 80 000 |
| gorilla | orangutan | 10 000 000 | 13 000 000 | 80 000 |
| polar bear (Alaska) | polar bear (Scandinavia) | 50 000 | 150 000 | 4000 |
| brown bear (Alaska) | brown bear (Scandinavia) | <100 000 | 100 000 | 45 000 |
| polar bear (Alaska) | brown bear (Alaska) | <100 000 | 200 000 | 45 000 |
| polar bear (Alaska) | brown bear (Scandinavia) | <100 000 | 100 000 | 45 000 |
| polar bear (Scandinavia) | brown bear (Alaska) | <100 000 | 200 000 | 45 000 |
| polar bear (Scandinavia) | brown bear (Scandinavia) | <100 000 | 200 000 | 45 000 |
| polar bear (Alaska) | American black bear | 500 000 | 900 000 | 50 000 |
| brown bear (Alaska) | American black bear | 600 000 | 1 000 000 | 50 000 |
4. Discussion
Our results demonstrate that PSMC can be used to infer the timing of divergence between lineages under a wide range of demographic scenarios, although the accuracy with which divergence time is detected is influenced both by demography and by the quality of the data available for analysis. The extension of the simulated F1 hybrid PSMC (hPSMC) framework to unphased haploidized data, which mirrors the type of data that are available for many published genomes, produces results that are comparable to those from phased data (figure 1a,b). However, pre-divergence population size will affect the inferred transition time, with population sizes more than 10 000 appearing to diverge earlier than the truth (figure 1b).
A known, potentially confounding feature of PSMC is that rapid changes in ancestral effective population size are recovered as more gradual transitions [8]. In the context of hPSMC, this means that we cannot apply a purely qualitative approach to estimating population divergence time by increases in inferred ancestral population size. Even using simulated phased data without any post-divergence gene flow (figure 1a) inferred ancestral population size begins to increase gradually before the divergence event. Therefore, we believe that a framework of comparing simulated population divergence events hPSMC results to those for real data (see above) is essential for reliable divergence-time estimation with hPSMC.
Our simulation results also show that hPSMC is highly sensitive to post-divergence gene flow (figure 1c). This sensitivity suggests that the approach may be a useful tool to infer the timing of the end of gene flow between two diverging populations, rather than the time of the initial divergence. As expected from population genetic theory, no divergence is detected when one or more migrants move between populations per generation post-divergence [31,32]. With smaller amounts of gene flow (here, 0.1 migrants per generation), divergence is detected, but the precision of the time estimate of that divergence is less than with no post-divergence migration (figure 1c).
The capacity of hPSMC to capture the end of gene flow between populations differentiates this approach from the more commonly used approach to detecting divergence using PSMC, which is to overlay PSMC plots generated separately for the two parent lineages and infer divergence by detecting shared ancestry [8–12]. Conveniently, these two approaches appear to capture different aspects of the divergence process. Overlaying PSMC plots detects the end of panmixia, whereas hPSMC detects the end of gene flow. Very strong allopatric barriers to gene flow might result in similar estimates of divergence time from these two approaches, as the end of gene flow will occur simultaneously with divergence. However, incomplete isolation or post-divergence gene flow may cause hPSMC to produce divergence estimates that are substantially more recent than those from overlain PSMC. Using hPSMC in conjunction with overlain PSMC plots may therefore provide additional insights into the divergence process, including an indication of the likelihood of post-divergence gene flow.
Like other forms of PSMC-based analysis, hPSMC requires assumptions about the rate of mutation and generation time that can profoundly impact inference. Because the mutation rate is assumed to be constant across the genome, any local variation, as may be due to the effects of purifying or balancing selection, is ignored. In addition, if the assumed mutation rate differs from the true genome-wide average, estimates of divergence times will be skewed proportionally from the true divergence time. In addition, longer generation time estimates produce larger PSMC inferred ancestral population sizes [8]; therefore, incorrect inference of the ancestral population size will affect the inferred range of most likely divergence times. Mutation rates and generation times can be difficult to estimate reliably [30,33–37], and the results of any PSMC-based analysis should be interpreted within the context of these limitations.
While the simulations presented above are based on relatively simple demographic models that assume a lack of post-divergence gene flow, the same simulation framework can be applied to other, more complex demographic scenarios in order to observe the influence of specific demographic parameters on the shape of the hPSMC plot. For example, if we assume models where populations are large at the time of divergence and maintain prolonged post-divergence gene flow, haploidized data produce hPSMC plots that are consistent with a more ancient divergence than the truth (electronic supplementary material, figures S18–S21 and accompanying text). Finally, given the influential role of pre-divergence Ne on haploidized hPSMC plots, it is important that any simulated data used for comparison with a real dataset exhibit the same pre-divergence ancestral population size as the real data.
(a). Great apes
Our hPSMC-based estimates of divergence times within the lineages of great apes (table 1) are mostly similar to estimates produced using different molecular approaches, although variation between the fossil record and molecular estimates of divergence times within the great apes has long made these estimates contentious [30,38]. One surprising result of our analysis is the extremely recent inferred divergence time between chimpanzees and bonobo (table 1). Today, chimpanzees and bonobos are separated by the Congo River, which is thought to have formed approximately 1.5–2 Ma [39] and to be a strong barrier to gene flow [40]. Previous PSMC-based estimates of chimpanzee and bonobo divergence, which were estimated by overlaying PSMC plots, suggested that the two lineages diverged 1.5–3 Ma [11], supporting the hypothesis that the Congo River has always been a strong barrier to gene flow. Our hPSMC results indicate divergence between chimpanzees and bonobos occurred only 350–400 ka, which we hypothesize may reflect the different aspects of the divergence process that are captured by the two PSMC-based methods. Overlaying PSMC plots to estimate divergence assumes that any difference in ancestral population size indicates population divergence. However, population structure and admixture can also produce different ancestral population size estimates without necessarily indicating that gene flow between populations has ended [8]. In contrast, hPSMC is more sensitive to gene flow (figure 1c) and will therefore describe the time when significant gene flow ended. In this context, it can be interpreted that our results suggest that chimpanzees and bonobos may have experienced a long period of population structure with gene flow from 1.5 Ma to 300–450 ka. Interestingly, a comparison of excess allele sharing between a bonobo genome and the genomes of central, eastern and western chimpanzees found no evidence for gene flow between bonobos and any one particular population of chimpanzees [21]. However, the different chimpanzee populations are estimated to have diverged within the last 500 ka [11], and some evidence of post-divergence gene flow between chimpanzee populations has been inferred [11,41]. If gene flow did occur between chimpanzees and bonobos, then it therefore must have occurred prior to the isolation between the three populations of chimpanzees.
Our estimates of the time of divergence between the African great apes (human, chimpanzee, bonobo and gorilla) all have large confidence intervals (table 1). This is in part because the transition from infinite ancestral population sizes to a period of shared ancestry is not as abrupt in these real datasets as it tends to be in simulated datasets (figure 3a). Figure 1c shows that this same phenomenon is observed with low levels of post-divergence gene flow. The wide confidence intervals estimated for divergence among great ape lineages may be partly the result of low levels of post-divergence gene flow near the time of speciation. It is also possible that other violations of the assumptions of PSMC, including purifying selection and variation of mutation rates within or among lineages may influence these results. Another possibility is that hPSMC could be detecting the effect of a genetic mosaic of divergent and non-divergent genomic regions, as may occur when two species speciate via strong divergent selection [42], or speciation under ‘genome hitchhiking’ [43,44]. Future analysis of the patterns of genetic variation and rates of mutation along these lineages will be necessary to fully understand why these observed transitions occur more slowly than expected from simulation.
(b). Bears in the genus Ursus
The timing of divergence between bear lineages in the genus Ursus has been a matter of much recent debate [17,18,24,45–47]. This is due in part to the paucity of fossils representing the early divergence of this lineage [48] and to post-divergence hybridization, which may be common among bears [18,19,24,45]. Molecular estimates of the timing of divergence between polar bears and brown bears range from 300 ka to 5 Ma [17,24]. A recent population genetic analysis of 89 polar and brown bear genomes concluded that these two lineages probably diverged 350–500 ka [24]. In contrast, PSMC-based estimates of the divergence between brown bears and polar bears have failed to identify a period during which the two lineages converged to the same population size [17], which has been interpreted to suggest a very old divergence between the lineages [17].
In our hPSMC analyses, all of the divergences estimated between polar bears and brown bears—both within and between lineages—occur within the last 200 000 years. We hypothesize that these remarkably recent divergences, which disagree with evidence from the fossil record [48], are probably the result of recent admixture among these lineages [18,19,24]. For example, we infer that brown bears in Alaska and Sweden diverged less than 100 000 years ago. Today, Alaskan and European brown bears are isolated by a variety of geographical and physical barriers, including the Bering Strait. During the last ice age, however, brown bears occupied a more or less continuous range from western Europe to Canada's Yukon Territory [45,49]. Data from mitochondrial DNA indicate a major expansion of brown bears out of Beringia beginning around 30–35 ka [45], which may explain the recent gene flow between Swedish and Alaskan brown bears (figure 3b).
Similarly, hPSMC suggests that brown bears and polar bears diverged less than 200 ka (table 1), which is considerably more recent than the timing of divergence inferred using a population genetics approach [24] and more recent than the age of the oldest known polar bear fossil, which dates to approximately 110 ka [50]. The hPSMC-based estimate of divergence is also probably influenced by post-divergence gene flow. Alaskan brown bears, including the individual used in this study, are known to have a small, but variable component of polar bear ancestry as the result of post-divergence hybridization with polar bears within the last 20 ka [18,19]. However, between-species divergences estimated using the Swedish brown bear, which has not been shown to have any polar bear ancestry, also suggest a recent divergence (table 1). This is less well explained, because neither polar bears nor Swedish brown bears have been shown to have detectable introgressed ancestry from the other species [18,24]. However, as the tests used to detect introgression used the Swedish bear as the purportedly un-admixed individual, future work in comparison with other, potentially less admixed, brown bears might reveal some polar bear ancestry in this Swedish brown bear.
5. Conclusion
We have shown that hPSMC or PSMC analysis of simulated F1 hybrid individuals can be used to estimate population divergence times with low-coverage unphased data. hPSMC provides a distinct perspective with regard to divergence than other methods, including overlaying PSMC plots. While overlaying PSMC plots detects the end of panmixia, hPSMC detects the end of gene flow. Very strong allopatric barriers to gene flow might make these two estimates the same. However, incomplete isolation or post-divergence gene flow may cause hPSMC to produce divergence estimates that are substantially more recent than those from overlain PSMC. In our case studies using real data from great apes and bears, we inferred divergence times that were largely consistent with estimates from other methods. However, our assessments of recently diverging lineages—chimpanzees and bonobos and polar bears and brown bears—are suggestive of a divergence process that includes post-divergence gene flow rather than an abrupt transition from panmixia to isolation. While other methods are available to infer the timing of divergence between lineages, such as MSMC [9], diffusion approximations for demographic inference [51] and identity by state tract length [52], most methods for genome based inference of divergence time require high coverage and phased genomic data, often from multiple individuals. hPSMC is particularly useful for estimating divergence time from low-coverage datasets, such as those found in ancient DNA studies, because it does not require the ability to call heterozygous sites or phase haplotypes. We suggest that hPSMC may be a valuable tool for estimating divergence in these common scenarios, and that, in combination with other approaches, can provide important new insights into the process of population subdivision and speciation.
Supplementary Material
Authors' contributions
J.A.C., R.E.G. and B.S. designed the experiment. J.A.C. and A.E.R.S. performed the analyses. All authors contributed to the interpretation of results and writing of the manuscript.
Competing interests
We have no competing interests.
Funding
This work was supported by grants from the Packard Foundation and the Gordon and Betty Moore Foundation.
References
- 1.Kimura M. 1968. Evolutionary rate at the molecular level. Nature 217, 624–626. ( 10.1038/217624a0) [DOI] [PubMed] [Google Scholar]
- 2.Zuckerkandl E, Pauling L. 1962. Molecular disease, evolution, and genic heterogeneity. In Horizons in biochemistry (eds Kasha M, Pullman B), pp. 189–222. New York, NY: Academic Press. [Google Scholar]
- 3.Bromham L, Woolfit M. 2004. Explosive radiations and the reliability of molecular clocks: island endemic radiations as a test case. Syst. Biol. 53, 758–766. ( 10.1080/10635150490522278) [DOI] [PubMed] [Google Scholar]
- 4.Worobey M, Han G-Z, Rambaut A. 2014. A synchronized global sweep of the internal genes of modern avian influenza virus. Nature 508, 254–257. ( 10.1038/nature13016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fleischer-Dogley F, Kettle CJ, Edwards PJ, Ghazoul J, Määttänen K, Kaiser-Bunbury CN. 2011. Morphological and genetic differentiation in populations of the dispersal-limited coco de mer (Lodoicea maldivica): implications for management and conservation. Divers. Distrib. 17, 235–243. ( 10.1111/j.1472-4642.2010.00732.x) [DOI] [Google Scholar]
- 6.Pamilo P, Nei M. 1988. Relationships between gene trees and species trees. Mol. Biol. Evol. 5, 568–583. [DOI] [PubMed] [Google Scholar]
- 7.Hudson RR. 1991. Gene genealogies and the coalescent process. Oxford Surv. Evol. Biol. 7, 1–44. [Google Scholar]
- 8.Li H, Durbin R. 2011. Inference of human population history from individual whole-genome sequences. Nature 475, 493–496. ( 10.1038/nature10231) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schiffels S, Durbin R. 2014. Inferring human population size and separation history from multiple genome sequences. Nat. Genet. 46, 919–925. ( 10.1038/ng.3015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lamichhaney S, et al. 2015. Evolution of Darwin's finches and their beaks revealed by genome sequencing. Nature 518, 371–375. ( 10.1038/nature14181) [DOI] [PubMed] [Google Scholar]
- 11.Prado-Martinez J, et al. 2013. Great ape genetic diversity and population history. Nature 499, 471–475. ( 10.1038/nature12228) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Prüfer K, et al. 2014. The complete genome sequence of a Neanderthal from the Altai Mountains. Nature 505, 43–49. ( 10.1038/nature12886) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Freedman AH, et al. 2014. Genome sequencing highlights the dynamic early history of dogs. PLoS Genet. 10, e1004016 ( 10.1371/journal.pgen.1004016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hudson RR. 2002. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics 18, 337–338. ( 10.1093/bioinformatics/18.2.337) [DOI] [PubMed] [Google Scholar]
- 15.Green RE, et al. 2010. A draft sequence of the Neanderthal genome. Science 328, 710–722. ( 10.1126/science.1188021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nielsen R, Paul JS, Albrechtsen A, Song YS. 2011. Genotype and SNP calling from next-generation sequencing data. Nat. Rev. Genet. 12, 443–451. ( 10.1038/nrg2986) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller W, et al. 2012. Polar and brown bear genomes reveal ancient admixture and demographic footprints of past climate change. Proc. Natl Acad. Sci. USA 109, E2382–E2390. ( 10.1073/pnas.1210506109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cahill JA, et al. 2013. Genomic evidence for island population conversion resolves conflicting theories of polar bear evolution. PLoS Genet. 9, e1003345 ( 10.1371/journal.pgen.1003345) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cahill JA, Stirling I, Kistler L, Salamzade R, Ersmark E, Fulton TL, Stiller M, Green RE, Shapiro B. 2014. Genomic evidence of geographically widespread effect of gene flow from polar bears into brown bears. Mol. Ecol. 24, 1205–1217. ( 10.1111/mec.13038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eberle M, Kallberg M, Chuang H-Y, Tedder P, Humphray S, Bentley D, Margulies E. 2013. Platinum Genomes: a systematic assessment of variant accuracy using a large family pedigree. In 60th Annu. Meet. Am. Soc. Human Genet., 22–26 November, Boston, MA. [Google Scholar]
- 21.Prüfer K, et al. 2012. The bonobo genome compared with the chimpanzee and human genomes. Nature 486, 527–531. ( 10.1038/nature11128) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cortez D, Marin R, Toledo-Flores D, Froidevaux L, Liechti A, Waters PD, Grützner F, Kaessmann H. 2014. Origins and functional evolution of Y chromosomes across mammals. Nature 508, 488–493. ( 10.1038/nature13151) [DOI] [PubMed] [Google Scholar]
- 23.Li B, Zhang G, Willersleve E, Wang J.2011. GigaDB dataset—genomic data from the polar bear ( Ursus maritimus ). GigaScience . ( ) [DOI]
- 24.Liu S, et al. 2014. Population genomics reveal recent speciation and rapid evolutionary adaptation in polar bears. Cell 157, 785–794. ( 10.1016/j.cell.2014.03.054) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.International Human Genome Sequencing Consortium. 2001. Initial sequencing and analysis of the human genome. Nature 412, 860–921. ( 10.1038/35057062) [DOI] [PubMed] [Google Scholar]
- 26.Li H. 2013. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. arXiv:1303.3997v2 [q-bio.GN].
- 27.Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R. 2009. The sequence alignment/map format and SAMtools. Bioinformatics 25, 2078–2079. ( 10.1093/bioinformatics/btp352) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schliebe S, Wiig Ø, Derocher A, Lunn N, orp(IUCN SSC Polar Bear Specialist Group) 2008. Ursus maritimus (polar bear). IUCN red list of threatened species. http://www.iucnredlist.org/details/22823/0.
- 29.Nachman MW, Crowell SL. 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156, 297–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Langergraber KE, et al. 2012. Generation times in wild chimpanzees and gorillas suggest earlier divergence times in great ape and human evolution. Proc. Natl Acad. Sci. USA 109, 15 716–15 721. ( 10.1073/pnas.1211740109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wright S. 1931. Evolution in Mendelian populations. Genetics 16, 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Slatkin M. 1987. Gene flow and the geographic structure of natural populations. Science 236, 787–792. ( 10.1126/science.3576198) [DOI] [PubMed] [Google Scholar]
- 33.Zhu YO, Siegal ML, Hall DW, Petrov DA. 2014. Precise estimates of mutation rate and spectrum in yeast. Proc. Natl Acad. Sci. USA 111, E2310–E2318. ( 10.1073/pnas.1323011111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Conrad DF, et al. 2011. Variation in genome-wide mutation rates within and between human families. Nat. Genet. 43, 712–714. ( 10.1038/ng.862) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tremblay M, Vézina H. 2000. New estimates of intergenerational time intervals for the calculation of age and origins of mutations. Am. J. Hum. Genet. 66, 651–658. ( 10.1086/302770) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hobolth A, Christensen OF, Mailund T, Schierup MH. 2007. Genomic relationships and speciation times of human, chimpanzee, and gorilla inferred from a coalescent hidden Markov model. PLoS Genet. 3, e7 ( 10.1371/journal.pgen.0030007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Helgason A, Hrafnkelsson B, Gulcher JR, Ward R, Stefánsson K. 2003. A populationwide coalescent analysis of Icelandic matrilineal and patrilineal genealogies: evidence for a faster evolutionary rate of mtDNA lineages than Y chromosomes. Am. J. Hum. Genet. 72, 1370–1388. ( 10.1086/375453) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Green RE, Shapiro B. 2013. Human evolution: turning back the clock. Curr. Biol. 23, R286–R288. ( 10.1016/j.cub.2013.02.050) [DOI] [PubMed] [Google Scholar]
- 39.Beadle LC. 1981. Inland waters of tropical Africa. New York, NY: Longman. [Google Scholar]
- 40.Myers Thompson JA. 2003. A model of the biogeographical journey from Proto-pan to Pan paniscus. Primates 44, 191–197. ( 10.1007/s10329-002-0029-1) [DOI] [PubMed] [Google Scholar]
- 41.Won Y-J, Hey J. 2005. Divergence population genetics of chimpanzees. Mol. Biol. Evol. 22, 297–307. ( 10.1093/molbev/msi017) [DOI] [PubMed] [Google Scholar]
- 42.Via S. 2012. Divergence hitchhiking and the spread of genomic isolation during ecological speciation-with-gene-flow. Phil. Trans. R. Soc. B 367, 451–460. ( 10.1098/rstb.2011.0260) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Feder JL, Egan SP, Nosil P. 2012. The genomics of speciation-with-gene-flow. Trends Genet. 28, 342–350. ( 10.1016/j.tig.2012.03.009) [DOI] [PubMed] [Google Scholar]
- 44.Nosil P, Harmon LJ, Seehausen O. 2009. Ecological explanations for (incomplete) speciation. Trends Ecol. Evol. 24, 145–156. ( 10.1016/j.tree.2008.10.011) [DOI] [PubMed] [Google Scholar]
- 45.Edwards CJ, et al. 2011. Ancient hybridization and an Irish origin for the modern polar bear matriline. Curr. Biol. 21, 1251–1258. ( 10.1016/j.cub.2011.05.058) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cronin MA, McDonough MM, Huynh HM, Baker RJ. 2013. Genetic relationships of North American bears (Ursus) inferred from amplified fragment length polymorphisms and mitochondrial DNA sequences. Can. J. Zool. 91, 626–634. ( 10.1139/cjz-2013-0078) [DOI] [Google Scholar]
- 47.Cronin MA, Amstrup SC, Garner GW, Vyse ER. 1991. Interspecific and intraspecific mitochondrial DNA variation in North American bears (Ursus). Can. J. Zool. 69, 2985–2992. ( 10.1139/z91-421) [DOI] [Google Scholar]
- 48.Wayne R, Van Valkenburgh B, O'Brien S. 1991. Molecular distance and divergence time in carnivores and primates. Mol. Biol. Evol. 8, 297–319. [DOI] [PubMed] [Google Scholar]
- 49.Barnes I, Matheus P, Shapiro B, Jensen D, Cooper A. 2002. Dynamics of Pleistocene population extinctions in Beringian brown bears. Science 295, 2267–2270. ( 10.1126/science.1067814) [DOI] [PubMed] [Google Scholar]
- 50.Ingólfsson Ó, Wiig Ø. 2009. Late Pleistocene fossil find in Svalbard: the oldest remains of a polar bear (Ursus maritimus Phipps, 1744) ever discovered. Polar Res. 28, 455–462. ( 10.1111/j.1751-8369.2008.00087.x) [DOI] [Google Scholar]
- 51.Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. 2009. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5, e1000695 ( 10.1371/journal.pgen.1000695) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Harris K, Nielsen R. 2013. Inferring demographic history from a spectrum of shared haplotype lengths. PLoS Genet. 9, e1003521 ( 10.1371/journal.pgen.1003521) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.