Heterodyne frequency-domain multispectral diffuse optical tomography of breast cancer in the parallel-plane transmission geometry

Abstract

Purpose:

The authors introduce a state-of-the-art all-optical clinical diffuse optical tomography (DOT) imaging instrument which collects spatially dense, multispectral, frequency-domain breast data in the parallel-plate geometry.

Methods:

The instrument utilizes a CCD-based heterodyne detection scheme that permits massively parallel detection of diffuse photon density wave amplitude and phase for a large number of source–detector pairs (10⁶). The stand-alone clinical DOT instrument thus offers high spatial resolution with reduced crosstalk between absorption and scattering. Other novel features include a fringe profilometry system for breast boundary segmentation, real-time data normalization, and a patient bed design which permits both axial and sagittal breast measurements.

Results:

The authors validated the instrument using tissue simulating phantoms with two different chromophore-containing targets and one scattering target. The authors also demonstrated the instrument in a case study breast cancer patient; the reconstructed 3D image of endogenous chromophores and scattering gave tumor localization in agreement with MRI.

Conclusions:

Imaging with a novel parallel-plate DOT breast imager that employs highly parallel, high-resolution CCD detection in the frequency-domain was demonstrated.

1. INTRODUCTION

Breast cancer is the second most commonly diagnosed cancer and the second leading cause of cancer death in the United States.¹ While the mortality rate of breast cancer has decreased significantly in recent years, the overall number of women affected remains large.

Presently, many imaging modalities are in use for the detection, diagnosis, and management of breast cancer; each technique has advantages and disadvantages. X-ray mammography employs ionizing photons to create high resolution projection images. Its relatively low cost and high patient throughput has made this modality the most common screening tool for breast cancer. However, x-ray mammography has limited sensitivity [e.g., ∼35% in women under 50 (Ref. 2)], especially in women with radiographically dense breasts;^3–5 the diagnostic technique also exposes women to ionizing radiation. Contrast-enhanced MRI screening is much more sensitive than mammography (∼85%),⁶ but it is also much more expensive, time consuming, and less common in the clinic. Moreover, many women with metallic implants or kidney failure are excluded from contrast-enhanced MRI. Finally, ultrasound tools have not yet been demonstrated to be sufficient for screening applications.⁷ Thus, potential roles for diffuse optical tomography (DOT) in screening of subpopulations (e.g., radiographically dense breasts) are apparent, and since DOT does not use ionizing radiation, it can be readily applied as a supplement to x-ray mammography in women with high risk of developing breast cancer (e.g., as determined by the Gail model).^8,9 These women will be screened more frequently than the remainder of the population, and they start screening at a younger age; thus, they will receive a larger x-ray dose from screening over their lifetimes.

After lesion identification, the techniques of MRI, ultrasound, x-ray computed tomography or tomosynthesis, and PET can all be applied to stage the malignancy. These tools, however, often rely on tissue structure rather than function (x-ray, ultrasound), can be relatively expensive (MRI, PET), will expose women to additional ionizing radiation (x-ray, PET), and often have comparatively low patient throughput (ultrasound, PET, MRI). Moreover, several authors have demonstrated that optical monitoring of a lesion throughout therapy (e.g., neoadjuvant chemotherapy) can predict the final pathological response earlier than established tools.^10–15 Thus, there is a current clinical need to expand the range of cancer screening options, especially for specific subpopulations and in staging lesions by tissue function or metabolism, rather than by tissue structure.^12,16–22

DOT mammography utilizes an array of near-infrared (NIR) light sources and detectors on the tissue surface to illuminate and probe breast tissue. In DOT, these transmitted light fluence rate signals provide the data needed for computational reconstruction of the 3D distribution of tissue scattering and absorption. Further, spectroscopic information from data collected at several wavelengths can be utilized to reconstruct tomograms of intrinsic or extrinsic chromophore concentrations in tissue and tissue scattering parameters.^23,24 The primary endogenous breast tissue chromophores (in the NIR) are oxy- and deoxyhemoglobin.²⁵ These spatial maps provide insight into local tissue function, e.g., heightened local hemoglobin concentrations may identify angiogenic regions. Previous work has demonstrated that DOT can be used to differentiate malignant and benign tumors,^{13,22,26–30} and that it holds potential to provide statistical separation of complete responders and partial responders and thereby inform chemotherapy treatments.^{14,15,31–33} Notably, DOT’s lack of ionizing radiation permits serial imaging throughout the course of therapy, potentially permitting dynamic optimization of therapy for individual patients.

Although other geometries have been used,^34–36 DOT systems for breast cancer typically utilize an imaging geometry which spatially distributes sources and detectors circumferentially (ring, fiber optic delivery)^37–42 or in parallel-planes.^22,43–46 In addition to the imaging geometry, these systems can differ by data type. Time-domain (TD) systems utilize temporal broadening of ∼100 ps pulses of light transiting tissue to obtain tissue optical properties (scattering and absorption) as a function of wavelength. Frequency-domain (FD) systems are the Fourier analog of the TD systems, wherein input signals are amplitude modulated (e.g., at ∼100 MHz), and the phase shifts and attenuation of the transmitted signal are captured.⁴⁷ Lastly, continuous wave (CW) acquisition systems measure only attenuation; CW data cannot fully separate tissue scattering and absorbing properties, though this limitation can be partially ameliorated using a multispectral approach.^23,48 DOT imaging systems thus vary in the combination of multispectral implementations, data-type, and source–detector arrangements, thereby requiring trade-offs involving cost, information content, and speed.

The DOT instrumentation to be presented and demonstrated herein builds on lessons learned from previous systems,^22,24,49 which utilized a small number of FD remission measurements at multiple wavelengths to measure bulk optical properties, along with many multispectral CW measurements in transmission in order to reconstruct relative chromophore concentrations and scattering parameters. The present instrument implements a CCD-based gain-modulated heterodyne detection scheme,^50–53 thereby generating very large FD data sets at a high spatial sampling density (approximately 10⁶ source–detector pairs) in 35 min/scan; to our knowledge, the device provides the largest DOT data set reported in a clinical setting. The primary advantage of the camera-based system over fiber-based systems is full coverage of the breast with a higher density of source–detector pairs; other advantages are more subtle, e.g., more source–detector pairs offer more measurement redundancy which helps to flag unanticipated systematic and random errors and which can improve data fidelity through adjustable spatial averaging. Further, the present instrument implements dual 3D profilometry systems permitting the determination of the breast boundary, real-time signal normalization, and independent regularization of absorption and scattering in the DOT reconstruction algorithm for improved image contrasts.

From the data, 3D tomographic images of chromophore concentrations and scattering parameters are reconstructed using a model-based iterative optimization approach that accounts for the nonlinearity and ill-posedness of the inverse problem. This inversion was performed with the toast++ software package,⁵⁴ which employs a finite-element model to simulate light propagation in highly scattering inhomogeneous media by numerically solving the frequency-domain diffusion equation. Reconstruction is then performed by a nonlinear conjugate gradient solver that iteratively minimizes a norm of the difference between model and measurement data by adjusting the model parameters. A regularization term is added to the cost function to control high-frequency noise artifacts in the reconstructed images. Notably, spatially dependent regularization was not used.

Herein we discuss the new instrumentation and present imaging results from phantom experiments used to optimize our reconstructions and demonstrate the ability to separate absorption/scattering contrasts as well as detect multiple chromophores. We also present an image reconstruction from a breast cancer patient showing endogenous contrast and exhibiting spatial agreement with MRI images taken of the same patient.

2. EXPERIMENT

2.A. Clinical breast imager

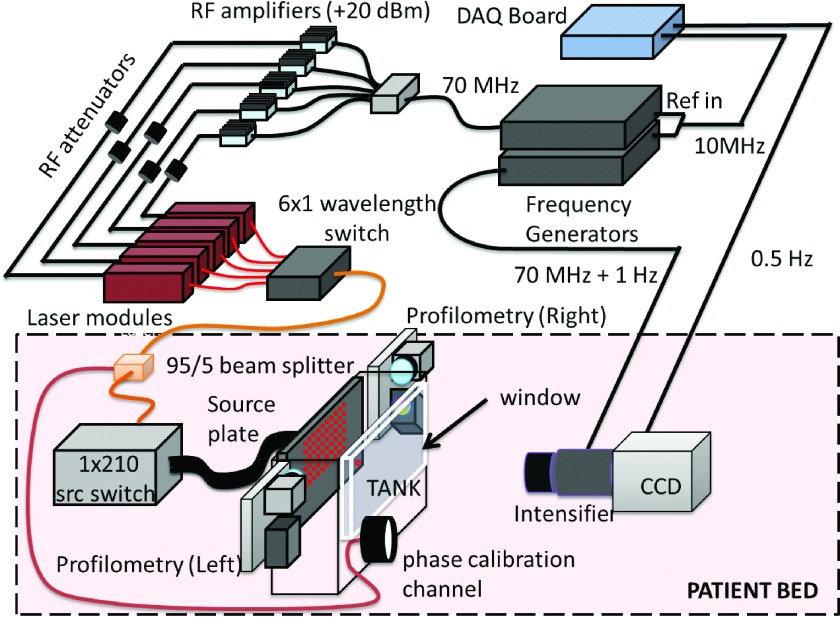
The DOT breast imager currently resides in the Perelman Center for Advanced Medicine at the University of Pennsylvania. A schematic of the instrument components is shown in Fig. 1. Briefly, the source component of the imager consists of five fiber-coupled and amplitude-modulated lasers (660, 690, 785, 808, and 830 nm) connected to a piezoelectric optical switch (Piezojena, FiberSwitch MM 6 × 1). The output from this wavelength switch is then connected to a custom 1x210 channel galvanometer source position switch. The outputs from the position switch are coupled to 600 μm diameter fibers, the distal ends of which are arranged in an 11 × 19 rectangular grid (8 mm spacing) on one side of the imaging volume. The switch time between sources is <2 ms, and the optical power at the breast surface is approximately 16 mW (or less) for all wavelengths and sources. We note that the position switch permits individualized optimization of the spatial extent of data collection and thus offers the possibility for reduced data collection time; however, we did not explore this optimization in the initial demonstration of the instrument.

FIG. 1.

Schematic of DOT breast imager. Five RF modulated (70 MHz) laser modules are switched through each source position (in series) to yield multispectral data. A 210 channel spatial position switch directs laser light to 209 source positions and to a calibration source channel on the input plate. The patient breast is inserted in the tank between the source plate and window. Profilometry devices on both sides of the tank image the surface of the breast. Light exiting the tank window is measured by a RF gain-modulated (70 MHz + 1 Hz) image intensifier and CCD. The acquisition cycles through source positions at a rate of 0.5 Hz.

In order to reduce the dynamic range required for the detectors and to minimize air boundaries, the breast is immersed in a matching fluid of dilute Intralipid (Baxter) with optical properties similar to breast tissue. In the transmission geometry, source positions are located in a rectangular grid on one of the compression plates, and the opposite plate is imaged with a CCD detection system (Fig. 1). Light from the source fibers travels through the breast and Intralipid-ink matching solution in the tank and exits through an antireflection coated imaging window. The detection system consists of a Xenon 25 mm f/0.95 C-Mount Lens (Schneider Optics, Germany) placed in front of an RF gain-modulated image intensifier- (Lambert Instruments, II8MD) mounted CCD (Andor, iXon DV887).

At a typical plate separation of 6 cm and a maximum source–detector distance of 9 cm (due to signal-to-noise), a limited-angle cone-beam geometry with cone aperture of 96° is achieved. The system also utilizes ancillary light sources for data correction and normalization. In order to calibrate for drifts in the amplitude due to systematic and random fluctuations of the apparatus, one (additional) source fiber is taken from the spatial position switch and is attached to the source plate at a position far from other source fibers and from the breast location. Further, a 95/5 fiber beam splitter is employed between the wavelength switch and the spatial position switch in order to route a source beam to the front of the imaging window for another concurrent measurement that enables correction for phase drifts. Motion artifacts are ameliorated by the gentle compression of the breast and by the increased patient comfort facilitated by design improvements of the imaging platform. Importantly, the data normalization (see Sec. 2.D) and the main system camera can detect motion when it occurs, and this information provides a means for the removal of data with possible artifacts from the analysis.

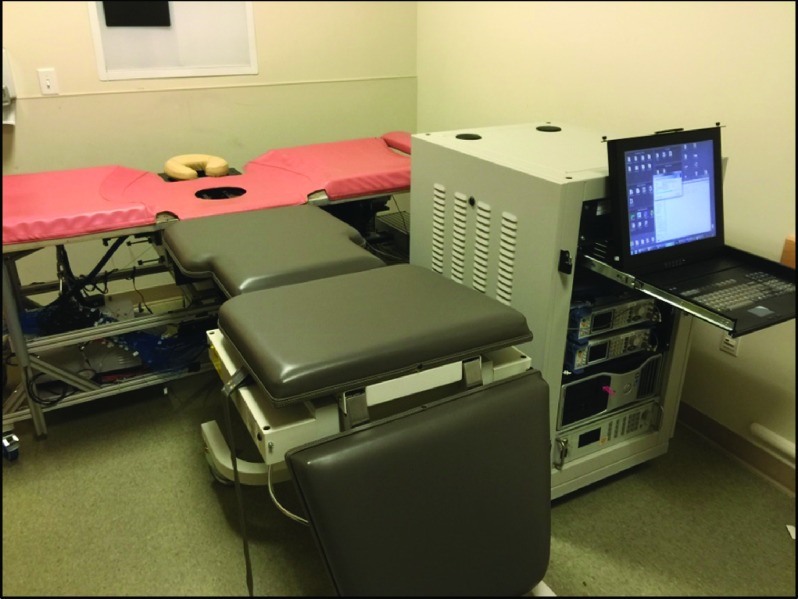
Photographs of the system in the patient room are shown in Fig. 2. The patient lies prone on the gray bed (for sagittal compression) or perpendicularly along the biopsy bed (axial). One breast is inserted into the breast tank. It is held in a soft compression (typically 6 cm) between a translatable source plate and a window. The imaging platform and instrument rack are displayed in Fig. 3 with the optical, mechanical, and electrical components labeled.

FIG. 2.

The breast imaging instrumentation in the mammography wing of Perelman Center for Advanced Medicine at the Hospital of the University of Pennsylvania (HUP). The photo shows the DOT instrument setup for patient measurement. The patient lies in the prone position with her head on the head rest and her body along the gray exam table (sagittal) or along the orange biopsy bed (axial). (See color online version.)

FIG. 3.

Breast imaging instrumentation in the mammography wing of the Perelman Center for Advanced Medicine at the Hospital of the University of Pennsylvania showing the various components of the instrument inside the patient bed (left) and the instrument rack (right).

2.B. Frequency-domain heterodyne detection

Frequency-domain DOT systems utilize light that is amplitude-modulated at radio frequencies. These sources produce diffuse photon density waves in turbid media.^55,56 Detectors must capture both the amplitude of the modulated signal (“AC,” in analogy to electrical current) and its phase. This modulation occurs in addition to a constant offset (“DC”). In homodyne systems, detection must be fast enough to capture the modulation (typically 70–100 MHz).^50,57,58 In the present instrument, we apply a heterodyne approach wherein the source is modulated at f_s = 70 MHz and the detector gain is modulated at a frequency with a slight offset (f_d = f_s + f_cc, where f_cc = 1 Hz). The heterodyne approach typically has better signal-to-noise than homodyne schemes because a low pass filter can be applied to isolate the signal and because detection is carried out at the cross-correlation frequency (f_cc = 1 Hz).⁴⁷ Heterodyne detection schemes are also better able to concurrently monitor and correct for amplitude and phase variation (e.g., as with our phase correction source), thereby facilitating correction for instrumental drifts over the measurement period.

The modulation frequencies at f_s and f_d are derived from a pair of phase-locked frequency generators (Rohde and Schwarz, SMA100A). The lasers are amplitude-modulated at a frequency of f_s = 70 MHz; thus the light source power density at the source fiber is given by

$${\displaystyle S_s({\mathbf{r}}_s,t)=S_{\mathrm{dc}}\left({\mathbf{r}}_s\right)+S_{\mathrm{ac}}\left({\mathbf{r}}_s\right)cos\left(2\pi f_{s}t\right).}$$ (1)

Here r_s denotes the spatial position of the source. The measured fluence rate, Φ, after the light passes through the sample in the tank is given by

$${\displaystyle \mathrm{\Phi }({\mathbf{r}}_s,{\mathbf{r}}_d,t)={\mathrm{\Phi }}_{\mathrm{dc}}({\mathbf{r}}_s,{\mathbf{r}}_d)+{\mathrm{\Phi }}_{\mathrm{ac}}({\mathbf{r}}_s,{\mathbf{r}}_d)cos\left(2\pi f_{s}t+\theta ({\mathbf{r}}_s,{\mathbf{r}}_d)\right),}$$ (2)

wherein Φ_dc, Φ_ac, and θ represent the DC amplitude, AC amplitude, and AC phase shift, respectively. Their values are dependent on the optical properties of the medium, the source position r_s, and the detector position r_d. Henceforth, we will drop explicit reference to r_s and r_d in these expressions and assume that the equations refer to diffuse light measured for a specific source–detector pair (i.e., corresponding to a single light source and a single pixel detector); these omissions simplify notation in the equations below.

By under-driving the gain-modulation of the image intensifier, we are able to produce a gated gain curve with frequency f_d; the gain modulation is essentially a series of pulses with narrow time-width and a repetition period set by the reciprocal of f_d. This gain modulation can be modeled as a Dirac comb with peaks at t = nT_d, where T_d = 1/f_d and n is an integer. This method is a commonly used technique for gated detection and sampling. The equation for the gain, in this case, is

$${\displaystyle G\left(t\right)\equiv \sum _{n=-\infty }^{\infty }{G}_0\hspace{0.17em}\delta (t-n{T}_d).}$$ (3)

Here G₀ is an effective gain constant which will ultimately be normalized. The measured signal, M, at the CCD is therefore the product of Eqs. (2) and (3),

$${\displaystyle M\left(t\right)=\mathrm{\Phi }\left(t\right)G\left(t\right)=\left({\mathrm{\Phi }}_{\mathrm{dc}}+{\mathrm{\Phi }}_{\mathrm{ac}}cos(2\pi f_{s}t+\theta )\right)\times \left(\sum _{n=-\infty }^{\infty }{G}_0\hspace{0.17em}\delta (t-n{T}_d)\right),}$$

$${\displaystyle M\left(t\right)=\frac{G_0}{T_d}({\mathrm{\Phi }}_{\mathrm{dc}}+{\mathrm{\Phi }}_{\mathrm{ac}}cos(2\pi (f_s+f_{\mathrm{cc}})t+\theta ))+\frac{G_0{\mathrm{\Phi }}_{\mathrm{dc}}}{2T_d}cos\left(2\pi f_{s}t\right)+\frac{G_0{\mathrm{\Phi }}_{\mathrm{ac}}}{4T_d}cos(2\pi (2f_s+f_{\mathrm{cc}})t+\theta )+\frac{G_0{\mathrm{\Phi }}_{\mathrm{ac}}}{4T_d}cos(2\pi \left(f_{\mathrm{cc}}\right)t+\theta )+\frac{G_0}{T_d}\sum _{n=2}^{\infty }\left[\frac{G_0{\mathrm{\Phi }}_{\mathrm{dc}}}{2}cos\left(2\pi n{f}_{s}t\right)\right.+\frac{G_0{\mathrm{\Phi }}_{\mathrm{ac}}}{4}\left(cos(2\pi (f_s-n{f}_d)t+\theta )\right.+\left.cos(2\pi (f_s+n{f}_d)t+\theta )\left.\right)\right].}$$ (4)

Equation (4) gives the light fluence-rate incident on the CCD for a given pixel. Note that a DC and a 1 Hz difference frequency term arise. All other terms oscillate at a frequency of ∼70 MHz or greater. Since the response time of the detection is limited by our CCD exposure time (∼100 ms), the terms with modulation frequencies greater than 10 Hz will average to zero and leave us with

$${\displaystyle M\left(t\right)\propto G_0{\mathrm{\Phi }}_{\mathrm{dc}}+\frac{G_0{\mathrm{\Phi }}_{\mathrm{ac}}}{4}cos(2\pi f_{\mathrm{cc}}t+\theta ).}$$ (5)

Equation (5) is used to determine Φ_dc, Φ_ac, and θ from the raw data; these parameters, in turn, are utilized in our reconstruction.

2.C. Breast profilometry

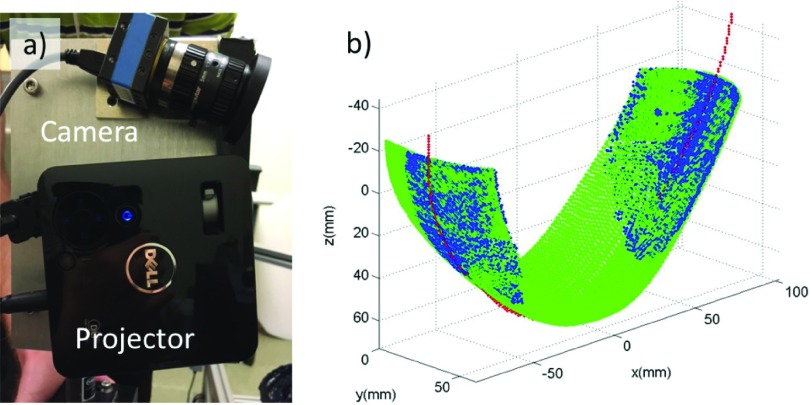
Information about the breast boundary facilitates 3D segmentation for image reconstruction. Other systems acquired such information using a 3D camera.⁶⁸ This imager employs two sets of profilometry cameras and projectors that utilize fringe projection profilometry techniques^59,60 to determine the breast boundary. The profilometry apparatus used in the DOT imager system is shown in Fig. 4(a). Each unit consists of a projector (M110, Dell) and a small CMOS camera (DMK 72AUC02, The Imaging Source) with a 5 mm lens (H0514-MP2, The Imaging Source) mounted on a custom aluminum block on both sides (i.e., between the source and detection plates) of the imaging volume.

FIG. 4.

Profilometry data used to determine breast boundary. (a) Photograph of the camera and projector with custom mount. (b) 3D point cloud generated by fringe profilometry (blue), and the breast outline trace (red) from the front CCD camera scaled and translated to match side surfaces. The point cloud and the trace are used to generate a 3D surface fit for the whole breast (green) which will be employed for image segmentation in the reconstructions. (See color online version.)

The profilometry apparatus uses a phase-shift fringe projection technique to obtain 3-D coordinates of points on the breast surface. Specifically, a sequence of sinusoidal light intensity fringe patterns (with preselected spatial phase-shifts) are projected onto the inferior side of the breast. The camera captures images of these fringe patterns from the breast surface. The measured phase at each camera pixel determines a 2-D matrix of phases (i.e., the phase map). Each element in the phase map corresponds to a point on the surface of the breast. By using calibration data from the camera–projector system with an object of known size and location, each number in the phase map matrix can be transformed into a physical point on the surface of the breast. This procedure is then repeated on the superior side of the breast, and thus, two 3-D clouds of points on the breast surface are created. In most cases, at least some portion of the breast is obscured from the profilometry system. To generate a profile of this region of the breast surface, another image is taken using the primary (CCD) camera; this image derives an outline of the bottom of the breast. Combining this outline with the two point-clouds (i.e., from the superior and inferior profilometry measurements) enables surface fitting, from which a map of the entire breast surface is derived.

2.D. Data normalization

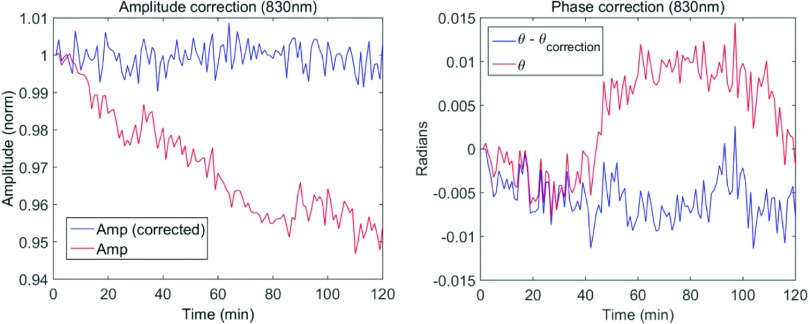
Two types of normalization methods are used to compensate for the drift in the amplitude and phase over the course of the imaging scan (due to temperature changes, movement in the fibers, etc). To correct for the slow amplitude drifts, we use an additional source fiber placed far from the breast that is measured after every 10th source position measurement. In addition, a fraction of the light entering the position switch is split off and concurrently measured with each individual measurement to correct for any fluctuations in the phase due to components upstream of the imaging volume. The results of these correction methods are shown in Fig. 5. Note that this per-measurement correction of phase drift is one advantage of heterodyne detection. Individual differences in measurements between source fibers and detector positions were normalized via measurement of a homogeneous reference phantom, as described in Sec. 3.D.

FIG. 5.

Time series data showing real-time data normalization methods used for the amplitude (left) and phase (right). The red curve is the uncorrected signal, and the blue curve is the corrected curve. The amplitude is corrected using the calibration source and the phase is corrected with the phase calibration channel. The data here are actually down-sampled signals, i.e., they are obtained by averaging over four adjacent pixels. (See color online version.)

3. THEORY

For 3D image reconstruction of chromophore concentrations and scattering parameters inside the phantoms and breast tissue, we employ a multispectral nonlinear iterative optimization scheme based on the minimization of an objective function Ψ consisting of a weighted data fit term (likelihood) and a regularization term (prior),

$${\displaystyle \mathrm{\Psi }\left(\mathbf{X}\right)={‖\frac{F\left(\mathbf{X}\right)-{\mathbf{Y}}^{\left(\mathrm{meas}\right)}}{\sigma }‖}^2+\tau R\left(\mathbf{X}\right).}$$ (6)

Here X is the vector of coefficients of the discretized set of reconstructed parameters, F is a forward model for light propagation in the inhomogeneous scattering media, Y^(meas) is the vector of measurements, σ is a vector of measurement confidence estimates, R is a regularization functional, and τ is the regularization hyperparameter.

Since our measurements are made in the frequency-domain, we use the diffusion equation in the frequency-domain as the light transport model F, implemented with a finite element method, and provided by the toast++ modeling and reconstruction software suite.⁵⁴ The forward model simulates the measurement system by computing logarithmic amplitude and phase shift for given nodal model parameters at each wavelength for each source at the transmission surface. The reconstruction scheme then employs a Polak–Ribiere scheme to iteratively minimize the objective function [Eq. (6)].

It should be further noted that we apply a multispectral reconstruction strategy²⁴ that directly reconstructs the chromophore concentrations c_i and parameters A and b of the scattering model. This approach helps to constrain the inverse problem. The scheme applies parameter transformations of the form

$${\displaystyle {\mu }_a\left(\lambda \right)={\mu }_a^{\left(\mathrm{bkg}\right)}\left(\lambda \right)+\sum _{i=1}^D{c}_i{ϵ}_i\left(\lambda \right),{\mu }_s\left(\lambda \right)=A{\lambda }^{-b}}$$ (7)

that map the absorption coefficient μ_a and scattering coefficient μ_s at a given wavelength λ to the model parameters c_i, A, b, given extinction spectra ϵ_i for all D reconstructed chromophores. ${\mu }_a^{\left(\mathrm{bkg}\right)}$ denotes the background absorption consisting of any chromophores that are assumed known and are excluded from the reconstruction. The coefficient vector X then consists of the discretized values of c_i, A, b, and the transformation Eq. (7) is used to map to optical coefficients μ_a, μ_s for evaluation of F at each input wavelength λ.

In order to prepare the measurement data obtained from the frequency-domain imaging system for the image reconstruction procedure, a number of data preprocessing steps are applied.

3.A. Data and parameter transformations

The frequency-domain diffusion equation evaluates a complex-valued surface exitance J⁺. To match the model to the data, Φ_ac and θ provided by the data acquisition system, we perform the transformation

$${\displaystyle ln\hspace{0.17em}{\mathrm{\Phi }}_{\mathrm{ac}}=Re(ln{J}^{+}),\theta =Im(ln{J}^{+}),}$$ (8)

and Y is composed of ln Φ_ac,  θ pairs for all sources at all CCD pixels for all measurement wavelengths. Likewise, the parameter space is rescaled by mapping to logarithmic parameters,

$${\displaystyle \hat{\mathbf{X}}=ln\hspace{0.17em}\mathbf{X}.}$$ (9)

This logarithmic rescaling ensures positivity of the recovered parameters. The gradients $\hat{\mathbf{r}}$ of the transformed parameter vector are given by

$${\displaystyle \hat{\mathbf{r}}=\frac{\partial \mathrm{\Psi }}{\partial \hat{\mathbf{X}}}=\mathbf{X}\frac{\partial \mathrm{\Psi }}{\partial \mathbf{X}}.}$$ (10)

3.B. Data confidence estimates

The confidence values σ in Eq. (6) are computed from estimates of the standard deviation of the measurement values. We expect (and assume) that the standard deviation of the reference measurements on a homogeneous medium is a function of the distance between source and detector location; it is larger for larger source–detector separations wherein signal levels are smaller. In practice, for each source and each wavelength, CCD reference measurements of ln Φ_ac and θ are collected in 1 mm wide bins according to distance d to source position. The standard deviations for each bin are computed assuming a normal distribution, and an estimate of σ(d) is obtained by linear interpolation between each bin. The corresponding σ value is then assigned to each CCD measurement.

3.C. Data subsampling and smoothing

After transformation of the gated raw CCD images to frequency-domain data and cropping of the image, the measurement data consist of a grid of 147 × 219 log-amplitude and phase measurements for each of the 209 source positions. This grid was cropped to a 96 × 168 grid to eliminate boundary effects for measurements close to the tank boundaries and interfaces. The resulting data grid was further smoothed and down-sampled with a Gaussian filter to a 12 × 21 grid.

For each source position, a cutoff source–detector distance of 90 mm is applied to eliminate measurements with insufficient signal-to-noise ratio. At a sample thickness of 60 mm, this approach produces a cone-beam geometry with a cone aperture of 96°.

An 11 × 19 = 209 grid of source positions was used for the reconstructions resulting in data sets consisting of 22 511 log amplitude and phase measurements for each of the five wavelengths.

3.D. Difference reconstruction

To compensate for unknown systematic measurement errors and discrepancies that cannot be incorporated into the model, such as losses in optical fibers and at interfaces, a reference measurement Y^(ref) on a homogeneous phantom was performed in addition to the target measurement Y^(tgt), and the reconstruction was carried out based on the difference between the target and reference data. The reference measurement was simulated with the forward model, given the estimates of the optical properties X^(ref) of the reference material. The reconstruction then operated on an adjusted data set ${\tilde{\mathbf{Y}}}^{\left(\mathrm{meas}\right)}$ given by

$${\displaystyle {\tilde{\mathbf{Y}}}^{\left(\mathrm{meas}\right)}={\mathbf{Y}}^{\left(\mathrm{tgt}\right)}-{\mathbf{Y}}^{\left(\mathrm{ref}\right)}+F\left({\mathbf{X}}^{\left(\mathrm{ref}\right)}\right).}$$ (11)

3.E. Regularization

Reconstruction requires inclusion of a regularization term R(x) in the cost function to account for the ill-posedness of the problem and the presence of measurement errors. In essence, regularization constrains the space of unknowns by penalizing certain types of solutions from the candidate distributions.

We consider R to be of the form

$${\displaystyle R\left(x\right)={\int }_{\mathrm{\Omega }}r\left(\right|\nabla x\left|\right)dr,}$$ (12)

where r is an image-to-image mapping and

$${\displaystyle \left|\nabla x\right|=\sqrt{{\left(\nabla x\right)}^{\mathit{T}}\nabla x}.}$$ (13)

The Frechet derivative of r evaluated at x is given by

$${\displaystyle \mathcal{L}\left(x\right)=-\nabla \cdot k\nabla }$$ (14)

with diffusivity

$${\displaystyle k=\frac{r^{\prime }\left(\right|\nabla x\left|\right)}{\left|\nabla x\right|}.}$$ (15)

In this framework, Tikhonov regularization is given by the choice of

$${\displaystyle r\left(x\right)=\frac{1}{2}|\nabla x{|}^2,\mathcal{L}\left(x\right)={\nabla }^2}$$ (16)

and an approximation to the total variation functional is given by

$${\displaystyle r\left(x\right)=T\sqrt{|\nabla x{|}^2+T^2}-T,\mathcal{L}\left(x\right)=\nabla \cdot \frac{T}{\sqrt{|\nabla x{|}^2+T^2}}\nabla ,}$$ (17)

where T is a threshold parameter.

The regularization hyperparameter τ in Eq. (6) determines the relative weighting between the likelihood and prior terms. Different strategies for determining τ exist. We used an L-curve approach, where the prior term is plotted against the likelihood term at the stopping point of a reconstruction for a range of values of τ, and the optimal value of τ is taken to coincide with the point of highest curvature of the plot.

We used phantom measurements of objects of known contrast suspended in a homogeneous background liquid for computing the optimal regularization settings for our instrument. We found that the reconstruction process inherently reconstructed scattering features with higher contrast and higher resolution than absorption features. This can be attributed to differences in the sensitivity profiles of the two parameters. To account for this effect in the reconstruction, we used a total variation prior for the absorption parameter, and a Tikhonov prior for the scattering parameter, as well as two separate hyperparameters (τ_μs = 10τ_μa). τ_μa was evaluated by an L-curve evaluation for each of the reconstruction problems. The use of different regularization functionals for the two parameters may be justified by the observation that the reconstruction of scattering is obtained with one order less smoothness than absorption. Thus a regularization that sharpens the absorption parameter is not needed for the scattering parameter.⁶¹

3.F. Breast-background segmentation

For the reconstruction from clinical breast measurements, we utilized the profilometry system described in Sec. 2.C to segment the reconstruction volume into breast and background domains. The initial values for the model parameters of the background region were then assigned from the known optical parameters of the Intralipid and ink solution, while the initial parameters for the breast volume were determined in a preliminary global parameter reconstruction step that regarded the breast domain as homogeneous and recovered the mean values of the chromophore concentrations and scattering parameters. These were then used as initial parameter values for the spatially resolved reconstruction.

4. TISSUE PHANTOM EXPERIMENTS AND RESULTS

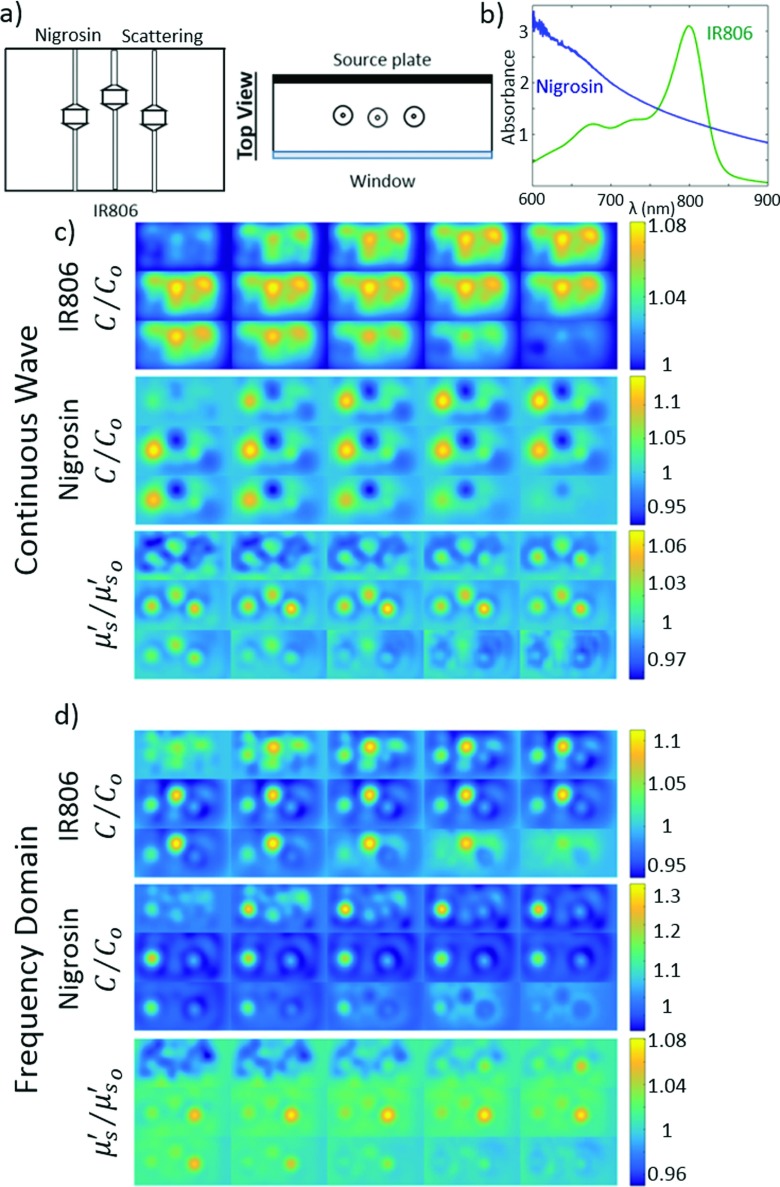
The capabilities of the DOT imager and reconstruction schemes were tested with tissue phantoms that roughly mimic the optical properties and contrast of breast tissue. Hollow targets, 16 mm in diameter with 1 mm thick walls of Delrin connected to thin nylon tubing, were filled with optical contrast and submerged in a background solution.^62,63 The target size was chosen to be slightly smaller than tumors imaged in our previous study.²² The background solution consisted of water, Intralipid, and two optical dyes, Nigrosin and IR806. These features gave the phantoms an approximate absorption and scattering of μ_a = 0.004 mm⁻¹ and ${\mu }_s^{\prime }=0.8{\mathrm{mm}}^{-1}$ at 785 nm. A series of experiments were performed with 3 ×, 4 ×, and 6 × chromophore concentrations (Nigrosin, lower left, and IR806, center) and 2 × reduced scattering coefficient (Intralipid, lower right) targets relative to the background [see Fig. 6(a)]. The ${\mu }_s^{\prime }$ contrast was chosen to be on the same order as the contrasts seen in our previous study.²² A comparison of the integrated reconstructed contrasts to the expected contrasts is given in Table I. Notice that a significant fraction of the expected chromophore contrast is reconstructed; however, as expected, the reconstructed contrast saturates at the higher chromophore concentration due to the increased nonlinearity of the imaging problem.

FIG. 6.

3D reconstruction of tissue phantom in frequency-domain. (a) Diagram of the target phantoms. The lower left target is filled with Nigrosin at 6 × concentration relative to the background, the center target is filled with IR806 at 6 × concentration relative to the background, and the lower right target has a higher Intralipid concentration with $2\times {\mu }_s^{\prime }$ contrast in scattering relative to the background at 785 nm. In all panels, we show the contrast between the target chromophore concentrations (C) or target scattering (${\mu }_s^{\prime }$) with respect to their corresponding background value (C₀ or ${{\mu }_s^{\prime }}_0$) is shown. The background had concentrations of 3.67 × 10⁻² and 3.48 μM for IR806 and Nigrosin, respectively, and ${\mu }_s^{\prime }=0.8{\mathrm{mm}}^{-1}$ at 785 nm. (b) Absorption spectra of the Nigrosin (blue) and IR806 (green) dyes [(c) and (d)] are the CW and FD 3D reconstructions shown in 4 mm slices from top left to bottom right. In the CW reconstruction, the IR806 and scattering reconstructions have high crosstalk, and the Nigrosin reconstruction has relatively low contrast. In the FD reconstructions, crosstalk is significantly reduced. For each image, the top/left slices are closer to the source plane and the lower/right slices are closer to the detector plane. (See color online version.)

TABLE I.

Spatially integrated reconstructed contrast (chromophore concentration divided by background concentration) for the two chromophores at three different concentrations. The total integrated contrast of each target was calculated using a full width at half maximum analysis scheme. This integration over the whole volume of the targets allows us to compare the broadened reconstructed contrast to the true contrast of the target. At higher concentrations, saturation effects due to the increased nonlinearity of the perturbations become more evident. Note that for all three experiments, the expected reduced scattering coefficient relative to background is 2 × and the recovered integrated contrast is between 1.44 and 1.54.

Expected contrast (C/C0)	Reconstructed IR806 contrast (C/C0)	Reconstructed Nigrosin contrast (C/C0)
3	2.48	2.31
4	2.95	2.71
6	3.29	3.34

In Fig. 6, we present reconstructions of a phantom with targets having 6 × chromophore concentrations and $2\times {\mu }_s^{\prime }$ relative to the background and plot C/C₀ and ${\mu }_s^{\prime }/{{\mu }_s^{\prime }}_0$, where C and ${\mu }_s^{\prime }$ are the reconstructed chromophore concentrations and reduced scattering coefficient, C₀ and ${{\mu }_s^{\prime }}_0$ are the known background chromophore concentrations and reduced scattering coefficient, and C/C₀ and ${\mu }_s^{\prime }/{{\mu }_s^{\prime }}_0$ are the recovered target contrasts. These reconstructions highlight the importance of the phase data, as well as the multispectral capabilities of the DOT imager. As expected, FD imaging, which utilizes amplitude and phase data, reduces the crosstalk between absorption and scattering when compared to reconstruction using only CW data. Additionally, in the FD reconstruction, we observe a clear separation between the Nigrosin and IR806 targets, indicating the ability of the system to distinguish chromophores with different spectral features.

The spatial structure of the images is reasonably good, but the reconstructed contrast is less than expected based on the peak contrast. This effect has been observed previously in DOT devices;^26,49,64 it is largely a result of the spreading of the reconstruction contrast that arises when the target (in the reconstructed image) is broadened spatially compared to the true target dimensions (i.e., because of a partial volume effect). This broadening is exacerbated in 3D reconstructions because of the additional stretching in the longitudinal (through-slab) dimension. The effect can be seen in the comparison of the Nigrosin and IR806 reconstructions in Fig. 6(d). Each target has the same concentration of its particular chromophore; however, the peak concentration is lower in the IR806 reconstruction than in the Nigrosin reconstruction due to the greater spatial broadening of the IR806 target along the longitudinal axis. Note also that the Nigrosin target is shifted closer to the source plane compared to the IR806 target. Phenomena such as these are difficult to understand and control because the DOT reconstruction problem is nonlinear and depends on many factors. In the present case, for our parallel-plate reconstructions, the number of useful off-axis measurements is set by an algorithm that depends on pixel signal-to-noise and is different for each target. The off-axis cutoff is known to cause elongation (normal to plates) of objects, and cutoff differences can also induce uncontrolled spatial shifts normal to the plates. Future work, after signal-to-noise improvements, will explore these issues.

In addition, some underestimation of optical contrast can be due to systemic offsets inherent in the instrument or reconstruction method; ultimately, we can compensate for these sorts of effects with calibration phantoms.⁶⁵ Some artifacts are also apparent near the source plane; these artifacts near source and detector surfaces are well-known to arise in DOT, and methods exist to ameliorate them. One common approach to cope with this issue is spatially variant regularization.⁶⁶ In this paper, we opted not to apply this technique in order to avoid biasing the results toward the central imaging plane. This could have resulted in an artificial improvement of the phantom reconstruction, which did not contain surface features, but at the same time could have introduced a distortion in the breast reconstruction discussed in Sec. 5. When required, more aggressive regularization schemes should be used to suppress contrast near the boundaries. This particular experiment also exhibited noise in the reference measurement, which contributed to the artifacts near the source plane.

5. IN VIVO CANCER MEASUREMENTS

We imaged a 79-year-old postmenopausal Caucasian female with biopsy-confirmed malignant cancer. Ultrasound found hypoechoic nodules which spanned approximately 18 × 10 mm at the 3:30 region of the breast, 4 cm from the areolar margin. The subject’s breast was gently compressed to maintain a source–detector plate separation of ∼6 cm for the duration of the measurement. A left breast core biopsy confirmed the presence of invasive mammary carcinoma with ductal and lobular features and intermediate grade nuclei. The patient consented to participate in the study in accordance with the consent policies outlined by the University of Pennsylvania research ethics committee.

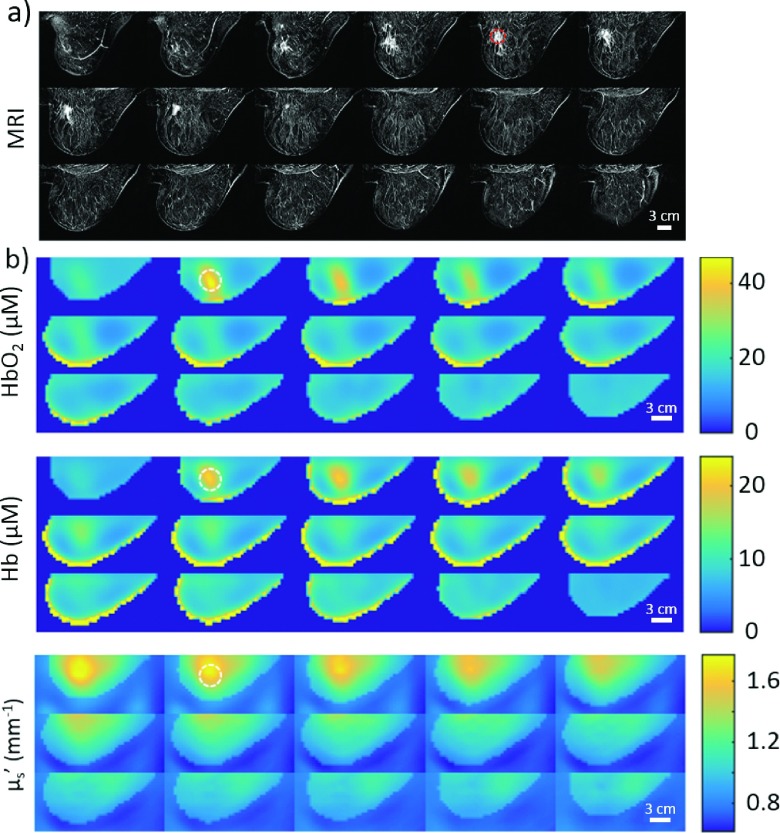
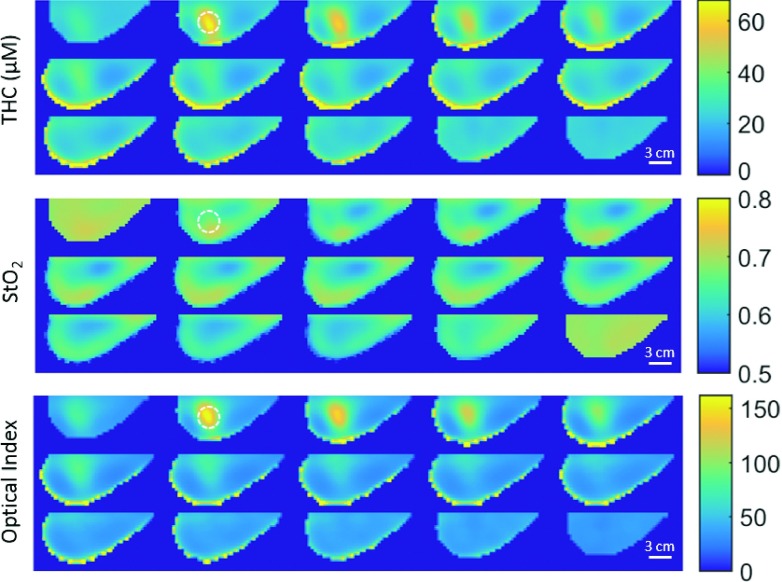
Figure 7 shows the DOT reconstructions of oxyhemoglobin concentration (HbO₂), deoxyhemoglobin concentration (Hb), and reduced scattering coefficient (${\mu }_s^{\prime }$), along with Dynamic Contrast Enhanced MRI (DCE-MRI) data from this subject. The DCE-MRI and DOT images were acquired in approximately the same breast geometry; however, the images were not acquired simultaneously, and the breast was slightly less compressed in the MRI than in the DOT measurement. Thus, in this case, the MRI can provide an approximate expected location for optical contrast in the DOT reconstructions but not an exact position, especially along the longitudinal axis. Corresponding 3D spatial maps of total hemoglobin concentration THC = HbO₂ + Hb, blood oxygen saturation StO₂ = HbO₂/THC, and an optical index $\mathrm{OI}=\mathrm{THC}\times {\mu }_s^{\prime }/{\mathrm{StO}}_2$ (Ref. 15) are shown in Fig. 8.

FIG. 7.

MRI and DOT images of the left breast of a 79-year-old post-menopausal Caucasian female with breast cancer, viewed as lateral to medial sagittal slices from the upper left. (a) Subtraction images from a DCE-MRI (Gadolinium). Tumor biopsy confirmed as invasive mammary carcinoma (ductal and lobular features) with intermediate grade nuclei. (b) 3D multispectral frequency-domain DOT reconstruction of the HbO₂ and Hb concentrations (μM) as well as the ${\mu }_s^{\prime }$ at 785 nm. The approximate tumor location in the MRI, as well as the corresponding area in each DOT image, is indicated by a dashed circle of 30 mm in diameter. Note, MRI and DOT breast compressions are similar but are not identical. Interesting features are apparent in the images with high HbO₂, Hb, and scattering near the tumor region (identified with biopsy clip in the MRI).

FIG. 8.

DOT reconstruction of the same breast as Fig. 7, again viewed as lateral to medial sagittal slices from the upper left. THC and StO₂ as well as the optical index ($\mathrm{OI}=\mathrm{THC}\times {\mu }_s^{\prime }/{\mathrm{StO}}_2$) at 785 nm. The dotted circles indicate the suspected tumor center in the DOT images and are 30 mm in diameter.

The optical index is a parameter which seeks to maximize optical contrast with the assumption that, compared to healthy tissues, tumors will have elevated levels of THC and ${\mu }_s^{\prime }$ and depressed levels of StO₂.²² The observed optical/physiological properties all fall within realistic values for the breast. Importantly in slice 2 of both Figs. 7 and 8, 8 mm from the medial plate/skin interface, the DOT images show significant contrast for multiple optical parameters. This location for the tumor corresponds approximately to the MRI-derived tumor location. We observe significant contrast in the tumor region for HbO₂ ∼ 3.1, Hb ∼ 2.2, ${\mu }_s^{\prime }\sim 1.7$, THC ∼ 2.7, and OI ∼ 11.6 when compared to the healthy region (i.e., as estimated from MRI and from other examinations). From the HbO₂ and Hb images in the same plane, the tumor is estimated to be 25–35 mm in diameter.

This initial case study demonstrates the ability of the new DOT instrumentation to image a large tumor. Due to the large tumor size, it is possible that surrounding tissues also have optical properties different from normal tissues; this effect could give rise to a further spatial broadening of the reconstructed tumor. Figure 7 shows somewhat imperfect geometrical registration of the tumor’s location in the two imaging modalities; however, the plate separations were different and no fiducial markers were utilized. On the other hand, it is well known that DOT has comparatively poor resolution in the longitudinal (through-slab) dimensions, an effect which has also been observed in our phantom experiments.

6. DISCUSSION

In this paper, we introduced and demonstrated a parallel-plate DOT breast imager that employed highly parallel, high-resolution CCD detection in the frequency-domain. Besides its large data-set, the instrument’s in situ normalization and additional spatial segmentation information for image reconstruction led to improved contrast and parameter separation compared to CW methods. Experiments on tissue phantoms were used to optimize reconstruction parameters for the separation of absorption and scattering contrasts as well as the separation of multiple chromophores. On the software side, separate regularization of absorption and scattering was found to lead to improved reconstruction. We demonstrated the instrument in a case study reconstruction of a breast cancer patient which showed reconstruction of endogenous chromophores and scattering with localization in agreement with MRI.

The research also identified important factors that should result in improved quantification and resolution in future imaging applications. To further improve SNR, potential hardware improvements include pixel binning to decrease readout noise, increasing the cross-correlation frequency to ameliorate noise near zero frequency, increasing the modulation frequency to improve phase contrast, increasing data acquisition frame-rate, and increasing laser power and stability. All of these improvements are readily implemented. Improved SNR would also allow for the use of data at longer source–detector separations, which, in turn, would improve the longitudinal resolution of the reconstructions. Still further resolution improvements could be achieved by increasing the number of sources and detectors and exploring different regularization techniques. Future work will also include systematic exploration of the impact of the number and spatial density of sources and detectors on reconstruction, e.g., on the quantification and localization of targets, as well as on spatial resolution and numerical stability.

In the future, the DOT imager will be utilized for focused work on several clinical applications. Examples of these applications include DOT imaging in populations with radiographically dense breasts or high genetic risk, in neoadjuvant chemotherapy monitoring, in exploration of novel optical contrast agents (e.g., exogenous absorption and fluorescence contrast agents), in construction of multimodal malignancy parameters based on optical data⁶⁷ and data from other medical imaging modalities, as well as in dynamic imaging (e.g., breast compression and decompression).

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.