A Mechanical Argument for the Differential Performance of Coronary Artery Grafts

Abstract

Coronary artery bypass grafting (CABG) acutely disturbs the homeostatic state of the transplanted vessel making retention of graft patency dependent on chronic remodeling processes. The time course and extent to which remodeling restores vessel homeostasis will depend, in part, on the nature and magnitude of the mechanical disturbances induced upon transplantation. In this investigation, biaxial mechanical testing and histology were performed on the porcine left anterior descending artery (LAD) and analogs of common autografts, including the internal thoracic artery (ITA), radial artery (RA), great saphenous vein (GSV) and lateral saphenous vein (LSV). Experimental data were used to quantify the parameters of a structure-based constitutive model enabling prediction of the acute vessel mechanical response pre-transplantation and under coronary loading conditions. A novel metric Ξ was developed to quantify mechanical differences between each graft vessel in situ and the LAD in situ, while a second metric Ω compares the graft vessels in situ to their state under coronary loading. The relative values of these metrics among candidate autograft sources are consistent with vessel-specific variations in CABG clinical success rates with the ITA as the superior and GSV the inferior graft choices based on mechanical performance. This approach can be used to evaluate other candidate tissues for grafting or to aid in the development of synthetic and tissue engineered alternatives.

Graphical Abstract

1. INTRODUCTION

Coronary artery grafts bypass (CABG) can restore long-term myocardial perfusion following advanced-stage coronary artery disease (Sabik et al., 2011). Annually more than 400,000 CABG procedures are performed in the United States alone. The health care cost of these CABG procedures is close to 200 billion USD (Lloyd-Jones et al., 2010; US Department of Health and Human Services, 2013). Despite decades of improvements to surgical techniques, approximately 6% of all CABGs fail in the first year, putting patients with compromised cardiovascular systems at greater risk of myocardial infarction and other pathologies (Carey et al., 2009). Failure rates depend strongly on the source tissue. For example, when collated from large clinical outcomes 15.3% of great saphenous veins fail in the first year while only 4.87% of internal thoracic artery failures occur (Calafiore et al., 1995; Cao et al., 2013; Cohen et al., 2001; Desai et al., 2004; Fiore et al., 1990; Fitzgibbon et al., 1996; Goldman et al., 2011; Hess et al., 2014; Loop et al., 1986; Maniar et al., 2002; Royse et al., 2000; Sabik et al., 2005; Zacharias et al., 2004). By comparison, when used as a CABG graft, the radial artery has an average first year failure rate around 9.78% (Calafiore et al., 1995; Cao et al., 2013; Cohen et al., 2001; Desai et al., 2004; Fiore et al., 1990; Fitzgibbon et al., 1996; Goldman et al., 2011; Hess et al., 2014; Loop et al., 1986; Maniar et al., 2002; Royse et al., 2000; Sabik et al., 2005; Zacharias et al., 2004). Although numerous factors contribute to the differential response, the mechanical mismatch of the grafted vessel with the host environment likely underlies a multitude of etiologies including ischemia, hemorrhage, dissection, inflammation, and restenosis (Bassiouny et al., 1992; Dobrin et al., 1989; Hofer et al., 1996).

Grafted vascular tissue must undergo an adaptive growth and remodeling process to retain optimal performance under the new mechanical loads imposed by the coronary circulation including altered blood pressure, flow, and axial force (Eberth et al., 2009a; Fung, 1991; Kamiya and Togawa, 1980; Rachev et al., 1998). These loads generate mechanical signals that are sensed by vascular endothelial, smooth muscle, and fibroblast cells eliciting gene expression pathways that lead to microstructural adaptations and tissue reorganization (Chien, 2007). Stress provides a continuum mechanics-based metric to assess the effects of loading on the local mechanical environment of vascular cells, specifically intramural stresses that act in the circumferential and axial directions as well as flow induced wall shear stresses acting on the endothelial-lined lumen (Humphrey, 2002; Zwolak et al., 1987). Biaxial mechanical testing, typically inflation and extension of a tubular tissue sample, and subsequent data processing in the framework of finite elasticity are necessary to quantify the intramural stresses in the vessel wall (Humphrey, 2002). Wall shear stress on the other hand, is dependent on the flow velocity profile and exponentially related to the vessel’s inner radius, a structural property. Compliance provides an additional structure-based measure that is fundamental to a graft’s performance in a pulsatile environment. Collectively, these passive mechanical responses are determined by the geometry, orientation, and composition of the extracellular matrix proteins present in the wall (Bank et al., 1996; Cox, 1978; Roach and Burton, 1957).

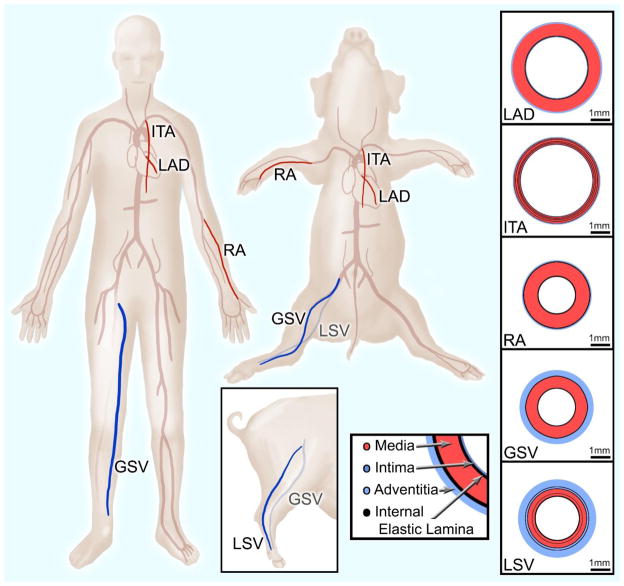
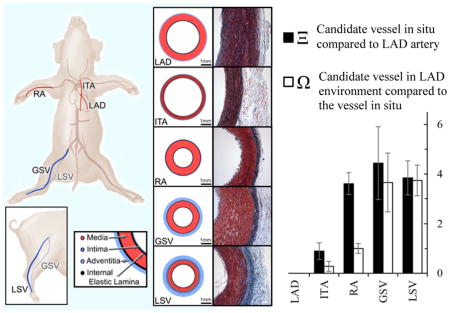
Currently, the most common tissue sources for grafting to the left anterior descending coronary artery (LAD) include the internal thoracic (also known as the internal mammary) artery (ITA), radial artery (RA), and great saphenous vein (GSV) (Athanasiou et al., 2011; Benedetto et al., 2015; Loop et al., 1986; Sabik et al., 2011). The anatomical and functional location of each graft vessel (i.e., ITA, RA, and GSV) along the vascular tree (Figure 1) determines the native mechanical loading environment, which in concert with vessel-specific properties, give rise to a vessel-specific homeostatic state. For example, the LAD and ITA nominally experience highly pulsatile blood flow, and as a result exhibit high mechanical compliance to dampen pulsatility and reduce cardiac preload (Berne and Levy, 2001; Konig et al., 2009). The RA is subjected to slightly lower blood pressures but less pulsatility than the LAD and ITA, resulting in a less compliant and more muscular structure (Chamiot-Clerc et al., 1998; Zambanini et al., 2005). The GSV and LSV are subjected to substantially lower pressures across a more narrow range, giving rise to a venous architecture that is structurally and compositionally different from its arterial counterpart (Berne and Levy, 2001; Canham et al., 1997; Dobrin et al., 1990; Dummler et al., 2011; Stick et al., 1993). Concatenate with hemodynamic loading, somatic growth influences these tissues to experience in situ axial load (Humphrey et al., 2009). This manifests as an axial extension as evidenced by an immediate retraction upon excision to relieve the axial force. These axial loads however, are very different than the neutral axial loads surgeons create during a CABG procedure (Khonsari et al., 2008).

Figure 1.

Translational schematic comparing vessel locations in human and porcine anatomy. Vessel wall diagrams are to scale based on geometric and histological data from the present study.

The differential performance of CABG grafts have been highlighted in numerous clinical studies that include long-term metrics such as graft patency (Athanasiou et al., 2011; Fitzgibbon et al., 1996; Loop et al., 1986), reintervention rates (Cohen et al., 2001), case-matching (Benedetto and Codispoti, 2013; Cohen et al., 2001), and meta-analysis (Athanasiou et al., 2011; Benedetto et al., 2015). These studies identified the ITA as the superior performer in terms of clinical outcomes due to its anatomical position – descending from the subclavian and running very close to the heart in its normal anatomical position – requiring only one site of anastomosis to achieve coronary perfusion (Sabik et al., 2011). In many cases however, the ITA is not available and a second source tissue needs to be selected. GSV grafts were historically the preferred choice due to their superficial anatomical position, non-branching morphology, and comparable caliber to coronary arteries (Effler et al., 1970; Loop et al., 1986). Other autologous source tissue options include RAs and GSVs, and far less commonly the right gastroepiploic artery or inferior epigastric artery (Fitzgibbon et al., 1996; Hess et al., 2014). RAs have similar caliber and have superficial location, but RAs suffer from susceptibility to vasospasm, calcification, intimal hyperplasia, and are relatively poor in patients with peripheral artery disease (Cheng and Slaughter, 2013).

Here we investigated if mechanical differences among autologous vascular tissue sources, particularly under pre- and post-grafting loading conditions, correspond with differences in clinical outcomes. To this end, we quantified the passive mechanical response of the healthy porcine LAD and a host of candidate vessels commonly used as coronary artery grafts. Obtained mechanical data were processed in a continuum mechanics-based framework, enabling prediction of each vessel’s mechanical response under varied loading conditions. Vessel-specific mechanical metrics that account for changes caused by grafting were developed and found to correlate with reported clinical outcomes. Our findings help explain differential outcomes following autologous grafting in the coronary artery, and can be extended towards the development and assessment of other grafting alternatives (i.e. alternative tissue sources and tissue engineered materials).

2. MATERIALS AND METHODS

2.1 Tissue Acquisition and Handling

All porcine tissue was obtained fresh from a local abattoir and dissections were performed immediately following tissue acquisition. Isolated blood vessels included the LAD, ITA, RA, GSV, and an additional vessel, the lateral saphenous vein (LSV) (Figure 1). While there is no true translational equivalent to the porcine lateral saphenous vein in humans, it is included due to its prevalence in other veterinary studies and similar caliber to the porcine great saphenous vein. American Yorkshire pigs were used in this study and all animals were 6 month old ± 1 week. All target vessels were dissected as a set from the same animal (n=6), and animal weights ranged from 102–113 kg. Upon dissection each vessel was stored in a sterile solution of 1% phosphate buffered saline (PBS) and refrigerated until mechanical testing could be performed, which was always within 24 hours of tissue dissection.

2.2 Biaxial Mechanical Testing

Mechanical testing was carried out using a Bose BioDynamic 5270 biaxial mechanical testing device. Vessels were cut to approximately 20 mm tubular sections, and initial measurements were taken of the unloaded length, outer diameter, and wall thickness. All measurements were made along the middle section of each vessel to avoid extreme conditions at proximal and distal ends. Each vessel was mounted into the testing chamber of the biaxial testing device; the chamber was filled with Krebs-Heisenleit solution (37 deg C and pH 7.4); and sodium nitroprusside (10⁻⁵ M) was flushed through the vessel and device tubing at 60 mL/min to elicit the fully relaxed (passive) state of the SMCs and to remove all air from the flow loop.

Each vessel was axially extended by approximately 40% of the unloaded length at a displacement rate of 0.01 mm/s and pressures of 60 mmHg, 100 mmHg, and 140 mmHg. The in vivo axial stretch ratio was then determined to be the intersection of resultant axial force vs. displacement curves. This phenomenological observation of in vivo axial stretch has been documented historically (Van Loon, 1976) and in our prior work (Eberth et al., 2009b). Each vessel then underwent five cycles of pressurization for preconditioning, helping to ensure reproducible results. For data collection, pressure was increased from 20 to 200 mmHg at a constant rate of approximately 1.3 mmHg/s while pressure-outer diameter and pressure-longitudinal force curves were recorded at an axial stretch ratio below the in vivo value. Data collection was then carried out at the approximated in vivo stretch ratio and again above the in vivo stretch ratio. Between tests, axial displacement was increased at a rate of 0.01 mm/s, and the vessel was allowed to acclimate for 15 minutes at the new stretch ratio. Each test was repeated three times (Eberth et al., 2009b; Zhou et al., 2013).

2.3 Zero Stress State

A radial, stress-relieving cut was made into 1 mm thick ring sections taken from the middle region of each vessel following mechanical testing (Fung, 1991). This radial cut causes ring sections to spring open into a sector. After allowing 30 minutes in PBS for each vessel to equilibrate, a digital image was taken of the resultant open sector using a Nikon Coolpix s3500 (resolution of 20 μm/pixel). Image-Pro 6.0 image analysis software was used to measure the sector thickness H, inner arc length L_i, and outer arc length L_o. From these data, cross-sectional area A and opening angle Φ of the sector were calculated using

$$H=\frac{2A}{L_i+L_o}\text{and}\mathit{\Phi }=\pi -\frac{L_o-L_i}{2H}.$$ (1)

Collectively, these data enable quantification of the zero stress state for each sample.

2.4 Data Analysis

Vessels are assumed to be 3-D thick-walled cylindrical tubes that experience an axisymmetric finite elastic deformation under applied pressure and longitudinal extension. Neglecting the contribution of vascular smooth muscle cells, the passive mechanical properties of vessels depend predominantly on the properties, amount, and spatial arrangement of collagen and elastin in the vessel wall. Through inflation-extension mechanical testing, sample luminal pressure P and axial stretch λ_z were controlled, and response data for the deformed outer radius r_o and axial force F were recorded. Under the assumption of tissue incompressibility, the deformed inner radius r_i is calculated as:

$$r_i=\sqrt{r_o^2-\frac{A}{\pi {\lambda }_z}}.$$ (2)

Likewise, the lumen area compliance is calculated as:

$$c=\pi \frac{\mathrm{\Delta }{r}_i^2}{\mathrm{\Delta }P}$$ (3)

The average circumferential σ_θ and axial σ_z wall stresses are calculated as:

$${\sigma }_{\theta }=\frac{{Pr}_i}{r_o-r_i},{\sigma }_z=\frac{F}{\pi \left(r_o^2-r_i^2\right)}.$$ (4)

The mid-wall circumferential λ_θ and axial λ_z stretch ratios are calculated as:

$${\lambda }_{\theta }=\frac{2\pi (r_i+r_o)}{L_i+L_o},{\lambda }_z=\frac{l}{L}$$ (5)

where l and L are the deformed and undeformed vessel lengths, respectively.

2.5 Theoretical Framework

For inflation and extension of an axisymmetric tube, its deformation is characterized by the right Cauchy-Green strain tensor

$$[C]=\mathit{diag}\left\{{\left(\frac{dr}{dR}\right)}^2,{\left(\chi \frac{r}{R}\right)}^2,{\lambda }_z^2\right\},\chi =\frac{\pi }{\pi -\mathit{\Phi }}$$ (6)

where r and R are the radial coordinates of an arbitrary point within the vessel wall before and after deformation.

Due to the incompressibility of the vessel wall

$$\frac{dr}{dR}\frac{r}{R}\chi {\lambda }_z=1$$ (7)

which after integration yields

$$r=\sqrt{r_o^2-\frac{1}{\chi {\lambda }_z}\left(R_o^2-R^2\right)}.$$ (8)

Given the zero-stress configuration, axial stretch ratio, and the deformed outer radius, the components of the strain tensor can be completely described. A diagrammatic representation of the zero-stress state and deformed configurations can be found in Zhou et al. (2013) and is consistent with that of other researchers Matsumoto and Hayashi (1996).

We use an analytical form of the strain energy function, whereby stress and stretch are related by the energy stored in the vessel wall as it is distended (Eberth et al., 2011; Zhou et al., 2014). This strain energy function was first described by Holzapfel and colleagues: (Holzapfel et al., 2000; Humphrey, 2002)

$$W={\varphi }_e{b}_0\left[\left({\lambda }_{\theta }^2+{\lambda }_z^2+{\left({\lambda }_{\theta }{\lambda }_z\right)}^{-2}\right)-3\right]+\frac{{\varphi }_c}{4}\sum _{k=1-4}\frac{b_{k1}}{2b_{k2}}\left\{exp\left[b_{k2}{\left({\sqrt{{\lambda }_{\theta }^2{sin}^2{\alpha }_k+{\lambda }_z^2{cos}^2{\alpha }_k}}^2-1\right)}^2\right]-1\right\}$$ (9)

The constitutive model of equation (9) is a structure-based strain-energy function. The first collection of terms and material constant b₀describe the isotropic, neo-hookean contribution of an elastin-dominated, non-collagenous extracellular matrix (Bersi et al., 2014; Gundiah et al., 2007; Holzapfel et al., 2000; Zulliger et al., 2004). The second term describes the anisotropic contribution of four collagen fiber families, where subscript k denotes a particular family of fibers oriented at a mean angle of α_k with respect to the longitudinal axis with material constants b_k1and b_k2. The four-fiber family model with 8 independent parameters gives an excellent representation of biaxial mechanical data without being over parameterized (Zeinali-Davarani et al., 2009). Histological evidence suggests that smooth muscle cell orientation is predominantly in the circumferential or diagonal directions (Cheng et al., 2013). Therefore the passive contribution of smooth muscle is “lumped” into the corresponding circumferential and diagonal fiber families (Ferruzzi et al., 2013). In this model α₁= 90 deg represents circumferentially oriented fibers, and α₂= 0 deg represents axially oriented fibers. Additionally α₃=−α₄ =α represents diagonally oriented fibers, with the value for α obtained from the model. Accordingly the stress-like and dimensionless parameters for these fiber families are equivalent so that b₃₁= b₄₁and b₃₂= b₄₂ respectively. ϕ is the area fraction of (e) elastin or (c) collagen compared to the total tissue as determined through histological analysis.

The following expressions are used to calculate the theoretical values for pressure and axial force from a given deformed configuration

$$P=\underset{r_i}{\overset{r_o}{\int }}{\lambda }_{\theta }\frac{\partial W}{\partial {\lambda }_{\theta }}\frac{dr}{r},F=\pi \underset{r_i}{\overset{r_o}{\int }}\left(2{\lambda }_z\frac{\partial W}{\partial {\lambda }_z}-{\lambda }_{\theta }\frac{\partial W}{\partial {\lambda }_{\theta }}\right)\mathit{rdr}.$$ (10)

Using data obtained through our mechanical testing and zero-stress state measurements, the material constants of the constitutive model were found for each vessel. The material parameters associated with the constitutive model were determined via non-linear regression of equation (10) which was implemented in Matlab 2010b (Mathworks. Inc) using the lsqnonlin subroutine. The lower and upper limits of the parameters were prescribed as b₀ and b_k1 ∈ [0, 105], b_k2 ∈ [0, 10], and α ∈ [0°, 90°]. The constitutive model was then used to predict the deformed configurations, stretch ratios, and average transmural stresses under prescribed, in situ and coronary, loading conditions.

The in situ and grafted loads include both transmural pressure and axial force. The value of in situ pressure for the LAD, ITA, RA, GSV, and LSV was taken from the literature (Table 3) and represents a rough estimate of the mean value throughout the cardiac cycle (Canham et al., 1997; Chamiot-Clerc et al., 1998; Dummler et al., 2011; Konig et al., 2009). For example, a pressure of 100 mmHg was selected as a loading condition for the LAD. The in situ axial force, on the other hand, was determined as a result of biaxial testing. The grafted coronary loads for the ITA, RA, GSV, and LSV were assumed to be the values of the pressure and axial force of the LAD in subsequent calculations.

Table 3.

Loads, structure, stretch, and stress for the LAD, ITA, RA, GSV, and LSV in situ or grafted under coronary loads. In situ pressure values obtained from literature [34, 35, 37, 39].

	P(mmHg)	F (N)	ri (mm)	c (10−6m2/kPa)	λθ	λz	σθ (kPa)	σz (kPa)
LAD	100	0.4 ± 0.12	2.29 ± 0.38	0.32 ± 0.11	1.31 ± 0.26	1.33 ± 0.02	66.7 ± 39.3	51.3 ± 10.4
	In Situ Loads		In Situ Structure		In Situ Stretch		In Situ Stress
ITA	100	0.35 ± 0.08	1.98 ±0.13	0.39 ± 0.13	1.17 ± 0.11	1.22 ± 0.07	67.1 ± 14.7	64.4 ± 17.2
RA	80	0.33 ± 0.21	0.9 ± 0.15	0.09 ±0.04	1.16 ± 0.23	1.17 ± 0.07	14.3± 3.12§	65.1 ± 34.2
GSV	20	0.26 ± 0.14	0.70± 0.39§	0.17 ± 0.12	0.93± 0.09§	1.24 ± 0.10	3.66± 0.67§	46.1 ± 44.7
LSV	20	0.16± 0.09§	1.54± 0.73§	0.89 ± 0.61	1.12± 0.14§	1.34 ± 0.17	7.40± 3.36§	28.6± 24.5§
	Grafted Loads		Grafted Structure		Grafted Stretch		Grafted Stress
ITA	100	0.4	1.97 ± 0.13	0.38 ± 0.13	1.17 ± 0.11	1.24 ± 0.07	67.9 ± 15.6	75.7 ± 14.3
RA	100	0.4	0.92± 0.12*	0.10 ± 0.06	1.17 ± 0.17	1.21± 0.05*	17.2± 4.00*	79.3 ± 20.1
GSV	100	0.4	1.10± 0.28*	0.15 ± 0.05	1.12± 0.14*	1.25 ± 0.09	22.8± 5.71*	93.5 ± 39.7
LSV	100	0.4*	1.91± 0.67*	0.23± 0.04*	1.35 ± 0.16	1.34 ± 0.19	49.4± 15.1*	74.2 ± 24.7

^§Signifies statistical significance from the LAD using one-way ANOVA with Dunnett’s Post Hoc test.

^*Signifies significance from the in situ to LAD replacement graft states using two-sided paired t-test at p<0.05.

2.6 Histological Analysis

Upon completion of mechanical testing, sections of each vessel were fixed in 4% fresh paraformaldehyde, followed by embedding in paraffin wax. Sections approximately 5 μm thick were stained with a combination of Verhoeff’s elastic and Masson’s trichrome stain (O’Connor and Valle, 1982). All vessels were sectioned and stained together to prevent batch-to-batch variations. Images were obtained using a Nikon E600 microscope with CCD camera and computer interface with Q Capture (QImaging). Each tested tissue was imaged at 4–6 different locations and the best representative image was selected for each tissue to be used for thresholding analysis. Mean and standard deviations for each group were therefore found from a sample size of n=6. Area fractions occupied by black, blue, and red pixels were quantified using ImageJ software (NIH) with the “Threshold_Colour” plugin, which serves to estimate fractions of elastin, collagen, and smooth muscle in each vessel, respectively (Landini, 2008). In an effort to maintain consistency across samples, unstained pixels were not considered, and threshold values were fixed. Black pixels were quantified using a bandpass filter from Brightness 0 – 83; blue pixels were quantified using a bandpass filter from Brightness 83 – 255 and Hue 33 – 230; and red pixels were quantified using a bandpass filter from Brightness 83 – 255 and bandstop filter from Hue 33 – 230. Thus, the sum of these areas was approximately 100% for each sample, and the contribution of other constituents (e.g., ground substance) was assumed to be negligible.

2.7 Comparison of Native and Grafted States

The normalized difference between each vessel (i.e., ITA, RA, GSV, LSV) in situ (IS) and the left anterior descending artery (LAD) in situ in terms of the deformed inner radius, compliance, circumferential stress, and axial stress are described by

$${\mathrm{\Xi }}_{ri}=\frac{2\left|r_i^{IS}-r_i^{\mathit{LAD}}\right|}{r_i^{IS}+r_i^{\mathit{LAD}}},{\mathrm{\Xi }}_c=\frac{2\left|c^{IS}-c^{\mathit{LAD}}\right|}{c^{IS}+c^{\mathit{LAD}}},{\mathrm{\Xi }}_{\sigma \theta }=\frac{2\left|{\sigma }_{\theta }^{IS}-{\sigma }_{\theta }^{\mathit{LAD}}\right|}{{\sigma }_{\theta }^{IS}+{\sigma }_{\theta }^{\mathit{LAD}}},{\mathrm{\Xi }}_{\sigma z}=\frac{2\left|{\sigma }_z^{IS}-{\sigma }_z^{\mathit{LAD}}\right|}{{\sigma }_z^{IS}+{\sigma }_z^{\mathit{LAD}}}.$$ (11)

Likewise, the normalized difference between (IS) and that same vessel grafted under coronary loads (G) is calculated in a similar manner to (11) by

$${\mathrm{\Omega }}_{ri}=\frac{2\left|r_i^{IS}-r_i^G\right|}{r_i^{IS}+r_i^G},{\mathrm{\Omega }}_c=\frac{2\left|c^{IS}-c^G\right|}{c^{IS}+c^G},{\mathrm{\Omega }}_{\sigma \theta }=\frac{2\left|{\sigma }_{\theta }^{IS}-{\sigma }_{\theta }^G\right|}{{\sigma }_{\theta }^{IS}+{\sigma }_{\theta }^G},{\mathrm{\Omega }}_{\sigma z}=\frac{2\left|{\sigma }_z^{IS}-{\sigma }_z^G\right|}{{\sigma }_z^{IS}+{\sigma }_z^G}.$$ (12)

Summing the above expressions generates two overall mechanical similarity scores

$$\mathrm{\Xi }={\mathrm{\Xi }}_{ri}+{\mathrm{\Xi }}_c+{\mathrm{\Xi }}_{\sigma \theta }+{\mathrm{\Xi }}_{\sigma z}\text{and}\mathrm{\Omega }={\mathrm{\Omega }}_{ri}+{\mathrm{\Omega }}_c+{\mathrm{\Omega }}_{\sigma \theta }+{\mathrm{\Omega }}_{\sigma z}.$$ (13)

Here values closest to zero indicate the smallest differences.

2.8 Statistics

Statistical analysis was performed with a two-tailed paired t-test and one-way or two-way ANOVA using GraphPad Prism 3.02 (San Diego, CA, USA). Dunnet’s post-hoc test was used for multiple comparisons to the control. Statistically significant differences was taken at a level of p < 0.05.

3. RESULTS

3.1 Blood Vessel Histology

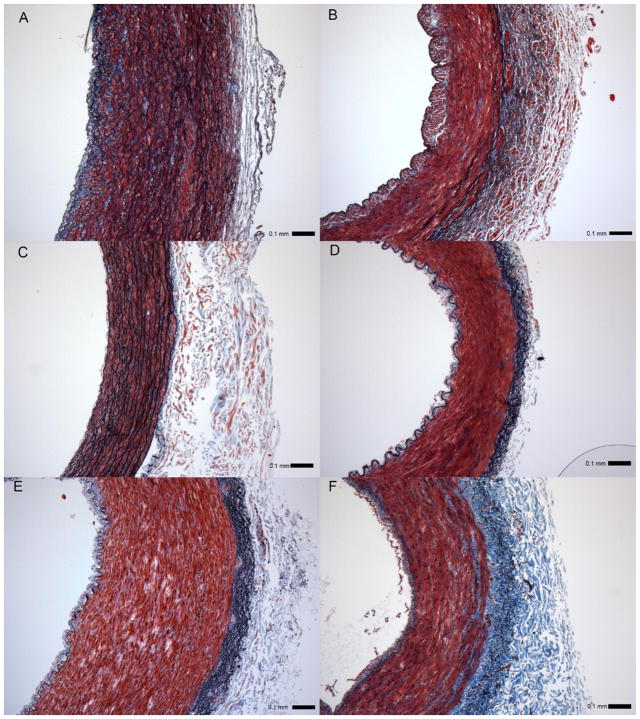
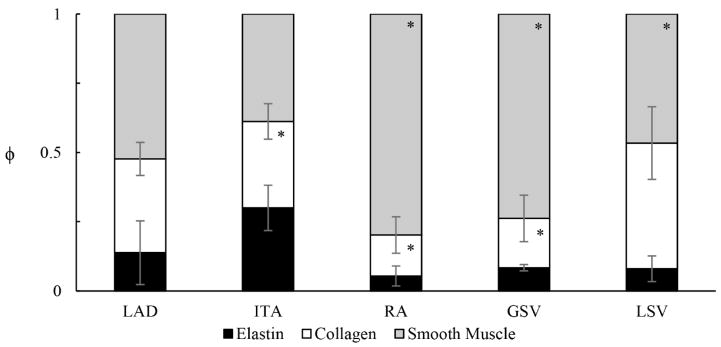
The microstructure of the vessels used in our comparative analysis varies considerably in spatial organization between anatomical locations, a feature reflective of its functional and native environment (Figure 2, Figure 3). Of note, the proximal LAD (Figure 2A) and ITA (Figure 2C) show numerous circumferentially oriented elastic lamellae in the media, whereas elastin is only somewhat evident in the media of the distal LAD (Figure 2B). Elastin is present as internal and external elastic laminas in the RA, GSV, and LSV (Figure 2D, E, and F, respectively). Despite these apparent differences, the only statistical difference in overall elastin content of any graft vessel and the LAD (ϕ_e =0.14 ± 0.12) was for the ITA (ϕ_e =0.30 ± 0.08) (Figure 3) while the collagen and smooth muscle fractions of the RA (ϕ_c =0.15 ± 0.07; ϕ_smc =0.80 ± 0.10) and GSV (ϕ_c =0.18 ± 0.08; ϕ_smc =0.74 ± 0.08), were found to be statistically different than the LAD (ϕ_c =0.34 ± 0.06; ϕ_smc =0.52 ± 0.06).

Figure 2.

Verhoeff – Masson’s stained cross-sections of (A) proximal and (B) distal left anterior descending artery - LAD approximately 2 cm apart; (C) internal thoracic artery - ITA, (D) radial artery - RA, (E) great saphenous vein - GSV, and (F) lateral saphenous vein - LSV. All images to scale with error bar = 0.1 mm.

Figure 3.

Area fractions ϕ of elastin (black), collagen (white), and smooth muscle (gray) determined by thresholding analysis of Verhoeff – Masson’s stained cross-sections for the internal thoracic artery (ITA), radial artery (RA), great saphenous vein (GSV), and lateral saphenous vein (LSV). *Signifies statistical significance with the LAD, mean ± SD, n=6 for each group.

3.2 Zero Stress State and Material Parameters

Table 1 shows the measurements obtained for the stress-free configuration of each vessel following biaxial testing. In the nearly zero stress state, the opening angle, responsible for homogenizing the circumferential stress through the vessel wall, was not found to be statistically different for any of the potential graft vessels and the LAD. There was however, statistically significant differences between the stress-free wall thickness of the ITA (H = 0.55 ± 0.06 mm) and LAD (H = 0.88 ± 0.11 mm). The RA and GSV were also found to be different from the LAD in terms of both inner (LAD = 10.4 ± 1.45; RA = 4.65 ± 1.21; GSV = 6.06 ± 1.74 mm) and outer (LAD = 13.8 ± 1.53; RA = 8.70 ± 1.63; GSV = 9.84 ± 2.32 mm) arc lengths. Based on biaxial testing data and stress-free measurements, the material parameters for the constitutive model were calculated and are shown in Table 2. Parameter b₁₁, representing the stress-like parameter in the exponential form for circumferentially oriented fibers, is significantly lower for the LSV than other vessels. Parameter b₂₁ is significantly different between the RA and LAD; this represents the stress-like parameter in exponential form for axially oriented fibers. The parameter for diagonally oriented fibers – b₃₁– is significantly different between the RA and LAD.

Table 1.

Vessel geometry of stress-free configuration.

	Outer arc-length (Lo) [mm]	Inner arc-length (Li) [mm]	Opening angle (Φ) [°]	Stress-Free Thickness (H) [mm]
LAD	13.8 ± 1.53	10.4 ± 1.45	70.1 ± 12.5	0.88 ± 0.11
ITA	13.4 ± 0.9	10.8 ± 0.86	44.9 ± 18.2	0.55 ± 0.06*
RA	8.70 ± 1.63*	4.65 ± 1.21*	45.2 ± 26.4	0.87 ± 0.06
GSV	9.84± 2.32*	6.06 ± 1.74*	51.5 ± 25.0	0.84 ± 0.05
LSV	12.0 ± 4.26	8.65 ± 4.35	67.8 ± 22.2	0.87 ± 0.15

^*Signifies statistical significance between graft tissue and the LAD using one-way ANOVA with Dunnett’s Post Hoc test at p<0.05.

Table 2.

Material Parameters for LAD, ITA, RA, GSV, and LSV obtained for a four-fiber constitutive model.

b0 [kPa]	b11 [kPa]	b12	b21 [kPa]	b22	b31 [kPa]	b32	α [°]	Residual
LAD 3.47 ± 2.83	18.7 ± 12.7	1.81 ± 2.92	1.96 ± 1.88	3.15 ± 2.08	7.51 ± 10.8	3.98 ± 1.4	40.5 ± 10.0	0.73 ± 0.34
ITA 17.5 ± 17.0	17.2 ± 5.74	0.34 ± 0.11	4.52 ± 3.70	3.38± 2.42	22.7± 30.6	4.05 ± 2.26	34.1 ± 13.2	0.52 ± 0.15
RA 5.17 ± 8.16	7.98 ± 11.3	0.64 ± 0.78	17.8± 10.8*	4.19 ± 2.02	17.8± 27.6*	3.73 ± 2.82	35.3 ± 4.98	0.52 ± 0.12
GSV 4.40 ± 5.85	6.95 ± 4.98	1.75 ± 2.93	14.0 ± 10.6	3.93± 3.16	24.5 ± 33.6	4.46 ± 2.55	37.7 ± 14.3	0.74 ± 0.23
LSV 5.53 ± 8.25	4.75± 4.03*	0.63 ± 0.62	0.91 ± 1.31	2.83± 3.09	2.62 ± 3.23	4.02 ± 2.97	42 ± 14.91	0.43 ± 0.23

^*Signifies statistical significance between graft tissue and the LAD using one-way ANOVA with Dunnett’s post hoc test at p<0.05

3.3 In Situ Structural and Mechanical Values

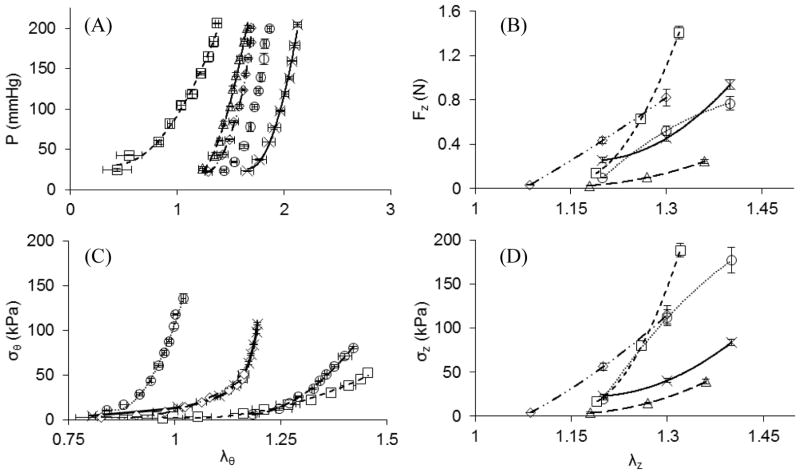
A representative sample of the measured pressure-deformed inner radius relationship at in situ conditions for each vessel shows similar behavior among the ITA, RA, GSV, and LSV (Figure 4A), while the LAD has a consistently larger lumen radius than the potential graft vessels. The $\text{GSV}(r_i^{IS}=0.70\pm 0.39\text{mm})$ and $\text{LSV}(r_i^{IS}=1.54\pm 0.73\text{mm})$ in situ radii (Table 3) were found to be different from the $\text{LAD}(r_i^{IS}=2.29\pm 0.38\text{mm})$. In situ area compliance can be interpreted from the tangential slope of Figure 4A and is shown in Table 3. Compliance values were not found to have a statistically significant difference. When comparing the axial force-axial distension at in situ pressures, the LAD fell within the group of tested blood vessels (Figure 4B) and the only statistically different in situ axial force from the LAD (F^IS =0.4 ± 0.12 N) was the LSV (F^IS =0.16 ± 0.09 N). The in situ circumferential stretches were statistically significant between the $\text{GSV}({\lambda }_{\theta }^{IS}=0.93\pm 0.09)$ and $\text{LSV}({\lambda }_{\theta }^{IS}=1.12\pm 0.14)$ compared to the $\text{LAD}({\lambda }_{\theta }^{IS}=1.31\pm 0.26)$ while axial stretches were not.

Figure 4.

Representative plots of (A) pressure-inner radius at in situ axial stretch, (B) axial force-stretch at in situ pressures, (C) circumferential stress-stretch at in situ axial stretch, and (D) axial stress-stretch at in situ pressures for the LAD ( ), ITA ( ), RA ( ), GSV ( ), and LSV ( ).

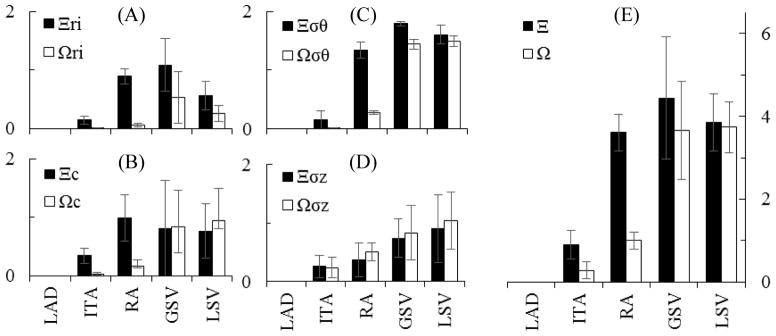
When circumferential stress-stretch is plotted (Figure 4C) an overall increasingly stiffer behavior is demonstrated at higher stretches especially for the ITA and LAD. Note that all data in Figure 4C is shown at the in situ axial stretch. Dramatic differences in the in situ circumferential stresses were observed for the $\text{RA}({\sigma }_{\theta }^{IS}=14.3\pm 3.1\text{kPa}),\text{GSV}({\sigma }_{\theta }^{IS}=3.66\pm 0.67\text{kPa})$, and $\text{LSV}({\sigma }_{\theta }^{IS}=7.40\pm 3.36\text{kPa})$ compared to the $\text{LAD}({\sigma }_{\theta }^{IS}=66.7\pm 39.3\text{kPa})$. The in situ axial stresses are much closer among the candidate tissues than the circumferential stresses and were only statistically different for the $\text{LSV}({\sigma }_z^{IS}=28.6\pm 24.5\text{kPa})$ compared to the $\text{LAD}({\sigma }_z^{IS}=51.3\pm 10.4\text{kPa})$ (Figure 4D; Table 3). Collectively, the differences in structural and mechanical properties were normalized and plotted for all vessels at in situ states compared to the LAD as indicated by Ξ in Figure 5. Using this approach, the ITA (Ξ =0.90 ± 0.34) is the best overall match to the LAD followed by the RA (Ξ =3.61 ± 0.44), LSV (Ξ =3.84 ± 0.69), and GSV (Ξ =4.44 ± 1.47).

Figure 5.

Comparison of normalized differences between vessels (ITA, RA, GSV, or LSV) in situ and the LAD (Ξ, ■) or between vessels in situ and that vessel under coronary loading (Ω,□). Subscripts (ri), (c), (σθ), and (σz) represent the normalized inner radius, compliance, circumferential stress, and axial stress respectively as plotted in (A), (B), (C), and (D) respectively while Ξ and Ω (no subscript) are the summation of those metrics (e). Mean ± SD, n=5 for each group.

3.4 Grafted Structural and Mechanical Values

Using a uniform prescribed mean pressure of 100 mmHg and the axial force measured for the LAD of 0.4 N to approximate coronary loading conditions for the graft tissue, deformed inner radius and compliance, circumferential stress and axial stress were calculated for the graft conditions of the coronary environment (Table 3). When comparing an autograft tissue in its in situ environment to that of the coronary environment we found statistically significant differences for the inner radius of the $\text{RA}(r_i^{IS}=0.9\pm 0.15;r_i^G=0.92\pm 0.12\text{mm}),\text{GSV}(r_i^{IS}=0.70\pm 0.39;r_i^G=1.10\pm 0.28\text{mm})$ and $\text{LSV}(r_i^{IS}=1.54\pm 0.73;r_i^G=1.91\pm 0.67\text{mm})$. The LSV (c^IS =0.89 ± 0.61; c^G =0.23 ± 0.04 10⁻⁶m²/kPa) also had a significant change in compliance. Despite the apparent increases in grafted axial stress shown in Table 3, statistically significant differences were only found in the circumferential direction. Specifically, the $\text{RA}({\sigma }_{\theta }^{IS}=14.3\pm 3.1;{\sigma }_{\theta }^G=17.2\pm 4.00\text{kPa}),\text{GSV}({\sigma }_{\theta }^{IS}=3.66\pm 0.67;{\sigma }_{\theta }^G=22.8\pm 5.71\text{kPa})$, and $\text{LSV}({\sigma }_{\theta }^{IS}=7.40\pm 3.36;{\sigma }_{\theta }^G=49.4\pm 15.1\text{kPa})$ all experience increased circumferential stress. The overall differences in structural and mechanical properties were normalized and plotted for all vessels at in situ states compared to the grafted environment as indicated by Ω in Figure 5. Using this approach, the ITA (Ω=0.28 ± 0.20) is the best overall match to the LAD followed by the RA (Ω=1.00 ± 0.20), GSV (Ω=3.66 ± 1.19), and LSV (Ω=3.74 ± 0.62).

DISCUSSION

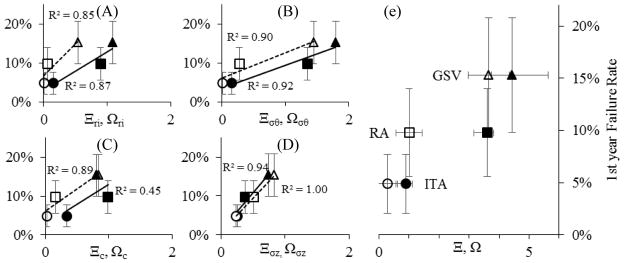
Landmark clinical studies have identified the existence of a performance differential for autologous vascular grafts based on anatomical tissue source location (Al-Sabti et al., 2013; Benedetto and Codispoti, 2013; Benedetto et al., 2015; Cheng and Slaughter, 2013; Cohen et al., 2001; Loop et al., 1986; Parissis et al., 2014; Raja et al., 2004; Sabik et al., 2011; Schwann et al., 2014). Although past clinical outcomes are inarguably a key determinant for CABG graft selection, the mechanisms of differential performance are not well explicated. Our data, and that of classic literature, shows that vascular tissues from functionally different origins have unique histoarchitecture (Cox et al., 1991). This histoarchitecture determines the inherent mechanical behavior dictating how a tissue remodels under the altered loading environment of the coronary vasculature (Figure 4). While vascular tissue remodeling is nominally an adaptive process that restores homeostasis, mechanical, compositional, and geometrical incongruities between the grafted and adjacent tissues can lead to deleterious outcomes that compromise lumen patency. The relationship between normalized difference in mechanical properties metrics – Ω and Ξ – versus first year CABG failure rate (Figure 6) suggests a positive relationship between graft failure rate and mechanical deviations. Further, our important findings suggest that a range of unique mechanical conditions exist for each of these tissues in situ and under coronary loading. Collectively, this information will help guide surgeons towards optimal tissue sources for bypass grafting, some of which are yet to be realized, and provide a basis for alternate therapeutic approaches such as tissue engineering (Carey et al., 2009; Hess et al., 2014).

Figure 6.

Relationship between the first year CABG failure rate (mean ± SD, [5–17]) and the state of the vessels in situ compared to the LAD (Ξ dashed line: ITA ●; RA ■; GSV ▲) or between the vessels in situ and that vessel under coronary loading (Ω solid line: ITA ○; RA□; GSV △). Subscripts (ri), (c), (σθ), and (σz) represent the normalized inner radius, compliance, circumferential stress, and axial stress as plotted in (A), (B), (C), and (D) respectively while Ω and Ξ (no subscript) are the summation of those metrics (E).

4.1 Structural and Mechanical Parameters and Vessel Selection

Although a multitude of logistical and practical criteria are used for surgical CABG vessel selection, matched inner radii in the in situ state has provided a historical foundation to initiate candidate vessels for transplantation. This fortunate selection criterion conveniently provides a common basis for comparison between grafts in situ and can be easily assessed using ultrasound. Under the increased pressure loading of the grafted environment however, the inner radii are modified from their in situ condition and is most evident for the GSV that experiences an increase in radius from 0.70 ± 0.39 to 1.10 ± 0.28 mm as indicated by Ω = 0.54 ± 0.44. These subtle differences may have a dramatic effect on wall shear stress, a known stimulus for remolding and intimal hyperplasia of venous grafts (Dobrin et al., 1989). Wall shear stress τ_w under steady Poiseuille flow has a cubic dependence on the deformed inner radius, namely

$${\tau }_w=\frac{4\mu Q}{\pi r_i^3},$$ (14)

where Q is the mean volumetric flow rate and μ the dynamic viscosity of blood (Berne and Levy, 2001). It should be noted that the GSV graft will also experience an increase in Q upon implantation from roughly 0.14 ml/s in the greater saphenous vein environment to 0.52 ml/s in the coronary vasculature, making the wall shear stress change less dramatic (Abraham et al., 1994; de Bruyne et al., 1996). Whereas comparable radii are important regulators of steady perfusion and steady shear stress, vascular compliance influences pulsatile perfusion and pulsatile shear stresses. Compliance is a contributing factor for anastomotic intimal hyperplasia, and the change in compliance from the in situ to the grafted environment is indicative of the nonlinear pressure-radius relationship (Ballyk et al., 1997). It is not surprising that the ITA has a similar compliance to that of the LAD considering their comparable microstructure and physiologic loading conditions.

Through mechanotransductive pathways intramural stresses apply physical signals to resident vascular cells (Zwolak et al., 1987). The stress distribution throughout the wall of the blood vessel also has important implications in health and disease with large opening angles shifting the circumferential stress distribution from the intima towards the adventitia (Wang et al., 2009). Veselý et al., (2015) found that the optimal opening angle in the human great saphenous vein for uniform stress distribution is around 40 degrees. In smaller pig studies than ours the opening angles were found to be considerably higher than our study (Guo and Kassab, 2004). This phenomenon does depend on the species and likely other taxonomic ranks (Rachev and Greenwald, 2003). Overall we did not find statistically significant differences between opening angles of our tissues. It is surprising, however, to see that the magnitude of mean circumferential stress differed so dramatically between graft tissues in situ and that the RA, GSV, and LSV had much higher stresses in the axial direction. Although the passive state of the smooth muscle cells contribute to a lower in situ stress than would be achieved with basal tone, an 18-fold difference exists between GSV (3.66 ± 0.67 kPa) and ITA (67.1 ± 14.7 kPa) so that Ξ=1.79 ± 0.04. The veins would also experience the greatest increase in circumferential stress upon grafting (GSV = 18.9 kPa, Ω = 1.44 ± 0.08; LSV = 42.0 kPa, Ω = 1.49 ± 0.09). In situ and grafted under coronary loading saphenous vein circumferential stresses ( ${\sigma }_{\theta }^{IS}=3.66\pm 0.67;{\sigma }_{\theta }^G\approx 22.8\pm 5.71\text{kPa}$), were within the range of the analogue human vessel reported in the work of Veselý et al., (2015) ( ${\sigma }_{\theta }^{IS}\approx 6;{\sigma }_{\theta }^G\approx 22\text{kPa}$). Enigmatically, the axial stresses were much higher than circumferential stresses in our study which are known to play a fundamental role in compensatory adaptation by blood vessels (Humphrey et al., 2009). Since axial prestretch is reduced with aging and disease conditions (Humphrey et al., 2009; Veselý et al., 2015) our tissue, taken from mature but young pigs, is likely at a higher stretch than those used for grafting. A likely contributing factor is the somatic growth and axial extension during development of these source tissues (i.e., extremities of the leg and arm). Moreover, the tested invariant force-pressure relationship that holds for arteries may need to be evaluated more extensively for venous structures (Van Loon, 1976). Given the assumption of material incompressibility, changes in axial extension influence other key parameters of Table 3 (e.g., radius, compliance, and circumferential stress). This relationship highlights the importance of biaxial measurements. While application of axial distension to CABGs might increase the difficulty of the procedures and put stress on the suture interface, it is worth further examination if it has the potential to reduce the incidence of graft failure in the vessels.

4.2 Framework for Evaluation of Candidate Vessels and Clinical Significance

In this work we have initiated two competing hypotheses to explain the differential outcomes of CABG procedures, each of which relies on the calculation of a comparative mechanical metric: 1) Ξ, a comparison of a graft vessel in situ to the LAD in situ, or 2) Ω, comparisons of a graft vessel in situ to that same vessel grafted under the loading conditions of the LAD. These subtle distinctions could have profound effects on how graft vessels are evaluated for candidacy in the future. Using both approaches the ITA was found to be the best mechanical choice followed by the RA. The results are less clear however, for the GSV and LSV raising the question, is it better for a graft to be more like the coronary artery (Ξ→ 0) or more like its native condition (Ω→0)? Unfortunately, the question does not have an immediate and clear answer. For example, it is tempting to assign a linear relationship to Figure 6 yet these clinical observations are limited to only three data points although the underlying dependence could be more complex. We do know however, that the normalized contribution of each of the individual parameters that make up Ξ (i.e.,Ξ_ri, Ξ_c, Ξ_σθ, Ξ_σz), is more evenly distributed than Ω, where Ω_σθ and Ω_σz contribute to 62–86% of the overall value. It is also provocative to consider a case where both Ξ and Ω intersect the origin in Figure 6. This would represent an idealized scenario where the coronary artery is used as a CABG graft resulting in zero first year failures. This is an unlikely, if not impossible scenario since the underlying cause of clinical failures are not isolated to mechanical reasons, yet it may provide insight into the importance of these two metrics. The high slopes of the linear fits used in Figure 6 suggest inner radius and axial stress as major contributors to clinical failure rates. The latter observation is profound since surgical guidelines for the CABG procedure recommend against applying axial loads. The answer to these questions and more will undoubtedly improve as clinical reports for other vessels (e.g., gastroepiploic or inferior epigastric artery) become available and are matched to mechanical data.

An important distinction between our in vitro study that considers vessels as replacement tissues for the LAD and the actual CABG procedure lies in how axial loads are applied. Current surgical guidelines for the CABG procedure advise against using excessive graft lengths to prevent kinking while tensile forces should be minimized to improve suture retention (Khonsari et al., 2008). This configuration puts vessels into neutral axial loading prior to reperfusion. Upon reperfusion however, small axial forces will be generated and can lead to bending and buckling. Still these stresses are far lower than those observed in situ resulting in a transplantation stress difference (Table 3). Khonsari points out “Saphenous vein grafts tend to shrink over time … shrinkage may cause tension on the anastomosis and predispose the graft to premature failure.” This observation is indicative of the stress-mediated growth and remodeling hypothesis aimed at restoration of in situ axial stresses described in the introduction. Regardless, the analysis described herein simplifies a complicated clinical procedure that involves bending and buckling instabilities that do not lend well to analytical approaches implemented within the framework of continuum mechanics.

In future investigations, the methods described here will be utilized in conjunction with a perfusion bioreactor to evaluate and control the vascular remodeling process and determine the dominance of the utility scores Ξ or Ω. Many theoretical studies have been proposed using stress-based growth and remodeling process for CABG for venous grafts and the current study has established the initial conditions for those future investigations which will determine the adaptability of the candidate tissues to new environments (Hwang et al., 2012; Ramachandra et al., 2014). We hypothesize that adaptability is dependent upon cellular function and the current state of the extra cellular matrix. In these future investigations, the grafted conditions applied by the ex vivo culture device will provide a prolonged remodeling stimulus, which we expect will lead to growth and remodeling within the cultured vessels. However, it is not clear whether vessels will continue to seek their initial homeostatic stress state indefinitely, take on a stress objective of a coronary artery, or a hybrid of both conditions.

While this investigation is focused on analyzing autologous CABG vessels, the outlined procedure is a universal approach that could be applied to other non-coronary grafting such as treatments for peripheral vascular disease. Beyond autologous grafts, the above methodology can give a more rigorous mechanical analysis of tissue engineered blood vessels (TEBVs) than is commonly presented. Generally, the mechanical data presented for TEBVs include uniaxial tensile tests, burst pressure, suture retention strength, and compliance, but these metrics do little to describe the functionality of the vessels in vivo (Konig et al., 2009; Shazly et al., 2015; Twal et al., 2014). Although the conditions most conducive to tissue growth will need to be identified, utilization of the current methods for mature vascular grafts could aid researchers in developing more functional TEBVs with quiescent properties (McFetridge and Chaudhuri, 2005). If the aforementioned grafts are to be used for grafting applications such as CABG where mechanical compatibility is paramount, it will be important to elucidate how the vessels develop a homeostatic state as it is influenced by biaxial loading. Moreover, ex vivo investigations under controlled mechanical stimuli could potentially allow researchers to define the homeostatic stress state for TEBVs. This would facilitate the creation of artificial grafts compatible with any mechanical loading conditions and thus any anatomical location.

4.3 Limitations

We hold that this investigation represents a meaningful contribution to the collective knowledge of vascular mechanics, but acknowledge that there are limitations to the study that merit further consideration. First and foremost, we assume that uniform loading of the grafted vessels is equivalent to that of a native LAD artery. This implies that we are considering an end-to-end anastomosed graft replacing a section of the LAD rather than following the surgical guidelines for a CABG procedure where vessels are initially under neutral axial loading. Furthermore, grafted conditions were assumed to be 100 mmHg at an axial force of 0.4 N, approximately representing the mean values experienced by the LAD. This does not account for the constant variation in stresses and strains caused by hemodynamic pulsatility and contraction of the myocardium. We also point out that all vessels were harvested taken from healthy, young pigs and that these vessels which would likely experience altered mechanics in disease and aging (Horny et al., 2011; Kamenskiy et al., 2015).

Of further note, histological differences exist between the proximal (Figure 2A) and distal (Figure 2B) sections of the LAD coronary artery due to the significant structural variations along its length. Based on our previous assumption of vessels organizing to homogenize stress at their homeostatic state, this change in histology would indicate that the loading environment changes significantly along the length of the LAD. As such, the optimal structure of a CABG graft of the LAD would vary according to where along its length it is being grafted. Moreover, the peripheral vessels of a quadraped are a less direct analogy to the human than the coronary vessels. Nowhere is this truer than for the LSV, a tissue that does not exist in the human but has applicability in veterinary medicine and laboratory studies (Figure 1). Moreover, the zero-stress state measurements were performed following mechanical testing therefore the supra-physiological loading conditions could potentially have an effect on opening angle measurements. This is likely a small contribution but one that should be considered in future work. Lastly, this investigation focused on the passive mechanics of the potential graft tissue. In highly muscular blood vessels such as the RA, GSV, or LSV, the stress state depends on smooth muscle activation and likely contributes to the low native circumferential stress values predicted in Table 3. An additional term could be added to account for active smooth muscle behavior (Baek et al., 2007; Cheng et al., 2013).

5. Conclusion

Mechanical loading is an important factor driving vascular growth and remodeling in autologous grafting of mature blood vessels. Differences in structural and mechanical characteristics, as demonstrated by our novel metrics Ξ and Ω, provide a reference to the extent that remodeling must occur in the grafted environment and provides supportive evidence for the differential performance of CABG grafts. The results of the current study are consistent with vessel-specific variations in clinical success rates and provides the groundwork for engineering a better material for CABG procedures. Further investigation and experimentation is necessary to determine if these metrics can be manipulated, acutely or chronically on native tissues, to improve CABG outcomes.