The RNA 3D Motif Atlas: Computational Methods for Extraction, Organization and Evaluation of RNA Motifs

Abstract

RNA 3D motifs occupy places in structured RNA molecules that correspond to the hairpin, internal and multi-helix junction “loops” of their secondary structure representations. As many as 40% of the nucleotides of an RNA molecule can belong to these structural elements, which are distinct from the regular double helical regions formed by contiguous AU, GC, and GU Watson-Crick basepairs. With the large number of atomic- or near atomic-resolution 3D structures appearing in a steady stream in the PDB/NDB structure databases, the automated identification, extraction, comparison, clustering and visualization of these structural elements presents an opportunity to enhance RNA science. Three broad applications are: (1) identification of modular, autonomous structural units for RNA nanotechnology, nanobiology and synthetic biology applications; (2) bioinformatic analysis to improve RNA 3D structure prediction from sequence; and (3) creation of searchable databases for exploring the binding specificities, structural flexibility, and dynamics of these RNA elements. In this contribution, we review methods developed for computational extraction of hairpin and internal loop motifs from a non-redundant set of high-quality RNA 3D structures. We provide a statistical summary of the extracted hairpin and internal loop motifs in the most recent version of the RNA 3D Motif Atlas. We also explore the reliability and accuracy of the extraction process by examining its performance in clustering recurrent motifs from homologous ribosomal RNA (rRNA) structures. We conclude with a summary of remaining challenges, especially with regard to extraction of multi-helix junction motifs.

Graphical Abstract

1. Introduction

This contribution concerns the computational extraction, analysis, and organization of RNA 3D motifs. In this introductory section, we define the different types of 3D motifs we observe in atomic-resolution RNA structures, discuss their properties and functions, and identify those that are amenable to current methods for extraction and clustering. Then we discuss, with reference to the wider goals of RNA bioinformatics, some reasons for systematically analyzing atomic resolution RNA 3D structures to identify, extract, and cluster 3D motifs, including construction of computational tools for RNA structure prediction and analysis. In the Materials and Methods section we discuss the selection of a target set of reliable, non-redundant (NR) RNA 3D structure files for analysis. We also provide computational details of methods currently used to build and maintain the RNA 3D Motif Atlas, see http://rna.bgsu.edu/rna3dhub/motifs [1]. In the Theory section, we provide the conceptual framework used to annotate, classify and cluster RNA motifs into coherent groups intended for downstream bioinformatic analysis. We begin the Results section by reviewing the current content of the RNA 3D Motif Atlas. Then we assess how well the current implementation of the computational pipeline organizes RNA 3D motif instances by tracking the clustering of motif instances from corresponding positions of homologous ribosomal RNA (rRNA) 3D structures from different organisms. We conclude with a summary of outstanding issues in extraction and classification of hairpin loops (HL) and internal loops (IL) and challenges in extending the 3D Motif Atlas to linker regions (defined below) and multi-helix junction (MHJ) loops.

Other workers have developed similar methods to identify, extract, and cluster RNA 3D motifs and websites to make them available in searchable formats [2–6]. This contribution is not meant as a comprehensive comparison of all the available methods, but as an attempt to provide detailed explanation of our own approach, as well as an extensive discussion of its limitations and the opportunities for future work in the field.

1.1 What are “RNA 3D Motifs”?

We use this term to refer to modular arrangements in 3D space of mutually interacting RNA nucleotides localized within the secondary structure, that is, nucleotides delimited by a set of mutually nested AU, GC, or GU cis Watson-Crick (WC) basepairs [7]. For our purposes, the secondary structure separates the nucleotides of the linear sequence into two disjoint classes, those that form the secondary structure, per se, and all the rest. The former comprise the WC-paired helices. The latter constitute the so-called “loops” and “linker segments” of RNA chains. These are the nucleotides that may form 3D motifs. Some ambiguity, however, remains regarding those nucleotides that form “isolated” WC pairs that occur within or between 3D motifs and which are not stacked contiguously on other WC pairs, on at least one side. It is not a simple, easily codified matter to decide which of these isolated pairs should be assigned to the secondary structure and which are best considered elements of the 3D motifs that surround them.

Strictly speaking, the Watson-Crick (WC) paired helices composing the secondary structure are also 3D motifs. While RNA helices are quite rigid, they nonetheless exhibit sequence- and context-specific structural variation. As this has been studied extensively elsewhere [8–11] we do not further consider RNA helices in this contribution.

The nucleotides forming the secondary structure generally comprise 60–70% of the nucleotides of structured RNAs. For example, just 60% form the secondary structure of 16S rRNA, while the remaining 40%, a significant fraction, constitute the loops and linkers [12]. In 2D representations of structured RNAs, these nucleotides are generally displayed as unstructured “loops,” separated by Watson-Crick paired helical elements, or as single-stranded “linkers,” joining distinct domains of the 2D structure. Such schematic representations seem to imply that these regions of the RNA are loosely structured or devoid of interactions. However, now that we have atomic-resolution structures for many structured RNAs, including the ribosomal RNAs (rRNA), we know that most loop regions are, in fact, structured by networks of non-Watson-Crick (non-WC) base-pairing, base-on-base stacking and base-to-backbone interactions [13]. We also verify that there is, in general, though not always, a one-to-one correspondence between individual “loops” in the 2D structures and modular 3D motifs.

1.2 Topological Classification of 3D Motifs

Nucleotides forming “loops” are bordered on all sides by helical elements and so the corresponding 3D motifs can be classified topologically by the number of flanking Watson-Crick pairs. (The reader should note this does not apply to nucleotides in linker segments). The simplest loops are “terminal” or hairpin loops (HL), flanked by just one Watson-Crick (WC) pair, where the RNA chain folds back on itself. Internal loops (IL) are embedded between two helical elements and are flanked on two sides by Watson-Crick pairs. They comprise two distinct segments of the RNA chain.

Multi-helix junction (MHJ) loops are formed from three or more independent, interacting chain segments and are flanked by an equal number of WC pairs. MHJ are further classified, at the 2D level, according to how many chain segments and flanking pairs they comprise. The simplest and most common are three-way junctions (3WJ), followed by four-way junctions (4WJ). In biological RNA molecules, MHJ loops of rank five to ten are observed [14,15]. Thus, MHJ loops are classified topologically according to the number of helical elements. However, this is a 2D classification. In fact, each topological category of MHJ comprises many different 3D motifs, differing among themselves in the arrangement in 3D space of the helices radiating from the junction [16]. The 3D arrangement of the helices is determined by detailed interactions between nucleotides at the junction, as well as distant tertiary interactions that orient and anchor the helices radiating from MHJ loops in 3D space. The relevance of this fact for RNA function became evident in studies of the mechanism of the self-cleaving hammerhead ribozyme, an RNA enzyme having a three-way junction (3WJ) at its active site. Long-range interactions between two of the helices far from the 3WJ site proved crucial for achieving the correct structure at the active site to make RNA catalysis possible [17,18]. Many outstanding issues remain regarding extraction and clustering of MHJ (see Results and Conclusion).

1.3 Modularity and Recurrence of 3D Motifs

For our purposes, RNA 3D motifs are collections of nucleotides that form dense networks of interactions, what mathematicians call connected graphs. As such, they form modular structural units, that are distinct and self-contained in the sense that interactions the motif forms with other molecules or parts of the same RNA depend on, or are contingent, upon the correct formation of interactions internal to the motif. A significant fraction of nucleotide interactions in modular motifs are “internal”, that is, they occur between nucleotides of the motif.

RNA 3D motifs may also be “recurrent.” These are motifs that are structurally similar, as defined below, and that occur in diverse contexts, not only in corresponding positions of homologous RNA molecules. “Diverse contexts” means different locations within a single RNA molecule as well as occurrences in molecules unrelated by homology. For example, the Sarcin/Ricin motif in loop E of 5S rRNA in H. marismortui occurs five times in the LSU rRNA of the same organism, cf. Section 4.1.2, and in other non-ribosomal RNAs. Recurrent motifs can vary in sequence but conserve the 3D structure and the types of interactions among comprising nucleotides. Many recurrent hairpin loops (HLs) and internal loops (ILs) are known, but far fewer recurrent MHJ loops appear to be recurrent.

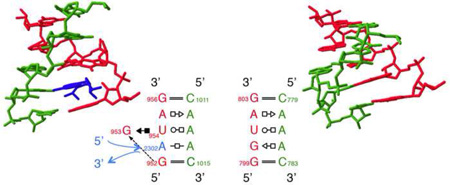
Continuing with the example of 5S rRNA, we note that all ribosomes except some mitochondrial ones contain this molecule, which is found in the central protuberance of the Large Subunit (LSU) on the side facing the Small Subunit (SSU). A recurrent IL called “loop E” in 5S rRNA interacts with a conserved IL in Helix 38 (H38), the “A-site finger” of the LSU rRNA that extends across the inter-subunit interface to contact the SSU. Within bacteria, loop E is highly conserved (see Figure 1) but in archaea and eukarya, it is substituted by a distinct but related 3D motif that has the same structure as the Sarcin/Ricin (S/R) motif, first identified in the Factor-binding site of the LSU rRNA [19].

Figure 1.

Annotated basepair diagrams for corresponding IL motifs in helix 4 of 5S rRNA (“loop E”). The first three are bacterial structures, and consist of seven stacked non-WC basepairs, including rare bifurcated (B) and water-inserted (W) basepairs cWW pairs. The archaeal and eukaryal versions of 5S loop E have the same structure as the highly-recurrent Sarcin/Ricin motif. The two eukaryal instances have an extra cis Watson-Crick basepair compared to the archaeal instance, and so are placed in different motif groups in the Motif Atlas.

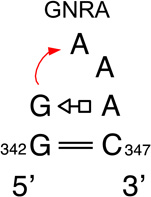
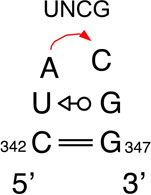
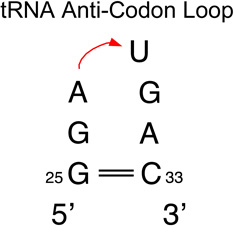
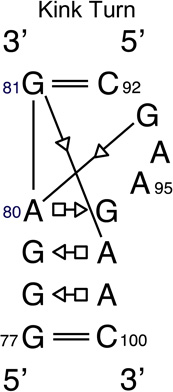
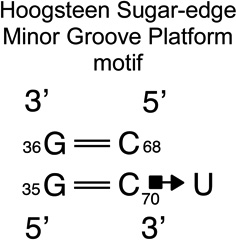
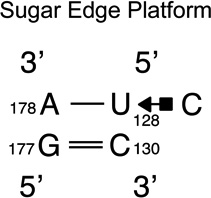
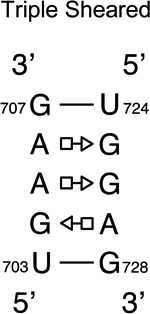
We provide a list of some common recurrent RNA 3D motifs that we have identified in the RNA 3D Motif Atlas in Table 1. Some of these are very familiar to RNA scientists and include GNRA and UNCG “tetraloops,” Anti-codon and TPsiC HL from tRNA, Sarcin/Ricin (S/R) and the related 5S rRNA “loop E” IL, kink turn motifs, C-loops, and the “11-nucleotide” GAAA loop receptor motif. Others do not have established names, but are found to be highly recurrent by the clustering algorithm. These are represented by their characteristic interactions, as noted by names like “tandem sheared pair,” indicating an IL motif comprising oppositely directed and stacked “sheared” (i.e. trans Hoogsteen-Sugar Edge) basepairs. Some recurrent motifs are represented by more than one motif group in the RNA 3D Motif Atlas, due to small structural differences, usually near the flanking basepairs of some motif instances, that are sufficient to trigger generation of new groups by the clustering procedure. For the most recurrent motifs, instances are found in a great diversity of RNA structures. Table 1 provides links to the Motif Atlas as well as schematic diagrams of exemplar instances.

Table 1.

Motif Name	Motif IDs (RNA 3D Motif Atlas 1.18)	Number of Structures	Number of instances
	HL_18781.9	25	30
	HL_67042.17, HL_71179.1, HL_74411.3, HL_33402.8, HL_48507.3, HL_11547.7, HL_90506.1, HL_82538.5, HL_19626.4, HL_86077.4, HL_48116.3, HL_61547.5, HL_92706.1, HL_57963.1, HL_79956.2, HL_70383.1, HL_08494.1, HL_62564.1, HL_79038.1, HL_15291.1, HL_96515.1	116	460
	HL_72498.17, HL_97270.8, HL_24544.6, HL_85534.6, HL_72543.3, HL_19066.1, HL_93771.1, HL_96309.1, HL_86123.2, HL_84888.1, HL_36151.1	81	137
	HL_39895.11, HL_27353.2, HL_21419.2, HL_15793.1, HL_21695.1	38	59
	HL_74465.7	17	18
	IL_65553.12, IL_77263.3, IL_34363.4, IL_28572.5, IL_37053.4, IL_48918.3, IL_34628.2, IL_37400.1, IL_65137.1, IL_21254.1, IL_37408.1, IL_59934.1, IL_68827.1, IL_40527.1, IL_91857.1	38	70
	IL_39199.8, IL_67828.2	41	74
	IL_44540.8, IL_67828.2	33	62
	IL_37976.1, IL_68859.1, IL_93568.6	26	67
	IL_13959.8	22	39
	IL_55938.8	15	27
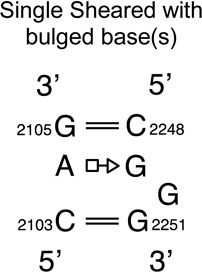
Tandem sheared with bulged base(s)	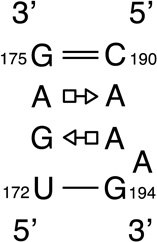IL_31555.8	12	15
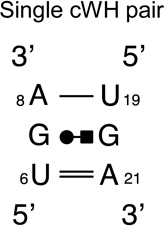
	HL_72498.17	65	78
	IL_85638.1	25	43

1.4 Sequence Signatures

Instances of the same RNA 3D motif can vary in sequence. A major motivation for extracting and organizing motifs by structural similarity is to document the range of sequence variation observed for each motif group, so as to define an empirical “sequence signature” for the motif. The sequence variation observed among 3D instances assigned to the same motif group can be augmented with sequence data from corresponding sites in homologous RNA multiple sequence alignments, although this needs to be done with care to ensure that the 3D structures of the motifs are conserved throughout the alignment. Such data inform probabilistic methods designed to predict 3D structures of RNA motifs from sequence [20]. Figure 1 shows annotated basepair diagrams for six instances of loop E from 5S rRNA in bacteria, archaea, and eukarya. These show that all 5S loop E motifs are structurally related, with the bacterial ones all forming the same types of basepairs, as indicated by the basepairing symbols, which are explained in Section 3. Therefore, the bacterial loop E motifs all belong to the same motif group. Figure 1 also shows that the archaeal and eukaryal loop E motifs form the same basepairs, but some of these pairs are different from those in the bacterial motif, showing that loop E motifs fall into two distinct groups. Moreover, Figure 1 illustrates that within each group, there are base substitutions, but that these preserve the basepairing type. Moreover, these substitutions are isosteric, as discussed below.

1.5 Autonomy, Induced Fit and Conformational Flexibility

RNA 3D motifs may also be “autonomous,” by which we mean RNA sequences that fold into their functional 3D structures independently of, or prior to, interactions with other structural elements or molecules. There is evidence from MD simulation and biophysical studies that some RNA 3D motifs are highly autonomous [21– 23]. These motifs form sufficient numbers of stabilizing interactions among their nucleotides to assume essentially the same structure regardless of the context in which they are found. A good example in this respect is loop E in helix 4 of 5S rRNA. In bacterial 5S rRNA, this loop is a highly symmetrical loop consisting of seven stacked non-WC basepairs, as shown in Figure 1. In archaeal and eukaryal 5S rRNA this loop takes the form of a Sarcin/Ricin (S/R) motif, an asymmetric motif in which each base forms at least one non-Watson-Crick basepair and three bases form a base triple (cf. Figure 1). MD simulations and thermodynamic studies have shown that each of these motifs are unusually stable even in the absence of their interacting partners [22–25].

Recurrent motifs tend to be autonomous, as apparently is the case for 5S loop E, but this is not always the case, especially for larger motifs, some of which require folding by induced fit to assume their functional forms. Such appears to be the case for the GAAA loop receptor (the so-called “11-nt motif”), which changes structure upon binding its cognate GAAA HL [26].

Other RNA motifs are conformationally flexible; their 3D structures change in response to changes in their environment, as an integral part of their function. The classic example is the IL in helix 44 of 16S rRNA, which functions to “decode” the codon/anti-codon interaction between mRNA and the incoming tRNA. This IL motif comprises two adjacent, unpaired adenosines (T. thermophilus 16S nucleotides A1492 and A1493) that are tucked inside helix 44 in the absence of tRNA but swing out when tRNA is bound to the A-site of the SSU, to interact with the first and second base-pairs of the codon/AC mini-helix. (See http://rna.bgsu.edu/rna3dhub/loops/view/IL_1J5E_056 for the “tucked in” conformation and http://rna.bgsu.edu/rna3dhub/loops/view/IL_1FJG_057 for the “swung out” conformation.) The interactions they form, and therefore the conformation of the decoding loop, depends on whether the bound tRNA is cognate, near-cognate, or non-cognate to the A-site codon presented by the mRNA, as documented by a series of ribosome structures [27–29]. When the interaction is cognate, the two bulged As form ideal “A-minor” interactions, i.e. Sugar-Edge basepairs with the mRNA/tRNA BPs. In this case, the conformation assumed by the motif is transduced into a signal to the large subunit to stimulate the elongation factor EF-Tu to hydrolyze ATP and release the amino-acyl end of the tRNA into the LSU A-site, leading to peptide bond formation [30].

1.6 3D Motif Functions and Motif Interchangeability

RNA 3D motifs are the primary loci of functional interactions in structured RNA molecules. They also provide structural variety to confer structural complexity to RNA that rivals that of proteins, by breaking up the linear monotony of the Watson-Crick double helix. Functions of individual motifs include the following: 1) To specifically bind small molecule ligands, proteins, or other RNAs; 2) to mediate tertiary interactions that allow RNA molecules to fold compactly; 3) to play architectural roles; 4) to provide nucleation sites to guide RNA folding; and 5) to create structural complexity by introducing branching points in the secondary structure. These are not exclusive roles: instances of the same motif can play multiple roles simultaneously, depending on the context in which they occur.

The function of many RNA 3D motifs is to mediate long-range tertiary interactions within the same RNA, with other RNA molecules, or with proteins or small molecules. The GNRA and TPsiC hairpin loops are examples of motifs that form tertiary interactions almost everywhere they are observed. GNRA HL present three stacked bases that interact in the minor grooves of target helices [31]. TPsiC or “T-loop” HL present intercalation sites for purines “bulged out” of other RNA motifs [32].

Some 3D motifs mediate interactions with other RNA molecules or with proteins. For example, several motifs in SSU, including the decoding site IL mentioned above, interact with mRNA and tRNA. Most RNA-protein interactions in 16S involve nucleotides found in loops. For example 60% of nucleotide-amino acid interactions in E.coli 16S rRNA involve loop nucleotides, even though these constitute just 42% of all 16S nucleotides [12].

Other RNA 3D motifs appear to primarily play architectural roles. These include the C-loops, which increase the helical twist of the RNA helix in which they are embedded [33–35], and the Kink-turns, which introduce a sharp bend or kink into helices in which they are found [36]. There is evidence from structure comparisons and MD simulations that kink-turns also function as hinges [37,38].

Finally, some motifs appear to play primarily stabilizing roles that guide RNA folding. For example, the very common UNCG hairpin loops appear to serve as nucleation sites for forming hairpin loop-stems because of their unusual thermodynamic stability [39,40]. This stability has been factored into structure prediction algorithms, such as the mFOLD program [41–43], to improve computational folding and structure predictability.

An important question that motivates the study of RNA 3D motifs is to determine which motifs can structurally or functionally substitute for each other, and are therefore functionally interchangeable. Such motifs constitute alternative, functionally equivalent, and modular building blocks for RNA nanotechnology [44]. An important source of data is provided by 3D structures of homologous molecules. Geometries and interactions of corresponding 3D motifs from homologous molecules can be compared to identify interchangeable motifs. In this way, for example, it is found that at least two different 3D motifs correspond to the IL called “loop E” in 5S rRNA [25,45–47]. The motif in bacterial and chloroplast 5S is distinct from the one found in archaeal and eukaryal 5S, which is identical in most cases to the Sarcin/Ricin of 23S rRNA (see Figure 1). The ribosome structures show that in all cases, archaeal, bacterial and eukaryal, 5S rRNA loop E interacts with a conserved IL in the “A-site Finger,” helix 38 of LSU rRNA.

1.7 Reasons for extracting and organizing RNA 3D Motifs

The motivation for this work in the wider context of understanding the role of RNA in living cells is the following: High throughput transcriptomic studies have shown that most of the DNA in eukaryal genomes (including human) is transcribed into RNA at some point in the life cycle of the organism, even though less than 2% actually codes for protein [48,49]. Large numbers of new RNA molecules have been identified in these studies. However, the biological characterization of RNA continues to lag far behind genomic and transcriptomic identification of new RNA molecules. Evidence that many of these RNAs are likely to be functional is provided by the high temporal and spatial specificity of their transcription, especially in the brain [50,51] and by sequence and structural conservation within or across phylogenetic groups. Moreover, given that the numbers, types and even sequences of proteins are highly conserved among mammals, and even among animals of all kinds, evidence is accumulating that evolutionary processes producing new animal species, for example the emergence of humans from the great ape lineage, may be driven in part by rapid RNA evolution [52–54]. Understanding the functions of new RNAs can be aided by predictions of their 2D and 3D structures. Methods for predicting 2D structures of RNAs are highly developed, although there is still room for improvement, but RNA 3D structure prediction, even starting from a reliable 2D structure, is still very challenging, as documented by the results of recent blind “RNA Puzzles” prediction competitions and reviews of the field [55–57]. We believe that careful study and comparison of the RNA 3D structures we already have, with each other and with aligned homologous sequences, can contribute to improving the methods of 3D RNA structure prediction.

Historically, experimental determination of RNA 3D structure has been time consuming and highly contingent on obtaining suitable crystals for diffraction. This is changing rapidly with the advent of atomic resolution cryo-EM, which now achieves atomic resolution of the same large RNA-containing complexes in multiple functional states with distinct conformations [58,59]. These advances promise a wealth of new structures to be analyzed and organized into accessible and useful formats.

1.8 Motifs that are not Readily Amenable to Identification and Extraction

Motifs commonly found in internal loops, hairpins, and some junctions are closed by Watson-Crick pairs and therefore are readily amenable to extraction and grouping, with only a few exceptions, as we describe in Section 3. However, not all interesting motifs are closed by Watson-Crick pairs. For example, in many large RNA molecules, structural domains are connected by single-stranded segments of the RNA chain. We call such segments “linkers.” For example the body domain of the SSU rRNA is connected to the head by a linker. Likewise, helix 44, which contains the decoding IL, is connected to the head domain by a linker. Moreover, the 3D structure reveals a large number of base-pairing and base-stacking interactions involving nucleotides in the linker and nearby helices, to form a highly structured “neck,” made of RNA, connecting these domains. The 3D motifs that constitute the neck in 16S are not identified or extracted by methods designed to extract HL, IL, or conventional MHJ [60]. New methods are needed to treat such motifs.

Long-range interactions represent another type of recurrent RNA 3D motif that is not extracted by methods targeting HL, IL, and MHJ loops. For example, GNRA HL, which form tertiary interactions almost everywhere that they occur, form recurrent motifs with their target receptors.

There do not appear to be many recurrent MHJ having a clearly defined consensus set of core nts and conserved inter-nucleotide interactions. Recent efforts to classify RNA 3WJ produced a small number of fairly broad classes characterized largely by differences in co-axial helical stacking at the junction [16]. Similar results were obtained for larger junctions [14]. New approaches will be needed to systematically identify and extract recurrent motifs formed by linkers, tertiary interactions, and higher-order MHJ.

1.9 Strategy for Assessing Motif Clustering

Any new clustering procedure needs to be assessed. The ideal clustering procedure groups together instances that are sufficiently similar and separates those that differ sufficiently to require distinct groups. If too many groups are generated, this leads to a plethora of singletons (groups with only one instance), some of which belong with other instances. With too few groups, heterogeneous instances are included in some groups making it difficult to derive sequence signatures for motifs or to make meaningful statements about the geometric variability of the instances.

An excellent source of RNA 3D motif instances for assessing current clustering procedures are the ribosomal RNA (rRNA) structures. The rRNAs represent an ideal test case because they contain a large number of IL and HL and have been solved from a variety of organisms representing all major phylogenetic domains [61– 66]. In addition, the function of the ribosome has been extensively studied, and detailed knowledge is available regarding the functional roles of each of the helical elements of the SSU and LSU rRNAs, including protein, tRNA, and mRNA binding sites and loci of functional conformational flexibility. Finally, a large number of aligned sequences are available for both the SSU and LSU rRNA of all major phylogenetic domains, including chloroplast and mitochondria. As a whole, these data provide good indications regarding which IL and HL in the SSU and LSU rRNAs are likely to be conserved in 3D structure and for which phylogenetic domains. In the Results section we will illustrate the approach using the hairpin loops of bacterial SSU rRNA. A complete analysis for HL and IL of SSU and LSU across all phylogenetic domains will be presented elsewhere.

In previous work, we compared the structures of corresponding HL and IL in rRNA using R3D Align, an online web application we constructed to locally align the 3D structures of homologous RNA molecules [67]. We found a high degree of structure conservation of motifs at corresponding locations. Here we ask into which motif group of the RNA 3D Motif Atlas corresponding loop instances from the representative rRNA structures of the NR set (see below) have been placed. If corresponding instances are placed in the same motif group, that is a sign that their geometries are strongly conserved. Where they are placed in different groups, this is a sign of variability in the geometry, including the internal base-pairing of the motif instance. Sometimes, corresponding motifs are placed in different, but structurally related groups. By comparing the clustering results with the expected variation in structure we can assess the reliability of the clustering approach. We define a successful clustering as one that reproduces the known similarities and differences among homologous corresponding motifs in homologous RNA molecules.

1.10 Incorporating Assessments of Quality of RNA 3D Data

The PDB is now providing structure quality information at the nucleotide level to indicate how well the modeled residues of a macromolecular structure fit the experimental electron density. One measure is the Real-Space Refinement statistic (RSR) calculated from the difference between the experimental electron density and that calculated from the 3D model [68]. Values range from 0 to 1, with smaller values indicating a better match to the data. RSR values are provided as part of PDB’s validation pipeline for new structures and for older structures deposited with structure factors [69]. PDB also computes percentile rank scores which facilitate comparison of RSR values between different structures. Using these data to filter out poorly modeled loop instances will improve the quality of data included in any collection of RNA 3D motifs.

2. Materials and Methods

2.1 Sources and Nature of Atomic-Resolution Structural Data

The Protein Data Bank (PDB) is the international, archival repository of experimental 3D structures of macromolecules of biological interest, including structures of RNA, DNA, and polysaccharide molecules in addition to proteins. As such, it contains entries for all author-deposited structures that meet its criteria for scientific originality and accuracy. The PDB therefore contains a large amount of information, much of which is redundant for purposes of identifying, classifying, and searching for structural motifs in RNA 3D structures. For example, there are now hundreds of structures of ribosomes, from a fairly small number of model organisms. Ribosome structures from the same organism generally differ from each other in the numbers and types of ligands bound, the functional state of the ribosome (including stage in the translation cycle), and the resolution of the underlying data and quality of the 3D modeling. These differences are reflected in small conformational changes in specific parts of the rRNA structures where binding takes place or in large domain motions (for example, rotation of the SSU “head” during translocation), but these differences are generally quite limited in their effects on the structures of most 3D motifs.

Therefore, before attempting to extract 3D motifs, we group PDB structures of the same type of RNA from the same organism into “equivalence classes,” to avoid being overwhelmed by these kinds of redundancy. All structures in the same equivalence class can then be ranked with suitable metrics to assess the reliability of the underlying experimental data and the quality of the 3D modeling. Using the top-ranking structures as representatives of each equivalence class, we form a non-redundant (NR) set to represent all 3D structures in further analyses. We have implemented procedures as a data pipeline to build NR sets of RNA-containing experimental 3D structures for the Nucleic Acid Database (NDB), the special purpose database that focuses on DNA and RNA structures [13,70].

Here we briefly summarize the procedures implemented and indicate some changes that are currently underway to take advantage of the features of the mmCIF file format, which recently superseded PDB format for all new structures in PDB/NDB.

2.1.1 Grouping RNA-containing 3D Structures into Equivalence Classes

In this section we describe a procedure to organize RNA-containing 3D structures from PDB based on the sequence of the longest RNA chains in the structures and their geometry. The procedure aims to identify all PDB files that represent the same molecule from the same organism and group them together into “Equivalence Classes.” Thus all structures that contain E. coli 16S rRNA belong in the same equivalence class, while all T. thermophilus 16S structures belong in a different class.

The procedure works at the level of entire files by analyzing only the longest chain in each file. This is because when the procedure was first implemented, the PDB was providing PDB-formatted files for all 3D structures. PDB format is limited to 99,999 atoms per file and so the 3D structures of large supramolecular complexes, such as ribosomes, were split into separate PDB-formatted files. Consequently the large and small ribosomal subunits (LSU and SSU) were placed in separate files, and so equivalence classes of these important molecules were synonymous with equivalence classes of 3D structure files. When X-ray structures contained more than one ribosome in the unit cell, these were separated into yet more files. NMR structures typically contain multiple models of the same molecule, all with the same sequence and all in the same file, and so we focused on the longest chain in the first model.

The procedure begins by identifying the longest chain in each RNA-containing 3D structure file, using the alphabetically first chain to break ties. We then deem a pair of structures to be equivalent if 1) the longest chains have roughly the same sequence (we use specific cutoffs for different ranges of lengths), 2) the “organism” annotations are consistent (we allow grouping of synthetic or unlabeled chains with labeled chains), and 3) the overall geometry is the same, as measured by geometric discrepancy being below 0.4 Å per nucleotide (see below for the definition of geometric discrepancy). Once we have found all pairwise equivalences between structures we extend by transitivity (“transitive closure”) to create groups of mutually equivalent structures. These groups are given identification strings and can be viewed online. For example, the T. thermophilus 16S equivalence class has identifier NR_all_42982.33 and can be viewed at http://rna.bgsu.edu/rna3dhub/nrlist/view/NR_all_42982.33. It contains 256 different 3D structures of this molecule with release dates ranging from the year 2000 to 2014.

2.1.2 Selection of Non-Redundant Sets of 3D Structures for Analysis

For the purpose of motif extraction, motif searching, and visual inspection, it is helpful to select just one structure out of each equivalence class, and it is useful to do this at different resolution thresholds. In our procedure, the structures in each equivalence class are ranked by the number of FR3D-annotated basepairs (of all types) per nucleotide (bp/nt), a useful metric for the quality of the 3D modeling of a structure. After setting a resolution threshold, for example, 4.0 Angstroms, all structures above the threshold are excluded, and from the remaining structures, the with the highest value of this metric is selected as the representative of the equivalence class at the given resolution threshold. In case of ties, we use the alphabetically first file. Moreover, in some 3D structures, there may be multiple versions of the same molecule as a result of the experimental procedure, and so we identify redundant chains within each structure and list out just one copy of each chain, again seeking to maximize the number of basepairs per nucleotide. In the case of multiple models, the lowest model number is chosen. For most equivalence classes, the representative structure has a value > 0.4 bp/nt.

Collecting together the representative structures from each equivalence class gives a Non-Redundant (NR) set of RNA-containing 3D structures. We make distinct sets at 1.5Å, 2.0Å, 2.5Å, 3.0Å, 3.5Å, 4.0Å, and 20.0Å resolution thresholds. Naturally, the NR set at 1.5 Ångström (1.5Å) or better resolution is much smaller than the NR set at 4 Å resolution. This list is posted each week on our website (see http://rna.bgsu.edu/rna3dhub/nrlist/release/1.89 for the most recent release) and on the NDB website (http://ndbserver.rutgers.edu/). NR lists are used for FR3D searches (see http://www.bgsu.edu/research/rna/web-applications/webfr3d.html) and for building new versions of the 3D Motif Atlas each month.

This implementation of the equivalence classes and NR sets ran stably on the BGSU RNA server from February of 2011 until December of 2014. Updates were made weekly. See http://rna.bgsu.edu/rna3dhub/nrlist/ for a list of releases, which indicates the growth in the number of non-redundant 3D structures over time from 1645 in February 2011 to 3145 in December 2014.

2.1.3 Changes in Data Formats and Availability

The PDB continued to use the original “PDB” format for 3D structure files until December 2014. This now outdated format was limited in the number of atoms that could be contained in one file and so large supramolecular complexes such as ribosomes had to be split over multiple PDB files. Since December 2014, all new structures are released with the “macromolecular Crystallographic Information File” or “mmCIF” format which allows all structures from the same structure determination experiment to be released exclusively as a single mmCIF file. This change in available data formats requires extensive changes in our data pipeline for creating equivalence classes of RNA structures and selecting the non-redundant sets. These changes are being implemented now and will be rolled out in 2016.

A major advantage of the mmCIF format is that structures of entire macromolecular complexes can be stored in a single file. Consequently, mmCIF files may contain several distinct RNA molecules, some or all of which may belong to distinct equivalence classes. For example, mmCIF files of prokaryotic 70S ribosome structures contain 16S, 23S and 5S rRNA, each of which belong in different equivalence classes. A further complication arises because, strictly speaking, each uniquely labeled RNA chain in an mmCIF file is defined operationally as a distinct RNA molecule. However, some RNA chains, viewed from an evolutionary perspective, belong together in a single molecular entity. For example, the 5.8S rRNA in eukaryal ribosomes is an integral part of the LSU rRNA, being homologous with the 5’-end of prokaryotic 23S rRNA. Therefore, 5.8S and LSU rRNA should be grouped into a single unit, which we call an “Integrated Functional Element” (IFE). At an operational level, RNA chains that belong together in one IFE are identified by virtue of their extensive inter-chain Watson-Crick basepairing.

2.2 Assessment of Motif Classification using Homologous rRNA Structures

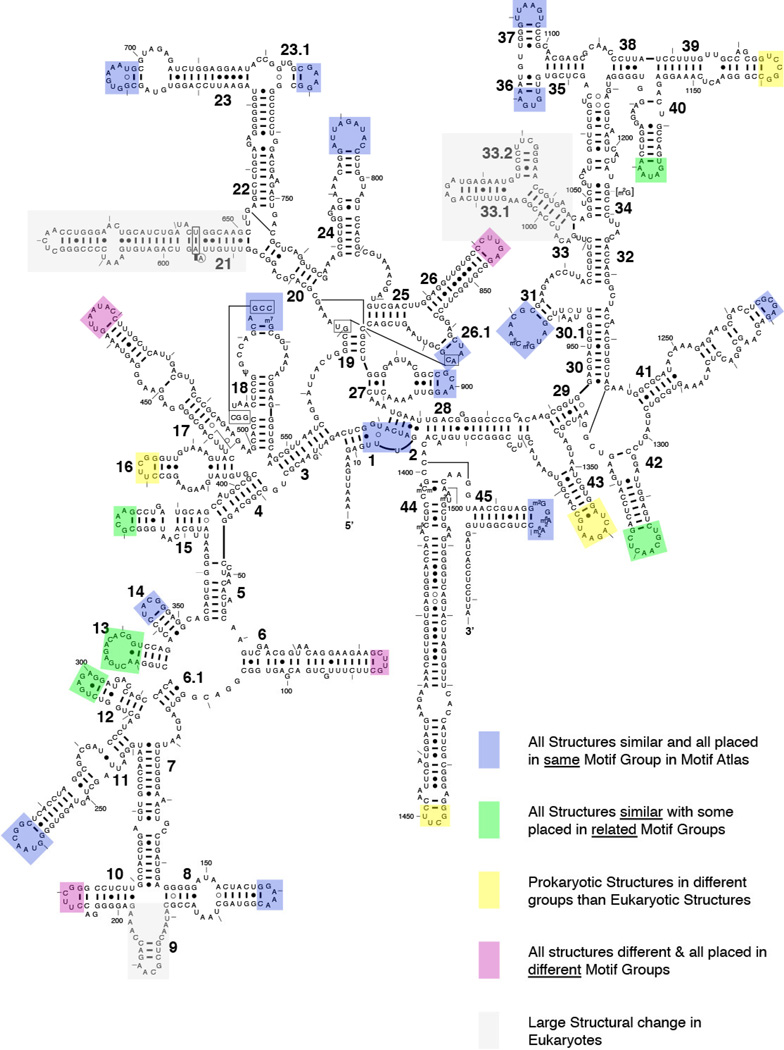
Metadata for the analysis of motif instance classification were obtained from PDB/NDB and rna.bgsu.edu, including loop and motif IDs and their URLs, PDB IDs and links to files from which each motif was extracted, motif sequences and the respective nucleotide ranges. This allowed each motif to be assigned to the respective molecule and helical element from which it was extracted and to be grouped with homologous motifs. The molecule names (SSU or LSU, Group I intron, Riboswitch, etc.) were added manually. HL and IL were placed on separate spreadsheet tables and sorted by motif ID and colored for easy visualization. Data were next sorted by molecule type and helical element to display corresponding motifs from homologous molecules together. The spreadsheet tables of “Hairpin loops” are provided in the Supplementary Materials. All motif instances were visually analyzed to evaluate motif clustering. The results of the analysis were summarized by marking motifs on 2D structure diagrams using colored rectangles to indicate the level of structural similarity, and therefore the success of the Motif Atlas clustering procedure to place motif instances from homologous locations in the appropriate motif group (See Results section 4.2.2).

3. Theory/Calculation

3.1 Theory: Principles of RNA 3D Motif Analysis and Classification

The RNA 3D Motif Atlas is designed to classify RNA 3D motifs according to 3D structural similarity. Consequently, some motif instances identical in sequence are assigned to different motif groups while other instances differing in sequence, or even in total number of nucleotides, are assigned to the same group. This is intentional and is based on many comparative observations of 3D structures of homologous RNA molecules. We see that loops with the same sequence can form different geometries in different contexts. Conversely, RNA 3D motifs occurring at corresponding positions in the 2D and 3D structure of homologous molecules can vary in sequence, including with respect to the total number of nucleotides, while forming otherwise very similar structures. The procedures we designed for extracting and clustering motifs are intended to place such motifs in the same motif group. In the Results section 4.2.2, we will assess how well that goal is achieved. In this section we provide the theoretical underpinnings for evaluating the structural similarity of RNA 3D motifs. First we discuss how it is that different RNA sequences can form very similar 3D structures and then we discuss how RNA 3D structures can accommodate varying numbers of nucleotides and still form essentially the same structure.

3.1.1 Basepair Families and Isostericity

Structurally similar RNA motifs can differ in sequence and still form the same 3D structure because of the structural similarity of the four RNA bases, two of which are purines (A and G), consisting of fused five- and six-membered heterocyclic rings, and two of which are pyrimidines (C and U), consisting of six-membered heterocycles. The two purines are very similar to each other in size and shape, as are the two pyrimidines. RNA bases, like those of DNA, are studded with functional groups, some of them Hydrogen-bonding donors and some acceptors. When two bases approach each other in the same plane, they can associate edge-to-edge if there is complementarity between their H-bond donors and acceptors. These highly characteristic interactions of nucleic acids are called base-pairs and they have been analyzed and catalogued comprehensively [71–73]. This analysis reveals that each base, whether purine or pyrimidine, can pair using any of three distinct edges, called the Watson-Crick (“W”), Hoogsteen (“H”) and Sugar (“S”) edges. All six combinations of edges are potentially possible, depending on the juxtapositions of H-bonding functional groups on the particular bases involved. Moreover, for each pair of edges, the bases can approach each other, when lying in the same plane, in two orientations, called cis and trans (“c” and “t”) and related by a 180° flip of one of the bases. Cis and trans refer to the relative orientations of the glycosidic bonds connecting the bases to the sugars. Therefore, there are twelve geometrically distinct basepairing families, distinguished by different pairs of interacting edges and whether the bases are oriented in cis or in trans. The basepairing families and the allowed base combinations for each family can be viewed and compared structurally on the RNA Basepair Catalog page of NDB (see: http://ndbserver.rutgers.edu/ndbmodule/services/BPCatalog/bpCatalog.html).

The canonical basepairs of the secondary structure belong to the cis Watson-Crick/Watson-Crick (“cWW”) family of basepairs. This family includes seven base combinations in addition to the canonical AU, UA, GC, and CG. All basepairs except the canonical cWW pairs are called “non-Watson-Crick.” Within each basepairing family, the pairs can be compared geometrically to identify which are isosteric and can substitute for each other in an RNA 3D motif without significantly perturbing the structure. We have defined a measure of isostericity called the “Iso-Discrepancy Index” (IDI), with units of Ångströms/nucleotide, to quantify the geometric similarity of two basepairs [73]. Comparison of all basepairs using IDI shows that only basepairs that belong to the same geometric family can be isosteric. The relevance of basepair isostericity to motif classification is therefore that motifs that differ in sequence can form geometrically similar motifs only if the basepairs formed by corresponding nucleotides are isosteric. This observation is fundamental to our choice of criteria to use to decide which motifs to group together, as explained in Section 3.2.4 below.

3.1.2 Defining the Core Nucleotides of Motif Instances

In this section we address how some RNA HL or IL can form very similar 3D structures while differing in the total number of nucleotides and in which cases these should be assigned to the same 3D motif group. Again, based on comparisons of corresponding motifs from 3D structures of homologous RNA molecules, many examples of this nature have been found. In most of these cases, the “extra” nucleotides found in the longer sequences are extruded or “bulged out” from the main body of the motif. These bulged out nucleotides generally do not interact with the rest of the nucleotides of the motif, except through covalent bonds in the backbone. The other nucleotides, which do interact with each other to form the network of internal stabilizing interactions that structures the motif, are found in all instances of the motif group. We assign these nucleotides to the “core” of the motif. The fundamental design decision we made for the 3D Motif Atlas was to place motif instances in the same motif group when they have the same number of core nucleotides and when these form sufficiently similar arrangements in 3D space, including basepairs from the same basepairing family as discussed above, irrespective of the positions of the “extra,” non-core nucleotides found in some instances.

3.1.3 Insufficiency of Grouping by Sequence Identity

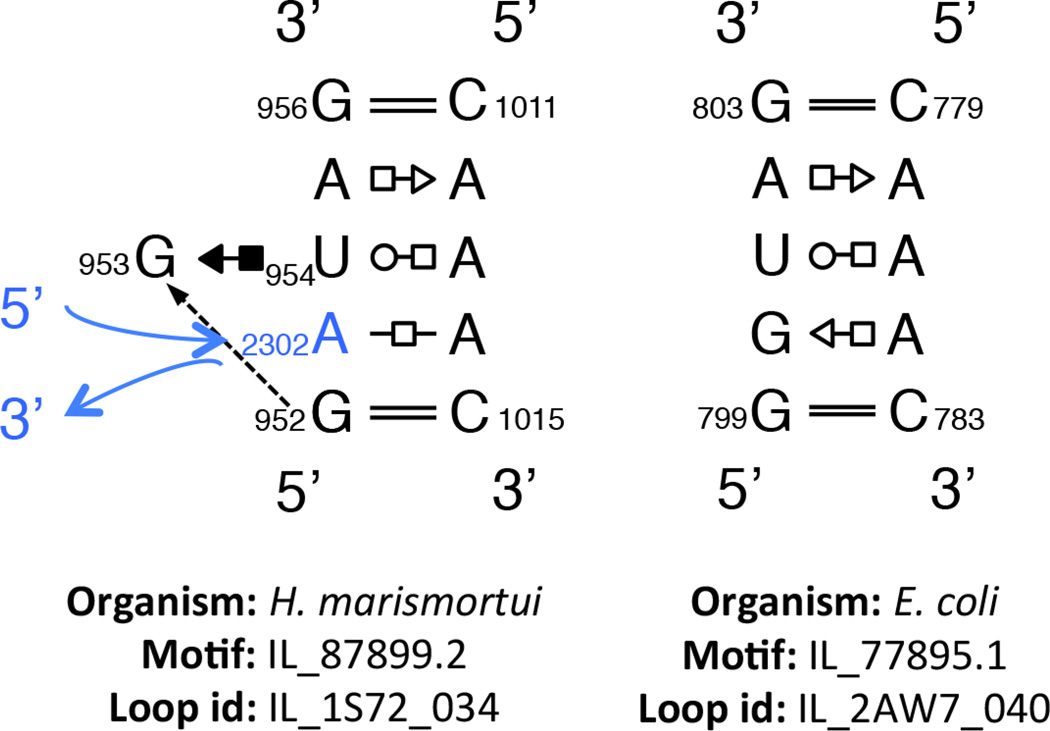
One might naively think that IL or HL having the same sequence (with or without the flanking WC basepairs) always share similar or identical geometries everywhere they occur, but in fact we find in the Motif Atlas many instances in which the same sequences form distinct geometries with substantial structural differences (C.L. Zirbel, unpublished results). A compelling example concerns multiple IL with sequence GGUAG*CAAAC. For example, loop instance IL_2AW7_040 from E. coli 16S rRNA forms a symmetric motif with three non-WC basepairs stacked between the flanking WC pairs (see: http://rna.bgsu.edu/rna3dhub/loops/view/IL_2AW7_040). However, the non-homologous loop instance with identical sequence, IL_1S72_034 from helix 38 of H. marismortui 23S rRNA has a base triple characteristic of the Sarcin/Ricin motif that creates a tertiary binding site that allows intercalation of A2302 from helix 81, which then pairs with A1014 in the loop (see: http://rna.bgsu.edu/rna3dhub/loops/view/IL_1S72_034 and click “Show neighborhood”). These structures are compared in Figure 2. Such examples show that even motifs that form stable non-WC basepairs are subject to induced fit conformational changes when presented with the appropriately positioned binding partners. These and other examples motivate grouping motifs by 3D structure and highlight the value of complementary 3D search capabilities for RNA motifs, that can accommodate bulged bases, as provided by FR3D (see http://www.bgsu.edu/research/rna/web-applications/webfr3d.html) [74].

Figure 2.

Example of two loops with the same sequence forming different structures. The left panel shows an internal loop from E. coli making a S/R-like motif using an intercalated base, shown in blue. The right panel shows a loop with an identical sequence but without the intercalated base it forms a different structure.

3.2 Calculations: Automated Pipeline for Motif Extraction and Grouping

In this section, we describe our approach to motif classification and explain how it is integrated into the automated pipeline for extraction and analysis of internal and hairpin loop RNA 3D motifs. The pipeline identifies a set of high quality 3D motif instances and clusters them into motif groups using the current non redundant 4.0Å list of 3D structures to populate the RNA 3D Motif Atlas.

The steps executed by the pipeline are as follows: An automated process is run weekly that 1) downloads all RNA-containing 3D structures from the PDB; 2) launches the FR3D annotation routines to annotate all pairwise base-pairing, base-stacking, and base-backbone interactions, as well as “near” interactions in new PDB files [75]; and 3) extracts all hairpin, internal, and junction loops from the 4.0Å NR list using the FR3D software suite developed and maintained by our group [75]. The construction of classes of equivalent 3D structures and of the NR list are explained in Section 2.2 above. Extraction and validation of motif instances is discussed next.

3.2.1 Extracting and validating HL and IL motif Instances

To facilitate automatic extraction of loop regions from RNA 3D structures, we added a new relation to the FR3D software suite called “borderSS” (“borders single-stranded region”). It is intended to aid in identifying the nucleotides that form the flanking base pairs that constitute the boundaries of each HL, IL and MHJ RNA motif [76]. The borderSS relation is motivated by the intuitive concept of “flanking base pairs” or “flanking nucleotides,” which refer to the canonical cWW pairs (GC, CG, AU, UA, GU, or UG) that form the boundaries between RNA hairpin, internal, and junction loops and the Watson–Crick helices to which they are attached. The borderSS relation is a binary, symmetric relationship that is defined to hold between two nucleotides belonging to the same RNA chain segment, if they form canonical cWW pairs that are nested within the secondary structure of the RNA molecule and when no nested AU, GC, or GU cWW pair is formed by any of the nucleotides between them in the covalent RNA chain. In the case of the closing basepair of a HL, the two nucleotides in question actually pair to each other. The use of the borderSS relation allows us to identify the start and end of each single-stranded region, whether it forms a HL by itself, an IL by associating with another RNA strand, or a multi-helix junction loop with additional single-stranded strand segments.

Next, the pipeline gathers all HL and IL from representative structures in the 4.0Å NR set and validates each loop as described in Petrov et al [1]. The 4.0Å NR sets are based largely on structures determined by X-ray crystallography. No NMR structures are included and only a small number of cryo-EM structures that have nominal resolution better than 4.0Å. We exclude all loops which have modified nucleotides, as the procedures for comparing geometries have not yet been extended to modified nucleotides. We include loops from structures that contain modified bases so long as the loops themselves do not contain any of the modified bases. We also remove loops with chain breaks or incomplete nucleotides. This results in the set of validated loops used for clustering into the motif groups that populate the Motif Atlas.

3.2.2 All-Against-All FR3D Searches and Alignments

Next, the pipeline makes all-against-all geometric comparisons of validated loops in order to identify those with sufficient geometric similarity to possibly be placed into the same motif group. We seek nucleotide to nucleotide alignments between loop instances so as to establish nucleotide correspondences for geometric discrepancy calculations (see below). To make the procedure robust against varying numbers and locations of bulged nucleotides, we consider one loop instance at a time, we temporarily exclude any bases which do not pair or stack with other bases in the loop, and we use the FR3D search tool to search for this reduced version of the loop in all other loop instances of the same motif type (for the present IL or HL) [75]. We constrain the search to respect the relative ordering of nucleotides within each strand. In principle, FR3D can return the best alignment to every other loop instance, but in practice we only consider alignments with geometric discrepancy less than 1 Å/nt. Geometric discrepancy is defined in the next section. For IL, we further restrict inclusion into the same motif group to pairs of instances for which the geometric discrepancy calculated for the flanking WC basepairs alone is also less than 1 Å/nt.

3.2.3 Calculation of Geometric Discrepancy

In this section we describe how we quantify the geometric similarity between two aligned sets of RNA nucleotides from 3D structures, for example two HL or two IL motifs. Superimposing the aligned nucleotides and calculating an RMSD between corresponding atoms is a natural approach, but aligned nucleotides may have different bases, for example, a purine in one motif aligned to a pyrimidine in the other, and bases differ in the number and relative positions of their atoms. A common choice would be to ignore the bases completely and simply superimpose the corresponding backbone atoms, but since the bases interact directly to form the stabilizing interactions that characterize motifs, we developed a different approach that allows us to directly compare the geometries of the bases [75]. For each base, we calculate a geometric center by averaging the locations of the heavy atoms (C, N, O). Then we optimally superimpose the base centers from the two loops and calculate the sum of squares of distances (in Ångströms) between corresponding base centers, which we call the location error, L². Within the optimal superposition, we also calculate the minimal angle of rotation (in radians) to bring corresponding bases into the same plane and orientation, so as to align their glycosidic bonds connecting base and sugar moieties. The sum of squares of these angles is the orientation error, A². The geometric discrepancy between the two loops is then calculated by $\frac{1}{m}\sqrt{L^2+A^2}$, where m is number of nucleotides. We express the discrepancy in units of Ångströms per nucleotide (Å/nt) [75]. The geometric discrepancy is used to compare two aligned loop instances, and also to compare the geometries of complete RNA chains when grouping RNA structures into equivalence classes.

3.2.4 Use of Maximal Cliques to Form Motif Groups

Next the pipeline groups together geometrically matched loops into motif groups. Our grouping is based both on the overall geometric similarity of the loop instances as well as annotations of base pairing in the loop instances.

Having made all-against-all alignments and geometric comparisons among all motif instances of a given type (for the present, HL or IL), as described above, we form a “motif similarity graph” with motif instances as vertices and edges connecting only those vertices for which the geometric discrepancy between the corresponding motifs is ≤ 1 Å/nt. To increase the homogeneity of motif groups, we remove edges between vertices corresponding to motif instances that have a conflicting basepair even if the discrepancy is less than 1 Å/nt. Conflicting basepairs occur when nucleotides i and j of the first instance are annotated with a different FR3D-annotated basepair than the corresponding nucleotides i and j of the second instance, e.g. tSH in the first and tWH in the second. Thus, an edge in the motif similarity graph exists only when two loops are geometrically similar and they have no conflicting basepairs.

Next we apply standard graph-theoretic algorithms to locate the largest clique in the motif similarity graph, where a “clique” is defined as a set of vertices with edges between each pair of vertices. The corresponding motif instances have mutually similar geometries and no conflicting basepairs and are therefore assigned to the same motif group and removed from the graph. We then apply the maximal clique algorithm again to find the next motif largest group, and so on until only disconnected vertices remain in the graph. These are placed in “singleton” motif groups consisting of just one member. New motif groups are provided with randomly generated identifiers, 5-digit numbers in the format IL_XXXXX for internal loops and HL_XXXXX for hairpin loops.

The procedure described above runs monthly, producing a release of the Motif Atlas approximately every four weeks. To provide continuity between releases of the Motif Atlas, motif groups that are unchanged keep the same 5-digit number from one release to the next, and those which have only small changes, such as the addition of a new member, have the name 5-digit number but have an increased version number, which comes after the 5-digit number. Thus, for example, IL_85647.7 is the 7th version of a Sarcin/Ricin motif group. This text string can be searched on the web to find the relevant Motif Atlas page.

4. Results

4.1 Overview of RNA 3D Motif Atlas Version 1.18

In this section we give brief summary statistics for version 1.18 of the RNA 3D Motif Atlas and we discuss some coherent, correctly-separated motif groups and a notable success dealing with instances containing “flipped” (i.e. anti-syn) bases. However, a careful inspection of the Motif Atlas shows some limitations in our clustering methodology. Notably, some groups contain individual instances which are geometrical outliers, relative to all other instances in the group. These instances should be separated from the others, but this is not currently done because they are within the limits of the geometric discrepancy cutoff. In addition, some groups contain instances with unusual backbone conformations that should be placed into separate groups, but remain because they escape the conflicting basepair criterion.

4.1.1 Summary Statistics

We begin the analysis of motif extraction and organization with a statistical summary (see Table 2) of the latest release of the RNA 3D Motif Atlas, version 1.18 (http://rna.bgsu.edu/rna3dhub/motifs). Release 1.18 of the Motif Atlas was compiled from HL and IL motifs extracted from version 1.71 of the 4.0Å NR list, which consisted of 834 PDB files. Release 1.18 comprises 2410 IL motif groups instances, grouped into 372 IL motif groups and 1475 HL instances, grouped into 316 HL motif groups. There are 175 IL containing just one motif instance (“singletons”) and another 65 groups with only two instances. Similarly, there are 154 singleton HL motif groups and 51 with just two instances. Note that while the number of singleton motif groups is large, only 175/2410 = 7.3% of IL and 154/1475 = 10.4% of HL instances belong in singleton groups. On the other hand, 1136/2410 = 47% of IL instances fall into the 10 largest IL groups and 599/1475 = 40% of all hairpin loop instances fall into the 10 largest HL groups. This indicates that while there are many singleton groups, most HL and IL loop instances are recurrent and fall within a relatively small number of distinct motif groups. Singleton groups are discussed in more detail below.

Table 2.

Summary statistics for 3D Motif Atlas Version 1.18. Link for IL: http://rna.bgsu.edu/rna3dhub/motifs/release/il/1.18 Link for HL: http://rna.bgsu.edu/rna3dhub/motifs/release/hl/1.18 This table summarizes the distrubution of number of nucleotides as well as the number of instances for internal loop and hairpin loop groups.

	Internal Loop Groups	Hairpin Loop Groups
Number of Instances	2404	1475
Number of Motif Groups	372	316
Range of Number of Instances/Group	1–371	1–328
Mean Instance Count/Group	6.46	4.66
Number of Singleton Groups	175	154
Range of Number of Internal Core Nucleotides	1–32	1–32
Mean Number of Internal Core Nucleotides	6.89	6.14
Range of Total Nucleotides	5–37	3–38
Mean Number of Total Nucleotides	11.99	9.56
Mean Number of Interactions/Motif	10.76	6.60
Mean Number of Interactions/Total Nt	1.05	0.78

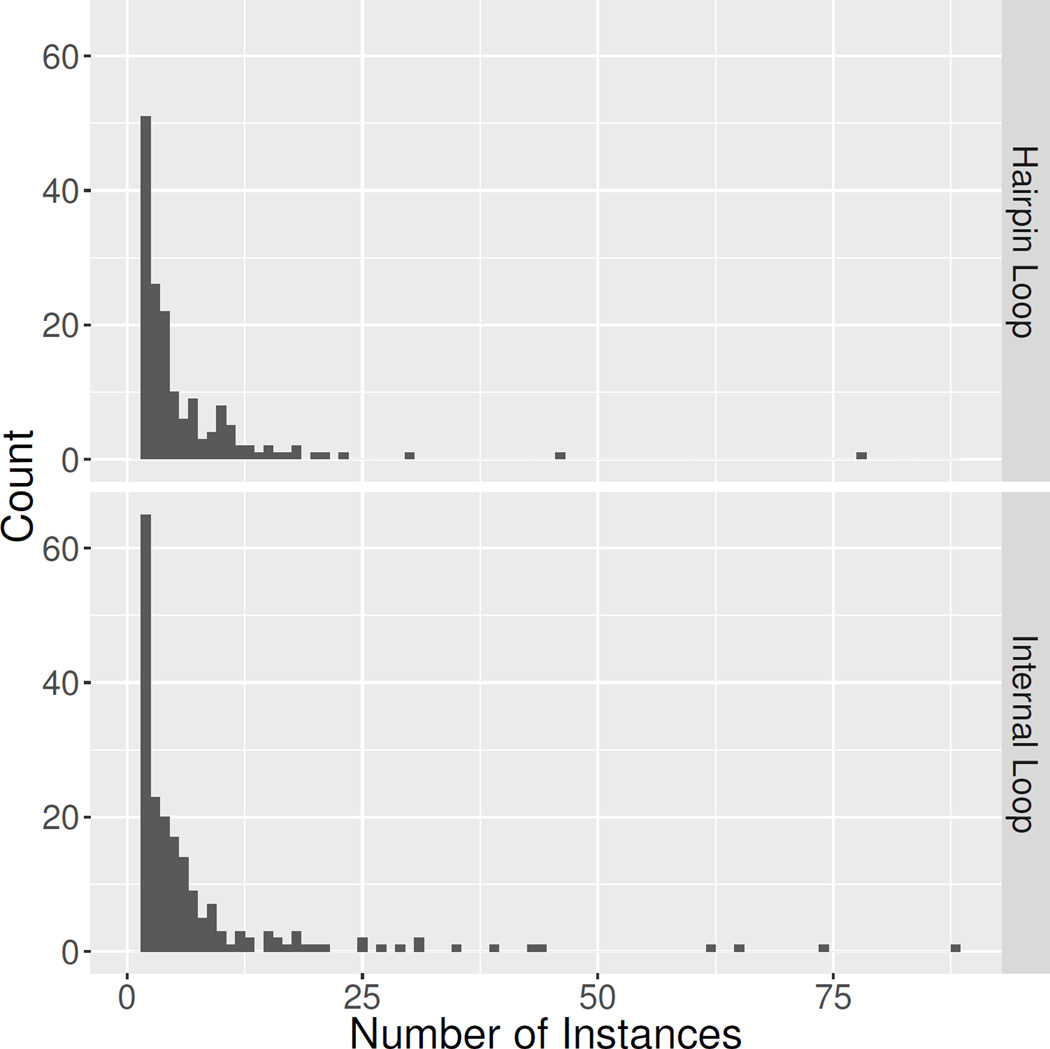
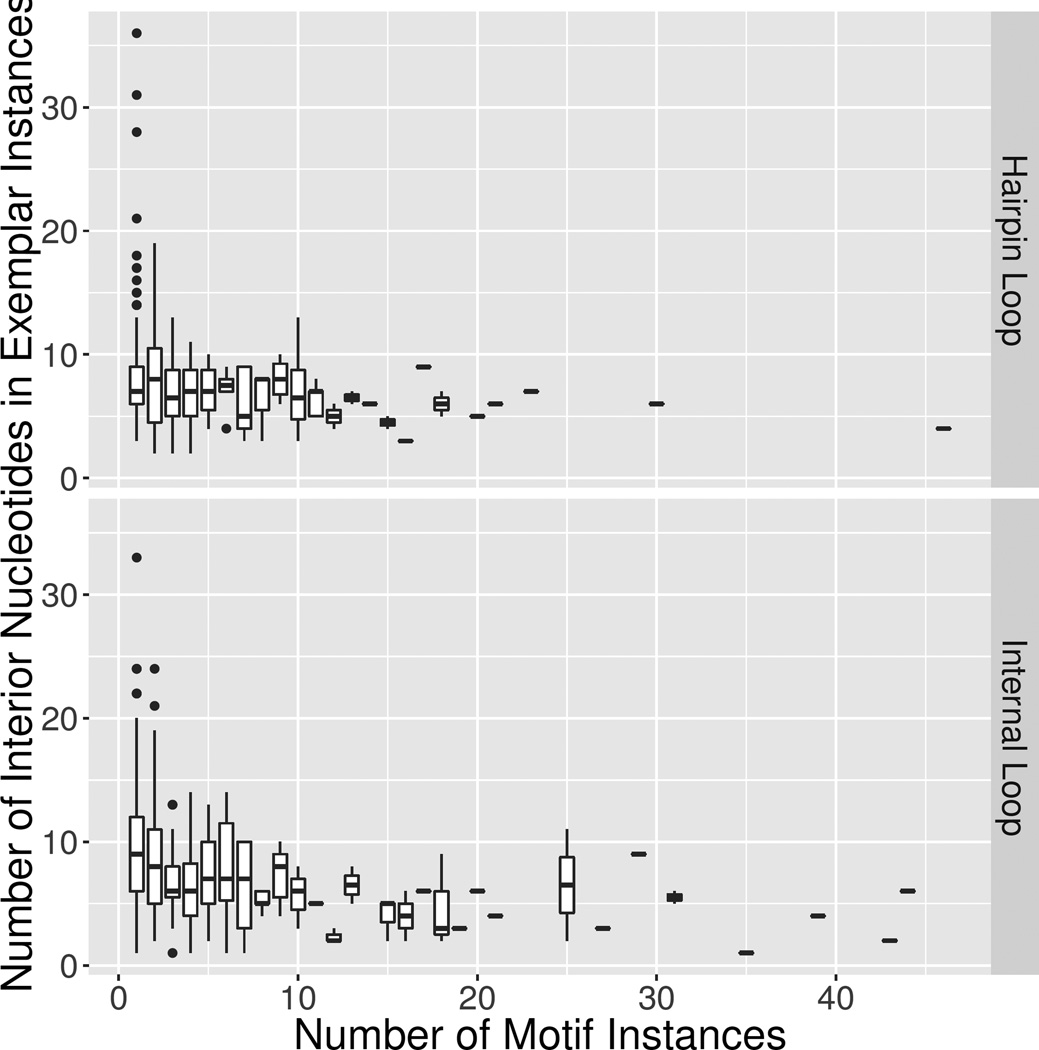
The largest IL motif group contains 371 instances, each having a small number of bulged bases. The second largest group contains 321 instances, each having one non-canonical cWW pair; the third largest group has 88 members comprising two adjacent non-canonical cWW pairs and the fourth group has 74 members, featuring a bulged base forming a cHS platform with a flanking basepair. The largest HL groups, are the GNRA hairpin loops, with 328 motif instances, T-loops with 78 instances, and UNCG tetraloops with 46 instances, reflecting the highly recurrent nature of these important 3D motifs. Figure 3 shows distributions of the numbers of instances in each motif group for HL and IL. These graphs show that only a small number of groups have large numbers of instances. The mean number of instances is just 6.46 for IL and 4.66 for HL. These and other summary statistics are provided in Table 2. We conclude that the current Motif Atlas indicates that the number of highly recurrent HL and IL motifs is rather small, but these groups contain the majority of motif instances.

Figure 3.

Distribution of number of instances per motif family. The figure does not include the singleton groups, which contain 175 of the 372 of the internal loops and 154 of the 316 hairpin loops. It is also truncated along the abscissa to only include groups with less than 100 instances. This removes the largest hairpin loop group HL_67042.17 (327 instances), and the two largest internal loops groups IL_48256.2 (371 instances) and IL_92602.2 (315 instances).

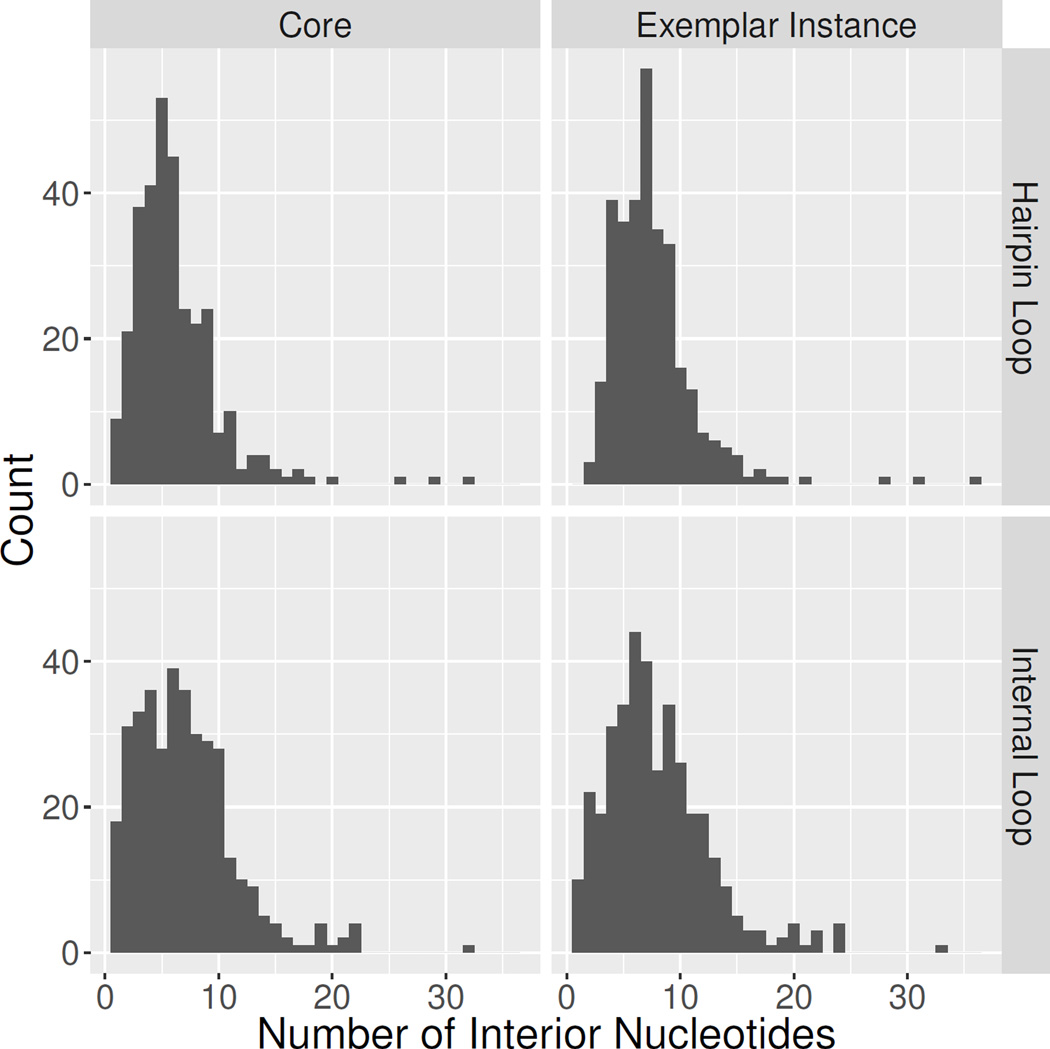
Figure 4 shows the distributions of the numbers of interior nucleotides of HL and IL motif groups in the Motif Atlas. Counts of interior nucleotides exclude the flanking basepairs of each motif (four nucleotides for IL and two nucleotides for HL). The histograms labeled “Core” count the number of core interior nucleotides in each motif family, as explained in Section 3.1.2, whereas the histograms labeled “Exemplar instance” count the number of interior nucleotides in the exemplar instances representing each motif group, which is generally larger because of the presence of non-core, bulged nucleotides. The number of core interior nucleotides varies from 1 to 36 for IL groups and 1 to 34 for HL groups. The total number of nucleotides of exemplar instances, including flanking pairs, varies from 5 to 37 for IL and 3 to 38 for HL. The histograms show that most groups have fewer than 10 nucleotides, but that IL motifs tend to be somewhat larger than HL motifs. There are a small number of motifs with 20 or more nucleotides.

Figure 4.

Distribution of number of motif instances per motif group across release 1.18 of the RNA 3D Motif Atlas. Top panels for HL, bottom panels for IL. Left panels show histograms of the number of interior (excluding the flanking WC pairs) core (non-bulged) nucleotides across the 316 HL and 372 IL motif groups. Right panels show histograms of the number of interior nucleotides in the exemplar instance for each motif group, including any bulged nucleotides.

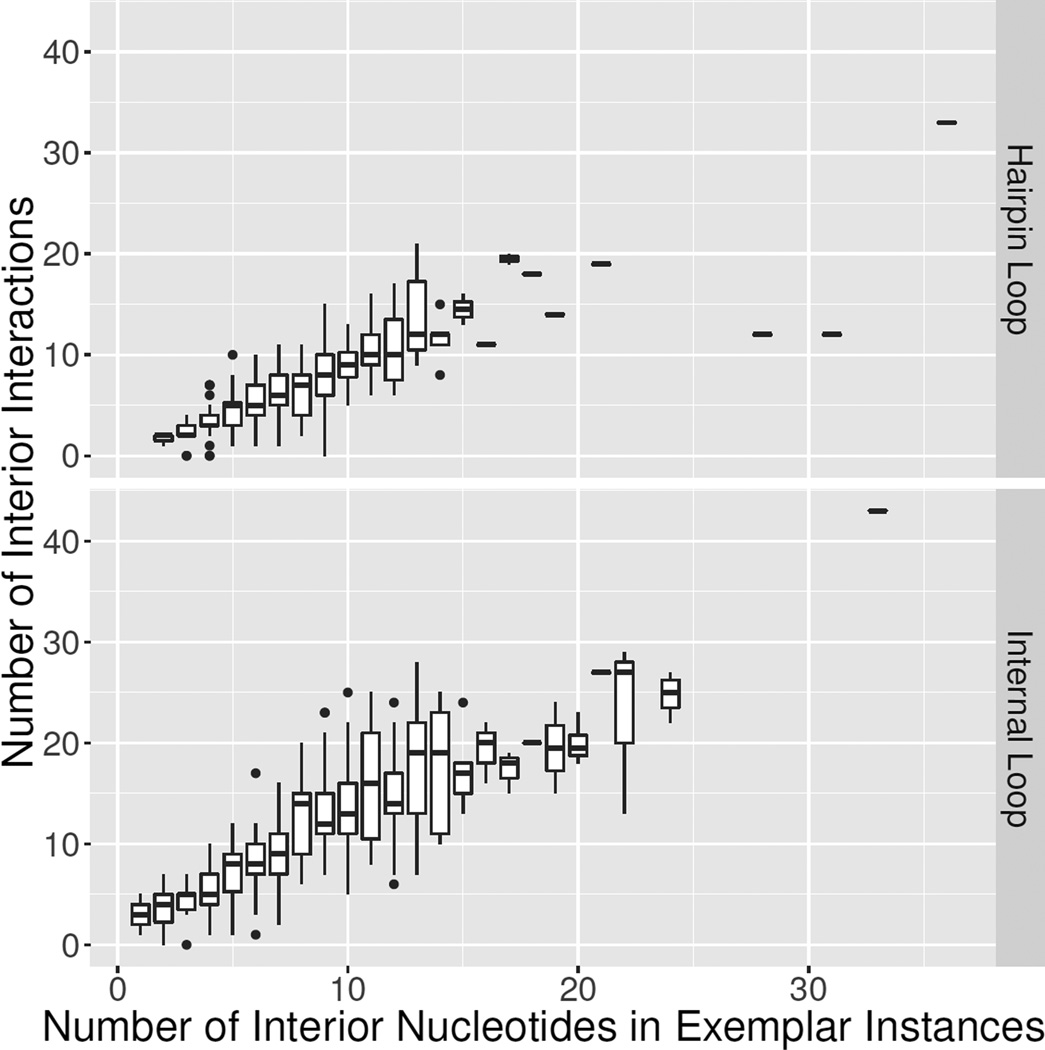
The distributions in the numbers of interactions among nts of each motif group are plotted as a function of the sizes of the motif groups in Figure 5 as a box and whisker plot. In a box and whisker plot, the box indicates the range of the middle two quartiles of the distribution and the whisker, the full distribution, with the exception of outliers, which are indicated by dots. For each group, the size is represented by that of the exemplar instance. This figure shows that nearly all motif groups have one or more internal interactions to structure them.

Figure 5.

Box plots showing range in the number of interactions among nucleotides in exemplar instances representing each motif group, as a function of number of interior nucleotides for each exemplar instance. Counts are FR3D-annotated base-pairing, base-stacking and base-backbone interactions. Data are from 3D Motif Atlas v. 1.18 (Internal loops: http://rna.bgsu.edu/rna3dhub/motifs/release/il/1.18, Hairpin Loops: http://rna.bgsu.edu/rna3dhub/motifs/release/hl/1.18).

Similarly, Table 2 shows that the mean number of interactions per motif is 10.76 and 6.60 for IL and HL respectively. Moreover, the number of interactions tends to increase linearly with the motif size. The range in the number of interactions also tends to increase with the sizes of the exemplar instances. Finally, IL groups have more interactions per nucleotide than hairpin groups with a mean of 1.05 versus 0.78 for HL groups, as shown in Table 2.

4.1.2 Examples of Coherent Motif Groups

A large number of motif groups show excellent levels of homogeneity within the group. For example, motif group IL_49493.8 (link: http://rna.bgsu.edu/rna3dhub/motif/view/IL_49493.8), has 18 instances of the Sarcin/Ricin (S/R) IL motif from a variety of non-homologous locations, including four locations in the archaeal 23S rRNA (H. marismortui) and one from the 5S rRNA of the same organism (cf. Figure 1). There are eight distinct interior sequences (that is, excluding the flanking WC basepairs, which vary in predictable ways). All 18 instances share the central GUA cSH-tWH base triple and the neighboring tHH and tHS basepairs, although these basepairs are annotated as “near” pairs of the same type for some instances [75]. A subgroup of five instances has an AC base combination making the tHH basepair between positions 3 and 11, rather than the more common AA base combination. All but one instance has an AG base combination for the tHS basepair between positions 6 and 9; RNase P has an AA base combination for this tHS basepair. These base substitutions in the tHH and tHS basepairs are isosteric. The motif group shows considerable variability in the annotations of the basepairs made between the nucleotides in positions 2 and 12, with fourteen instances having a tSH or near tSH basepair, but three with near cSW and one with a bifurcated basepair. These annotations are considered to be “non-conflicting” and so they can co-exist in the same motif group.

The Motif Atlas contains 11 other coherent IL motif groups which contain variants of the Sarcin/Ricin motif. These can be seen by visiting IL release 1.18 at http://rna.bgsu.edu/rna3dhub/motifs/release/il/1.18 and entering “sarcin” in the filter box. The motif groups differ in the numbers and types of non-WC basepairs on one end of the standard S/R motif, although group IL_95652.6 is notable for having a conserved base insertion at position 13, which makes a long-range basepair, and group IL_98073.2 which lacks the characteristic GUA base triple because the G is substituted by A or U, and these bases bulge out of the motif.

4.1.3 Inconsistent 3D Modeling: Flipped Bases

As noted in [1], roughly one third of motif groups with more than one member have at least one instance with at least one base which is rotated 180° about the glycosidic bond (i.e. “flipped”), compared to corresponding bases in other instances in the same group. Such bases will look approximately correct when viewed in 3D; they will stack and appear to pair with some of the same bases, but on closer inspection they will not form the same basepairs with their neighbors, leading us to conclude that they are most likely not correctly modeled. The 180° flip about the glycosidic bond changes the configuration of the base from the more common anti to the rarer syn glycosidic conformation. Often, two loop instances with such a base flip between them will occur at corresponding positions in homologous RNA molecules, so it is appropriate that they are placed in the same motif group. We can conclude that our method successfully groups a large number of similar loop instances together in spite of their having anti-syn flipped bases. Unfortunately, since a flipped base contributes roughly 0.3 to 0.4 Å per nucleotide to the geometric discrepancy, a base flip plus additional geometric variation may push a loop completely out of the motif group to which it belongs and into a singleton motif group. Clearly, one would need to devise additional flexibility in the grouping to bring such instances into the correct motif group or to screen out inadequately modeled motifs using energy criteria or Real-Space Refinement Statistics.

4.1.4 Unusual Backbone Orderings

A coherent but somewhat strained motif group is the main kink-turn group, IL_65553.12, which has 29 instances. Superposition of all instances shows quite good agreement on the overall geometry of the motif, but six instances of the group (IL_3RW6_002, IL_4W23_017, IL_4BPP_017, IL_3U5F_019, IL_3J7A_016, and IL_2AW7_014) have an unusual 1-3-2-4 strand order in the shorter strand, in which the third base of the strand is stacked between the first and second base of the strand. All instances but the first come from the ribosomal SSU, but the first comes from the constitutive transport element (CTE) of simian type D retroviral RNA [77]. It is not surprising that such an unusual strand arrangement is conserved across all ribosomal SSU structures (including T. thermophilus loop IL_1FJG_011, which is placed in singleton motif group IL_21254.1), but it is quite surprising that the same unusual strand arrangement occurs in an otherwise unrelated RNA molecule. A similar strand-order issue occurs with motif group http://rna.bgsu.edu/rna3dhub/motif/view/IL_64847.2. These unusual backbone orderings result in non-conflicting basepairs compared to other instances, and so evade the screens meant to split such instances into separate motif groups. As a result, the consensus list of basepair interactions for the motif group has extra basepairs, being a union over somewhat-conserved basepairs. It is an open question, whether this motif group should be split into two groups, to reflect the different backbone orderings, or kept as one group, given the similarity in the overall geometry.

4.1.5 Outliers within Motif Groups

Some motif groups are fairly coherent with low discrepancy between most instances, but with one or more outliers. While these outliers are geometrically similar and do not contain conflicting base pairs they can nonetheless differ considerably from the other instances in the group. A clear example is IL_77895.1 (http://rna.bgsu.edu/rna3dhub/motif/view/IL_77895.1), which contains a single outlier instance (IL_3J7A_061) having discrepancy 0.84 or higher with respect to the rest of the group (but less than 1.0), while the other instances all have geometric discrepancy < 0.7 among themselves. The outlier seems to be poorly modeled since it has no FR3D-annotated basepairs. Consequently there is no obvious basis for excluding it as there are no basepair conflicts with the consensus pairing observed in the group. Fortunately, such instances are fairly rare, occurring in about 15% of motif groups that have more than one element. We anticipate that once we filter motif instances on the basis of their Real Space Refinement (RSR) statistics, we will eliminate most of these poorly-modeled instances such as these.

4.1.6 Singleton Motif Groups

As discussed above, about half of the IL and HL motif groups in the Motif Atlas are singletons, containing just one motif instance (175 IL out of 372 total groups and 154 HL out of 316 total groups). These large numbers of singleton groups require explanation, as they may cause the reader to question the effectiveness of the clustering algorithm described above. To gain insight into the nature of these groups, we examined them manually. We find that many of these motif instances come from recent eukaryal ribosomal 3D structures, which have extensive expansion segments with novel motifs not found in the homologous bacterial or archaeal rRNAs. Other singleton groups arise from small differences in the flanking basepairs of individual motif instances that are very similar to those in larger motif groups. For example, the singleton motif group IL_09333.1 (see http://rna.bgsu.edu/rna3dhub/motif/view/IL_09333.1) consists of a well-structured IL that is very similar to loop instances in the 5-member group IL_86994.2 (see http://rna.bgsu.edu/rna3dhub/motif/view/IL_86694.2). The instances in the larger group have an additional non-canonical cWW basepair on one end. Finally, other singleton groups come from small RNA molecules with no homologues in the dataset and present unique geometries.

To further explore the singleton groups, we made box and whisker plots to display the distributions of the sizes of all motif groups as a function of the number of instances they contain, as shown in Figure 6. This plot clearly shows that all large HL and IL motifs, i.e. those motifs with > ~15 interior nts, are either singleton or doubleton groups. By contrast, all motif groups with large numbers of instances (>10 members) consist of motifs that are small in size (<11 interior nts). Furthermore the median number of interior nucleotides for the motif groups with one or two members are higher than for larger groups as shown by the box plots in Figure 6. This data are consistent with the idea that especially large 3D motifs are unlikely to be recurrent.

Figure 6.

Box and whisker plot of number of interior nucleotides in exemplar instances versus the number of motif instances in Motif Release 1.18. Top panel is HL groups and bottom panel is IL groups. The box plot represents the range of interior nucleotides for motifs with the given size. Singletons are the leftmost group with size 1. The means are indicated by the bold lean in each box while the bars around each box cover the first and third quartile. Outliers are indicated with dots. A small number of motif groups have more than 50 instances, but all are small in size (< 10 nts) and very homogeneous.

4.2 Assessment of Motif Clustering in the 3D Motif Atlas

In this section we summarize the results of an assessment we carried out of the procedures described above to group together geometrically similar motifs [78]. The success of an automatic clustering procedure is best evaluated by comparing its output to that produced manually by domain experts. The first step is to assemble data sets that include sufficient numbers of instances forming distinct groups to test the ability of the method to discern true from false negatives as well as true from false positives. Reliable manual classifications of the same data make it possible to validate the automated procedure. Instances belonging to the same groups should be similar, but not identical and there should be sufficient numbers of distinct yet related groups, to adequately challenge the performance of the algorithm. The basic premise of this study was therefore that corresponding HL and IL from homologous RNA molecules are likely to be conserved in 3D structure, and therefore should be grouped by automated procedures into the same motif groups in the Motif Atlas. The methodology was described in Section 2.2.

4.2.1 Results of HL Clustering in tRNA

Recurrent motif instances are frequently found at corresponding positions in the 2D and 3D structures of homologous RNA molecules. First we consider transfer RNA (tRNA) structures, and in the next section, SSU rRNA structures. A more complete study, including the LSU rRNA, will be presented elsewhere. While there are many different atomic-resolution tRNA structures in PDB/NDB, thus presenting a rich data set, tRNAs are relatively small RNA molecules (70–90 nucleotides), and only offer for analysis three distinct hairpin motifs, the dihydrouracil or “D-loop”, the anti-codon (“AC-”) loop, and the Thymidine-Pseudouridine-Cytosine (“TPsiC-”) loop [79], one MHJ loop (either a 4- or 5-way junction), and generally no internal loops. We evaluated the clustering of the HL from tRNA and found, as expected, that practically all T-loops from tRNA are clustered together, whereas D-loops, which are more loosely structured and more variable in length, are placed in several different, but related motif groups by the Motif Atlas pipeline [78]. The anti-codon loops from tRNA 3D structures also form more than one motif group (see Table 2). Most of the instances are assigned to a single group (HL_74465.7), in which the conserved U33 in the AC-loop forms the characteristic U-turn. The motif instances in this group assume the conformation that binds the complementary mRNA codon sequence. The other motif groups are populated by AC-loop instances distorted by interactions with tRNA-modifying proteins, principally cognate aminoacyl-tRNA synthetases (“aaRS”) that bind and unfold the anti-codon to “read” its sequence to ensure correct recognition. Overall, the Motif Atlas performs well in clustering the three types of HL motifs found in tRNAs.

4.2.2 Results of HL Clustering in SSU rRNA

A far richer source of loop motifs is the ribosome. Until recently however, the database of structures was limited to a handful of prokaryal structures at atomic resolutions, including the large subunit (LSU) of one archaeon (H. marismortui) and three bacteria (E. coli, T. thermophilus, and D. radiodurans), and just two small subunit (SSU) structures, (E. coli and T. thermophilus). Subsequently, two eukaryal SSU and LSU structures (S. cerevisiae and T. thermophila) became available followed by several mitochondrial structures. Motifs from these structures were available when the RNA 3D Motif Atlas v. 1.13 was compiled. The structures analyzed for motif extraction were from release 1.56 of the NR sets (http://rna.bgsu.edu/rna3dhub/nrlist/release/1.56), and included representative SSU rRNA structures from T. thermophilus (PDB file 1FJG), E. coli, (PDB file 2AW7), S. cerevisiae (PDB file 3U5F), and T. thermophila (PDB file 4BPP), and LSU rRNA from T. thermophilus (PDB file 4NVV), E. coli (PDB file 2QBG), H. marismortui (PDB file 1S72), D. radiodurans (PDB file 4IOA), T. thermophila (PDB file 4A1B), and S. cerevisiae (PDB file 3U5H).

Figure 7 summarizes the analysis of clustering in the Motif Atlas of HL from 16S rRNA structures, carried out as described in Section 2.2. The results for each HL are displayed on the E. coli secondary structure using color-coded rectangles to indicate the results of the clustering. Blue boxes indicate similar structures across all organisms, as judged by manual comparison of structures, and corresponding HL placed in the same motif groups of the Motif Atlas, i.e. successful clustering. Green rectangles indicate similar structures, some of which have small, identifiable differences, and therefore are placed in distinct, but related motif groups. Yellow rectangles indicate that the corresponding bacterial and eukaryal loops have structural differences and are placed in different groups, with bacterial motifs in one group and eukaryal motifs in a second group. Finally pink rectangles identify locations where most or all of the loops are different and are placed into different structures. In no case were loops judged to have different structures placed in the same motif group. Neither were any loops judged to be similar placed in unrelated motif groups.

Figure 7.

Bacterial 16S rRNA secondary structure (E. coli sequence). Each hairpin loop in a conserved region is assessed based upon the conservation across E. coli (2AW7), T. thermophilus (1FJG), S. cerevisiae (3U5F), and T. thermophila (4BPP). The coloring of each box on the hairpins indicates the results of clustering in motif atlas version 1.18. Loops which form similar structures and are placed in the same group are placed in blue boxes. Loops which are similar in structure across all loops and are placed in related groups are in green. Loops which form different structures between Prokaryotes and Eukaryotes are in pink. Finally, the regions which some large differences between Prokaryotes and Eukaryotes are shown with grey boxes. The data is in Supplemental Data 1.

The analysis indicates that 22 out of the 32 hairpin loops in bacterial SSU rRNA are conserved in structure among bacterial and eukaryal ribosomes, as indicated by the blue and green boxes in Figure 7, which were classified correctly as such by the Motif Atlas. These are the hairpin loops capping helices 2, 8, 11, 12, 13, 14, 15, 18, 21, 23, 23.1, 24, 26.1, 28, 31, 33.1 36, 37, 40, 41, 42, and 45. The green boxes indicate that among these structurally conserved loops, the Motif Atlas places some motif instances in different groups, including HL capping h12, h13, h15, h40 and h42. A closer analysis reveals that these HL differ among themselves in a small number of interactions, so the clustering algorithm correctly places them in different, but structurally related motif groups. The hairpin loops of helices 16, 21, 39, 33.1, 43, and 44 are conserved separately among bacterial structures and among eukaryal structures and so are marked with yellow boxes; the 3D motifs found in the Bacteria differ from those found in Eukarya. In each case, the bacterial loops were placed in the same groups and the eukaryal in different ones. The HL of helices 21 and 33.1 are conserved in bacteria, but no equivalent HL exist in Eukarya because these helical elements are very different in Eukarya. The Motif Atlas clusters the bacterial loops of h21 and h33.1 correctly. Finally, several hairpin loops (HL 6, 10, 17, and 26.1) have structures that differ among most of the organisms and are accordingly placed by the Motif Atlas into unrelated groups (Figure 7, pink boxes). HL 9, 21 and 33.2 were not analyzed because equivalents do not exist in Eukarya and they are very different among bacteria.

There are no cases where structurally related HL motifs of 16S are grouped by the Motif Atlas into unrelated groups or vice versa. We conclude that overall the Motif Atlas does an excellent job clustering HL motif instances from representative, high quality bacterial and eukaryal structures. This result highlights the importance of carefully using structural constraints when clustering motifs.

4.3 Identifying RNA 3D Motifs from Sequences and Computed 2D Structures

A key motivation for building and maintaining the RNA 3D Motif Atlas was to learn the interaction network and typical sequence variability for recurrent RNA motifs, so as to more easily identify them in the predicted secondary structures of novel RNAs. This project has come to fruition with the publication of a software package called “JAR3D” (“Java-based Alignment of RNA using 3D structure”) [20]. Because each motif group consists of aligned instances with non-conflicting basepair interactions, we can identify a consensus set of basepairs and the observed base combinations making each consensus basepair and use basepair isostericity rules [12] to assign a probability score for each possible base substitution. Furthermore, we use base-backbone interactions detected in the 3D structures to further tailor the probability scores assigned to possible base substitutions. We previously showed that base-backbone interactions are highly associated with base conservation [80]. We can also model sites and likely lengths of insertions where bulged bases are seen to occur in some instances of a motif group. Because of the nested nature of most basepairs in RNA IL and HL, we use Stochastic Context-Free Grammars (SCFG) as the basis for the probabilistic models for sequence variability, enhanced by Markov Random Fields (MRF) to handle base triples, crossing interactions, and basepairs on the same strand. We develop SCFG-MRF models for each motif group in each release of the Motif Atlas [20,81].

Given one or more sequences of an RNA IL or HL, JAR3D scores the sequence(s) against all motif groups and sorts them according to a linear combination of the probability score and an edit distance between the input sequences and known sequences from 3D structures. We find that JAR3D is quite accurate in identifying the correct motif group, even with novel sequences as input that differ from all known sequences [81]. Moreover, having multiple sequence variants for the same motif greatly increases the accuracy of JAR3D, in the same way that WC covariations observed between nucleotides provides evidence for WC-paired helices conserved across homologous RNA molecules.

We noted above that there are twelve IL motif groups with different variants of the Sarcin/Ricin motif. This causes no difficulties for JAR3D. When inputting novel sequences from a multiple sequence alignment, JAR3D easily identifies which variant of the Sarcin/Ricin motif is present, but often other variants also score well, helping to confirm that the sequences represent a Sarcin/Ricin motif. Singleton motif groups are a double-edged sword. On the one hand, JAR3D makes reasonable models based on a single instance, because it uses basepair isostericity to extend the range of accepable sequences to many more than are observed in 3D. On the other hand, the sheer number of singleton motif groups results in occasional false positive matches, especially when inputting a single novel sequence.

As new RNA 3D structures are solved, new motif groups will be added to the RNA 3D Motif Atlas, and JAR3D will be able to identify new motifs. Also, existing motif groups will acquire new sequence variants, and so JAR3D’s performance on existing motif groups will improve as well.

5. Discussion

5.1 Remaining Issues and Challenges in HL and IL Motif Extraction and Classification

5.1.1 “Isolated” or “Embedded” cWW Basepairs in HL and IL

Determining which “isolated” cis Watson-Crick (cWW) pairs should be considered integral parts of 3D motifs and which should be considered part of the secondary structure and thus used to split large motifs is a major problem for MHJ motifs as discussed in the next section, and also for some HL and IL motifs. For example, the large 15-nt HL in 5S rRNA called “loop C” is not correctly extracted by the current algorithm populating the RNA 3D Motif Atlas. The 3D structure is conserved in all 5S rRNA, but we discuss the E.coli version for specificity. Loop C in E.coli 5S rRNA comprises nucleotides 34–48, with the flanking cWW pair included. The 3D structure shows that C38 and G44 form an isolated cWW pair within loop C. This pair is highly conserved and therefore does not appear in 2D structures as there are no WC co-variations to allow its detection. Moreover, the 3D structure shows that it is an integral part of the HL motif (i.e., “embedded”) and therefore should not be assigned to the secondary structure and labeled a flanking pair. However, current motif extraction programs identify it as the flanking pair and consequently split loop C into a smaller HL (nts 38–44, HL_2QBG_001) and an adjacent IL (nts 34–38/44–48, IL_2QBG_004). As will be discussed in Section 5.2.1 for a MHJ, rectifying this situation is not a simple matter, because there are other cases in which an isolated cWW pair should be retained as part of the secondary structure. In these cases the adjacent motifs are distinct and should not be merged into one larger motif.

5.1.2 Composite Motifs and Motifs that Extend Beyond their Flanking Pairs

An issue that challenges the very definition of a 3D motif concerns “composite” motifs. These are generally two or more IL (or perhaps an HL and an IL, or an IL and an MHJ) that are close to each other in the secondary structure and interact extensively with each other. In certain cases, the interactions are so extensive in relation to the sizes of the motifs that it is likely that the interactions play an important role in forming the observed 3D structure. 5S rRNA loop A provides an example of a 3WJ and small IL that interact in this way (see Section 5.2).

Helix h6 of E. coli 16S rRNA presents a striking example of a series of IL that form a composite internal loop motif. Helix 16 forms the “spur” feature of bacterial 30S ribosomes. The 2D structure shows four relatively simple internal loops, including a two-base bulged loop (G64 and A65) separated by two WC pairs from a three-base asymmetric loop (G68, G100, and A101), followed by two more WC pairs and another two-base bulged loop (A71 and A72). Finally, there are three more WC pairs and a one-base bulged loop (G94). However, in the 3D structure it is apparent that all these internal loops interact with each other to form a single composite 3D motif stabilized by an integrated network of non-WC base pairs forming base triples with the intervening WC pairs and extended base stacking. These interactions change the normal stacking of the helix, increase the helical twist and provide RNA docking sites that promote tertiary interaction with the HL of h15 and the IL of h8 to structure the lower part of the body (Domain 1) of 30S. These observations argue that motifs such as the composite motif in 16S h6 should be treated as integrated modules and should appear somewhere in the RNA 3D Motif Atlas, probably in addition to, rather than in place of the individual “simple” motifs that compose them. This example was discussed extensively in a previous publication, to which the reader is referred [60].

5.2 Challenges Posed by MHJ

Multi-helix junction (MHJ) loops pose a number of similar and some additional challenges.

5.2.1 “Embedded” cWW Basepairs in HL and IL

“Embedded” cWW pairs, often highly conserved in sequence, occur more often in MHJ than in HL or IL. In bacterial 16S rRNA for example, a total of six MHJs were found to contain such pairs [12]. They occur in four 3WJ (defined by helices h4/h5/h15, h20/h21/h22, h32/h33/h34 and h38/h39/h40), one 4WJ (H29/h30/h41/h42) and one 5WJ (h3/h4/h16/h17/h18). Correctly identifying these Watson-Crick basepairs as part of the MHJ and not as flanking pairs is necessary to correctly extract these MHJ from the 16S 3D structures. However, the current motif extraction pipeline assigns these to the secondary structure. Making the correct assignments is complicated by the fact that there are situations where there is just one Watson-Crick pair between a MHJ and an adjacent IL or HL (or between two IL or between an IL and an HL), that in fact should be assigned to the secondary structure, so that the two motifs are treated as distinct. An example is the first cWW pair of Helix 41, C1303/G1334, which separates a conserved IL consisting of three non-WC pairs, from the 4WJ, h29/h30/h41/h42. The IL is not part of the MHJ 29/30/41/42. To maintain the distinction it is necessary to assign the C1303/G1334 pair to the secondary structure. These examples illustrate the nature of the challenges in correctly extracting MHJ from 3D structures.

5.2.2 Importance of Nearby Tertiary Interactions to MHJ

The 3WJ of 5S rRNA, “loop A,” is an example of a structured MHJ that depends on a nearby IL for some stabilizing interactions. Loop A is formed by helices 1, 2 and 4 of 5S rRNA. There is a conserved IL in helix 2, just two basepairs away from loop A, that consists of a single bulged base. This base extends into the major groove of the 3WJ to form a base triple with a flanking pair of the 3WJ. This base triple stacks between a second base triple and a non-WC pair formed by junction nts to stabilize co-axial stacking of helices 2 and 4. This description should impress on the reader that it is unlikely that the loop A 3WJ would form this geometry without the participation of the bulged base from the IL, located two basepairs away from the 3WJ per se. This strongly suggests that, to be useful for RNA nanotechnology applications, all essential parts of complex motifs such as MHJ will need to be identified and extracted as modular functional units. Developing methods to do this correctly presents a additional challenge to MHJ extraction.

5.2.3 Variations in Numbers of Helical Elements

The topological classification based on RNA secondary structures suggests that MHJ should first be classified by number of helices. However, structure comparisons and evolutionary considerations suggest otherwise. For example, it is well known that all tRNA’s form a “clover-leaf” secondary structure, organized by a 4WJ, but in some tRNAs there is a fifth “variable” helix. However, in 3D these MHJ are very similar with regard to the stacking of the D-stem on the Anti-codon stem and of the TPsiC stem on the aminoacyl acceptor stem. The 5^th variable stem does not significantly alter the 3D structure of the four conserved helices on the tRNA MHJ. This suggest that at the 3D level it may sensible, in some cases at least, to cluster motifs with differing numbers of helices in related if not the same motif groups, especially when they are related by homology as well as geometry. Devising suitable procedures to do so pose additional challenges for future work.

6. Conclusions

Generally, the RNA 3D Motif Atlas performs a very robust clustering of motif instances. Its automated analysis process results that agree with manual analysis, yet can be done in a fraction of the time and thus can be carried out on a regular basis. In addition, the Motif Atlas outputs various visualization pages and files which aid manual analysis, such as windows to view and superimpose the 3D coordinates of motif instances, alignments of motif instances with lists of interactions, lists of motifs classified in the same group or related groups, along with sequence variants and calculations of geometric discrepancies between motif instances. Overall, the Motif Atlas is an excellent program suite for automatically analyzing and classifying RNA tertiary motifs.

Internal, junction, and hairpin loops that appear in secondary structures are, in most cases, instances of recurrent modular RNA motifs. Different sequences can form the same recurrent 3D motif, as a result of structure-neutral mutations. RNA 3D motifs are defined by listing the conserved pairwise interactions between corresponding core nucleotides (including base-pairing, -stacking, and -phosphate interactions). Motifs can be classified according to structural or functional similarity. During evolution, global structural changes occur more slowly than sequence changes, even when these changes result, through a combination of base substitutions, and nucleotide insertions or deletions, in significant changes in local 3D motif structure, as seen, for example with loop E of 5S rRNA. When such motifs are involved in crucial long-range interactions, such as the interaction between 5S and 23S rRNA, the global function is preserved as a result of a “motif swap” in which 3° or 4° contacts are mediated by geometrically distinct but functionally equivalent 3D motifs. A challenge for future versions of the 3D Motif Atlas will be to identify and link functionally equivalent motifs, as well as, all structural variants of conformationally flexible motifs.

Highlights.

• Up to 40% of nucleotides in structured RNAs are in hairpin, internal and junction loops

• Loops are structured by non-Watson-Crick base-pairing and -stacking interactions

• RNA 3D motifs found in loops can be extracted and clustered into motif groups

• Many RNA 3D motif geometries are modular and recurrent with similar non-WC pairing

• Corresponding motifs in homologous structures frequently conserve 3D structure

Abbreviations

HL

Hairpin Loop

IL

Internal Loop

3WJ

3-way Junction

4WJ

4-way Junction

MHJ

Multi-Helix Junction

2D structure

Secondary structure

PDB

Protein Data Bank

NDB

Nucleic Acid Database

WC

Watson-Crick

non-WC

non-Watson-Crick

BP

basepair

NR

Non-redundant

nt

nucleotide

S/R

Sarcin/Ricin

mRNA

messenger RNA

tRNA

transfer RNA

rRNA

ribosomal RNA

SSU

small ribosomal subunit

LSU

large ribosomal subunit