Digital design of multimaterial photonic particles

Significance

We present an approach for the facile fabrication of dielectric particles having the size of an optical wavelength yet endowed with a complex multimaterial internal nanoscale architecture. This methodology amounts to “digitally designing” the particle by precisely allocating the desired material at prescribed coordinates within the 3D volume of the particle. The digital design of such a photonic particle enables sophisticated strategies for controlling light scattering. As an example, without changing the size of a core–shell particle, its optical scattering strength can be tuned above or below that afforded by its constitutive materials by changing the core–shell diameter ratio. This work may lead to the development of new optical coatings and paints with exotic functionality.

Abstract

Scattering of light from dielectric particles whose size is on the order of an optical wavelength underlies a plethora of visual phenomena in nature and is a foundation for optical coatings and paints. Tailoring the internal nanoscale geometry of such “photonic particles” allows tuning their optical scattering characteristics beyond those afforded by their constitutive materials—however, flexible yet scalable processing approaches to produce such particles are lacking. Here, we show that a thermally induced in-fiber fluid instability permits the “digital design” of multimaterial photonic particles: the precise allocation of high refractive-index contrast materials at independently addressable radial and azimuthal coordinates within its 3D architecture. Exploiting this unique capability in all-dielectric systems, we tune the scattering cross-section of equisized particles via radial structuring and induce polarization-sensitive scattering from spherical particles with broken internal rotational symmetry. The scalability of this fabrication strategy promises a generation of optical coatings in which sophisticated functionality is realized at the level of the individual particles.

The prospect of exercising complete control over the internal 3D structure of multimaterial microparticles and nanoparticles produced in a scalable fashion has profound implications for scientific disciplines ranging from photonics (1, 2) to biomedicine (3–5), and for a multitude of industrial applications, such as cosmetics, sunscreen lotions, optical coatings, and paints (6–8). For example, most paints are emulsions containing dielectric “photonic particles” designed to optimize optical scattering through judicious selection of size—typically on the order of an optical wavelength—and refractive index (9). Further tailoring their scattering characteristics requires tuning an internal high refractive-index contrast nanoscale architecture, which remains an outstanding fabrication challenge despite recent progress (10–14). Indeed, the process kinetics in bottom-up and top-down particle fabrication strategies impose fundamental constraints on the extent of structural control and the magnitude of refractive-index contrast. To date, there is no viable approach for what may be termed “digital design” of a photonic particle: the precise placement of disparate materials compartmentalized at independently addressable coordinates within a particle at the scale of an optical wavelength. Such structural control is envisioned to introduce entirely new optical functionalities that exploit the particle’s resonances (15), such as the elimination of backscattering and increasing the directionality of optical scattering (16–20). Nevertheless, mapping out the phase function of a single isolated photonic particle—to verify its functionality without ensemble averaging—has proven so far to be prohibitively difficult, leading to measurements being carried out on scaled-up particles at longer wavelengths [typically in the microwave spectrum (15)].

Due to the inherent difficulty in achieving such digital design of photonic particles, efforts have been directed instead at structuring the morphology of surfaces to manipulate the scattering of light. Efforts in this direction range from exploiting planar photonic crystals to plasmonic structures and metasurfaces to control the directionality of optical scattering (21–23) or optical polarization (24), and even achieve zero refractive index (25). These patterned surfaces typically involve a large array of elements that—combined—achieve the desired optical functionality. Moreover, many of these structures use metallic components that introduce unwanted optical losses.

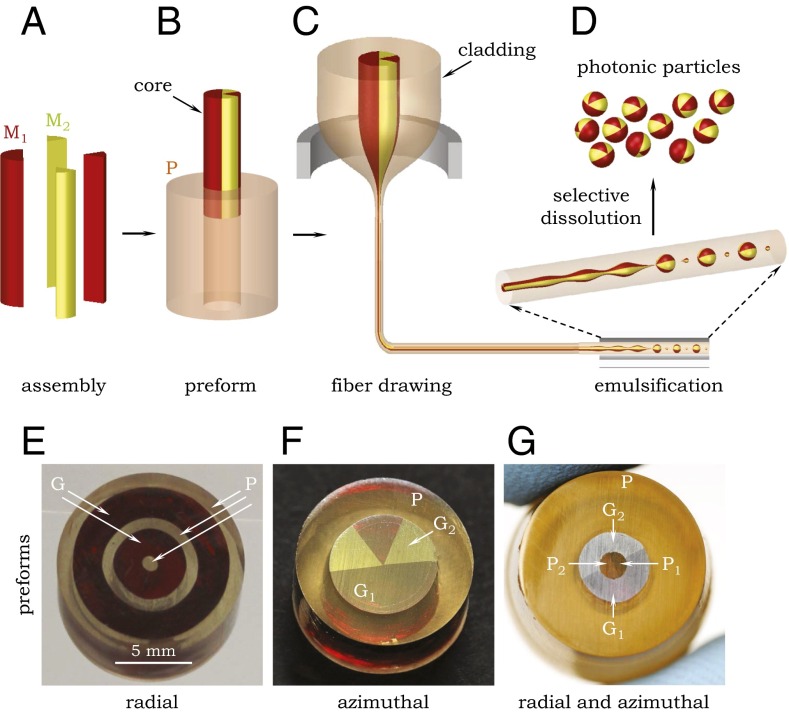
We present here a scalable fabrication strategy for engineering the internal geometry of all-dielectric multimaterial photonic particles, which provide access to sophisticated optical scattering capabilities. The key to addressing the challenge of particle digital design is exploiting a recently discovered in-fiber fluid instability (26–28) that produces spherical particles having—in principle—arbitrary internal structure. A centimeter-scale axisymmetric cylindrical “core” rod is assembled as a prototype of the intended particle structure in a LEGO-like procedure from prefabricated segments of different materials, which is then embedded in a cladding matrix to form a “preform” (29–31). A fiber that is thermally drawn from this preform with reduced transverse feature size defines the initial conditions for a cylinder-to-sphere geometric transformation by thermally inducing the Plateau–Rayleigh capillary instability (PRI) (32, 33) at the heterogeneous interfaces along the whole fiber length (26–28). Because the geometric morphing associated with this fluid instability is predictable, the axially symmetric core is converted into spherical particles with a target architecture that follows from the macroscopic preform structure. The uniqueness and versatility of this processing strategy is brought out here by realizing (i) radial control in multilayered particles with predictable layer thicknesses, (ii) azimuthal control in particles with discrete rotational symmetry, and (iii) combined radial and azimuthal engineering in four-material core–shell particles having Janus core and shell with well-controlled relative orientation of the azimuthally structured layers.

The efficacy of digitally designed photonic particles for rationally controlling optical scattering is confirmed via two key experiments. First, we tailor the radial structure of a high-index contrast all-dielectric core–shell particle to tune the optical scattering cross-section—without changing the particle size—to reach values above or below that of equally sized particles of the constitutive materials. This feature is verified through mapping out—for the first time (to our knowledge)—the phase function of a single photonic particle by combining evanescent field excitation with near-field optical scanning microscopy, instead of relying on an ensemble measurement. Second, we verify that breaking the internal rotational symmetry of a particle with spherical external morphology produces polarization-dependent scattering. Exploiting the scale invariance of our fabrication strategy (27), we first produce in both cases larger-scale particles (∼10–40 μm in diameter) to confirm the internal structure through direct structural and compositional imaging, and then carry out the optical experiments on reduced-scale photonic particles in which the structure is established through single-particle optical scattering. Such particles may serve as designer optical scattering elements for constructing new synthetic photonic materials and structures.

Results

In-Fiber Fabrication Strategy.

The starting point of our fabrication methodology (shown schematically in Fig. 1) is the construction of a centimeter-scale preform prepared using macroscopic processes, such as extrusion (34), casting, etc. (SI Appendix). This preform contains a prototype of the targeted particle architecture in the form of a multimaterial cylindrical core assembled from preshaped segments of the desired materials (Fig. 1 A and B). The core is embedded in an amorphous cladding that facilitates thermal drawing into a fiber (Fig. 1C), thereby reducing the core diameter to the scale of the intended particle size (27)—potentially ranging from millimeters down to tens of nanometers (27, 35). Surface energy at the core-cladding interface, and at interfaces within the core itself, is exploited to initiate the PRI upon reducing the viscosity via thermal treatment (26). The result is a thermally induced emulsification of the whole core length, thereby morphing it into an ordered and oriented necklace of structured spherical particles (26) to be released from the fiber through selective dissolution of the cladding (Fig. 1D). The dynamics of the breakup process is shown in Movie S1, where six parallel cores in a fiber are thermally treated and undergo a physical transformation from microthreads to a 2D array of spheres. We focus here on thermally compatible combinations of polymers (28) and soft glasses (26, 27, 36, 37) that afford high optical refractive-index contrasts, but a broader range of materials can be exploited in this process, such as crystalline semiconductors including silicon and germanium (38) and even globular biomaterials (28).

Fig. 1.

General strategy for the digital design of multimaterial photonic particles independently in the radial and azimuthal directions. (A) Segments of two materials, M₁ and M₂, are produced that may be assembled into an axisymmetric cylinder or core. (B) The core is provided with a polymer (P) cladding to form a preform. (C) The preform is thermally drawn into an extended continuous fiber that is subsequently heated leading to well-ordered and oriented emulsification of the core: its breakup into spheres in a low-viscosity state driven by surface tension. (D) The particles are harvested by selective dissolution of the cladding. (E–G) Optical micrographs of preform cross-sections showing (E) radial control in a multilayer structure (G, As₂S₃; and P, PES), (F) azimuthal control with broken rotational symmetry [G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7; and P, PES], and (G) control over the combined radial and azimuthal geometry [G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7; P₁, PES; P₂, PEI; and P, PES]. Fibers produced from the preforms in E–G are shown in Figs. 2, 4, and 5, respectively.

Examples of preform cross-sections produced by multimaterial coextrusion (34) are presented in Fig. 1 E–G (SI Appendix, S1: Overview of the Preform Preparation Process and S2: Structured-Preform Fabrication): first, a preform core composed of alternating cylindrically nested layers of a glass (G, As₂S₃) and a polymer [P, polyethersulfone (PES)]; second, a core with broken azimuthal symmetry formed of two glasses [G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7] assembled from wedged segments; and third, a core combining radial and azimuthal structural engineering, consisting of a glass–core/polymer–shell geometry in which both layers have a Janus structure—thus juxtaposing four materials. Uniquely, the different layers with broken rotational symmetry in the last example may be oriented at will with respect to each other. These selected examples highlight the potential for digitally designing the cylindrical core prototype, which is facilitated by its large size. We now proceed to show that a thermally induced PRI-driven process in fibers drawn from these preforms indeed produces particles with the desired geometry and associated optical functionality.

Control over the Radial Structure.

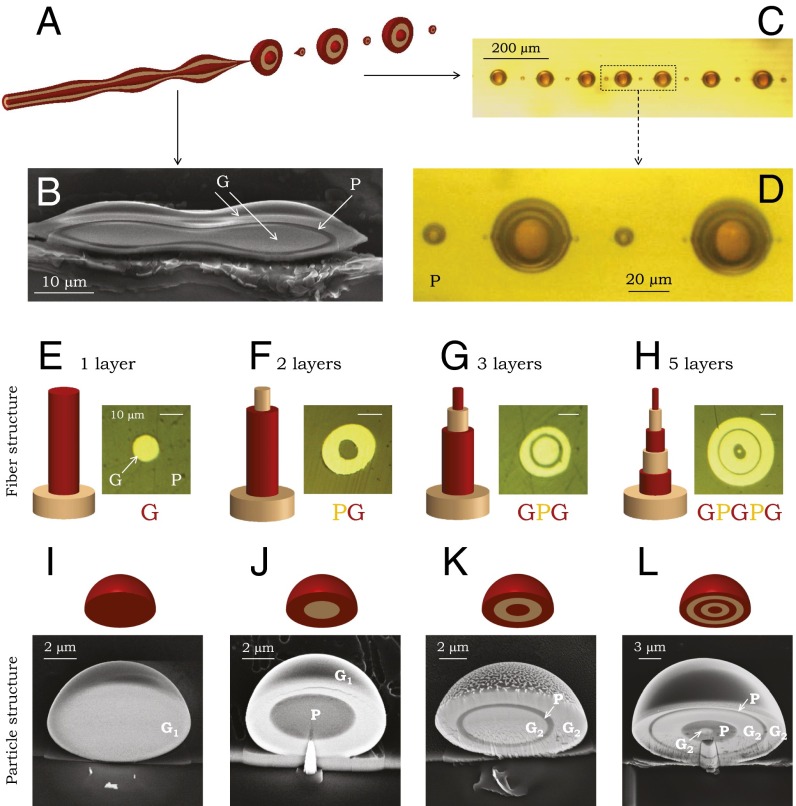
The initial conditions for in-fiber fabrication of spherical multilayered particles are defined by a fiber core with nested layers. Because the instability growth time—as described in the classical Tomotika model—is linear in the diameter of the cylindrical interface between two viscous fluids (39), the cylindrical multilayer core structure (Fig. 2A) breaks up from the innermost layer outward (Fig. 2B) and yields multilayered spherical particles upon heating the fiber (Fig. 2 C and D). The feasibility of this strategy is established by direct imaging of microparticle realizations with increasing number of layers, starting from a unimaterial glass particle (Fig. 2 E and I) to a five-layer particle with alternating glass and polymer shells (Fig. 2 H and L). Micrographs of the harvested particles after sectioning them at midplane reveal smooth, sharp interfaces, and the integrity of the extracted particles after selective dissolution of the polymer cladding—using a solvent that is detrimental to exposed internal structures—indicates that the spherical-shell layers form in an orderly sequence (from the inside out) without pinching. Furthermore, the spherical symmetry and concentricity of the internal particle interfaces (Fig. 2 I–L) is markedly improved with respect to those in the initial fiber (Fig. 2 E–H), thereby confirming a theoretical prediction that perturbations in the fiber core are smoothed out during the surface-tension–driven breakup process (40)—which relaxes the fabrication tolerances at the preform and fiber levels.

Fig. 2.

Control over particle structure in the radial direction. (A) Schematic of a fiber containing a cylindrical core consisting of nested shells undergoes the PRI-driven breakup into spherical multilayer particles. The cladding is not shown for clarity. (B) SEM micrograph of a three-layer core sectioned using a focused ion beam (FIB) with the PRI arrested before complete breakup of the core (G, As₂S₃; and P, PES). (C and D) Optical transmission micrographs of five-layer particles after breakup held in the polymer (P) cladding separated by smaller multilayered satellite particles. (E–H) Optical reflection micrographs of fiber multilayered-core cross-sections (G, As₂S₃; and P, PES). Schematics of the fiber structures are also shown. (I–L) SEM micrographs of multilayer particles after sectioning with a raster-scanning low-current FIB. Schematic of the particles are shown above each panel. G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7; P, PES.

Although the thicknesses of the layers in the particle are related deterministically to those of the cylindrical shells in the drawn fiber (28, 40), the dynamics of the PRI nevertheless constrains the relative shell diameters for which the breakup results in the intended layered structure. It is well established from the classic Tomotika model that the breakup period of a viscous thread embedded in a viscous matrix is proportional to the diameter of the thread (39). The breakup period is related to the instability wavelength having the highest growth rate. If the core diameter is much smaller than that of the shell $d_{\text{core}}/d_{\text{shell}}\ll 1$, then the resulting breakup period of the core may—in turn—be significantly smaller than that of the shell. Consequently, instead of the desired core–shell structure, multiple smaller core particles forming a linear chain extending between the antipodes of the particle are obtained inside a single shell (28, 40).

We confirm these predictions experimentally (SI Appendix, Fig. S12) by inducing the PRI-driven breakup in PES–core, As₂S₃–shell structures that differ in the ratio of the core-to-shell diameters $d_{\text{core}}/d_{\text{shell}}$. First, when $d_{\text{core}}/d_{\text{shell}}=0.7$, the sinusoidal modulations resulting from the PRI along the interfaces occur simultaneously upon heating and the target core–shell structure is obtained. Second, with $d_{\text{core}}/d_{\text{shell}}=0.5$, the modulation along the interfaces are independent to some degree, and we obtain a subset of particles in which the core–shell structure does not develop. Instead, we sometimes obtain two core particles within the shell. Third, with $d_{\text{core}}/d_{\text{shell}}=0.2$, the growth of the PRI-induced modulations along the interfaces are independent and the core breaks up into spherical particles before the shell breaks up altogether. Consequently, the shells after formation contain several core particles. Furthermore, the satellite particles are formed of the shell material only. The crossover that occurs between the stable (core–shell) and unstable (multiple cores in a shell) regimes at $d_{\text{core}}/d_{\text{shell}}\approx 0.5$ is borne out by calculations based on a linear stability analysis (28) and direct fluid-dynamical simulations (40). The potential for forming strings of particles along the axis of a larger particles is exploited below in inducing polarization-sensitive optical scattering.

Control over the Optical Scattering Efficiency in Core–Shell Particles.

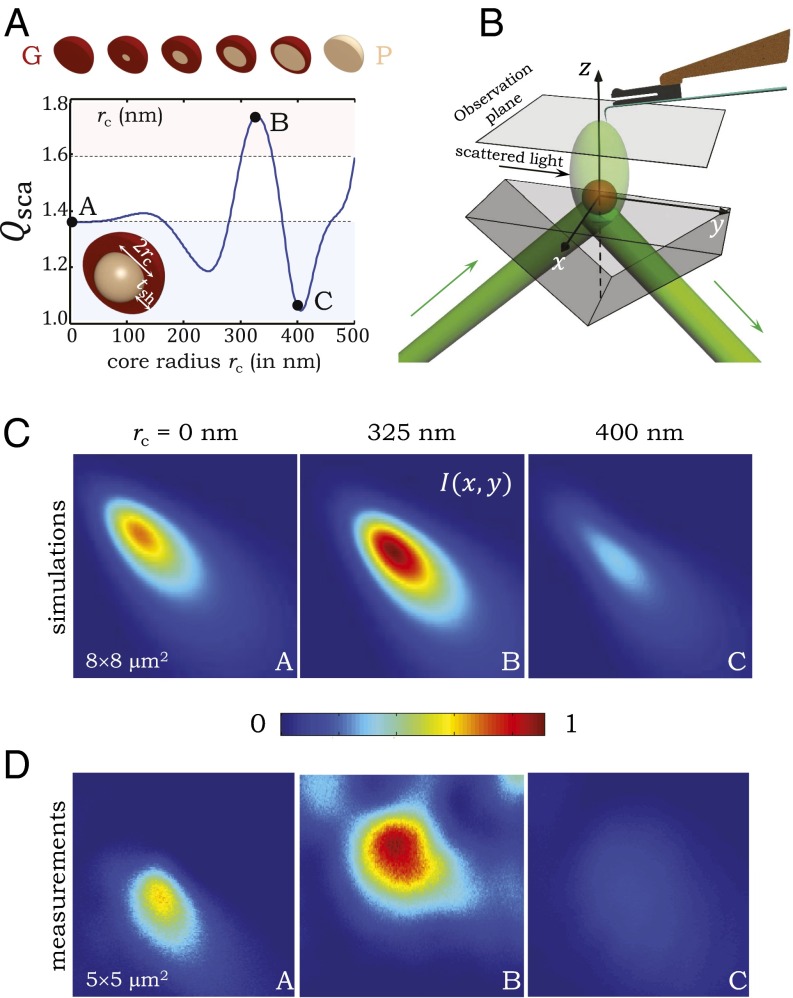
To date, tailoring the optical scattering efficiency $Q_{\text{sca}}$ [defined as the ratio of the scattering to geometric cross-sections (41)] from particles have relied on either changing their size or refractive index. Realizing high $Q_{\text{sca}}$, as necessary, for example, in optical coatings to achieve opacity in thin layers without absorption, typically necessitates increasing the refractive index, an approach fundamentally limited by naturally available materials (42). We proceed to show here that multilayer dielectric particles with controlled radial structure and high refractive-index contrast (without incorporating metals) enable rational control over $Q_{\text{sca}}$ solely through the internal architecture. This point is made clear through a calculation of $Q_{\text{sca}}$ at a wavelength $\lambda =532$ nm for a core–shell particle of fixed radius $a=500$ nm (polymer–core and glass–shell refractive indices are $n_{\text{c}}=1.5$, $n_{\text{s}}=2.51+i0.28$, respectively), which reveals a modulation in $Q_{\text{sca}}$ while varying the core radius $r_{\text{c}}$ between two limits: an all-glass particle ($r_{\text{c}}=0$) and an all-polymer particle ($r_{\text{c}}=a$) (Fig. 3A). Thus, by adjusting an internal geometric degree of freedom, $Q_{\text{sca}}$ may be varied below or above that of equisized unimaterial particles made of either of the constitutive materials, as a result of multipolar interferences [$ka=\left(2\pi /\lambda \right)a\approx 6$].

Fig. 3.

Tailoring the scattering cross-section in high refractive-index contrast core–shell photonic particles. (A) Calculated $Q_{\text{sca}}$ for a core–shell particle of fixed outer radius 500 nm; core is the polymer (P) PES having radius $r_{\text{c}}$, whereas the shell is the glass (G) As₂S₃ (refractive indices given in text). Wavelength used in the calculations is 532 nm. (B) Schematic of the optical system for dark-field near-field optical scanning microscope (NSOM), which is based on a Nanonics MultiView 4000 NSOM working in standard collection mode. (C) Calculated scattered field intensities from three particle structures corresponding to cases A, B, and C in A. (D) Measured intensity distributions corresponding to those in C.

We confirm these theoretical predictions by examining specifically designed and manufactured particles having three different core–shell ratios, structures A ($r_{\text{c}}=0$ nm), B $(r_{\text{c}}=325$ nm), and C $(r_{\text{c}}=400$ nm) highlighted in Fig. 3A, and selected to confirm that varying $r_{\text{c}}$ can reduce or enhance $Q_{\text{sca}}$. Critically, to isolate the effect of the internal particle structure on $Q_{\text{sca}}$ and eliminate the impact of particle–particle interactions, we carry out the measurements on one single particle. The formidable challenge of identifying the extremely weak scattered signal off a single particle from the strong background of incident light is addressed by constructing a dark-field light-scattering setup in which the particle is excited by an evanescent optical field at a wavelength of 532 nm (Fig. 3B; Methods). Measurements of the scattering phase functions for structures A, B, and C are plotted in Fig. 3D. The measurements presented in Fig. 3D are “absolute” in the sense that the same intensity scale is used for the three particles. Although symmetry in standard Mie scattering based on propagating plane wave excitation excludes any cross-polarization terms in the scattering matrix, the exponentially decreasing amplitude in the evanescent-wave–scattering arrangement introduces an asymmetry that leads to cross-polarization terms. Consequently, the scattered intensity depends on the specific polarization and direction of the incident beam. The results shown in Fig. 3D correspond to p-polarized incidence.

To model this evanescent excitation scenario, the usual Mie theory (41)—describing scattering of a propagating electromagnetic plane wave from spherical particles—falls short. Although previous modeling attempts either generalize Mie theory or rely on purely computational techniques (43, 44), we make use instead of a recent theoretical advance in which the conventional Mie theory is directly applied to scattering of evanescent waves through a complex-angle rotation of the standard Mie solution (45, 46). By rotating both the direction and the distribution of the incident electric $\overrightarrow{E}\left(\overrightarrow{r}\right)=\hspace{0.17em}{\widehat{R}}_y(-\gamma )\overrightarrow{E}\hspace{0.17em}\left[{\widehat{R}}_y\left(\gamma \right)\overrightarrow{r}\right]$ and magnetic $\overrightarrow{H}\left(\overrightarrow{r}\right)=\hspace{0.17em}{\widehat{R}}_y(-\gamma )\overrightarrow{H}\hspace{0.17em}\left[{\widehat{R}}_y\left(\gamma \right)\overrightarrow{r}\right]$ fields by a complex angle $\gamma$, a $z$-propagating plane wave can be transformed into an evanescent field (46); here, $\overrightarrow{E}$, $\overrightarrow{H}$, and $\overrightarrow{r}$ are electric field, magnetic field, and position vectors, respectively, and ${\widehat{R}}_y\left(\gamma \right)$ is a vector-rotation operator around the $y$ axis by an angle $\gamma$. By exploiting this complex-angle rotation methodology to calculate the field scattered by spherical core–shell particles excited by the evanescent-field configuration in Fig. 3B, we predict the scattered intensity distribution $I(x,y)$ in a plane 2 μm above the particle (Fig. 3C), which is in excellent agreement with the measurements (Fig. 3D).

Engineering the Azimuthal Structure.

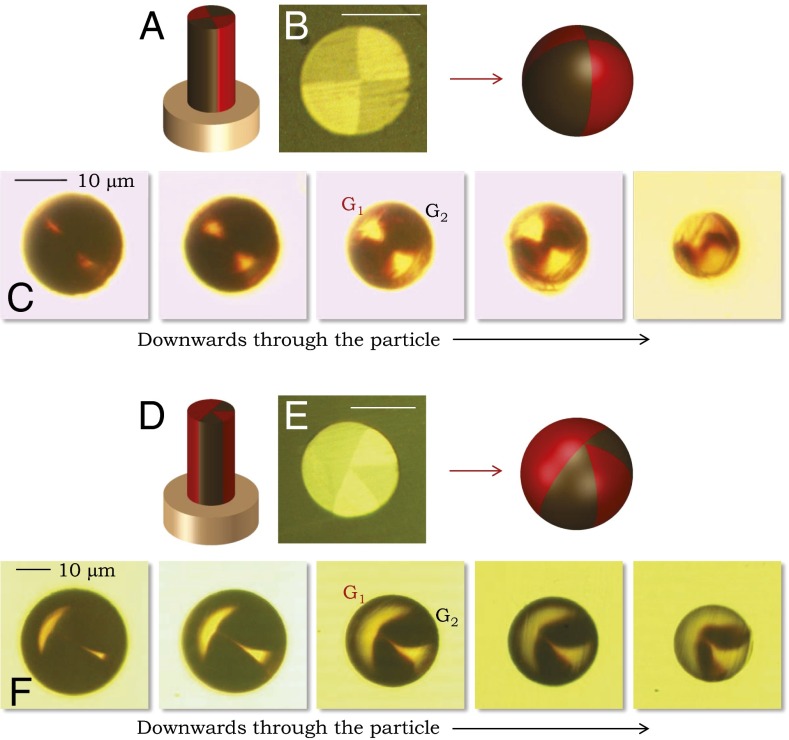
Structuring a spherical particle azimuthally—rather than radially—has traditionally been a more demanding fabrication task, and to date is limited to “Janus” structures in polymers in which two materials are compartmentalized in two hemispheres or only the surface is treated (47–49). Although symmetry principles may potentially enable higher-order discrete rotational symmetry through directed template growth, arbitrary control over the azimuthal structure of a spherical particle displaying no symmetry is out of reach of current approaches. The in-fiber breakup strategy permits sophisticated yet facile and systematic azimuthal-symmetry engineering via core segmentation. Two examples of “beach ball” particles in Fig. 4—consisting of alternating segments of two different glasses G₁ and G₂—illustrate this unique capability: (i) a particle exemplifying discrete fourfold rotational symmetry by arranging G₁ and G₂ in equally sized quadrants (Fig. 4 A–C); and (ii) a particle with broken sixfold rotational symmetry by substituting one G₁-sextant with G₂ (Fig. 4 D–F). We compare the particle structures to that of the preform and fiber by optically imaging successive layers revealed within the particle through gradual polishing.

Fig. 4.

Control over the azimuthal structure. (A–C) Beach ball particle with fourfold discrete rotational symmetry. (A) Schematic of the fiber structure; (B) optical reflection micrograph of the fiber cross-section and schematic of the resulting particle; and (C) optical transmission micrographs through a single particle while polishing axially through it. (D–F) Same as A–C for a spherical particle lacking rotational symmetry, produced by reversing one sextant (from G₂ to G₁) in a structure with sixfold discrete rotational symmetry. Throughout, G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7; and P, PES.

Combined Control over the Radial and Azimuthal Structure.

The above-described procedures for radial and azimuthal structuring are independent and may thus be realized simultaneously in a single geometry. We highlight this unique capability by combining elements of radial and azimuthal engineering to produce core–shell particles (radial control) where each layer has a Janus structure (azimuthal control). Moreover, we control the relative orientation of the two broken-symmetry layers with respect to each other. The resulting particle thus comprises four materials carefully compartmentalized within the 3D volume of the particle as confirmed by combined structural and compositional imaging (Fig. 5 A–D). Another example of combined radial and azimuthal structural control in a trimaterial particle (two glasses and one polymer) is shown in Fig. 6 in which four thin high-index glass threads are embedded in a low-index polymer surrounded by a high-index thin glass shell. The disparity between the diameters of the glass threads and the polymer results in the threads first breaking up into four parallel strings of smaller particles followed by breakup of the polymer into spherical particles containing the smaller glass particles. Movie S2 shows the real-time breakup dynamics of this fiber, whereas Movie S3 shows the internal particle structure obtained by 3D confocal optical microscopy. Such a multimaterial particle has broken spherical symmetry with a preferred optical axis along the particle strings.

Fig. 5.

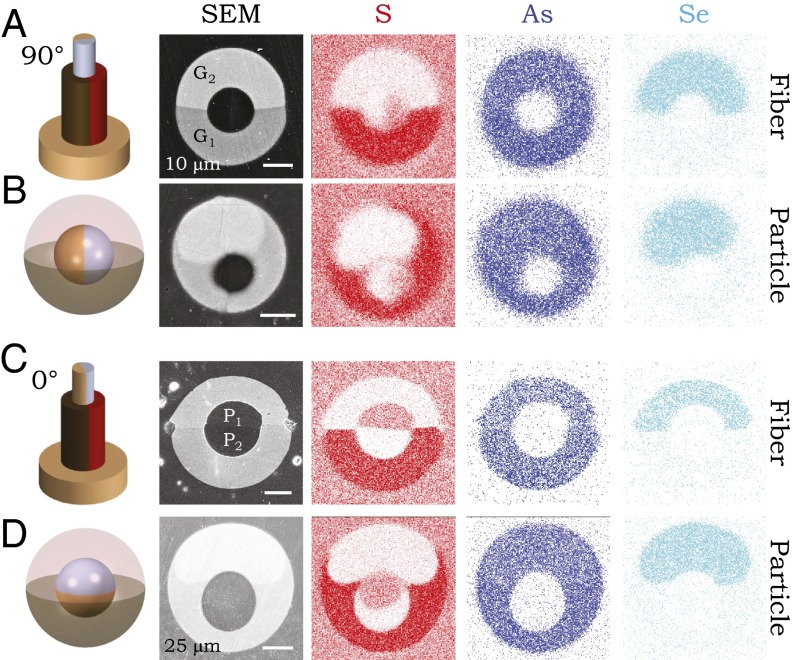
Combined radial and azimuthal control over a particle’s internal architecture. (A) A double-Janus particle: a core and shell each consisting of two halves of different materials. Here, the two symmetry-breaking axes are orthogonal. From Left to Right: A schematic of the fiber structure, SEM micrograph of the fiber cross-section, and energy-dispersive X-ray spectroscopy micrographs identifying the elements S, As, and Se. (B) Same as A, except the cross-sections are midplane through a particle resulting from the breakup of the fiber in A. (C and D) Same as A and B, except the symmetry-breaking axes in the core and shell are parallel. G₁, As₂S₃; G₂, Ge_1.3(As₂Se₃)_98.7; P₁, PES; P₂, PEI.

Fig. 6.

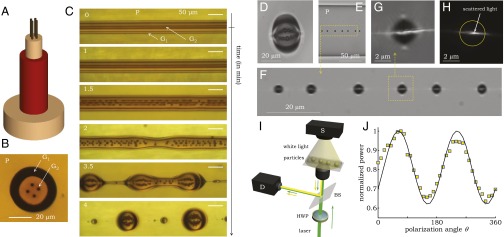
Broken azimuthal symmetry in a spherical particle enables polarization-sensitive scattering. (A) Schematic of the fiber structure that produces strings of high-index contrast nanoparticles within a photonic particle. (B) Optical transmission micrograph of the fiber cross-section. (C) Optical transmission micrographs capturing the fiber breakup dynamics during thermal treatment. First, the four G₂ [Ge_1.3(As₂Se₃)_98.7] inner threads break up in parallel strings of smaller particles, and then the polymer cladding P (PES) and thin glass shell G₁ (As₂S₃) subsequently break up. Time is indicated in the Top Left corner of each panel. (D) Optical transmission micrograph through a microparticle produced in C. (E) Transmission optical micrograph of a section of fiber containing a necklace of 3-μm–diameter particles with the same structure as in D. (F) Higher-magnification micrograph of a section of the fiber in E. White light is used in imaging, whereas a green laser is imaged in reflection (the horizontal white line) and scatters strongly parallel to the axis along which the internal high-index nanoparticles are aligned. (G) A micrograph of a single particle from F with combined laser and white-light scattering. (H) Micrograph of laser light scattering from a single particle (white light turned off). The yellow circle is a guide to the eye and corresponds to the particle surface. (I) Schematic depiction of the optical arrangement for measuring the polarization-dependent scattering. The yellow beam indicates the transmitted white light used to align the sample, whereas the green one corresponds to the laser radiation used to measure the backscattering. HWP, half-wave plate; BS, beam splitter; S, source; D, detector. (J) Sinusoidal modulation of the integrated scattered intensity (squares) as a function of incident polarization angle. The maximum occurs when light is polarized along the direction of the internal nanoparticle strings. Squares are the data, and the solid line is a sinusoidal fit.

Polarization-Dependent Optical Scattering.

Azimuthal structural engineering of a particle can enable controlling the polarization of electromagnetic waves. In particular, a spherical photonic particle with broken internal azimuthal symmetry of sufficiently high refractive-index contrast exhibits polarization-dependent scattering. When a plane wave illuminates a spherical particle whose diameter is much smaller than the wavelength, there is no phase shift between the electric fields components polarized parallel and perpendicular to the scattering plane. We designed the internal structure of the particles in Fig. 6 A–C such that the four lines of high refractive-index small nanoparticles inside each particle (Fig. 6 D–F) break its azimuthal symmetry by scattering light in a similar fashion to finite cylinders (Fig. 6 G and H). We demonstrate polarization-dependent scattering from these structured particles using the arrangement shown in Fig. 6I, where linearly polarized monochromatic light is focused on a single particle and backscattered light is collected in reflection mode while the incident polarization is rotated (Methods). We observe significantly stronger scattering when the incident polarization is aligned parallel to the internal lines of nanoparticles with respect to the orthogonal polarization (Fig. 6J).

Discussion

The desire to impart form to matter has driven much of our technological mastery over nature. We have shown here that such control can be extended to the internal architecture of spherical multimaterial photonic particles—ones at the scale of an optical wavelength combining multiple high-index contrast materials. By exploiting an in-fiber fluid instability, multiple materials—including polymers and glasses—are compartmentalized at designated radial and azimuthal positions in the coordinate system of the particle. The critical feature that distinguishes our approach is that the structure is encoded at a macroscopic scale in the preform and the characteristic length scale is then translated down across orders of magnitude via thermal drawing (35). Furthermore, the relative orientation of the azimuthal structures in each radial layer may be varied—a feature unique to our fabrication strategy and currently inaccessible to other approaches. The process is efficient, scalable, in principle scale-free, and only minimal modifications to the procedure are required to change the target particle architecture, thereby enabling the digital design of photonic particles endowed with unprecedentedly sophisticated structures, which have implications for introducing new optical scattering capabilities without changing the particle size or materials selection.

A future road map emerges: starting from a desired far-field or near-field optical scattering phase function for a single particle, what is the particle structure (the internal 3D refractive-index distribution) that is required? This inverse optical problem has not yet been solved in its entirety (50, 51). Furthermore, although we have exercised here control over the real part of the refractive index of the internal architecture of a photonic particle, it is possible to extend this approach to other physical attributes, such as the imaginary part of the refractive index (corresponding to optical gain or loss according to its sign). Gain may be imparted by doping a polymeric section of the particle with a fluorescent dye or with quantum dots, which may lead to particles satisfying the conditions for so-called PT symmetry and other non-Hermitian photonic structures (52). Moreover, nonoptical physical attributes of the particles, such as the direction of their thermal emissivity (53), may be controlled through multimaterial structural engineering.

Methods

Scattering-Strength Measurements.

Particles are extracted by dissolving the polymer cladding using dimethylacetamide at room temperature and are then deposited on a coverslip that is placed on the prism. The intensity distributions were measured across a 10 × 10-μm² plane situated at a height ≈2 µm above the particle using a Nanonics MultiView 4000 tuning-fork near-field scanning optical microscope in standard collection mode. Scattered light is collected using a Cr-Au–coated tapered silica fiber probe (Nanonics) with 50-nm–diameter aperture connected to a photon multiplying tube (Hamamatsu; H7421). See SI Appendix, S5.1: Scattering-Strength Measurements, for further details.

Polarization Measurements.

The particles are retained in the fiber without removing the cladding such that they all have the same orientation with respect to the fiber axis. The sample is first illuminated with white light to identify and align the particle (Fig. 6 E and F), and then with a green linearly polarized laser (532-nm wavelength) focused at approximately midplane of the particle. Images are recorded using a Nikon Eclipse Ti microscope. With the white light turned off, we imaged the scattered green light across a single particle (Fig. 6H) and evaluate the integrated scattered intensity as a function of incident polarization. See SI Appendix, S5.3: Polarization Measurements, for further details.