Classification of odorants across layers in locust olfactory pathway

Abstract

Olfactory processing takes place across multiple layers of neurons from the transduction of odorants in the periphery, to odor quality processing, learning, and decision making in higher olfactory structures. In insects, projection neurons (PNs) in the antennal lobe send odor information to the Kenyon cells (KCs) of the mushroom bodies and lateral horn neurons (LHNs). To examine the odor information content in different structures of the insect brain, antennal lobe, mushroom bodies and lateral horn, we designed a model of the olfactory network based on electrophysiological recordings made in vivo in the locust. We found that populations of all types (PNs, LHNs, and KCs) had lower odor classification error rates than individual cells of any given type. This improvement was quantitatively different from that observed using uniform populations of identical neurons compared with spatially structured population of neurons tuned to different odor features. This result, therefore, reflects an emergent network property. Odor classification improved with increasing stimulus duration: for similar odorants, KC and LHN ensembles reached optimal discrimination within the first 300–500 ms of the odor response. Performance improvement with time was much greater for a population of cells than for individual neurons. We conclude that, for PNs, LHNs, and KCs, ensemble responses are always much more informative than single-cell responses, despite the accumulation of noise along with odor information.

the anatomy of the olfactory pathway shows striking architectural similarities across different animal species (Kay and Stopfer 2006). Odorants are first detected by receptor neurons, and the signal is then transmitted to glomeruli in the olfactory bulb (mammals) or antennal lobe (AL) (insect), where olfactory information is processed by an interconnected network of excitatory and inhibitory neurons. A hallmark of this network configuration is the emergence of oscillatory activity, which ranges between 10 and 30 Hz in insects (Ito et al. 2009; Laurent and Davidowitz 1994; Stopfer et al. 1997; Tanaka et al. 2009) or wider ranges of frequencies in vertebrates (Kay 2014; Kay et al. 2009). Olfactory information then travels to deeper brain structures, such as the piriform cortex in mammals and the mushroom body (MB) in insects, where further processing occurs.

Quick behavioral responses require that minimal time is spent on information processing before the signal is relayed to centers for motor planning. Studies in several species generally agree that a few hundred milliseconds suffice to elicit behavioral responses, although the exact time depends on experimental methodology and task complexity (Abraham et al. 2004; Rinberg et al. 2006; Uchida and Mainen 2003; Vickers and Baker 1996). Studies of olfactory information content based on neural recordings from fish and insects show a similar range: one hundred to several hundred miliseconds are required for accurate classification (Friedrich and Laurent 2001; Krofczik et al. 2009; Mazor and Laurent 2005; Namiki and Kanzaki 2008; Raman et al. 2010; Wilson et al. 2004). In the AL, the identity of an odorant was shown to be coded by populations of first-order neurons (Wehr and Laurent 1996). The exact results of different classification measures used by different groups depend to some extent on the numbers of neurons recorded, but several studies suggest that the code is robust enough that only small fraction of the available neuronal assembly might be necessary for accurate classification (Stopfer et al. 2003).

In locust, the AL network consists of ∼800 projection (PNs) and ∼300 local inhibitory neurons, which together produce ∼20-Hz oscillations during an odor response (Bazhenov et al. 2001a, 2001b). Information then travels downstream to ∼50,000 Kenyon cells (KCs) of the MB and to the lateral horn (LN) where different classes of ∼100 neurons (LHNs) further process the incoming signal (Gupta and Stopfer 2012; Laurent 1996). The neural code representing odors varies in format among these areas. PNs represent odor stimulus through reliable sequences of synchronized and alternating assemblies of activated cells (Wehr and Laurent 1996). KCs encode odorant stimuli sparsely (Perez-Orive et al. 2002), while the LHNs (classes C1-4), which receive direct stimuli from the PNs, respond to all odors with vigorous spiking (Gupta and Stopfer 2012).

Previous modeling studies (Assisi et al. 2007; Bazhenov et al. 2001a; Nowotny et al. 2005; Papadopoulou et al. 2011) explored only a small part of the circuitry present in the locust olfactory pathway. Here we constructed a more complete model, including feedback interactions between several olfactory layers [PN, LN, KC, GABAergic neuron (GGN), LHN], and we used that detailed multilayer model to test how odorant classification in different layers depends on the integration time and the size of the neural population. We found that, particularly for PNs, only a small fraction of the population was needed for accurate discrimination. Furthermore, only a few optimally wired neurons downstream from the PNs could classify delivered stimuli with high accuracy. Individual PNs clustered into a few distinct groups and revealed greater accuracy either for high- or low-odor concentrations of odors, but not for both.

The time needed for accurate odor classification depended on the similarity of the odors and ranged between less than 100 ms for distinct odors to several hundred milliseconds for very similar odorants. Furthermore, the odor-specific temporal structures of neuronal firing were preserved at the higher stages of olfactory processing because the neuronal integration time affected classification performance of both KC and LHNs. A large population of neurons showed a significant decrease in error rate with time, while individual neurons demonstrated only marginal improvement in classification as time progressed.

MATERIALS AND METHODS

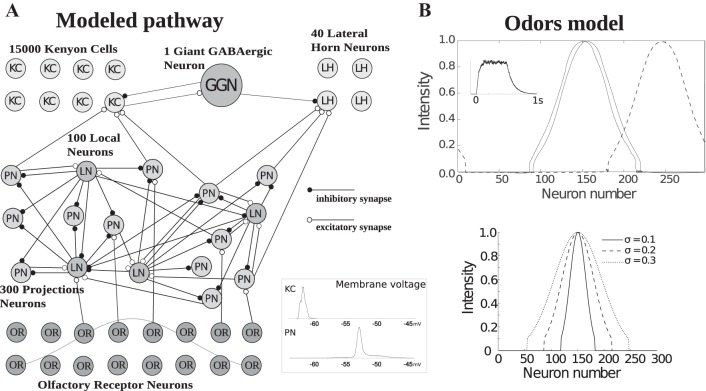
The model of the olfactory pathway included four types of neurons: 300 PNs and 100 inhibitory LNs within the AL, 15,000 KCs, 40 LHNs, and a single giant GGN in the MB. PNs and LNs were modeled by Hodgkin-Huxley equations, and their interaction produced an oscillatory rhythm at ∼20 Hz (Bazhenov et al. 2001a, 2001b). To model the follower neurons, including LHNs and large numbers KCs, we used computationally efficient map-based models (Assisi et al. 2007; Rulkov et al. 2004). We also used a map-based model for GGN to facilitate modeling synaptic interactions between GGN, KCs and LHNs. The inhibitory drive to KCs and LHNs was produced by GGN (Gupta and Stopfer 2012; Papadopoulou et al. 2011); full details of the wiring connecting these neurons are given in Fig. 1A.

Fig. 1.

Network structure and stimulation procedure. A: monosynaptic pathways directly connect PNs to KCs and PNs to LHNs. Inhibition is activated by excitatory input from the KCs to GGN, and then GGN inhibits KCs and LHNs. Inset at bottom show histogram of membrane voltages for map and Hodgkin-Huxley model; voltage trace from single KC (top) and PN (bottom) neuron was selected. OR, olfactory receptor. B, top: activation of PNs by two similar (solid lines) and one different odorant (dashed line). Similarity between odors can be seen as the distance between the identities of activated PNs. Quantitatively, similarity was defined as the distance between the two most active neurons in the population, denoted here as a “shift.” Inset shows the temporal profile of the input waveform delivered to PNs and LNs; note the variable, noisy component added to the input pulse. Bottom: activation of PNs by three different odor concentrations. Concentration is defined by the width of the distribution such that more PNs are recruited by higher concentrations.

Olfactory stimulation of LNs and PNs followed the procedure described in Assisi et al. (2007); an example of an injected current waveform is shown in Fig. 1B, top left inset. The intensity of a stimulus delivered to PNs and LNs was defined by a Gaussian distribution truncated at 0.1 to avoid stimulating all AL neurons, which does not occur in vivo (Fig. 1B). Each simulated odorant stimulated a different subset of AL neurons. We defined similarity between two odorants (shift) by the distance between two different groups of activated PNs. We tested 300 different odorants, each at 5 different concentrations. In most cases, the stimulus lasted 1 s and was presented in 10 trials that each contained a different noise component.

Antennal lobe.

The AL model followed equations and parameters used in Bazhenov et al. (2001a, 2001b). Three hundred PNs and 100 LNs were modeled by single-compartment Hodgkin-Huxley model (Hodgkin and Huxley 1952). The LN cell model included a transient Ca²⁺ current (Laurent et al. 1993), a calcium-dependent potassium current (Sloper and Powell 1979), a fast potassium current (Traub and Miles 1991), and a potassium leak current. PN model included a fast sodium current (Traub and Miles 1991), a fast potassium current (Traub and Miles 1991), a transient K⁺ A-current (Huguenard et al. 1991) and a potassium leak current.

Fast GABA (LNs to PNs, LNs to LNs) and nicotinic cholinergic (PNs to LNs) synaptic currents were modeled by first-order activation schemes (Destexhe et al. 1994), and slow GABAergic (between LNs to PNs) synaptic currents were modeled by second-order activation schemes (Bazhenov et al. 2001b; Destexhe et al. 1996).

MB and LH.

To implement large numbers of neurons postsynaptic to the PNs, we modeled them with computationally efficient map-based models (Assisi et al. 2007; Rulkov et al. 2004). KCs (15,000) and LHNs (40) were modeled as regular spiking neurons. Equations and parameters for KCs and LHNs were the same as in Bazhenov et al. (2005):

$$x_{n+1}=f_{\alpha }\left(x_n,x_{n-1},y_n+{\beta }_n\right)$$

$$y_{n+1}=y_n-\mu \left(1+x_n\right)+\mu \left(\sigma +{\sigma }_n\right)$$

$$f_{\alpha }\left(x_n,x_{n-1},u\right)=\{\begin{array}{cc}\alpha /\left(1-x_n\right)+u& x_n\le 0\\ \alpha +u\hfill & 0\le x_n\le \alpha +u\text{and}{x}_n\le 0\hfill \\ -1\hfill & x_n\ge \alpha +u\text{or}{x}_{n-1}>0\hfill \end{array}$$

The parameter μ (affecting slow dynamics of the membrane) was drawn for each neuron from a uniform distribution in the interval of 0.0012 ± 0.00068 for KCs and fixed to 0.0005 for LHNs to match more closely population response of the cells, as recorded in vivo. To introduce variability in KCs, we set σ = 0.06 + e, where e was drawn for each KC from an exponential distribution with mean 0.0072. For other cell types σ = 0.06. Input variables were proportional to the injected current I, β_n = Iβ_e, σ_n = Iσ_e, and we limited the synaptic input β_n to the range of [−1;1]. The rest of parameters were set to α = 3.65, β_e = 0.03, σ_e = 1. Initial conditions x₀ = x_n = x_n−1 = σ − 1, y₀ = x₀ − α/(1 − x).

GGN is a nonspiking cell, and its response characteristics were tuned to replicate responses recorded in vivo (Gupta and Stopfer 2012) (see Fig. 2) with the following equations:

$$x_{n+1}=\alpha f\left(x_n\right)-y_n$$

$$y_{n+1}=y_n+\mu \left(1+x_n\right)-\mu \left(\sigma +{\sigma }_n\right)$$

$$f\left(x_n\right)=\{\begin{array}{cc}2& x_n>3\\ x_n-\frac{x_n^3}{27}& -3\le x_n\le 3\\ -2& x_n<-3\end{array}$$

where α = 0.8, μ = 0.005, σ = −0.5, and initial conditions: x₀ = σ − 1, y₀ = α (x₀ − x₀³/27) − x₀.

Fig. 2.

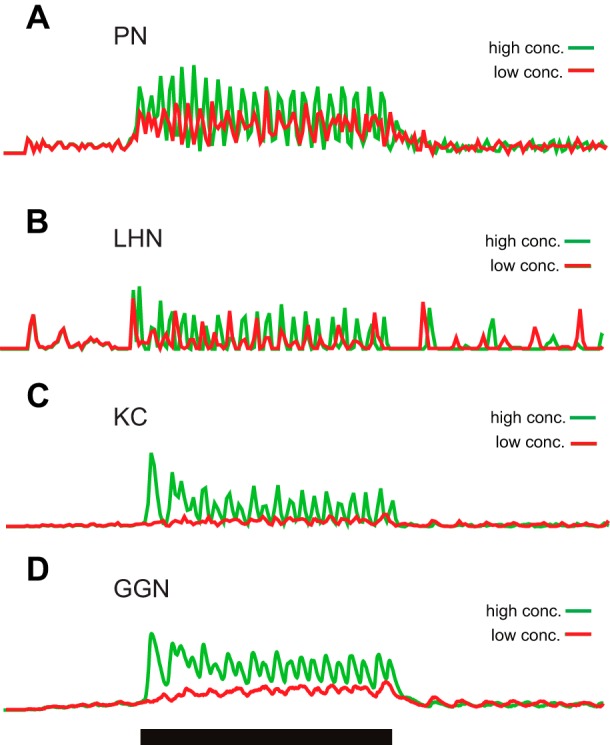
Model response patterns of different cell types. The spikes produced by all model neurons of each type [PNs (A), LHNs (B), and KCs (C)] were binned into 10-ms sliding window and plotted over time. Red lines, low odor concentration (0.15). Green lines, high odor concentration (0.25). D: membrane voltage of GGN. Black bar shows 1-s stimulation.

To model synaptic connections, we used a map-based equation for the conductance and synaptic current (Rulkov and Bazhenov 2008). Excitatory synapses (PN → KC, PN → LHN, KC → GGN) followed these equations:

$$g_{n+1}^{\text{syn}}=\gamma g_n^{\text{syn}}+\{\begin{array}{cc}{\text{G}}_{\text{ACh}}/{\text{S}}_{\text{Dend}},& \text{spike}\\ \text{0,}& \text{otherwise}\end{array}$$

$$I_n=\{\begin{array}{cc}-g_n\left(x_n^{\text{post}}-{\text{E}}_{\text{ACh}}\right),& x_n^{\text{post}}-{\text{E}}_{\text{ACh}}>0\\ \text{0,}& \text{otherwise}\end{array}$$

where maximum conductances (in dimensionless units, see Bazhenov et al. 2005) were set to G_ACh (PN → KC) = 0.00066, G_ACh (KC → GGN) = 0.5, G_ACh (PN → LHN) = 0.007, decay constant γ = 0.4, reversal potential E_ACh = 0, ratio between size of soma and dendrite S_Dend = 165 × 10⁻⁶. x_n^post refer to x_n on postsynaptic site. A spike was generated when on presynaptic site x_n^pre ≥ α + y_n^pre + β_n^pre or x_{n − 1}^pre.

Inhibitory synapses (GGN → KC, GGN → LH) followed these equations:

$$g_{n+1}^{\text{syn}}=\gamma g_n^{\text{syn}}+\{\begin{array}{cc}1/\left[1+\frac{\text{exp}\left(\frac{-x_n^{\text{pre}}+1.5}{1.5}\right)\cdot {\text{G}}_{\text{GABA}}}{{\text{S}}_{\text{Dend}}}\right],& x_n^{\text{pre}}>-1.4\\ 0,& \text{otherwise}\end{array}$$

$$I_n=-g_n\left(x_n^{\text{post}}-{\text{E}}_{\text{GABA}}\right)$$

Maximum conductances were fixed to G_GABA (GGN → KC) = 0.00004, G_GABA (GGN → LH) = 0.00045. Since GGN is not a spiking neuron, the threshold of x_n was set to −1.4 on the presynaptic site to trigger activity.

The size of the network (Fig. 1A) was set to 1/3 of a locust olfactory network for computational efficiency. Connection probability between different types of cells was set in the following way: p(PN → KC) = 0.3, p(PN → LHN) = 0.7 [an estimate based on dense convergence observed in Gupta and Stopfer (2012)]. There was only a single GGN, so all connectivity probabilities to and from the GGN are one, p(KC → GGN) = p(GGN → KC) = p(GGN → LH) = 1.

The inset shown in Fig. 1A shows example voltage histograms of simulated PNs (Hodgkin-Huxley model) and KCs (map-based model). The sources of variability in the model included 1) noise in the simulated input from olfactory receptors; 2) variability in baseline voltage of PN neurons; and 3) random variation in parameters that affect the dynamics of the membrane voltage and network connectivity. Introducing such variability in the model led to membrane voltage variability like that observed in vivo.

Error rate analysis.

To characterize how information about odor stimuli is transformed across layers of the olfactory pathway, we measured classification error rate attained by different models when separating two given odorants at a fixed concentration for a given population of cells (MacLeod et al. 1998).

Population responses can be represented in a vector space where each dimension characterizes spiking of a single neuron (Gochin et al. 1994); to construct the vectors, we used spike counts binned within a fixed time window (“integration time”). The response of a population of neurons was then characterized by its vector, A. When stimulating the network by K = 10 trials of two different odorants, two groups of vectors were obtained, A_i and B_i, i = 1,…,10. The average vector for each group was calculated, <A> and <B>. Then each response trial was classified by comparing the Euclidean distances between the vector representing trial A_i or B_i and two average vectors representing odorants, <A> and <B>. The percentage of trials when the distance between a trial of odor A and the mean representation of A was larger than the distance to the mean representation of another odor B, |A_i − <A>| > |A_i − <B>|, was counted as an error (the same calculation was done for the second odorant B). The error rate was calculated as the fraction of incorrectly classified trials for both odors; an error rate of 0.5 corresponded to chance performance. To test the effect of the size of the population on the error rate, we varied the number of neurons included in the analysis, including a case when the spike train of a single neuron was analyzed.

To characterize the overall trends of error rate in single neurons (Fig. 3), we measured the slope of the line approximating the values of error rates across concentrations for each difference in similarity between two odorants (odorant shift). The histogram of the slopes (first derivative) summarized lines for all shifts in neurons which had nontrivial error rate profiles (i.e., not all error rate values equal to 0.5).

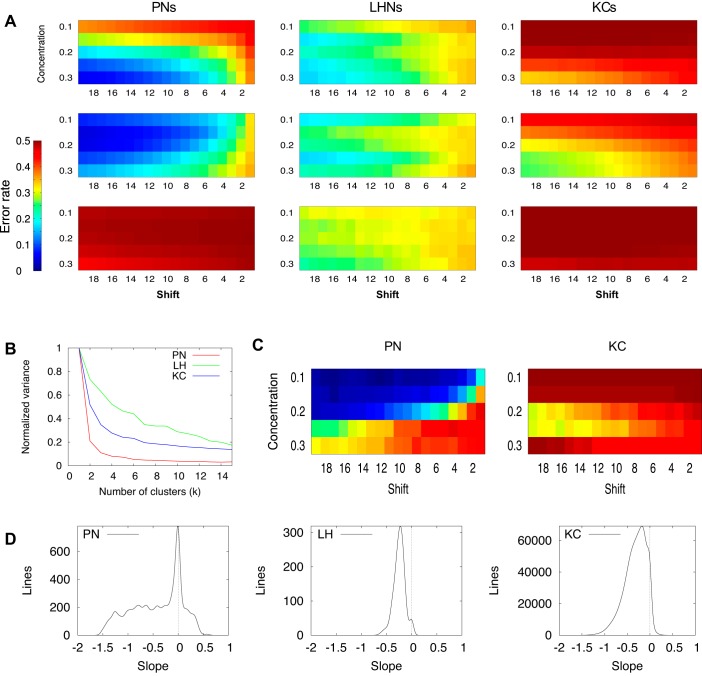
Fig. 3.

Classification performance by single neurons. A: average classification error rate profiles obtained by K-means clustering (k = 3): PNs (left), LHNs (middle), and KCs (right). X-axis is odor similarity (from low to high). Y-axis is odor concentration (0.1, low concentration; 0.3, high concentration). Color of the heat map is error rate with a maximum of 0.5 (chance level for 2 odors). B: total variance as a function of number of clusters used in decomposition. Variance was computed as the sum of distances between the cluster and all points belonging to that cluster (summed for all clusters). C: examples of two single-cell error rate profiles: PN (left), KC (right). D: distribution of the error rate vs. concentration slopes. For each odor pair, we computed the slope of line approximating error rate as a function of concentration (a slice of a particular color from error concentration profiles shown in A), giving 20 slopes per neuron. The distribution of all slopes for all cells is plotted in B. Cells with completely flat profile with error rate 0.5 were omitted from this analysis.

K-means clustering was used (MLPACK library) to determine the typical shapes of error rate profiles. To compute the total variance for a given k, the error profile for each cell was represented as a vector. Euclidean distances between a cluster center and its points were computed and then summed for all clusters. To normalize these results, the total variance for a given k was divided by the total variance for k = 1.

We sought to compare the error rate estimated from the population responses as described above (referred to as network or population error rate) to the error rate from ensemble n of single neurons (referred to as the statistical error rate below), so we calculated the statistical error rate S(n). We first estimated the average error rate, p, of a single neuron of a given type as described above (see, e.g., Fig. 5C), and we used this value to represent the probability of classification error when the responses of a single randomly selected neuron are used to classify the odor. We defined the population response by a subset of n neurons as erroneous when the majority (>50%) of these neurons misclassifies the odor. If p is the probability that a single neuron will make an error, then the probability that a randomly chosen subset k out of n neurons will give an incorrect answer while the (n − k) remaining neurons gives a correct answer is p_k(n) = p^k (1 − p)^{n − k}. There are $\left(\begin{array}{c}n\\ k\end{array}\right)$ subsets of the size k in a population of n neurons. Thus the statistical probably that more than 50% of the neurons in a population of n neurons would classify the odor erroneously can be estimated as

$$S\left(n\right)={\displaystyle {\sum }_{k=\lfloor n/2\rfloor +1}^n}\left(\begin{array}{c}n\\ k\end{array}\right)p^k{\left(1-p\right)}^{n-k}$$

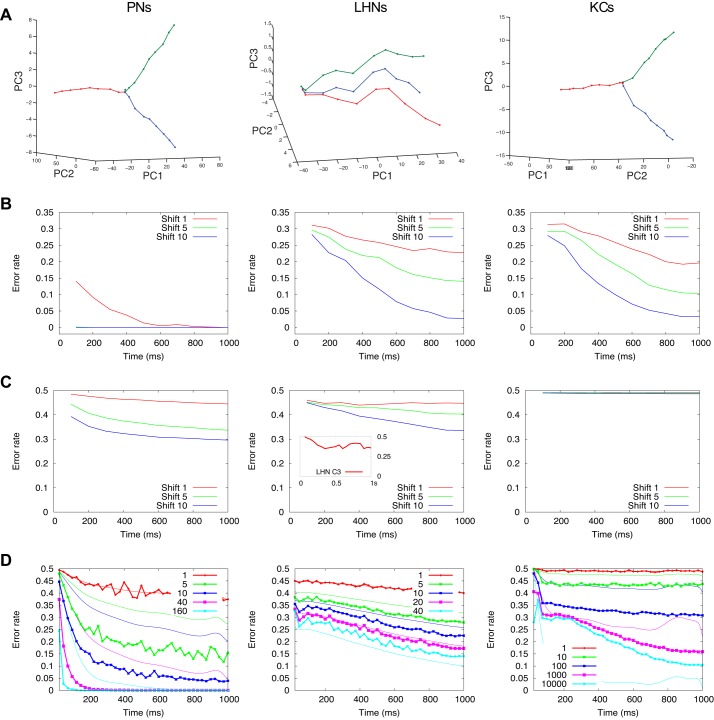
Fig. 5.

Role of stimulus duration on classification error. A–D: columns in the graph show data for PNs, LHNs, and KCs. Results are shown for odor distances 1 (red), 5 (green), 10 (blue), and concentration C = 0.2. A: representation of 3 odors for increasing integration time projected to first 3 principal components. Each point is an average of 10 trials; each line connects points with increasing integration time, starting with 100 ms to 1,000 ms. The distance between odor representations increased with integration time. B: population error (for entire network of each type) as a function of integration time. C: average single-cell error rate for PNs, LHNs, and KCs. Inset shows average classification error rate for single LHNs recorded in vivo (6 LHN neurons, class C3; replotted from Gupta and Stopfer 2012). D: error rate estimated from different size subsets of neurons. Thick lines with points show populational network error rate. Thin lines show estimated statistical error rate; lines were additionally smoothed for better readability of the plots. Increasing the size of each population leads to faster decreases in error rates as integration time increases for PNs and KCs, and to lesser extent, for LHNs.

where the sum is taken over all k > n/2.

Trajectories in coding space.

To visualize the neurons' population dynamics, we averaged spiking activity from all trials and measured the number of action potentials for each neuron in overlapping windows of specific durations. By stepping the time window forward in increments of 2.5 ms, we produced trajectories in a high dimensional coding space with each dimension corresponding to a single neuron and each point in the trajectory to the activity of all neurons within a given time window. Principal component analysis (PCA) reduction into the first three dimensions was used for graphing the results. A smoothing window was applied to each trajectory.

Experimental data.

Electrophysiological recordings were made from adult locusts raised in a crowded colony. Animals were restrained, and the brain was exposed, perfused with fresh locust saline, and desheathed (Laurent and Naraghi 1994). Recordings from PNs were made with 16-channel silicon probes (NeuroNexus Technologies, Ann Arbor, MI) and were amplified by a custom amplifier (BES, Caltech). Signals were sorted in Igor (Wavemetrics, Portland, OR) by the Spike-O-Matic algorithm (Pouzat et al. 2002).

Intracellular recordings from LHNs were made using sharp glass micropipettes filled with 0.5 M potassium acetate (P87 horizontal puller, Sutter Instrument, 60–200 MΩ), and signals were amplified (Axoclamp-2B; Molecular Devices) and sampled at 15 kHz (LabView software; PCI-MIO-16E-4 DAQ cards; National Instruments) (Gupta and Stopfer 2012).

RESULTS

We used the model of the locust olfactory circuit (Fig. 1A) to simulate responses to 300 different odorants at 5 different concentrations (Fig. 1B). The spiking outputs of PNs, LHNs, and KCs were binned within specific time windows and analyzed to reveal how odor representations evolve as they progress through multiple stages of the olfactory system.

Cell responses.

The model neurons responded in ways that were similar to neurons recorded in vivo (Fig. 2). PNs responded to a 1-s odor stimulation on average with 5.5 spikes (Mazor and Laurent 2005). KCs responded sparsely with less than 10% of the KC population responding to each odor, and each responsive KC generated on average five spikes (Perez-Orive et al. 2002). LHNs responded to every odor with an average of 11.5 spikes (Gupta and Stopfer 2012). GGN responded to odors with a nonspiking response (Fig. 2D), reflecting the oscillatory output of AL, transmitted through the KCs (Papadopoulou et al. 2011). As in vivo, all cell populations showed odor-elicited oscillations, evident in the spike counts made in sliding 10-ms windows (Fig. 2); as in vivo, the oscillations driving the whole circuit were generated by the interactions of PNs and LNs in the AL (Bazhenov et al. 2001b). The oscillation frequency was primarily determined by the time scale of the fast inhibitory connections from LNs to PNs (Bazhenov et al. 2001b), and its amplitude was determined by the number of activated PNs and the degree of synchrony across active PNs, which provides an indirect measure of odorant concentration, as observed in vivo (Ito et al. 2009). Stages downstream from the AL showed somewhat weaker oscillatory behavior and in some cases with modified rhythm (e.g., resulting from the feedback loop between KCs and GGN).

Classification error of single cells.

We first tested the classification performance of single neurons from different olfactory layers. For each pair of odors and each odor concentration (see Fig. 1), the error rate was calculated using binned spike trains of single neurons (see materials and methods). We represented the neuron's response to each odor trial as a point in one-dimensional space, with each point reflecting the number of spikes produced by the neuron within a specific time window. Responses gathered over the entire stimulation time (1,000 ms) were used for the discrimination task, and the classification performance of each neuron was evaluated independently.

For each neuron, we calculated a classification error profile: the average error rate it achieved with given pairs of odors with different degrees of similarity, and a range of concentrations. Examples of two such profiles are shown in Fig. 3C. Only a few distinct types of profiles were observed across all of the neurons. Single neurons with analogous profiles suggest these neurons shared similar classification performance for a given set of odor similarities and concentrations. To determine the number of distinct profiles, we performed K-means cluster analysis. It revealed that the profiles of individual PNs fell largely into three groups. Characteristic representatives of these three types of profiles are shown in Fig. 3A. For PNs, these three groups together well-described the error profiles observed across the entire PN population. The red line in Fig. 3B shows, for a given number of clusters, the fraction of unexplained variance; for PNs, the first two clusters alone explain 80% of the variance. The variance became almost flat for k > 3, indicating that increasing numbers of clusters beyond the first three did not significantly decrease the total variance (measured as the distance of cell profiles to their respective clusters). One-half of the PN population performed at chance when distinguishing between any two odorants; see Fig. 3A, left bottom, which shows a flat error rate profile centered around 0.5. The remainder of the PNs most often showed decreasing error rates as the difference between odors (odor shift) increased and as concentration increased (see example in Fig. 3A, left top). Some PNs showed the opposite trend, having profiles with minimal error rate either for low or intermediate odor concentrations (Fig. 3A, left middle), and for a few PNs this trend was even more pronounced; the profile for one such PN is shown in Fig. 3C, left. This unusual trend can be explained by odor saturation: higher odor concentrations activate larger populations of receptor neurons, causing overlaps in the neuronal populations responding to different odors. Randomized network connectivity between layers of olfactory processing can cause increased sensitivity in some downstream neurons to the overlap in populations of the upstream neurons and thus degrade the discrimination capabilities of particular neurons at specific concentrations. To quantify the error rate profiles, for each neuron and each distance between odors we then calculated the slope (linear approximation) of the error rate across concentrations in the profile. With this measure, a negative slope, for example, indicates that the error rate decreases as odor concentrations increase. Figure 3D, left, shows the distribution of such slopes for all distances between odors and all neurons. We found more neurons showed negative slopes (error rate decreases as concentration increases) than positive slopes (error rate increases with odor concentration); thus more PNs perform like those in the example shown in Fig. 3A, left top, rather than those shown in Fig. 3A, left middle.

A similar analysis of LHN classification error profiles (Fig. 3A, middle) revealed, as for PNs, a decrease in error rate as odor difference increased. In contrast to PNs, however, LHNs maintained a constant error rate across odor concentration. The error profiles of the two cell types had similar shapes, as shown by the three cluster representations. Notably, unlike the PNs, the variance in error rate across LHNs did not decrease abruptly when more clusters were used in the decomposition analysis (Fig. 3B, green line), which would be the case when few very distinct clusters explained most of LHN profiles.

KCs also had classification error rate profiles with less variability than those of PNs. Some KCs showed essentially no classification success (Fig. 3A, right bottom); typically, KCs displayed a slight decrease in error rate as odor difference and concentration increased (Fig. 3A, right top and middle). A minority of KCs exhibited highly specific responses not exemplified by the cluster means, such as the example shown in Fig. 3C, right.

All three main cell types (PNs, LHNs, KCs) tended to have higher error rates for low odor concentrations, illustrated as a negative slope across concentrations (Fig. 3D). PNs revealed the widest distribution of gradients, implying that many PNs are highly sensitive to a particular concentration of an odor while performing much worse for a different concentration. In contrast, LHNs showed a narrow distribution, suggesting that large numbers of LHNs performed equally well across the entire range of odor concentration. The average PNs and LHNs classification error rate was in the 25–45% range, varying with the extent of difference between the odors. In terms of single-cell average performance, single KCs performed the worst of the three main cell classes; KC classification error rate varied between 40 and 50%, and only a minority of KCs showed higher classification success for a given stimulus (neurons showing flat profiles with error rates of 0.5 were not included in the histograms plotted in Fig. 3D).

Classification error in populations of cells.

Since olfactory information is represented by populations of neurons (Laurent 1996), we examined how classification error rate depends upon the size of the population. We used an approach similar to that described in the previous section; however, here we represented a population response to each odor input as a vector in N dimensional space, where N was the number of neurons of a given type used in the analysis. We found that population errors were always lower than individual cell error rates for all cell types (Fig. 4A). When an entire population of cells was used for the analysis, error rates dropped to nearly zero. In the case of PNs, the error rate dropped within the first 100 ms; KCs and LHNs needed more time (Fig. 4B). As with the analysis of single cells, we observed a decrease in error with increasing distance between odors.

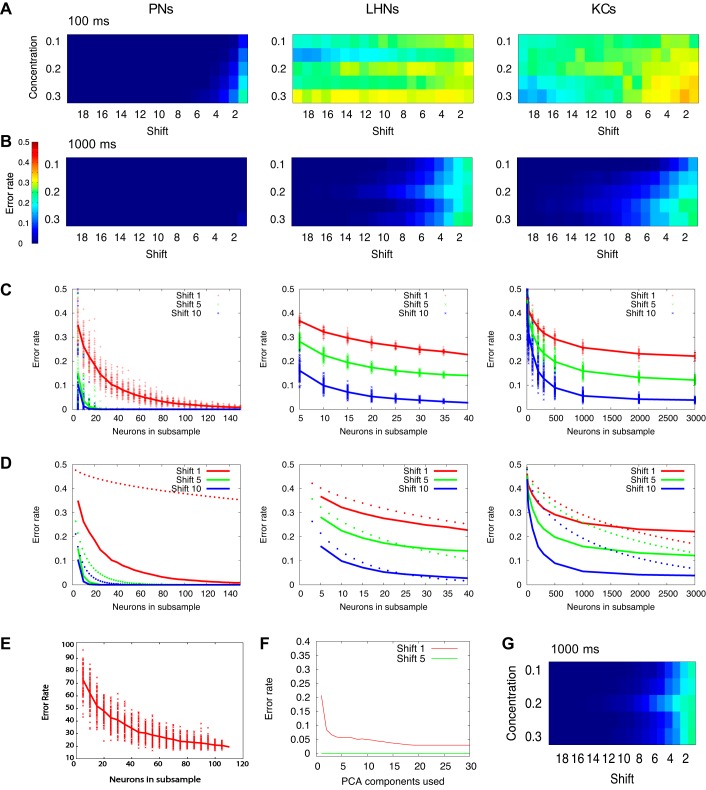
Fig. 4.

Classification performance by population of neurons. A–D: columns show results for PNs, LHNs, and KCs. A: error rates based on the time window of the first T = 100 ms. B: error rates for the full T = 1 s odor presentation. C: error rate as a function of the subset of neurons used for classification. For each sampling size, we drew 100 random subsets of neurons and calculate its error rate (each subset is represented by 1 dot in the graph). All data are shown for odor distances 1 (red), 5 (green), and 10 (blue), and concentration C = 0.2. D: comparison of populational network error rate (solid lines) and statistical error (dotted lines). Axis and colors have the same meaning as in C. E: classification error rate for subsets of PNs recorded in vivo (replotted from Stopfer et al. 2003). F: error rate as a function of number of the most significant PCA components used for classification, averaged across odorants with odor distances 1 and 5, integration time 1 s. G: LHN error rates for connections with random connection strengths from PNs to LHNs. Each original connection strength was multiplied by a random value drawn from the uniform distribution [0.5;1.5]. Color code is as in A and B.

When we tested differently sized subsamples of the population, we found that the error decreased as the size of the population increased (Fig. 4C). PNs revealed a rapid decrease in error rate; for pairs of similar odors (distance of 5) classification performance was nearly perfect, given about 30 or more randomly selected neurons (based on 100 randomly selected sets). For pairs of odors that were more different from each other (distance of 10), around 20 neurons were sufficient to achieve extremely low error rates. Notably, some subsamples consisting of just a few neurons reached perfect classification, in close agreement with results from PNs recorded in vivo [Fig. 4E; adapted from Stopfer et al. (2003, Fig. 6E)]. For both LHNs and KCs, error rates rapidly declined as subsample size increased, but, unlike the case of PNs, the error rates asymptoted without approaching zero (Fig. 4C).

Fig. 6.

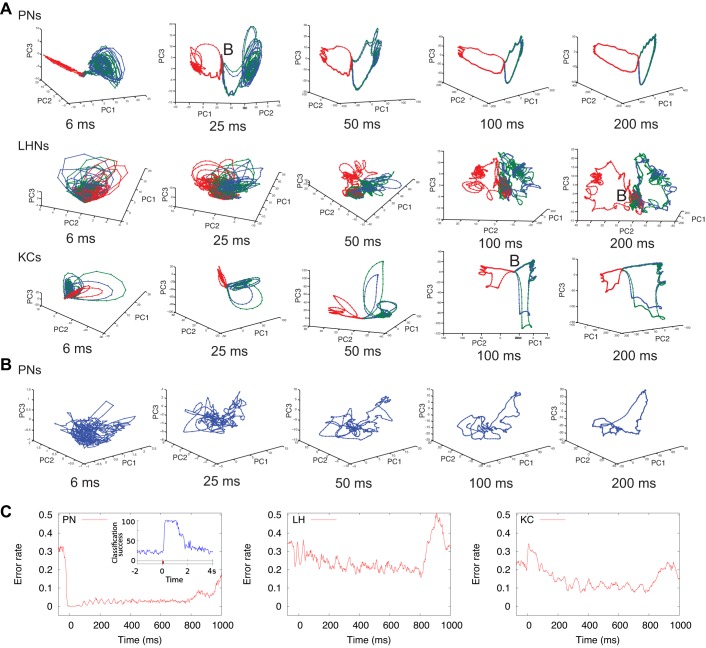
Role of integration window time in odor classification. A: population trajectories projected into first 3 principal components. Each point is an average of 10 odor trials; integration window slides forward in 2.5-ms steps. Points from the same odorant are connected with lines of the same color (odor distance between green and blue is 5, odor distance between blue and red is 100); in all cases concentration C = 0.2. B: baseline activity. Population trajectories of 14 simultaneously recorded locust PNs, averaged across 10 trials are shown. C: error rate across time obtained with 50-ms moving integration window. We used similar odors (shift 5), concentration = 0.2. Inset in left panel: classification success for the 14 PNs recorded from locusts, across time using 50-ms window (Brown et al. 2005).

Intuitively, one might expect to find an improvement in discrimination performance when the neural population increases. It is not clear, however, whether this improvement can be explained entirely by the larger population size, or whether it also depends on the variety of tuning of individual neurons within the population. If the first is true, then adding more neurons with the same average behavior to the population analysis (thus, e.g., eliminating the “noise” present at the level of a single neuron or small population) would lead to the same improvement observed in the population of AL neurons tuned to specific odor features. To test this, we computed expected statistical error rates (see materials and methods section) for a population of statistically identical neurons.

The dotted lines in Fig. 4D show error based on the pure population averaging of the estimated single-neuron performance (depicted in detail in Fig. 5C below); the solid lines are identical to the network population error rates shown in Fig. 4C. The difference between two (especially for PNs) suggests that classification performance based on the cell population of the network cannot be simply reduced to the smoothed average of single-neuron performance, and that the structure of the responses across populations of neurons matters. In the case of KCs, we observed that statistical error continued to decrease (Fig. 4D, right, dotted lines), and, for very large subsets of neurons, fell below the network error rate (Fig. 4D, right, solid lines). This may be explained by the fact that the average single KC error rate derives from a relatively small set of very informative neurons, and a large set of neurons whose contribution to classification is very small (see the representative clusters in Fig. 3A). As such, the population network error rate remains constant once the subset of neurons is large enough to include those informative neurons, while statistical error continues to decrease toward zero because only the size of the subset, not its structure, defines the error rate.

Effect of synaptic strength variability on classification error.

In our model, all synaptic connections from PNs to the following layers had the same synaptic strength. Biological neurons may have synapses of different strengths, and plasticity mechanisms can potentially modulate the strengths of signals coming through them. To test how classification performance may change with plasticity, we first introduced random variations in synaptic strength between PN and LHNs. The resulting error rate (see Fig. 4G) was very similar to the baseline model with uniform strengths (compare middle column in Fig. 4B for 1,000 ms; similar results were obtained for 100 ms, not shown). This result also shows that our results, and the olfactory circuitry, are robust against random variations in synaptic strength.

Plasticity may shape connections between neurons in a nonrandom way, and we previously showed that spike timing dependent plasticity operating on connections from the AL to the MB can increase the sparseness of odor representation by KCs and improve classification (Finelli et al. 2008). Here, we applied PCA as a way to optimize the synaptic output of the PN population. The first PCA component can be interpreted as a vector of weights for an “ideal” downstream observer reading the entire PN population; each synaptic connection to that “ideal” cell would be determined by a coefficient of the given PCA component. This “ideal” downstream cell would become very sensitive, for a given stimulus, to PNs that capture most of the population activity variance, and less sensitive to PNs that do not contribute to the variance. Subsequently, we can project the PN population code into the subspace defined by PCA component(s) and measure the error rate in the same way we do in normal coding space. If classification succeeds, it would imply that a single (first) component is sufficient to express the variability needed for proper odor identification. Otherwise, we can start adding additional PCA components, thus allowing additional dimensions to express the variability needed for proper odor separation. Again, coefficients of each additional component can be treated as synaptic weights to another “ideal” downstream observer capturing the remaining variability of PN output. The result of such an iterative process can be seen in Fig. 4F, where we measured the error rate of an increasingly large population of “ideal” cells. It can be seen that the use of even a few optimally tuned cells can lead to very good classification results. While an explicit implementation of this sort of synaptic plasticity between PNs and downstream neurons would go beyond the scope of this paper, this result suggests the possibility that plasticity mechanisms might be able to tune synaptic weights to achieve better classification performance than we reported above.

Classification performance vs. integration time.

We next investigated how classification error rate is affected by the response history available to downstream neurons, starting from the beginning of the stimulation. Thus we tested how error rate changes as odor-sampling time is increased.

In our simulations, increasing odor-sampling time produced an increasingly large distance between odor representations in coding space, thus providing better classification performance. Figure 5A shows with representative examples how the distance between odor representations develops over time for three odorants that are more or less similar to one another. The entire population of neurons was included in the analysis, and a three-dimensional PCA projection was used to visualize responses. In these experiments, the neurons integrated their input for successively longer time periods. The results show that, for short integration times, the points representing the population response to a given odor are very close to each other. However, as the integration time increases, the points continuously diverge (odor points are connected with a line).

The improvement in performance at the population level can be seen quantitatively in Fig. 5B. For PNs, classification of odors with 90% success (10% error) was attained within 200 ms even for odorant pairs with distance = 1 (very similar odors); for more different odorant pairs, classification was nearly perfect by 100 ms. Similarly, rapid classification by PNs has been reported in locust (Brown et al. 2005; Saha et al. 2013). For LHNs and KCs, average classification error rates ranged between 5 and 30% and decreased slowly as integration time increased. For all cell types, more distinct odors were generally classified faster.

Figure 5C shows the average classification error rate for single PNs, LHNs, and KCs. The average KC profile consists of a flat line at around 0.5, which corresponds to the sparse responses of the KC population. We found that increasing the integration time improved classification by single neurons less than it did when the entire population was included in the analysis. Figure 5D shows a plot of classification error vs. time for increasingly large populations of neurons. Both the network error rate and statistical error rate are provided for each population size. We observed that population error rate was lower than the statistical rate for smaller cell populations, but in LHN and KC networks it reversed once the population size exceeded a threshold. This result was similar to that observed before in simulations with increasing network size (Fig. 4D). The error rate obtained with single LHN neurons agrees well with results obtained in vivo from locust LHNs (inset in Fig. 5C, middle, shows classification error for single LHN class C3; Gupta and Stopfer 2012). We conclude that populations of neurons benefit far more substantially from longer integration times than do single neurons, and that this effect cannot be explained simply as the probabilistic product of including a larger number of uniformly behaving neurons. This finding should be taken into account when drawing conclusions about the role of integration time in performance based on small subsamples of experimentally recorded neurons.

The optimal size of the “read out” integration window for different cell types.

PNs and KCs/LHNs represent sequential layers of olfactory processing. As information moves through this network, what is the optimal integration time for downstream neurons to provide the best classification performance? In the previous section, we considered decoding based on continuous “integration” of the input by downstream neurons starting from the beginning of odor stimulation. We found (Fig. 5) that having access to more of the history of an odor response improves classification performance at the level of cell population. This effect was strongest for very similar odors. Now we ask how classification performance depends on the size of the integration window when subsequent integration windows of such fixed size are used (short “snapshots”).

For this analysis, we used three different odorants, two similar and one very different (odor distance 5 and 100). First, for all three main types of neurons (PNs, KCs, LHNs), we visualized the trajectory of the population response using PCA, with spikes binned into sliding windows of different size from 6 ms to 200 ms, with a small time step of 2.5 ms. The entire population of neurons of each class was used for the analysis. Our approach is similar to that used previously in experimental studies (Mazor and Laurent 2005; Raman et al. 2010; Stopfer et al. 2003), except that we considered a wider range of binning windows (previous experimental studies usually tested 100–200 ms windows).

The spatio-temporal structure of the response trajectory changed significantly as the integration window increased (Fig. 6A). Small windows revealed multiple oscillatory loops (Fig. 6A, left), with each loop representing a single oscillatory cycle in the AL local field potential (the main frequency generated by PNs is about 20 Hz, which corresponds to the 50-ms duration of a single cycle). As the window lengthened closer to 50 ms and beyond (Fig. 6A, right), the segment of repeated loops started to unfold into a smoother trajectory. The initial unfolding part of the trajectory corresponded to the transient response at the odor onset, and the rest represented the stationary part of the response, commonly referred as the “fixed point.” While our results are in agreement with previous experimental findings (e.g., Mazor and Laurent 2005), our analysis using smaller time windows of less than 50 ms clearly shows that the “fixed point” actually represents a state with complex oscillatory dynamics that become invisible when longer time windows (>100 ms) are applied.

All three cell types revealed oscillatory behavior when their responses were analyzed with brief time bins, but the transition to unfolded trajectories became apparent when using different window sizes for different cell types. For PNs, a 50-ms window was sufficient to reveal the distinct trajectories of similar odorants, but this window was too brief to reveal such structure in responses of LHNs. This result suggests that, to attain similar levels of performance, different integration windows should be used for piecewise decoding by different cell types. This result is consistent with analyses shown in Fig. 5B, where we observed that the PN population reached its optimal performance much more rapidly, starting from beginning of the stimulation, than the KC or LHN populations.

To compare the model's behavior with recordings made in vivo, we plot in Fig. 6B the reduced-dimension trajectory of 14 PNs responding to a 1-s pulse of hexanol. As in the model data, increasing the integration window helped to unfold the complex shape of the PN population trajectory into a simpler one. In the responses recorded in vivo, we did not observe clear loops representing 20-Hz oscillations, likely because 1) we averaged activity of all PNs without aligning them to a common local field potential reference (something not available with this data set); and 2) we had access to only a small subset of the entire PN population (14/∼800 neurons).

Recordings made in vivo from the locust PNs show that the transient onset and offset components of the response contain more information about the odor than the stationary component of the response (“fixed point,” Mazor and Laurent 2005). To explore this result in our model, we measured the error rate over successive integration windows comprising the trajectory (Fig. 6C). Using similar odors (odor distance 5) and 50-ms windows for spike binning to match conditions used in the locust, we found that classification performance of the PN population reached its peak very quickly: the first 50-ms window was already optimal. The error rate then remained nearly constant. Overall, this result is in good agreement with analyses of recordings made from locust PNs (Fig. 6C, left, inset). In contrast, the same analysis conducted on responses of KCs and LHNs showed error rates that, on average, slowly decreased from one 50-ms window to the next (although the error rate showed significant fluctuations) over the first ∼500 ms. In sum, the results presented in Figs. 5 and 6 suggest that the PN population may attain optimal classification of even very similar odors much faster than the KC and LHN populations. As expected, using odor pairs that were more distinct reduced the time required for optimal odor classification by any population.

DISCUSSION

In this study, we compared odor representations at different stages of processing in the locust olfactory system. We modeled circuitry in the AL, MB, and LH, focusing on odor representations by the PNs, KCs and LHNs. Our work revealed significant changes between encoding strategies applied by the AL neurons and their downstream counterparts: neurons in the MB and LH. Many individual PNs of the AL showed a preference for a specific range of odor concentrations, especially for dissimilar odors. KCs and LHNs displayed more uniform properties, with many cells showing similar performance to decode odor concentration. Notably, we observed a small subset of KCs showing high specialization for narrow concentration ranges. (The specificity of single KCs to particular odors observed in vivo would not be seen in our profiles, because the result for each distance of odors was averaged across many different tested odor pairs.) In all cases, when neurons of a specific type were analyzed together as a population, they displayed better classification performance than individual neurons. This improvement was quantitatively different for the uniform population (consisting of identical neurons) and the spatially structured population (actual olfactory circuitry, consisting of unique and different neurons) as shown in Fig. 5D; we are not aware of other studies showing this difference. In all cases, increasing the size of the actual olfactory network led to much faster decrease in classification error than when the size of the uniform (consisting of identical neurons) population was increased.

Neuron populations also benefited more from longer durations of odor decoding: discrimination performance continued to improve as the length of the odor stimulation increased, while individual cells reached asymptotic performance levels soon after odor onset.

Error rates for population vs. single cells for different cell types.

Single PNs, in general, showed a more diverse error rate profile than LHNs and KCs. We found that many PNs were best able to discriminate odors at specific concentrations. Importantly some neurons performed better for low odor concentrations and others for high concentrations. In contrast, except for a small fraction of cells, many KCs showed a flat profile with an error rate close to 0.5 (chance), a direct consequence of their sparse firing (Perez-Orive et al. 2002, 2004). Within the small fraction, few KCs were generally good at classification, reaching 10% error rate for distant odors; some others performed better for particular concentrations. Classification based on responses of single LHNs was generally less successful than for responses of single PNs. PNs also did not show diverse profiles for different odor distances and concentrations. This is probably because LHNs receive densely convergent input from PNs and extract from it rather general features of odorant stimuli (Gupta and Stopfer 2012). Classification success measured from single LHN recordings made in vivo varied widely, depending on the class of LHN. Connectivity used in our model led to results matching those obtained with the C3 class of LHN neurons (Gupta and Stopfer 2012).

Classification improved when responses of whole cell populations were considered. When the entire PN population was probed with a selected range of odor similarity, the error rate decreased almost to zero. PNs recorded in vivo also classified odors better when the full recorded population was used (Stopfer et al. 2003). When populations of KCs and LHNs were used, the error rate was substantially lower than when single cells were used, although for these cell types longer integration time was needed.

Our study predicts that population responses are needed to accurately identify odors, but only small subsets of neurons are needed for accurate classification between odor pairs. Indeed, a study in locust showed that responses of 10 PNs allowed a classification success rate of 75–90% (Stopfer et al. 2003). Geffen et al. (2009) showed that only the five most useful PNs were enough to predict the odorant stimulus with 95% success. Vertebrates show a comparable ability to classify odors with a subset of neurons; in mouse optimally selected sets of five mitral cells showed 84% success in classifying five different odorants (Shusterman et al. 2011), and similar results were reported for zebrafish (Friedrich and Laurent 2004). Lesion studies in rats showed that even small remnants of the olfactory bulb were sufficient for rats to perform odor discrimination tasks (Lu and Slotnick 1998), and fewer than 100 neurons in the piriform cortex were needed to predict behavioral results (Miura et al. 2012). In our model, 10 PNs sufficed to reach on average 95% classification success rate for distant odors; with 25 PNs, all randomly selected, the success rate exceeded 95%. To reach 95% classification success for very different odors, 30 LHNs on average were needed, and KCs needed about 1000 randomly sampled neurons.

A simple probabilistic model of the ensemble error rate revealed that the population of uniformly behaving neurons does not fully explain the decrease in error with increasingly large cell populations. The statistical error rate derived for the probabilistic model remained higher than the one based on an analysis of the network responses in all simulations, except when populations of LHNs and KCs exceeded some threshold size. This finding emphasizes the role of the structure of the population code, which cannot be reduced to average properties of the cell response. While we did not explore possible roles that synaptic plasticity may play in tuning the performance of downstream neurons, our indirect measurements based on PCA revealed that downstream neurons with optimally tuned synaptic weights could reach very high classification success. Only a few such neurons are needed to reach classification error rates near zero. This is in agreement with our laboratory's previous work (Finelli et al. 2008). Further studies of plasticity are needed to thoroughly explore this prediction.

Odor sampling time.

An ongoing debate in olfactory research concerns the timing of odor sampling. One view is that odor information accrues over time at some neural location, enabling animals to perform better on olfactory tasks if they can delay behavioral responses until sufficient information has accumulated (speed-accuracy trade-off). Another view is that animals successively sample only within short time windows (Zariwala et al. 2013), each of which provides sufficient information to drive appropriate behaviors. On the one hand, mammalian behavioral data suggest that a single sniff (<200 ms in rats) may be enough to discriminate odors (Uchida and Mainen 2003); on the other hand, response accuracy on difficult tasks improves with longer exposures to odor, including more sniffs (Abraham et al. 2004; Rinberg et al. 2006; Slotnick 2007).

In zebrafish, discrimination between population activity patterns which represent related odors also improves over time (Friedrich and Laurent 2001). Behavioral studies on insects show similar timescales of a few hundred milliseconds for odor identification (Smith and Menzel 1989; Vickers and Baker 1996; Wright et al. 2009). Results from PN recordings in various insect species show a similar range of discrimination time, although somewhat different measures were reported for different species [130–230 ms in Drosophila (Wilson et al. 2004), 100–150 ms in locust (Mazor and Laurent 2005), 100–150 ms in Bombyx mori (Namiki and Kanzaki 2008), ∼150 ms in honeybees (Krofczik et al. 2009)]. It was suggested that odor decorrelation in the locust depends on local excitatory interneurons (Assisi et al. 2012).

In our model, classification improved with integration time for all three tested cell types. The PN population performed better than the others, reaching 95% classification success within a 200-ms window, even for extremely close odor pairs. KCs and LHNs needed 400 ms to reach perfect classification for many odors. Notably, the discrimination task presented to our model was very difficult, with the most distinct odor pairs sharing 90% overlap, and some pairs with 99% overlap (based on identities of PNs and LNs activated by receptor input). More distinct odor pairs can be classified much faster. Similarities in early olfactory coding between insect and mammalian pathways (Kay and Stopfer 2006) probably contribute to the similar timescales for classification performance dynamics observed in direct physiological recordings in rats (Cury and Uchida 2010), in mice (Shusterman et al. 2011), and those reported in our model.

The complementary view suggests that, instead of continuously integrating its input, the olfactory system encodes odorant identity piecewise and progresses by individual snapshots. Individual integration windows defining the snapshots could be generated by either a behaviorally imposed rhythm, such as sniffing in vertebrates, or distinct oscillatory cycles generated by reciprocally connected neural circuits, occurring with ∼10- to 30-Hz frequency in the insect AL (Ito et al. 2009; Laurent and Naraghi 1994; Stopfer et al. 1997; Tanaka et al. 2009) and follower neurons (Broome et al. 2006). In the locust, the information contained by PNs in a single oscillatory cycle (50–100 ms) may provide enough information to correctly classify odor and concentration by downstream neurons (Stopfer et al. 2003). Abolishing oscillations reduces odor specificity in the responses of KCs (Perez-Orive et al. 2004) and β-lobe neurons (MacLeod et al. 1998), and abolishing oscillatory synchronization of PNs in honeybees disrupts fine odor discrimination (Hosler et al. 2000; Stopfer et al. 1997).

Although the information contained within a single cycle might suffice to describe some aspects of the odorant, it is clear that the identities of spiking PNs change reliably oscillatory cycle by cycle, and that these patterns of activity change with the odor (Wehr and Laurent 1996), providing the substrate for beneficial, longer integration. Friedrich et al. (2004) show that in zebrafish, odor information can be conveyed in by neural circuits in parallel on different time scales. Patterns that become evident within individual 20-Hz oscillatory cycles are useful for odor categorization, and patterns on longer time scales (>100 ms) are particularly useful for odor identification (and improve over time as they decorrelate). Thus the same olfactory circuitry can, at first, broadly classify and then precisely specify an odor (Friedrich and Laurent 2001).

We used our model to analyze how the lengths of integration windows used for encoding changed the representations of odorants. As visualization in PCA space shows, LHNs needed longer windows than PNs to obtain distinct trajectories. When using 100-ms windows or longer, the trajectory can be divided into four distinct segments: baseline; initial transient; steady-state oscillatory segment [commonly referred as the “fixed point” (Mazor and Laurent 2005)]; and return transient to the baseline. Similar structures can be found in responses of the mammalian olfactory bulb (Bathellier et al. 2008). Using smaller time windows, our study revealed the oscillatory structure of the “fixed point.” Furthermore, we found that the first 50 ms of PN responses was sufficient for optimal classification. This timing agrees with analyses of recordings made in vivo (Brown et al. 2005). Some studies reported longer times, ∼250 ms, are needed (Stopfer et al. 2003), but the difference may be explained by the way odors are delivered. Downstream cell populations of KCs and LHNs needed longer times to reach optimal classification.

Model predictions.

Our model leads to several predictions that can now be tested in vivo. 1) The odor-specific temporal structure of responses in olfactory neurons extends from lower to higher stages of the olfactory processing. That, together with the recent finding of the temporal channel linking KCs and its followers in β-lobe (Gupta and Stopfer 2014), suggests that temporal structures of odor responses may propagate across multiple layers of the olfactory pathway. 2) The PNs may cluster into a few distinct classes with respect to their response profiles to extensive sets of different odors and concentrations. This rich repertoire of the PNs response properties helps to improve discrimination by the entire PN population in a way that exceeds a mere sum of the responses of a statistically identical PN population of the same size. This specificity of PN responses may arise from synaptic wiring and thus may suggest that specific wiring in the insect olfactory system plays an important role in precise odor discrimination. 3) Predicting network classification performance by first averaging across a population of neurons and then considering the network of such “averaged” identical neurons (as sometimes needed to be done when only limited set of neurons is available in experimental recordings) cannot fully explain classification performance of the real network consisting of “nonidentical” neurons tuned to specific odor features.

Conclusion.

Recordings made in vivo of a substantial fraction of the neurons responsible for population coding of olfactory signals are still not technically feasible by standard electrophysiological tools. Attempts to provide insight into odorant classification in neurons downstream from PNs are scarce. The model proposed in this paper provides insights into population coding at different stages of the locust olfactory pathway and allows comparisons of classification performance over time by olfactory neurons at different positions along the olfactory system.

GRANTS

This research was supported by the National Institutes of Health-National Institute on Deafness and Other Communications Disorders (R01 DC012943 and R01 DC011422).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: P.S., T.K., N.G., M.S., and M.B. conception and design of research; P.S. and T.K. performed experiments; P.S., T.K., and M.B. analyzed data; P.S., T.K., N.G., M.S., and M.B. interpreted results of experiments; P.S. and T.K. prepared figures; P.S. drafted manuscript; P.S., T.K., N.G., M.S., and M.B. edited and revised manuscript; P.S., T.K., N.G., M.S., and M.B. approved final version of manuscript.