Response reliability observed with voltage-sensitive dye imaging of cortical layer 2/3: the probability of activation hypothesis

Abstract

A central assertion in the study of neural processing is that our perception of the environment directly reflects the activity of our sensory neurons. This assertion reinforces the intuition that the strength of a sensory input directly modulates the amount of neural activity observed in response to that sensory feature: an increase in the strength of the input yields a graded increase in the amount of neural activity. However, cortical activity across a range of sensory pathways can be sparse, with individual neurons having remarkably low firing rates, often exhibiting suprathreshold activity on only a fraction of experimental trials. To compensate for this observed apparent unreliability, it is assumed that instead the local population of neurons, although not explicitly measured, does reliably represent the strength of the sensory input. This assumption, however, is largely untested. In this study, using wide-field voltage-sensitive dye (VSD) imaging of the somatosensory cortex in the anesthetized rat, we show that whisker deflection velocity, or stimulus strength, is not encoded by the magnitude of the population response at the level of cortex. Instead, modulation of whisker deflection velocity affects the likelihood of the cortical response, impacting the magnitude, rate of change, and spatial extent of the cortical response. An ideal observer analysis of the cortical response points to a probabilistic code based on repeated sampling across cortical columns and/or time, which we refer to as the probability of activation hypothesis. This hypothesis motivates a range of testable predictions for both future electrophysiological and future behavioral studies.

we use information derived from our sensory systems to interact dynamically with the external sensory world. Our senses help us avoid being hit by a speeding car in a crosswalk or instantly recognize a face in a sea of strangers. Our individual sensory experiences are fleeting, yet much of what we understand about neural processing of sensory stimuli has been inferred from data averaged across repeated presentations of a specific sensory input. Implicit in this analysis is the assumption that the trial average is a valid model for the code the brain uses to represent our sensory experiences. However, the trial average itself is not ethologically relevant. There is no a priori reason to expect a trial-averaged neural signal to reflect features of the dynamic neural code. Even given trial-average differences, it is the across-trial variability that determines which stimulus parameters are effectively encoded (Abbott and Dayan 1999; Averbeck et al. 2006; Beck et al. 2012). In this study, we consider this concept of reliability, or how well individual trials can be differentiated or decoded given knowledge of characteristics of a trial average. From a theoretical perspective, the role of trial-to-trial variability has been explored, particularly in the context of single neurons or the joint activity of pairs of neurons (Butts and Goldman 2006; Churchland et al. 2010; Cohen and Kohn 2011), but at a population level the concept is not well understood.

The rodent vibrissa (whisker) system is a powerful model system for detailed investigation of neural circuitry in early sensory pathways (for review see Petersen 2007) and is emerging as an important model system for behavior. Rodents are capable of choosing between different textures and patterns of whisker stimulation (Carvell and Simons 1990; Morita et al. 2011; Wolfe et al. 2008) and of performing object detection and localization (O'Connor et al. 2010a, 2010b). Nevertheless, the specific stimulus features that are encoded in these tasks are not known. One hypothesis is that sporadic high-velocity “slip-stick” events observed during texture discrimination as a whisker is moved across a surface are relevant stimulus features (Jadhav et al. 2009; Wolfe et al. 2008). Experiments in our laboratory and others' have shown that both the frequency of stimulus detection in behavioral experiments (Ollerenshaw et al. 2012; Stüttgen et al. 2006; Stüttgen and Schwarz 2008; Waiblinger et al. 2015) and the spike frequency in the thalamus and cortex with extracellular recordings (Boloori et al. 2010; Pinto et al. 2000; Shoykhet et al. 2000; Simons 1978; Wang et al. 2010) are modulated by the velocity of the whisker movements. However, neither of these approaches can allow a direct measurement of population response on single trials.

In this study, we consider reliability in the context of the encoding of whisker deflection velocity using in vivo voltage-sensitive dye (VSD) imaging of the rat barrel cortex in an anesthetized preparation. The VSD imaging employed measures population activity in putative cortical layer 2/3 on a single trial with sufficient fidelity as to differentiate stimulus-evoked activity on a single stimulus presentation (Ollerenshaw et al. 2014). Consistent with previous VSD studies (Ollerenshaw et al. 2012; Petersen et al. 2003a) and many decades of trial-averaged electrophysiological evidence, we show that the trial-average amplitude of cortical activation increased with whisker deflection velocity. Despite these trial-average trends, we show that knowledge of trial-average trends was not sufficient to accurately classify response observed on only single trials. By examining the variability of the single-trial distribution, we find that the stimulus velocity instead modulated response frequency. We propose a probabilistic framework that changes the conceptual map between observed trial-average activity and the expected distribution of activity on single trials. The probability of activation framework suggests additional testable predictions and hypotheses for sensory neural coding and behavior.

METHODS

Animals.

All procedures were approved by the Institutional Animal Care and Use Committee at the Georgia Institute of Technology. Data from six adult female Sprague-Dawley rats (250g-330 g) were used in this study. Data from four additional animals were excluded on the basis of predetermined criterion due to inadequate signal quality as reflected in the signal-to-noise ratio, predominantly caused by inadequate or uneven dye penetration.

Surgical preparation.

Animals were sedated with isoflurane (5%) and injected with pentobarbital sodium (50mg/kg ip) for long-term anesthesia. A tail vein catheter was inserted, and pentobarbital sodium (4.5mg/ml) was delivered continuously and adjusted to maintain an anesthetic depth at which no toe- or tail-pinch reflex was observed. Heart rate, oxygen saturation, respiratory rate, and temperature (37°C) were monitored continuously to ensure a constant level of anesthetic depth throughout the experiment. Once anesthetized, the animal was stabilized in a stereotaxic frame. A craniotomy was performed over the barrel cortex (stereotaxic coordinates: 0.5–4.0 mm caudal to the bregma and 3.0–7.0 mm lateral to the midline), and the dura was removed. A dental cement well was created around the craniotomy to hold dye and saline. The cortical surface was kept moist with sterile dye or saline throughout the entire experiment.

VSD imaging.

Voltage-sensitive dye (VSD) imaging measures subthreshold activity from supragranular layers of the barrel cortex (Kleinfeld and Delaney 1996; Petersen et al. 2003a). The dye is not targeted to supragranular layers specifically; instead, the limiting factor for the origin of the VSD signal (as with all optical imaging techniques in the visible spectrum) is the loss of signal at deeper depths due to light scattering in biological tissue. Previous studies have shown using simultaneous whole cell recordings that the VSD signal are linearly correlated with subthreshold voltage traces of layer 2/3 pyramidal neurons (Cohen et al. 1978; Petersen et al. 2003a). However, the VSD signal is not exclusive and potentially represents activity from other sources such as apical dendrites from other layers. Importantly, previous studies have estimated that these contributions are likely not more than 10% of the signal (Petersen et al. 2003a). In our study, VSD (RH1691, 2 mg/ml; Optical Imaging) was placed on the surface of the brain and mixed regularly with a micropipette every 5–10 min for 1.5–2 h to allow sufficient time for diffusion into the cortex. Next, the unbound dye was removed by multiple washes with sterile saline. The cortex was illuminated with a 150-W halogen lamp passed through an excitation filter (621–643 nm). A long-pass emission filter was used (>665 nm). Images were recorded with a high-speed charge-coupled device camera (MiCAM2; SciMedia) as depicted in Fig. 1. A ×1 objective lens was combined with a ×0.63 condenser lens, resulting in a total magnification of ×1.6. The camera was focused ∼300 μm below the surface to target activity from layer 2/3. Forty to 60 trials for each stimulus condition were recorded for analysis. Image resolution was ∼20 μm/pixel.

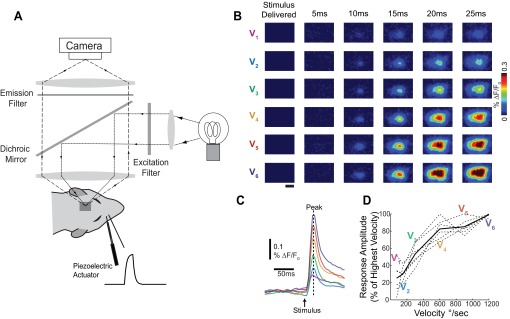
Fig. 1.

Trial-average cortical response amplitude was modulated by stimulus strength. A: a schematic of the voltage-sensitive dye (VSD) imaging system. A piezoelectric actuator delivered controlled mechanical deflections of a whisker with variable velocity. The surface of the cortex was stained with VSD, and images were recorded on a high-speed charge-coupled device camera every 5 ms. B: representative cortical responses to whisker deflections of variable velocity (V₁, lowest). Images were averaged over 60 trials. Scale bar (1 mm) applies to all images. %ΔF/F₀, response amplitude. C: corresponding time series to the images shown in B. Time series were calculated by averaging over a circular region of interest the size of 1 cortical column (∼400-μm diameter) centered over the barrel corresponding to the deflected whisker. The peak response frame determines the response amplitude. D: the trial-average response amplitude for each data set (dashed lines, n = 6 whiskers, 4 animals) and the resulting mean (solid black line). Trial-average response amplitude increased with velocity in all data sets.

Whisker deflections.

Controlled whisker deflections were delivered with piezoelectric bending actuator (range of motion: 1 mm; bandwidth: 200 Hz; Polytec PI) attached to a glass pipette. The whiskers were trimmed to 15 mm, and the whisker tip was placed inside the pipette and positioned 10 mm from the whisker base. The saw-tooth deflection consisted of an 8-ms exponential rise phase and an 8-ms exponential decay phase. The velocity of the whisker deflection was varied by changing the rostral-caudal distance the whisker moved by the piezoelectric actuator. The duration of the deflection remained constant. The angle of deflection at the whisker base was calculated from the measured distances (distance from whisker pad, deflection distance), assuming triangular geometry. The six velocities (V₁ to V₆) were calibrated using high-speed videography to be 75, 150, 300, 600, 900, and 12,00°/s, respectively, in the rostral-caudal plane. During our calibration procedures, we observed that the whisker was reliably deflected with every presentation of the stimulus using this method. This method of whisker deflections has been used extensively previously to deliver precisely controlled whisker deflections (Millard et al. 2013; Ollerenshaw et al. 2014; Wang et al. 2010). However, given the nature of the data presented in this study, we took additional precautions to ensure that the whisker deflections were delivered reliably. The distance from the whisker base was carefully placed at 10 mm from the whisker pad. Even given this precaution, a 1-mm misplacement can dramatically affect the absolute velocity delivered. Therefore, our analyses focus on trends within single experiments and do not compare absolute values across animals. Because the animal was anesthetized and immobilized in these experiments, the location of the whisker within the diameter of the pipette was maintained within a given preparation.

In most animals, noise trials in which no stimulus was delivered were also recorded. In data sets in which noise trials were not recorded, 40 prestimulus frames were used to approximate noise trials. Dual whisker deflections were delivered using two individually calibrated piezoelectric actuators at equal velocity, both in the rostral-caudal plane.

Image analysis and transformation into time series.

All data analysis was done in custom-written software in MATLAB (The MathWorks, Natick, MA). For each trial, a background image (F₀) was created by averaging 40 prestimulus frames (200-ms interval). The stimulus-evoked VSD signal was calculated as the percent change from this background image: %ΔF/F = (F − F₀)/F₀ × 100. Analyses of response amplitude were performed on time series derived from VSD image series. VSD time series were calculated by averaging over a circular region of interest (ROI) with a 10-pixel radius (∼200 μm) from the center of activation in the onset frame (determined manually, usually 10 or 15 ms after stimulus delivery) from an average of all trials. The onset frame has previously been shown to be restricted to a single cortical column (Petersen et al. 2003a). The use of a spatially restricted ROI resulted in an increased signal-to-noise ratio and allowed the detection of even small activations that were stimulus evoked. For calculation of the center of mass and image presentation only, images were filtered with a spatial averaging filter (400 × 400 μm, ∼1 barrel). To display response amplitude for all data sets on the same scale, single-trial response amplitudes were normalized by the maximum single-trial response amplitude observed in each data set. Average response amplitudes were normalized by the maximum average response.

Ideal observer classification by stimulus velocity.

An ideal observer was tasked with classification of trials by response amplitudes (r) into six stimulus velocity categories V₁, V₂, …, V₆ (Wang et al. 2010). Response amplitude r is the peak response frame from the barrel-specific time series derived from VSD images described above. The temporal dynamics of the VSD response were exceptionally stereotyped, and the peak frame is consistent across all stimuli within a single preparation. For each velocity V_i, a probability distribution, P(r|V_i), was estimated using bootstrapped estimates of the sample mean. Bootstrapped sampling was performed with replacement. The set of six velocity distributions formed the trial-average classifier. The same classifiers were used in all decoding frameworks throughout the study. The input to the model, the response estimate r was modulated by changing the number of trials used to calculate r. A given subsampled response amplitude r was sorted into the velocity class with the maximal likelihood estimator (given a flat prior):

$${\hat{V}}_{MLE}=\arg \hspace{0.17em}{\max }_{V_i}\hspace{0.17em}\hspace{0.17em}P({\mathit{\text{r|V}}}_{\text{i}})\mathrm{.}$$

The result was a 6 × 6 performance matrix in which the [j, k] element was the frequency of assigning a single trial to V_k when the actual stimulus was V_j. The “actual classification performance” was defined as the frequency that a given trial was correctly classified, summed across stimuli, or simply the average of the diagonal of the performance matrix.

The “optimal classification performance” for a given classifier was limited only by the overlap between the velocity distributions. Conceptually, it was the frequency of correctly classified trials if the response amplitudes were sampled directly from the classifier distributions:

$$Optimal\hspace{0.17em}performance=100\cdot {\displaystyle \sum _{V_i}{\displaystyle \underset{r\in R_i}{\int }P\left(r|V_i\right)P\left(V_i\right)dr},}$$

where R_i is the range of response amplitudes over which velocity V_i had the maximum probability and P(V_i) = 1/6, the relative frequency at which a given velocity stimulus was presented. Extreme errors were trials in which the assigned velocity class, V_k, differed from the actual stimulus class, V_j, such that |k − j| ≥ 2. For simulations of multiple whisker presentations, the maximum likelihood estimation was calculated from the effective response amplitude, r̄, which was the mean of n (1, 3, or 10) randomly selected trials.

Response frequency analysis.

Single-trial time series were calculated by averaging over the same barrel-sized ROI used to create average time series described previously. Each trial was determined to be either a “response” or “no-response” trial based on the presence or absence of a measurable stimulus-evoked activity. As the temporal response was extremely stereotyped across velocities, an average time series from 0 to 250 ms after stimulus delivery was used as a filter (or template). The filter included frames in which the activity had not yet reached the cortex, to ensure that changes in fluorescence were stimulus locked. Individual trials were matched to the template by pointwise multiplication and summed (dot product). The resulting match score quantified how well each single trial matched the template:

$$Match\hspace{0.17em}Score={\displaystyle \sum _{k=0}^{K-1}x\left(k\right)\ast h\left(k\right)=x\cdot h},$$

where x is the single-trial time series, h is the averaged time series filter, and K is the length of the filter. Match score distributions from both noise trials and stimulus trials were calculated. A classification threshold was set at 3 SD above mean scores of noise trials. Stimulus trials with match scores above this threshold were considered response trials. Note that the use of a high threshold (a match score above the 99.7 percentile of the noise distribution) resulted in a greater number of false negatives (a misclassification of a true response as a no-response trial) while limiting the probability of false-positive misclassifications. The high threshold level was chosen to highlight the existence of large response amplitudes to small velocity stimuli; however, the results presented in this report were consistent for all threshold levels (0–3 SD above noise). Note that the threshold choice is required only for qualitative assessment, because significance tests were not used on the sorted data sets.

Probability of activation simulations.

We discussed two possible models that could generate the observed average VSD responses, the continuum model and the probability of activation model. As a demonstration of the unique characteristics of each model, we simulated single-trial distributions with identical trial-average statistics but originating with the assumptions of the two possible models. These simulations are meant to demonstrate the qualitative differences between the models and are not quantitatively representative of any specific parameter of actual data. The single trials from all data sets were normalized (as described above) such that they could be plotted on the same axis and considered a single data set. Briefly, each trial was normalized relative to the largest single trial observed within a given preparation such that the maximum response amplitude is fixed at 1. For the simulated continuum hypothesis data, distributions were assumed to be normally distributed about the observed mean of each velocity category with a standard deviation (SD) equal to that of the noise distribution. For the probability of activation data, the “no-response distribution” was Gaussian with identical mean and variance of the actual noise distribution (trials where no stimulus was presented). The “response distribution” was also Gaussian, with a mean and SD estimated from only trials assumed to be response trials. In this analysis, unlike in the formal analysis above, response trials are sorted by an absolute threshold (3 SD above the noise distribution mean). Simulated response frequencies at each velocity were randomly drawn from binomial distributions measured from real data. A trial was randomly assigned as response or no response and then assigned an amplitude randomly drawn from the corresponding distribution described above.

Calculation of activated area.

To determine the spatial spread of the cortical activation, we estimated the extent of the VSD image activated following a whisker deflection. Specifically, the activated area analysis was performed on a time-averaged VSD image that included data from two frames (15 and 20 ms after stimulus delivery). Each image was filtered with a spatial averaging filter (100 × 100 μm) to reduce high-frequency spatial noise prior to analysis. The mean and SD of the noise were calculated using all pixel intensities in the noise image. The threshold was set at 2 SD above mean noise (determined from a prestimulus noise frame). Regions of the image that surpassed this activity threshold were considered active. Trial-average area represents the mean of all the activated areas of single trials.

Analysis of rising slope in VSD signal.

We defined the rising slope of the measured VSD signal as the maximum derivative, or change in signal between any two frames, that occurred during the stimulus onset to peak response. This calculation was performed on both trial-averaged time series and single-trial time series that were used for the response amplitude analysis.

Multiwhisker spatial classification.

A spatial template-matching algorithm was used to classify single trials from simultaneous whisker deflection. This algorithm was adapted from a previously published method (Millard and Stanley 2013). In each data set (n = 3 animals), trials (data set 1, 100 trials; data sets 2 and 3, 50 trials) were collected for individual whisker deflections and for both whiskers deflected simultaneously. Two-dimensional images were transformed from a one-dimensional vector representing individual barrel columns. A representative barrel map of 32 barrel columns was registered as described previously, and the mean change in fluorescence within each barrel region was calculated. N is the number of barrel columns (maximum of 32) that fell within the VSD image. Trial-average and time-average (15–20 ms) images from individual whisker deflections and simultaneous whisker deflections were transformed in this way to create spatial templates for each stimulus category: whisker 1 alone (T₁), whisker 2 alone (T₂), both whiskers (T₃), and no stimulus (T₄). We assumed a constant noise model with covariance (Σ) to account for uneven staining of the cortex. Single trials (y) were time-averaged and mapped to one dimension in the same manner as for the templates and then sorted by choosing the least-squares template, T_LS, that minimized the weighted mean squared error:

$$T_{LS}=\arg \min {\hspace{0.17em}}_{\begin{array}{l}{T}_i=\\ T_{1,\dots ,T_4}\end{array}}{\left(y-T_i\right)}^{\prime }{\displaystyle {\sum }_{-1}\left(y-T_i\right).}$$

RESULTS

Population responses to whisker deflections were studied using voltage-sensitive dye imaging (VSD) as illustrated in Fig. 1A. Single punctate whisker deflections of different velocities were delivered by a computer-controlled piezoelectric actuator in the rostral-caudal plane (see methods). Images were recorded every 5 ms and the fluorescence quantified as percent change from background. Figure 1B shows trial-average images for six different velocity whisker deflections (V₁ to V₆): 75, 150, 300, 600, 900, and 1,200°/s, which span the expected behavioral threshold for detection of the punctate deflection of an individual whisker (Ollerenshaw et al. 2012; Stüttgen and Schwarz 2008). Consistent with previous studies, the neural activity started locally over the primary barrel column ∼10 ms after stimulus presentation (Fig. 1B) and then spread into neighboring barrel columns (Ollerenshaw et al. 2012, 2014; Petersen et al. 2003a; Wang et al. 2012). In our hands as well as in previous VSD studies, location of the onset of cortical activity is topographic and determined by the identity of the deflected whisker, allowing a direct alignment with the underlying barrel map. Time series shown in Fig. 1C were created by averaging temporally (images over trials) and then spatially (over a circular ROI approximately the size of 1 cortical barrel column: 400-μm diameter) corresponding to the deflected whisker (see methods). Increasing the velocity of the stimulus increased the trial-average peak amplitude (or simply response amplitude) of the VSD response (Fig. 1D) across all experiments (n = 6 whiskers, 4 animals). These trial-average VSD data are consistent with previous electrophysiological (Boloori et al. 2010; Pinto et al. 2000) and VSD findings (Petersen et al. 2003a; Wang et al. 2012) which demonstrated that as the velocity of a whisker deflection increased, the trial-average activity increased.

Trial-average differences were not sufficient to allow for single-trial velocity discrimination.

The previous analysis is a replication of imaging and electrophysiological studies (Lee and Simons 2004; Petersen et al. 2003a; Pinto et al. 2000; Wang et al. 2010). Figure 1 shares an important characteristic with these previous analyses: the analysis begins by collapsing the data across trials. Here, we collapse across trials by averaging VSD time series from multiple trials, but with other methodologies this takes the form of a computing firing rate, average single-cell trace, or another summary metric. Many techniques, including (but not limited to) intracellular recording, extracellular recordings, calcium imaging, and two-photon imaging, do not have sufficient signal-to-noise ratio to estimate a population response within a single trial. Because of this shortcoming, computing a summary metric across trials is a necessary first step. VSD imaging, on the other hand, has sufficient signal-to-noise ratio to estimate population activity on a single trial. This unique characteristic of VSD allows us to test the assumption that the trial average can substitute effectively for single trials for a model of the neural code. This hypothesis cannot be evaluated well with other methods. In this study we specifically tested whether single-trial response could be classified into a whisker deflection velocity category using knowledge of the trial-average population response.

To test this hypothesis, we define a trial-average classifier for each data set. The trial-average classifier is a set of response distributions created from bootstrapped estimates of the trial average (mean) for each of six velocities. Bootstrapping is a subsampling methodology (n = 10, with replacement) that estimates the variability of a sample parameter (trial-average response amplitude). As the number of trials increases, the bootstrapped distribution will tend to center on the overall sample mean. The SD of the trial-average classifiers are estimates of the standard error of the mean (SE). A representative example of a set of trial-average distributions is shown in Fig. 2A. The observed trial-average sample peak of this specific data set is represented as a black dot.

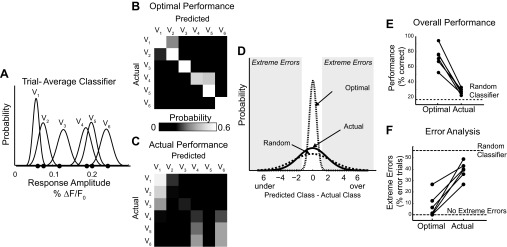
Fig. 2.

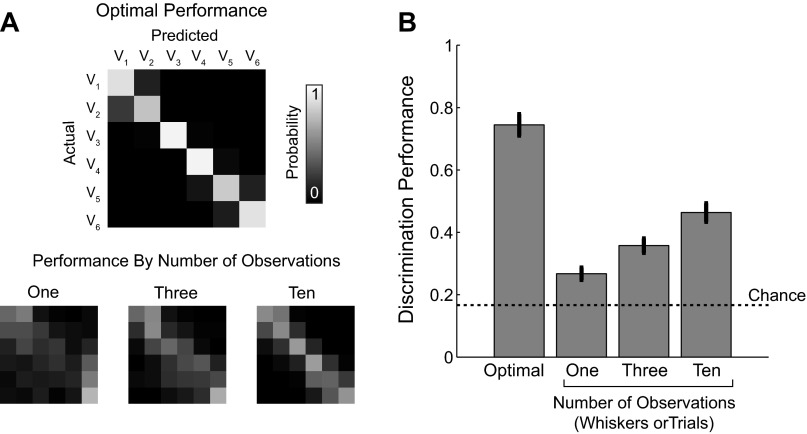
Classification of single trials by an ideal observer performed near chance. A: representative example of a trial-average classifier. Black dots represent actual observed trial-average time series peaks and appear in velocity order (closest to origin V₁, maximum V₆). B: the optimal performance of the classifier shown in A is limited only by the overlap of the velocity response distributions. The probability of classifying an observation from velocity V_j as coming from V_k is represented graphically as element [j, k] in the performance matrix. The presence of a strong diagonal represents a high number of correctly sorted trials. C: the actual performance matrix of the ideal observer given true single-trial response amplitudes. D: distribution of the errors associated with classification. Using the notation described above, the error = j − k. E: the percentage of trials correctly classified under both the optimal and actual conditions across all data sets. Optimal and actual performance from individual data sets are connected with a line. F: the percentage of error trials that are extreme |j − k| ≥ 2 in both the optimal and actual performance conditions.

If the single trials were perfectly modeled by the trial average, the theoretical performance would be limited only by the area of overlap of each of the distributions (referred to as the optimal classifier performance). In other words, if it were possible to infer something about the single trial (the ethologically relevant measure) from a collapsed metric such as the trial-average response amplitude, we would expect an ideal observer to be able to effectively classify trials using the information available in these classifiers.

We tested this hypothesis using maximum likelihood estimation. Briefly, given an input response amplitude r, drawn from the boot-strapped distributions, the trial is classified as the stimulus velocity with the maximum likelihood of having created that response. Optimal performance is visualized in matrices showing the frequency of trials predicted to be in each class (columns) for each actual input velocity (rows). A representative performance matrix is shown in Fig. 2B. In all our data sets, the optimal performance matrix has a strong diagonal representing a high number of correctly classified trials (72.9% ± 10.4%, mean ± 1 SD). If the trial averages were perfect models of single trials and differed only due to experimental noise, one would expect an ideal observer to correctly classify a trial ∼72% of the time.

Because VSD imaging allows us access to single trials, we were able to use the same decoding framework to classify experimentally observed single-trial response amplitudes. The decoding performance on single trials was substantially less than optimal. On average, we correctly classified 27.7% ± 3.7% of trials, which is about 11% more than if the classifications among six equally likely velocities were purely random. The performance of each individual data set is shown in Fig. 2E.

This result is not surprising. The SD of the trial-average classifiers distributions are estimates of the SE of the sample mean. Given a sample size greater than one, the SE necessarily underestimates the SD of the population (the true single-trial variability). Because these trial-average classifiers are also the distributions that would be used to assess the statistical significance of the trial averages, this simulation demonstrates that trial-average metrics, represented in this analysis by the trial-average classifier, are not representative of single trials (the scientifically relevant unit of the neural code).

It is interesting to observe that the actual performance of an ideal observer using this framework was not just noisy but approached random classification, particularly when we considered the scale of the errors. In the example shown in Fig. 2C, a trial from even the lowest velocity (V₁) was classified as one of the highest velocities (V₅); similarly, a trial from the highest velocity was mistaken classified as the lowest (V₁). To quantify this across data sets, we considered any trial that was misclassified by two velocity classes or more away as an extreme error (Fig. 2D). In the optimal case, the percentage of errors predicted to be extreme was 7.8% with an SD of 10.3%. The actual observed percentage of extreme errors was five times greater, on average, 38.9% ± 7.4%. The percentage of misclassified trials that are expected to be extreme errors using a random classifier is 56.2% (Fig. 2F).

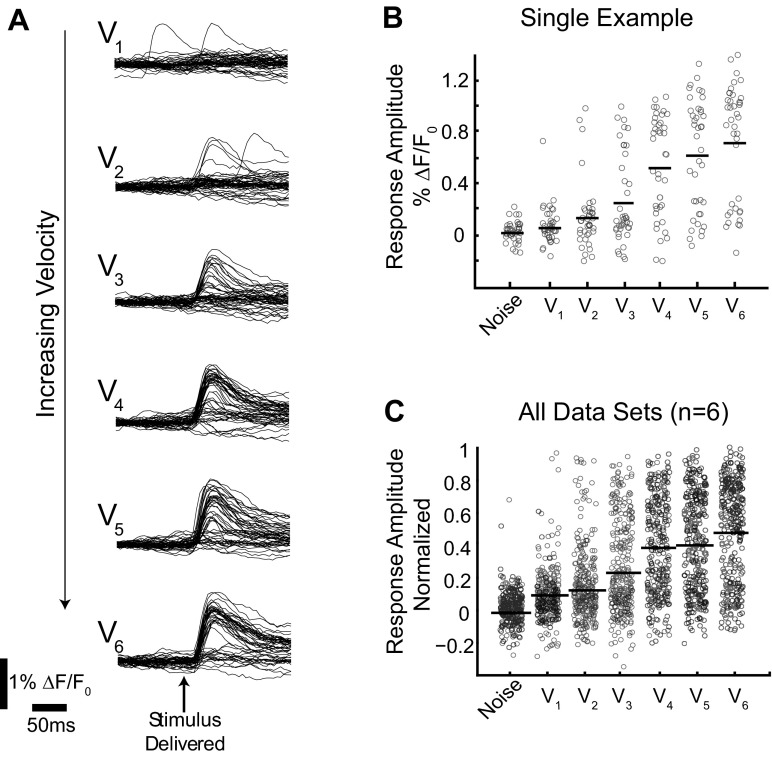
The poor performance of the ideal observer using a trial-average classifier on single trials demonstrates that the single trials are not well modeled by the trial-average response. To investigate how this occurs, we considered single-trial distributions directly. Figure 3A shows the time series associated with single trials from a representative data set. There is large variability in the response amplitude across all velocities. Consistent with the high number of extreme errors made when decoding with a trial-average classifier, the response amplitude from a single trial in response to a low velocity can equal the magnitude of the response from a trial observed in response to a high velocity. A jittered scatter plot shows the same data with a single data point representing the peak response amplitude frame (open circle) for each single trial at each velocity (Fig. 3B). The mean response is indicated with a solid black line. As previously observed, the mean (trial average) increased with velocity, but a given response amplitude on a single trial can be the result of any velocity. The corresponding plot with all single trials from all data sets (n = 6 whiskers, 4 animals) is shown in Fig. 3C. From this representation of the data, it is clear that knowledge of the peak response amplitude is not sufficient to classify individual trials into velocity categories.

Fig. 3.

Single-trial response amplitudes were characterized by a high level of variability. A: all single-trial VSD time series from a representative data set. V₁ is the lowest velocity, whereas V₆ is the highest. B: the peak response amplitude from each single trial shown in A is represented as an open circle in the jittered scatter plot. C: all single-trial response amplitudes from all 6 data sets are shown in a jittered scatter plot. Data sets are normalized such that the peak single trial from any data set has a response amplitude of 1.

Single-trial responses were well-described by a probability of activation model.

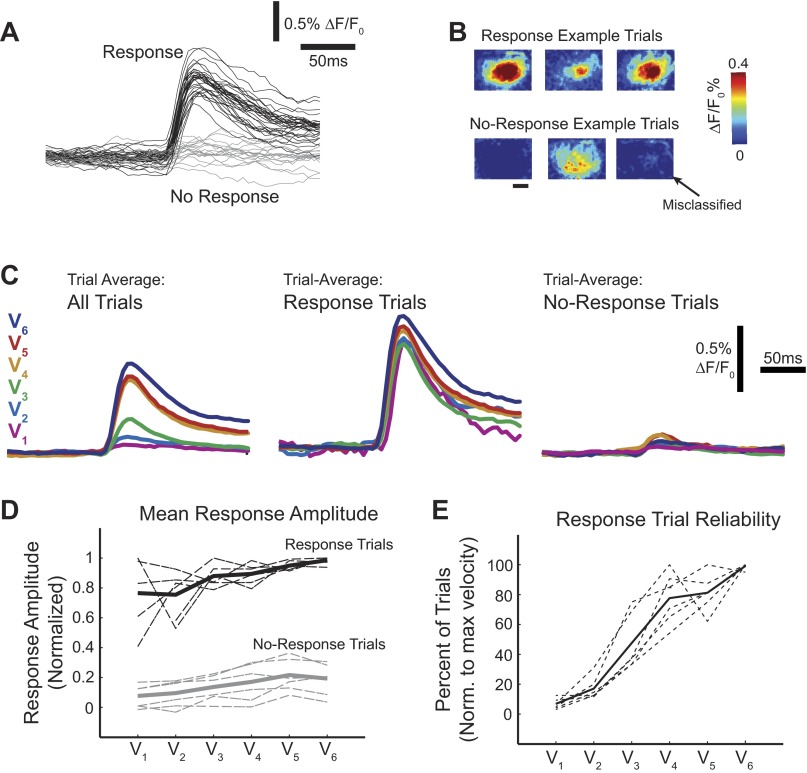
It must be determined how, given such variability in the response amplitude, there are substantial differences in the trial-average amplitude between velocities across all animals. In all data sets, for a given velocity, we observed a subset of trials in which the stimulus-evoked response was not measurably increased from the prestimulus activity. These trials were distinctly different from the trials in which there was clearly an evoked response (Fig. 3A). We sorted trials on the basis of presence or absence of a stimulus-evoked response on individual trials using a matched-filter algorithm (see methods). We defined two categories: 1) response trials, in which poststimulus fluorescence was distinguishable from noise, and 2) no-response trials, in which poststimulus fluorescence was not different from noise. An example set of sorted time series, as well as example corresponding single-trial images, is shown in Fig. 4A. The magnitude of the response and no-response trials was not distinguishable by an absolute threshold, but the response trials all exhibited a clear, spatially specific activation over the primary barrel column as well a stimulus-locked increase in fluorescence in the corresponding time series. No-response trials exhibited either nonspecific background activity or no stimulus-specific changes at all. In a small number of trials sorted as no-response trials, there was actually a very small spatially localized signal. We consider these trials to be response trials misclassified as no-response trials, but the change in activity was so small as to not be distinguished from noise fluctuations by our sorting criteria (Fig. 4B).

Fig. 4.

Response frequency was modulated by stimulus strength. A: single trials were qualitatively and quantitatively separable into 2 groups: trials with stimulus-evoked activity (response trials; black) and those without (no-response trials; gray). B: example single-trial images from trials shown in A demonstrate variability within the groups. Shown are 3 response trials with variable response amplitude (top). Three no-response trials (bottom) were chosen to represent the types of trials that comprise this category, including a misclassified trial. C: when all trials were included in the average time series of a single data set, there were large differences between the velocities (left), but when the average of only response trials (middle) or only no-response trials (right) was considered, the differences were dramatically reduced. D: results were consistent across all data sets (n = 6 whiskers, 4 animals; dashed lines) for both the response (black) and no-response (gray) average responses. The mean for both groups is depicted with a solid line. Note that higher variability is associated with conditions with the fewest number of trials (low velocities for response trials, high velocities for no-response trials). E: the frequency of response trials increased with stimulus velocity for all data sets (dotted lines), as well on average (mean; solid line).

When response or no-response trials were considered alone, the differences between the velocities were dramatically reduced. The ordered nature of the velocities was sometimes even lost: low velocities had larger mean response amplitudes than higher velocities, as shown in Fig. 4C. The means of response and no-response groups for individual data sets are shown as dashed lines in Fig. 4D. Once sorted, the absolute amplitude of response and no-response trials was no longer strongly modulated by the stimulus velocity. However, the number of trials sorted into the response category, which we call the “response frequency,” increased with stimulus strength (Fig. 4E). This was true for every data set collected. Note that the response frequency was considered relative to the velocity (not always the highest velocity) with the highest number of response trials for each data set. Importantly, no velocity in any data set showed a perfect response rate. Although the frequency of response trials always increased with velocity, the absolute response frequency was highly variable between data sets.

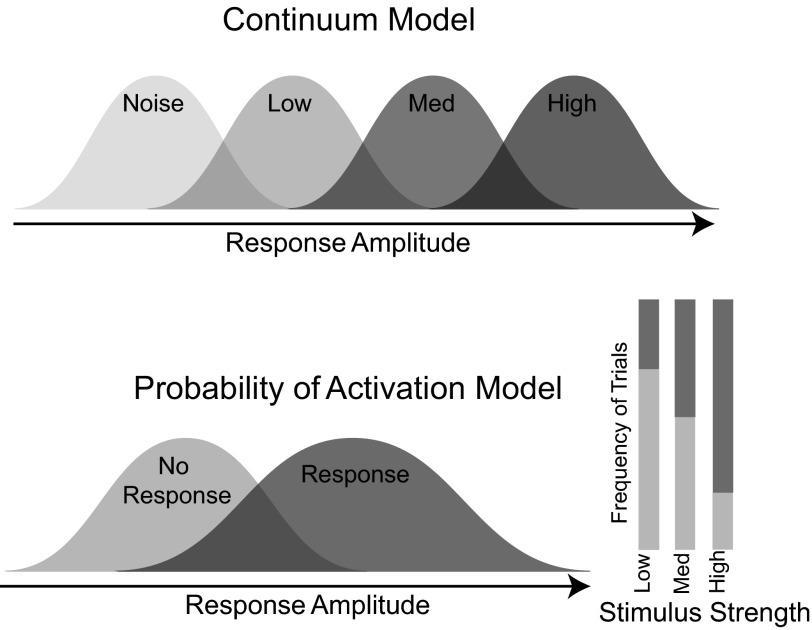
The presence of two distinct types of responses suggests a model for the encoding of the whisker deflection velocity that is distinctly different from that predicated from knowledge of the trial-average responses alone. Historically, we (Boloori et al. 2010; Ollerenshaw et al. 2014; Wang et al. 2010) and others (Ito 1985; Pinto et al. 2000; Simons 1978) have implicitly assumed a model in which the stimulus strength was encoded by the strength of the population response on a single trial (the trial-average classifier). We refer to this as the continuum model because it proposes graded response with increasing deflection velocity (Fig. 5, top). This continuum model also represents the traditional interpretation of intracellular and extracellular recordings when responses from one or a few cells across trials are used as a model for the entire population on a single trial. However, the same mean response profile we observed can also be created from a discrete “probability of activation” model formed from two possible response categories, a response and a no-response class (Fig. 5, bottom). The differences in the mean response occur by changes in the number of observations sampled from each distribution.

Fig. 5.

Two possible encoding schemes. The continuum model (top) has graded response amplitude with increasing stimulus strength [low, medium (med), and high velocities]. For the probability of activation model (bottom), the frequency of response trials increases with increasing stimulus strength; however, the response and no-response distributions are conserved across stimulus strength.

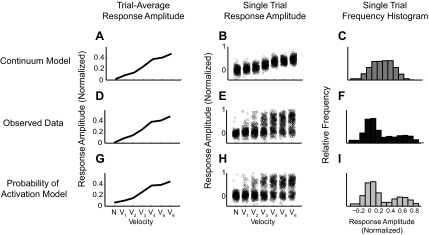
It is not possible to distinguish between the probability of activation model and the continuum model with only a trial-average response. For example, Fig. 6 shows two possible single trial-distributions simulated from hypothetical realizations of both the continuum (Fig. 6, A–C) and probability of activation models (Fig. 6, G–I). Both models result in the same trial-average measurements (Fig. 6, A, D, G), making the source of the responses ambiguous. The primary differences between the two models are revealed in a more thorough examination of trial-to-trial variability. For the continuum model, in addition to increased mean response with velocity, three additional observations are evident. First, the minimum and maximum observed responses increased with the mean and with velocity (Fig. 6B). Second, when pooled across velocities, the aggregate distribution of the responses is multimodal, reflecting the graduated increase in amplitudes with velocity (Fig. 6C). Third, knowledge of the amplitude of a single-trial response reduces the uncertainty about which of the stimuli could have produced that response. In contrast, the range of achievable responses does not change with increasing velocity in the probability of activation model (Fig. 6H). When pooled, this distribution is bimodal (Fig. 6I). Note that although bimodality is supporting evidence of a probability of activation model, it is not actually necessary, because it is also dependent on the overall difference between signal and noise distributions in a given data set, which is often determined by data quality, not data content. The key difference between the two models, however, is that in the probability of activation model, the single-trial amplitude does not convey information, or reduce the uncertainty, about strength of the stimulus. Observed VSD single-trial distributions in Fig. 6, E and F (same data as in Fig. 3C), are more consistent with the probability of activation model.

Fig. 6.

Observed single-trial response distributions were consistent with the probability of activation model. A–C: continuum model simulations. A: mean response amplitude vs. velocity. B: a jittered scatter plot of the underlying single trials. C: a combined histogram of response amplitude of single trials from all velocities. The same analyses were done on the observed VSD single trials (D–F) and probability of activation model simulations (G–I). Notice that the range of achievable response amplitudes for each velocity is constrained in the continuum model but not in the probability of activation model. The observed data are consistent with the probability of activation model.

Trial-average trends in rising slope do not reflect differences on single trials.

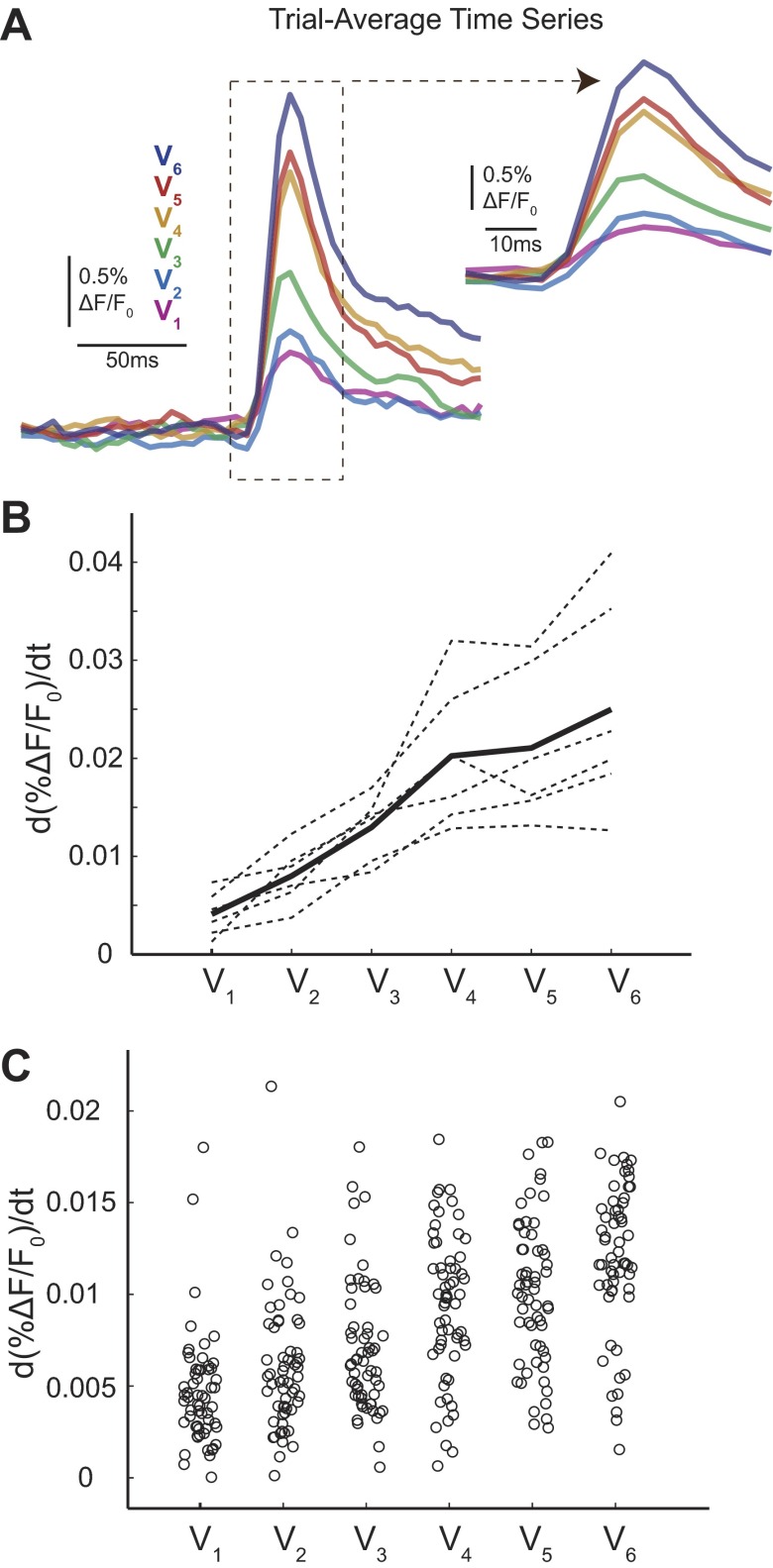
Response amplitude is not the only parameter that has been studied historically only as a trial average. Extracellular recordings and intracellular recordings interpreted as a trial average have reported differences in the rising slope with deflection velocity (Pinto et al. 2000; Wilent and Contreras 2004). Using our VSD imaging data, we also considered these additional trends both as a trial average and on the single trials. Rising slope was calculated as the maximum derivative or change in the magnitude of the signal between any two frames (from stimulus delivery to the peak). Consistent with previous trial-average single-unit extracellular and intracellular literature, we observed a correlation between whisker deflection velocity and rising slope when this analysis was performed on trial-average time series. Representative trial-average time series highlighting this trend are shown in Fig. 7A with a summary across animals shown in Fig. 7B (dotted lines represent individual animals, bold line indicates the animal average). Qualitatively, these responses are very similar to trial-average time series previously reported in intracellular recordings (Wilent and Contreras 2004). However, reliable differences in rising slope were not observed when we considered the single-trial distributions. Figure 7C shows a scatter plot of the rising slope of all single trials from a typical animal. As with response amplitude, the minimal and maximum rising slope of the single-trial distributions did not change with deflection velocity. Therefore, given knowledge of the rising slope of a single trial, an ideal observer would not be able to classify these trials by velocity.

Fig. 7.

A trend in rising slope exists on trial-average time series but not on single trials. A: representative trial-average time series from 1 data set. Inset highlights the rising slope differences between the traces. B: trial-average rising slope responses for each of the 6 data sets (n = 6 whiskers, 4 animals; dotted lines). Solid line shows mean. C: jittered scattered plot for 1 representative data set (same as in A) shows that rising slope trends are not observed on single trials with significant variability similar to amplitude distributions.

Trial-average trends of activated area do not reflect differences on single trials.

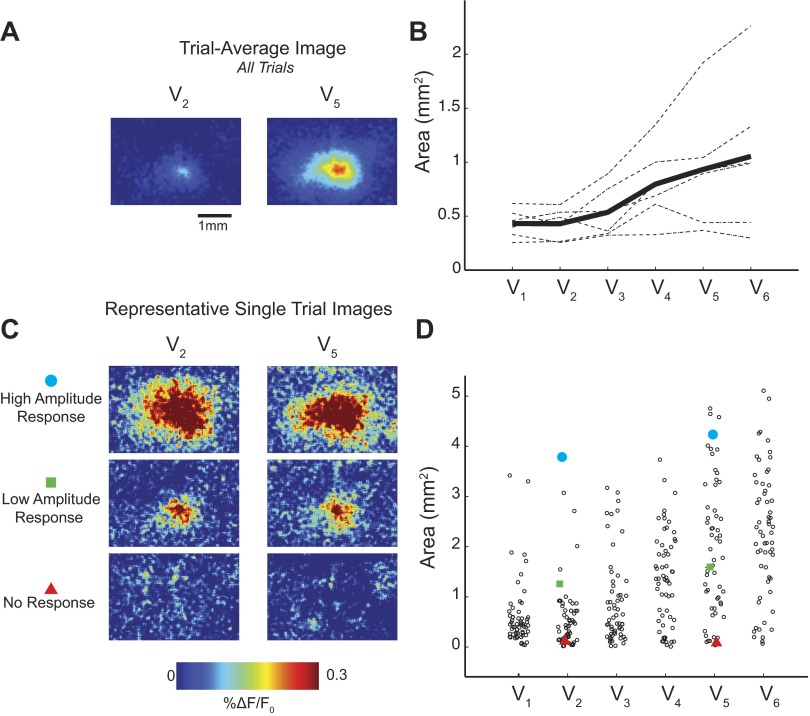
As exhibited in Fig. 1B and previous studies (Petersen et al. 2003a; Wang et al. 2012), the area of cortex activated by the whisker deflection also appears to covary with the whisker deflection velocity when summarized as a trial average. We quantified the relationship between activated cortical area and velocity. We defined activated area as the region of cortex within an image with %ΔF/F₀ greater than 3 SD of the background noise. Similar to both rising slope and response amplitude, we observed a trial-average correlation between activated area and deflection velocity. Representative trial-average images are shown in Fig. 8A, summarized across animals in Fig. 8B. Although this trial-average trend is apparent in both our trial-average images in Fig. 8A as well as in the original examples in Fig. 1A, these differences are not representative of differences in area of the single trials. In Fig. 8C, we also show amplitude-matched single-trial images from two different velocities (V₂: 150°/s; V₅: 900°/s). From comparison of the high-amplitude, low-amplitude, and no-response single-trial images, it is clear that the activated area varies greatly between trials. Despite the strong trial-average trend, it is straightforward to find examples of V₅ (900°/s) trials with dramatically less activated area than a chosen trial from V₂ (150°/s). The distributions of activated areas from all trials and all velocities in a single animal are shown in Fig. 8D, similarly to Fig. 3B. Although measurements of area performed on single trials can be noisy, it is still apparent that all velocities are capable of activating both large (maximum) and small (minimum) cortical areas. This trend was observed in all animals.

Fig. 8.

A trend in area exists in trial-average images but not on single trials. A: representative trial-average images from 2 velocities (V₂, 150°/s; V₅, 900°/s) show apparent change in activated area. B: trial-average areas for each data set (n = 6 whiskers, 4 animals; dashed lines). Solid lines show an increasing trend (mean). C: representative amplitude-matched single trials with high (top) and low (middle) response amplitude, as well as no-response trials (bottom), demonstrate the variability of the activated area across trials. D: single-trial distributions from 1 representative example show extensive variability. Specific trials shown in C are identified by red triangles (no response), green squares (low amplitude), and blue circles (high amplitude) for V₂ and V₅.

Encoding stimulus strength within the probability of activation model requires multiple redundant sensors or events.

The probability of activation model predicts that deflection is not encoded by the response in a single barrel column. This is troubling since velocity is likely an important parameter for sensory perception (Jadhav et al. 2009). Outside of controlled laboratory experiments, however, a rat would rarely perceive a stimulus, whether it is an object or wind stimulus, using only a single whisker. Multiple observations of the same stimulus, whether on the same whisker over time or over an array of multiple whiskers, could provide an estimate of the strength of stimulus. For instance, a weak stimulus may activate 2 barrel columns out of 10, or result in an observable activation in 2 of 10 whisks across an object. Similarly, a strong stimulus may activate all 10 barrels or respond on every single whisk across an object. This hypothesis can easily be simulated by adapting the same maximum likelihood decoding framework used in Fig. 2 to include a variable number of observations. We simulated having access to multiple observations by averaging 3 or 10 single trials into a single response variable prior to classification. Overall accuracy of the classification increased with increasing number of observations of the stimulus. In Fig. 9A, there are increasingly prominent diagonals in the performance matrices as the number of trials increased from 1 to 3 to 10 observations. This was true across all data sets (Fig. 9B). This conceptual model suggests that velocity discrimination performance would increase with additional samples or observations of the stimulus given the probability of activation model. Note that because the difficulty of the classification task depends on arbitrary experimental decisions such as the number of velocities, we do not consider the specific number of whiskers or the exact performance values reported here to be biologically relevant. The observation that increasing the number of observations increases the performance would hold in all nontrivial classification paradigms given the probability of activation hypothesis.

Fig. 9.

Additional observations increased velocity classification performance. A: example performance matrices for the optimal discrimination performance (top) and the performance matrix for an increasing number of observations (1, 3, and 10 observations; bottom). The same labels and scale bar apply to all performance matrices. B: quantification of increased performance across all data sets (n = 6 data sets, 4 animals). Bar graph shows means ± SE.

The key assumption in this conceptual simulation in Fig. 9 was that population response measurements that encode the stimulus velocity are not coupled and instead are redundant estimates of the same stimulus parameter. In other words, the proposed velocity-encoding scheme requires that it is possible for one barrel column to respond while another adjacent barrel column does not. If the responses of neighboring whiskers were trivially coupled by a network state variable, VSD imaging artifact, or other confounding variable, then no new stimulus intensity information could be gained by increasing the number of observations.

To our knowledge, within-trial population response correlations between neighboring barrel have not been experimentally studied using VSD or otherwise. When considered as a trial average, the findings across an array of studies are collectively inconclusive: some studies observe sublinear population responses (Civillico and Contreras 2006; Mirabella et al. 2001; Simons 1985), others supralinear (Ego-Stengel et al. 2005; Shimegi et al. 1999 2000), and some no change at all (Drew and Feldman 2007).

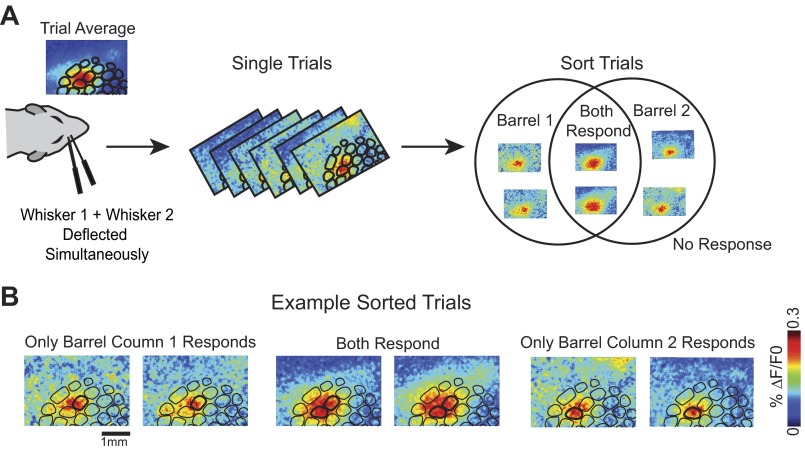
We examined the cortical activity in response to simultaneous deflection of two whiskers on single trials to determine whether or not adjacent barrel columns are deterministically coupled within a single trial. In three additional experiments (3 animals, 4 pairs of whiskers), two adjacent whiskers were deflected both individually and simultaneously. The neural activity was recorded using VSD imaging as before. Consistent with previous studies, the trial-average VSD image from simultaneous deflection was spatially similar to summed responses of the two individual whiskers (Fig. 10A). On a subset of single trials, however, even though both whiskers were physically deflected, the spatial extent of the cortical response more closely resembled trials in which only one whisker was deflected (Fig. 10B). This preliminary evidence suggests that it is possible for only one barrel column to respond given the simultaneous deflection of two whiskers: the responses across whisker barrels are not strongly coupled. Although this spatial assessment is qualitative, it was repeatable across animals. We repeated the same experiment in three separate animals, using four pairs of whiskers (data sets) in total. In each animal, we observed subsets of trials in which one or the other barrel column responded.

Fig. 10.

Simultaneous whisker deflections resulted in trials with a response in only 1 whisker barrel. A: schematic of the dual whisker experimental paradigm. Trial-average image from dual whisker deflections resembled a linear sum of 2 responding whisker barrels. Single-trial responses exhibit variable response spatial profiles. Trials were sorted into 4 response categories: barrel 1 responds, barrel 2 responds, both barrels respond, and no response. B: example single-trial images (15–20 ms after stimulus presentation) from each of the 3 response categories. Scale bar (1 mm) applies to all images.

We additionally observed that the frequency of the possible trial types was supportive of the general probability of activation model. To estimate frequency, we sorted images from single trials recorded in response to dual whisker deflections based on a spatially matched filter algorithm (see methods) and recorded the number of trials that most resembled the spatial profile of four categories: each whisker individually responds (barrel column 1 alone, barrel column 2 alone), both barrel columns respond, and neither respond. The observed frequencies for two data sets (from 3 animals) are shown in Table 1. Two observations support the probability of activation model in the interpretation of the data. First, trials in which two whiskers are deflected but only one barrel column responds are common. In all data sets, single barrel column responses to dual whisker deflections were at least 10% of trials, as much as 41% in some data sets. Individual barrel column responses from both whiskers were observed. Second, the frequency of single barrel column responses was consistent with the observed probability of activation in the single whisker deflection data (Table 1). In data set 1, for example, the response frequency for individual whisker deflection was lower than in the other data sets (62% and 76%, respectively, for whisker 1 and whisker 2). Consistent with a probabilistic model, the number of single barrel column response trials for the dual deflection data was higher (22% and 19%). Additionally, in data set 3, the response of whisker 2 alone was very low (32%), and this is reflected in the number of overall no response trials (neither whisker responses) in the dual whisker deflection stimulus (32%). Taken together, these observations support the hypothesis that barrel column circuits are not coupled within a single trial and can act as redundant encoders of stimulus intensity. It is important to note that whereas the existing evidence suggests that the spatial profile of responses resembles the combined and probabilistic responses of single whisker deflections, this is not evidence of independence of response amplitude or probability of response.

Table 1.

Spatial classification of simultaneous whisker deflection trials

	Single Whisker Deflection		Dual Whisker Deflection
	Wk1 response frequency	Wk2 response frequency	Wk1+ Wk2 response	Wk1 response only	Wk2 response only	No response
Data set 1	0.62	0.76	0.51	0.22	0.19	0.08
Data set 2	0.90	0.66	0.68	0.08	0.22	0.02
Data set 3	0.62	0.32	0.52	0.14	0.02	0.32
Data set 4	0.66	0.76	0.70	0.14	0.08	0.08

Frequencies are presented as probability estimates: the number of observed trials in each category divided by the total number of recorded trials. Wk, whisker.

In summary, we have demonstrated that trial-average trends are insufficient as evidence to support inferences about characteristics of the neural code directly. With respect to whisker VSD data specifically, the variability within the single-trial distributions in amplitude, rising slope, and area instead support a probability of activation framework in which the strength of the sensory input is encoded not in a graded cortical response amplitude, but instead probabilistically and redundantly (across trials or experiences). In addition, we provide evidence that cortical columns that represent input from different whiskers are separable, potentially allowing for velocity information to be encoded probabilistically across the whisker array.

DISCUSSION

In this report, we present evidence that the stimulus strength is not encoded by graded changes in response amplitude within a cortical/barrel column. Specifically, the correlation between deflection velocity and trial-average VSD response amplitude results primarily from modulation of response frequency, not absolute amplitude. An ideal observer analysis showed that differences in trial-average response amplitudes were not sufficient information to allow classification of trials into velocity categories; instead, the observer made large classification errors. Although highly variable, there was structure in the single-trial distributions. We observed that single trials from all velocities divided into two groups: response and no-response trials. Once sorted, amplitude differences between velocities were dramatically reduced. Additionally, trial-average trends in rising slope and activated area did not reflect differences in single trials.

Two surprising aspects of the VSD single trial responses were at odds with the continuum model and led us to the probability of activation model. First, we failed to observe activity in response to some (even very strong) whisker deflections. Because no-response trials are effectively an absence of evidence, when considered in isolation, these trials might be attributable to technical limitations of the VSD methodology, such as requiring many neurons to be active simultaneously for a detectable signal or variable background activity. However, we also observed high-amplitude responses to minimal velocities, including those velocities predicted to be significantly subthreshold in an awake, behaving animal. In fact, some number of trials in all velocities achieved maximal response amplitude. This observation is distinct from the observation of no-response trials because it is dependent not on an absence of evidence but on positive evidence of activity. Under the continuum model, it would be unlikely to observe the maximum response amplitude to a slow, subthreshold, whisker deflection; it would be exceptionally unlikely to observe them with the frequency we observed in the VSD data. Although subtle, it is important to note that the VSD data reported presently are not supportive of an all-or-none bimodality. Instead, response amplitude was extremely variable, taking on any possible value: a “something-or-nothing” distribution. Taken together, we believe the dual inconsistencies of the observed response distribution are impossible to reconcile with the continuum hypothesis, leading us to propose a probabilistic hypothesis for the encoding of whisker intensity information.

Given our proposed model, it is essential to consider the VSD evidence and the probability of activation hypothesis in the context of existing extracellular and intracellular data. The VSD signal is limited to activity in supragranular layers of cortex due to light loss by scattering from deeper depths (Petersen and Diamond 2000), and we specifically targeted layer 2/3 with the imaging as a representation of the suprathreshold output of layer 4 projections to 2/3. Although VSD is not specific to cell soma or any cell type, in vivo VSD activity has previously been shown to be linearly correlated with layer 2/3 pyramidal neurons in the barrel cortex (Cohen et al. 1978; Petersen et al. 2003a). Given only the data in this study, we cannot rule out the possibility that the probabilistic responses are specific to layer 2/3, particularly given that layer 2/3 has characteristically low firing rates and high trial-to-trial variability (Crochet et al. 2011; Kerr et al. 2007; Petersen et al. 2003a; Sato et al. 2007; Wilent and Contreras 2004).

However, after critically reevaluating existing literature, we find the probability of activation hypothesis does appear remarkably consistent with existing extracellular and intracellular data across layers. Spiking data are almost exclusively considered as part of a trial average. We and others have assumed that that a small subset of neurons represent the population: that the trial-average or a combined peristimulus time histogram (PSTH) can be used to estimate the variability and extremes of the population responses on single trials (Ma et al. 2006; Pouget et al. 2003; Wang et al. 2010). It is interesting to observe retrospectively that there is actually no positive evidence for this assumption. Instead, probabilistic and often absent responses are characteristic not only of individual neurons but also of the behavioral output: psychometric curves recorded from animals performing a whisker detection task. Focusing on electrophysiological evidence, previous studies of layer 2/3 neurons reported trials in which a whisker deflection did not cause any spikes within the experimentally observed subset of the population. This was true even with high stimulus intensities (Kerr et al. 2007; Petersen et al. 2003b; Sato et al. 2007; Wilent and Contreras 2004). In the cortical input layer, layer 4, neurons often respond to transient high-velocity events, such as the set of stimuli used in this study, with a single spike or no spike at all (Lee and Simons 2004; Wang et al. 2010). In single-unit recordings, trials with no experimentally observed activity not only exist, but the frequency of such trials is inversely correlated with deflection velocity, consistent with our present interpretation. Consequently, the trial-average firing rate of a single neuron, or PSTH, is similar to an estimate of the reliability of an individual neuron across trials. This reinterpretation demonstrates that the continuum model was built from an assumption made in an absence of evidence: neural activity was assumed to have occurred even when none was experimentally measured. The nonspecificity of the VSD signal, although in some contexts considered a limitation, is uniquely capable of analyzing the population responses separate from this ubiquitous, but unsubstantiated, assumption of reliability of the population response.

The results presented in this report also allow an intriguingly simple interpretation of canonical behavioral experiments. Behavioral experiments have shown that the probability of detection increases with stimulus velocity (Ollerenshaw et al. 2012; Stüttgen and Schwarz 2008), which we observed as an increased probability of response in our VSD signal. A probabilistic behavioral output is matched with a probabilistic neural signal. In fact, existing behavioral data from our laboratory and others (Ollerenshaw et al. 2012; Stüttgen and Schwarz 2008) show that the detection threshold (the deflection velocity at which behaving animals respond to a whisker stimulus 50% of the time) is between 200 and 300°/s. This is the same range of stimulus intensities in which we observed a 50% probability of response in this study. It is possible to interpret these behavioral results in the context the continuum model, but the simplest interpretation, where detection occurs when the activity crosses an absolute threshold, cannot account for the observed behavioral results. Previously, more complex models such as an accumulation of evidence model were used to match observed behavior with the neural recordings (Ollerenshaw et al. 2012).

The probability of activation model makes the specific prediction that a behaving animal could not discriminate deflection velocity with information from only a single whisker. This is consistent with behavioral evidence currently available. Existing behavioral paradigms show that animals respond more often to stronger stimuli and that the dynamic range of detectable stimuli can be modulated by previous or ongoing stimuli (Ollerenshaw et al. 2014; Waiblinger et al. 2015). Though these paradigms demonstrate complex behaviors and capabilities of rodents, they are not evidence of velocity discrimination. To our knowledge, no study has shown that an animal can be trained to discriminate whisker deflection velocities. Such a study requires a demonstration that animals can respond less often to stronger stimuli or differently (i.e., alternative forced choice) within a set of stimuli with variable intensity.

One of the biggest limitations of this study is the use of an anesthetized preparation. Although it is impossible to know for certain how anesthesia influences the observed effect, an attractive hypothesis is that the observed bimodality is related to different processing of stimuli in the “up” and “down” brain states characteristic of an anesthetized cortex (Civillico and Contreras 2012; Petersen et al. 2003b). Brain-state fluctuations likely contribute to the variability of the VSD signal. Because we did not record any indicator of cortical state, we cannot specifically exclude this hypothesis. However, several observations suggest that a causal role for up and down states in determining the observed response frequency is unlikely. First, the frequency of no-response trials is stimulus specific, whereas the stimuli are delivered in pseudorandom order. Each stimulus condition samples from relatively equal occurrences of the up and down states; therefore, state should affect all stimuli equally. Without a more complex nonlinear relationship between state and response frequency, simple state fluctuations are not sufficient to explain the stimulus-dependent differences. Second, the dual whisker deflection data suggest that one part of the cortex can respond while a neighboring region of the cortex does not. If up and down states were determining this response/no-response characteristic, then one would have to conclude that neighboring whisker barrels could be in opposing states at the same time. Although possible, this is inconsistent with existing literature (Petersen et al. 2003b). Since neither the probability of activation hypothesis nor the continuum hypothesis has been observed experimentally in awake animals, both potential models should be considered when techniques that allow for recording of entire populations on a single trial in awake animals are perfected.

Intriguingly, the instantaneous velocity of whisker deflection is analogous to simplistic characterizations of the strength of inputs in other pathways, such as sound intensity in audition or luminance/contrast in vision, both of which are represented by an increased trial-average response amplitude. Most existing theories of neural computation, both in the barrel cortex and in other sensory modalities, rely on local differences in the amplitude of the population response to encode stimulus parameters (Ma et al. 2006; Pouget et al. 2003; Seriès et al. 2004). If the absolute strength or magnitude of a population response is not informative within a single experience or a cortical column, it reduces the power of such proposed codes. Perhaps most strikingly, the results of the ideal observer model demonstrate that changes to parameters measured or inferred from the trial average, including but not limited to the current examples of response amplitude, rising slope, and activated area, would not represent a feature available for decoding stimulus information during active perception.

We propose a framework in which the strength of the sensory input is encoded not in a graded cortical response continuum but probabilistically by distinct, spatially separable subpopulations of neurons (different cortical columns). Different spatial patterns across columns could encode the equivalent stimulus information or percept while limiting the scientific usefulness of direct inference from a trial-average signal. We do not suggest that the data presented in this work, or any single scientific study, are sufficient to entirely prove a new hypothesis. Instead, the VSD data become a starting point to propose the probability of activation model as a testable alternative interpretation of existing intracellular, extracellular, and behavioral data.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant R01NS48285. C. A. Gollnick and D. C. Millard were supported by the National Science Foundation Graduate Research Fellowship Program.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

C.A.G., D.C.M., R.V.B., and G.B.S. conception and design of research; C.A.G. and A.D.O. performed experiments; C.A.G. and D.C.M. analyzed data; C.A.G. and G.B.S. interpreted results of experiments; C.A.G. prepared figures; C.A.G. and G.B.S. drafted manuscript; C.A.G. and G.B.S. edited and revised manuscript; C.A.G., D.C.M., A.D.O., R.V.B., and G.B.S. approved final version of manuscript.