Temporal and spatial tuning of dorsal lateral geniculate nucleus neurons in unanesthetized rats

Abstract

Visual response properties of neurons in the dorsolateral geniculate nucleus (dLGN) have been well described in several species, but not in rats. Analysis of responses from the unanesthetized rat dLGN will be needed to develop quantitative models that account for visual behavior of rats. We recorded visual responses from 130 single units in the dLGN of 7 unanesthetized rats. We report the response amplitudes, temporal frequency, and spatial frequency sensitivities in this population of cells. In response to 2-Hz visual stimulation, dLGN cells fired 15.9 ± 11.4 spikes/s (mean ± SD) modulated by 10.7 ± 8.4 spikes/s about the mean. The optimal temporal frequency for full-field stimulation ranged from 5.8 to 19.6 Hz across cells. The temporal high-frequency cutoff ranged from 11.7 to 33.6 Hz. Some cells responded best to low temporal frequency stimulation (low pass), and others were strictly bandpass; most cells fell between these extremes. At 2- to 4-Hz temporal modulation, the spatial frequency of drifting grating that drove cells best ranged from 0.008 to 0.18 cycles per degree (cpd) across cells. The high-frequency cutoff ranged from 0.01 to 1.07 cpd across cells. The majority of cells were driven best by the lowest spatial frequency tested, but many were partially or strictly bandpass. We conclude that single units in the rat dLGN can respond vigorously to temporal modulation up to at least 30 Hz and spatial detail up to 1 cpd. Tuning properties were heterogeneous, but each fell along a continuum; we found no obvious clustering into discrete cell types along these dimensions.

the dorsolateral geniculate nucleus (dLGN) integrates and transforms the output of the retina into information that can be used by the primary visual cortex (V1). Evidence from physiology (Cleland et al. 1971; Hubel 1960; Hubel and Wiesel 1961; Kuffler 1953) and anatomy (Guillery 1966; Sherman and Koch 1986) has shown that receptive fields of neurons in the dLGN resemble those of their retinal inputs. However, the presence of interneurons (Wang et al. 2011a, 2011b), neuromodulatory inputs (Erisir et al. 1997; Varela 2014), and feedback from V1 (Erisir et al. 1997) indicate that the dLGN could shape visual responses, and thereby the perception of the animal, according to behavioral requirements.

Individual neurons in the dLGN are tuned to visual signals in limited spatial frequency and temporal frequency bands. This tuning reflects signal processing in both the retina and the dLGN, and filters the spatial and temporal spectra of visual information available to V1. Such filtering could serve many adaptive functions, such as reducing redundancy (Attneave 1954; Barlow 1961; Dan et al. 1996; van Hateren 1992), producing sparse responses to stimuli (Olshausen and Field 1996), or emphasizing behaviorally relevant signals (O′Carroll et al. 1997).

We used sine gratings to measure the spatial and temporal tuning of dLGN neurons. Sine gratings are widely used to characterize the early visual system (Carandini et al. 1997; Movshon et al. 1978; Sceniak et al. 1999). They provide a parametric family of spatial patterns that can isolate a system's responsiveness to core features of contrast, spatial frequency, phase, orientation, and temporal frequency (reviewed in Wandell 1995). If early visual processing were linear, these measurements would be sufficient to explain responses to more complex stimuli, including natural stimuli. To the extent that processing is nonlinear, these measurements could still provide the foundation for models that account for higher order interactions (Rust and Movshon 2005; Victor et al. 1977).

The spatial and temporal frequency tuning of neurons in the retina and the dLGN have been measured in multiple species (Cheng et al. 1995; Enroth-Cugell and Robson 1966; Grubb and Thompson 2003; Hale et al. 1979; Hawken et al. 1996; Heine and Passaglia 2011; Hochstein and Shapley 1976; Kirby and Wilson 1986; Schade 1956; Shapley and Perry 1986; Xu et al. 2002; Van Hooser et al. 2003, 2013). All these studies, however, used anesthetized preparations or explanted retinas such that the nonretinal inputs contributing to the dLGN responses were either modified or absent. Since the first studies of the dLGN (Hubel 1960; Hubel and Wiesel 1961), responses of the awake and anesthetized dLGN have been compared. Many studies have reported that anesthesia (macaque monkey, Alitto et al. 2011; cat, Kang and Malpeli 2009) or arousal (rabbit, Bezdudnaya et al. 2006; Swadlow and Weyand 1985; macaque, Ramcharan et al. 2000) alter dLGN responses (but see mouse, Niell and Stryker 2010). However, very few have compared spatiotemporal tuning properties across these different conditions (Alitto et al. 2011; Bezdudnaya et al. 2006; Kang and Malpeli 2009).

In this study we measured the tuning properties of the dLGN in the unanesthetized rat. Rodents are becoming an important model to study visual circuits because of their ability to perform complex behaviors (Busse et al. 2011; Creer et al. 2010; Harvey et al. 2012; Meier et al. 2011; Zoccolan et al. 2009), their applicability to studying visual diseases (Sekirnjak et al. 2011), and the relative ease of applying genetic techniques to modify circuit function (Morozov 2008; Thomas and Capecchi 1987). The functional properties of the early visual system of rodents have been studied for decades (Anderson et al. 1977; Fukuda et al. 1979; Kriebel 1975; Lennie and Perry 1981), but the tuning properties of the dLGN had not been studied in detail in any awake rodent.

METHODS

All procedures were conducted with the approval and under the supervision of the Institutional Animal Care and Use Committee at the University of California San Diego. Fifteen male Long-Evans rats (Harlan) were used for this study.

Surgery.

Adult hooded male rats (Rattus norvegicus; older than postnatal day 90, >P90) were deeply anesthetized using 5% isoflurane. Ringers solution (15 ml/kg) was provided for hydration, and atropine (0.05 mg/kg) was injected to control secretion. Keflex antibiotic (15 mg/kg sc) was given prophylactically. The scalp was shaved and sterilized with 70% isopropyl alcohol/Betadine pads. The rat's head was held in position using a standard rat stereotaxic frame (Stoelting, Wood Dale, IL) to allow surgery according to precise stereotaxic coordinates (Paxinos and Watson 2008). Sensorcaine (0.1 ml) was injected into the scalp, and an incision was made over the left dLGN (4.5 mm posterior, 3.5 mm lateral from bregma). After the fascia over the skull was removed, a craniotomy was drilled over the putative dLGN center (dimensions: 1.5–2 mm mediolateral, 2–3 mm anteroposterior).

For chronic awake recordings, a resealable recording well was created as follows. We cut the bottom off of a sterile 0.2-ml polypropylene microcentrifuge tube (Eppendorf, Hauppauge, NY). The cylindrical upper section of the tube (0.5 cm in diameter, 1 cm high) was attached to the skull surrounding the craniotomy using surgical glue (VetBond; 3M, Saint Paul MN). The removable cap of this tube provided a secure, watertight, and sterile seal for the recording well. For head fixing, we used a custom-machined holder mounted directly to a stereotaxic micromanipulator (Kopf Instruments, Tujunga, CA). Two threaded stainless steel guide tubes were secured to this holder with screws such that the guide tubes extended from left to right in stereotaxic coordinates and lay parallel to one another in the same horizontal plane. During surgery, the micromanipulator and holder were used to position these guide tubes near the skull just anterior and posterior to the attached Eppendorf well. Five or six small titanium screws were also implanted across the exposed skull surface to enhance anchoring of dental cement. Dental cement was then applied to the exposed skull outside the Eppendorf well to permanently secure the Eppendorf well and the two stainless steel guide tubes to the anchor screws and skull. Surgical wounds were closed with surgical glue and all exposed skull surfaces covered with dental cement. After the cement cured, the screws were removed from the holder to release the implanted guide tubes. Rats were then removed for postoperative care and recovery. In subsequent recording sessions, connecting the implanted head cap to the stereotaxically positioned custom holder with the screws identically reproduced the head position as it was during surgery, thereby providing a stereotaxic coordinate frame. Postoperatively and for the duration of chronic recordings, implanted rats were given cephalexin antibiotic (50 mg/kg oral daily) prophylactically.

For acute anesthetized recordings, a similar stereotaxic head cap was prefabricated by attaching the two guide tubes to the custom holder and embedding them in dental cement, keeping an opening in the center where the craniotomy would be. During surgery, after the craniotomy was completed and covered with Gelfoam (Pfizer, New York, NY), the prefabricated head cap was positioned over the craniotomy stereotaxically as described above and fastened to the exposed skull with a small amount of dental cement. For acute recordings, we did not use anchor screws in the skull or attach an Eppendorf well. The prefabricated head cap was discarded at the end of the experiment.

Head fixing rats.

Rats were constrained in a sock, and the rat's headpiece was fixed with a screw threaded through stereotaxically implanted guide tubes (see Surgery, above). This led to stable recording sessions lasting about 120 min and allowed for recording of single units lasting 10–20 min in duration. Each rat was used for recording for a duration between 3 and 12 wk.

In their first week of head-fixed recording, rats were acclimated to restraint with a mild sedative, midazolam (0.3–0.6 mg/kg). At this low dose (compared with therapeutic dose of 4–5 mg/kg), rats whisked vigorously, held their eyes open, and responded to external stimulation. After the first week, rats were weaned from midazolam. Most units were recorded in nonmedicated rats (recordings typically continued for 3–12 wk).

Stimulus presentation.

Stimuli consisted of a spatially uniform field modulated sinusoidally in time, slow-drifting (≤4 Hz) sinusoidal spatial gratings, or spatially uniform flickering white noise. Recordings were made in a darkroom (background luminance <0.1 cd/m²). One of two monitors [Westinghouse L2410NM (LCD) or ViewSonic PF790-VCDTS21611 (CRT)] was used to present visual stimuli. Both monitors were empirically linearized, and all stimuli were presented at a frame rate of 60 Hz and a mean luminance of 25 cd/m. Using photodiode measurements, we confirmed for both monitors that contrast was independent (<5%) of spatial or temporal frequency. For both monitors, due to 60-Hz sampling, the gratings with 16-Hz sinusoidal modulation had an effective theoretical contrast of 0.94, compared with 1.0 for other frequencies. If anything, this would cause us to underestimate response to high frequencies.

For LCD displays, kinetics is a particular concern. The nominal response time of our LCD monitor, the time required to transition from black to white (luminance level 0 to 255) or white to black (255 to 0) was 4 ms, fast relative to the frame duration (17 ms). We further measured the time required for the slower luminance transitions (gray to gray, 86 to 170 or 170 to 86). These transitions were slower (8 ms) but still faster than the duration of the frame. We also checked for response coherence at the refresh rate and found none for either monitor (not shown). Finally, we empirically confirmed that the distributions of spatial and temporal frequency tuning properties we report were not different between CRT- and LCD-driven units [by either Kolmogorov-Smirnoff (KS) test or ANOVA].

The monitor was placed approximately tangent to the field of view, 30 cm (LCD) or 20 cm (CRT) from the rat's right eye, such that the display filled at least 85° × 60° of visual field in both cases. Simultaneous with the start of each frame update, a 5-V synchronizing transistor-transistor logic (TTL) pulse was sent to the recording computer. Delayed rendering of the stimulus (frame drops) often occurred in the first few frames of the trial; we used only the data after any such frame drops. If any frames were dropped later in a trial, the entire trial was excluded from analysis. Our stimuli were constructed using the Psychophysics toolbox (Brainard 1997; Kleiner et al. 2007; Pelli 1997). Custom MATLAB (The MathWorks, Natick, MA) scripts were used to present either stochastic noise stimuli or drifting gratings stimuli to the right eye of the rat (Meier et al. 2011).

Electrophysiological recording.

For recordings in unanesthetized animals, the chronic Eppendorf well was exposed and an extracellular electrode [tungsten (FHC, Bowdoin, ME) or pulled quartz microelectrodes filled with Ringer solution] was inserted stereotaxically with a micromanipulator (Kopf Instruments) to defined coordinates (4.5 mm posterior, 3.5 mm lateral to bregma) corresponding to the location of the dLGN in the rat brain (Paxinos and Watson 2008) The electrode was lowered while the recorded activity was monitored for visual responses. Putative dLGN units were found 4–5 mm ventral relative to bregma skull surface.

Voltage traces were amplified (10-1,000 times) and filtered (1 Hz–10 kHz) (AM1800; AM Systems, Sequim, WA), digitized (NIDAQ PCI-6259; National Instruments, Austin, TX), and stored in a local computer. Synchronizing TTL pulses from the stimulus computer were recorded simultaneously on a separate channel. After each session, the well was washed thoroughly with antibiotic solution (Baytril, 0.05mg/ml), cleaned thoroughly with neutral saline, and plugged with silicone gel until the next session.

The unanesthetized animals in this study were not performing any visual task, and we did not record an EEG. Therefore, we cannot know if the rats were “alert.” We monitored, however, for two indirect signs of drowsy/inattentive state: 1) eyelids partially or fully closing, as observed by the infrared eye-tracking camera, or 2) dLGN neurons entering a rhythmic bursting firing mode. In this same preparation it was previously shown (Flister and Reinagel 2010) that this rhythmic firing mode in the dLGN comprises mostly bursts resembling low-threshold calcium bursts and is accompanied by an increase in synchronous power in the alpha band of the local field potential. (This firing pattern is readily distinguished from the case in which single bursts occur intermittently mingled among tonic spikes during awake recordings). If or when the rat appeared drowsy or inattentive by either of these criteria, we used mild stimuli (clapping hands, gently brushing tail, squirting water in mouth) to arouse them or ended the recording session if these measures were ineffective.

For recording under anesthesia, animals were removed from the surgery table and immediately transferred to the recording rig while still under anesthesia. The isoflurane concentration was reduced to the minimum necessary to keep the animal anesthetized (not moving and unresponsive to toe pinch) while still eliciting robust visual responses in the dLGN. Recording continued up to 5 h from the start of surgery, after which the animal was euthanized. We found no evidence of systematic long-term eye position drift in the preparation; receptive field locations were highly stable upon remapping (data not shown). Furthermore, we made no attempt to control the focus of the eye.

Eye tracking.

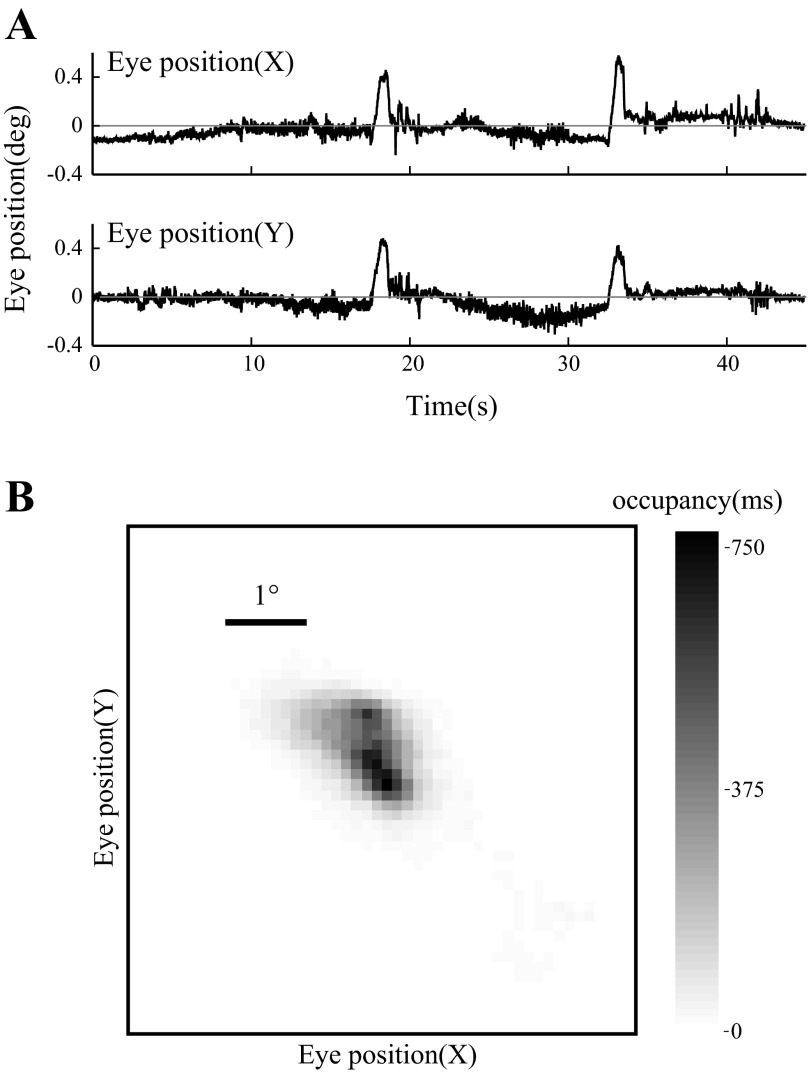
The rat's eye position was monitored using an infrared tracker (EyeLink 1000; SR Research, Kanata, ON, Canada). Calibration was achieved by rotating the rat around the axis of the eyeball and measuring the mean position of captured corneal reflection as a function of physical angle. Clear artificial tears were applied to the eyes to keep them moist. Excess tears were removed using a cotton swab. Tracking data was digitized using the EyeLink Toolbox (Cornelissen 2002). When stimulated by noise or touch (see above), rats made low-amplitude (<5°) saccades, consistent with some reports (Hikosaka and Sakamoto 1987). In this experiment we did not see large saccades such as reported by Chelazzi et al. (1989). After saccades, the eye position typically decayed back to the “neutral” position, which we define operationally as the mean eye position over the course of the experiment. In our preparation, saccades were infrequent (<1 Hz) and often were absent when the rat was undisturbed (Fig. 1A).

Fig. 1.

Eye position during visual stimulation. A: recorded horizontal (X) and vertical (Y) eye position as a function of time during a 45-s trial in which a drifting grating was presented. The 0° position is operationally defined as the mean eye position over the recording session. B: eye position density represented in 2-dimensional space during the trial plotted in A. Grayscale indicates amount of time spent at each location in ms. Scale bar, 1° visual angle.

Eye position was stable within a few degrees over the 30–45 s of a grating presentation (Fig. 1, A and B). Preliminary experiments showed that in our preparation, over the course of many minutes, rats maintained their eye position within a 5° circle around the mean eye position in >65% of samples and within 15° in >95% of samples. The stability of eye position was sufficient for us to ensure the receptive field remained within the full-field grating stimulus for the duration of the recording. However, eye movements could affect the phase of the grating relative to the receptive field for all but the lowest spatial frequencies probed (see for example the rasters in Fig. 6C). Thus we do not report the absolute phase of the stimulus in our analysis. Instead, we used drifting (not counterphase) gratings and computed the neuron's response independently for each short trial (see below) such that phase differences from trial to trial would not affect our measure of the amplitude of the response.

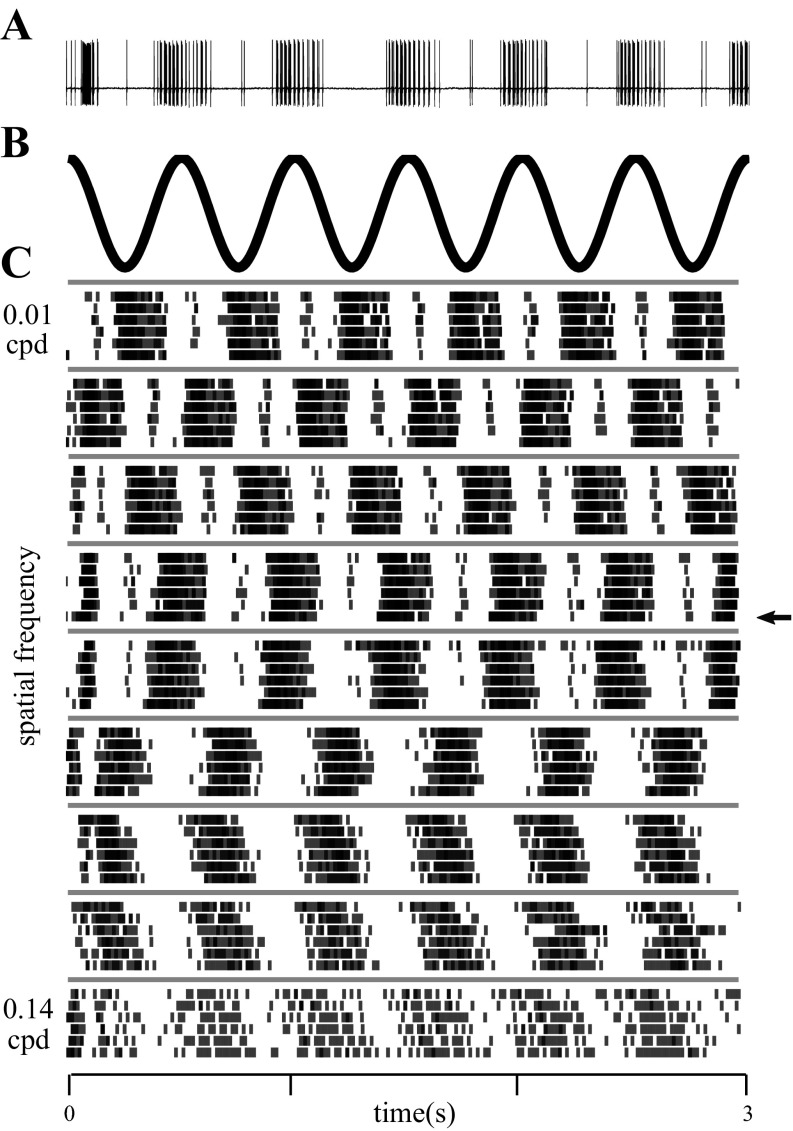
Fig. 6.

Responses of a single unit to drifting gratings of different spatial frequencies. A: voltage trace from a single unit recorded from the dLGN of an awake rat. The raster corresponding to this trial is marked with an arrow in C. B: stimulus luminance at an arbitrary point on the display, as a function of time. Temporal frequency was 2 Hz for 6 complete cycles within the 3-s duration of a trial, regardless of spatial frequency. C: rasters for this single unit obtained for all spatial frequencies, where each row indicates responses for a single trial and each tic mark indicates the time of a single action potential. The 6 trials recorded at each spatial frequency were interleaved during the experiment but are grouped by spatial frequency for display. The time axis at bottom applies to all panels.

Single-unit isolation.

Units were recorded from the dLGN under stereotaxic guidance. Single units were identified as negative (tungsten FHC electrode) or positive (quartz microelectrode) deflecting spikes of much larger amplitude than noise or any other spikes (e.g., see Fig. 2A). Units were studied only if the visual responses exhibited a spatially compact receptive field; diffuse visual responses would be expected from the adjacent visually responsive vLGN (Spear et al. 1977). Rough spike sorting criteria were used to characterize the single unit during the experiment. All analyses shown were performed on more stringent offline sorting using KlustaKwik (Harris et al. 2000). Units were kept for analysis if they met several criteria: 1) thresholded spike waveforms were aligned at the positive peak and all waveforms formed a well-isolated cluster; 2) spike shape was relatively constant; and 3) there were no refractory violations. Spike amplitude variation was common for well-isolated single units, depending on the preceding interspike interval. Care was taken to include as many of the spikes as possible despite this amplitude variation.

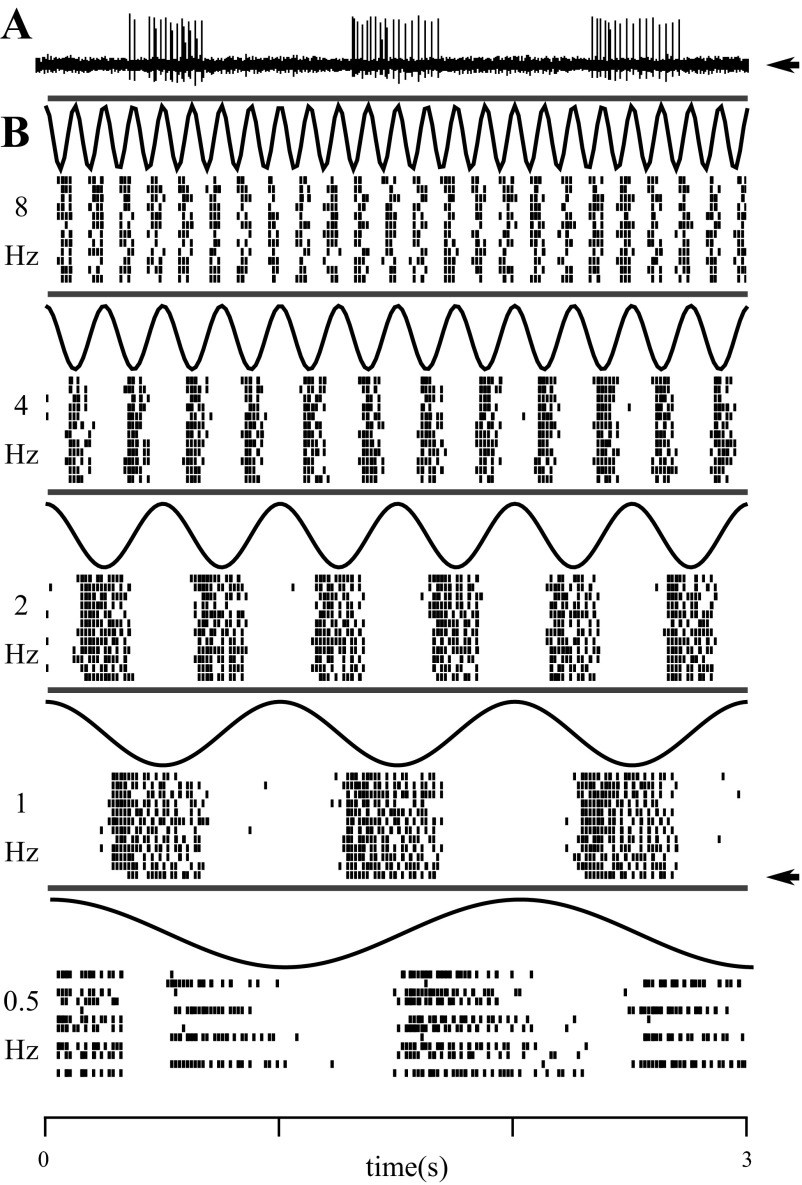
Fig. 2.

Responses of a single unit to full-field modulation at different temporal frequencies. A: voltage trace from a single unit recorded from the dLGN of an awake rat. The raster corresponding to this trial is marked with an arrow in B. B: black curves show the luminance time courses sampled at the frame rate (integrated within frame). Each row of a raster indicates responses for a single trial, and each tic mark indicates the time of a single action potential. The 12 trials recorded at each temporal frequency were interleaved during the experiment but are grouped by frequency for display. The time axis at bottom applies to all panels.

Single-unit characterization.

Once the receptive field location was roughly mapped (using a flashlight on a tangent screen), the position of the rat relative to the monitor was adjusted such that the receptive field of the unit was approximately centered on the monitor display. In some neurons (n = 69) we mapped receptive field location and structure to high resolution using spatiotemporal white noise stimuli. On this basis we classified 38 units as OFF cells and 31 as ON cells; the remaining 61 units were unclassified. Each single unit was characterized in multiple ways. We measured the temporal frequency tuning of the cell at 0 cpd (spatially uniform stimuli) by modulating luminance sinusoidally with time (0.5–16 Hz). Vertical drifting gratings of various spatial frequencies (0.01–1 cpd) were presented to measure the spatial frequency tuning of the cell. These stimuli were at full contrast (100%) on a linearized monitor with a frame rate of 60 frames/s. For spatial frequency tuning, drift frequency was 2 or 4 Hz. This drift frequency was chosen to drive maximal neural responses without engaging the optokinetic reflex (Fuller 1985; unpublished observations). Each “trial” consisted of a 2- or 3-s presentation of a specific spatial/temporal frequency, and frequencies were interleaved in pseudorandom order without gaps until each stimulus was presented once, and this sequence was repeated three or more times. For all stimuli, the mean luminance on the screen was 25 cd/m².

To measure the first-order Weiner kernel, full-field spatially homogenous stimuli were presented at a frame rate of 60 Hz. On each frame, the luminance was sampled from a Gaussian distribution centered at the gray value for the monitor with SD chosen such that mean ± 2SD spanned the dynamic range of the monitor. Random samples that were below mean − 2SD were set to zero luminance, whereas samples above mean + 2SD were set to full luminance. Each trial was 30 s long, seeded with random luminance at the start of the trial to obtain a random sequence of luminance on each trial.

Fano factor.

To determine the variability of spike count in repeated presentations of the same visual stimulus, we measured the Fano factor (FF), which is defined as the variance in spike count from trial to trial in some stimulus-locked time window, divided by the mean spike count in that window (Teich 1989). In this article we report the FF averaged over nonoverlapping time windows of length 16.67 ms, computed exactly as by Kara et al. (2000). We analyzed all 4- and 2-Hz temporal modulation responses for which we had at least 3 repeats of at least 2-s duration (thus a minimum of 24 sinusoid cycles). We verified that restricting analysis to cells with twice this many repeats did not alter our results; thus we do not think we have underestimated variability due to under sampling, at least for these small counting windows. Longer continuous segments and more repeats would have been required to adequately explore long counting windows. Measuring variability by Allan factor instead of Fano factor (as in Kara et al. 2000) yielded the same results (not shown).

Burst analysis.

Bursts in the dLGN attributed to low-threshold calcium spikes are conventionally identified by clusters of two or more spikes with interspike intervals of <4 ms (250 Hz) preceded by a lack of spikes for more than 100 ms. These criteria reflect the biophysics of de-inactivation of the low-threshold calcium channel and have been validated to identify low-threshold calcium spikes in the anesthetized cat preparation with the use of intracellular recordings (Lu et al. 1992; Wang et al. 2007). In our data, paired interval distributions are consistent with a distinct cluster roughly matching these criteria, but we have no intracellular data to verify that they are due to calcium spikes. We report the fraction of firing events that are bursts (where all the spikes within a burst are considered part of a unitary firing event), using the 100 ms/4 ms criteria. Results were not qualitatively changed by altering the interval criteria. Analysis was restricted to trials in which we recorded ≥10 spikes.

Temporal frequency tuning.

The responses of each single unit were temporally discretized at the stimulus refresh rate (60 Hz). Response power estimates were calculated on a trial-by-trial basis as the Fourier transform of the autocorrelation function (Wiener-Khinchin theorem). This was repeated for each trial for a specific temporal frequency and across all temporal frequencies. The f1 response amplitude for each trial was measured as the square root of the power at the stimulus temporal frequency. Correlograms and spectra were inspected to verify that the computed f1 amplitude corresponded to a peak in the spike train power spectrum. Of the 130 units recorded, we recorded temporal frequency tuning curves for 100 units (75 using CRT, 25 using LCD), all of which are included in the analysis. Of the 32 units recorded in anesthetized rats, temporal frequency responses were recorded from 16 units (all 16 using CRT), all of which are included in the analysis. We found no difference in temporal frequency tuning attributable to display type.

Spatial frequency tuning.

Methods for spatial frequency analysis were similar to those of temporal frequency analysis. The responses of each single unit were temporally discretized at the stimulus refresh rate (60 Hz). To mitigate the effects of small eye movements on stimulus phase, response power estimates were calculated on a trial-by-trial basis as the Fourier transform of the autocorrelation function (Wiener-Khinchin theorem). This was repeated for each trial for a specific spatial frequency and across all spatial frequencies. The f1 response amplitude for each trial was measured as the square root of the power at the stimulus temporal frequency (integrated within a frequency band of 1.53–2.46 Hz or 3.53–4.46 Hz for 2- and 4-Hz stimuli, respectively). Of the 130 units recorded in awake rats, we measured spatial frequency tuning in 111 units. Of these, 28 units were rejected from analysis because the spike train power spectrum had no peak at the stimulus frequency and/or the responses were nonstationary (inconsistent tuning curves or a large change in mean rate between repeats). Of the 32 units recorded in anesthetized rats, we measured spatial frequency tuning in 10 units, all of which passed the above criteria and were included in analysis.

It should be noted that in the present study, we did not transform the stimulus to conform to the spherical nature of the retina (per Heine and Passaglia 2011). Therefore, our estimates of spatial frequency cutoffs place only a lower bound on the actual spatial frequency cutoff of neurons. Specifically, if the receptive field was not perfectly centered on the monitor, high-frequency cutoff could be underestimated by as much as 20%.

To determine if our measured f1 amplitude was significantly above the noise, a resampling approach was taken. For each recorded trial, we generated a set of shuffled control spike trains by randomly reordering the interspike intervals, thus maintaining the spike number and interspike interval distribution. The f1 power of each resampled spike train was calculated using the methods described above. A “virtual” experiment was simulated using one reshuffled spike train for each recorded trial, and the f1 amplitudes of 100 such virtual experiments were used to obtain a mean and SD of the noise floor at each frequency. For all units included in this study, the actual f1 response was more than 2 SDs from the estimated noise floor mean for multiple spatial or temporal frequencies.

Normalized tuning curves.

For both temporal and spatial frequency responses, tuning curves were shuffle corrected and then normalized as follows: at each spatial or temporal frequency, we subtracted the average power of the shuffled spike trains (see above) from the power in the original spike train. Each shuffle corrected tuning curve was then divided by its maximal value such that each normalized tuning curve had a maximal value of 1. Note that this does not set the minimal value to 0 (the minimal value is allowed to be negative). The population average normalized curve was calculated by averaging the normalized values in each frequency bin. Since different units were characterized at different spatial and temporal frequencies, each frequency bin had different number of units contributing to it.

White noise analysis.

For white noise analyses, we drove the cells with a spatially uniform field whose luminance was updated each video frame (16.6 ms) to a new value drawn from a Gaussian distribution. The resulting stimulus had a white spectrum up to the Nyquist frequency (30 Hz). We discretized the neural responses and the stimuli into 1-ms bins. For purpose of analysis, we idealized the stimulus as a constant luminance throughout the frame with sharp jumps to new luminance values immediately after a new frame starts. All receptive fields were centered on the monitor prior to recording. The latency of the response was corrected for the delay with which stimulus was rendered at the receptive field. For anesthetized cells, this was well approximated as 8.33 ms. For awake animals, monitor positioning was less precise. For some (n = 19), we had recorded a spatiotemporal receptive field, allowing us to map the receptive field center for an exact correction, which was 7.46 ± 3.45 ms. For remaining cells from awake animals (n = 14), we used this mean 7.46 ms for latency correction. We verified that the heterogeneity of latency we observed is equivalent in the subset of cells that had an exact latency correction.

For each spike, the stimulus that preceded the spike was extracted (spanning 300 ms before the spike to the time of the spike). The spike-triggered average (STA) is defined as the average of these extracted stimuli. The frequency power spectrum was calculated from the Fourier transform of the STA and normalized such that the total power from 0 to 60 Hz equals 1 before being averaged across units.

Even the idealized stimulus contains power at frequencies surpassing the frame rate because of the sharp transitions. In practice, the high frequencies are weaker in LCD displays and stronger in CRTs. If these higher frequencies drive a visual response in the dLGN, we would be able to detect this. Nevertheless, frequencies above the Nyquist limit are only weakly present, and therefore our estimate of the neural response should be considered a lower bound for frequencies above 30 Hz.

Of the 130 units recorded in awake rats, we recorded responses to white noise from 33 units (19 with CRT, 14 with LCD), all of which were included in the analysis. Of the 32 units recorded in anesthetized rats, 19 were tested with white noise (all with CRT), all of which were included in the analysis. We found no difference in temporal frequency sensitivity attributable to display type (but see Analysis of individual differences).

Analysis of individual differences.

To detect if heterogeneity of physiological properties was attributable to differences between rats, we computed mean results separately for each animal and used KS tests to compare the distributions obtained from different animals, as well as ANOVA to find the variance attributable to animal identity. For most measures reported in this study, there was no significant difference between rats. For results where intersubject differences were suspected on the basis of any of these analyses, we defined the population heterogeneity as the standard deviation divided by the mean for all units. To quantify within-animal heterogeneity, we determined the standard deviation divided by the mean of units for each animal separately and defined within-animal heterogeneity as the weighted average of this value across animals, weighted by the number of units contributed by that animal.

In the case of white noise analysis, a large fraction of the variance in tuning properties could be attributed to intersubject variability. Specifically, a single outlier rat contributed 14 units with significantly different temporal frequency sensitivity from the 19 units contributed by 4 other (“typical”) rats. Results from this rat are therefore analyzed separately for population average curves (see Fig. 4I) and identified as “outlier” in the population distributions (see Fig. 5). The outlier rat was studied using a CRT display. We attribute the difference to animal and not display because the units recorded with CRT in other rats were consistent with LCD recordings in other rats and different from units in this outlier rat. For example, the distribution of temporal frequency cutoffs was not distinguishable for units recorded with LCDs vs. CRTs in other rats (KS test, P = 0.933), whereas the distribution of temporal frequency cutoffs recorded from the outlier rat vs. other rats using CRTs was significantly different (KS test, P = 0.019).

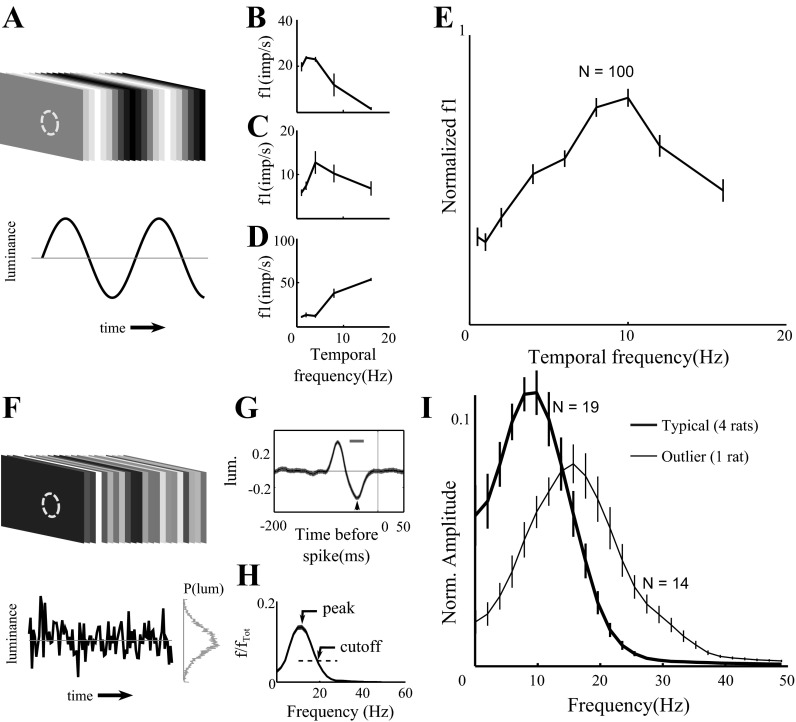
Fig. 4.

Temporal frequency tuning of dLGN responses. A: spatially homogenous visual stimulus was modulated sinusoidally at different temporal frequencies. Temporal frequency tuning curves are shown for 3 representative dLGN neurons (B–D, shared x-axis) with preference for different temporal frequency ranges. E: the average normalized temporal frequency tuning curve (n = 100 units). Curves and error bars indicate means ± SE. We found no difference between CRT and LCD responses to sinusoidal modulation at any of these temporal frequencies, so their data are combined. F: in white noise experiments, spatially homogenous visual stimuli were modulated temporally by sampling from a Gaussian distribution of luminance from each frame (16.6 ms); stimulus and response were sampled for analysis at 1-ms precision. G: spike-triggered average (STA) of response to a full-field Gaussian white noise stimulus for 1 example cell. Arrow indicates the latency to first peak of the STA, whereas the bar indicates the half-width of the first peak of the STA. H: temporal frequency tuning curve of the unit shown in G, defined as the Fourier transform of the STA. Total integrated power between 0 and 60 Hz was normalized to 1. The peak response and the cutoff response (defined as 1/e × peak response) are labeled. I: the average normalized temporal frequency tuning curve based on Fourier analysis of the STA. Error bars indicate ±SE. Data from units recorded in typical rats (thick curve; n = 19 units from 4 rats) and from units recorded in one outlier rat (thin curve; n = 14 units) are plotted separately.

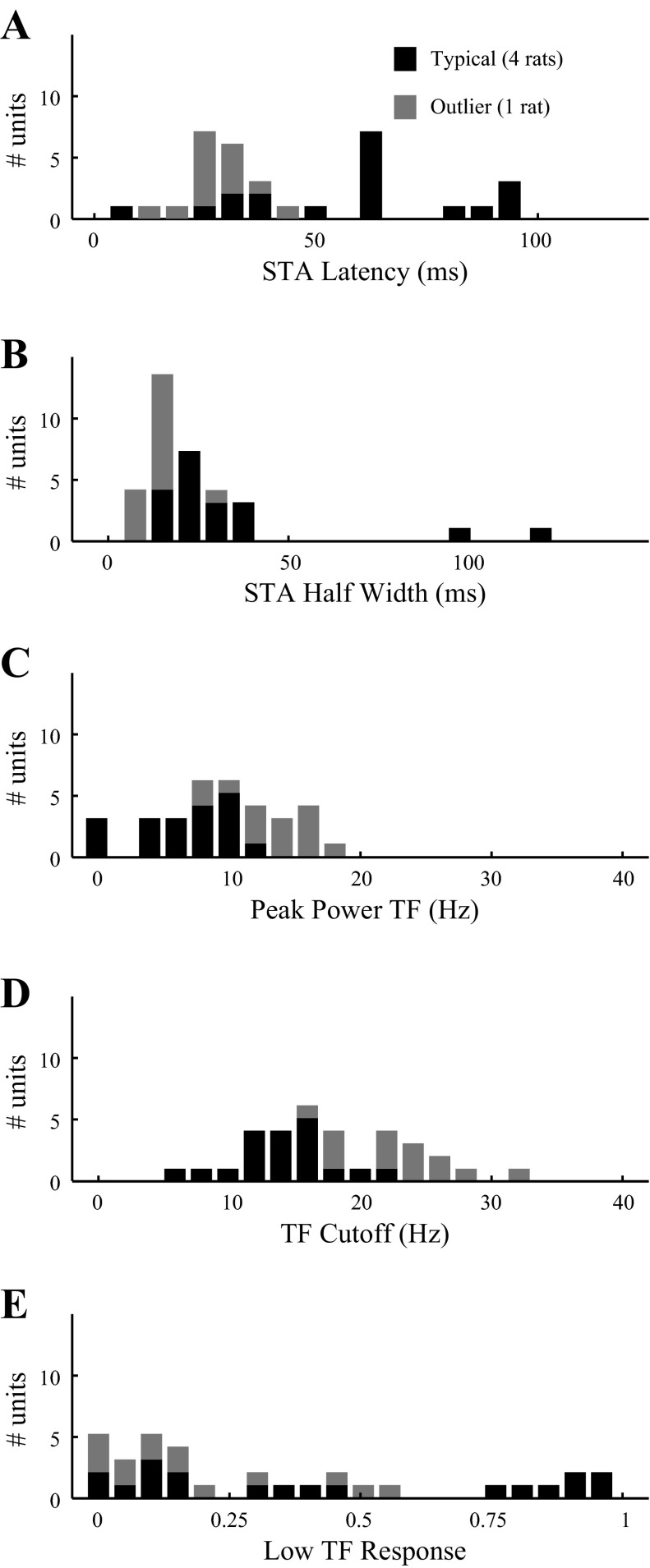
Fig. 5.

Distribution of temporal frequency tuning properties of dLGN neurons. Results are from dLGN neurons probed with Gaussian white noise, analyzed as shown in Fig. 4, F–I. A: latency to the first peak of the STA (e.g., arrow in Fig. 4G). B: width at half maximum of the first peak of STA (e.g., bar in Fig. 4G). C: the peak temporal frequency of the tuning curve (see Fig. 4H). D: the high-frequency cutoff (see Fig. 4H). E: power transmitted at the lowest temporal frequency (0 Hz) as a fraction of the power at peak frequency. Data from units recorded in typical rats (black bars; n = 19 units from 4 rats) and from units recorded in one outlier rat (gray bars; n = 14 units) are plotted separately. TF, temporal frequency.

This outlier rat differed from typical rats in one other respect: the neural reliability, or Fano factor. For example, with 4-Hz visual stimulation, units from the outlier were more reliable (FF = 0.32 ± 0.16, 0.33; n = 10) than units from other rats (FF = 0.58 ± 0.24, 0.57; n = 74), and the difference between the distributions was highly significant (KS test, P = 0.001). With 2-Hz stimulation the same effect was seen (outliers: FF = 0.34 ± 0.14, 0.30; n = 9, vs. typical rats: FF = 0.55 ± 0.23, 0.54; n = 76), although the difference in the distributions was less significant (P = 0.02). The higher reliability could have contributed to this rat's higher temporal frequency response.

In all other respects the outlier rat was not distinguishable from other rats. There was no significant difference in the distribution of f0, f1, and f1/f0 (not shown; cf. Fig. 3) or in its spatial frequency tuning characteristics (see Fig. 7). There was no significant difference in bursting. For example, with Gaussian white noise stimuli, burst fractions in the outlier rat were 0.05 ± 0.04, 0.04 (n = 12 units) compared with 0.06 ± 0.08, 0.02 (n = 17) in the remaining rats (KS test, P = 0.682). Bursting in response to 2- and 4-Hz stimulation also was not significantly different (not shown).

Fig. 3.

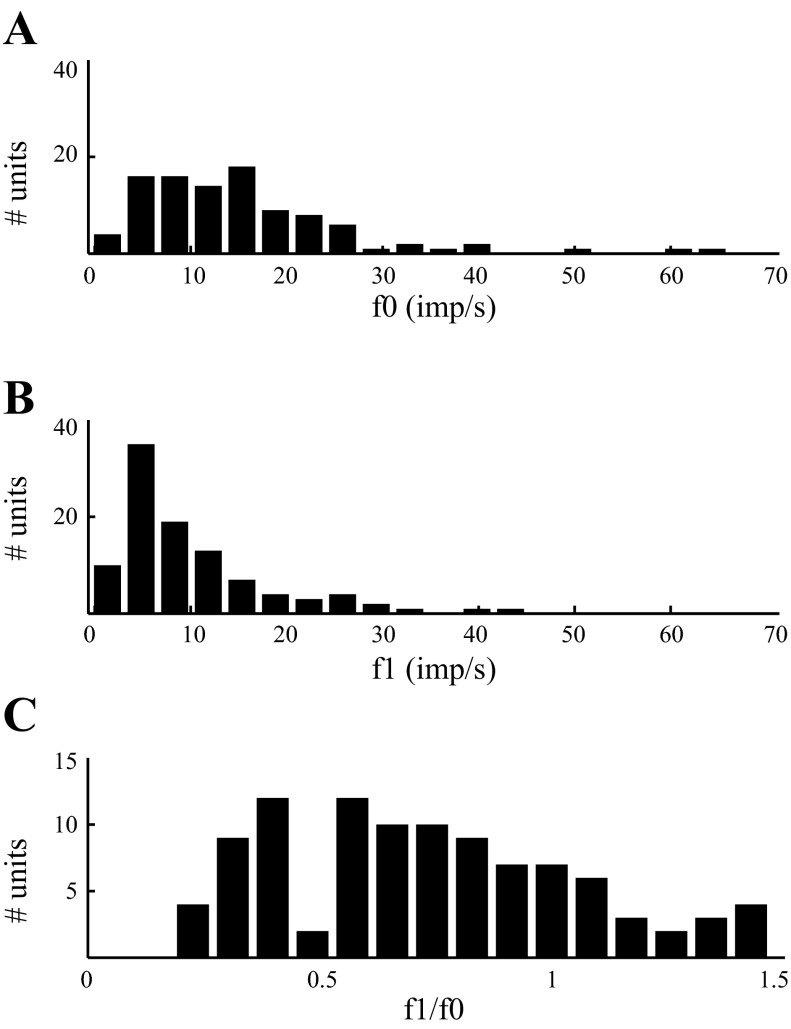
Visual response of dLGN neurons to full-field temporal modulation. Spatially homogenous visual stimulus was modulated sinusoidally at 2 Hz. A: distribution of f0 responses (average firing rate) of single units (n = 100, 75 with CRT and 25 with LCD). B: distribution of f1 responses (modulation of firing rate) of the same units shown in A. C: distribution of relative modulation of firing rates (f1/f0) for the neurons shown in A and B. Results from LCD- and CRT-driven units are combined, because we found no significant difference in any of these distributions. imp/s, Impulses/s.

Fig. 7.

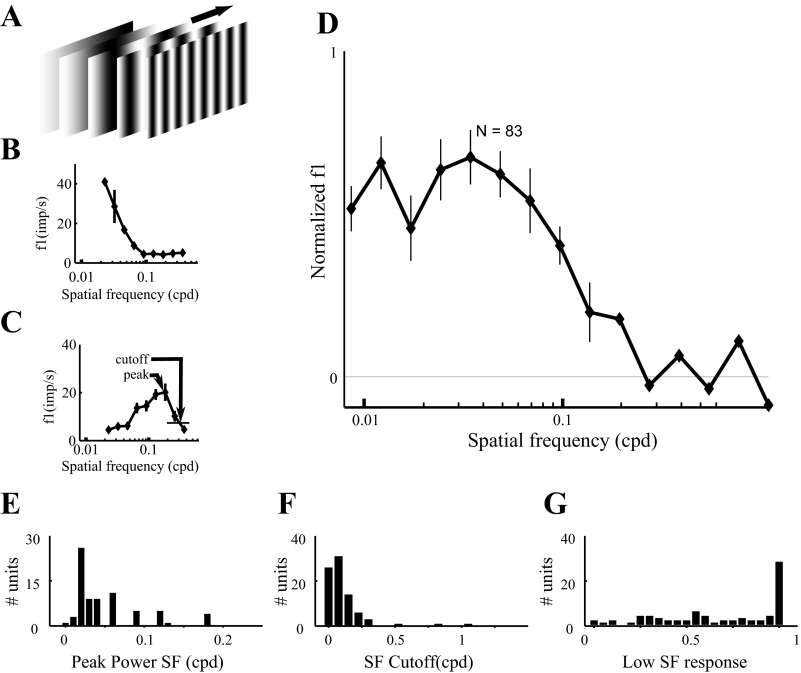
Spatial frequency tuning of dLGN neurons. Results are from 83 dLGN neurons probed with drifting gratings, as in Fig. 6. A: vertical gratings of different spatial frequencies were drifted across the receptive field at 2 or 4 Hz. Spatial frequency tuning curves are shown for 2 cells (B and C, respectively). D: the average normalized spatial frequency tuning curve (n = 83 neurons). Curves and error bars indicate means ± SE. E: the spatial frequency corresponding to the maximal response (“peak” in C). F: the high spatial frequency cutoff (“cutoff” in C). G: power transmitted at the lowest spatial frequency (0.02 cpd) as a fraction of the power at peak frequency. Results from LCD- and CRT-driven units are combined, because we found no significant difference in responses to 2- or 4-Hz modulation. SF, spatial frequency.

We do not know what caused this rat to be different from others; no difference in procedures, history, or training data could be identified. Unexplained individual differences in alertness, arousal, attention, or anxiety are common and should be considered possible factors. It would be valuable to quantify these behavioral traits in future experiments.

Preliminary reports.

A preliminary account of these physiology methods, including surgical implant design, head-fixed recording methods, integration with stimulus display, and eye-tracking hardware and software, has been presented previously in abstract form (Flister and Reinagel 2010; Sriram et al. 2011).

RESULTS

We recorded from 100 single units in the dorsolateral geniculate nuclei (dLGN) of unanesthetized Long-Evans rats while they passively viewed spatially homogenous, temporally sinusoidal visual stimuli of different temporal frequencies. The visual responses of an example OFF cell are summarized in Fig. 2. This well-isolated single unit was strongly modulated by changes in luminance on the screen (Fig. 2A). This cell was modulated by every temporal frequency tested (Fig. 2B). This cell fired preferentially when the luminance on the screen was low.

First, we characterized the mean firing rates and extent of rate modulation of dLGN cells. For the example cell shown in Fig. 2, the f0 response (mean firing rate) to a 2-Hz visual stimulus was 23.5 spikes/s, and the f1 response (modulation of firing rate about the mean at the same frequency as the stimulus) was 31.6 spikes/s. Over the population of dLGN cells (n = 100), the strength of the visual response varied widely (Fig. 3). For example, the mean firing rate in response to modulation at 2 Hz (f0, Fig. 3A) ranged from 0.9 to 63.6 spikes/s, averaging 15.9 ± 11.4, 13.8 (mean ± SD, median). For 2-Hz stimuli, the modulation of firing rate about the mean (f1, Fig. 3B) ranged from 0.86 to 42.7 spikes/s, averaging 10.7 ± 8.4, 8.2. The relative modulation (f1/f0) ranged from 0.18 to 1.46, averaging 0.73 ± 0.32, 0.68 (Fig. 3C).

The trial-to-trial variability of a neuron's response to repeated presentation of the same stimulus was measured by the Fano factor (FF; methods). We found that variability was sub-Poisson, consistent with previous findings in the dLGN awake monkey (Alitto et al. 2011) and several anesthetized preparations (Alitto et al. 2011; Andolina et al. 2007; Kara et al. 2000; Victor et al. 2007). The Fano factor in 16.7-ms counting windows was FF = 0.53 ± 0.23, 0.52 with 2-Hz visual stimuli (n = 85) and FF = 0.55 ± 0.25, 0.51 with 4-Hz visual stimuli (n = 84).

Neurons in the dLGN fire stereotyped bursts that can be identified by standard interspike interval criteria (methods). We found that bursts identified by these criteria were present but infrequent in the dLGN responses of unanesthetized rats during visual stimulation. The fraction of firing events that were classified as bursts was 0.06 ± 0.07, 0.03 (n = 29) in responses to Gaussian white noise, 0.09 ± 0.12, 0.03 (n = 96) in responses to spatially uniform 2-Hz temporal modulation, and 0.10 ± 0.11, 0.06 (n = 95) in responses to 4-Hz temporal modulation.

Temporal filtering properties.

The strength of modulation of firing rate was generally dependent on the temporal frequency of the stimulus (Fig. 4). We determined the temporal frequency tuning curves of the same 100 dLGN neurons described above (Fig. 4, A–E). The units displayed heterogeneous tuning properties, with some individual units showing peak responses at low temporal frequencies (<4 Hz, 14/100; Fig. 4B), intermediate temporal frequencies (4–10 Hz, 71/100; Fig. 4C), and high temporal frequencies (>10 Hz, 15/100; Fig. 4D). To summarize the frequency response of the population as a whole, we averaged their normalized tuning curves. For each cell the temporal frequency tuning curve (f1 as a function of temporal frequency, e.g., Fig. 4, B–D) was normalized by its maximal response. The average of these normalized tuning curves (Fig. 4E) shows that as a population, cells in the rat dLGN are best driven by stimuli around 10 Hz. In this experiment we found no difference between cells driven by LCD (n = 25) or CRT (n = 75) displays for temporal frequencies up to 12 Hz; 16-Hz stimuli were only tested using CRT monitors.

In the sinusoidal modulation experiment we could only test a few discrete temporal frequencies, so the peak response frequency and x could not be estimated precisely. To further characterize the temporal response properties in rat dLGN, we recorded the responses of 33 single units while the animals were viewing a spatially uniform visual stimulus temporally modulated with Gaussian white noise (Fig. 4F). The average stimulus preceding a spike (spike-triggered average, STA) was computed for each cell (Fig. 4G). We also computed the normalized power spectrum of each STA (Fig. 4H). Together these curves capture the linear dependence of spiking on the visual stimulus. We define the high-frequency cutoff of a neuron as threshold 1/e of maximum power (“cutoff” in Fig. 4H). To express the relative power at low temporal frequency, we calculate the ratio of the power in the lowest frequency band (0–2 Hz) to the power in the peak frequency band. This produces an index between 0 (strictly bandpass) and 1 (low pass).

In this experiment, units recorded from one rat were significantly different from units of the other four rats (see methods, Analysis of individual differences), so these were analyzed separately. To summarize the temporal response profile for the population of dLGN cells, we computed the average normalized STA power spectrum (Fig. 4I). In the average spectrum for the four typical rats (n = 19 units; thick curve), the peak temporal frequency was 9.77 Hz, the high-frequency cutoff was 19.53 Hz, and the low temporal frequency response index was 0.55. Thus results from broadband temporal stimuli (Fig. 4I; thick curve) were qualitatively consistent with the results obtained with sequential, sinusoidal modulation (Fig. 4E). In these typical rats, we found no difference between units driven by LCD (n = 14) or CRT (n = 5) displays. In the outlier rat (n = 14 units; thin curve), units were more responsive to high temporal frequencies. The peak temporal frequency was 15.63 Hz, the high-frequency cutoff was 27.39 Hz, and the low temporal frequency response index was 0.21. All units from the outlier rat were driven by CRT stimuli.

To characterize the heterogeneity of temporal tuning across the population, we extracted five descriptive parameters from each cell: 1) the time to the first STA peak before the spike (a measure of response latency), 2) the width of the first peak at half maximum (a measure of response transience), 3) the peak temporal frequency in the power spectrum of the STA, 4) the high-frequency cutoff in the STA power spectrum, and 5) the normalized power at low temporal frequency. We again found heterogeneity across the population of cells. Including units from all rats, latency (arrow in Fig. 4G) ranged from 7 to 100 ms (Fig. 5A). The width of the first peak of the STA (bar in Fig. 4G) ranged from 11 to 122 ms (Fig. 5B). The peak temporal frequency (“peak” in Fig. 4H) ranged from 0.16 to 19.6 Hz (Fig. 5C). The high-frequency cutoff (“cutoff” in Fig. 4H) ranged from 7.9 to 33.6 Hz (Fig. 5D). The low-frequency response index ranged from 0.005 to 0.99 (Fig. 5E).

In the four typical rats (n = 19 units; Fig. 5, black bars), the latency was 61.6 ± 25.7, 66.2 ms; STA half-width was 36.7 ± 27.5, 27 ms; peak temporal frequency was 8.3 ± 3.6, 9.5 Hz; temporal frequency cutoff was 15.3 ± 3.6, 15.6 Hz; and fraction of response at low temporal frequency was 0.47 ± 0.37, 0.39. Units from the outlier rat (n = 14 units; gray bars) had shorter latencies (29.8 ± 8.1, 29.2 ms), shorter STA half-widths (17.57 ± 4.73, 16.5 ms), higher peak temporal frequencies (14.4 ± 2.9, 14.95 Hz), higher temporal frequency cutoffs (24.2 ± 4.5, 23.8 Hz), and less fractional response to low temporal frequency (0.21 ± 0.20, 0.14). The distributions of parameters from the outlier rat were significantly different from other rats' (KS <10⁻³) for all these measures but low temporal frequency response (KS = 0.17). Animal identity accounted for significant variance (ANOVA, P <10⁻³) for all measures but STA half-width (P = 0.067).

In summary, we showed that dLGN neurons in the typical rat fire robustly, are strongly modulated by visual stimuli, are best driven around 10 Hz, and respond well to temporal modulation from 5 to 15 Hz. Neurons sensitive to higher temporal frequencies were found in one rat. In the heterogeneous population, we found individual cells that filtered out low temporal frequency signals and others that responded robustly above 30 Hz.

Spatial filtering properties.

Next, we turned to the spatial frequency response properties of the rat dLGN. To determine the spatial frequency sensitivity of dLGN neurons, we recorded the responses of 83 single units in the dLGN to a full-field grating stimulus at full contrast with a temporal frequency of either 2 or 4 Hz. Spatial tuning properties were not significantly different between the cells tested at 2 Hz and the cells tested at 4 Hz. Responses of one representative OFF cell are summarized in Fig. 6. The raw voltage trace in response to a drifting grating for one 3-s trial (Fig. 6A) shows the quality of isolation of the unit and reveals that the firing rate was modulated over time by the stimulus (Fig. 6B) at this spatial frequency. The drift speed was adjusted such that the temporal frequency of modulation was the same for all spatial frequencies. The responses to all repeats of all spatial frequencies are summarized by rasters grouped by spatial frequency (Fig. 6C). For this example cell, both the mean firing rate (f0) and the modulation of the firing rate (f1) depended on the spatial frequency of the grating. The highest mean rate at any spatial frequency was 68 spikes/s. For this cell, the spatial frequency eliciting the greatest modulation at the temporal frequency of the stimulus (f1) was 0.06 cpd. At this peak spatial frequency, this cell's responses were modulated by 77% of the mean rate (f1/f0).

The 83 single units we recorded were heterogeneous in spatial frequency tuning. There was no difference found between LCD (n = 41) and CRT (n = 42). In response to drifting grating stimuli (Fig. 7A), some cells responded selectively to low spatial frequencies (Fig. 7B), whereas other cells were selective for higher spatial frequencies (Fig. 7C). The population tuning curve shows that, on average, cells in the dLGN of awake rats respond best to spatial frequencies of 0.03–0.06 cpd (Fig. 7D).

To quantify the distribution of tuning properties across the population, we extracted the peak spatial frequency and high-frequency cutoff (1/e of maximum power; see Fig. 7C) for each cell (see Fig. 7F), as well as the power of the response to the lowest spatial frequency (0.02 cpd) as a fraction of the power at peak frequency. The spatial frequency that drove the cell best ranged from 0.008 to 0.18 cpd, averaging 0.056 ± 0.045, 0.034 cpd (n = 83 cells; Fig. 7E). The upper spatial frequency cutoff of these cells ranged from 0.01 to 1.1 cpd, averaging 0.15 ± 0.16, 0.12 cpd. Most units (77 of 83) had cutoff spatial frequency below 0.3 cpd (Fig. 7F). The response to very low spatial frequency ranged from 0 to 1 times the response at the same cell's peak spatial frequency, on average, 0.68 ± 0.33, 0.74 (Fig. 7G).

Importance of unanesthetized recording.

Because our primary interest is linking physiology to behavior, we characterized response properties in the unanesthetized preparation (Figs. 1–7). To test whether this was necessary, we also recorded a small sample of cells (from different rats) under light isoflurane anesthesia. All anesthesia experiments used CRT monitors. The properties observed in this small sample were inconsistent with random sampling from the distributions we measured in the awake rat, however, so these cells are not included in the results above.

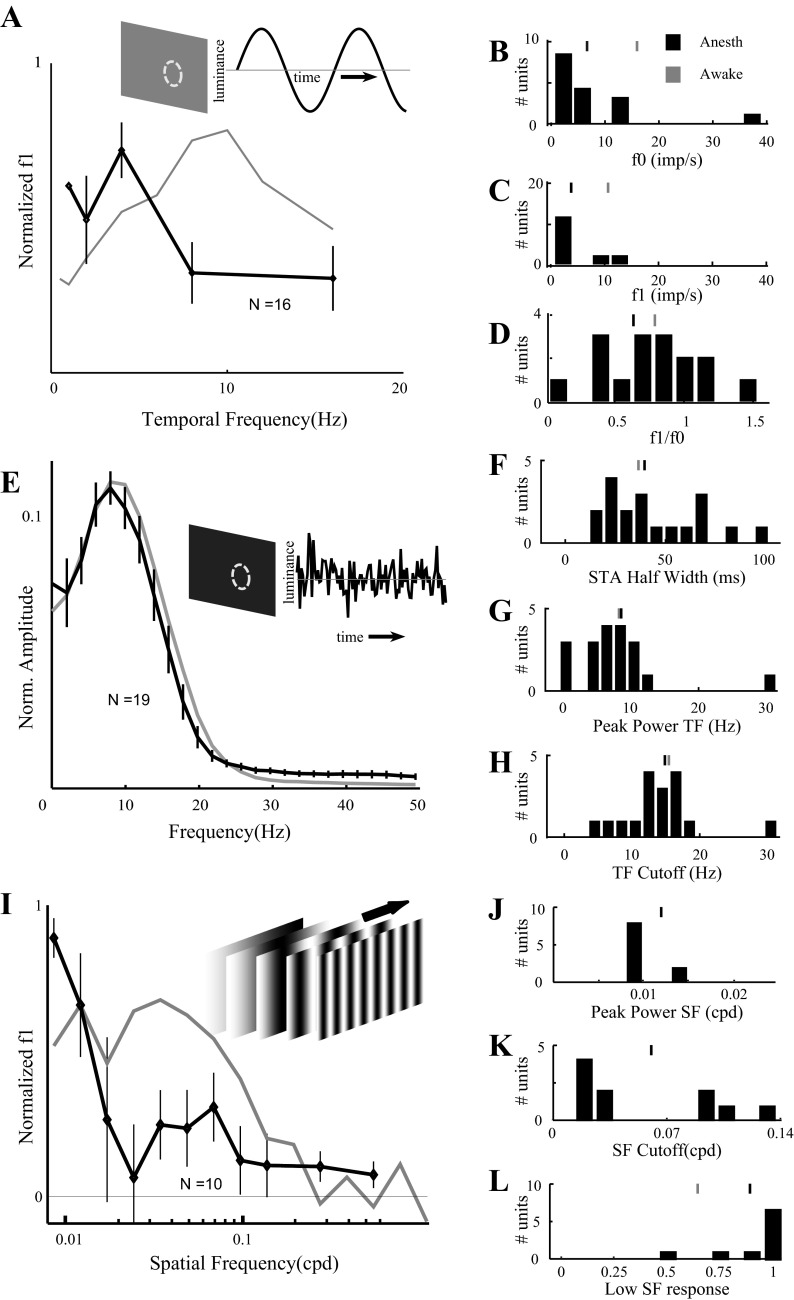
For example, we measured temporal frequency tuning with sinusoidal modulation for an additional 16 cells under isoflurane anesthesia (16 different electrode penetrations in 5 different rats; Fig. 8A, black). At the population level, anesthetized cells preferred lower temporal frequencies (2–4 Hz) compared with cells from unanesthetized rats (Fig. 8A, gray). The distribution of mean firing rates was significantly different from the unanesthetized sample (Fig. 8B, cf. Fig. 3A; KS test, P = 4.1e-6). Specifically, dLGN cells in anesthetized rats had lower firing rates (f0 = 6.7 ± 9.02, 4.6 spikes/s vs. 15.9 ± 11.4, 13.8 spikes/s in awake rats). The f1 distribution was also significantly different (Fig. 8C, cf. Fig. 3B; KS test, P = 6.7e-6). Specifically, dLGN cells in anesthetized rats were less modulated (f1 = 3.8 ± 4, 2.2 spikes/s vs. 10.7 ± 8.4, 8.2 spikes/s in awake rats). Relative modulation (f1/f0) was comparable (Fig. 8D, cf. Fig. 3C; KS test, P = 0.72).

Fig. 8.

Temporal and spatial frequency tuning properties of dLGN neurons differ under anesthesia. A: population average of normalized temporal frequency tuning curves for 16 neurons from anesthetized rats (black). Error bars indicate ±SE. Compare with results from unanesthetized rats in Fig. 4E (shown in gray). B: distribution of average firing rate (f0) at 2 Hz for 16 cells from anesthetized rats (cf. Fig. 3A). C: the modulation of firing rates (f1) at 2 Hz (cf. Fig. 3B). D: relative modulation of firing (f1/f0; cf. Fig. 3C). Tic marks in B–D indicate population means from anesthetized (black) and awake (gray) rats. E: population average of normalized temporal frequency tuning curves obtained using Gaussian white noise stimuli for 19 units from anesthetized rats (black). Error bars indicate ±SE. Compare with results from typical unanesthetized rats (cf. thick curve in Fig. 4I; shown in gray). F: distribution of STA half-widths from anesthetized rats (cf. black bars in Fig. 5B). G: distribution of peak power from anesthetized rats (cf. black bars in Fig. 5C). H: distribution of temporal frequency cutoff from anesthetized rats (cf. black bars in Fig. 5D). Tic marks in F–H indicate population means from anesthetized (black) and typical awake rats (gray). I: population average of normalized spatial frequency tuning curves from 10 dLGN units recorded under anesthesia (black). Error bars indicate ±SE. Compare with results from unanesthetized rats (cf. Fig. 7D; curve shown in gray). J: distribution of best spatial frequency from anesthetized rats (cf. Fig. 7E). Mean of distribution from awake rats is off scale (0.052 cpd). K: distribution of spatial frequency cutoff from anesthetized rats (cf. Fig. 7F). Mean of distribution from awake rats is off scale (0.15 cpd). L: distribution of low spatial frequency responses from anesthetized rats (cf. Fig. 7G). Tic marks in J–L indicate population mean from anesthetized (black) and awake (gray) rats.

Anesthesia did not significantly affect response reliability as measured by the Fano factor. With isoflurane, responses to 2-Hz temporal modulation had FF = 0.61 ± 0.31, 0.54 (n = 11 units), comparable to that in awake rats (FF = 0.53 ± 0.23, 0.52). Likewise, with 4-Hz temporal modulation, units in anesthetized rats had FF = 0.59 ± 0.28, 0.53 (n = 10 units), comparable to results in awake rats (FF = 0.55 ± 0.25, 0.51). This result is in agreement with similar findings in the monkey dLGN (Alitto et al. 2011).

In our experiment, isoflurane did not increase the burst frequency observed in our dLGN recordings. The fraction of firing events that were defined as bursts (methods) in anesthetized rats was 0.04 ± 0.08, 0.02 for the Gaussian white noise stimulus (n = 19), 0.02 ± 0.02, 0.01 for 2-Hz sinusoidal modulation (n = 13), and 0.02 ± 0.04, 0.01 for 4-Hz modulation, comparable to the values obtained in awake recordings (above). In the case of 4-Hz stimuli, bursting was significantly lower in the population of cells recorded under anesthesia than in the awake preparation (KS test, P = 0.005). This was surprising because anesthesia often increases bursting in the dLGN in other preparations. Perhaps our plane of anesthesia was relatively light or our awake rats were not as alert or engaged as in other behavioral studies. Also, we note the absence of secondary anesthetic agents in our case.

We recorded temporal white noise responses from 19 cells (15 different penetrations in 6 different isoflurane-anesthetized rats) and compared them with response of units from typical awake rats. The population spectrum (Fig. 8E, black) was similar to that obtained from cells recorded from typical awake rats (Fig. 8E, gray). The population spectrum recorded under anesthesia had a slightly lower peak frequency (7.8 Hz, compared with 9.77 Hz in awake rats) and a slightly lower high-frequency cutoff (15.7 Hz, compared with 19.53 Hz in awake rats), and the power at low frequency relative to peak frequency was slightly greater (0.71, compared with 0.55 in awake rats). Individual units recorded under anesthesia showed slightly lower peak latencies (47.7 ± 17.2, 54 ms; not shown, cf. 61.6 ± 25.7, 66.2 ms in awake rats, Fig. 5A; KS test, P = 0.01), similar peak widths (Fig. 8F, cf. Fig. 5B, black; KS test, P = 0.46), similar peak temporal frequency (Fig. 8G, cf. Fig. 5C, black; KS test, P = 0.95), similar cutoff frequency (Fig. 8H, cf. Fig. 5D, black; KS test, P = 0.74), and similar low-frequency response (not shown, cf. Fig. 5E black; KS test, P = 0.74).

We collected spatial frequency tuning curves from 10 additional single units in anesthetized rats (10 different penetrations in 4 different rats). This small sample was sufficient to reveal that the population average tuning curve differed (Fig. 8I, cf. Fig. 7D). Under isoflurane the peak spatial frequency (0.01 ± 0.003, 0.008 cpd; Fig. 8J) was significantly lower (cf. Fig. 7E; KS test, P = 0.01). The cutoff spatial frequency (0.06 ± 0.05, 0.01 cpd; Fig. 8K) was significantly lower (cf. Fig. 7F; KS test, P = 0.025). Transmission of the lowest spatial frequency (relative to peak frequency) was higher (0.88 ± 0.18, 1.0; Fig. 8L, cf. Fig. 7G), but this difference was not significant (KS test, P = 0.11).

In summary, units recorded under light isoflurane anesthesia were not comparable to those recorded in unanesthetized animals.

DISCUSSION

We have characterized the temporal and spatial filtering characteristics of single units in the dLGN of unanesthetized rats. These are the first quantitative measurements of dLGN spatiotemporal filtering properties in an unanesthetized rodent.

Temporal response properties.

We measured the temporal filtering properties of dLGN neurons using full-field spatially homogenous, temporally sinusoidally modulating stimuli and also using spatially uniform temporal white noise. Results from the two methods were in qualitative agreement, suggesting that temporal filtering by the dLGN is approximately linear within the regime we explored. Although dLGN neurons showed considerable variability in tuning properties, the average dLGN neuron showed peak responses at 10 Hz and still responded significantly at 16 Hz. This frequency is well above previously characterized peaks and cutoffs measured in the dLGN of anesthetized mice using patterned gratings (Grubb and Thompson 2003). It is possible this difference is explained by anesthesia (see below).

The peak temporal frequencies we find in awake rat (14 Hz for CRT stimuli; Figs. 4E, 4I, and 5C) are comparable to that of sustained cells in the awake rabbit dLGN (11 Hz; Bezdudnaya et al. 2006) or parvocellular neurons in the awake macaque monkey (15 Hz; Alitto et al. 2011), and much lower than that of transient cells of the rabbit or magnocellular neurons of the macaque. Temporal frequency cutoff in awake rat (25 Hz at 1/e maximum response for CRT stimuli; Figs. 4H and 5D) was substantially less than that of macaque parvocellular neurons (average 32 Hz at 1/2 response). We note, however, that rabbit and macaque units were characterized with optimal spatial frequency gratings, whereas we used spatially uniform stimuli.

The optimal temporal frequency for driving dLGN neurons in the awake rat is well above the temporal frequencies typically used in mouse and rat visual behavior experiments (1.5Hz, Busse et al. 2011; 0 Hz, Meier et al. 2011; Meier and Reinagel 2011; Prusky et al. 2000; but see Umino et al. 2008). Nevertheless, stimulus onset responses could engage units tuned to high frequency. Moreover, a substantial subpopulation of dLGN neurons is well driven by these low temporal frequencies and could therefore underlie the observed behavioral performance.

Spatial response properties.

We measured the spatial filtering properties of dLGN neurons with drifting sinusoidal gratings. We found diverse spatial tuning properties, with an average peak frequency of 0.05 cpd and high-frequency cutoff of up to 0.25 cpd. On a linear approximation, spatial tuning curves have a direct relation to receptive field structure. We found both low-pass tuning curves (Fig. 7B), corresponding to weak surround antagonism and spatial integration, and bandpass tuning (Fig. 7C), implying strong antagonism and spatial differentiation. When the tuning curves reported were fit to a difference-of-Gaussian model (Enroth-Cugell and Robson 1966), the estimated receptive field center diameters (2σ of center Gaussian) ranged from 1° to 13° (analysis not shown). We also measured receptive fields using spatiotemporal white noise (Chichilnisky 2001; Reid et al. 1997) with similar results (data not shown). Thus the spatial tuning we find in awake rat is consistent with the range of receptive field sizes reported in the awake rabbit (Swadlow and Weyand 1985). In the awake rabbit, 84% of units were classified as having “concentric” receptive fields based on spatial mapping. In rough agreement, more than half the cells we recorded in awake rat had reduced power at low spatial frequency indicative of surround antagonism (Fig. 7G). Unsurprisingly, high spatial frequency cutoff in the awake rat (0.12; Fig. 7F) was lower than that of parvocellular units in the macaque even out to 15–20° eccentricity (Alitto et al. 2011), and much less than that of magnocellular neurons. Neurons in the awake macaque also showed stronger surround antagonism than we found in rat.

The spatial filtering properties we found in the awake rat dLGN correspond well to those measured in the rat retina (Heine and Passaglia 2011), despite the fact that the retinal data were collected from anesthetized rats. This suggests that the effect of anesthesia we observed may arise in the dLGN circuitry and not in its retinal inputs. Conservation of tuning from retina to dLGN is consistent with the view that dLGN cells receive inputs from one or, at most, a few retinal ganglion cells (Sherman and Koch 1986).

We note that spatial and temporal frequency tuning in the dLGN are not independent (Cai et al. 1997; Troy 1983). Because of limited recording duration we could not fully sample the joint parameter space. In this article we have described temporal frequency tuning only for low spatial frequency (0 cpd), and spatial frequency tuning only at moderate temporal frequency (2–4 Hz). Also, we measured spatial responses with drifting not counterphasing gratings, so we could not determine linearity of spatial summation (X- vs. Y-like character) for this neural population.

Heterogeneity.

We found that dLGN neurons in unanesthetized rats are heterogeneous in spatial and temporal tuning. We considered whether this heterogeneity was attributable to individual differences between animals, multiple distinct cell types, dependence on spatial location in the dLGN, or dependence on receptive field location in visual space. The heterogeneity in most physiological properties was not due to individual differences between rats, with the following exceptions.

In the case of relative modulation (Fig. 3C), identity of rat accounted for significant variance (ANOVA, P = 1.5 × 10⁻³), but this was a minor factor in explaining heterogeneity. The heterogeneity of the overall sample (n = 100 units, 6 rats) was 0.44 (SD/mean; see methods). The average heterogeneity within animal was similar (0.42).

In the white noise analysis, units recorded from one rat (n = 14) were significantly more responsive to high temporal frequencies (Fig. 5, black vs. gray). This individual rat accounted for some but not all of the heterogeneity. The heterogeneity in latency (SD/mean) was 0.46 overall and 0.33 within animal. For peak temporal frequency, population heterogeneity was 0.41 vs. 0.30 within animal; for temporal frequency cutoff, population heterogeneity was 0.31 vs. 0.21 within animal; for low frequency index, population heterogeneity was 0.92 vs. 0.80 within animal. In the case of STA half-width, there were two outlying units (>100 ms) recorded from two different (otherwise typical) rats; the remaining 31 units had half-widths <50 ms (Fig. 5B). Differences between rats also contributed to heterogeneity, however. Among units with half-widths <50 ms, heterogeneity was 0.35 overall vs. 0.27 within-animal. The one rat identified as an outlier on the basis of high temporal frequency responses also had significantly lower neural variability (Fano factor). We did find that Fano factor was negatively correlated with a high temporal frequency cutoff in the population as a whole (r = −0.43) and among only units from other rats (r = −0.45), although the correlations were not significant (P = 0.06 and P = 0.08, respectively).

In the spatial frequency experiment, one rat had significantly different spatial frequency cutoffs from all other rats, but this was because two of the four units recorded in that rat were outliers (0.60 and 1.10 cpd, cf. mean 0.15 cpd; Fig. 7F). Another such unit (cutoff 0.85 cpd) was recorded in a different rat. Leaving aside these three exceptional units, the population heterogeneity in the remaining 80 units was 0.62, and the within-animal heterogeneity was almost as great, 0.57. In summary, individual differences do exist, but response properties are heterogeneous within each animal.

We found no evidence for clustering of our dLGN cells into discrete cell types according to tuning properties. Each individual parameter fell along a continuum with a unimodal distribution. The data set was too small for generalized multidimensional clustering, but no clusters were apparent by inspecting several two- and three-parameter combinations.

The units we recorded were sparsely distributed throughout the dLGN volume, more concentrated near the center. We did not see any obvious spatial organization within the dLGN of tuning properties, considered singly or in combination. Therefore, we could not attribute the heterogeneity in physiological properties to the anatomical locations of the units.

In many mammals, spatial resolution of visual neurons declines with eccentricity (Derrington and Lennie 1984; Hoffmann et al. 1972; Swadlow and Weyand 1985). Rats lack a defined area centralis or fovea, and we found no correlation between receptive field eccentricity and either spatial frequency cutoff or temporal frequency cutoff. The absence of such a correlation is consistent with reports of the rat retina (Heine and Passaglia 2011), the mouse dLGN (Grubb and Thomson 2003), and the mouse V1 (Neill and Stryker 2008).

On anatomical grounds it is likely that the rat dLGN contains distinct cell types that are spatially organized within the dLGN according to retinal ganglion cell classes and their projection patterns (Discenza and Reinagel 2012; Huberman et al. 2008, 2009). Weak gradients or fine structure within the dLGN might not be detectable in our data because we did not sample densely in any individual rat. Selection bias could be part of the reason we did not identify distinct physiological types; we only recorded cells with compact receptive fields and central receptive field locations (between 0° and 60° horizontally and ±20° vertically). Cells with large or peripheral receptive fields might represent distinct classes of neurons with different tuning properties. We were not able to test linearity of spatial summation, which distinguishes X-type and Y-type cells in the rat retina (Heine and Passaglia 2011). In summary, we presume that distinct physiological types do exist in the rat dLGN, but our study was not optimized for cell type classification.

Effect of anesthesia.

We found that both temporal and spatial frequency tuning as measured with sinusoidal stimuli were different under isoflurane anesthesia. We conclude that recordings of dLGN neurons from awake animals will be necessary to obtain measurements directly applicable to modeling visual behavior. Our goal was not to provide a thorough characterization of the distribution of tuning curves in the anesthetized state, but only to determine if anesthesia matters. Nevertheless our limited data are in broad agreement with previous reports comparing anesthetized to awake responses in the dLGN. Visual responses have been recorded from the dLGN of anesthetized mice (Grubb and Thompson 2003; Marshel et al. 2012; Piscopo et al. 2013; Zhao et al. 2013) and in their isolated retina in vitro (Farrow and Masland 2011; Marco et al. 2013; Rivlin-Etzion et al. 2011; Wang et al. 2011c). Our results in anesthetized rat dLGN are consistent with measurements made in the anesthetized mouse dLGN, in that cells of anesthetized animals are best driven by lower temporal frequencies (4–8 Hz). We note, however, that some individual units did respond to 8- and 16-Hz modulation in the sinusoidal stimulus experiment; these units were simply rarer than in awake animals.

Our results are consistent with previous reports that firing rate decreased and temporal and spatial frequency tuning shifted to lower frequencies under anesthesia in monkeys (Alitto et al. 2011) and cats (Kang and Malpeli 2009; cf. Lee et al. 1992) or inattentive state in rabbits (Bezdudnaya et al. 2006; Swadlow and Weyand 1985). In rabbit, an inattentive state did not alter concentricity of receptive fields, but in our hands the rat cells recorded under anesthesia were more likely to be spatially low pass (Fig. 8L), implying a reduction in surround antagonism.

We do not know the mechanism underlying the effects of isoflurane we observed. Isoflurane could affect thalamic relay cells by directly hyperpolarizing them (Krasowski and Harrison 1999; Reis and Puil 1999) and also indirectly by affecting the local inhibitory network (Detsch et al. 2002; Krasowski and Harrison 1999). Hyperpolarization could shift thresholds by increasing the synaptic input required to elicit spikes and could evoke nonlinear effects through changes in the intrinsic properties of the relay cell. Given that the spatial integration and temporal precision of visual responses are shaped by local feed forward and feedback inhibition in this circuit (Isaacson and Scanziani 2011), alterations to the local inhibitory network could also alter the tuning properties of relay neurons.

We found that anesthesia weakens dLGN responses, reducing response amplitude and sensitivity to high spatial and temporal frequencies, compared with responses in animals that were awake but passive and unengaged. Conversely, we speculate that increased arousal or task engagement could strengthen and sharpen neural responses to improve visual coding, even at the level of the dLGN. In mice, running increased response amplitude in V1 but not dLGN (Niell and Stryker 2010), but in monkeys, selective attention was shown to increase dLGN responses to relevant visual stimuli (McAlonan et al. 2008).

From our data, we do not know if each individual cell in the rat shifts its spatial and temporal frequency response during anesthesia or if a different subpopulation of neurons is preferentially active under anesthesia. In either case, later visual processing regions (V1 and higher visual areas) receive a substantially different picture of the visual input under light isoflurane anesthesia.

Summary.

Our data show that the rat dLGN is more visually responsive, and more sensitive to higher spatial and temporal frequencies, than was generally assumed or previously reported. We have measured only a few of the response properties of rat dLGN neurons; much work remains. The methods and findings reported here can provide a foundation for further characterization of the rat dLGN, inform interpretation of rat visual behavior, and assist modeling of the circuits underlying visual response properties in rodent V1.

GRANTS

This work was supported by National Eye Institute Grant R01EY016856-02, a James S. McDonnell Foundation Scholar Award, and a San Diego Foundation Blasker Award.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

B.S., P.M.M., and P.R. conception and design of research; B.S. and P.M.M. performed experiments; B.S. analyzed data; B.S., P.M.M., and P.R. interpreted results of experiments; B.S. prepared figures; B.S. drafted manuscript; B.S., P.M.M., and P.R. edited and revised manuscript; B.S., P.M.M., and P.R. approved final version of manuscript.