Effects of GABA_A kinetics on cortical population activity: computational studies and physiological confirmations

Abstract

Voltage-sensitive dye (VSD) imaging produces an unprecedented real-time and high-resolution mesoscopic signal to measure the cortical population activity. We have previously shown that the neuronal compartments contributions to the signal are dynamic and stimulus-dependent (Chemla S, Chavane F. Neuroimage 53: 420–438, 2010). Moreover, the VSD signal can also be strongly affected by the network state, such as in anesthetized vs. awake preparations. Here, we investigated the impact of the network state, through GABA_A receptors modulation, on the VSD signal using a computational approach. We therefore systematically measured the effect of the GABA_A-mediated inhibitory postsynaptic potentials (IPSPs) decay time constant (τ_G) on our modeled VSD response to an input stimulus of increasing strength. Our simulations suggest that τ_G strongly modulates the dynamics of the VSD signal, affecting the amplitude, input response function, and the transient balance of excitation and inhibition. We confirmed these predictions experimentally on awake and anesthetized monkeys, comparing VSD responses to drifting gratings stimuli of various contrasts. Lastly, one in vitro study has suggested that GABA_A receptors may also be directly affected by the VSDs themselves (Mennerick S, Chisari M, Shu H, Taylor A, Vasek M, Eisenman L, Zorumski C. J Neurosci 30: 2871–2879, 2010). Our modeling approach suggests that the type of modulation described in this study would actually have a negligible influence on the population response. This study highlights that functional results acquired with different techniques and network states must be compared with caution. Biophysical models are proposed here as an adequate tool to delineate the domain of VSD data interpretation.

voltage-sensitive dye imaging (VSDI) offers the possibility to visualize in real-time the cortical network activity of large neuronal population with high spatiotemporal resolution (Grinvald et al. 1999; Grinvald and Hildesheim 2004; Chemla and Chavane 2010b). This makes it an ideal technique to study the dynamics of cortical processing at the mesoscopic level. The technique is based on voltage-sensitive dyes (VSDs), which bind to the cells membrane and transform linearly variations of membrane potential into variations of fluorescence. The recorded VSD signal is therefore a complex signal that combines a large amount of intermingled components (including all layers of the circuitry, all cell types, i.e., excitatory, inhibitory, and glial, and all neuronal compartments, i.e., somas, axons, and dendrites), whose relative contributions are difficult to disentangle from each other (see Chemla and Chavane 2010b for a review on the subject).

To understand the multicomponent origin of the VSD signal, we developed a detailed biophysical model (Chemla and Chavane 2010a) based on known neural properties of the visual cortical network and adjusted to reproduce the dynamics of experimental VSD signal (Reynaud et al. 2007, 2012). Although the size of the cortical column is limited to approximately one single pixel of optical imaging, it provided us with a detailed reconstruction of the signal and its dynamics. The model suggested that inhibitory cells, spiking activity, and deep layers contributions are playing a small although nonnegligible role in the overall signal (20%), while 60% of the signal comes from the dendritic activity of excitatory neurons in superficial layers [see discussion in Chemla and Chavane (2010a) for explanation on the origin of this nonlinear prediction]. Importantly, we showed that those contributions were dynamically modulated with time and thalamic input strength. However, VSDI studies are done in a variety of experimental and arousal conditions. One concern is therefore that VSD signal origin may not be identical in those studies since different network states could affect the relative contribution of the various components to the VSD signal. Actually, anesthesia seems to affect differently evoked potentials and VSD responses (Devonshire et al. 2010). Hence one may question how much VSD signal is comparable across those studies performed on various arousal states, for instance, in awake (Slovin et al. 2002; Chen et al. 2006; Reynaud et al. 2012) vs. anesthetized (Grinvald et al. 1994; Sharon and Grinvald 2002; Chavane et al. 2011) animals. Lastly, another recent concern is that VSD molecules, in themselves, seems to affect GABA_A receptors, resulting in a potential prolongation of inhibitory postsynaptic current (IPSC) decays by 32 ± 5% (Mennerick et al. 2010). Although this in vitro study has not been replicated in vivo, it is worth considering such an effect on the VSD signal from a theoretical perspective.

In this study we therefore investigated how cortical population dynamics, as measured by VSDI, are affected by differences of network state and VSD-mediated GABA_A receptor modulation. For this purpose, we manipulated a single parameter in our model (see materials and methods), the decay time constant of GABA_A-mediated IPSCs (τ_G), since affected by most anesthetics (see Table 2 and results). Here we reveal that τ_G strongly affects the neuronal response dynamics and contrast response function as would be measured by VSDI. The predictions of our model were confirmed in VSDI experiments made in V1 of five monkeys at different arousal states (see materials and methods). Finally, we show that the VSD-mediated τ_G prolongation suggested by Mennerick et al. (2010) would actually lead to minor changes of the VSD signal, having negligible consequences on the population signal.

Table 2.

Effect of general anesthetics on GABA_A-mediated IPSCs decay time constant and amplitude

Anesthetics	IPSC Decay Time Constant (τG)	IPSC Amplitude	Underlying Mechanisms on GR	References
Isoflurane	++	–	Direct action on postsynaptic GR to block IPSCs but 2 different sites for amplitude and decay mechanisms	Banks and Pearce 1999
Isoflurane	++	++	More channel opening	Hemmings et al. 2005
Isoflurane	+	0	Presynaptic site	Ogawa et al. 2011
Halothane	++	0	Prolong Cl− channel currents via an increase of intracellular calcium	MacIver et al. 1991
Halothane	++	–	Direct action on postsynaptic GR	Banks and Pearce 1999
Halothane	++	–	Reduce the agonist unbinding rate	Li and Pearce 2000
Barbiturates	0	++	Increase probability of long (stable) vs. short openings	MacDonald et al. 1989
Barbiturates	++	0	Prolong Cl− channel currents via direct action on GR	MacIver et al. 1991
Barbiturates	++	++	Direct action on GR	Mathers et al. 2007
Propofol	++	++	Decrease GR desensitization but unknown mechanisms	Orser et al. 1998
Propofol	++	0	Enhance gating of the GR by GABA	Hemmings et al. 2005
Ketamine	0	0	—	Hemmings et al. 2005
Benzodiazepines	++	0	Increase the agonist binding rate	MacDonald et al. 1989
Benzodiazepines	++	++	Reduce the agonist dissociation rate	Mellor and Randall 1997

GR = GABA_A receptors; IPSC, inhibitory postsynaptic current. ++, Prolongation at clinically relevant concentrations; +, prolongation at nonclinically relevant concentrations; –, reduction at clinically relevant concentrations; 0, no changes at clinically relevant concentrations or not mentioned in the literature. The ketamine anesthetic is only informative as it mainly acts through NMDA receptors.

MATERIALS AND METHODS

Biophysical Model Implementation and GABA_A Receptor Modulation

In Chemla and Chavane (2010a), we proposed a detailed biophysical and realistic cortical column model with compartmental neurons, which allows us to compute linearly the VSD signal. More precisely, this column comprised 180 compartments (up to 10) Hodgkin-Huxley neurons (small pyramidal in layer 2/3, spiny stellate in layer 4 and large pyramidal in layer 5 are excitatory and represent 80% of the cells, while inhibitory smooth stellate interneurons in each layer represent the remaining 20%) and has a horizontal area of 50 × 50 μm, corresponding to one pixel of optical imaging. Recurrent connectivity between those neurons was inspired by Binzegger et al. (2004) while lateral interactions were tuned in strength and synapses numbers to fit excitatory and inhibitory distributions, respectively, from Buzás et al. (2001) and Buzás et al. (2006), enabling us to simulate the dynamics induced by a hypercolumn of ∼750 μm. Synaptic background activity similar to in vivo measurements for a large network was introduced in the form of two stochastic ionic conductances (i.e., Ornstein-Uhlenbeck equations) using the model of Destexhe et al. (2001). Finally, thalamic afferent inputs to layer IV cells are simulated using random spike trains whose rate was manipulated (from 0 to 100 Hz) to study the influence of different cortical regimes on the VSD signal. Importantly, individual input-output relationships (F–I curves) of excitatory and inhibitory neurons have been initially fitted to reproduce intracellular recordings from Nowak et al. (2003), and in a second step the recurrent network of neurons has been tuned to reproduce the contrast response function (CRF) of excitatory and inhibitory V1 neurons in vivo (Contreras and Palmer 2003). The resulting biophysical model is thus a balanced local network of excitatory and inhibitory neurons, background activity and horizontal interactions, that behaves realistically in response to different levels of activity (thalamic inputs), both at the single neuron and the global network level (see the schematic representation of the model in Fig. 1).

Fig. 1.

Biophysical model implementation: model representation with recurrent network (red arrows, for clarity only the main connections are represented) connecting 6 populations of neurons (excitatory: pyramidal and spiny stellate cells; and inhibitory: smooth stellate cells) in the 3 main layers of the cortical structure, background activity (green arrows) simulating realistic synaptic bombardment to embed the column into a larger network, lateral connections between neighboring columns (blue dashed arrows), and input signals from the thalamus (large red arrow). The model offers the possibility to compute the voltage-sensitive dye (VSD) signal with a linear formula taking into account the dye concentration (blue gradient), and the membrane potential at each compartment. [Reprinted from Neuroimage, Vol. 53, Chemla and Chavane, “A biophysical cortical column model to study the multi-component origin of the VSDI signal,” Pages 420–438, Copyright (2010), with permission from Elsevier.]

The VSD signal is computed by linearly integrating, for each layer L, the level of depolarization (V) of each compartment (i), membrane surface (S), and staining (λ):

$$\text{VSD}={\displaystyle \sum _L{\text{VSD}}^L}\text{with}{\text{VSD}}^L={\lambda }^L{\displaystyle \sum _i{V}_i{S}_i}$$

This first assumption assumes that the dye, which has a lipophilic and a lipophobic part (Grinvald et al. 1999), stains all membranes independently of the neuron type (Grinvald and Hildesheim 2004), as evidenced from two-photon imaging (Denk et al. 1994; Yuste et al. 1997; Kuhn et al. 2008; Homma et al. 2009) or single photon confocal imaging (Fine et al. 1988; Ferezou et al. 2006). Importantly, dye attenuation (Fig. 1, color gradient) was taken into account to calculate the compartments' contributions across layers (supragranular, granular, and infragranular layers). Note that as we restricted our stimulation duration to a few hundred of milliseconds, the dye signal would be less likely to be contaminated by changes of slow hemodynamic intrinsic signals (see Shoham et al. 1999) that contribute to the fading of the fluorescent signal with cortical depth. Light scattering is another factor but its amplitude is an order of magnitude smaller (see Grinvald et al. 1999). We used the distribution of fluorescence intensity (λ parameter) estimated by Lippert et al. (2007), i.e., λ² = 0.95, λ⁴ = 0.05, and λ⁵ = 0. The model has been implemented using both NEURON (Hines and Carnevale 1997) and neuroConstruct (Gleeson et al. 2007) softwares (see Chemla and Chavane 2010a for more details). We used this cortical column modelization to study the effect of modulating one biophysical parameters on the VSD signal, e.g., τ_G.

Anesthetic-mediated or VSD-mediated modulation of GABA_A receptor kinetics was investigated by manipulating the decay time constant of GABA_A-mediated IPSCs, respectively, either considering that all GABA_A receptors are affected or only receptors of neurons stained by the dye, i.e., neurons in superficial layers. In our model, the synaptic interactions are modeled by using the general equation that describes transmitter-activated ion channels in the Hodgkin-Huxley formalism (Hodgkin and Huxley 1952):

$$I_{\text{syn}}\left(t\right)=g_{\text{syn}}\left(t\right)\left(V-E_{\text{syn}}\right),$$ (1)

where I_syn is the synaptic current, g_syn(t) is a time dependent conductance that will increase at the arrival of a presynaptic spike, V is the postsynaptic membrane potential, and E_syn is the reversal potential of the considered channel. The parameter E_syn and the function g_syn can thus be used to characterize different types of synapses, e.g., AMPA and GABA_A for excitatory and inhibitory synapses respectively in this model.

More particularly, we used the simplified kinetic model of GABA_A synaptic receptors proposed by Destexhe et al. (1998), which uses the following two-states diagram:

$$C+T\underset{\beta }{\overset{\alpha }{\rightleftharpoons }}O,$$ (2)

where C and O represent respectively the closed and open states of the channel, T represents the concentration of neurotransmitter molecules, assuming to be released in a brief pulse at each arrival of a presynaptic spike, and α and β are voltage-independent forward and backward rate constants. If r is defined as the fraction of the receptors in the open state, it is then described by the following first-order kinetic equation:

$$\frac{dr}{dt}=\alpha \left[T\right]\left(1-r\right)-\beta r$$ (3)

The postsynaptic current of GABA_A receptors is given by:

$$I_{{\text{GABA}}_{\text{A}}}=G_{{\text{GABA}}_{\text{A}}}r\left(V-E_{{\text{GABA}}_{\text{A}}}\right),$$ (4)

where G_GABAA is the maximal conductance of Cl⁻ channels and E_GABAA its reversal potential (E_GABAA = E_Cl⁻ = −70 mV). In this framework, τ_G corresponds to the inverse of the parameter β.

Parametric Analysis and Statistical Procedure

For the majority of cortical cells, τ_G falls within a range from 2 to 10 ms (Otis and Mody 1992; Mody et al. 1994; Nusser et al. 2001; Mody and Pearce 2004). Longer τ_G >10 ms can be found but under nonphysiological conditions such as in neuronal cultures (Mennerick et al. 2010; Chisari et al. 2011), in vitro studies at room temperature (Kapur et al. 1997; Sceniak and MacIver 2008), or studies under barbiturates anesthesia (Mathers et al. 2007). More seldom inhibitory postsynaptic currents with decay time constants >20 ms have also been reported for neurogliaform cells that mediate the so-called third form of GABA_A-receptor-mediated inhibition GABA_A,slow (see Capogna and Pearce 2011 for a review on the subject). In this study, we limited the range of τ_G within the physiological values of 2 to 20 ms. Table 1 summarizes this range (τ_G = 1/β), as well as the conditions in which they are found in the literature.

Table 1.

Range of β-values (hence τ_G) used in this study

β, ms−1	τG, ms	Conditions
0.5	2	Physiological (e.g., CTX/HPC pyramidal cells at 37°C)
0.4	2.5
0.2	5
0.1	10
0.05	20	Nonphysiological (room temperature or under barbiturates)	GABAA,slow (e.g., NGFC)
0.02	50–75	HPC neurons in culture (Mennerick et al. 2010)

Row 6 reports the β-value of Mennerick et al. (2010), not tested in this study. CTX, cortex; HPC, hippocampus; NGFC, neurogliaform cell.

To assess differences in VSD signal parameters, before and after changes in τ_G, we ran model simulations in the following: 1) for each trial, the model configuration (including cell positions, network connections, background noise, and thalamic inputs) is generated once and, except for the parameter τ_G, is kept in all other aspects constant; 2) from one trial to the other, the model configuration is recalculated. We then obtained sets of samples (100 trials) on which we can perform two-samples Wilcoxon signed-rank test analyses with P < 0.01 considered significant to compare their means pairwise. To investigate the effect of anesthetic-mediated modulation, we made pairwise comparisons between τ_G = 2 ms and higher values (see range of τ_G values in Table 1). To investigate the effect of VSD-mediated modulation, we made pairwise comparisons between each τ_G and τ_G + 32%. All the following results have been plotted using the statistical software package R (https://www.r-project.org/, 2008) and its wilcox.test function (with argument paired = TRUE). We used a boxplot representation for VSD parameters distribution to graphically visualize the median, the 25 and 75% quartiles, and the minimum and the maximum of the data set. We also superimposed a one-dimensional scatter dot violin-like plot of the data (closely packed, nonoverlapping gray points) to give additional precision of the distribution (see Fig. 2, C–E, Fig. 3A, and Fig. 4, B and C).

Fig. 2.

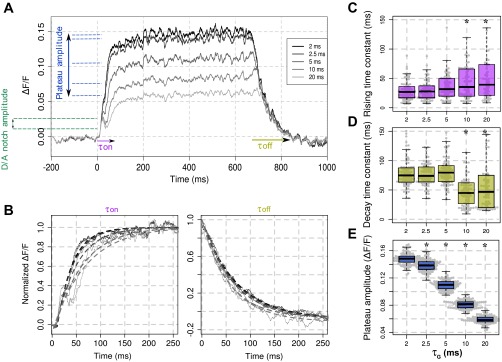
Effects of τ_G modulation on the VSD signal dynamics. A: averaged (100 trials) time course of the modeled VSD signal in response to a 600 ms static Gaussian luminance stimulus (40 impulses/s, stimulus onset at t = 0) for the different values of τ_G (gray scale). B: onset (left) and offset (right) of the modeled VSD responses, after normalization with respect to their maximum. τ_on and τ_off of each VSD trials have been computed using an exponential fitting (dotted lines, see materials and methods, Eq. 5). Box-plot diagrams of the rising time constant parameter τ_on (C); the decay time constant parameter τ_off (D); and the plateau amplitude (E) of the modeled VSD response as a function of τ_G are shown. *Significant differences with the condition τ_G = 2 ms (P < 0.01, see materials and methods).

Fig. 3.

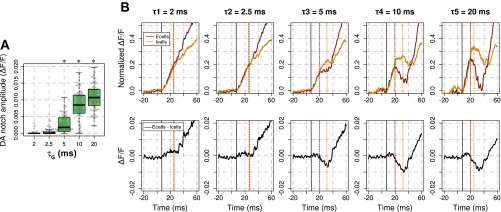
Towards an understanding of the deceleration-acceleration (DA) notch formation. A: box-plot diagram of the DA notch amplitude of the modeled VSD signal plotted in Fig. 2A for the different values of DA. *Significant differences with the condition τ_G = 2 ms (P < 0.01). B: onset of the VSD signal time courses decomposed into excitatory cell activity (Ecells, burgundy lines) and inhibitory cells activity (Icells, orange lines), normalized to the maximum total VSD response, and plotted for 5 τ_G values at top (2, 2.5, 5, 10, and 20 ms). The corresponding time courses of the difference between Ecell and Icell activities are plotted in black at bottom. Corresponding vertical dashed lines indicate times of local maxima computed from response onset marked by the solid black lines.

Fig. 4.

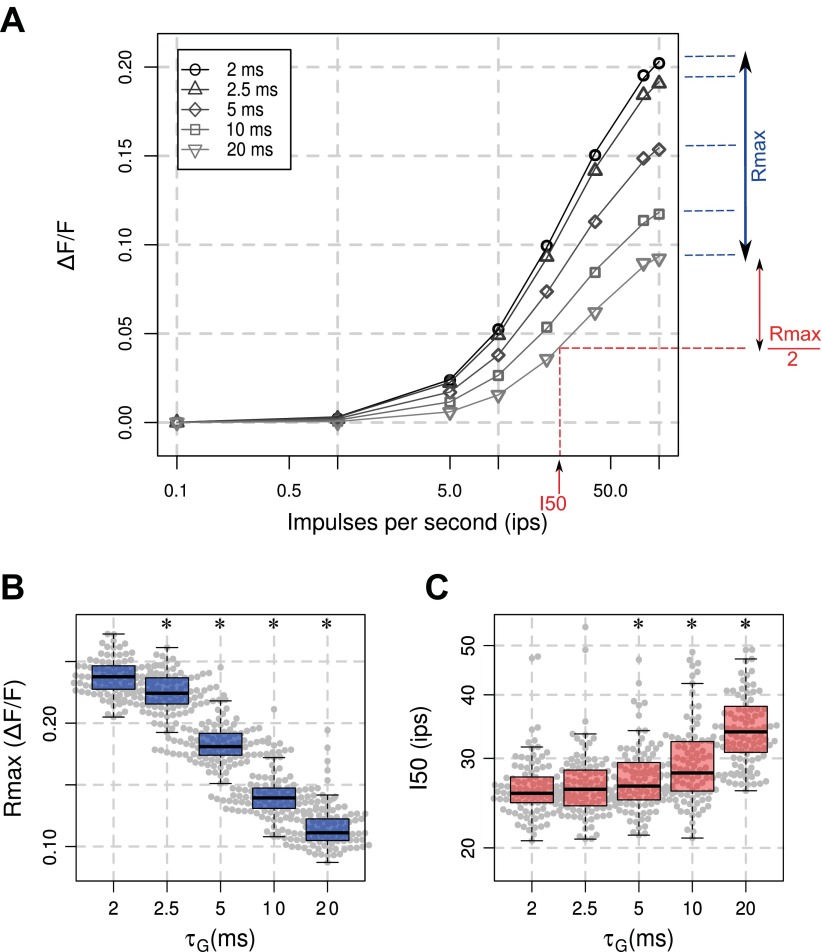
Effects of τ_G modulation on the input response function of the VSD signal. A: the modeled VSD signal, averaged over 600 ms at steady state, is plotted as a function of thalamic input rate, for the 5 considered values of τ_G (gray scale, different markers). Each trace has been fitted with a Naka-Rushton function (see materials and methods, Eq. 6). Box-plot diagrams of R_max (B) and I₅₀ (C) as a function of τ_G are shown. *Significant differences with the condition τ_G = 2 ms (P < 0.01).

Experimental Procedures

The experiments were conducted on five monkeys (3 male Macaca mulatta and 2 female M. fascicularis) in three different protocols: awake (n = 2), anesthetized (n = 2), and awake with two arousal states that serves as his own control (n = 1). Experimental protocols have been approved by the Marseille Ethical Committee in Neuroscience (Approval A10/01/13, Official National Registration 71-French Ministry of Research). All procedures complied with the French and European regulations for animal research, as well as the guidelines from the Society for Neuroscience.

Surgical preparation and VSDI protocol.

All protocols started with head holder and chamber implantation over the right hemisphere. Subsequently the dura-mater of the primary visual cortex (V1) was removed surgically and a silicon-made artificial dura-mater was inserted under aseptic conditions to insure a good preparation and an optimal optical access to the cortex (Arieli et al. 1995). Before recordings, the cortex was stained for 3 h with the VSD RH-1691 (Optical Imaging) prepared in artificial cerebrospinal fluid (aCSF) at a concentration of 0.2 mg/ml and filtered through a 0.2-μm filter. After this staining period, the chamber was rinsed thoroughly with filtered aCSF to wash off any supernatant dye, the artificial dura-mater was inserted back in position, and the chamber was closed with transparent agar and cover glass. Subsequently, optical signals were recorded from a focal plane ≈300 μm below the cortical surface using a Dalstar camera (512 × 512 pixels resolution, frame rate of 110 Hz) driven by the Imager 3001 system (Optical Imaging). Excitation light was provided by a 100-W halogen lamp filtered at 630 nm and fluorescent signals were high-pass filtered at 665 nm. The surgical preparation and VSDI protocol have been described in detail in Reynaud et al. (2012).

Behavioral task in awake and control protocols.

Monkeys (n = 3) were trained to fixate a red target presented in the center of the screen for the entire duration of the trial (799 ms). We monitored the eye positions (sampling rate: 1 kHz, ISCAN ETL-200 Eye Tracking System) using the REX package under the QNX operating system (Hays et al. 1982) and both online behavioral control and image acquisition were heartbeat triggered. A trial was successful when the monkey maintains his gaze on the red target within a window of 2° diameter. As expected from previous studies (e.g., Busettini and Frölich 2014), fixational behaviors were similar in awake vs. drowsy states, presenting similar median distances to the fixation point (0.39 and 0.37°, respectively) and similar median absolute deviation (0.53 and 0.33°, respectively). As a reward, a drop of mashed apple was delivered to the monkey just after the end of the trial. An intertrial interval of 8 s was set for dye bleaching prevention.

Anesthetized protocol.

Monkeys (n = 2) were initially anesthetized with intramuscular ketamine (10 mg/kg), midazolam (0.2 mg/kg), and robinul (0.05 mg/kg). Then, continuous anesthesia was induced with an intravenous propofol bolus (2.5 mg/kg) and maintained with slow intravenous propofol infusion (0.3 mg·kg⁻¹·min⁻¹), while monkeys were artificially ventilated. Eyes were dilated using atropine and contact lenses were placed to prevent drying. During the experimental protocol, physiological parameters, i.e., temperature, heart frequency, concentration of expired carbon dioxide, and oxygen saturation level, were monitored continuously and collected every 30 min. At the end of experimental recordings, the propofol infusion was stopped and the animal recovered in a very short time (15 min on average).

Drowsiness state induction in control protocol.

The drowsy state of the animal (n = 1) was induced by intranasal administration of 0.2 ml midazolam (7-chloro-imidazo, 0.1 mg/kg). Midazolam is a short-acting (short elimination half-life: 2–6 h) hypnotic-sedative drug with anxiolytic and amnestic properties. From the benzodiazepines class of tranquilizer drugs, the pharmacologic effects of midazolam are mediated through a majority of GABA_A receptors (those containing α₁-, α₂-, α₃-, or α₅-subunits, see Sigel 2002 for a review) and as a positive allosteric modulator (i.e., ligand binding to allosteric sites of GABA_A receptors causing increased efficiency of the main site) potentiates the inhibitory effect of the available agonist GABA (see Table 2), thereby leading to a calming and anxiolytic effect. To estimate the cerebrospinal fluid concentration of the injected dose (D_midazolam = 0.9 mg), we proceeded in the following way. We deduced from Walbergh et al. (1991) that ∼15% of midazolam nasal administration is found in the plasma (P_plasma ≈ 0.15). In a second step, the cerebrospinal fluid concentration should be of 30% of the plasma concentration (Henry et al. 1997; Maurer et al. 2005; P_CSF ≈ 0.3). If we assume the same proportion in the monkey, the CSF concentration was estimated with the following formula:

$$\frac{{\mathrm{D}}_{\text{midazolam}}\times {\mathrm{P}}_{\text{plasma}}\times {\mathrm{P}}_{\text{CSF}}}{{\mathrm{M}}_{\text{midazolam}}\times V_{\text{CSF}}}\approx 8\hspace{0.17em}\mu \text{M}$$

where monkey CSF volume V_CSF ≈ 15 ml and midazolam molar mass M_midazolam = 325.78 g/mol.

Visual stimulation.

The visual stimuli consisted of drifting gratings (FS = 3 cpd, FT = 3 Hz) displayed on the screen, either full-field (24°) or locally (1 or 2°) centered on (−1°, −2°) from the center of the fixation. Six different contrast levels (mean luminance set to 15 cd/m and Michelson contrast between 2.5 and 80%) were used for the full-field gratings (6 full-field conditions), while only 80% contrast was used for the two local stimulation conditions (done in the control protocol only). In addition, two blank conditions, i.e., where no visual stimulus was presented on the screen, were presented to the monkey. The stimuli were computed online using VSG2/5 libraries (VSL v8) on Matlab and were displayed on a 22 inch CRT monitor at a resolution of 1,024 × 768 pixels, a refresh rate of 100 Hz and at a viewing distance set to 57 cm.

Data analysis.

Stacks of images were stored on hard-drives for offline analysis with MATLAB R2014a (MathWorks), using the Optimization, Statistics, and Signal Processing Toolboxes. The evoked response to each stimulus was computed in four successive basic steps. First, the recorded value at each pixel was divided by the average value before stimulus onset (“frames 0 division”) to remove slow stimulus-independent fluctuations in illumination and background fluorescence levels. Second, this value was subsequently subtracted by the value obtained for the blank condition (“blank subtraction”) to eliminate most of the noise due to heartbeat and respiration (Shoham et al. 1999). Third, a linear detrending of the time series was applied to remove residual slow drifts induced by dye bleaching (Chen et al. 2008; Meirovithz et al. 2009). Finally, the response is averaged within a region of interest (ROI) in V1 (7,269 pixels equivalent to a region radius of 1.4 mm). The rationale of this average is to increase the signal-to-noise while keeping the dynamics the same. Indeed, we presented full-field stimuli that will generate similar dynamics for all pixels in the ROI. To check for this assumption, we did a correlation analysis between this averaged response and the response of each individual pixel of the ROI and demonstrate that the averaged time course is highly correlated with all pixels (median values of R² from 0.87 to 0.97 for the lowest and the highest contrast condition, respectively). Thus the averaged dynamics is indeed a good physiological measure to be compared with the model's single pixel, better than an experimental single pixel that will be a noisier representative of the same dynamics.

Data Fitting

Rising and decay time constants of the simulated and physiological VSD responses (respectively, Fig. 2, C and D, and Fig. 5, A and B) are quantified using an exponential fitting (Eq. 5), respectively, on the onset and the offset epochs (calculated from the moment the signal starts to, respectively, rise, i.e., time 0 in Fig. 2B, left, and decline, i.e., time 0 in Fig. 2B, right) of the response normalized to its maximum:

$$F_{\text{exp}}\left(t\right)=a+k\left(1-e^{\frac{-\left(t-\text{offset}\right)}{\tau }}\right)\left(t\ge \text{offset}\right)$$ (5)

Fig. 5.

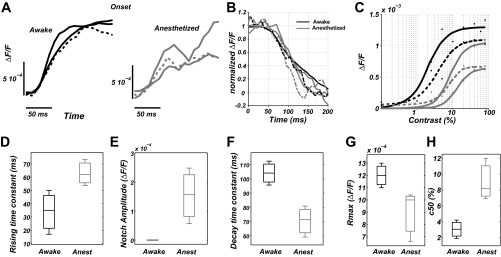
Experimental VSD data. A, left: onset of averaged experimental VSD responses obtained in awake (solid line) and control (dashed line) protocols (3 awake monkeys) in response to full-field drifting gratings at high contrasts. Right: onset of averaged experimental VSD responses obtained in anesthetized (solid line) and control (dashed line) protocols (3 anesthetized monkeys) in response to full-field drifting gratings of high contrasts. B: offset of the averaged experimental VSD responses (2 awake monkeys and 3 anesthetized monkeys). Same color/linestyle code as in A. C: experimental contrast response function for awake (black lines) and anesthetized (gray lines) states. Each trace has been fitted with a Naka-Rushton function (see materials and methods, Eq. 6). Dashed lines correspond to the contrast response function of the same monkey enrolled in the control protocol, i.e., before (black, awake state) and after (gray, drowsy state) midazolam administration. Boxplot diagrams revealing the difference in rising time constant (D); DA notch amplitude (E); decay time constant (F); R_max (G); and C₅₀ (H) between awake (black) and anesthetized (gray) conditions are shown.

where a denotes the offset, k the amplitude, offset the temporal offset, and τ the time constants of the fit.

Note that we also tested two other fitting procedures to check whether the deceleration-acceleration (DA) notch dynamics influence the evaluation of changes in the onset time constants. In the first one, we performed the exponential fit only through the start of the response (not shown), while in the second one we used a linear combination of an exponential and a difference of Gaussian (DoG) functions (see Eq. 6) to separate the DA notch component from the exponential dynamics (data not shown):

$$F\left(t\right)=F_{\text{exp}}\left(t\right)+k{k}_2\left(e^{\frac{-{\left(t-\left(t_{\text{c}}-\frac{{\text{offset}}_2}{2}\right)\right)}^2}{{\sigma }_2}}-e^{{\frac{-(t-{\left(t_{\text{c}}+\frac{{\text{offset}}_2}{2}\right))}^2}{{\sigma }_2}}^{}}\right)$$ (6)

where σ₂ denotes the variance of each Gaussian functions, while k₂ and t_c are respectively the amplitude and the time of the center point of the DoG. Both procedures gave very similar results than the simple exponential fit (comparison of τ_on values when applying, respectively, Eq. 6 vs. Eq. 5: ranging from 30.3 ± 15.7 vs. 28.6 ± 16.2 ms for τ_G = 2 ms to 60.9 ± 35.3 vs. 51.8 ± 40.6 ms for τ_G = 20 ms). Nevertheless, we used the former procedure for computing rising time constants of our experimental data (Fig. 5D) to get rid of variability in the dynamics of the experimental DA notch.

Input response function are fitted to a Naka-Rushton equation (Eq. 7), where R denotes the response of the cell and I the input levels (Fig. 4, B and C). R_max, I₅₀, and n are, respectively, the maximum response rate, the semisaturation input rate, equivalent to the semisaturation contrast C₅₀ of the CRF (Fig. 5H, experimental conditions) and the exponent of the input response function.

$$R\left(I\right)=R_{\max }\frac{I^n}{I_{50}^n+I^n}$$ (7)

RESULTS

Effects of τ_G Modulation on the Cortical Population Dynamics as Measured by the VSD Signal

First we argue that, among many parameters, τ_G is a simple though key parameter to account for the effect of anesthesia. The effect of general anesthetics on the GABA_A receptor has been studied extensively (MacIver et al. 1991; Orser et al. 1998; Banks and Pearce 1999; Li and Pearce 2000; Hemmings et al. 2005; Mathers et al. 2007; Ogawa et al. 2011). Table 2 reports the effect of most general anesthetics used in VSD studies on GABA_A-mediated IPSCs decay time constant and amplitude, as well as the possible underlying mechanism on GABA_A receptors (see Weir 2006 for a review). Most of them enhance GABA_A-mediated inhibition by prolonging τ_G in a dose-dependent manner (Table 2, 2nd column). However, the kinetic mechanisms underlying this common effect remain controversial (see Table 2, 4th column, as an example of several possible mechanisms found in the literature). The modulation of IPSCs amplitude is in contrast less consistent between studies: a modulation has been only reported in about half of the considered studies and the direction of the modulation (increase or decrease) is not clear (Table 2, 3rd column). We therefore only considered the modulation of τ_G as the simplest key parameter to model the effect of anesthetics.

VSD signal dynamics depend on τ_G.

What are the main effects of τ_G modulation on the VSD response dynamics? Figure 2A shows the temporal evolution of the modeled VSD signal for various values of the parameter τ_G from 2 to 20 ms, in response to a 600-ms thalamic input. Note that the fractional signal (ΔF/F) depends on an arbitrary linear transformation from the level of depolarization to the amount of fluorescence (see Chemla and Chavane 2010a for more details). First, we quantified on each trial the modeled response rising and decay time constants, respectively, τ_on and τ_off (see materials and methods, Eq. 5, Fig. 2B). A small but significant increase (Fig. 2C, τ_on) and decrease (Fig. 2D, τ_off) were observed only for values ≥10 ms when compared with the time constants of the VSD response obtained for τ_G = 2 ms (see materials and methods, Wilcoxon signed-rank test with P < 0.01). On the contrary, we observed a strong decrease in plateau amplitude of the VSD response with τ_G (Fig. 2E), the amplitude being significantly smaller for all τ_G values ≥ 2.5 ms when compared with the VSD response amplitude obtained for τ_G = 2 ms (P < 0.01).

Another striking feature of the response dynamics revealed when increasing τ_G by the model in Fig. 2A, dashed green lines, is that the VSD signal shows an early transient deceleration of the VSD signal: the so-called DA notch (Sharon and Grinvald 2002). Our model shows that the notch amplitude increases with τ_G (Fig. 3A), only significantly for τ_G values ≥ 5 ms compared with the notch amplitude obtained for τ_G = 2 ms (P < 0.01). Sharon and Grinvald (2002) hypothesized that the DA notch is related to the transient increase of disynaptic cortical inhibition following excitatory thalamic input. Using our model, we plotted the onset of the decomposed signal time course arising from excitatory and inhibitory neurons when increasing τ_G (see Fig. 3B, top, vertical dashed lines mark local maxima of the responses that have been normalized to the maximum global VSD response), as well as the time course of the difference between excitatory and inhibitory contributions to the VSD signal (Fig. 3B, bottom). We observe different dynamics for excitatory and inhibitory cells activity, respectively, denoted Ecells and Icells in the following. For large value of τ_G, we observe that Ecells start to descelerate and eventually decrease at a time when Icells continues to rise (Ecells reach a local maximum at 17.1 ± 0.49 ms after response onset for τ_G = 5 ms, 14.3 ± 0.13 ms for τ_G = 20 ms and a local minimum at 24.5 ± 0.36 ms for τ_G = 5 ms, 31.3 ± 0.27 ms for τ_G = 20 ms), resulting in a decrease of the net recurrent excitatory activity. This decrease thereafter reduces the drive to inhibitory cells, which themselves reduces consequently. Lastly, Icell activity becomes less prominent (Icells reach a local maximum at 22.8 ± 0.81 ms after response onset for τ_G = 5 ms, 25.5 ± 1.01 ms for τ_G = 10 ms, 19.5 ± 0.15 ms for τ_G = 20 ms and a local minimum at 25.8 ± 1.35 ms after response onset for τ_G = 5 ms, 37.1 ± 1.29 ms for τ_G = 20 ms) allowing Ecell activity to increase again thanks to the constant thalamic input. This phase-shift between Ecells and Icells is well captured by the time course of the difference between excitatory and inhibitory VSD signals (Fig. 3B, bottom), which shows a biphasic behavior, Icell activity becoming strong enough (negative values) to transiently slow down the global (Ecells + Icells) population signal. This general effect is becoming stronger for higher inhibition, hence higher τ_G. This suggests that the DA notch arises from the precise timing of balanced excitation and inhibition, these balanced dynamics being phase shifted by the changes of GABA_A kinetics. Our results therefore predict that this notch should mostly occur in anesthetized preparations (τ_G ≥ 5 ms).

VSD input response function depends on τG.

The above results were obtained at a given thalamic input rate, i.e., 40 impulses/s (ips), but we have shown that the origin of the VSD signal changes with input rate (Chemla and Chavane 2010b). Figure 4A shows the input response function of the VSD signal for eight different thalamic rates (from 0.1 to 100 ips) and for various values of the parameter τ_G. Figure 4 shows a gradual change of the input response function when increasing τ_G. The maximum response rate R_max (Fig. 4B) and the semisaturation input rate I₅₀ (Fig. 4C) were extracted with a Naka-Rushton function (Eq. 6). Naturally, R_max (Fig. 4B) exhibits the same tendency than the plateau amplitude (Fig. 2E, P < 0.01). In the other hand, the significant increase in I₅₀ for τ_G values ≥5 ms (Fig. 4C, P < 0.01) suggests that the operating range of the input response function will shift towards higher input rate when increasing anesthesia level.

Experimental validation of the model predictions.

In summary, our model makes predictions on the dynamics and the contrast response function of the VSD signal following an increase of τ_G, presumably mediated by anesthetics. To test these predictions, we compared the VSD signals measured in monkey V1 in awake and anesthetized conditions, in response to full-field drifting gratings presented at various contrasts (see materials and methods, Fig. 5). Experimental data from five monkeys were pooled: two in awake behaving protocols (Reynaud et al. 2012), two in semichronic anesthetized experiments, and a last monkey that served as his own control since both states were tested on the same session (administration of midazolam, i.e., a positive GABA_A modulator, during a behaving session).

Figure 5, A and B, shows the averaged time course of VSD signals in normal conditions (black) or with a pharmacological agent increasing τ_G (gray), the dashed line corresponding to the same monkey before or after midazolam administration. Our VSD experimental data confirm that anesthesia, most likely through GABA_A receptor potentiation, reduces response amplitude, increases the response time constant τ_on, and decreases the decay time constant τ_off in agreement with the model predictions (Fig. 2). Remarkably, although the DA notch was not detectable in awake conditions for all three monkeys (Fig. 5A, left), inducing anesthesia or a drowsy state (dashed curve) unveiled for all monkeys a clear DA notch (Fig. 5A, right). Note that DA notch was also unveiled by midazolam administration in response to local drifting grating stimulation (not shown).

In four of these monkeys, we also measured the CRF (Fig. 5C) in awake conditions (black) and anesthetized (gray), the dashed line being for the same monkey before (black) and after (gray) midazolam injection. The measured contrast response functions clearly confirmed the model prediction, i.e., a decrease of the amplitude and the contrast sensitivity when the animal is anesthetized (gray curves shift to the right and down, Fig. 5C).

Not only were those predictions confirmed qualitatively but also quantitatively, when applying a direct comparison with the model temporal dynamics. More precisely, in this paragraph, we will compare how much τ_G has to be increased in the model (from reference τ_G = 2 ms) to account for the changes observed experimentally on various parameters of the response dynamic. Physiological VSD dynamics exhibits, respectively, an 85 and a 32% difference in τ_on and τ_off between awake and anesthetized conditions (τ_on: 34 ± 16.5 ms in the awake state vs. 63 ± 9.9 ms in the anesthetized state, Fig. 5D; τ_off: 104.1 ± 8.4 ms in the awake state vs. 70.4 ± 10.9 ms in the anesthetized state, Fig. 5F) consistent with the difference generated by the model when increasing τ_G above 10 ms (τ_on: 81% for τ_G = 20 ms, Fig. 2C; τ_off: 40% for τ_G = 10 ms, Fig. 2D). The amplitude of the DA notch observed only in the anesthetized condition is ∼20% of the VSD signal amplitude (i.e., 1.5 10⁻⁴ ± 9.5 10⁻⁵, Fig. 5E), consistent with the model prediction when increasing τ_G above 10 ms (i.e., τ_G ≥ 10 ms, Fig. 3A). Regarding the contrast response function parameters, Fig. 5G reports a 25% difference in R_max (1.2 10⁻³ ± 1 10⁻⁴ in the awake state vs. 0.9 10⁻³ ± 2.1 10⁻⁴ in the anesthetized state), very similar to the model prediction when increasing τ_G above 5 ms (25% for τ_G = 5 ms, Fig. 4B). Finally, Fig. 5H shows a 196% difference in physiological C₅₀ (3.05 ± 1.15% in the awake state vs. 9.03 ± 2.65% in the anesthetized state), whereas the model predicted an increase of only 40% in I₅₀ when increasing τ_G to the most extreme values (Fig. 4C). Please note that this absolute comparison of visual contrast to the models' thalamic input rate is delicate and not fully relevant. Nonetheless, such difference is reduced if one compare the C₅₀ values in the same animal for two arousal states, revealing a 64% increase between awake and drowsy state of the animal (C₅₀ = 4.2 before vs. 6.9 after midazolam administration, Fig. 5C, dashed lines). This comparison of values between computational predictions and experimental observations suggests that increasing τ_G from 2 to 10 ms in the model is likely to correspond to the awake-anesthetized state change in our experimental conditions. Accordingly, midazolam administration at 8 μM (see materials and methods) should prolong the IPSCs decay time constant by ∼400% (i.e., about the difference between τ_G = 2 ms and τ_G = 10 ms), consistent with what could be extrapolated from a previous study (Verbny et al. 2005).

Quantification of VSD-Mediated GABA_A Receptor Function Potentiation

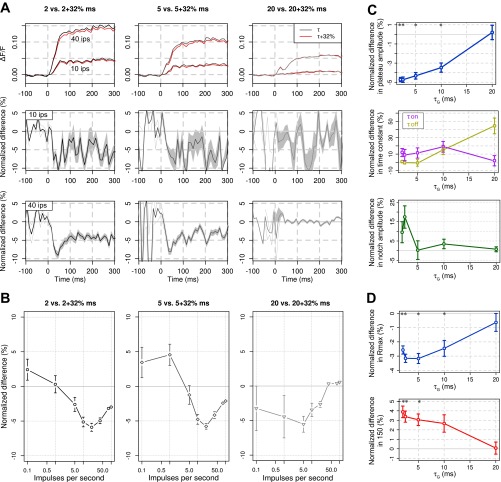
Lastly, we wanted to take advantage of our model to test the impact that the VSD RH1691 can itself have on GABA_A-mediated IPSCs (Mennerick et al. 2010). Indeed, these last authors showed in vitro a prolongation of IPSCs by 32 ± 5% measured in the presence of 0.3 μM RH1691. Whether such effect exists in vivo still need to be confirmed. Furthermore, the effect disappears after washout of the dye, which is the normal imaging condition. However, because of the importance for the interpretation of VSD signals, we wanted to probe what would be the effect of such extreme-worst-case prolongation of the GABA_A-mediated IPSCs on the VSD signal. Figure 6A shows that a 32% modulation of τ_G has actually only a mild global effect [red curves with modulation (f_mod), gray-scale curves without modulation (f)] on the temporal evolution of the VSD signal, tested for different initial values of τ_G (2, 2.5, 5, 10, and 20 ms, top row). To unravel the effect, we computed the normalized difference of amplitude values [Fig. 6A, middle and bottom rows, df = (f_vsd − f)/f]. At low τ_G values, the decrease of signal amplitude by VSD-like modulation of GABA_A receptor is peaking transiently to a value of about 10% of the signal amplitude at 35 ms, converging to a steady-value of 5% at 100 ms after stimulus onset, for both 10 and 40 ips input rate (Fig. 5A, middle and bottom rows). This effect diminishes when increasing the initial τ_G to fully disappear for τ_G values longer than 10 ms (Fig. 6A, bottom row, τ_G = 20 ms). Figure 6B confirms this significant effect for the transient peak amplitudes of the normalized difference observed for values of input rate ≥5 ips (P < 0.01) but also reveals that the effect is maximal for intermediate input rate of 5–20 ips.

Fig. 6.

RH1691 specific effects on the modeled VSD signal. A, top: VSD responses before (gray-scale traces) and after (red traces) a 32% modulation of τ_G (2, 5, and 20 ms are plotted in columns) for 2 thalamic input rates (10 and 40 ips). Corresponding normalized differences [df = (f_mod − f)/f] are plotted at bottom, where shaded gray areas represent means ± SE. B: similarly to the VSD dynamics, normalized differences of the input response function of the VSD signal are computed and plotted here for the three different values of τ_G (2, 5, and 20 ms, gray-scale and markers). C: statistical effect of a 32% prolongation of τ_G on the principal VSD time course characteristics. The normalized differences in plateau amplitude (blue), time constants (τ_on and τ_off, pink and yellow), and notch amplitude (green) are respectively shown in top, middle, and bottom. D: statistical effect of a 32% prolongation of τ_G on the input response function parameters. The normalized differences in R_max (blue) and I₅₀ (red) are, respectively, shown at top and bottom. Error bars are means ± SE. *Significant differences (see materials and methods, P < 0.01).

To gauge the functional impact of the 32% modulation of τ_G, we computed the normalized difference on the different characteristics of the VSD time course (see Fig. 2), and the input response function parameters (see Fig. 4), and assessed the statistical significance of those paired differences (see materials and methods, Wilcoxon signed-rank test with P < 0.01). We conclude that a small (∼3 to 5%) yet significant effect on VSD plateau amplitude (Fig. 6C, top), R_max, and I₅₀ (Fig. 6D) exists for the first three or four initial values of τ_G. This effect decreases to 0% difference for τ_G = 20 ms. On the contrary, the effect on VSD notch amplitude and rising and decay time constants (Fig. 6C, middle and bottom) is not statistically significant for any of the τ_G values [mean differences: 6.28 ± 3.24% (P = 0.38) for the notch amplitude, 10.39 ± 6.24% (P = 0.32) for τ_on, 11.84 ± 4.49% (P = 0.46) for τ_off].

DISCUSSION

The novel finding reported in this paper, using a computational cortical column model, is the provision of a means of investigating the origin of the effect of GABA_A receptor modulation on the cortical population dynamics, as measured by the VSD signal, as well as specifically looking at the RH1691 VSD-mediated effect on the VSD signal dynamics. We show that increasing τ_G decreases plateau amplitude and R_max while it increases I₅₀ and the DA notch. All these predictions were clearly confirmed qualitatively and quantitatively by experimental recordings in the awake state or after injection of an anesthetic to the animal. Our simulations also suggest that the putative RH1691-dependent slow down of GABA_A (Mennerick et al. 2010) would modulate the VSD signal but only by <5%. This latter result was nonetheless important to estimate because RH1691 is one of the most used VSD in vivo for the past 15 yr. If the dye action on GABA_A would have impacted more strongly the population physiological response, this could have had major scientific implications. Therefore, it was very important to quantify how much the VSD-induced GABA_A slow down (Mennerick et al. 2010) could affect the global VSD signal. Our results unveil that the effect is negligible, clarifying this important issue.

Our general approach is based on three assumptions: 1) the anesthesia level affects GABA_A kinetics; 2) enhancing GABA_A synaptic inhibition, i.e., prolonging τ_G, affects the network activity; and 3) the VSD signal is sensitive enough to detect those changes in network activity. We will discuss the relevance of these assumptions below.

The effects of anesthetics on brain activity and their underlying mechanism of action have been of growing interest (Simons et al. 1992; Antkowiak 1999; Heinke and Koelsch 2005; Loepke and Soriano 2008; Alitto et al. 2011; Haider et al. 2013). The anesthesia level affects the inhibitory network in part by prolonging τ_G (Table 2). Our model predicts that this will slow down the rising time constant and fasten the decay time constant of VSD responses. A prediction verified experimentally. This opposite effect may be surprising at first glance but underlies the fact that onset and offset are subtended by different mechanisms, an active recruitment of recurrent networks followed by a relaxation from sustained activity to return to spontaneous state. This is actually reinforced by results obtained by Bair et al. (2002) and Sit et al. (2009), who have also observed, using single-unit activity in anesthetized monkeys and VSDI in awake monkeys respectively, that onset and offset dynamics obey to different rules, the first one depending on stimulus properties and the latter one not. However, the most striking effect we observed when increasing τ_G is a reduction in response amplitude of the global VSD signal confirming several experimental studies using other recordings in V1 of rodents (Vizuete et al. 2012), cats (Ikeda and Wright 1974; Villeneuve and Casanova 2003), and S1 of squirrel monkeys (Chen et al. 2005), with various anesthetic agents (e.g., desflurane, halothane, isoflurane, and urethane) but also in lateral geniculate nucleus neurons of macaque monkeys (Alitto et al. 2011). Therefore, the two first assumptions we made are reasonable. Importantly, this reduction in amplitude with anesthesia was also observed for sensory-evoked VSD responses with anesthesia in the rat barrel cortex (Devonshire et al. 2010), demonstrating that the VSD signal can capture such changes in network activity. Actually there is now a large set of evidence coming from different laboratories and across many experimental conditions that clearly shows that the VSD signal reflects linearly changes of membrane potential (Cohen et al. 1974; Petersen and Sakmann 2001; Petersen et al. 2003; Ferezou et al. 2006) and nonlinearly changes in spiking rate (Arieli et al. 1995; Jancke et al. 2004; Chen et al. 2012) but also with local field potential or EEG (Arieli et al. 1996; Civillico and Contreras 2005) with a high sensitivity. Therefore, our third assumption is also verified.

The second characteristic of the VSD dynamics affected by the anesthesia level is the semisaturation input rate I₅₀ of the input response function, equivalent to the semisaturation contrast C₅₀ of the CRF. Although less abundant, the literature is also consistent with our result. Ikeda and Wright (1974) reported an increase in contrast threshold of neurons in the cat V1 under increasing halothane anesthesia. In the monkey, similar observation can only be done across studies when comparing C₅₀ values from Geisler and Albrecht (1997) (anesthetized, C₅₀ ≈ 43) and from Nassi et al. (2014) (awake, C₅₀ ≈ 28). This effect is specific to the cortex (Alitto et al. 2011). Note that the absolute values of semisaturation constant are different from our experimental values, which is expected since VSD mainly reflects subthreshold activity (Chemla and Chavane 2010).

Another major feature of the VSD response dynamics revealed in this study is the early and transient DA notch. Our simulations suggest that the DA dynamics reflect the transient decorrelation in the time course of excitatory and inhibitory cells activities with increasing anesthetic level (Fig. 3B). The VSD literature on mammals is in line with this prediction since DA notch have been reported in the anesthetized cat (Sharon and Grinvald, 2002; Onat et al. 2011a,b) but never observed in the awake behaving monkey (Slovin et al. 2002; Chen et al. 2006; Meirovithz et al. 2010; Reynaud et al. 2012). This dynamics is consistent with rapid sequences of excitation followed by inhibition classically observed in primary sensory areas, e.g., in visual (Anderson et al. 2000), auditory (Wu et al. 2008), or somatosensory (Wilent and Contreras 2004) cortexes, which are very likely to be involved in rapid processing of cortical responses (Reynaud et al. 2012). Our model acts in a high conductance state (see Chemla and Chavane 2010a, their materials and methods) and supports the existence of a transient shunting mode of inhibition at response onset (Borg-Graham et al. 1998), shaping sensory processing (Monier et al. 2003; Ozeki et al. 2009; Isaacson and Scanziani 2011). This transient increase of inhibition at stimulus onset has also been proposed to reduce trial-to-trial response variability in both anesthetized and awake state (Monier et al. 2003; see Churchland et al. 2010 for a review). Our result suggests that the exact early interplay between excitation and inhibition, a fundamental processing of transient thalamic inputs, is affected by anesthesia and directly reflected in the DA notch characteristic of the VSD signal. The recent paper of Kozyrev et al. (2014) further supported this hypothesis by showing that high-frequency repetitive transcranial magnetic stimulation diminishes the DA notch by weakening intracortical inhibition.

Although in full accordance with the literature, we further tested our model predictions experimentally. Consequently, we have measured V1 response to a contrasted drifting grating in awake and anesthetized monkeys in different animals but also a control on the same animal. In the latter, to closely match to the sole manipulation of the parameter τ_G used in our simulations, we used an anesthetic agent specific for the GABA_A receptor, e.g., midazolam, unlike more general anesthetics classically used in VSDI studies, e.g., isoflurane that also target various other proteins. In the anesthetized protocol, we used an intravenous infusion of propofol, whose main action on GABAergic IPSCs duration has also been reported (see Table 2). Note that testing the general effect of the anesthesia would probably also result in cognitive impairment that is not supposed to affect the very low-level properties and simple behavioral task (fixation) we tested here. The main effects of GABA_A modulation as predicted by our model were all clearly confirmed by experimental data. Importantly, varying the contrast of the visual stimuli now provides preliminary missing data in monkey, directly comparing the effect of anesthetics (e.g., benzodiazepines in this study) on the contrast response function during the same experiment.

In conclusion, this computational study provides a tool to draw more accurate comparisons of VSD signals across arousal states. As any measure of neuronal response, VSD dynamics is strongly affected by anesthetics levels. One specific feature of the VSD signal, the DA notch, could actually be used as a probe to inspect the early desynchronization between excitation and inhibition. Further experiments further scrutinizing this link will be needed. Importantly, our study showed that the effect of the RH1691 dye itself on the functioning of the network is negligible. However, other VSDs, such as the di-4-ANEPPS, might have a stronger impact (Mennerick et al. 2010; see also Grandy et al. 2012). In a next stage, inspecting the impact of excitatory conductances modulations (AMPA, NMDA) may also reveal fundamental aspects of network dynamics (Rangan et al. 2005). This study underlines that care should be taken when comparing functional results acquired across different network states with various techniques. We argue here that realistic biophysical models are an important tool to guide both the interpretation and the relevance of experimental data.

GRANTS

We acknowledge funding from the European Community (FET Grants FACETS FP6-015879 and BrainScaleS FP7-269921) and the ANR BalaV1 (ANR-13-BSV4-0014-02).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

S.C. and F.C. conception and design of research; S.C. and F.C. performed experiments; S.C. analyzed data; S.C. and F.C. interpreted results of experiments; S.C. prepared figures; S.C. drafted manuscript; S.C. and F.C. edited and revised manuscript; S.C. and F.C. approved final version of manuscript.