Predicting binaural responses from monaural responses in the gerbil medial superior olive

We recorded from principal neurons of the gerbil medial superior olive (MSO), measuring how firing rate varied with interaural correlation and interaural time delay (ITD). We also recorded subthreshold monaural responses to wideband tone complexes. Wideband rate-ITD functions were predicted in considerable detail by cross-correlating the monaural responses, suggesting that to explain ITD sensitivity in MSO one need not postulate a major computational role of binaural interaction beyond a simple linear addition of monaural inputs.

Abstract

Accurate sound source localization of low-frequency sounds in the horizontal plane depends critically on the comparison of arrival times at both ears. A specialized brainstem circuit containing the principal neurons of the medial superior olive (MSO) is dedicated to this comparison. MSO neurons are innervated by segregated inputs from both ears. The coincident arrival of excitatory inputs from both ears is thought to trigger action potentials, with differences in internal delays creating a unique sensitivity to interaural time differences (ITDs) for each cell. How the inputs from both ears are integrated by the MSO neurons is still debated. Using juxtacellular recordings, we tested to what extent MSO neurons from anesthetized Mongolian gerbils function as simple cross-correlators of their bilateral inputs. From the measured subthreshold responses to monaural wideband stimuli we predicted the rate-ITD functions obtained from the same MSO neuron, which have a damped oscillatory shape. The rate of the oscillations and the position of the peaks and troughs were accurately predicted. The amplitude ratio between dominant and secondary peaks of the rate-ITD function, captured in the width of its envelope, was not always exactly reproduced. This minor imperfection pointed to the methodological limitation of using a linear representation of the monaural inputs, which disregards any temporal sharpening occurring in the cochlear nucleus. The successful prediction of the major aspects of rate-ITD curves supports a simple scheme in which the ITD sensitivity of MSO neurons is realized by the coincidence detection of excitatory monaural inputs.

NEW & NOTEWORTHY

We recorded from principal neurons of the gerbil medial superior olive (MSO), measuring how firing rate varied with interaural correlation and interaural time delay (ITD). We also recorded subthreshold monaural responses to wideband tone complexes. Wideband rate-ITD functions were predicted in considerable detail by cross-correlating the monaural responses, suggesting that to explain ITD sensitivity in MSO one need not postulate a major computational role of binaural interaction beyond a simple linear addition of monaural inputs.

accurate sound source localization can be essential for survival. The submillisecond differences in arrival time between the ears, the interaural time differences (ITDs), are a dominant cue for localization in the horizontal plane, especially at low frequencies. The medial superior olive (MSO) plays a key role in this process (Brown and May 2005). Two bilateral excitatory and two bilateral inhibitory inputs make up the core afferent circuitry of the MSO. The role of inhibitory inputs, one from the ipsilateral lateral nucleus of the trapezoid body and the other from the contralateral medial nucleus of the trapezoid body neurons, is still debated (Franken et al. 2015; Myoga et al. 2014; Pecka et al. 2008; Roberts et al. 2013; van der Heijden et al. 2013). The excitatory inputs originate from spherical bushy cells in the anteroventral cochlear nuclei on both sides (Thompson and Schofield 2000), and their role in sound localization is understood in greater detail.

It is commonly accepted that MSO neurons act as coincidence detectors of their monaural excitatory inputs (Goldberg and Brown 1969; Yin and Chan 1990). The internal delays of both excitatory inputs give each MSO cell its own “best ITD,” the interaural delay in the stimulus leading to maximal excitation. Although the origin of internal delays is debated, the general features of ITD selectivity in the MSO are in agreement with coincidence detection as proposed by Jeffress (1948), reviewed in Vonderschen and Wagner (2014). The integration of the monaural inputs can be alternatively described by schemes of coincidence detection or cross-correlation, or by linear summation combined with a nonlinear expansive excitability (Colburn et al. 1990; van der Heijden et al. 2013). Such schemes, which produce similar predictions of ITD selectivity, correctly predict the best ITD of MSO neurons from the timing of the excitatory inputs as assessed from the neuron's response to monaural stimuli (Goldberg and Brown 1969; van der Heijden et al. 2013; Yin and Chan 1990). Several studies, however, suggest that such cross-correlation schemes may fail to reproduce other aspects of binaural responses (Batra et al. 1997; Batra and Yin 2004; Franken et al. 2015). All of these earlier tests were performed using tonal stimuli, and although they may provide insight into the underlying mechanisms of ITD tuning, the relevance of tonal responses to everyday sound localization is limited.

In this study we explore whether the prediction of binaural MSO responses from their monaural inputs can be generalized beyond predicting best ITDs for tones. The idea is as follows. If a simple cross-correlation between monaural inputs suffices to accurately predict binaural responses of a more general and common type, there is little need to postulate a major computational role for somatic integration in MSO cells beyond the linear summation of ipsi- and contralateral inputs found by van der Heijden et al. (2013). Such a major computational role has been suggested in previous studies (Agmon-Snir et al. 1998; Brand et al. 2002; Franken et al. 2015; Jercog et al. 2010; Pecka et al. 2008; van der Heijden et al. 2013; Zhou et al. 2005). If, on the other hand, systematic deviations between cross-correlation predictions and actual ITD tuning are observed, these may point to the nature and relevance of possible nonlinear interactions between ipsi- and contralateral inputs. We characterized the ITD selectivity of MSO cells by measuring firing rate in response to wideband stimuli with varying ITD. The resulting wideband rate-ITD functions in MSO have a damped oscillatory shape (Yin and Chan 1990), a pattern resembling the autocorrelation function of band-limited waveforms. Yin and Chan (1990) showed a reasonable similarity between an example wideband rate-ITD curve and the cross-correlogram of spike trains obtained with monaural stimulation, thus providing a first, basic test of the predictability of wideband ITD tuning from monaural data. In this article we report a systematic and extensive test, based on subthreshold monaural responses, which allowed us to use moderate sound intensities and to overcome the limitations of using monaurally evoked action potentials as a proxy for monaural inputs (Batra and Yin 2004). Using the measured responses to monaural wideband stimuli as inputs to a cross-correlation model, we predicted the wideband rate-ITD function, which we then compared with the wideband rate-ITD functions recorded from the same MSO neurons.

MATERIALS AND METHODS

Animal Procedures

All experiments were conducted in accordance with the European Communities Council Directive (86/609/EEC) and were approved by the institutional animal ethics committee. Young-adult female Mongolian gerbils (average body mass 60 g) were anesthetized intraperitoneally with a ketamine-xylazine solution (114 and 17 mg/kg body wt, respectively). Reflexive state was monitored throughout the experiment by performing the hind-paw pinch-reflex test and was maintained by regular administration of ketamine-xylazine solution (one-third of induction dose). Body temperature was maintained at 37°C using an electrical heating pad.

The head was fixed using a metal head plate that was glued to an exposed rostrodorsal part of the skull. Both pinnae were removed, providing access to the ear canal for placing the tubes for delivering sound stimuli. The animal was fixed in a supine position. The skin, connective tissue, salivary glands, and lymph nodes above the trachea were surgically removed, followed by a tracheotomy, after which the animal kept breathing independently. Both bullae were exposed by removing the overlying muscles and making openings in the bone using a scalpel and forceps. The opening of both bullae equalizes the effect on low-frequency middle ear transfer (Ravicz et al. 1992). A 0.7- to 0.9-mm-diameter craniotomy was made on the right side using a drill. The craniotomy was located ∼2 mm rostrally from the stapedial artery and in the middle between the cochlea and medial wall of the skull. When needed the craniotomy was extended by drilling in the vicinity of the first craniotomy. The meninges were left intact. The angle of the electrode insertion point could be changed with the use of a fixed-pivotal-point, custom-built positioning device on which the animal rested throughout the experiment.

In Vivo Juxtacellular Recordings

Recordings were made with thick-walled borosilicate glass microelectrodes having a resistance of 4–7 MΩ when filled with recording solution. Pipettes were filled with solution that contained (in mM) 138 K-gluconate, 8 KCl, 10 Na₂-phosphocreatine, 4 MgATP, 0.3 Na₂GTP, 0.5 EGTA, and 10 mM HEPES (pH 7.2 with KOH). Recordings were made from fewer than 10% of the cells using extracellular solution that contained (in mM) 135 NaCl, 5.4 KCl, 1 MgCl₂, 1.8 CaCl₂, and 5 mM HEPES (pH 7.2 with NaOH). Some of the electrodes had biocytin (0.1%) added to the solution. No specific differences could be found between the responses of cells recorded with either solution, so we pooled them for the analysis.

Pipettes had high positive pressure (∼100 mbar) during brain surface penetration. Immediately after successful penetration of the brain surface, the pressure was lowered to 20–30 mbar and we waited for a few minutes before making a recording to minimize the impact of brain tissue movements relative to the electrode. The location of the MSO somatic layer was identified on the basis of the local field potential (“neurophonics”; Biedenbach and Freeman 1964; Clark and Dunlop 1968; Galambos et al. 1959; Mc Laughlin et al. 2010), as described previously (van der Heijden et al. 2013). Field potentials were evoked using monaural click stimuli (2-ms duration) presented alternately to either ear. Once the somatic layer was reached, the pipette was advanced slowly and its resistance was monitored closely. Contacting a neuron resulted in a gradual increase in resistance, after which we released positive pressure. The electrode was then forwarded up to 10 μm to increase and stabilize seal resistance. Typically, the resistance reached a value of 20–40 MΩ. All the recordings were done in current-clamp mode while the seal resistance was regularly monitored. In case of evident changes in cell response, the recordings were stopped. Data were acquired using a Multiclamp 700B amplifier (Molecular Devices, Foster City, CA) with custom software written in MATLAB (The MathWorks, Natick, MA).

Stimuli

Auditory stimuli were generated using custom software written in MATLAB and realized through a 24-bit digital-to analog channel processor [RX6; Tucker Davis Technologies (TDT), Alachua, FL; 111.6 kHz], programmable attenuator (PA5; TDT), and an amplifier (SA1; TDT). Stimuli were delivered to the ear canals in a close-field fashion through Shure speakers (frequency range 22 Hz to 17.5 kHz) and a pair of small (length ∼11 cm) tubes.

Three types of stimuli were used for this study: irregular tone complexes presented monaurally, irregular tone complexes presented binaurally (noise delay stimulus), and broadband Gaussian noise with varied interaural correlation. The frequency range of all stimulus types was 50-3,000 Hz; the tone complexes consisted of 30 components. The sound pressure level (SPL) range for monaural and ITD delay stimuli was 20–40 dB above hearing threshold. The total SPL of the noise was 15 dB higher than the SPL per tone of the tone complex stimuli in order to achieve the same effective SPL level. Hearing threshold was defined as the lowest SPL of monaural click stimulus to which neurophonics could be evoked.

Monaurally presented stimuli were frozen within recordings from one cell; their 22-s duration and 2,950-Hz bandwidth ensure that the waveforms were representative of the statistical ensemble of these wideband stimuli. The waveforms for all the other stimuli were recomputed for a different instance of their presentation but were kept the same within one instance for all different stimulus conditions and repetitions.

Monaural Stimulation

Monaural responses were evoked using “zwuis,” an irregular tone complex stimulus (see Fig. 2, A and B; van der Heijden and Joris 2003, 2006) with the following properties. Thirty distinct pure tone components with an irregular spacing in the frequency range of 50-3,000 Hz were chosen in such a way that no second-order or third-order distortion products present in the response could have a frequency of any of the stimulus components. Duration of presentation was ∼22 s (including 1 s each for pre- and poststimulus baselines). All stimulus components had the same amplitude and a random phase (van der Heijden and Joris 2006; Versteegh and van der Heijden 2012).

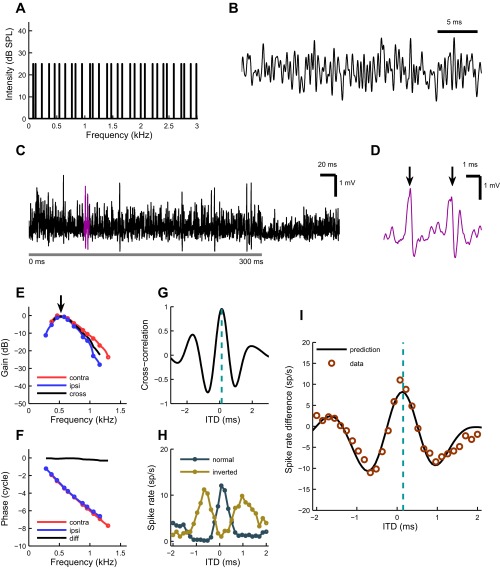
Fig. 2.

Predicting difcor of an MSO neuron. A: power spectrum of irregular tone complex stimulus (“zwuis”). The 30 components have equal magnitudes and span a 3-kHz bandwidth in irregular intervals. B: an excerpt of the zwuis stimulus waveform, the result of mixing the 30 frequency components shown in A. C: a typical MSO neuron response, recorded juxtacellularly, to a noise delay stimulus. Stimulus starts at 0-ms time point (with a 3-ms ramp) and lasts for 300 ms (gray horizontal bar). The highlighted segment is shown separately in D. D: segment from the juxtacellular recording of an MSO neuron shown in C. The 2 largest events are action potentials (arrows) that were identified offline by thresholding the derivative of the response. E: MSO neuron's frequency response to monaural zwuis (tone complex) stimulation. Blue and red colors represent ipsi- and contralateral ear responses, respectively. The circles are data points, and the lines are interpolated values. Best frequencies (BF) of contralateral (0.54 kHz) and ipsilateral ear (0.51 kHz) are indicated with an arrow. The response magnitudes are estimated with respect to the magnitude of the stimulus SPL (30 dB for this cell) and normalized to the dominating monaural response. Black line represents the cross-spectrum of monaural responses (see results). F: phases to which the neuron “locks” monaurally for each frequency component. Color coding is the same as in E. The circles are data points, and the lines are interpolated values. Black line shows the phase difference (contra minus ipsi). G: cross-correlation function (“crosscorr”) of the neuron, showing how ipsilateral and contralateral ear transfer functions correlate linearly. The cyan bar indicates the peak of the function, the expected best ITD (0.13 ms). H: rate-ITD functions. The stimuli presented to both ears had either the same (“normal”; dark blue line) or opposite polarity (“inverted”; dark yellow line). I: comparison of measured and predicted difcor functions. The circles represent a difcor function, which is obtained by subtracting the inverted rate-ITD function from the normal rate-ITD function. The prediction (solid black line) is estimated by scaling the crosscorr in ordinate direction (indirect conversion from cross-correlation to spike rates) to fit the difcor points by least squares. Note that such scaling does not alter the extrema locations of the prediction. Cyan bar indicates the expected best ITD (0.13 ms). The best ITD of the difcor was 0.12 ms. The data variance explained by the model was 91%. All data are from the same cell.

Delay Functions

Rate-ITD functions were obtained by presenting the zwuis stimulus binaurally with a systematically varying time delay between the ears. ITD was varied over a range chosen after evaluation of the frequency response of the neuron: for neurons preferring lower frequencies, wider ranges were applied than for the higher frequency neurons. Stimuli were delayed in equal steps in a random order with 20 repetitions for each condition. Positive ITDs corresponded to the signal leading at the contralateral ear. The duration of a single presentation was 300 ms, followed by a 100-ms silence period, resulting in a total stimulus duration of 170 s.

For a large subset of cells an inverted rate-ITD function was obtained by inverting the polarity of the stimulus in the contralateral ear. To distinguish between the responses to the two stimuli, we call the former “normal rate-ITD function” and the latter “inverted rate-ITD function.”

Difcor.

To emphasize the fine-structure component of the neuron's ITD sensitivity, we plotted difcor function (Joris 2003; Joris et al. 2006) when possible. This was achieved by subtracting responses of inverted rate-ITD function from normal rate-ITD function.

Rate vs. Interaural Correlation Functions

Rate vs. interaural correlation functions were obtained from a binaurally presented broadband Gaussian noise [50- to 3,000-Hz bandwidth, 300-ms burst for each condition, 20 different correlation values (conditions), and 20 repetitions; total duration of stimulus: 162 s]. For a detailed explanation of the method see Louage et al. (2006). Briefly, a single noise token is generated by mixing two independently drawn Gaussian broadband tokens. The same stimulus is always presented at the contralateral side. For the ipsilateral ear, for every new condition, a new noise token is generated by mixing the same two independent tokens, but with varying weighting coefficients. The difference between the coefficients of contralateral and ipsilateral presentation composites determines the normalized correlation between the stimuli and covers the full correlation range from ρ = −1 (anti-correlated) to ρ = 1 (correlated). The correlation stimulus was presented at the best ITD.

Admission/Selection Criteria for the Data

Criteria for a successful MSO juxtacellular recording.

Field-potential reversal is an established method for detecting the MSO somatic layer (Biedenbach and Freeman 1964; Galambos et al. 1959; Mc Laughlin et al. 2010). In all our experiments MSO was approached from the ventrolateral to the dorsomedial direction. During this approach the polarities of the field potentials indicated the location of electrode as follows: 1) the ipsilateral potential was negative, indicating a local sink, and the contralateral potential was positive before reaching the somatic layer; 2) the ipsilateral potential reversed as the electrode entered the somatic layer; 3) while in the somatic layer, the field potentials had the same polarity; and 4) leaving the somatic layer resulted in the reversal of the contralateral field potential. We considered a cell an MSO cell if the field potentials were of the same polarity just before the electrode made contact with the cell. In the same animal it was always verified that further penetration led to a second reversal. For 33 experiments, the electrode penetration track was marked using biocytin, Alcian blue, or DiI at the end of the experiment. All 16 penetrations that could be recovered histologically indicated that electrodes penetrated the somatic layer of the MSO.

Juxtacellular recordings have been shown to be suitable for resolving both sub- and suprathreshold activity of a single MSO unit (van der Heijden et al. 2013). The resistance between the electrode and the cell varied across different cells. Only those recordings for which the initial seal resistance was between 20 and 70 MΩ were accepted as valid juxtacellular recordings.

Baseline-based criteria for recording stability.

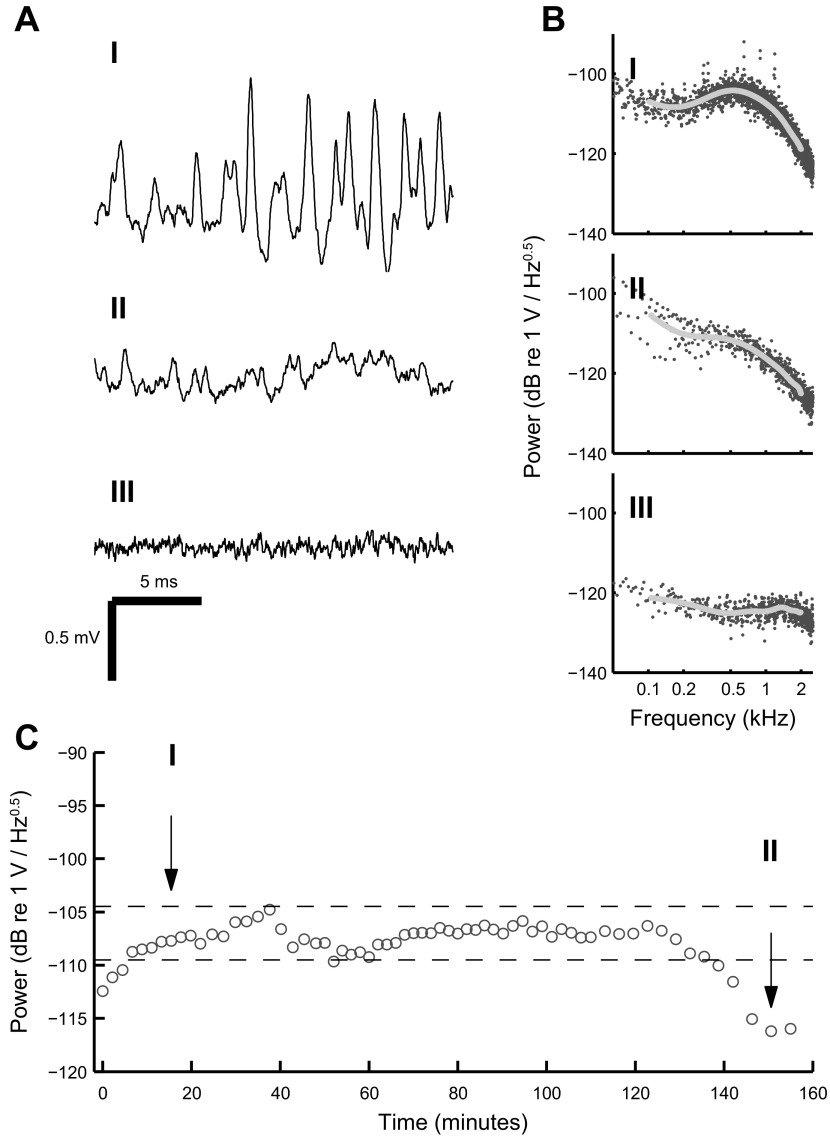
All the stimuli included either 1- or 2-s-duration pre- and poststimulus baselines. We used these baseline periods to evaluate the stability of the recordings over time (Fig. 1). Stable recordings are indispensable when attempting to predict one set of responses from another. A power spectrum was generated for each baseline period of all the recordings. Most neural events are in the millisecond range, resulting in a peak of the power spectrum at around 1 kHz (Fig. 1BI). For all the recordings from a cell we determined the baseline power spectra amplitudes at 1 kHz and then plotted them sequentially (from the first recording till the last). This allowed us to observe whether there were any changes in the recorded spontaneous activity of the cell, which in turn represents the recording stability (Fig. 1C). Recordings were considered stable if during the time course the power spectra amplitudes did not deviate more than 5 dB from an arbitrary threshold, which was different for each cell. The threshold was chosen in such a way that the 5-dB window would include the largest number of sequential recordings from a cell. These recordings were used for further analysis. Field recordings, unsuccessful juxtacellular configuration with a cell and unknown objects that increased electrode resistance but showed no signs of electrophysiological activity, exhibited no peaks in their baseline power spectra (Fig. 1, BII and BIII). These cases were excluded from further analysis.

Fig. 1.

Evaluating recording stability using prestimulus baselines. A: 3 examples of recorded prestimulus baselines illustrating the juxtacellular configuration (I), reduced contact (II), and lack of direct contact (field recording; III). B: power spectra of the waveforms shown in A. Spontaneous MSO activity comes about as a peak at around 0.5 kHz on the power spectrum (I). This peak is not present when either the contact with the cell is poor (II) or the electrode is not in contact with a cell (III). Gray line shows the fit on the power spectrum between 0.1 and 2 kHz. C: changes in the power spectrum value at 1 kHz in the time course of recordings from one MSO cell. The total duration of the electrode contact with the cell was 155 min. Horizontal dashed lines indicate a 5-dB window used as a criteria for recording selection. Arrows with numbers indicate which baselines are shown from the time courses in AI and AII. The measured resistances for configurations I, II, and III were 36, 21 and 7 MΩ, respectively.

Criteria for data quality.

To confirm that recordings were made from ITD-sensitive cells, we performed a single-sided ANOVA test (function “anova1” in MATLAB) for the rate-ITD functions. P < 0.01 was considered statistically significant. Those cells for which the responses had significant differences in their means for different conditions (time delays) were considered binaural, and the data were used for further analysis. These criteria were applied only to difcor data (see below).

To eliminate possible stimulus-independent changes in a cell's response to noise delay stimuli, we set an additional criterion for the difcor functions. After fitting a difcor with a Gabor function (see below), we estimated the ratio between the offset and the amplitude of the envelope and set the threshold for this ratio at 0.2. This binaural consistency criterion selects against cases in which the cell response changed between direct and inverted noise delay stimuli presentations. Some of the cells showed highly reduced ITD sensitivity or changes in the spontaneous firing rates, which will affect difcor. Only difcors for which these ratios were <0.2 were used for further analysis.

For rate vs. interaural correlation functions, we used a “dynamic range” criterion. The dynamic range of a correlation function was defined as the difference between the average spike rates at the three highest stimulus correlation values and the average spike rate for the five correlation values centered around ρ = 0. The rationale behind this criterion was to discern the cells with poor response to the stimulus and exclude them from predictions that were based on the rate vs. interaural correlation functions without excluding the cells that could be envelope sensitive. After comparing the variances accounted for by the power function fit on the data, we determined a reasonable dynamic range threshold to be 5 spikes/s. Rate vs. interaural correlation functions with a dynamic range below 5 spikes/s were considered unreliable for prediction modeling and were not considered further.

Data Analysis

Event detection.

Action potential detection was done offline based on the statistics of the negative peak values in the derivative of recorded waveforms (van der Heijden et al. 2013). Only if the histogram of local minima exhibited a clear bimodality did the separation between the modes define a threshold derivative that could be used to identify the action potentials; if the distribution did not show a clear bimodality, the recording was rejected from further analysis. The characterization of the monaural inputs (which were used to make the binaural predictions) is based on the long-term spectra of subthreshold responses. We therefore also restricted the analysis of binaural responses to the sustained part of the responses, cutting out the first 10 ms of the waveforms obtained with binaural stimulus presentations.

Fitting functions.

Binaural data were fitted using two functions as described below. Such fits allowed us to compare measured data with predictions. Every fit was optimized using the least-squares method (function “lsqcurvefit” in MATLAB), and the variance accounted for was estimated for each instance. A one-dimensional Gabor function (simply referred to as “Gabor function”) has been used previously in fitting binaural models (Leibold and van Hemmen 2005) and data (Franken et al. 2014).

Linear representation of monaural inputs.

Response amplitude and phase were determined by Fourier analysis of the recorded responses to monaural zwuis tone complexes, leading to a representation of the effective monaural input to the neuron that is a linearly filtered version of the stimulus. Statistical significance of each spectral component was tested by a Rayleigh test (P < 0.001) applied to the phase values obtained by segmenting the response waveform into 10 equally long, nonoverlapping segments (Versteegh and van der Heijden 2012). The significant frequency components were plotted as a relative signal gain over the stimulation intensity. The phases of significant components were presented versus the respective stimulus components. Normalized cross-correlation functions were obtained from these monaural transfer functions by computing the normalized cross-spectrum and converting it to the time domain by a Fourier transform. More information about stimulus generation, analysis, and interpretation of results is provided in van der Heijden and Joris (2006) and Versteegh and van der Heijden (2012).

To check the effects of monaurally evoked action potentials on the predictions, we compared predictions from monaural responses with truncated action potentials with predictions from responses with action potentials included. The presence of the relatively small numbers of monaurally evoked action potentials, which contributed at most 0.5%, on average, of the whole response duration, did not affect the cross-spectrum and predictions. The predictions presented in this study were therefore based on the waveforms with the spikes present.

Gabor fit.

Difcor functions were fitted with a Gabor function,

$$G\left(\tau \right)=A+B{e}^{-0.5{\left(\frac{\tau -{\tau }_0}{w}\right)}^2}\cos 2\pi \left(f\tau -{\phi }_0\right),$$ (1)

where τ is time (ms), A is the offset (spikes/s), B is the amplitude (spikes/s), τ₀ is the peak time of the envelope (ms), w is the width of the envelope (ms), f is the frequency (kHz), and φ₀ is the start phase of the cosine (cycle).

Rate-ITD functions were fit with a modified Gabor function with an additional power parameter that allowed us to reshape the Gabor function before fitting it on the data. The modified function (“pGabor”) can be written as

$$G_p\left(\tau \right)=A+Bg(p,e^{-0.5{\left(\frac{\tau -{\tau }_0}{w}\right)}^2}\cos 2\pi \left(f\tau -{\phi }_0\right)),$$ (2)

where g(p, x) = (x + 1)^p/2 and p is the additional parameter, the power of the modifying function. This modification results in an asymmetric envelope of the fit, which more faithfully represents the measured rate-ITD functions with their “rectified” appearance.

Power function fit.

Rate vs. interaural correlation functions were fitted using a generalized version of the power function (Shackleton et al. 2005), where the new addition is the “parabola” component with its weighting factor, C. This function can also be used to fit non-monotonic rate vs. interaural correlation functions that have an envelope or “polarity-tolerant” component (Joris 2003):

$$y\left(x\right)=A+B{\left(\frac{1+x}{2}\right)}^p+C{x}^2,$$ (3)

with A, B, C, and p corresponding to the offset, amplitude, weighting parabola coefficient, and power parameters, respectively.

RESULTS

We presented multitone stimuli to juxtacellularly recorded MSO cells in anesthetized Mongolian gerbils to test to what extent binaural responses could be predicted from monaural responses. The stimuli were presented at 20–40 dB SPL above hearing threshold to ensure that MSO neurons were most sensitive to frequencies close to their characteristic frequency (CF). Best frequencies (BF) were, on average, 0.95 ± 0.32 kHz (mean ± SD; range 0.27–1.35 kHz; n = 60). All MSO neurons in this study are therefore “low-frequency” neurons. The low intensity of stimuli resulted in subthreshold-dominated monaural responses and varying response types upon binaural stimulation. Binaural responses of the neurons were evaluated only on the basis of action potentials. We looked into the extent to which an MSO neuron functions as a cross-correlator of its monaural inputs by cross-correlating its monaural responses and comparing predicted with measured binaural responses. As further detailed in materials and methods, we used two different methods, difcor and rate-ITD (rITD) functions, to predict binaural ITD sensitivity from monaural responses, depending on the available data. Difcor predictions look at the neuron's sensitivity to the fine structure of the stimulus. Rate-ITD functions show a neuron's general ITD sensitivity regardless of which frequencies the neuron responds to. First, we present the method of difcor prediction and its comparison with the data and after that, the data and predictions of rITD functions.

Linearized Rate-ITD Curves

Wideband rITD functions of binaural neurons generally show a mix of sensitivity to stimulus fine structure and envelope, and the two contributions can be largely separated by subtracting and summing the curves obtained with different interaural polarities (Joris 2003). Denoting the regular and polarity inverted versions of the rITD curve as rITD+ and rITD−, respectively, their difference rITD_DIFF isolates the fine-structure component of ITD sensitivity. It is a linearized version of the rITD function in that it asymptotes to zero for large positive and negative ITD values and has a more symmetrical envelope than the raw rITD+ and rITD− (Joris 2003; Joris et al. 2006). In correlograms of monaural responses, the difference correlogram (“difcor”) closely resembles the cross-correlation function of the effective (filtered) waveforms to the two ears (Mc Laughlin et al. 2014), and this resemblance motivated the current approach. We derived the transfer characteristics of the monaural inputs to each MSO neuron from its subthreshold response to monaural tone complexes, computed the cross-correlation function, and compared it with the measured rITD_DIFF data (see materials and methods).

From a total of 87 cells, both normal and inverted rITD functions were obtained, allowing an analysis of the fine-structure, oscillatory component of wideband ITD tuning using rITD_DIFF curves. Of these 87 cells, 62 passed the statistical criteria for binaurality (ANOVA; P < 0.01). Application of the binaural consistency criterion (See materials and methods, Criteria for data quality) led to a collection of 47 cells from 31 animals.

Responses to Monaural Stimulation Can Be Used to Predict Fine-Structure Sensitivity to ITDs

The basis of our model is the responses of MSO cells to monaurally presented tone complexes (zwuis stimulus) presented at 20, 30, or 40 dB SPL per tone. Fourier analysis of the raw waveforms, which were dominated by subthreshold excitatory postsynaptic potentials (EPSPs), yielded a representation of the monaural response characteristics of each ear in terms of linear transfer functions (see materials and methods, Linear representation of monaural inputs).

Figure 2A shows the power spectrum of the zwuis stimulus with 30 equal amplitude components spaced irregularly within a 3-kHz bandwidth. A segment of the zwuis waveform is shown in Fig. 2B. An example of the response of a juxtacellularly recorded MSO neuron to a noise delay stimulus is depicted in Fig. 2C. In this example the stimulus started at the 0-ms time point with a 3-ms ramp and lasted for 300 ms (gray horizontal bar), which was followed by a 100-ms silent period. The highlighted segment of the recording is expanded and shown in Fig. 2D. During stimulus presentation the neuron responded with action potentials (Fig. 2D, arrows). Figure 2E shows the frequency responses (circles) obtained from contralateral (red) and ipsilateral (blue) stimulation for a typical MSO cell. These responses provide a measure for the phase-locked response of the neuron to the 30 stimulus components. The peak response is the BF. For the neuron presented in Fig. 2, the BF of the contralateral ear was 0.51 kHz and that of the ipsilateral ear was 0.53 kHz. The depicted frequency responses can be seen as linear transfer functions from the ear canal to the subthreshold responses of the neuron.

The corresponding phase curves are shown in Fig. 2F. The phase difference (contralateral minus ipsilateral) is plotted as a solid black line. For each monaural response a complex transfer function was calculated. A cross-spectrum was then produced by multiplying the contralateral ear transfer function with a complex conjugate of the ipsilateral ear transfer function (Fig. 2E, solid black line). The inverse Fourier transform of the cross-spectrum yielded the cross-correlation function, or “crosscorr” (Fig. 2G). Such a function represents the normalized correlation between the two linearized monaural responses. The peak of the crosscorr is indicated by the cyan line (0.13 ms).

Normal and inverted rITD functions (Fig. 2H) were measured by varying the ITD of a wideband multitone stimulus. The stimulus of the normal rITD function was identical in the two ears (apart from the ITD); the stimulus for the inverted rITD function was obtained by inverting the stimulus polarity in one ear. Subtraction of the inverted rITD function from the normal one resulted in a difcor function (Fig. 2I, circles). The difcor function reflects the dependence of ITD sensitivity on the fine structure and has a tendency to linearize the dependence on interaural correlation (Joris 2003). Binaural responses were determined using only action potentials. Since there is no direct way to convert cross-correlation values into spike rate differences, we scaled the cross-correlation function by a single factor for optimal overlap with the measured difcor function in the least-squares sense (Fig. 2I, black line). Note that such rescaling does not affect the shape of the function or the location of its extrema. The cyan bar in Fig. 2I indicates a close match to the best ITD of Fig. 2G and to the measured best ITD of this cell, which was 0.12 ms.

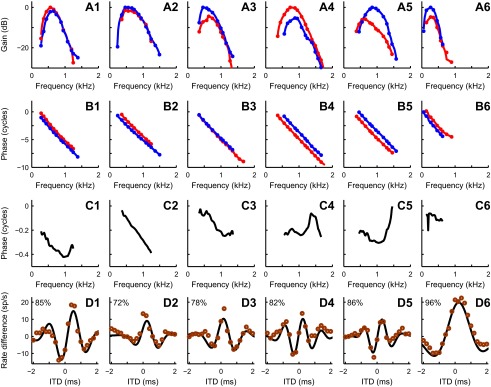
Figure 3 shows monaural and binaural responses with the predictions for six additional MSO neurons (cells 1–6). The color scheme and the methods are the same as in Fig. 2. Monaural response magnitudes (A) and their phases (B) were used to produce a difcor prediction (D, solid line) as described above. The predictions were compared with the measured difcor (D, circles) by estimating the variance of the data accounted for by the model (percentages in D). For these six cells, the variances accounted for ranged from 72% to 96%. Figure 3C shows the phase difference dependence on the frequency. The irregular shapes of many of these curves shows that the relation between the two inputs is not a simple delay, which would yield a straight line through the origin. Similar irregularities were previously found in the MSO of the gerbil (Fig. 10 of Day and Semple 2011; Figs. S4 and S5 of van der Heijden et al. 2013) and in the MSO of the cat (Fig. 10C of Yin and Chan 1990; Figs. 1–4 of Batra et al. 1997). Some of the pairs of magnitude-frequency curves in Fig. 2A show an interaural difference in frequency tuning, again showing that a simple delay is not sufficient to describe the interaural disparity of the inputs. A detailed analysis of asymmetric frequency tuning is beyond the scope of the present study.

Fig. 3.

Examples of difcor predictions for 6 MSO cells. Magnitudes (A) and phases (B) of responses to monaural stimulation are shown together with phase differences (C) and measured difcors (circles, D) and their predictions (solid line; D) for 6 MSO neurons (cells 1–6). Color coding and methods are the same as in Fig. 2. For cells 2–6, the y-axis scaling is the same as for cell 1. The percentage values in D indicate the variance explained by the model on the measured data. Best frequencies for contralateral and ipsilateral ear and best ITDs for each cell, respectively, are as follows: cell 1, 0.54 and 0.61 kHz, 0.47 ms; cell 2, 0.56 and 0.54 kHz, 0.14 ms; cell 3, 0.65 and 0.53 kHz, 0.18 ms; cell 4, 0.80 and 0.84 kHz, 0.21 ms; cell 5, 0.62 and 0.89 kHz, 0.28 ms; cell 6, 0.29 and 0.24 kHz, 0.28 ms.

Fig. 4.

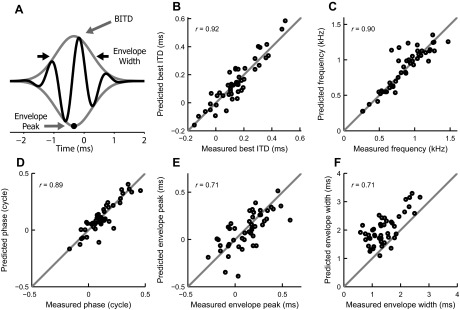
Comparing model and difcor fit parameters on a population level. A: data and models were fit with a Gabor function (black line), which is defined by a phase offset, oscillation frequency, full width at half maximum of the envelope (black arrows), and envelope peak time (black circle). Best ITD is determined by the starting phase and oscillation frequency. Two additional parameters, offset and amplitude (distance between envelope peak and trough), are not indicated because they are not considered in this study. B–F: scatter plots of Gabor fit parameters best ITD (B), frequency (C), starting phase (D), envelope peak time (E), and full width at half maximum of the envelope (F) for difcors and their predictions of the MSO neurons for which difcor predictions were available (n = 47). Gray lines indicate identity. Values in each plot show the Pearson's correlation coefficient r.

For a more exhaustive comparison between predictions and data, we fitted both to a standard Gabor function (Fig. 4A, solid black line) using least squares (see materials and methods). The Gabor function is a sinusoid multiplied by a Gaussian envelope. The binaurally relevant parameters of the Gabor function are the starting phase and oscillation frequency, and the temporal position of the envelope peak and its width. The best ITD can be derived from these four parameters.

Figure 4, B–F, shows correlations between the parameters of fits on data and on predictions: best ITD (B), frequency (C), phase (D), envelope peak time (E), and envelope width (F). DC offset and envelope size are not informative for comparisons between data and model and thus are not included in this study. Pearson's correlation coefficient is indicated at the top left of each plot. Gray lines are the identity lines. Note that the model is systematically predicting a somewhat wider envelope of the response than shown by the data (Fig. 4F). Apparently the central peak of a difcor is higher (relative to the secondary peaks) than what a cross-correlation of monaural inputs would produce (see Fig. 3D1–D4). The other parameters show no obvious biases.

Rate-ITD Function Predictions

From a total of 84 cells for which responses to noise with varied interaural correlation were recorded, 32 (from 24 animals) passed the dynamic range criterion for rate vs. interaural correlation (rIC) functions (see materials and methods, Criteria for data quality). Most cases that did not pass the criterion had low overall spike rates at the moderate intensities used, which did not allow a sufficiently accurate characterization of the rIC functions.

Responses to Monaural Stimulation Can Also Be Used to Predict a Neuron's Rate-ITD Function

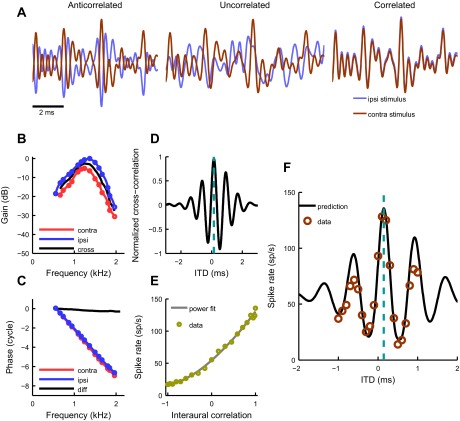
When possible, we recorded the response of MSO neurons to changing interaural correlation using a noise-mixing technique (see materials and methods). The resulting rIC function allowed us to predict the rITD function. An example is shown in Fig. 5. The waveforms presented to the ipsi- and contralateral ear for this stimulus are illustrated in Fig. 5A. The stimulus is anti-correlated when the polarities are opposing (left), uncorrelated when the polarities are unrelated in any systematic way (middle), and correlated when the polarities are identical (right). The small shift between waveforms in the correlated case was imposed intentionally for illustrational purposes to demonstrate that both stimuli are identical. Figure 5, B–D, shows the same information as described for Fig. 2, namely, the monaural frequency (B) and phase (C) responses and the resulting cross-correlation function (D). Figure 5E depicts the measured relationship between the output rate of the neuron and the correlation between left and right ear stimuli; the solid line is a power function fit (see materials and methods). For all the cells the increase in correlation from uncorrelated (ρ = 0) to perfectly correlated (ρ = 1) resulted in an increase in firing rate, and 7 of 32 cells showed higher output rates for anti-correlated stimuli (ρ = −1) than for uncorrelated ones (ρ = 0). Such non-monotonic behavior indicates a polarity-tolerant or envelope component in the response. An example of a polarity-tolerant cell is shown in Fig. 6C4. For 28 rIC functions the power fit p parameter values were 3.1 ± 1.4 (range 1.3–6.9).

Fig. 5.

Predicting binaural responses of an MSO neuron. A: excerpts of stimulus waveforms with varied interaural correlation when the presentations between ipsilateral and contralateral ears are anti-correlated (left), uncorrelated (middle), and correlated (right). The slight mismatch between waveforms in the example of correlated stimuli was imposed only for illustrational purposes. B: frequency response of an MSO neuron to monaural zwuis stimulation. Blue and red circles represent ipsilateral and contralateral ear responses, respectively. Best frequencies of the contralateral and ipsilateral ears were 1.23 kHz and 1.33 kHz, respectively. The response magnitudes are estimated with respect to the magnitude of the stimulus SPL (20 dB for this cell) and normalized to the maximum of the dominating monaural response. Black line represents the cross-spectrum of monaural responses (see results). C: phases to which the neuron “locks” monaurally for each frequency component. Color coding is the same as in B. Black line shows the phase difference (contra minus ipsi). D: a cross-correlation function (“crosscorr”) of the neuron. A crosscorr shows how ipsilateral and contralateral ear transfer functions correlate linearly. The cyan bar indicates the peak of the function (0.15 ms). E: the neuron's response to noise with varying interaural correlation (see materials and methods). Yellow circles are data, and the solid line is a power fit. F: comparison between the measured and predicted ITD rate functions of the neuron. Using the spike rate values for each interaural correlation (E), the cross-correlation function (D) was converted into a rate-ITD function prediction (solid black line). Circles represent measured data; best ITD of the neuron was 0.14 ms. Cyan bar indicates the expected best ITD (0.15 ms). All data are from the same cell.

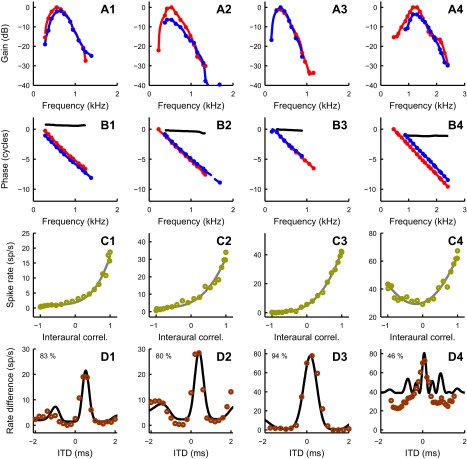
Fig. 6.

Examples of rate-ITD function predictions for 4 MSO cells. For cells 1–4, magnitudes (A) and phases (B) of monaural responses together with interaural correlation sensitivity (C) are used to predict the rate-ITD function (D; solid line) and compare it with the measured one (D; circles) (see Fig. 5 and results for more details). The solid line in C is a power fit function. Color coding is the same as in Fig. 5. The percentage values in D indicate the variance of the measured data explained by the model. Best frequencies for contralateral and ipsilateral ears, best ITD, and power value of power fit (p; see materials and methods) for each cell, respectively, are as follows: cell 1, 0.54 and 0.61 kHz, 0.47 ms, 4.38; cell 2, 0.49 and 0.47 kHz, 0.3 ms, 3.25; cell 3, 0.33 and 0.36 kHz, 0.2 ms, 3.12; cell 4, 1.23 and 1.31 kHz, 0.08 ms, 0.68. Cell 1 is also shown in Fig. 3 as cell 1. Cell 4 is an example of an MSO neuron that is prominently sensitive to the envelope component of the stimulus.

Using the relation between the interaural correlation and output rate (Fig. 5E), we translated the crosscorr function into a predicted (expected) rITD function (Fig. 5F, solid line) and compared it with the measured one (Fig. 5F, circles). For conversion from interaural correlation responses, we used the power fit function. The expected best ITD for the cell was 0.15 ms, whereas the noise delay function peaked at 0.14 ms.

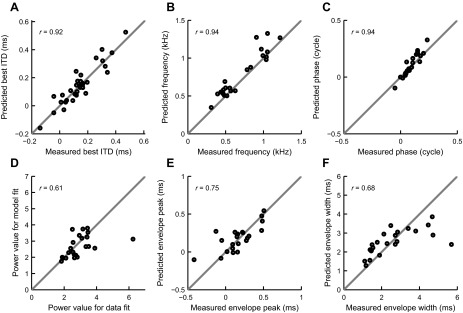
Four additional examples of rate-ITD function predictions are shown in Fig. 6. The color scheme is the same as for Fig. 5. For each of cells 1–4 in Fig. 6, magnitudes (A) and phases (B) of monaural responses are plotted together with rIC functions (C). Figure 6D shows the measured (circles) and predicted (solid line) rate-ITD functions. Values indicate the percentage of the variance of the data accounted for by the prediction, ranging from 46% to 94%. For the assessment of the accuracy of the prediction, we used a modified Gabor function as a fit. Since rITD functions, unlike difcors, do not have comparable sizes of peaks and troughs because the spike rates are only positive, we modified the Gabor function by adding a power parameter, p, analogous to the power value in the functions used for fitting the rIC function data. A value p = 1 corresponds to an “undistorted” Gabor function; increasingly higher values of p correspond to an increasing degree of “rectification” by enhancing the peaks and reducing the troughs. We fitted both the data and predictions with this modified Gabor function. Some of the rITD functions had only one peak (or trough) across the measured ITD range, and fitting of such data with the modified Gabor fit was overdetermined because no envelope could be meaningfully determined. For that reason we excluded 9 cells from the Gabor parameter comparison, but we did include them in the best ITD comparison. Figure 7 compares the parameters of the fits for the data and predictions: the best ITD (A), frequency (B), phase (C), power value (D), envelope peak (E), and envelope width (F). Phases and frequencies once again showed the strongest correlations, whereas the envelope width showed the worst. That is most likely due to the Gabor fit having difficulties in finding the most suitable envelope for rITD functions since they show less oscillatory behavior than difcors; note that the biggest discrepancies arise for the values of the largest envelope widths on the data fits. The largest outlier in Fig. 7D and two largest outliers in Fig. 7, E and F, come from the same pair of cells. The underlying cause of the parameter mismatch for these cells is the discrepancies between locations of secondary peaks in measured and predicted rITD functions. These discrepancies gave rise to Gabor fits with very different envelopes, which resulted in envelope-related parameter mismatch (power, envelope peak, and envelope width). The Pearson's correlation coefficient (r = 0.61) in Fig. 7D is reported with the outlier being excluded. We found that the underestimation of the envelope width (Fig. 7F, rightmost points) happened only for the cells with very low average best frequency (the mean of BF values for contralateral and ipsilateral ears); mean BF for those cells was below 600 Hz.

Fig. 7.

Comparison of model and rate-ITD function fit parameters on a population level. A–F: scatter plots of power-modified Gabor fit parameters (A, best ITD; B, frequency; C, starting phase; D, power; E, envelope peak time; F, full width at half maximum of the envelope) for rate-ITD functions and their predictions of the MSO neurons for which the predictions and fits were available (n = 32 for A, n = 23 for B–F). Gray lines indicate identity. Values in each plot show the Pearson's correlation coefficient r. Correlation coefficient in D is reported with the outlier excluded.

Figures 4B and 7A show the relationships between the measured and predicted best ITDs from difcor (Fig. 4B, n = 43) and rITD functions (Fig. 7A, n = 31). For difcor best-ITDs, the Pearson's correlation coefficient was 0.92, the same as for rITD functions. We estimated absolute mismatches between the predicted and measured best ITDs; on average, they were 43 ± 35 and 50 ± 37 μs for difcor and rITD function predictions, respectively.

DISCUSSION

Summary of Findings

We recorded sub- and suprathreshold responses of MSO neurons to wideband stimuli at moderate levels. The cross-correlation functions of monaural, subthreshold-dominated responses were used to directly predict the binaural rITD_DIFF data (Fig. 2) and the rITD function data by incorporating the nonlinear relation between interaural correlation and firing rate, measured with a mixed-noise technique (Fig. 5). Predicted ITD sensitivity was compared with the measured responses through a standard fitting function. We found that cross-correlation accurately accounted for binaural temporal parameters (phase and frequency) but did less well reproducing the exact envelope of measured ITD sensitivity functions.

Predicting ITD Tuning by the Cross-Correlation of Monaural Inputs

Best ITDs were accurately predicted from cross-correlating subthreshold monaural inputs (Figs. 4B and 7A), in agreement with previous work based on monaurally evoked action potentials (Goldberg and Brown 1969; Moushegian et al. 1975; Spitzer and Semple 1995; Yin and Chan 1990) and subthreshold responses (van der Heijden et al. 2013). Mismatches between predicted and measured best ITDs were not systematic and were generally smaller than 50 μs. Based on physiologically relevant ITD range measurements (Maki and Furukawa 2005), a 50-μs delay at low frequencies translates into sound source angles of 20°–30°, comparable with the minimum resolvable angle in gerbils, which is at least 25° (Carney et al. 2011). Thus our overall prediction accuracy is comparable with the gerbil's behavioral acuity in sound localization.

Our rITD_DIFF functions had a damped oscillatory shape that was well captured by Gabor functions and that resembled rITD_DIFF functions obtained in the inferior colliculus of cats (Mc Laughlin et al. 2008). Oscillation rate, oscillation phase offset, and envelope position of the rITD_DIFF functions were well predicted (Fig. 4, C–E). Envelope width was systematically overestimated (Fig. 4F), corresponding to a slight underestimation of the main peak height in individual cases (Fig. 3). The underestimation may reflect the failure of rITD_DIFF functions to fully linearize the relation between stimulus correlation and spike rate. When this relation is highly supralinear (power ≫2), the subtraction of normal and polarity-inverted curves will flatten but not fully straighten it. Such higher p values were regularly encountered in the present study (see results), and the range of p values was similar to that found in the IC of the guinea pig (Shackleton et al. 2005) and cat (Mc Laughlin et al. 2014). Another related factor that has likely contributed to the underestimation of the central peak is the sharpening of phase locking in the cochlear nucleus compared with the auditory nerve (AN). Cross-correlation functions of the effective stimuli produce accurate predictions of linearized correlograms (difcors) in the AN but are often too symmetric to match well the difcors from bushy cells with their sharp central peak (Joris et al. 2006; Louage et al. 2005). Figure 9C of Louage et al. (2005) shows the sharpness of the central peaks that cannot be matched by Gabor functions (compare our Fig. 3). Thus the mismatches in Fig. 3D, rather than undermining the adequacy of coincidence detection to characterize MSO responses, reveal the limitations of modeling monaural inputs by a linearly filtered version of the acoustic stimulus. Overcoming this limitation would require an event-based analysis in which the cross-correlation functions are replaced by correlograms, but this is beyond the scope of the current study.

The raw wideband rITD functions (Figs. 5 and 6) had a damped oscillatory shape similar to that of the rITD_DIFF functions, but in addition showed a substantial degree of “rectification”: a selective enhancement of peaks and flattening of troughs. They strongly resemble wideband rITD functions in cat MSO (Yin and Chan 1990). Comparison of modified Gabor fits with a power parameter that captured the amount of nonlinearity (Fig. 7) revealed that the monaural predictions accounted well for the starting phase and oscillation rate (Fig. 7, B and C) but did less well predicting the envelope characteristics (Fig. 7, D–F) The poorer match of the envelope parameters may originate in part from using more fit parameters and the risk of “overfitting” the data; in particular, envelope width (Fig. 7F) and power value (Fig. 7D) likely interact, because they both control peakedness. This trade-off may account for the spread in Fig. 7, D–F. Interestingly, the systematic underestimation in peakedness in the rITD_DIFF predictions (Figs. 3C and 4F) did not reoccur in the predictions of the raw rITD functions, indicating that our use of rIC functions (Fig. 6C) adequately captured the nonlinearities that had limited the rITD_DIFF predictions. This finding is the physiological counterpart of the successful use of interaural correlation in modeling a large body of psychophysical data (Colburn 1996; Sayers and Cherry 1957).

Lack of Evidence for Asymmetries in Processing Binaural Inputs

The main aim of our study was to test to what extent binaural responses could be predicted from monaural responses. The monaural responses are dominated by fast fluctuations, which are the EPSPs, but additionally, inhibitory postsynaptic potentials (IPSPs) are present, as well (Franken et al. 2015; Grothe and Sanes 1994; Roberts et al. 2013, 2014). These monaural synaptic inputs are modified as they interact with voltage-dependent ion channels (Franken et al. 2015; Khurana et al. 2011; Mathews et al. 2010; Scott et al. 2010). Even though our somatic recordings do not allow us to further dissect the monaural signals, the possibility to control the ipsi- and contralateral inputs separately, in combination with the anatomical segregation of the excitatory inputs, provides a unique opportunity to study the somatic integration of these monaural inputs. Brand et al. (2002) observed a broadening of the window for ITD detection and a shift of best ITDs toward 0 μs in the presence of the glycine receptor antagonist strychnine. They proposed a model in which contralateral IPSPs affected the early phase of ipsilateral EPSPs more than their late phase. Subsequent modeling and experimental studies showed that to create the differential impact on early and late phases of the EPSP, fast kinetics and/or high conductance was needed for the glycinergic inputs, and it is still debated to what extent these requirements match the physiological characteristics of these inputs (Leibold 2010; Myoga et al. 2014; Roberts et al. 2014; Zhou et al. 2005). Recently, Franken et al. (2015) presented evidence suggesting that the strychnine-induced shift originally observed by Brand et al. (2002) and Pecka et al. (2008) was caused by an off-target effect on I_h channels. The present experiments also do not support this well-timed inhibition theory, since we did not find evidence for the predicted differential filtering of ipsi- and contralateral inputs during their interaction. Our ability to predict binaural responses from monaural responses argues against strong shifts resulting from nonlinear interactions between ipsi- and contralateral inputs. The successful prediction of entire rITD functions confirms and strengthens previous evidence in favor of coincidence detection as the basic mechanism of ITD tuning (Goldberg and Brown 1969; Yin and Chan 1990), as originally proposed by Jeffress (1948), even though this apparently simple scheme may involve complex interactions between I_h, Kv1, and Na channels and both excitatory and inhibitory conductances (Khurana et al. 2011; Roberts et al. 2014; Scott et al. 2010), and we cannot exclude the possibility that some of the small deviations we found in our predictions are caused by these interactions (Franken et al. 2015). Similarly, in vivo recordings did not yield evidence for asymmetries in the rising phase of EPSPs from either side (Franken et al. 2015; van der Heijden et al. 2013). Asymmetries in the origin of the axon, as proposed by Zhou et al. (2005), seem not to be borne out by the typically somatic axonal origin in most MSO neurons (Kuwabara and Zook 1999; Rautenberg et al. 2009; Scott et al. 2005, 2007). Franken et al. (2015) found evidence for systematic shifts in ITD in some gerbil MSO neurons when cross-correlating monaural EPSP period histograms, showing that their ITD tuning often deviated from instantaneous coincidence detection. A direct comparison with their results is not easy, since they used high-intensity binaural beats at frequencies typically much below CF, whereas we used broadband stimuli at intensities not far above the absolute hearing threshold.

Comparison to Avian ITD Tuning

In overall methodology the present study resembles those of Fischer et al. (2008, 2011) in the nucleus laminaris of the barn owl. Both studies used juxtacellular recordings to obtain a linear representation of monaural inputs, which in turn led to predictions of ITD tuning. The major common finding between the avian studies and our study is the successful prediction of ITD tuning from cross-correlating the monaural responses, indicating that nonlinear binaural interactions are unlikely to make a strong contribution to their ITD tuning. The major difference is the adequacy of a linear representation of the monaural inputs. The avian rITD functions are symmetric and lack the strong rectification and dominance of a central peak that characterizes the mammalian rITD functions. The comparatively linear character of the avian system may reflect both physiological and anatomical aspects (Macleod and Carr 2011. The high CFs of the avian AN fibers in the barn owl (up to 8 kHz) tend to linearize the neural representation of the acoustic of individual inputs, resulting in cycle histograms of high-CF avian AN fibers that are sinusoidal, i.e., faithfully reflect the stimulus waveform (Köppl 1997), and a similar faithfulness is preserved in the nucleus laminaris (Funabiki et al. 2011). In contrast, the lower CF mammalian cycle histograms are strongly peaked in the AN and become further sharpened at the level of the cochlear nucleus (Joris et al. 1994). The sharpening and rectification is clearly visible in the periodograms of monaural MSO responses in van der Heijden et al. (2013). In the avian system the large number of monaural inputs to each nucleus laminaris neuron is likely to further linearize the neural representation of the monaural waveforms, particularly if the timing differs somewhat among individual inputs (Macleod and Carr 2011). In contrast, mammalian MSO neurons have a comparatively small number of monaural inputs (Couchman et al. 2010).

Conclusion

In sum, not only the best ITDs but the entire ITD tuning of MSO neurons in response to wideband sounds are well predicted by a straightforward cross-correlation of monaural responses. This supports the Jeffress (1948) hypothesis that ITD sensitivity is realized by a simple coincidence detection of monaural inputs. The imperfections in the predictions most likely mainly originate from modeling the monaural inputs by the bandpass-filtered acoustic waveform: unlike the avian system, where the inputs carry a faithful representation of the (bandpass filtered) acoustic waveform, monaural inputs to MSO show strong nonlinear distortion in the form of rectification and temporal sharpening. We conclude that an improved understanding of the major aspects of ITD tuning (temporal acuity, range of best ITDs, etc.) should not be primarily sought in the details of processing by MSO neurons themselves but in a better characterization of the monaural inputs and their convergence onto MSO.

GRANTS

This work was supported by the Dutch Fund for Economic Structure Reinforcement (FES 0908 “NeuroBasic PharmaPhenomics Project”).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.P. performed experiments; A.P., J.G.G.B., and M.v.d.H. analyzed data; A.P., J.G.G.B., and M.v.d.H. interpreted results of experiments; A.P. prepared figures; A.P., J.G.G.B., and M.v.d.H. drafted manuscript; A.P., J.G.G.B., and M.v.d.H. approved final version of manuscript; J.G.G.B. and M.v.d.H. conception and design of research; J.G.G.B. and M.v.d.H. edited and revised manuscript.