Distinct α- and β-band rhythms over rat somatosensory cortex with similar properties as in humans

Abstract

We demonstrate distinct α- (7–14 Hz) and β-band (15–30 Hz) rhythms in rat somatosensory cortex in vivo using epidural electrocorticography recordings. Moreover, we show in rats that a genuine β-rhythm coexists alongside β-activity that reflects the second harmonic of the arch-shaped somatosensory α-rhythm. This demonstration of a genuine somatosensory β-rhythm depends on a novel quantification of neuronal oscillations that is based on their rhythmic nature: lagged coherence. Using lagged coherence, we provide two lines of evidence that this somatosensory β-rhythm is distinct from the second harmonic of the arch-shaped α-rhythm. The first is based on the rhythms' spatial properties: the α- and β-rhythms are demonstrated to have significantly different topographies. The second is based on the rhythms' temporal properties: the lagged phase-phase coupling between the α- and β-rhythms is demonstrated to be significantly less than would be expected if both reflected a single underlying nonsinusoidal rhythm. Finally, we demonstrate that 1) the lagged coherence spectrum is consistent between signals from rat and human somatosensory cortex; and 2) a tactile stimulus has the same effect on the somatosensory α- and β-rhythms in both rats and humans, namely suppressing them. Thus we not only provide evidence for the existence of genuine α- and β-rhythms in rat somatosensory cortex, but also for their homology to the primate sensorimotor α- and β-rhythms.

several rhythms have been observed in the mammalian sensorimotor cortex, of which the α- (7–14 Hz) and the β-band (15–30 Hz) rhythms are the best documented (Crone et al. 1998; Jasper and Andrews 1938). The sensorimotor α-rhythm has been reported in a whole range of species, from small rodents to primates and is thought to be related to the excitability of the somatosensory cortex (Anderson and Ding 2011; Semba et al. 1980; Sobolewski et al. 2011). The sensorimotor β-rhythm has been reported almost exclusively in primates, and there is good evidence that it plays a role in motor functions (for an overview, see Kilavik et al. 2013; Pavlidou et al. 2014). In contrast to a pure motor function, intracranial studies have demonstrated coherent β-rhythms over both motor and somatosensory cortex (Brovelli et al. 2004; Szurhaj et al. 2003; Witham and Baker, 2007). This widespread sensorimotor β-rhythm has recently been shown to be modulated independently of motor functions in a top-down somatosensory attention task (van Ede et al. 2014a). This strongly suggests that it also plays a role in somatosensory processing.

In contrast to the intracranial studies, which argue for coherent β-rhythms over both motor and somatosensory cortex, source localization studies using the magnetoencephalogram (MEG) have provided mixed results. In one series of studies, the focus was on the late event-related desynchronization (ERD) after movement, and it was concluded that the sensorimotor β-rhythm is produced by the precentral motor cortex, whereas the sensorimotor α-rhythm originates from the postcentral somatosensory cortex (Hari and Salmelin 1997; Salmelin and Hari 1994; Salmelin et al. 1995). In other studies, focused on spontaneous activity and early ERD, it was concluded that the postcentral somatosensory cortex also generates a β-rhythm (Gaetz and Cheyne 2006; Jones et al. 2009). In the study by Jones et al. (2009), the conclusion was supported by simulations of a neuroanatomically and biophysically realistic computational model of somatosensory cortex. Surprisingly, this model was able to generate a β-rhythm as a result of near-synchronous α-band input signals to layer 4 and layer 2/3 neurons (corresponding to, respectively, feedforward and feedback input).

In rodents, there have been numerous reports of a sensorimotor α-rhythm (Nicolelis et al. 1995; Semba et al. 1980; Sobolewski et al. 2011; Vanderwolf 1975; Wiest and Nicolelis 2003). In contrast, sensorimotor β-rhythms in rodents have only been reported in two contexts: in vitro under appropriate neurochemical stimulation conditions (Kramer et al. 2008; Roopun et al. 2006), and in vivo within a motor circuit involving the basal ganglia and primary motor cortex (Leventhal et al. 2012). The β-rhythm has not been reported in the rodent somatosensory cortex in vivo, and this is surprising given the popularity of this model system.

There are at least three possible reasons for this. First, compared with the sensorimotor α-rhythm, the sensorimotor β-rhythm has much smaller amplitude and possibly also a smaller degree of phase preservation. As a result, the β-peak in the power spectrum will be much less pronounced. Second, a β-peak in the power spectrum may have been occluded by (or interpreted as) the second harmonic (Oppenheim et al. 1989) of the sensorimotor α-rhythm, whose arch-shaped waveform is well documented (Gastaut et al. 1952; Kaplan 1979). Third, in rodents, the β-rhythm may be absent over somatosensory regions and may instead arise from motor cortex only. However, as also alluded to above, several studies in human and nonhuman primates have previously demonstrated that the β-rhythm is also prominent in somatosensory areas (Brovelli et al. 2004; van Ede et al. 2014a; Witham and Baker 2007), and it is thus well conceivable that this is also the case in rodents.

In this paper, using epidural electrocorticography (ECoG) recordings, our objective is to rule out the third alternative by demonstrating somatosensory β-rhythms in rats in vivo. More specifically, our objective is to demonstrate the existence of a genuine β-rhythm that coexists alongside the β-activity that is thought to reflect the second harmonic of the arch-shaped somatosensory α-rhythm. To demonstrate this, we use a novel quantification of rhythmicity, called lagged coherence (Fransen et al. 2015). Compared with power, lagged coherence does not depend on waveform amplitude, but only on the degree to which the phase of band-limited neural activity is preserved over time. In humans, we previously demonstrated that lagged coherence is better suited to identify and isolate the somatosensory α- and β-rhythms than Fourier power (Fransen et al. 2015). To demonstrate somatosensory β-rhythms in rats, first we compare the power and lagged coherence spectra over rat somatosensory cortex. Next, we confirm the arch-shaped waveform of the somatosensory α-rhythm and evaluate to what extent the resulting phase-amplitude coupling (PAC) between α- and β-band activity can explain the amplitude fluctuations and phase of β-band activity. Last, we evaluate whether both α- and β-band rhythms are generated by a common source. For this we make use of two lines of evidence: one based on the topography of the rhythms, and one based on lagged phase-phase coupling.

If there is a functional homology between the somatosensory rhythms in human and rats, this homology predicts that rat somatosensory cortex must also generate β-band rhythms. After we demonstrate this to be the case, we provide some additional evidence for the homology of the sensorimotor α- and β-rhythms over somatosensory cortex in rodents and primates using the data of a tactile stimulation experiment. We demonstrate that both rhythms are modulated by a tactile stimulus in the same way in rats as in humans: following the tactile stimulus, the amplitudes of both rhythms are suppressed with a comparable time course in both species.

MATERIALS AND METHODS

Animals

Data were collected in 10 male adult Long-Evans rats that were on a reversed day-night schedule. Access to food and water was ad libitum. All procedures were in accordance with international, national and institutional ethical guidelines for animal experiments and were approved by the Animal Ethical Committee of the Radboud University Nijmegen. Of these 10 animals, 3 did not have α- or β-band peaks in either the power or the lagged coherence spectra of their neurophysiological data. As our interest is in characterizing these α- and β-band rhythms over somatosensory cortex, these three animals were excluded from all analyses described below.

Data Acquisition

High-density micro-ECoG arrays were implanted on the dura over the somatosensory cortex. In animals 1–5, the polyimide electrode arrays were implanted over the left somatosensory cortex and contained 32 disk-shaped electrodes with a diameter of 480 μm and an interelectrode distance of 1,000 μm (center-to-center). In animals 6–10 the polyimide electrode arrays were implanted over the right somatosensory cortex and contained 78 disk-shaped electrodes with a diameter of 100 μm and an interelectrode distance of 610 μm. The ECoG arrays were slid in place via a trepanation hole in the skull on top of the head, which was sealed after surgery to allow for chronic recordings in freely moving animals. To confirm their location and orientation, the electrode arrays were coregistered postmortem to the anatomical and functional regions of the brain in five animals. The electrode arrays, their implantation and the procedure of their coregistration to functional brain areas are described in detail in Dimitriadis et al. (2014a, 2014b).

Electrophysiological data were recorded using a Digital Lynx acquisition system (Neuralynx) at a sample frequency that differed across animals, but was at least 2,959 Hz. All recorded potentials were referenced to an electrode over trunk or hindlimb sensorimotor cortex. During recordings, animals were placed in a light- and sound-proofed chamber and monitored using an infrared camera. Recordings started after the animal ceased explorations and grooming, which normally took about 15 min. Using video recordings, we confirmed in five animals that they spent most (i.e., 80–95%) of the recorded time in quiet wakefulness.

Epochs of ongoing activity.

In all animals, we collected ongoing neuronal activity that we partitioned into epochs of 2 s. When the data were collected in sessions during which tactile stimuli were presented, we only used epochs that did not contain any stimuli in the 1.9 s before the beginning of the epoch, nor during the epoch itself. Approximately 1,300 ± 350 epochs were collected per animal.

Epochs containing tactile stimulation.

To compare the stimulus-induced modulations of the sensorimotor rhythms between rats and humans, we collected data from both species. For the rat data, we recorded the ECoG in six of the rats while they were presented with brief tactile stimuli. We selected 2-s epochs that were centered on stimulus onset and in which no additional stimuli were presented in the 1.9 s before stimulation, nor during the epoch itself. For each animal, we collected between 1,349 and 5,942 such epochs.

Human Data

To evaluate the homology between rodents and humans of the event-related desynchronization in the α- and the β-band, we reused data from the 20 human participants who participated in the study described in van Ede et al. (2011). In this study, we recorded the MEG using a system with 275 axial gradiometers (CTF MEG; MISL, Coquitlam, British Columbia, Canada), which was housed in a magnetically shielded room. For each subject, we selected 438 ± 49 (mean ± SE across participants) epochs in which a brief tactile stimulus was presented to all fingers of either the left or the right hand. Epochs lasted 2 s and were centered on stimulus onset. No additional stimuli were presented in the 1.9 s before stimulation, nor during the epoch itself.

Tactile Stimulation Protocols and Apparatus

In rat.

Six of our ten rats were presented with tactile stimuli on the whisker pad contralateral to the implanted ECoG array. These stimuli were presented using a head-mounted stimulator identical or highly similar to the one described in Dimitriadis et al. (2014a). Tactile stimuli were produced by protracting a plastic pin onto the whisker pad and retracting it after 0.020 s (20 ms). Stimuli were presented at semirandomized interstimulus intervals ranging from 1 to 10 s. Animals were habituated to the stimulator and stimuli in the week prior to the recording sessions. Stimuli were collected over several weeks in multiple recording sessions that lasted about 1 h each. The animals were not involved in any task.

In human.

Tactile stimuli were produced by piezoelectric Braille cells (Metec, Stuttgart, Germany). A single Braille cell consisted of four pairs of pins that can be protracted and retracted. Five such cells were built into a graspable device (see van Ede et al. 2011), one for each finger. Both the left and the right hand were placed on one such graspable stimulation device. Tactile stimuli were produced by protracting all pins and retracting them back into the cells after 0.020 s, rendering the subjective experience of a tap on all finger tips of a single hand. The stimuli were presented equally often to the left and the right hand, at 2-s interepoch intervals. These stimuli were part of a localizer that occurred in between task-blocks, and participants did not need to do anything with them.

Data Preprocessing

Data were analyzed using FieldTrip (Oostenveld et al. 2011), an open-source MATLAB toolbox developed at the Donders Institute for Brain, Cognition and Behaviour (Nijmegen, The Netherlands), together with custom-written code. Malfunctioning ECoG electrodes were identified during impedance recordings and removed from the data (see Table 1). For the 2-s epochs from all three data sets (rat ongoing data, rat tactile stimulation data, and human tactile stimulation data), we performed four preprocessing steps. First, we removed line noise by subtracting from the data the sinusoids at integer multiples of 50 Hz, which were obtained by the discrete Fourier transform. Second, we removed the DC component from each epoch by subtracting the average over all the samples in that epoch. Third, we down-sampled all epochs to 1,000 Hz. Finally, we visually inspected all epoch for the presence of artifacts in a semiautomated fashion and removed contaminated epochs from the data.

Table 1.

Number of electrodes and number of broken electrodes per animal

	Rat Number
	1	2	3	4	5	6	7
No. electrodes	32	32	32	32	32	64	32
No. broken electrodes	0	2	0	4	8	19	2

Generation of Synthetic Signals with a Nonsinusoidal α-Rhythm

In the remainder of the materials and methods section, we make several points regarding the spectra of nonsinusoidal α-band rhythms with an arch-shaped waveform. To illustrate these points, we generated such signals and embedded them in noise. For each signal, an α-frequency (f₀) was selected from a normal distribution with a mean of 8.5 Hz and a standard deviation of 0.5 Hz. Then a nonsinusoidal α-rhythm was created by concatenating a broad and a narrow waveform. The broad waveform was the first half (the peak) of a sine with a frequency of f₁ = 0.625f₀ Hz, and the narrow waveform was the second half (the trough) of a sine with a frequency of f₂ = 2.5f₀ Hz. The amplitude of the broad waveform was set to 1 and the amplitude of the narrow waveform was set to f₁/f₂, which ensures a smooth transition between the waveforms. Concatenating the two waveforms resulted in a combined waveform with a length of 1/f₀. From this combined waveform, a 2-s signal was created by concatenating this waveform with itself. We introduced nonstationarity in the signal by drawing the amplitude of each repetition of the combined waveform from a log normal distribution that was obtained by taking a normally distributed random variable (with mean 0 and standard deviation 0.5) and using it as the exponent of the number e. To increase its comparability with physiological signals, we then added brown (1/f²) noise such that the signal-to-noise ratio was 1.16 (Nunez 1981a, 1981b). Finally, we subtracted the average of each signal, effectively removing the DC component. In this way, we synthesized a set of 1,000 signals, each with a length of 2 s.

Quantifying Rhythmicity Using Lagged Coherence

We measured the presence of rhythmic activity using lagged coherence (Fransen et al. 2015). Rhythmicity is defined as the consistency of the phase relations over a certain time interval (lag). We applied the well-known coherence measure (Lachaux et al. 1999; Rosenberg et al. 1989) to signals in non-overlapping epochs recorded at the same site. Accordingly, lagged coherence [λ(f)] is the coherence between a signal x_n and its lagged version (x_n+1) at a specific frequency (f):

$$\lambda \left(f\right)=\left|\frac{{\displaystyle {\sum }_{n=1}^{N-1}\mathit{F}{\left({\mathit{x}}_n\right)}_f\mathit{F}{\left({\mathit{x}}_{n+1}\right)}_f^{\ast }}}{\sqrt{\left({\displaystyle {\sum }_{n=1}^{N-1}{\left|\mathit{F}{\left({\mathit{x}}_n\right)}_f\right|}^2}\right)\left({\displaystyle {\sum }_{n=1}^{N-1}{\left|\mathit{F}{\left({\mathit{x}}_{n+1}\right)}_f\right|}^2}\right)}}\right|$$ (1)

In this equation, F(x_n) denotes the Fourier transform of the signal x_n. The superscript asterisk (*) denotes the complex conjugate. We use |z| to denote the absolute value of z. The signals x_n (for n = 1, . . . , N) are ordered equal-length data segments that were cut from the original, longer signal. The length of each data segment equals the length of 3 cycles at frequency f. In our calculations, the segments are adjacent and non-overlapping, although this is not necessary for the calculation of lagged coherence. Fourier coefficients were calculated in combination with a Hanning taper. Note that calculating Fourier coefficients on tapered signals with a frequency-dependent length is equivalent to the so-called wavelet method (Bruns 2004), and the resulting coefficients are also known as wavelet coefficients.

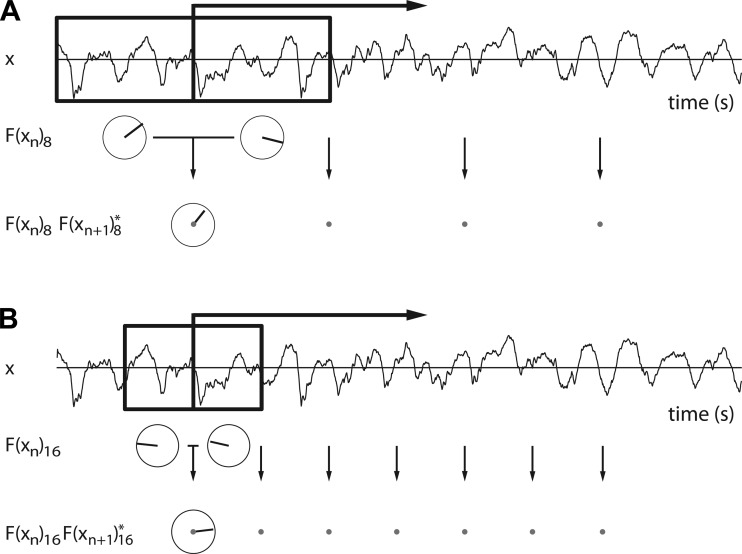
To illustrate what lagged coherence quantifies, we give an example in Fig. 1. Two subsequent data segments are highlighted in Fig. 1A. For each of these segments, the Fourier coefficient F(x_n)₈ at 8 Hz is calculated. Next, the first segment's Fourier coefficient is multiplied with the complex conjugate of the second segment's Fourier coefficient to obtain their amplitude-weighted phase difference: F(x_n)₈F(x_n+1)₈^*. These complex numbers are depicted in polar coordinates below the corresponding arrows in Fig. 1A, with the length of the vector representing amplitude, and its angle representing the phase difference between the two segments. The average of these amplitude-weighted phase differences across all adjacent segment pairs in the data is called the lagged autospectrum. The amplitude of the lagged autospectrum increases with the consistency of the phase relations in each pair of segments, but it also depends on the amplitude of the Fourier coefficients. To correct for the latter, we divide the lagged autospectrum by these amplitudes. That is, we divide the numerator of Eq. 1 by the square root of two sums of squared amplitudes: the sums of the squared amplitudes of the first and those of the second segments. This results in a complex number with an absolute value between 0 and 1; this absolute value is lagged coherence. In summary, lagged coherence at 8 Hz quantifies the consistency of the phase differences at 8 Hz across all segment pairs. Similarly, lagged coherence at, say, 16 Hz quantifies the consistency of F(x_n)₁₆F(x_n+1)_16* across all pairs of 0.1875-s-long segments. As such, lagged coherence is a frequency-indexed measure of rhythmicity.

Fig. 1.

The calculation of lagged coherence. A: 2-s raw data trace from rat 1. The boxed area marks two data segments, together lasting 0.75 s (6 cycles at 8 Hz). The Fourier coefficients at 8 Hz are represented in polar coordinates underneath each segment. Per pair of adjacent data segments, the Fourier coefficient of the first segment is multiplied with the complex conjugate of the Fourier coefficient of the second segment. The resulting amplitude weighted phase-relations are represented in polar coordinates underneath the black arrow. To obtain lagged coherence, these are then summed over all pairs, and the result is normalized (see text). B: same as A, but now showing the segments and Fourier coefficients that are used in the calculation of lagged coherence at 16 Hz.

If a signal is perfectly rhythmic (e.g., a sine function), then future phases are perfectly predictable, and lagged coherence equals 1. On the other hand, if the signal is fully arrhythmic (e.g., white noise), the future phases are fully unpredictable, and lagged coherence equals 0. To identify rhythms in physiological data, it is not useful to statistically test whether the lagged coherence values are significantly different from 0 or 1, because these null hypotheses are false for trivial reasons, such as an imperfect spectral resolution (a consequence of the short window lengths used for calculating lagged coherence). Therefore, to identify rhythms, we calculate a so-called lagged coherence spectrum (lagged coherence as function of frequency) and look for peaks in this spectrum, which we consider as evidence for rhythmic activity.

The Performance of Lagged Coherence Compared with Fourier Power for the Identification of Neuronal Oscillations

Measured neuronal activity comprises both rhythmic and transient components. These components are thought to originate from different neuronal mechanisms (Chan et al. 2011; Fetz 2013; Kaneoke and Vitek 1996; Riehle et al. 1997). The rhythmic activity is typically investigated using tools based on or inspired by the Fourier transform (Gross 2014; Wacker and Witte 2013). The Fourier transform dissects a signal into a set of sinusoids, such that the sum of all sinusoids equals the observed signal. Typically, from this transform, a Fourier power spectrum is calculated, and peaks in this spectrum are interpreted as indexes of neuronal oscillations. This is misleading because it ignores the fact that Fourier power reflects not only the neuronal oscillations in the signal, but also all transient activity. This is particularly troubling because neuronal activity comprises irregular high-amplitude transients (Freyer et al. 2009). As we demonstrate in Fig. 2, such high-amplitude transients can produce peaks in the Fourier power spectrum. This illustrates that not all peaks in this spectrum reflect rhythmic activity. These peaks are especially pronounced when wavelet-transforms are calculated that are based on short data segments. Recently, we have demonstrated that the performance of lagged coherence is superior to that of power for the identification of the somatosensory rhythms in ongoing human neuronal activity as measured by MEG (Fransen et al. 2015). This improved performance is likely due to the fact that, unlike Fourier power, lagged coherence is a direct measure of the rhythmicity at a particular frequency.

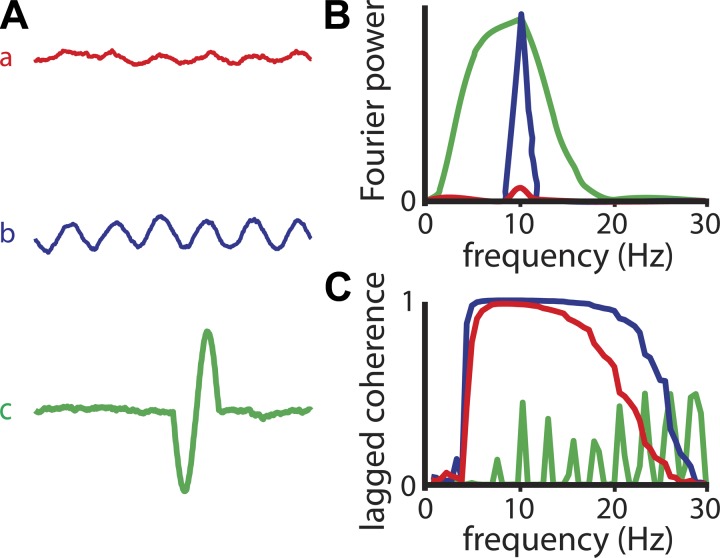
Fig. 2.

Fourier power does not directly reflect a signal's rhythmicity, but lagged coherence does. A: waveforms can vary in their amplitude and rhythmicity. Waveforms a and b have the same rhythmicity and only differ in their amplitude, whereas waveforms b and c have the same Fourier amplitude at 10 Hz, but differ in their rhythmicity. B: Fourier power spectra for signals a, b, and c. C: lagged coherence spectra for signals a, b, and c.

To illustrate the differential performance of lagged coherence and power, we show their spectra for several synthetic signals in Fig. 2. Two rhythmic signals a and b are constructed by adding 1/f noise to a 10-Hz sine wave of low (a) or high (b) amplitude. One nonrhythmic signal c is constructed by adding one cycle of this 10-Hz sine to a signal with 1/f noise. All signals have the same length. The power spectra of all three signals have a peak at 10 Hz (Fig. 2B). In itself, the height of this peak is not informative about the rhythmicity of the signal. Instead, it reflects the amplitude of a 10-Hz sinusoid that best fits the signal, and this amplitude does not tell us anything about whether the signal itself is rhythmic or not. For example, the peak amplitude (square-root power) of signals b and c is approximately equal, whereas that of signal a is much smaller (Fig. 2B). In contrast, the peak amplitude of the lagged coherence spectrum is much more informative of the signal's rhythmicity: signals a and b are both rhythmic at 10 Hz, and both have a peak lagged coherence value of 1 (Fig. 2C). In contrast, signal c is much less rhythmic, and this is reflected by a much lower lagged coherence value at 10 Hz. We should point out that the signal-to-noise ratio in these three signals is very high. This means that the lagged coherence peaks are almost at their theoretical maximum (i.e., 1). They are also quite broad as a result of spectral leakage. The more noise (or nonrhythmic activity) is added, the narrower the lagged coherence peak. In summary, in contrast to Fourier power, lagged coherence does not depend on the amplitude of the sinusoid that best fits the signal, but only on the rhythmicity of the signal itself.

Quantifying Phase-Amplitude Coupling

As can be seen from Fig. 5C, an α-rhythm with an arch-shaped waveform has power in both the α- and the β-bands. In fact, the β-power in this signal is concentrated in the sharp troughs of the α-rhythm. This concentration of β-power at a particular phase of the α-rhythm is known as PAC between the α-phase and β-amplitude. We investigated this pattern using a regression analysis in which we quantified the extent to which the β-amplitude envelope (i.e., the instantaneous β-amplitude as a function of time) could be explained by the simultaneous α-phase. For each animal, we first determined the frequencies at which the α- and β-lagged coherence are maximal, and denote these by f_α and f_β, respectively. Then, in three steps, we calculated the proportion of explained variance (PEV) of the amplitude time series at f_β by the simultaneous phase time series at f_α. In the first step, using a wavelet approach (three cycles of a complex exponential, tapered by a Hanning window), for every epoch, we calculated the β-amplitudes at intervals of 0.016 s. Per epoch, the epoch-averaged β-amplitude was subtracted from this time series, after which the time series were concatenated across epochs. In the second step, using the same wavelet approach, we calculated the complex α-phase at the same intervals. These complex time series were also concatenated across epochs. In the third and final step, the concatenated β-amplitude time series was regressed on two predictors: the concatenated complex α-phase time series and its complex conjugate. This analysis is equivalent to a regression of the β-amplitude time series on the real and the imaginary part of the complex α-phase time series. From this regression analysis, we obtained both the preferred phase of the PAC and the strength of this coupling, which was quantified as the PEV of the β-band activity.

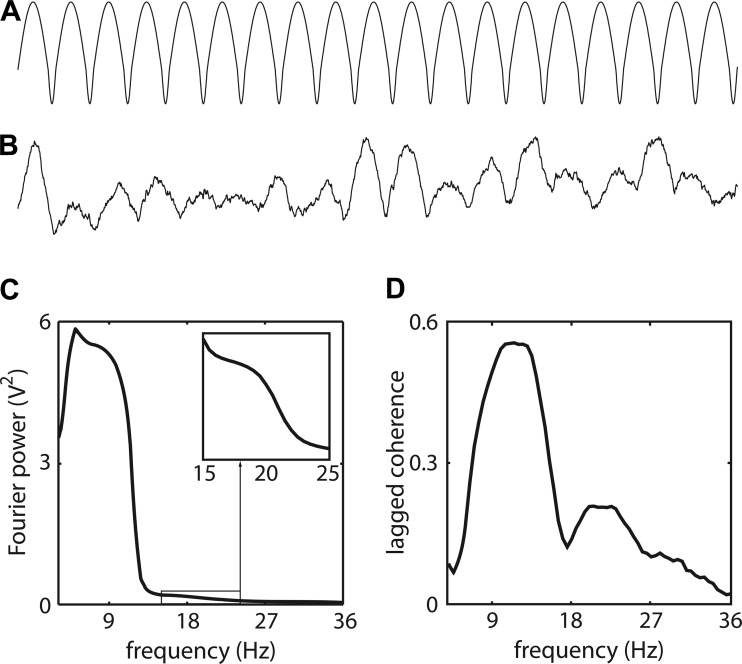
Fig. 5.

An α-rhythm with an arch-shaped waveform has peaks in its power and lagged coherence spectra in both the α- and β-bands. A: a synthetic nonsinusoidal α-rhythm with broad peaks and narrow troughs. B: same as A, but now including fluctuations of the waveform amplitude over time, and after 1/f² noise was added. C: the power spectrum of the synthetic signal shown in B. The spectrum between 15 and 25 Hz is enlarged in the boxed area. D: the lagged coherence spectrum of the synthetic signal shown in B.

To test whether a PEV is large enough to reject the null hypothesis that α-phases and β-amplitudes are independent, we used a trial-shuffling procedure. This procedure involved shuffling the order in which the β-amplitude time series were concatenated across epochs. This creates a mismatch between the epochs from which the β-amplitude fluctuations were obtained and those from which the complex α time series were obtained. We repeated the trial-shuffling procedure for 200 different epoch orders and calculated the PEV for each of them. From these 200 PEVs, we calculated one-sided 99.5% probability intervals for the PEV under the null hypothesis of uncorrelated α-phase and β-amplitude fluctuations. The value of 99.5% corresponds to a critical P value of 0.05 in combination with the Bonferroni correction (N = 10 animals). If the observed PEV exceeds this one-sided PEV probability interval, then the null hypothesis of independence between α-phase and β-amplitude is rejected.

Quantifying Topographic Similarity Between Rhythms at Different Frequencies

If the α- and β-rhythms are produced by the same neuronal generator, then their topographies should be identical. To evaluate this, we quantified the overlap between the spatial topographies of lagged coherence at its peak frequencies in the α- and β-bands (denoted by f_α and f_β). For this quantification, we used the Pearson correlation coefficient between the lagged coherence topographies at f_α and f_β (i.e., a correlation across the channel-dimension). We did this separately for every animal.

Because the lagged coherence spatial distributions are noisy, even when both rhythms are produced by the same neural generator, one cannot expect this correlation to be 1. To deal with the noise in the lagged coherence topographies, we quantified both the reliability of each topography and the similarity between the α- and β-topographies by means of a split-half procedure. This split-half procedure involved partitioning the set of epochs for each animal into two complementary sets of equal size (2 partitions). We calculated the split-half reliability of the α- and the β-lagged coherence topographies by calculating the Pearson correlation between the partition-specific topographies, separately for the α- and the β-frequency. We made 100 random split-half partitions, and, for each of these, the two split-half reliabilities (one for α and one for β) are combined by taking the product of their square roots. The motivation for this particular way of combining the split-half reliabilities is that the product of the reliabilities' square roots is an upper bound to the correlation of the α- and the β-partition-specific topographies (Lord et al. 1968). This upper bound is obtained when the neural generators for the α- and the β-rhythm are identical. This upper bound served as a baseline with which we must compare the between-frequency correlations between the partitions: the correlation between the α-topography in partition 1 and the β-topography in partition 2, and vice versa. These two correlations are combined by taking their average, and this is further denoted as topographic similarity. From the distributions of both the topographic reliability and similarity over the 100 random split-half partitions, we obtained their means and calculated stability intervals. Stability intervals reflect the degree to which topographic reliability and similarity vary across random splits. We calculated a stability interval as the interval containing 95% of the 100 topographic reliability (respective similarity) values.

Quantifying Phase-Phase Coupling Using Cross-Frequency Lagged Coherence

A nonsinusoidal α-rhythm that has energy in both the α- and the β-band repeats itself in such a way that the α- and β-phase in one cycle of this rhythm are equally predictable of the α- and β-phase in the next cycle of this rhythm. However, the frequency band with the largest signal-to-noise ratio (in this case α) will be more predictive, because the phase estimate of the rhythm will be more accurate. Therefore, if the β-rhythm (at the β-site) is the second harmonic of a nonsinusoidal α-rhythm, then we expect the future β-phase to be coupled more strongly to the present α-phase than to the present β-phase. We first substantiated this prediction by an analysis of our synthetic signals. To quantify the coupling strength between the present α-phase and the future β-phase, we calculated cross-frequency lagged coherence. This measure is similar to within-frequency lagged coherence, except that it is the coherence between a signal (x_n) at frequency f₁ and the lagged version of that same signal (y_n+1) at another frequency f₂:

$$\lambda \left(f_1,f_2\right)=\left|\frac{{\displaystyle {\sum }_{n=1}^{N-1}\mathit{F}{\left({\mathit{x}}_n\right)}_{f_1}\mathit{F}{\left({\mathit{y}}_{n+1}\right)}_{f_2}^{\ast }}}{\sqrt{\left({\displaystyle {\sum }_{n=1}^{N-1}{\left|\mathit{F}{\left({\mathit{x}}_n\right)}_{f_1}\right|}^2}\right)\left({\displaystyle {\sum }_{n=1}^{N-1}{\left|{\mathit{F}({\mathit{y}}_n+1)}_{f_2}\right|}^2}\right)}}\right|$$ (2)

Note the use of the different symbols, x_n and y_n+1, for the data segments from which the Fourier coefficients for the different frequencies are calculated. The length of the epochs x_n (for n = 1, . . . , N) is equal to three cycles at frequency f₁, whereas the length of the epochs y_n (for n = 1, . . . , N) is equal to three cycles at frequency f₂. The epochs x_n and y_n are centered at the same time points, indexed by n. These time points are separated in time by a lag equal to (f₁ + f₂) × (3/2), which ensures that all segment pairs x_n and y_n+1 are adjacent and non-overlapping (Fig. 3A).

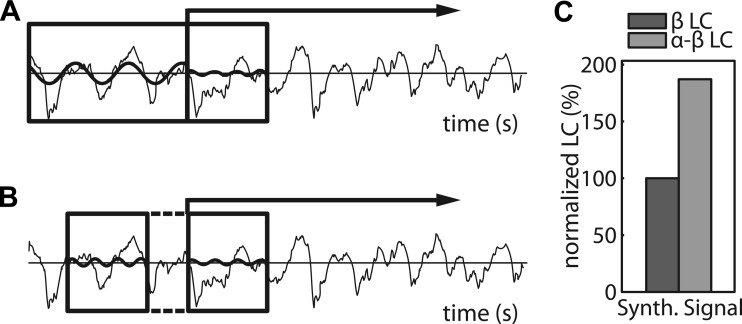
Fig. 3.

Cross- and within-frequency lagged coherence (LC) are both assessed with 3 cycles per frequency. A: 2-s raw data trace from rat 1. The boxed areas mark data segments that are denoted x_n (left) and y_n+1 (right) in the main text on cross-frequency LC. The contribution of a frequency-specific Fourier component to a segment is shown as a sinusoid, whose amplitude and phase correspond one-to-one to the corresponding Fourier coefficient. The Fourier coefficient F(x_n)_f1 corresponds to the sinusoid that is superimposed on x_n. And the Fourier coefficient F(y_n+1)_f2 corresponds to the sinusoid that is superimposed on y_n+1. B: same as A, but now the boxed areas mark data segments that correspond to y_n (left) and y_n+1 (right), and the superimposed sinusoids correspond to F(y_n)_f2 and F(y_n+1)_f2. Note that, in contrast to Fig. 1B, these segments are nonadjacent (see the dashed lines). C: lagged phase-phase coupling in the synthetic signal that was used in Fig. 3, between present and future β (β-LC) and between present α and future β (α-β-LC).

The cross-frequency α-β-lagged coherence values were compared with the within-frequency β-β-lagged coherence values. For comparability, we calculated the within-frequency lagged coherence at the same time points with the same lag and the same number of cycles in each data segment. This way, the two calculations match with respect to the number of cycles that are used for the phase estimates and with respect to the time interval between the two phase estimates. Note that, with this lag, the two segments used to estimate the β-phases have a gap between them (Fig. 3B), which is different from the calculation of (within-frequency) lagged coherence reported elsewhere in this paper. This assessment of the lagged phase-phase coupling favors the cross-frequency α-β-lagged coherence, because this measure involves segments that follow each other without a gap in between. We confirmed this bias by applying this analyses to our synthetic signals, where the cross-frequency lagged coherence was approximately twice as high as the lagged within-frequency lagged coherence at f₂ (Fig. 3C). Prior to averaging over animals, we normalized the lagged coherence values by expressing them as a percentage of the β-lagged coherence in the so-called β-sites (the 25% electrodes with the largest β-band coherence) for ease of interpretation; note that this does not in any way alter the results. We tested whether there were significant differences between the α-β- and β-β-lagged coherence using a pairwise t-test.

Time-Frequency Representations of Power and Their Modulation by Tactile Stimulation

If the α- and β-rhythms in rat somatosensory cortex play the same role in sensory processing as the ones in human sensorimotor cortex, then these rhythms should respond to tactile stimuli in the same manner in both species. To assess this, in both species, we characterized the time- and frequency-resolved response to a brief (0.020 s) tactile stimulus. For the human MEG data, per participant, we first had to select somatosensory channels, and we did this on the basis of the stimulus-induced β-suppression, as described in detail by van Ede et al. (2011).

The calculation of these time-resolved power spectra involved a sliding time window with a width of 3 cycles at each frequency, which was advanced in steps of 0.005 s. Prior to calculating the Fourier coefficients, the signals were multiplied with a Hanning taper. We expressed all power estimates as a percentage of the average baseline power, with the baseline covering an interval of 0.5 s before stimulus onset.

RESULTS

Rhythmic α- and β-band Activity Over the Rat Somatosensory Cortex

We used micro-ECoG (Dimitriadis et al. 2014b, 2014a) to perform chronic recordings of ongoing electrophysiological activity over the rat somatosensory cortex (see materials and methods and Fig. 4A). We investigated rhythmicity in these recordings using the lagged coherence measure (Fransen et al. 2015). Rhythmicity is the extent to which a signal is periodic, allowing for the prediction of future phases on the basis of the present one. Lagged coherence is a frequency-indexed measure of rhythmicity (see materials and methods). There is an important difference between lagged coherence and Fourier power: Fourier power at a given frequency is not informative of the rhythmicity of the signal at that frequency, but instead reflects the amplitude of the sinusoid, with the same frequency, that best fits the signal. The amplitude of this best-fitting sinusoid does not tell us anything about whether the signal itself is rhythmic or not. As a result, a peak in the Fourier spectrum cannot simply be interpreted as a rhythm at that frequency (Fig. 2). In contrast, the lagged coherence spectrum does not depend on the amplitude of this best-fitting sinusoid and only reflects to what extent that signal is rhythmic at each frequency. Because we are interested in identifying whether the rat somatosensory cortex contains a β-band rhythm, we will primarily report lagged coherence values, rather than Fourier power.

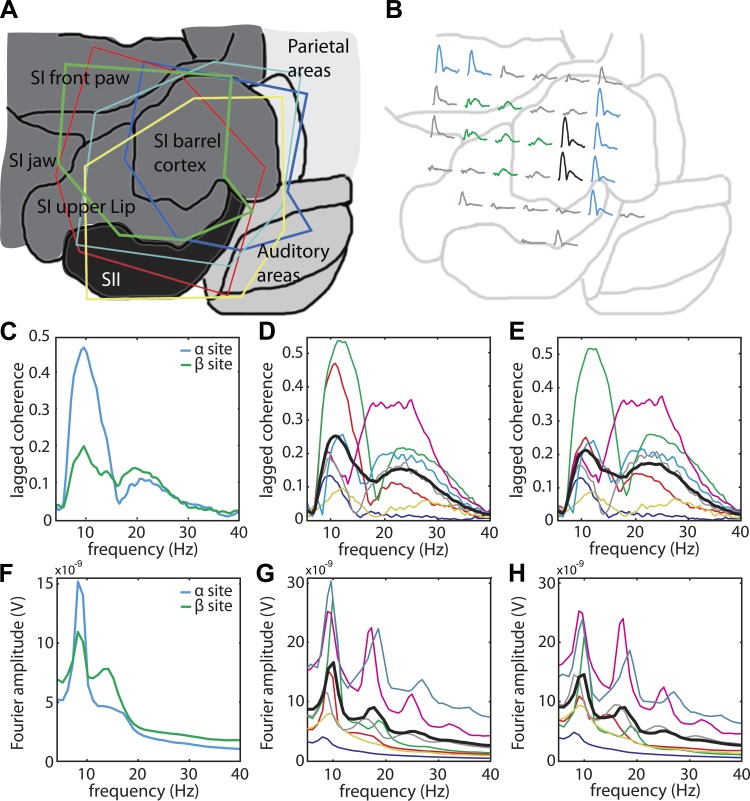
Fig. 4.

Lagged coherence and Fourier spectra of cortical activity over rat somatosensory cortex contain peaks in both the α- and the β-bands. A: the outline of 5 electrode arrays projected on a flattened brain map. B: for rat 1 (green outline in A), we show the lagged coherence spectrum between 4 and 40 Hz at each electrode location. The 25% electrodes that together make up the α-site are depicted in blue; the 25% electrodes that make up the β-site are depicted in green. Electrodes that are in both groups are depicted in black. C: the lagged coherence spectra of rat 1 are plotted separately for the α- and the β-site. D: the lagged coherence spectra at the α-sites are shown for each animal, and for all animals averaged (thick black line). The spectra in C are shown again in D and E, but now in red. E: same as D, but now the lagged coherence spectra are shown for the β-sites. F–H: same as C–E, but showing Fourier amplitude spectra.

A crucial observation in the present study pertains to the difference between the recorded cortical sites with respect to the rhythms they generate. This is obvious from the fact that the corresponding lagged coherence spectra in the different recording sites are not simply scaled versions of one another. For example, in animal 1, the lagged coherence spectra of some sites only peak in the α-band (7–14 Hz), whereas others only peak in the β-band (15–30 Hz) (Fig. 4B). These differences between the spatial patterns of the α- and the β-band rhythms were more pronounced when identified by means of lagged coherence compared with power, and this is one of the important reasons for why we adopted the former measure for this study. In the subsection Distinct Neural Generators for the α- and β-Rhythms Over Rat Somatosensory Cortex, we provide a systematic comparison of the α- and the β-band lagged coherence topographies. In what follows, we mainly focus on lagged coherence spectra (i.e., lagged coherence as a function of frequency).

To average the results across the 10 animals in our study, we have to deal with the heterogeneity across the somatosensory cortex: 1) not every recording site shows rhythmicity, and 2) there are individual differences in the animals' α- and β-band topographies. For every animal, we selected the 25% electrodes with the largest α-band lagged coherence, as well as the 25% electrodes with the largest β-band lagged coherence. In the following, these will be denoted as, respectively, the α- and the β-sites. Averaging the lagged coherence spectra within each site produces spectra with an α- as well as a β-peak (see Fig. 4C for rat 1, and Fig. 4, D and E, for all animals, together with their average shown as a thick line). Importantly, because in each animal the spectra for both sites show an α- as well as a β-peak, this demonstrates that 1) neither peak is an artifact of site selection, and 2) there is overlap between the α- and the β-band topographies. The overlap is substantial in several animals, and, therefore, the difference between the average lagged coherence spectra in Fig. 4, D and E, is not spectacular. However, when we directly quantify the degree of overlap between these spatial topographies, these differences turn out to be highly reliable (see Fig. 7).

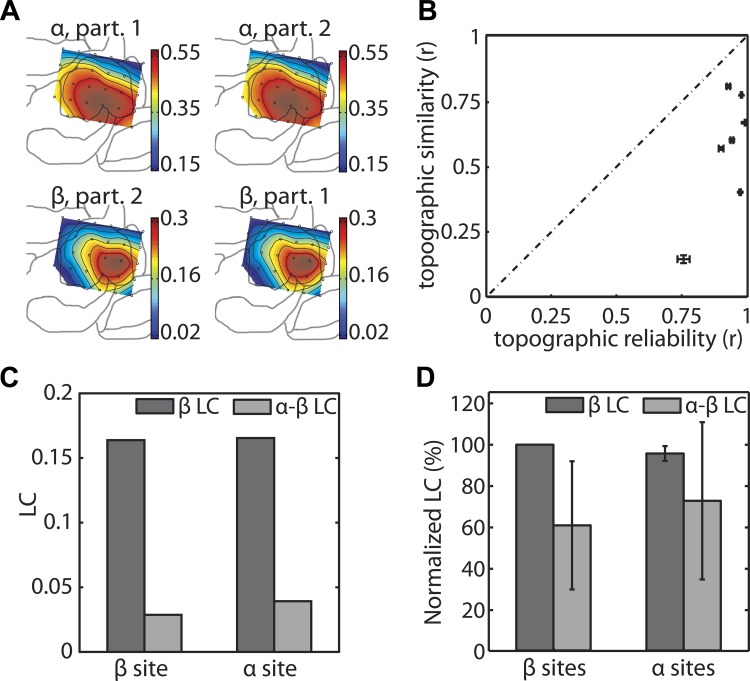
Fig. 7.

Spatial and spectral evidence for a genuine somatosensory β-rhythm that cannot be explained as the second harmonic of a nonsinusoidal α-rhythm. All panels on the left are based on data from rat 2, whereas those on the right combine data from all animals. A: the spatial distribution of lagged coherence (LC) at 10.5 Hz (α) and 23.5 Hz (β) for two complementary partitions of the data of rat 2. Color denotes LC. B: the topographic similarity between the α- and β-LC is plotted against the topographic reliability at these frequencies. The vertical and horizontal error bars denote the split-half 95% stability intervals of the topographic similarity and reliability. Note that A and B are the only ones in this figure that pertain to the spatial distribution of LC; the remaining panels pertain to comparisons of different types of LC, which are performed separately for the α- and the β-sites. C: for rat 2, we show the within-frequency β-LC and the cross-frequency α-β-LC. We did this separately for the α- and the β-sites. D: same as C, but now for the average normalized LC values. Normalization across animals was performed by expressing every LC value as a percentage of the within-frequency β-LC at the β-sites. Error bars represent the 95% confidence intervals, calculated on the basis of the variance across animals.

In rat 1, the heterogeneity of the lagged coherence spectra over space is accompanied by heterogeneity in its Fourier amplitude spectra (Fig. 4F). However, in most animals, the Fourier spectra are more homogeneous over space compared with the lagged coherence spectra (spatial topographies not shown). We recently demonstrated this ability of lagged coherence to overcome the smeared Fourier power topographies in human sensorimotor cortex (Fransen et al. 2015). Furthermore, although all Fourier spectra contain α-peaks (Fig. 4, G and H), the β-peaks in the individual Fourier spectra appear to systematically coincide with the harmonics of these α-peaks. In the following, we will ask to what extent the β-peaks in the lagged coherence spectra may reflect such harmonic activity also.

Part of the β-Band Activity Is Due to the Nonsinusoidal Waveform of the α-Rhythm

The sensorimotor α-rhythm is known to be nonsinusoidal: the α-waveform's peak is much broader than its trough, resembling an arch, such as caricaturized in Fig. 5A (Gastaut et al. 1952; Kaplan 1979). This rhythm has broad peaks and sharp troughs, and the duration of one period (peak + trough) places this rhythm in the α-band. To investigate whether the observed power and lagged coherence spectra (often, with a peak in both the α- and the β-band) could be produced by this nonsinusoidal waveform, we performed a simulation study in which we analyzed a simulated signal with a nonsinusoidal waveform. To make the signal physiologically plausible, we generated a nonstationary version of it and added 1/f noise (Fig. 5B). The details of the synthesis of this signal are described in the materials and methods section (Generation of Synthetic Signals with a Nonsinusoidal α-Rhythm).

The results with respect to the power spectrum show a peak at one over the signal's period (in the α-band), but also a second one (albeit much weaker) at twice this frequency (in the β-band) (Fig. 5C). This peak in the β-band is known as the peak of the second harmonic, because it occurs at twice the frequency of the waveform. Importantly, this harmonic β-band peak is also present in the lagged coherence spectrum (Fig. 5D), with the peak frequencies in both the α- and the β-band slightly shifted to the right compared with the corresponding peak frequencies in the power spectrum. Thus also the β-band peaks in the lagged coherence spectra in Fig. 5 might reflect a nonsinusoidal α-rhythm, rather than a distinct β-band rhythm. In what follows, we investigate whether the β-sites contain an α-band rhythm whose arch-shaped waveform can explain part of the activity at the frequency of the β-band rhythm. In parallel, we look for evidence in the data that points to a distinct β-band rhythm that coexists alongside this arch-shaped α-rhythm.

To investigate whether the β-sites contain an α-band rhythm with an arch-shaped waveform, we performed a linear model analysis in which we predicted the instantaneous β-amplitude (i.e., the β-amplitude envelope) from the instantaneous α-phase (see materials and methods). This type of coupling is commonly known as PAC, and the linear model analysis is highly related to the PAC measure proposed by Maris et al. (2011). The β-amplitude envelope for a given signal was calculated at the peak frequency in the β-band of its lagged coherence spectrum. The instantaneous α-phase that served as a predictor in the linear model analysis was calculated at the peak frequency of the α-band power spectrum. All analyses were performed at the β-sites.

If an α-rhythm has an arch-shaped waveform and is present in the β-sites, then the α-phase should predict a statistically significant proportion of the variance in the β-amplitude envelope. We evaluate this statistical significance by comparing the PEV with its probability distribution under the null hypothesis that β-amplitudes and α-phases are statistically independent. In fact, under this null hypothesis, β-amplitude envelopes and α-phase signals can be exchanged between epochs without changing the probability of the data. By randomly exchanging amplitude envelopes and phase signals between epochs, we obtained a one-sided probability interval for the PEV under the null hypothesis. The upper limit of these probability intervals is shown as thick black lines in the bars in Fig. 6B. This upper limit corresponds to a statistical test with a critical P value of 0.007, which was obtained by applying the Bonferroni correction to the usual critical P value of 0.05.

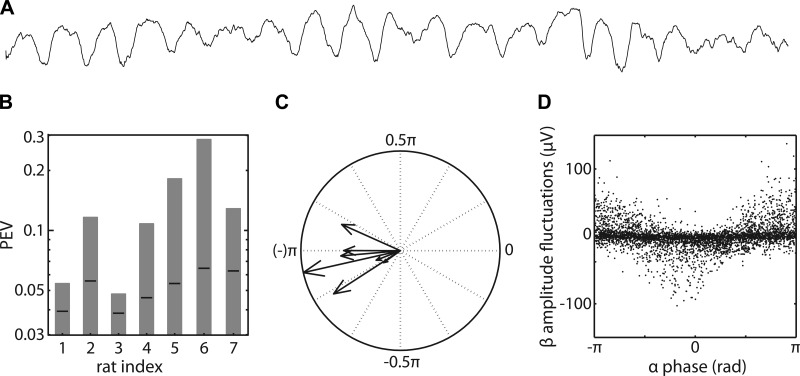
Fig. 6.

The phase of α-activity is associated with amplitude fluctuations in the β-band. A: 2-s raw data trace from rat 2. B: the proportion of the β-band amplitude fluctuations that is explained by the α-phase in each animal (rat indexes 1–7). Note that the PEVs are plotted on a logarithmic scale. The PEV values are significant at P < 0.05 (corrected for multiple comparisons) when they exceed the black lines. These black lines denote the one-sided 99.5% probability interval of the proportion of β-band amplitude fluctuations that are explained by the α-phases in another epoch. C: the angle (in radians) of each vector denotes the preferred coupling phase at which β-amplitude is maximal in that animal. Phase ±π corresponds to the trough of the α-rhythm. The length of each vector denotes the PEV of that animal, plotted on a logarithmic scale. D: per animal, the instantaneous β-amplitude fluctuations are plotted against the instantaneous α-phase for the 10 epochs in which the α-power is largest.

In all animals, the PEV is significantly larger than the upper limit under the null hypothesis, providing strong evidence that these animals have a nonsinusoidal α-rhythm in the β-sites (Fig. 6B).

If this nonsinusoidal rhythm has an arch-shaped waveform (Fig. 5), then the β-amplitude should be maximal at the trough of the α-rhythm. This is because the trough is much sharper than the peak, and this results in a much stronger local correlation with the β-wavelet that is used to calculate the amplitude envelope (see materials and methods). Our linear model analysis not only allows one to calculate the PEV, but also the preferred coupling phase, which should be ±π for an arch-shaped rhythm. In our animals, the preferred coupling phase was −0.93π ± 0.09π (mean ± 95% confidence interval), which provides strong evidence that the observed α-rhythm indeed has an arch-shaped waveform (Fig. 6C).

Although we confirm the existence of a somatosensory α-rhythm with an arch-shaped waveform in the β-sites, this does not necessarily mean that a genuine β-rhythm does not coexist in the same brain areas. One piece of evidence that points in this direction comes from the linear model analysis: more than 70% of the variance in the β-amplitude envelopes cannot be explained by the α-phase. Admittedly, part of this unexplained variance may be noise. However, even in those epochs in which the α-power is the largest, much of the β-amplitude fluctuations are not phase-locked to the α-rhythm (Fig. 6D). Rather than focusing on negative evidence for a genuine β-rhythm (i.e., the inability of the arch-shaped α-rhythm to explain all β-band power), in the following, we now present some positive evidence.

Distinct Neural Generators for the α- and β-Rhythms Over Rat Somatosensory Cortex

Although we demonstrated in the previous section that the waveform of the α-rhythm is such that it generates peaks in both the α- and β-bands, there is a clear difference in the spatial distribution of the α- and β-rhythms, as depicted in Fig. 4B for rat 1. (Although, in this animal, the difference seems to correspond to different functional regions, this could not be reproduced in the other animals.) This raises the question whether there is also positive evidence for the existence of a genuine β-rhythm that coexists alongside the β-band rhythmicity that is due to the α-rhythm's nonsinusoidal waveform. Here, we address the problem of quantifying whether or not the β-peak in the lagged coherence spectrum reflects both harmonic β-band activity and a genuine β-rhythm. To test whether the β-band lagged coherence peak mainly reflects such a harmonic or whether it mainly reflects a genuine β-rhythm, we use two independent measures: 1) the similarity of the topographies of the α- and β-rhythms, and 2) the predictive strength of α- compared with β-phases for the prediction of future β-phases.

The first measure quantifies the extent to which the α- and β-rhythms are colocalized. If the α- and β-rhythms are produced by the same neural generator, then the spatial distribution of lagged coherence at the β-peak frequency should match the topography at the α-peak frequency. In rat 1, the α- and β-topographies are quite different (Fig. 4A). In rat 2, on the other hand, the topographies are more similar, although not identical (Fig. 7A, top vs. bottom). To quantify the similarity of these topographies, we calculate the Pearson correlation between the spatial topographies of α- (Fig. 7A, top) and β-lagged coherence (Fig. 7A, bottom) for every animal. The resulting correlations vary greatly between animals: they range from 0.14 to 0.80 (Fig. 7B, vertical axis). This variability across animals may be due to between-animal differences in the overlap of both topographies. However, they may also be (partly) due to between-animal differences in the reliability of the α- and β-topographies themselves. If the topographies are unstable over time, then the topographic similarity is likely to be lower simply due to the unreliability of these topographies. Thus the combined topographic reliability of the α- and β-lagged coherences forms the upper bound for the topographic similarity, and this upper bound is shown by the dashed line in Fig. 7B (see materials and methods for a description and motivation of the precise way the combined topographic reliability was calculated). Whether the α- and β-topographies differ from each other is, therefore, determined by whether the topographic similarity is lower than can be expected from this upper bound. To test this, we quantify the reliability of the α- and β-topographies by means of split-half reliability coefficients (see materials and methods). Calculating a split-half reliability coefficient of a data set starts by partitioning the set of epochs into two halves. Next, for each of these halves, the lagged coherence topographies are calculated. For example, in Fig. 7A, we show the α- and the β-lagged coherence topographies separately for each of the two partitions. The split-half reliabilities of these topographies are equal to their between-partition correlations, separately for the α- (Fig. 7A, top) and the β-band (Fig. 7A, bottom). If the topographic similarity is approximately equal to this upper bound (i.e., if the error bars overlap with the diagonal in Fig. 7B), then we conclude that the α- and β-rhythm are produced by the same neural generator. All animals have high topographic reliabilities, which can only occur if these topographies are sufficiently stable over time. In contrast, although the α- and β-topographies overlap (similarity > 0), the topographies are more dissimilar than can be expected from their reliability (as indicated by the fact that all topographic similarities lie well below the dashed line in Fig. 7B). In other words, the α- and β-topographies are stable over time, and, although they overlap, they are significantly different from one another.

The second measure provides information about the independence of the β- from the α-rhythm. Specifically, this second measure quantifies the predictive strength of the present α- and β-phases for the prediction of future β-phases. If the α- and the β-rhythms are produced by a single neural generator, as in the case of a nonsinusoidal α-rhythm, then the present phase of the α-rhythm should predict the future phase of the β-rhythm. To quantify the strength of this cross-frequency prediction, we calculated the cross-frequency lagged coherence (see materials and methods) and compared it with the ordinary (within-frequency) lagged coherence. If the β-rhythm is the second harmonic of a nonsinusoidal α-rhythm, then we expect the α-β cross-frequency lagged coherence to be larger than the β-β within-frequency lagged coherence. This expectation was confirmed by an analysis of our synthetic signal: for this signal, the α-β-lagged coherence (0.17) was about 80% larger than the β-β-lagged coherence (0.094, Fig. 3C).

We calculated the α-β- and the β-β-lagged coherence separately for the α- and β-sites. In rat 2, for both sites, the present β-phase is a much better predictor of the future β-phase than the present α-phase (Fig. 7C). In each site, the α-β-lagged coherence is less than one-third of the β-β-lagged coherence. We obtained the averaged results for the 7 animals that have reliable α- and β-rhythms. Prior to averaging, we normalized all lagged coherence values relative to the β-lagged coherence in the β-sites (Fig. 7D). In the β-sites, the α-β-lagged coherence is significantly less (P < 0.05) than the β-β-lagged coherence. In the α-sites, the α-β-lagged coherence and the β-β-lagged coherence are approximately equal. In combination with the fact that, for the synthetic signal, the α-β-lagged coherence is much larger than the β-β-lagged coherence, these results demonstrate the existence of a somatosensory β-rhythm with its own neural generator.

Tactile Input Suppresses α- and β-Band Power in Both Rat and Human Somatosensory Cortex

The α- and β-rhythms, such as the ones we identified in rat somatosensory cortex, are also known to be present over human sensorimotor cortex. In both species, both the power and lagged coherence spectra over somatosensory cortex have a peak in the α- as well as in the β-band. Furthermore, in both species, the lagged coherence peaks are at slightly higher frequencies than the power peaks (Fig. 8, A and B; see also Fransen et al. 2015). To further test for the homology of these rhythms, we also asked whether these rhythms are modulated by tactile input in the same way in both species. A well-documented finding in human studies is that, following presentation of a tactile stimulus on one hand, there is an induced suppression of both α- and β-band power over the contralateral sensorimotor cortex (Bauer et al. 2006; Gaetz and Cheyne 2006; van Ede et al. 2011, 2014a). Here, we replicate this result in humans and demonstrate a highly similar modulation in rat somatosensory cortex.

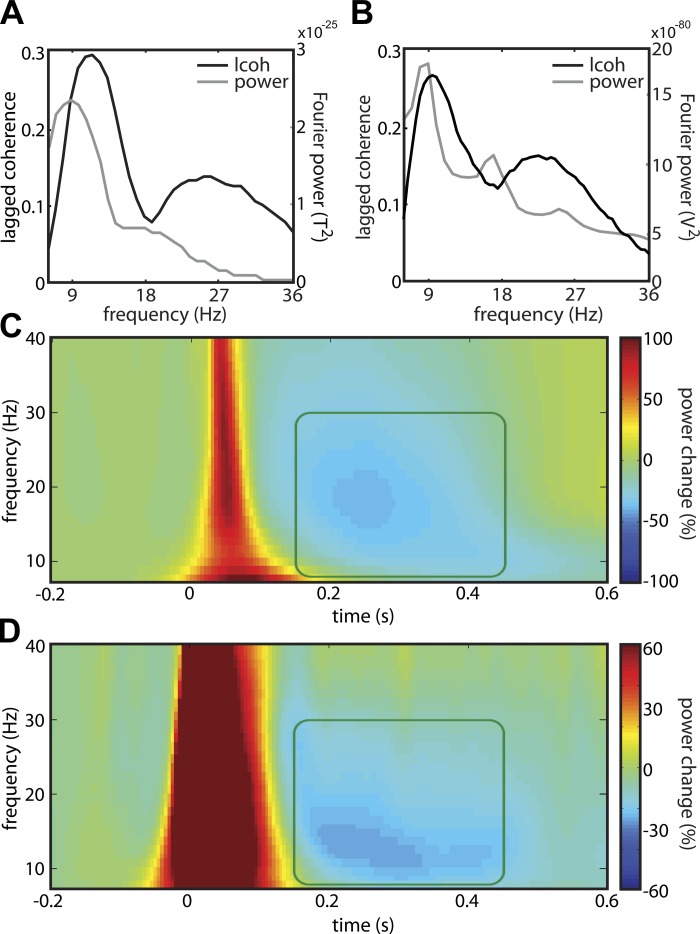
Fig. 8.

In the somatosensory cortexes of both human and rat, tactile input suppresses α- and β-band power between 0.15 and 0.45 s after stimulus onset. A: lagged coherence (black) and power (gray) spectra of MEG data over human somatosensory cortex. B: same as A, but for ECoG data over rat somatosensory cortex. C: time-frequency resolved power, plotted as a percentage of the average power during baseline in a synthetic MEG electrode over contralateral primary sensorimotor cortex and averaged over 20 humans. The power is time-locked to a brief tactile stimulus presented to all fingers of the contralateral hand at 0 s. The boxed area spans from 8 to 30 Hz, and 0.15 to 0.45 s. D: same as C, but plotted for all ECoG electrodes over rat somatosensory cortex. Here, the stimulus was presented to the contralateral upper lip.

Neural activity was measured using MEG in 20 human subjects, who were presented with tactile stimuli on all fingers of the left or right hand (van Ede et al. 2011). In Fig. 8C, we show the baseline-corrected time-frequency power representation of an MEG site over the contralateral sensorimotor cortex, with time 0 corresponding to the presentation of the brief (0.020 s) tactile stimulus. Approximately 0.15 s after stimulus onset, the power in the α- and β-bands decreases (Fig. 8C, highlighted area). This suppression lasts for about 0.3 s and is followed by a β rebound, an increase in β-power relative to the prestimulus baseline.

We also presented tactile stimuli on the upper lip of 6 awake, unrestrained rats and recorded ECoG activity over the contralateral somatosensory cortex (Fig. 8D). Although the color scale of the time-frequency power representation is dominated by the strong initial evoked response, there is also a clear power decrease in the α- and the β-bands. Interestingly, the timing and frequency profile of this power decrease is very similar to the one in humans (Fig. 8C): the decrease is band-limited between 8 and 30 Hz, starts ∼0.15 s after stimulus onset, and lasts for ∼0.3 s.

Although not central to the current paper, it is interesting to note the difference between the two species with respect to the size of the initial evoked response. There are at least two possible reasons: 1) we did not match the stimulus intensity between the two experiments, and 2) for biophysical reasons, the epidural ECoG electrodes may reflect the evoked response in the intracellular currents much better than the gradiometers of the MEG system. The data also differ with respect to the β-rebound: whereas it is present in human sensorimotor cortex, there is no evidence for a β-rebound in the rat somatosensory cortex.

DISCUSSION

We have demonstrated the existence of a β-rhythm in the rat somatosensory cortex. Together with the α-rhythm in the same area (but not necessarily the same exact sites), these rhythms likely constitute the homologues of the human sensorimotor rhythms. Much of our evidence is obtained using lagged coherence, a novel measure that quantifies rhythmicity separately at each frequency of interest. We demonstrate that the β-rhythm coexists alongside β-activity that is due to the typical arch-shaped waveform of the somatosensory α-rhythm. Strong positive evidence for this distinction comes from the fact that the α- and β-rhythms have different topographies. In addition, despite the fact that the α-phase is much better preserved over time, the present β-phase can be predicted significantly better by past β-phases than by past α-phases. Finally, we demonstrated an interesting functional homologue with the human somatosensory cortex: α- and β-band power over rat somatosensory cortex responds in a very similar way to a tactile stimulus (i.e., they are suppressed between 0.15 and 0.45 s) as their human counterparts.

Cross-Species Consistency of Somatosensory Rhythms

It has been well established that rhythmic neuronal activity is one of the best conserved phenotypes in mammalian evolution (Buzsaki et al. 2013). This conservation allows species to increase their brain size, without compromising on the duration of computations or on the extent of local-global integration. The strong conservation reflects the existence of as yet unknown functional requirements on temporal processing that are independent of brain volume and anatomical connectivity.

For many, but not for all, rhythms, conservation in mammals has been demonstrated. In this paper, we have focused on rhythmic activity in rat primary somatosensory cortex. In primates, there is both α- and β-band rhythmic activity in the somatosensory cortex (Brovelli et al. 2004; Crone et al. 1998; Gaetz and Cheyne 2006; Witham et al. 2007). Also for rat somatosensory cortex, there is substantial evidence for the existence of α-band rhythmic activity (Nicolelis et al. 1995; Semba et al. 1980; Sobolewski et al. 2011; Vanderwolf 1975; Wiest and Nicolelis 2003), which is thought to be a homolog of somatosensory α-rhythms in other mammals (Buzsaki et al. 2013; Kaplan 1979; Montaron et al. 1979; Sobolewski et al. 2011). Surprisingly, despite the popularity of the rat somatosensory cortex as a model system, there have been no reports of distinct β-band rhythmic activity in this area. There are several reasons for this: 1) the β-rhythm has traditionally been considered a purely motor rhythm that resides in motor rather than somatosensory cortex; 2) the presence of a rhythm in a particular frequency band has traditionally been based on a peak in the power spectrum, and the power in the sensorimotor β-rhythm may be too low to produce a clearly discernible peak. Moreover, in those cases where the power spectrum did show a β-peak, this may have been attributed to the nonsinusoidal α-waveform. In the following sections, these points will be discussed in detail.

Evidence for conservation across species does not only come from the rhythmic activity itself, but also from how it is modulated by sensory stimulation and movement. For the human sensorimotor rhythms, is has been demonstrated that, following a tactile stimulus, their power decreases (ERD; Pfurtscheller and Da Silva 1999). We showed the same phenomenon for the rat somatosensory rhythms and thereby extended a similar observation by Sobolewski and colleagues (2011), who already described this for the somatosensory α-rhythm.

In the remaining discussion, we will ignore the individual differences between our rats (N = 10), even though they were prominent. In three animals (rats 7, 9, and 10), there was hardly any rhythmic activity in the α- and/or the β-band, as demonstrated by the very low split-half reliability of their lagged coherence topographies. Interestingly, also in humans, there are substantial individual differences in the spectral signature of the sensorimotor rhythms (α- and β-peak, α-peak only, β-peak only, no peaks). Unfortunately, because journal articles typically show only averages across subjects, these individual differences often remain undocumented. However, we have observed them in a whole range of studies on attentional modulations over the human sensorimotor cortex (van Ede et al. 2010, 2011, 2012a, 2014a, 2014b). Thus, not only is the existence of the two sensorimotor rhythms consistent over the different mammalian species, but possibly also the individual differences in the degree to which they are expressed in their members.

The Sensorimotor β-Rhythm

The β-rhythm is thought to arise in a network involving the cortex and the basal ganglia (Leventhal et al. 2012; Williams et al. 2002). Within cortex, the sensorimotor β-rhythm is classically thought to arise from motor, rather than somatosensory, regions (Brovelli et al. 2002; Pfurtscheller et al. 1997) and, therefore, has been mainly considered as a motor rhythm. In line with this, there is extensive evidence for a modulation of this rhythm by most aspects of movement: from movement execution (Jasper and Penfield 1949; Rougeul et al. 1979), offset (Pfurtscheller et al. 1997, 1998), planning (Leocani et al. 1997), preparation (Pfurtscheller et al. 1998; Zhang et al. 2008), inhibition (Pogosyan et al. 2009; Swann et al. 2009), and switching (Cheyne et al. 2012; Gilbertson et al. 2005; Stoffers et al. 2001), to movement imagery (Brinkman et al. 2014; Schnitzler et al. 1997) and observation (Babiloni et al. 2002; Koelewijn et al. 2008; Orgs et al. 2008, Pavlidou et al. 2014). Furthermore, strong evidence for the motor function of the sensorimotor β-rhythm comes from the clear β-peak in the cortico-muscular coherence: the coherence between the extracranial activity over the sensorimotor cortex and the EMG (Baker et al. 1997; Salenius et al. 1997).

In addition, over the past decade, several invasive studies have reported a genuine β-rhythm in somatosensory cortex as well (Brovelli et al. 2004; Witham et al. 2007; Witham and Baker 2007). This β-rhythm was found to be distinct from the somatosensory α-rhythm. This is not trivial, as one of the most distinguishing features of the sensorimotor α-rhythm is its arch-shaped waveform (Gastaut et al. 1952; Kaplan 1979), which causes a β-peak in the power spectrum. We too present evidence for a contribution of this nonsinusoidal waveform to the β-power. We even show that an arch-shaped α-waveform can introduce a rhythmicity peak in the β-band of the lagged coherence spectrum. However, we also demonstrate that a genuine β-rhythm coexists alongside this harmonic β-activity. This is in line with recent evidence from multiunit activity and ECoG recordings in primates. There, it has been shown that neurons in primate somatosensory cortex fire in phase with local β-oscillations (Witham et al. 2007), and that this somatosensory β-rhythm drives the one in motor cortex (Brovelli et al. 2004; Witham et al. 2007).

Given this connectivity, the β-rhythms over somatosensory and motor cortex are probably not distinct. In fact, there is evidence that the β-rhythms in both the somatosensory and motor cortex form one coherent network (Brovelli et al. 2004) and are functionally homogenous. The function of β-rhythms in this coherent network is a topic of active theorization, as evidenced by the many reviews that have recently been published on this topic (Cannon et al. 2014; Cheyne 2013; Engel and Fries 2010; Kilavik et al. 2013; Pavlidou et al. 2014). However, in line with the involvement of both somatosensory and motor regions, a growing body of evidence suggests that this rhythm plays a cognitive role that is not unique to the motor system. For example, the sensorimotor β-rhythm is modulated by several cognitive tasks, such as somatosensory attention (van Ede et al. 2012b, 2014b). Moreover, it has been shown that the cortico-muscular β-band coherence cannot be interpreted as evidence for a strict motor function of the β-rhythm either: we recently demonstrated that this cortico-muscular coherence can be modulated by a sensory paradigm in the absence of any movement requirements (van Ede et al. 2014a).

We should note that, in contrast to this idea of one homogenous sensorimotor β-rhythm, there is a well-documented β rebound at about 20 Hz that has been reported to have a different topography from other β-modulations, namely one that does not include primary somatosensory cortex. The localization of the β rebound to motor cortex has been reported both after the offset of a movement (Brovelli et al. 2002, Jurkiewicz et al. 2006; Pfurtscheller et al. 1996) and of a tactile stimulus (Gaetz and Cheyne 2006). This motor origin is in agreement with our present findings: as we did not find any evidence for the presence of a β rebound over the somatosensory cortex. We speculate based on its differential connectivity pattern and functional modulation that this rebound is generated by different circuits than the sensorimotor β-rhythm. In this context, special attention is warranted to work by Leventhal et al. (2012), as theirs is the only study, other than this one, that has reported a sensorimotor β-rhythm in the rat. They studied the β-rhythm at about 20 Hz in the motor cortex and the basal ganglia and demonstrate that it was not strictly modulated by movements or their suppression. Instead, they observed that the increase of β-synchronization after the offset of a cue is specific to those cues that are used to determine motor behavior. This may indicate that also the β-rebound plays a cognitive role.

Identifying the Sensorimotor β-Rhythm Using (Lagged) Coherence

In this paper, we identified neuronal oscillations on the basis of rhythmicity, instead of in the usual way, on the basis of Fourier power. Rhythmicity is the degree of phase preservation over time, and we quantified this by lagged coherence. This measure allowed us to identify the β-rhythm as a peak in the lagged coherence spectrum. We have previously used lagged coherence to identify and localize the two sensorimotor rhythms using extracranial signals obtained by the MEG in humans and demonstrated that it outperforms Fourier power for this purpose (Fransen et al. 2015).

Interestingly, Leventhal et al. (2012) too identified β-rhythms, not based on the power spectrum, but on a measure of coherence: they used the coherence between areas in the network formed by cortex and basal ganglia. Coherence, both over time (lagged coherence) and over space, has the advantage over Fourier power that it does not depend on waveform amplitude (except via its contribution to the signal-to-noise ratio). Instead, it only depends on the degree of phase preservation between two signals and expresses this by a number between zero (no phase preservation) and one (perfect phase preservation). The fact that the only two reports of β-rhythms in vivo in rodents (and other nonprimates) have been based on coherence measures implies that studying coherence across time and/or space is a promising strategy for further studies of these sensorimotor rhythms in nonprimates.

GRANTS

This study was supported by the European Union's Framework Programme (FP7/2007–2013) Contract Grant 600925 (G. Dimitriadis and E. Maris); and the British Academy (Newton Fellowship) (F. van Ede).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

A.M.M.F. and E.M. conception and design of research; A.M.M.F., G.D., and F.v.E. performed experiments; A.M.M.F. analyzed data; A.M.M.F., F.v.E., and E.M. interpreted results of experiments; A.M.M.F. prepared figures; A.M.M.F. drafted manuscript; A.M.M.F., F.v.E., and E.M. edited and revised manuscript; A.M.M.F., G.D., F.v.E., and E.M. approved final version of manuscript.