Eliciting and Measuring Betrayal Aversion using the BDM Mechanism

Abstract

Betrayal aversion has been operationalized as the evidence that subjects demand a higher risk premium to take social risks compared to natural risks. This evidence has been first shown by Bohnet and Zeckhauser (2004) using an adaptation of the Becker – DeGroot – Marschak mechanism (BDM, Becker et al. (1964)). We compare their implementation of the BDM mechanism with a new version designed to facilitate subjects’ comprehension. We find that, although the two versions produce different distributions of values, the size of betrayal aversion, measured as an average treatment difference between social and natural risk settings, is not different across the two versions. We further show that our implementation is preferable to use in practice as it reduces substantially subjects’ mistakes and the likelihood of noisy valuations.

1. Introduction

Recent experimental evidence shows that people demand a higher risk premium when the source of risk is another person rather than nature (see Bohnet and Zeckhauser (2004), Bohnet et al. (2008)). Moreover, they prefer to opt out from a trust game and let their earnings be determined by a payoff – equivalent lottery to avoid learning whether their co – player betrayed them (Aimone and Houser (2011), Aimone and Houser (2012), Aimone and Houser (2013)). This evidence reveals that people anticipate the psychological cost of betrayal that they suffer on top of monetary costs.

This phenomenon, commonly referred to as betrayal aversion, has been first investigated by Bohnet and Zeckhauser (2004) (BZ, henceforth) using an adaptation of the Becker – DeGroot – Marschak mechanism (BDM, see Becker et al. (1964)). Their design compares so – called minimum acceptance probabilities (MAPs) between a social risk and a natural risk situation. A MAP is defined as the minimum probability of the good outcome that subjects require to choose a risky bet rather than a certain payoff. The finding that MAPs are on average higher in the social risk compared to the natural risk setting has been interpreted as evidence that subjects are betrayal averse.

In this paper, we ask whether different implementations of the BDM mechanism affect the elicitation of values and the measurement betrayal aversion in the BZ design. Our question is particularly important for two main reasons. First, recent evidence shows that the BDM mechanism may be empirically not reliable due to its complexity and to subjects’ misconceptions of the incentive structure (see, e.g., Cason and Plott (2014)). Second, the MAP design uses the BDM mechanism in an unusual way compared to the previous literature as it elicits a probability instead of a price. In most applications, the BDM mechanism is used in selling or buying tasks and subjects are asked the minimum price demanded to give up an object or the maximum price they would be willing to pay to buy the object. The MAP design, instead, asks subjects to reveal the minimum value of a probability that they would require to play a lottery. Arguably this may further increase the complexity of the mechanism.¹

In our experiment we simplify the original BZ instructions and procedures to minimize the risk of misconceptions and ask whether this has an impact on the elicitation of betrayal aversion. Study 1, reported in Section 2, consists of two experimental conditions: the open-ended (OE) condition replicates the design and procedures of BZ, whereas the choice list (CL) condition introduces a novel instrument and procedures intended to facilitate subjects’ comprehension.

Our results from Study 1 show that the way the BDM mechanism is presented to subjects has a significant impact on elicited values. The two elicitation methods generate statistically different distributions of data, with the CL distribution of MAPs being more peaked and presenting less variation. However, when we compare the estimated size of betrayal aversion (the average difference of MAPs in the social versus the natural risk situation), we find no differences between OE and CL.

We ask next which method is preferable to use in terms of truthful revelation. To answer this question, in Study 2, we conduct a survey with a sample of undergraduate students, where we compare the experimental instructions of OE and CL used in Study 1 on the basis of perceived complexity and number of mistakes made in a set of comprehension questions. We show that our CL instructions are better understood than the OE instructions in terms of both perceived complexity and number of mistakes in the comprehension questions. We discuss the implication of these findings in our concluding section.

2. Study 1 – Two versions of the BDM mechanism for the elicitation of betrayal aversion

2.1. Experimental design and procedures

Our design consists of two treatments: the OE and the CL treatment. The OE treatment is an exact replication of BZ.² The CL treatment introduces a new instrument, procedures and instructions to measure betrayal aversion.

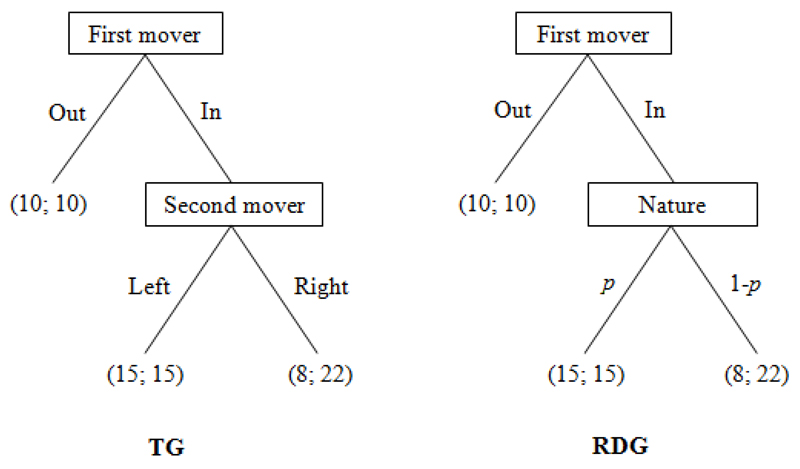
Following BZ, each of our treatments permits a between-subjects comparison of two conditions called trust game (TG) and risky dictator game (RDG).³ Figure 1 depicts the extensive form of TG and RDG. In both decision tasks, a first mover chooses between a certain and a risky option. The certain option gives 10 points to them and 10 to their counterpart. The risky option can produce either an unequal outcome of 8 points to the first mover and 22 to their counterpart or an equal split giving 15 points to both. While in TG, the outcome of the risky option is determined by a second mover, in RDG, it is determined by nature with the probabilities of outcomes (15; 15) and (8; 22) being respectively p and 1-p. This is the only difference between the two conditions.

Figure 1. Monetary payoffs in TG and RDG.

The variable of interest is the probability of the outcome (15; 15) which makes first movers indifferent between the certain and the risky option. Following BZ, we shall call this value the minimum acceptance probability (MAP). If the average difference in elicited MAPs between TG and RDG is positive, that is (MAP_TG – MAP_RDG > 0), subjects are on average betrayal averse as they require a higher risk premium in the social compared to the natural risk setting. In what follows, we describe our two treatments in detail.

Open ended (OE) elicitation of betrayal aversion (Bohnet and Zeckhauser (2004))

Both in TG and RDG, each first mover is asked to state directly the MAP by writing it down on their answer sheet. In particular, in TG each first mover is asked the following question:

“KEY QUESTION: How large would the probability p of being paired with a Person Y who chose Option 1 minimally have to be for you to pick Alternative B over Alternative A? (like any probability it must lie between 0 and 1).”⁴

At the same time, second movers are asked to reveal their strategy using the strategy method (Selten (1967)), namely they are asked whether they would choose to be trustworthy or not in case their first mover chooses In (Alternative B according to BZ labels). After collecting the answers, the experimenter computes the actual fraction of trustworthy second movers in the session and determines the decision of first movers according to their stated MAP. If their MAP is greater than the actual fraction of trustworthy second movers, they are deemed to choose Out (Alternative A). If, instead, their MAP is less or equal than the actual fraction of trustworthy second movers, they are deemed to choose In (Alternative B) and the outcome depends on their second mover’s choice. This mechanism to determine first movers’ action is known to first movers but unknown to second movers. Second movers only know that first movers will make a choice between In and Out.

In RDG, recipients are simply asked to wait for the decision of first movers. Each first mover is instead asked the following:

“KEY QUESTION: How large would the probability p of the lottery producing Option 1 minimally have to be for you to pick Alternative B over Alternative A? (like any probability, it must lie between 0 and 1).”

The mechanism to determine outcomes is similar to TG except that the elicited MAP is compared with a probability p which is predetermined before the experiment and unknown to subjects. If the stated MAP is greater than p, the subject is deemed to choose Out (Alternative A), while if the MAP is less or equal than p, the subject is deemed to choose In (Alternative B). At the end of the session the experimenter reveals the actual value of p and the lottery is implemented.

The advantage of the open-ended version is that it is fast to implement and it elicits values with high precision, because subjects can state “point” valuations. The main disadvantage is that, in standard implementations like selling or buying tasks, it is not clear whether subjects fully understand the functioning of the bidding mechanism (see Harrison and Rutstrom (2008)). In the context of probability elicitation, there is the risk that the mechanism and the wording of the “KEY QUESTION” may be even more obscure to subjects compared to standard implementations. For example, in a selling task the typical question would be something like “What’s the lowest price at which you would sell?” which less likely creates comprehension problems compared to the probability elicitation setting described above.

Our innovation – Choice list (CL) elicitation of betrayal aversion

The procedure used to elicit the decisions of second movers is identical to the OE treatment. First movers, instead, are presented with a choice list table. In TG, the first column of the table reports all the possible fraction of second movers choosing Left from “20 out of 20” to “0 out of 20” for a total of 21 rows. In the second column, subjects are asked to circle In or Out for each row. In RDG, everyone is told that a draw from an urn with a predetermined number of green and yellow balls will determine the outcome for the subjects who choose In. The first column of the table displays all the possible fractions of yellow balls (see Online Appendix A.3 for an example of the table). First movers have to circle In or Out for each possible number of yellow balls in the urn. It is further explained to subjects that only one row is relevant for earnings (the one corresponding to the actual number of trustworthy second movers or to the actual number of yellow balls), but that they will know which row is relevant only after they have taken their decisions.

We expect subjects to choose In in the first row of the table when the outcome (15; 15) is certain and switch to Out when the risk of being the sucker [unlucky] increases. We infer the MAPs from subjects’ choices by taking the middle point between the last probability for which they choose In and the first probability for which they choose Out going from the top to the bottom of the table.⁵

The CL treatment varies three elements compared to the OE treatment: the choice list format, the descriptions of second movers’ actions as frequencies instead of probabilities and the text of the instructions adding more detailed explanations and examples to make the mechanism as clear as possible (see Online Appendix A.2). The advantage of using the choice list format is that it is generally easy to explain to participants and it minimizes subjects’ confusion. However, it has two potential disadvantages. First, it elicits only interval values rather than “point” valuations and is, thus, less precise than the open-ended method. Second, it can be prone to framing effects, such as for example, subjects’ tendency to switch in the middle of the table rather than at their “true” value (see, e.g., Andersen et al. (2006)). Regarding the presentation of probabilities as frequencies, evidence from psychology has shown that statistical reasoning is improved if problems are presented using frequencies rather than percentages or probabilities (see Gigerenzer and Hoffrage (1995)). Thus, expressing the problem using frequencies may help subjects understand the functioning of the BDM mechanism.⁶

Procedures

All the sessions were conducted at the University of Nottingham. We used the instructions and control questions from Bohnet et al. (2008) for the OE treatment.⁷ We developed novel instructions and control questions for the CL treatment (see Online Appendix A.2). All the experimental sessions in both treatments were composed of several parts. In Part 1, we conducted the experiment reported in this paper and in the other parts we conducted other experiments reported in a companion paper (Cubitt et al. (2015)). Subjects knew of the existence but no details about subsequent parts while they were completing Part 1.

Our sample is composed by undergraduate student participants from various disciplines recruited via ORSEE (Greiner (2015)). Our sample was balanced across treatments in terms of relevant characteristics: in OE (CL) we had 50% (51%) females; 81% (82%) whose country of origin was a European country; average age was 20.4 (20.2); they participated on average in 3.5 (3.7) experiments before taking part in our sessions (t – test, p – value = 0.491). We conducted 16 sessions with 272 subjects in OE and 8 sessions with 320 subjects in CL. The OE and CL sessions were conducted one year apart (2011 and 2012, respectively) in the exact same period of the year. All outcomes were described as point earnings and converted at an exchange rate of £0.2 per point. Average hourly earnings were around £8.

2.2. Experimental Results

Result 1

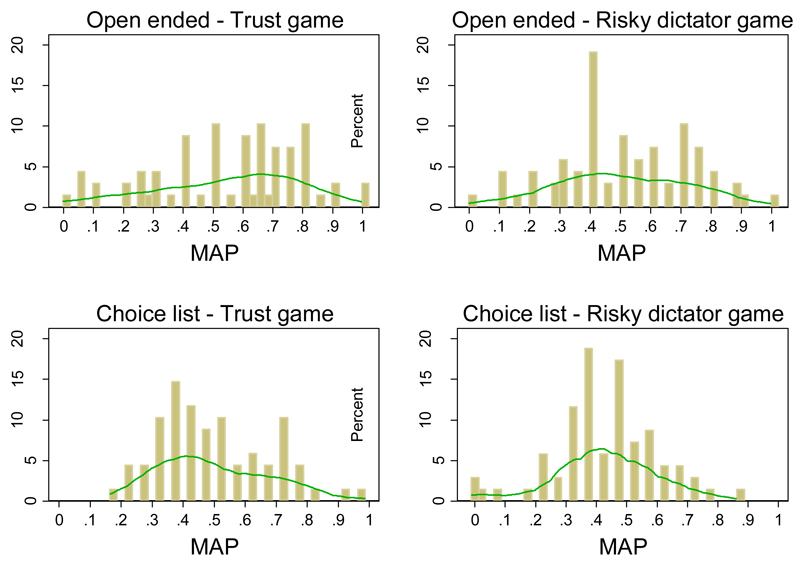
The two elicitation methods yield significantly different distributions of MAPs. CL generates significantly less variation and a more peaked distribution compared to OE.

Support

The support for Result 1 comes from Figure 2, where we show the histograms and estimated kernel density functions of MAPs in OE (two upper panels) and CL (two lower panels). The distribution of MAPs is statistically different across elicitation methods both in TG and RDG according to Kolmogorov – Smirnov tests (p = 0.029 and p = 0.042, respectively). OE generates a less peaked distribution as suggested by the kernel density estimates and less dispersion around the mean as revealed by the significantly higher standard deviation in OE compared to CL (standard deviations are 0.23 and 0.18, respectively; two – sided Levene test, p = 0.003). This is true also looking separately at TG and RDG (standard deviations are 0.25 and 0.22 in OE and 0.18 and 0.17 in CL, respectively; two-sided Levene-tests, p = 0.012 and p = 0.055, respectively).⁸

Figure 2. Distribution of MAPs across treatments.

Result 2

Betrayal aversion (MAP_TG - MAP_RDG) is 0.04 in OE and 0.07 in CL. Econometric analysis reveals that the size of betrayal aversion is not significantly different between the two elicitation methods.

Support

As a first step, in Table 1 we report the average MAP in each treatment for both methods separately and for the pooled sample. The size of betrayal aversion (MAP_TG − MAP_RDG) is similar across the two methods (0.04 in OE and 0.07 in CL). While the MAPs from TG and RDG are not statistically different according to a Mann – Whitney U-test in the OE treatment (z = 1.156, p = 0.248), they are significantly different in the CL treatment (z = 1.809, p = 0.070).⁹

Table 1.

Betrayal aversion in CL and OE treatments (mean (Std. dev.)).

	MAPTG	MAPRDG	MAPTG – MAPRDG
CL (n = 137)	0.50 (0.18)	0.43 (0.17)	0.07* (0.17)
OE (n = 136)	0.54 (0.25)	0.50 (0.22)	0.04 (0.23)
All (n = 273)	0.52 (0.22)	0.47 (0.20)	0.05** (0.21)

Notes: **p < 0.05, *p < 0.10 according to two-sided Mann-Whitney U-test. Every MAP is treated as an independent observation. For the difference between MAPs, we report the pooled standard deviation.

Overall, we observe that betrayal aversion is significant in our sample (z = 2.162, p = 0.031), but less prominent compared to the original studies by Bohnet and co-authors (the average difference in MAPs between TG and RDG is 0.15 in Bohnet et al. (2008)). However, we also notice that other studies using BZ design have found smaller size of betrayal aversion in line with our results (0.07 in Hong and Bohnet (2007)¹⁰, 0.08 in Dreber et al. (2013), 0.07 Butler and Miller (2014), and 0.04 in Aimone et al. (2015) using a within-subject version of BZ design).

As a second step, we use regression analysis to directly compare the two methods. We report OLS regression estimates in Table 2. In Model (1), we regress the variable MAP on two treatment dummies: TG takes value 1 if the observation is collected in TG and zero otherwise and OE takes value 1 if the observation is collected using the OE version and zero otherwise. The estimated coefficient of TG suggests that MAPs increase significantly by 5 percentage points in TG compared to RDG. This supports the presence of significant betrayal aversion in our entire sample. Additionally, the OE’s coefficient reveals that MAPs elicited with the OE method are on average almost 6 percentage points higher than the ones elicited with the CL mechanism.

Table 2.

OLS regressions. Dependent variable: MAPs.

	(1)	(2)	(3)
TG	0.055**	0.053**	0.072**
	(0.025)	(0.024)	(0.029)
OE	0.059**	0.060**	0.079**
	(0.025)	(0.024)	(0.033)
TG × OE			-0.039
			(0.049)
Female		0.108***	0.108***
		(0.024)	(0.024)
Intercept	0.438***	0.383***	0.374***
	(0.019)	(0.023)	(0.025)
N	273	273	273
R2	0.037	0.103	0.105

Notes: Robust standard errors in parentheses. *p < 0.10, **p < 0.05, ***p < 0.01.

In Model (2) we control for the gender of the participants by including the dummy “Female”. The inclusion of this control has no effect neither on the size nor on the significance of the treatment dummies and improves the overall fit of the model as suggested by the R². Interestingly, females report significantly higher MAPs than males both in TG and RDG. This is in line with the finding that women tend to be generally more averse to risks than men (Croson and Gneezy (2009)).

Model (3) adds the interaction term between the variables TG and OE to Model (2). If the size of betrayal aversion elicited in CL is significantly higher than the one elicited in OE, we should expect the interaction term to be negative and significant. Although the sign is indeed negative, the coefficient is not significant. This leads us to conclude that, although the two methods generate different distributions of values, this does not translate in statistically different estimates of the average treatment difference between TG and RDG.

We ask next which of the two methods is preferable to use in practice. Drawing from the results of Study 1, we notice that different conclusions on the significance of betrayal aversion could be reached depending on the method used. Hence, it is important to assess which of the two methods is better suited to elicit subjects’ “true” valuations. We observe a general tendency of CL to generate less extreme values and less variation in the distribution of MAPs compared to OE. This could be due to a framing effect of the choice list, if subjects are led to switch more in the middle of the table. However, it could also be that subjects are less confused and these extreme values are in fact noisy valuations that the CL version helps to eliminate.

One way to assess whether this is the case is to check subjects’ understanding in OE and CL. We conjecture that the comprehension of procedural aspects of the mechanism will be inversely related to the noise present in the elicited distributions of MAPs, and thus measuring subjects’ understanding would reveal which method minimizes subjects’ misconceptions.

3. Study 2 – Assessing subjects’ understanding of the instructions

In Study 2, we conduct an online survey study where we compare the instructions of OE and CL.

3.1. Survey design and procedures

Our participants were undergraduate students (n = 209) from the University of Nottingham who had not taken part in the experiments reported in Section 2. We recruited subjects through ORSEE (Greiner (2015)). Upon their acceptance to participate in our online survey, subjects were told that the task was part of a research project and were invited to read an instruction document. After reading the instructions, they were asked a set of comprehension questions. Participants were informed before they started the task that they would not participate in the experiment. In Question 1, subjects had to answer the following: “How difficult do you think the instructions are?” on a scale from 0 to 10, where 0 corresponds to “very difficult” and 10 to “very easy.” Questions 2 and 3, each of which comprises three sub-items, were hypothetical scenarios where subjects in the role of the first movers were asked questions on the functioning of the BDM mechanism (see Online Appendix A.1 for the list of questions). Subjects were presented only the experimental instructions from TG. We assume that any difference would translate analogously to RDG. Participants were entered in a prize draw if they completed the task. There were two prizes of £50 each.

3.2. Survey Results

In Table 3 we report the average response (standard deviation) to Question 1 and the percentage of mistakes in Question 2 and 3. The self-reported assessment of difficulty (Question 1) reveals that CL is perceived significantly easier than OE (MWU-test, z = – 4.307, p = 0.000). Furthermore, when we look at the comprehension questions, we also find that, for all sub-items of Question 2 and 3, the percentage of mistakes is significantly lower in CL than OE. These results suggests that CL is significantly easier for subjects and that we were successful in reducing subjects’ confusion and mistakes.

Table 3.

Answers to comprehension questions in CL and OE

	CL (n = 107)	OE (n = 102)	Tests	p-value
Question 1	6.40 (2.34)	4.90 (2.40)	Mann-Whitney	0.000
Question 2
a)	5.6%	23.5%	χ2test	0.000
b)	14%	27.5%	χ2test	0.016
c)	15%	26.5%	χ2test	0.040
Question 3
a)	20.6%	32.4%	χ2test	0.053
b)	38.3%	59.8%	χ2test	0.002
c)	39.3%	60.8%	χ2test	0.002

Notes: all percentages are percentages of wrong answers.

4. Conclusion

In this paper, we have compared two implementations of the BDM mechanism for the elicitation of betrayal aversion in the BZ design. Overall, our results confirm the presumption that valuations elicited through the BDM mechanism may be biased due to subjects’ mistakes and misconceptions of the incentive system. We further show that these mistakes can be reduced by employing a set of instructions that make the decision situation as clear as possible.

Despite no difference was found in the estimated size of betrayal aversion across OE and CL elicitations, our results indicate that valuations are significantly noisier in the OE version (Table 3) and different conclusions on the significance of betrayal aversion could be reached depending on the method used (Table 1). Hence, researchers should be careful in using a version of the mechanism that minimizes subjects’ mistakes to make reliable inferences. In this sense, our CL version constitutes a significant improvement compared to OE.