When and Where to Transfer for Bayes Net Parameter Learning

Abstract

Learning Bayesian networks from scarce data is a major challenge in real-world applications where data are hard to acquire. Transfer learning techniques attempt to address this by leveraging data from different but related problems. For example, it may be possible to exploit medical diagnosis data from a different country. A challenge with this approach is heterogeneous relatedness to the target, both within and across source networks. In this paper we introduce the Bayesian network parameter transfer learning (BNPTL) algorithm to reason about both network and fragment (sub-graph) relatedness. BNPTL addresses (i) how to find the most relevant source network and network fragments to transfer, and (ii) how to fuse source and target parameters in a robust way. In addition to improving target task performance, explicit reasoning allows us to diagnose network and fragment relatedness across BNs, even if latent variables are present, or if their state space is heterogeneous. This is important in some applications where relatedness itself is an output of interest. Experimental results demonstrate the superiority of BNPTL at various scarcities and source relevance levels compared to single task learning and other state-of-the-art parameter transfer methods. Moreover, we demonstrate successful application to real-world medical case studies.

1. Introduction

Bayesian networks have proven valuable in modeling uncertainty and supporting decision making in practice (Pearl, 1988; Fenton and Neil, 2012). However, in many applications it is hard to acquire sufficient examples to learn BNs effectively from data. For example, in a small hospital or country there may be insufficient data to learn an effective medical diagnosis network. However, directly applying a network learned in another domain may be inaccurate or impossible because the underlying tasks may have quantitative or qualitative differences (e.g., care procedures vary across hospitals and countries). In this paper we investigate leveraging BNs in different but related domains to assist learning a target task with scarce data. This is an important capability in at least two distinct scenarios: (i) those where the source tasks are the same as the target, but have different specific statistics (e.g., due to different demographic statistics in another country), and (ii) those where the source tasks are related to the target in a piecewise way, (the target and source tasks are not the same, but share common sub-graphs, e.g., two hospitals share a subset of procedures; or two diseases share a subset of symptoms).

The proposed contribution falls under the topical area of transfer learning (Torrey and Shavlik, 2009; Pan and Yang, 2010) (also known as domain adaptation), which aims to significantly reduce data requirements by leveraging data from related tasks. Transfer has been successfully applied in a variety of machine learning areas for example, recommendations (Pan et al., 2012), classification (Li et al., 2012; Ma et al., 2012) and natural language processing (Collobert and Weston, 2008). Central challenges include computing when to transfer (transfer or not depending on relevance), from where (which of multiple sources of varying relevance) (Eaton et al., 2008; Mihalkova and Mooney, 2009) and how (how to fuse source and target information). These are crucial to ensure that transfer is helpful, and avoid ‘negative transfer’ risk (Pan et al., 2012; Seah et al., 2013a). Despite the popularity of transfer learning, limited work (Luis et al., 2010; Niculescu-mizil and Caruana, 2007; Oyen and Lane, 2012) has been done on transfer learning of BNs. Outstanding challenges in BN transfer include dealing automatically with from where to transfer, transferring in the presence of latent variables and transferring between networks with heterogeneous state spaces. In this paper we introduce the first framework that resolves these issues in a BN context, leveraging the structured nature of BNs for piecewise transfer, so multiple sources of partial relevance and potentially heterogeneous state spaces can be exploited.

In this paper we assume the target and source domain structures are provided¹ and concentrate on the challenges of learning the target network parameters in the presence of latent variables and from multiple sources of varying – continuous and/or piecewise – relevance. Importantly, we do not require that the source and target networks correspond structurally, or that node names are shared. Our novel solution involves splitting the target and source BNs into fragments (sub-graphs) and then reasoning explicitly about both network-level and fragment-level relatedness. Reasoning simultaneously about both is important, because pure fragment-level relatedness risks over-fitting if there are many sources. We achieve this via an Expectation Maximization (EM) style algorithm that alternates between (i) performing a Bayesian model comparison to infer per-fragment relatedness and (ii) updating a source network relatedness prior. This solves when and from where to transfer at both coarse and fine-grained level. Finally, the actual transfer is performed per-fragment using Bayesian model averaging to robustly fuse the source and target fragments, addressing how and how much to transfer. In this way we can deal robustly with a variety of transfer scenarios including those where the source networks are: (i) highly relevant or totally irrelevant, (ii) have the same or heterogeneous state spaces and (iii) uniform or piecewise (varying per sub-graph) relevance. Our explicit network and fragment relatedness reasoning also provides a diagnostic of which networks/domains are similar, and which sub-graphs are common or distinct. This is itself an important output for applications where quantifying relatedness, and uncovering the source of heterogeneity between two domains is of interest (e.g., revealing differences in treatment statistics between hospitals). To evaluate our contribution, we conduct experiments on six standard networks from a BN repository, comparing against various single task baselines and prior transfer methods. Finally, we apply our method to transfer learning in two real-world medical networks.

2. Related Work

Expert Elicitation. An advantage of BNs is their interpretable nature means that experts can define variables, structure and parameters in the absence of data. Nevertheless, learning BNs from data is of interest because there are many situations for which there is no available expert judgment, or where it may not be possible to elicit the conditional probability tables (CPTs). Studies have therefore tried to bridge the gap between these two paradigms. Most typically, experts specify a semantically valid network structure, and CPTs are learned from data. Recently, expert specified qualitative constraints on CPTs have been exploited to improve parameter learning. This is done, for example, via establishing a constrained optimization problem (Altendorf, 2005; Niculescu et al., 2006; de Campos and Ji, 2008; Liao and Ji, 2009; de Campos et al., 2009) or auxiliary BNs (Khan et al., 2011; Zhou et al., 2014a,b). In this study we exploit the ability of experts to easily specify a network structure and focus on transfer to improve quantitative estimation of parameters.

CPTs combination. When there is limited training data, researchers have attempted to construct CPTs from different relevant sources of information. Given a set of CPTs involving the same variables, conventional methods to aggregate them are linear aggregation (i.e., weighted sum) and logarithmic aggregation (Genest and Zidek, 1986; Chang and Chen, 1996; Chen et al., 1996). Based on this, the work of (Luis et al., 2010) introduced the DBLP (distance based linear pooling) and LoLP (local linear pooling) aggregation methods by considering the CPTs’ confidences and similarities learnt from the original datasets. This method highlighted the importance of measuring the weights/confidences of different CPTs. However, the method is a too simplistic heuristic: confidence values depend only on the CPT entry size and dataset size, without considering the fit to the target training data.

Transfer Learning. Transfer learning in general is now a well studied area, with a good survey provided by (Pan and Yang, 2010). Extensive work has been done on transfer and domain adaptation for flat machine learning models, including unsupervised transfer and analysis of relatedness (Duan et al., 2009; Seah et al., 2013b,a; Eaton et al., 2008). However, these studies have generally not addressed one or more of the important conditions that arise in the BN context addressed here, notably: transfer with heterogeneous state space, piece-wise transfer from multiple sources (a different subset of variables/dimensions in each source may be relevant), and scarce unlabeled target data (thus precluding conventional strategies that assume ample unlabeled target data, such as MMD (Huang et al., 2007; Seah et al., 2013b)).

Transfer Learning in BNs. In the context of transfer learning in BNs, the multi-task framework of (Niculescu-mizil and Caruana, 2007) considers structure transfer. However, it assumes that all sources are equally related and simply learns the parameters for each task independently. Kraisangka and Druzdzel (2014) construct BN parameters from a set of regression models used in survival analysis. However, this method cannot be generalized to transfer between BNs. The transfer framework of (Luis et al., 2010) covers a more similar parameter transfer problem to ours and proposes a method to fuse source and target data. However, the heuristic CPT fusion used assumes every source is both relevant and equally related. It is not robust to the possibility of irrelevant sources and does not systematically address when, from where, and how much to transfer (as shown by our experiments where this method significantly underperforms ours). The study (Oyen and Lane, 2012) considers multi-task structure learning, again with independently learned parameters. They investigate network/task-level relatedness, showing transfer performs poorly without knowledge of relatedness. However, they address this by using manually specified relatedness. Finally, a recent study (Oates et al., 2014) improves this by automatically inferring the network/task-level relatedness. However, they do not consider information sharing of parameters. In contrast, we explicitly learn about both network and fragment-level relatedness from data. None of these prior studies cover transfer with latent variables or heterogeneous state spaces.

A related area to BN transfer is transfer in Markov Logic Networks (MLNs) (Mihalkova et al., 2007; Davis and Domingos, 2009; Mihalkova and Mooney, 2009). In contrast to these studies, our approach has the following benefits: We can exploit multiple source networks rather than exactly on each; we automatically quantify source relevance and are robust to some or all irrelevant sources (rather than assuming a single relevant source); these MLN studies use the transferred clauses directly rather than weighting the resulting transfer by estimated relevance.

3. Model Overview

3.1. Notation and Definitions

In a BN parameter learning setting, a domain 𝓓 = {V, G, D} consists of three components: variables V = {X₁, X₂, X₃, …, X_n} corresponding to nodes of the BN, associated data D, and a directed acyclic graph G encoding the statistical dependencies among the variables. The conditional probability table (CPT) associated with every variable specifies the probability p (X_i|pa(X_i)) of each value given the instantiation of its parents as defined by graph G. Within a domain 𝓓, the goal of parameter learning is to determine parameters for all p(X_i|pa(X_i)). This is conventionally solved by maximum likelihood estimation (MLE) of CPT parameters $\theta ,\widehat{\theta }={\text{arg max}}_{\theta }\text{log}p(D|\theta ).$ We denote this setting Single Task Learning (STL). The related notation in this paper are listed in Table 1.

Table 1.

Notation used in this paper for the Bayesian network transfer learning task.

Index	Notation	Description
1	${𝓓}^t$	The jth fragment in target domain
2	${𝓓}_k^s$	The kth fragment in the sth source domain
3	Hs	Hypothesis of domain-level relatedness between 𝓓t and 𝓓s
4	$H_{jk}^s$	Hypothesis of fragment-level relatedness: $H_{jk}^s\in \{H_{jk1}^s,H_{jk0}^s\}$
5	$H_{jk1}^s$	Hypothesis of two fragments ${𝓓}_j^t$ and ${𝓓}_k^s$ share a common CPT
6	$H_{jk0}^s$	Hypothesis of two fragments ${𝓓}_j^t$ and ${𝓓}_k^s$ have distinct CPT
7	${𝓓}_j^t$	The data for the jth fragment in target domain
8	${𝓓}_k^s$	The data for kth fragment in the sth source domain

In this paper, we have one target domain 𝓓^t, and a set of sources ${\left\{{𝓓}^s\right\}}_{s=1}^S,S\ge 1.$ The target domain and each source domain have training data $D^t=\left\{d_1^t,d_2^t,\dots ,d_N^t\right\}$ and $D^s=\left\{d_1^s,d_2^s,\dots d_{M^s}^s\right\}.$ For transfer learning we are interested in the case where target domain data is relatively scarce: 0 < N ≪ M^s, and/or N is small relative to the dimensionality of the target problem N ≪ n². Following the definition of transfer learning in (Pan and Yang, 2010), we define BN parameter transfer learning (BNPTL).

Definition 1 BNPTL. Given a set of source domains {𝓓^s} and a target domain 𝓓^t, BN parameter transfer learning aims to improve the parameter learning accuracy of the BN in 𝓓^t using the knowledge in {𝓓^s}.

This task corresponds to the problem of estimating the target domain CPTs θ^t given all the available domains:

$${\widehat{\theta }}^t=\text{arg}\hspace{0.17em}\underset{{\theta }^t}{\text{max}}p({\theta }^t|{𝓓}^t,\{{𝓓}^s\})$$ (1)

If the networks correspond (V^t = V^s, G^t = G^s) and relatedness is assumed, then this could be simple MAP or MLE with count-aggregation. In the more realistic case of 𝓓^s ≠ 𝓓^t due to different training data sets with different statistics and thus varying relatedness; and potentially heterogeneous state spaces V, then the problem is much harder. More specifically, we consider the case where dimensions/variables in each domain do not correspond V_s ≠ V_t. They may be disjoint $V_s\cap V_t=\varnothing ,$ or partially overlap $V_s\cap V_t\ne \varnothing .$ However any correspondence between them is not assumed given (variable names are not used). In the following we describe an algorithm to maximize Eq (1) by proxy.

3.2. BN Parameter Transfer Learning

Typically, transfer learning methods calculate relatedness at domain or instance level granularity. However, in real-world applications, that relevance may vary within-domain – such that different subsets of features/variables may be relevant to different source domains. In order to learn a target domain 𝓓^t leveraging sources {𝓓^s} with piecewise relatedness, or heterogeneity V^t ≠ V^s and G^t ≠ G^s, we transfer at the level of BN fragments.

Definition 2 BN fragment. A Bayesian network of domain 𝓓 can be divided into a set of sub-graphs (denoted fragments) 𝓓 = {𝓓_f} by considering the graph G. Each fragment 𝓓_f = {V_f, G_f, D_f} is a single root node or a node X_i with its direct parents pa(X_i) in the original BN, and encodes a single CPT from the original BN. The number of fragments is the number of variables in the original BN.

To realize flexible BN parameter transfer, the target domain and source domains are all broken into fragments ${\mathbf{𝓓}}^t=\{{\mathbf{𝓓}}_f^t\},$ ${\mathbf{𝓓}}^s=\left\{\left\{{\mathbf{𝓓}}_f^s\right\}\right\}$. Assuming for now no latent variables in the target domain, then each fragment j can be learned independently ${\widehat{\theta }}_j^t=\arg {\max }_{{\theta }_j^t}p({\theta }_j^t|{\mathbf{𝓓}}_j^t,\{\left\{{\mathbf{𝓓}}_f^s\right\}\}).$ To leverage the bag of source domain fragments $\left\{\right\{{\mathbf{𝓓}}_f^s\left\}\right\}$ in learning each ${\theta }_j^t,$ we consider each source fragment ${\mathbf{𝓓}}_k^s$ as potentially relevant. Specifically, for each target fragment, every source fragment is evaluated for relatedness and the best fragment mapping is chosen. Once the best source fragment is chosen for each target, a domain/network-level relatedness prior is re-estimated by summing the relatedness of its fragments to the target. The knowledge from the best source fragment for each target is then fused according to its estimated relatedness.

To realize this strategy, four issues must be addressed: (1) which source fragments are transferable, (2) how to deal with variable name mapping, (3) how to quantify the relatedness of each transferrable source fragment in order to find the best one and (4) how to fuse the chosen source fragment. We next address each of these issues in turn:

Fragment Compatibility For a target fragment j and putative source fragment k with continuous sate spaces, we say they are compatible if they have the same structure. For fragments with discrete and finite state spaces, we say they are compatible if they have the same structure² and state space. That is, the same number of states and parents states³, so

$$compatible\left(G_j^t,G_k^s\right)=\{\begin{array}{l}1if\hspace{0.17em}{G}_j^t=G_k^s\hspace{0.17em}\&\hspace{0.17em}\text{dims}({\theta }_j^t)=\text{dims}({\theta }_k^s)\\ 0\text{otherwise}\end{array}$$

This definition of compatibility could be further relaxed quite straightforwardly (e.g., allowing target states to aggregate multiple source states) at the expense of additional computational cost. However, while relaxing the condition of compatibility would improve the range of situations where transfer can be exploited, it would also increase the cost of the algorithm by increasing the number of allowed permutations, as well as decreasing robustness to negative transfer (by potentially allowing more ‘false positive’ transfers from irrelevant sources). This is an example of pervasive trade-off between maximum exploitable transfer and robustness to negative transfer (Torrey and Shavlik, 2009).

Fragment Permutation Mapping For two fragments j and k determined to be compatible, we still do not know the mapping between variable names. For example if j has parents [a, b] and k has parents [d, c], the correspondence could be a − d, b − c or b − d, a − c. The function permutations$(G_j^t,G_k^s)$ returns an exhaustive list of possible mappings P_m that map states of k to states of j.

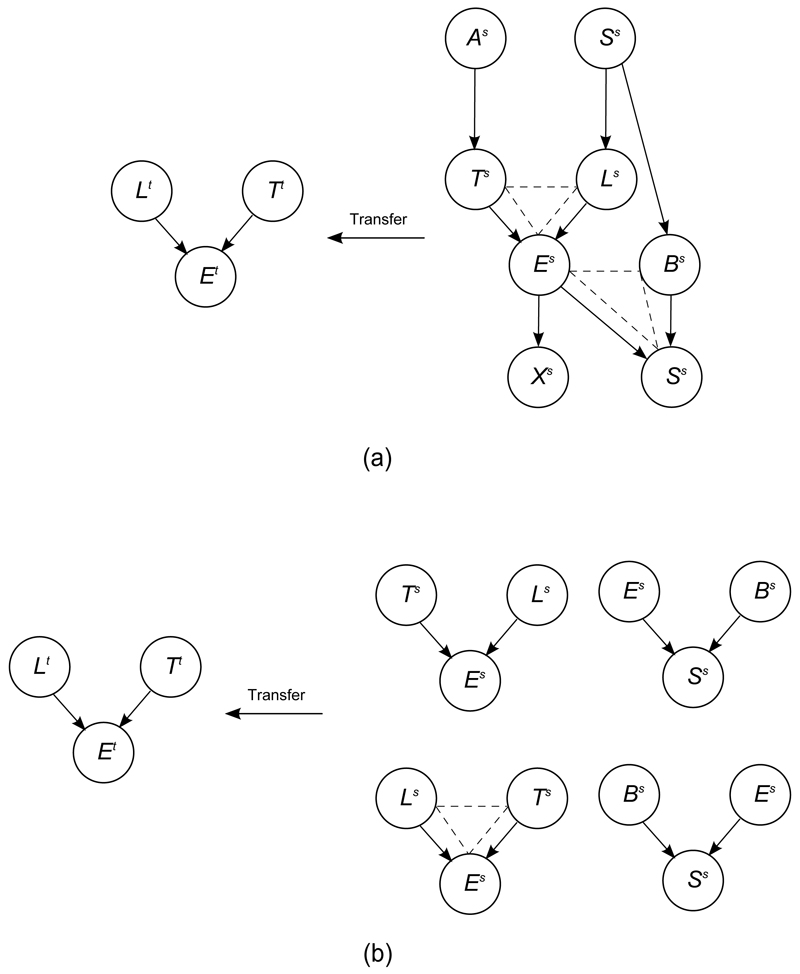
Here we provide an illustrative example of fragment-based parameter transfer: the target is a three node BN shown in the left part of Figure 1 (a), and the source is a eight node BN shown in the right part of Figure 1 (a). In Figure 1 (b), there are two source fragments ({T^s, L^s, E^s} and {E^s, B^s, S^s}) which are compatible with target fragment. Thus, there are four permutations of compatible source fragments (assuming binary parent nodes). All four of these options are then evaluated for fitness, and the best fragment and permutation is picked (shown with dashed triangle in Figure 1 (b)). Finally, this selected fragment and permutation will be fused with target fragment via our fusion function.

Figure 1.

A simple example to show the fragment compatibility measurement, and the permutations of all possible parental nodes in a fragment. (a) The dashed triangle represents source fragments {T^s, L^s, E^s} and {E^s, B^s, S^s}, which are compatible with the target fragment. (b) All the permutations of compatible source fragment, and the most fit one {L^s, T^s, E^s}.

We next discuss the more critical and challenging questions of how a particular target fragment G_j and specific permuted source fragment $P_m\left(G_k^s\right)$ are evaluated for relevance, and how relevant sources are fused.

3.3. Fitness Function

To measure the relatedness between compatible target and source fragments ${\mathbf{𝓓}}_j^t$ and ${\mathbf{𝓓}}_k^s$, we introduce a function fitness $({\mathbf{𝓓}}_j^t,{\mathbf{𝓓}}_k^s,p\left(H^s\right))$, where p(H^s) is a domain-level relatedness prior. Here we consider a discrete random variable indexing the related source s among S possible sources. So p(H^s) is a S-dimensional multinomial distribution encoding the relatedness prior. In this section, for notational simplicity we will use t and s to represent the jth target and kth source domain fragments under consideration.

A systematic and robust way to compare source and target fragments for relevance is to compute the probability that the source and target data share a common CPT (hypothesis⁴ $H_1^s$) versus having distinct CPTs (hypothesis $H_0^s$). This idea was originally proposed in a recent work (Zhou et al., 2015), which is called as Bayes model comparison (BMC) for hypotheses $H^s\in \left\{H_1^s,H_0^s\right\}$ is:

$$p\left(H_1^s|D^s,D^t\right)\propto {\displaystyle \int p\left(D^t|\theta \right)}p\left(\theta |D^s,H_1^s\right)p\left(H_1^s\right)d\theta ,p\left(H_0^s|D^s,D^t\right)\propto {\displaystyle \int p\left(D^t|{\theta }^t\right)p\left({\theta }^t|H_0^s\right)}p\left(H_0^s\right)d{\theta }^t.$$ (2)

where we have made the following conditional independence assumptions: $D^s\perp H_1^s$, $D^t\perp \left\{D^s,H_1^s\right\}|\theta$ and ${\theta }^t\perp D^s,H_0^s.$

For discrete likelihoods p(D|θ) and Dirichlet priors p(θ|H^s), integrating over the unknown CPTs θ, the required marginal likelihood is the Dirichlet compound multinomial (DCM) or multi-variate Polya distribution:

$$p\left(D^t|D^s,H_1^s\right)=\frac{\Gamma \left(A^{X^s}\right)}{\Gamma \left(N^{X^t}+A^{X^s}\right)}{\displaystyle \prod _{c=1}^C\frac{\Gamma \left(n_c^{X^t}+{\alpha }_c^{X^s}\right)}{\Gamma \left({\alpha }_c^{X^s}\right)}}$$ (3)

where c = 1 …C index variable states, $n_c^{X^t}$ is the number of observations of the cth target parameter value in data D^t, and $N^{X^t}={\sum }_c{n}_c^{X^t};{\alpha }_c^{X^s}$ indicates the aggregate counts from the source domain and distribution prior, and $A^{X^s}={\sum }_c{\alpha }_c^{X^s}.$

Maximal fitness(·) is achieved when the target data are most likely to share the same generating distribution as the source data. As we can see, previously proposed fitness function (Zhou et al., 2015) only addresses discrete data with Dirichlet conjugate priors. In this paper, we derive the analogous computations for continuous data with Gaussian likelihood with Normal-Inverse-Gamma conjugate priors.

$$p\left(D^t|D^s,H_1^s\right)={\displaystyle \prod _{i=1}^N(\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{2{\alpha }_m+1}{2}\right)}{\Gamma \left(\frac{2{\alpha }_m}{2}\right)}\sqrt{\frac{\Lambda }{2{\alpha }_m}}{\left(1+\frac{\Lambda {\left(d_i^t-{\mu }_m\right)}^2}{2{\alpha }_m}\right)}^{-\left(\frac{2{\alpha }_m+1}{2}\right)})}$$ (4)

where $\Lambda =\frac{{\alpha }_m{k}_m}{{\beta }_m\left(k_m+1\right)},$ the hyperparameters µ_m, k_m, α_m and β_m are updated based on the source data $D_k^s,$ which contains M samples with center at ${\overline{d}}^s$:

$$\{\begin{array}{c}{\mu }_m=\frac{k_0{\mu }_0+M{\overline{d}}^s}{k_0+M}\\ k_m=k_0+M\\ {\alpha }_m={\alpha }_0+\frac{M}{2}\\ {\beta }_m={\beta }_0+\frac{1}{2}{\displaystyle {\sum }_{i=1}^M{(d_i^s-{\overline{d}}^s)}^2+\frac{k_{0}M{({\overline{d}}^s-{\mu }_0)}^2}{2(k_0+M)}}\end{array}$$ (5)

Transfer Prior: The final outstanding component of BMC is how to define the transfer prior p(H^s). We assume that transfer is equally likely a priori within a given source domain, but that different source domains may have different prior relatedness. Thus we set the transfer prior for a particular fragment pair to the prior for the corresponding source network, i.e., $p(H_{jk1}^s)=p(H^s).$ The fragment transfer prior $p(H_{jk}^s)$ is then normalised as $p(H_{jk0}^s)=1-p(H_{jk1}^s).$

3.4. Fusion Function

Once the best source fragment ${\mathbf{𝓓}}_k^s$ is found for a given target fragment ${\mathbf{𝓓}}_j^t$, the next challenge is how to optimally fuse them. Our solution (denoted BMA) is to infer the target CPT, integrating over uncertainty about whether the selected source fragment is indeed relevant or not (i.e., if they share parameters or not – $H_1^s$ and $H_0^s$ in last section).

We perform Bayesian model averaging, summing over these possibilities. Specifically, we ask $p\left({\theta }^t|D^t,D^s\right)={\displaystyle {\sum }_{H^s}p({\theta }^t,H^s|D^t,D^s})$ which turns out to be:

$$\begin{array}{l}p\left({\theta }^t|D^t,D^s\right)=p(H_1^s|D^t,D^s)Dir(\theta ;\alpha +N^{X^t}+N^{X^s})+p(H_0^s|D^t,D^s)Dir(\theta ;\alpha +N^{X^t})\end{array}$$ (6)

where p(H^s|D^t, D^s) comes from Eq (2). This means the strength of fusion is automatically calibrated by the estimated relevance. Since there is no closed form solution for the sum of Dirichlets, we approximate Eq (6) by moment matching. For conditional Gaussian nodes, the weighted sum is also approximated by moment matching.

Moment matching (also known as Assumed Density Filtering (ADF)) is to approximate a mixture such as Eq (6) by a single distribution whose mean and variance is set to the mean and variance of the weighted sum. The estimated relatedness provides the weights $w_1=p\left(H_1^s|D^t,D^s\right)$, $w_0=p\left(H_0^s|D^t,D^s\right)$. Assuming the posterior mean and variance of the parameters in the related and unrelated condition are u₁, v₁ and u₀, v₀ respectively. Then the approximate posterior mean is u = w₁u₁ + w₀u₀, and variance is v = w₁(v₁ +(u₁ − u)² + w₀(u₀ − u)² (Murphy, 2012). For Gaussian distributions we can use this directly. For Dirichlet distributions with parameter vector α, the variance parameter $v=1/{\displaystyle \sum \alpha }$, and the mean parameter vector is u = vα.

3.5. Algorithm Overview

An overview of our BNPTL framework is given in Algorithm 1. Each target fragment is compared to all permutations of compatible source fragments and evaluated for relevance using BMC fitness. The most relevant source fragment and permutation is assigned to each target fragment. The network-level relevance prior is re-estimated based on aggregating the inferred fragment relevance for that source: $p(H^s)\propto {\sum }_{jk}p(H_{jk}^s|{\mathbf{𝓓}}_j^t,{\mathbf{𝓓}}_k^s).$ This way of updating the source network prior reflects the inductive bias that fragment should be transferred from fewer distinct sources, or that a source network that has already produced many relevant fragments is more likely to produce further relevant fragments and should be preferred.

Algorithm 1: BNPTL.

INPUT : Target domain 𝓓^t, Sources {𝓓^s}

OUTPUT: ${\theta }^t=\{{\theta }_j^t\}$ and p(H^s)

1 Initialize the domain-level relatedness p(H^s) (uniform);

2 repeat

3        for target fragment j = 1 to J do

4             for source network s = 1 to S and fragment k = 1 to K do

5                  if compatible $(G_j^t,G_k^s)$ then

6                       P = permutations$\left({𝒟}_k^s\right)$;

7                      for permutation m = 1 to M do

8                          measure relatedness:

                          $fitness({\mathbf{𝓓}}_j^t,P_m^{sk}({\mathbf{𝓓}}_k^s),p\left(H^s\right))=$

                          $p(H_{jk1}^s|D_j^t,P_m^{sk}\left(D_k^s\right));$

9                    end

10            end

11      end

12   end

13  for source network s = 1 to S do

14        Re-estimate network relevance: $p\left(H^s\right)\propto {\displaystyle {\sum }_{jk}p(H_{jk}^s|D_j^t,D_k^s);}$

15  end

16 until convergence;

17 for target fragment j = 1 to J do

18       Find the best source and permutation:

          $k^{\prime },s^{\prime },m^{\prime }=\arg \underset{}{{\max }_{k,s,m}}p(H_{jk1}^s|D_j^t,P_m^{sk}\left(D_k^s\right));$

19      ${\theta }_j^t=fusion({\mathbf{D}}_j^t,P_{m^{\prime }}^{s^{\prime }{k}^{\prime }}\left({\mathbf{D}}_{k^{\prime }}^{s^{\prime }}\right));$

20 end

21 return ${\theta }^t=\{{\theta }_j^t\}$ and p(H^s)

Finally, the most relevant source fragment for each target is fused using BMA. If there are missing or hidden data in the target domain, we start by running the standard EM algorithm in the target domain, to infer the states of each hidden variable. We use these expected counts to fill in D^t when applying BNPTL.

Properties. Our BNPTL has a few favorable properties worth noting: (i) If there is no related source fragment, then the most related source fragment will have estimated relatedness near zero and no transfer is performed $\left(p(H_1^s|D^t,D^s\right)\approx 0$ in Eq (6)). This provides some robustness to irrelevant sources (as explored in Section 4.7–4.8). (ii) Although we rely on an EM procedure to estimate fragment and source relatedness, starting from a uniform prior p(H^s), our algorithm is deterministic and we use only one run to get results, (iii) Explicitly reasoning about both fragment and network level relatedness allows the exploitation of heterogeneous relevance both within and across source domains.

Computational Complexity. The computational complexity of this algorithm lies in the total number of relatedness estimates. We treat a relatedness calculation as an elementary operation O(1). Assuming there are J target fragments, S′ compatible source fragments (typically much less than total number of source fragments S), and each fragment has v parent nodes. Then the time complexity of each EM iteration in BNPTL is: O(JS′v!). Where v! is the total number of permutations searched to transfer a compatible fragment pair. In practice it always converged in 10-30 EM iterations. For example, I took 0.47 seconds to process Asia network (see Table 4, row 7) on our computer (Intel core i7 CPU 2.5 GHz).

Table 4.

Performance (unknown correspondences and hidden variables) of STL and transfer learning methods: CPTAgg and BNPTL.

Name	Hidden Vars	STL	CPTAgg	BNPTL
Weather	None	0.03±0.02	0.02±0.02	0.02±0.02
	1	0.55±0.07*	0.41±0.00	0.45±0.01*
	2	0.59±0.00*	0.45±0.01	0.49±0.01*
Cancer	None	0.33±0.31	0.14±0.09	0.09±0.08
	1	0.33±0.28	0.12±0.09	0.09±0.09
	2	0.39±0.27	0.20±0.08	0.15±0.06
Asia	None	0.85±0.18*	0.73±0.22*	0.31±0.09
	1	0.93±0.18*	0.87±0.27*	0.42±0.15
	2	1.17±0.17*	0.93±0.27	0.63±0.26
Insurance	None	1.82±0.16*	1.51±0.13*	0.76±0.06
	3	1.96±0.15*	1.56±0.11*	0.87±0.05
	5	2.08±0.13*	1.66±0.11*	1.01±0.05
Alarm	None	2.43±0.15*	2.13±0.12*	0.66±0.06
	3	2.48±0.14*	2.20±0.14*	0.64±0.01
	5	2.47±0.14*	2.20±0.09*	0.79±0.06
Hailfinder	None	2.85±0.03*	2.47±0.02*	1.03±0.07
	5	2.84±0.03*	2.47±0.02*	1.00±0.05
	10	2.86±0.03*	2.49±0.03*	1.06±0.04

4. Experiments

We first evaluate transfer learning on 6 standard networks from the BN repository⁵ before proceeding to real medical case studies. Details and descriptions of these BNs can be found in Table 2

Table 2.

Descriptions of Weather, Cancer, Asia, Insurance, Alarm and Hailfinder BNs

Name	Nodes	Arcs	Paras†	M-ind‡	Descriptions
Weather	4	4	9	2	Models factors like rain and sprinkler, which can be affected by the weather condition and all determine the presence of wet grass (Russell and Norvig, 2009)
Cancer	5	5	10	2	Models the interaction between risk factors and symptoms for diagnosing lung cancer (Korb and Nicholson, 2010)
Asia	8	8	18	2	Used for a patient entering a chest clinic to diagnose his/her most likely condition given symptoms and risk factors (Lauritzen and Spiegelhalter, 1988).
Insurance	27	52	984	3	Used for estimating the expected claim costs for a car insurance policyholder (Binder et al., 1997).
Alarm	37	46	509	4	This network is a medical diagnostic application for patient monitoring and is classically used to explore probabilistic reasoning techniques in belief networks. (Beinlich et al., 1989).
Hailfinder	56	66	2656	4	Prediction of hail risk in northern Colorado (Abramson et al., 1996).

^†Total number of parameters in each BN.

^‡The maximum edge in-degree, the maximum number of node parents in each BN.

4.1. Baselines

We compare against existing strategies for estimating relatedness and fusing source and target data. For relatedness estimation, we introduce two alternative fitness functions to BMC:

Likelihood: The similarity between the fragments is the log-likelihood of the target data under the ML source parameters ${\widehat{\theta }}^s,{\sum }_l\log p(d_l^t|{\widehat{\theta }}^s).$

MatchCPT: The dis-similarity between the fragments is the K-L divergence between their ML parameter estimates $𝒦ℒ𝒟({\widehat{\theta }}^t,{\widehat{\theta }}^s)$ (Dai et al., 2007; Selen and Jaime, 2011; Luis et al., 2010).

For fusing source and target knowledge, we introduce two competitors to our BMA:

Basic: Use the estimated source parameter directly ${\widehat{\theta }}_j^s$. A reasonable strategy if relevance is perfect and the source data volume is high, but does not exploit target data and it is not robust to imperfect relevance.

Aggregation: A weighted sum reflecting the relative volume of source and target data (Eq (12) in (Luis et al., 2010)), it exploits both source and target data, but is less robust than BMC to varying relevance.

Neither Basic nor Aggregation is robust to varying relevance across and within sources (they do not reflect the goodness of fit between source and target), or situations in which no source node at all is relevant (e.g., given partial overlap of the source and target domain).

The algorithms implemented in MATLAB are based on functions and subroutines from the BNT⁶ and Fastfit/Lightspeed⁷ toolboxes. All the experiments were performed on an Intel core i7 CPU running at 2.5 GHz and 16 GB RAM.

4.2. Overview of Relatedness Contexts

Before presenting experimental results, we first highlight the variety of possible network-relatedness contexts that may occur. Of these, different relatedness scenarios may be appropriate depending on the particular application area.

Structure and Variable Correspondence: In some applications, the source and target networks may be known to correspond in structure, share the same variable names, or have provided variable name mappings. In this case the only ambiguity in transfer is which of multiple potential source networks is the most relevant to a target. Alternatively, structure/variable name correspondence may not be given. In this case there is also ambiguity about which fragment within each source is relevant to a particular target CPT.

Cross-network relevance heterogeneity: There may be multiple potential source networks, some of which may be relevant and others irrelevant. The most relevant source should be identified for transfer, and irrelevant sources ignored.

Continuous versus discontinuous relevance: When there are multiple potential source networks, it may be that relevance to the target varies continuously (e.g., if each network represents a slightly different segment of demographic of the population), or it may be that across all the sources some some are fully relevant and others totally irrelevant. In the latter case it is particularly important not to select an irrelevant source, as significant negative transfer is then likely.

Piecewise Relevance: Relevance may vary piecewise within networks as well as across networks. Consider a target network with two sub-graphs A and B: A may be relevant to a fragment in source 1, and B may be relevant to a fragment in source 2. For example, in the case of networks for hospital decision support, different hospitals may share different subsets of procedures – so their BNs may correspond in a piecewise way only. A target hospital network may then ideally draw from multiple sources. Note that this may happen either because (i) subgraphs in the target are structurally compatible with different sub-graphs in the multiple sources (which need not be structurally equivalent to each other), or (ii) in terms of quantitative CPT fit, fragments in the target may each be better fit to different sources.

Our BNPTL framework aims to be robust to all the identified variations in network relatedness. In the following experiments, we will evaluate BN transfer in each of these cases.

4.3. Transfer with Known Correspondences

In this section, we first evaluate transfer in the simplest setting, where structure/variable name correspondence is assumed to be given. This setting is same as (Luis et al., 2010): the transfer only happens between target/source nodes with the same node index $X_i^t=X_i^s,where{X}_i^t\in V_t,X_i^s\in V_s$ and V_t = V_s, G_t = G_s. (In our framework this is easily modelled by providing the prior $p(H_{jk1}^s)=0,$ and hence $p(H_{jk0}^s)=1,$ for non-corresponding pairs j ≠ k.) This setting has the least risk of negative transfer, because there is less chance of transferring from an irrelevant source CPT.

We use six standard BNs (Weather, Cancer, Asia, Insurance, Alarm and Hailfinder) to compare our approach (BMC fitness with BMA (BNPTL)) to the state-of-art (MatchCPT fitness with Aggregation fusion (CPTAgg) (Luis et al., 2010)). In this case we use “soft noise” to simulate continuously varying relatedness among a set of sources. The specific soft noise simulation procedure is as follows: For each reference BN three sets of samples are drawn with 200, 300 and 400 instances respectively. These sample sets are used to learn three different source networks. Because the source networks are learned from varying numbers of samples, they will vary in degree of relatedness to the target, with the 400 and 200 sample networks being most and least related respectively. Subsequently, 100 samples of each source copy are drawn and used used as the actual source data. Because node correspondences are known in this experiment, another baseline is simply to aggregate all target and source data. This method is referred as ALL, and also will be compared. Results are quantified by average KLD between estimated and true CPTs. In each experiment we run 10 trials with random data samples and report the mean and standard deviation of the KLD.

The results are presented in Table 3, with the best result in bold, and statistically significant improvements of the best result over competitors indicated with asterisks * (p ≤ 0.05). Compared with CPTAgg, BNPTL achieves 60.9% average reduction of KLD compared to the ground truth. These results verify the greater effectiveness of BNPTL even in the known correspondence setting, where the assumptions of CPTAgg are not violated. To demonstrate the value of our network-level relevance prior p(H^s), we also evaluate our framework without this prior (denoted BNPTL^np). The comparison between BNPTL and BNPTL^np demonstrates that the network-level relevance does indeed improve transfer performance. In this case it helps the model to focus on the higher quality/more relevant 400-sample source domain: even if for a particular fragment a less relevant source domain may have seemed better from a local perspective.

Table 3.

Performance (known correspondences) of STL, ALL and transfer learning methods: CPTAgg, BNPTL^np and BNPTL.

Name	STL	ALL	CPTAgg	BNPTLnp	BNPTL
Weather	0.02±0.02*	0.01±0.00	0.01±0.00	0.01±0.00	0.01±0.00
Cancer	0.33±0.31*	0.01±0.00	0.12±0.09*	0.10±0.07*	0.10±0.05*
Asia	0.85±0.18*	0.36±0.04	0.68±0.27	0.30±0.12	0.24±0.14
Insurance	1.82±0.16*	1.05±0.09*	1.47±0.17*	0.77±0.05	0.76±0.04
Alarm	2.43±0.15*	1.70±0.10*	2.19±0.13*	0.64±0.02	0.63±0.02
Hailfinder	2.85±0.03*	1.98±0.02*	2.44±0.04*	0.97±0.07	0.97±0.04
Average	1.38±0.14	0.85±0.04	1.15±0.12	0.47±0.05	0.45±0.05

The ALL baseline also achieves good results in Cancer and Weather networks. We attribute this to these being smaller BNs (node ≤ 5), so all the source parameters are reasonably well constrained by the source samples used to learn them, and aggregating them all is beneficial. However in large BNs with more parameters, the difference between the 200 and 400 sample source networks becomes more significant, and it becomes important to select a good source instead of aggregating everything including the noisier less related sources. In real-world settings, we may not have node/structure correspondence. Thus we do not assume this information is available in all the following sections.

4.4. Dependence on Target Network Data Sparsity

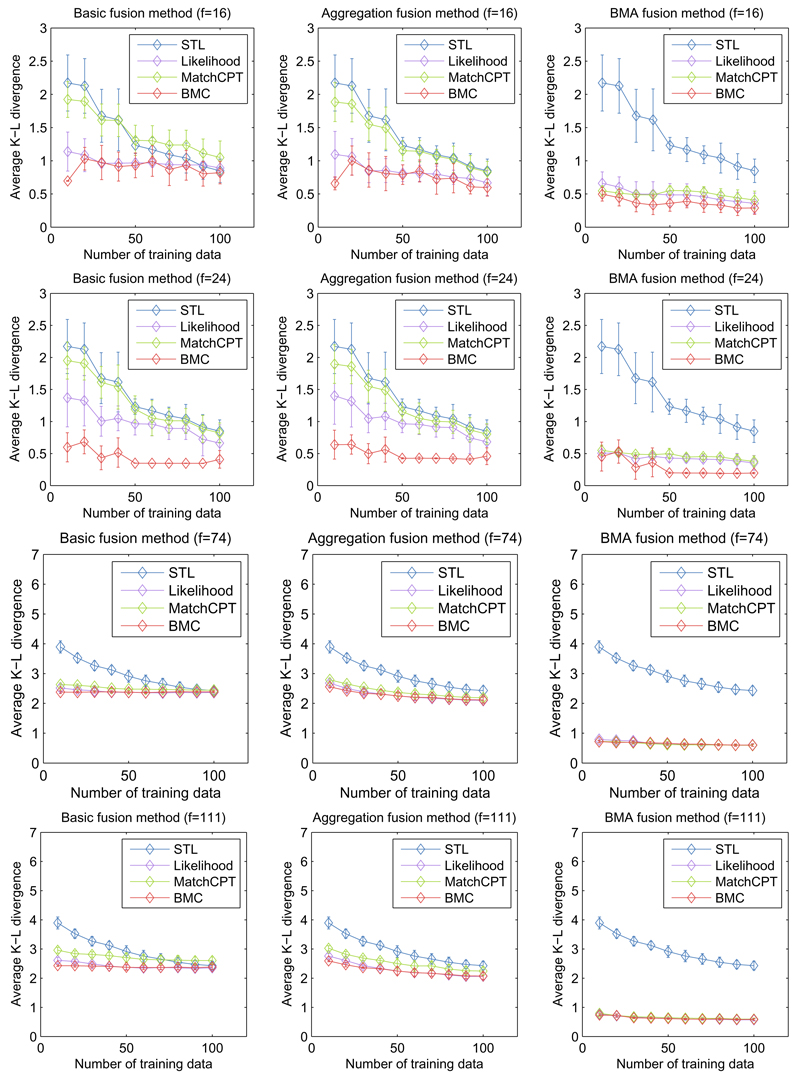
In this section, we explore the performance for varying number of target samples, focusing on the Asia and Alarm networks. Here the target and source domain are both generated from the Asia or Alarm networks, and the relatedness of the source domain varies (soft noise). For relatedness, we consider 2 conditions for the source domains: (i) two Asia/Alarm networks learned from 200 and 300 samples respectively, this results 16 source fragments in Asia network (Row 1 of Figure 2) and 74 source fragments in Alarm network (Row 3 of Figure 2), and (ii) three Asia/Alarm networks learned from 200, 300 and 400 samples respectively, this results 24 source fragments in Asia network (Row 2 of Figure 2) and 111 source fragments in Alarm network (Row 4 of Figure 2). The latter condition potentially contains stronger cues for transfer – if a good decision is made about which source network to transfer from. To unpack the effectiveness of our contributions, we investigate all combinations for different fitness methods and fusion methods under these settings.

Figure 2.

Transfer performance of varying target data volume and source relatedness (soft noise) in Asia and Alarm BNs. Top two rows: transfer learning with 16 and 24 source fragments in Asia BN. Bottom two rows: transfer learning with 74 and 111 source fragments in Alarm BN. Columns: Basic, Aggregation and BMA fusion.

In each sub chart of Figure 2, the x-axis denotes the number of target domain training instances, and the y-axis denotes the average KLD between estimated and true parameter values. The blue line represents standard MLE learning, green denotes transfer by MatchCPT fitness, purple shows transfer with likelihood fitness, and red line the results using our BMC fitness function. The columns represent Basic (source only), Aggregation and BMA fusion. As we can see from the results, the performance of transfer methods with BMC fitness function improves with more source fragments, especially in Asia network. Furthermore, algorithms with our BMC fitness function (red) achieve the best results in almost all situations. Even the simple basic fusion method gets reasonable learning results (< 0.50) using the BMC fitness function to choose among the 24 source fragments in Asia network. Also, our BMA fusion (right column) significantly outperforms other fusion methods. For instance, when there are 16 source fragments in Asia network (top row), the average performance of BMC fitness function in BMA fusion increased 25.4% and 29.3% compared with the same fitness function in Basic fusion and Aggregation fusion settings. Although these margins decrease with increasing source fragments, our BNPTL (BMC+BMA) is generally best.

4.5. Illustration of Network and Fragment Relatedness Estimation

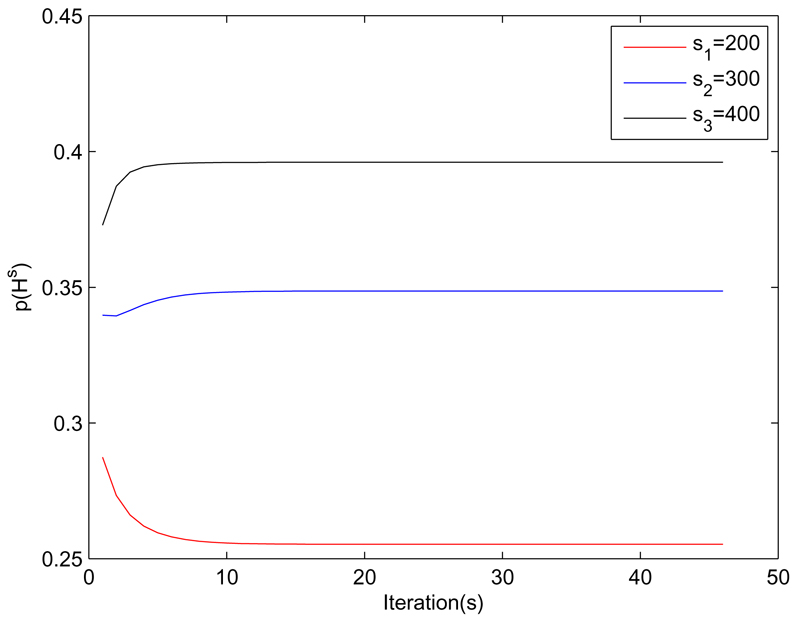
To provide insight into how network and fragment relatedness is measured in BNPTL, we continue to use the Asia network and its three sources (soft noise). Network Relatedness: Figure 3 shows the estimated relatedness prior p(H^s) for each source s over EM iterations. As we can see the network-level relatedness converges after about 10 iterations, with the relatedness estimates being in order of the actual source relevance.

Figure 3.

The estimated network relatedness p(H^s) between target Asia network and its three source copies of varying quality/relatedness.

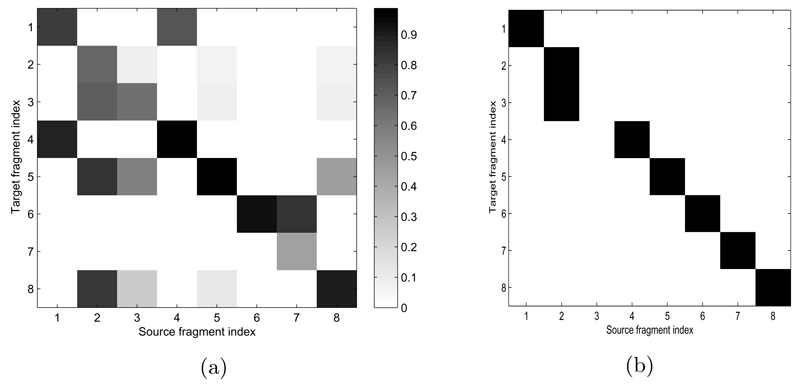
Fragment Relatedness: To visualize the inferred fragment relatedness, we record the estimated relatedness between every fragment in the target and every fragment in source 3 of the Asia network. This is plotted as a heat map in Figure 4(a), where the y-axis denotes the index of target fragment, and x-axis denotes the index of source fragment. Darker color indicates higher estimated relatedness $p(H_{jk1}^s|{\mathbf{𝓓}}_j^t,{\mathbf{𝓓}}_k^s)$ between two fragments j and k. Some incompatible source fragments have zero relatedness automatically. For each target fragment, the most related (darkest) source fragment is selected for BMA fusion. Although there is some uncertainty in the estimated relatedness (more than one dark cell per row), overall all but one target fragment selected the correct corresponding source fragment (Figure 4(b).

Figure 4.

Fragment relatedness experiment in Asia network. (a) The inferred fragment relatedness between target and source fragments. (b) The final selected source fragment for each target.

4.6. Robustness to Hidden Variables

In this section, we evaluate the algorithms on six standard BNs. We use the same sampled target and sources as in Table 3, but we introduce additional hidden variables in the target. We learn the target parameters by: conventional single task BN learning (EM with MLE), MatchCPT fitness with Aggregation fusion (CPTAgg) (Luis et al., 2010) (note that CPTAgg does not apply to latent variables, but we use their fitness and fusion functions in our framework), and our BNPTL. Three conditions are considered: (i) fully observed target data, (ii) small number of hidden variables and (iii) medium number of hidden variables. (In the hidden data conditions, the specified number of target network nodes are chosen uniformly at random on each trial, and considered to be unobserved, so the data for these nodes are not used.)

Table 4 summarises the average KLD per parameter. In summary, the transfer methods outperform conventional EM with MLE (STL) in all settings. Compared with the state-of-the-art CPTAgg, BNPTL also improves performance: improvement on 15 out of 18 experiments, with an average margin of 53.6% (the average reduction of KLD). Of the total set of individual target CPTs, 84.3% showed improvement in BNPTL over CPTAgg.

4.7. Exploiting Piecewise Source Relatedness

Thus far, we simulated source relevance varying smoothly at the network level – all nodes within each source network were similarly relevant. So all fragments should typically be drawn from the source estimated to be most relevant. In contrast for this experiment, we investigate the situation where relatedness varies in a piecewise fashion. In this case, to effectively learn a target network, different fragments should be drawn from different source networks. This is a setting where transfer in Bayesian networks is significantly different from transfer in conventional flat machine learning models (Pan and Yang (2010)).

To simulate this setting, we initialise a source network pool with three copies of the network, before introducing piecewise “hard noise”, so that some compatible fragments are related and others are totally unrelated. Specifically, we choose a portion (25% and 50%) of each source network’s CPTs uniformly at random and randomise them to make them irrelevant (by drawing each entry uniformly from [0,1] and renormalizing). This creates a different subset of compatible but (un)related fragments in each network. Thus piecewise transfer - using different fragments from different sources is essential to achieve good performance.

We consider two evaluation metrics here: the accuracy of the fragment selection - whether each target fragment selects a (i) corresponding and (ii) non-corrupted fragment in the source, and accuracy of the learned CPTs in the target domain. Table 5 presents the results, where our model consistently outperforms CPTAgg in Weather, Cancer and Asia networks. Although the fragment selection accuracy of BNPTL failed to outperform the CPTAgg in Insurance, Alarm and Hailfinder networks due to the greater data scarcities in their target networks, the general good performance (KLD) of BNPTL verifies that the framework still can exploit source domains with piecewise relevance. Meanwhile the fragment selection accuracy of BNPTL explains how this robustness is obtained (irrelevant fragments (Eq (2)) are not transferred (Eq (6))). In addition to verifying that our transfer framework can exploit different parts of different sources, this experiment demonstrates that it can further be used for diagnosing which fragments correspond or not (Eq (2)) across a target and a source – which is itself of interest in many applications.

Table 5.

The fragment selection performance of CPTAgg and BNPTL. The numbers 25% and 50% indicate different portions of irrelevant fragments in the sources. Note that chance here is much lower than 75/50% due to unknown network correspondence.

	25% random CPTs
Name
	Fragment Accuracy		KLD
	CPTAgg	BNPTL	STL	CPTAgg	BNPTL
Weather	61.0%*	90.0%	0.03±0.02*	0.01±0.00	0.01±0.00
Cancer	94.8%	96.0%	0.33±0.31	0.14±0.09	0.07±0.05
Asia	78.0%*	97.5%	0.85±0.18*	0.67±0.14*	0.18±0.00
Insurance	82.4%	70.7%*	1.82±0.16*	1.01±0.04*	0.74±0.02
Alarm	61.7%	58.8%*	2.43±0.15*	1.60±0.27*	0.57±0.02
Hailfinder	75.5%	62.4%*	2.85±0.03*	2.04±0.03*	0.79±0.02
Average	75.6%	79.2%	1.38±0.14	0.91±0.10	0.39±0.02
	50% random CPTs
Weather	57.0%*	74.5%	0.03±0.02*	0.01±0.00	0.01±0.00
Cancer	79.2%	82.4%	0.33±0.31	0.13±0.07	0.08±0.04
Asia	61.5%*	80.8%	0.85±0.18*	0.42±0.19	0.20±0.01
Insurance	65.9%	51.9%*	1.82±0.16*	0.97±0.05	0.90±0.04
Alarm	51.0%	46.4%*	2.43±0.15*	1.38±0.17*	0.63±0.04
Hailfinder	65.7%	49.9%*	2.85±0.03*	2.07±0.03*	0.43±0.02
Average	63.4%	64.3%	1.38±0.14	0.83±0.09	0.38±0.03

4.8. Robustness to Irrelevant Sources

The above experiments verify the effectiveness of our framework under conditions of varying source relatedness, but with homogeneous networks Vt = Vs. In this section we verify robustness to two extreme cases of partially and fully irrelevant heterogeneous sources.

Partially irrelevant In this setting, we use the same six networks from the BN repository, and consider each in turn as the target, and copies of all six networks as the source (thus five are irrelevant and one is relevant). Therefore the majority of the potential source fragments come from 5 irrelevant domains. Table 6 presents the results of transfer learning in these conditions. We evaluate performance with two metrics: (i) percentage of fragments chosen from the correct source domain, and (ii) the usual KLD between the estimated and ground truth parameters in the target domain.

Table 6.

Performance (domain-partially-irrelevant) of STL and transfer learning methods: CPTAgg and BNPTL.

Name	Domain Accuracy		KLD
	CPTAgg	BNPTL	STL	CPTAgg	BNPTL
Weather	80.0%*	100.0%	0.03±0.02*	0.01±0.00	0.01±0.00
Cancer	80.0%*	92.0%	0.33±0.31	0.11±0.07	0.07±0.04
Asia	77.5%*	85.0%	0.85±0.18*	0.49±0.15*	0.18±0.01
Insurance	97.8%	97.8%	1.82±0.16*	0.82±0.03*	0.51±0.02
Alarm	94.1%	82.7%*	2.43±0.15*	1.64±0.06*	0.70±0.03
Hailfinder	99.3%*	100.0%	2.85±0.03*	1.74±0.01*	0.84±0.02
Average	88.1%	92.9%	1.38±0.14	0.80±0.05	0.38±0.02

As shown in Table 6, our BNPTL clearly outperforms the previous state-of-the-art CPTAgg in each case. This experiment verifies that our framework is robust even to a majority of totally irrelevant source domains, and is achieved via explicit relatedness estimation $\left(p\left(H_1^s\right)\right)$ in Algorithm 1 and Eq (2)).

Fully irrelevant In this setting, we consider the extreme case where the source and target networks are totally different G_t ≠ G_s, V_t ∩ V_s = ∅. Note that since the source and target are apparently unrelated, it is not expected that positive transfer should typically be possible. The test is therefore primarily whether negative transfer (Pan and Yang, 2010) is successfully avoided in this situation where all source fragments may be irrelevant. Note that since the sources are totally heterogeneous, prior work CPTAgg (Luis et al., 2010) does not support this experiment. We therefore compare our algorithm to a variant using BMC fitness and Basic fusion function (denoted BMCBasic) and target network only STL.

The results are shown in Table 7, from which we make the following observations. (i) BNPTL is never noticeably worse than STL. This verifies that our framework is indeed robust to the extreme case of no relevant sources: $\left(p(H_0^s|D^t,D^s\right)$ is correctly inferred in Eq (2), thus preventing negative transfer from taking place (Eq (6)). (ii) In some cases, BNPTL noticeably outperforms STL, demonstrating that our model is flexible enough to achieve positive transfer even in the case of fully heterogeneous state spaces. (iii) In contrast, BMCBasic is worse than STL overall demonstrating that these properties are unique to our approach.

Table 7.

Performance (domain-fully-irrelevant) of STL and transfer learning methods: BMCBasic and BNPTL. The symbol ↢ represents the transfer relationship: target ↢ source. Here ‘Other’ represents the six BN repository networks with the target removed.

Transfer Setting	STL	BMCBasic	BNPTL
Asia ↢ Other	0.85±0.18*	0.34±0.02*	0.19±0.03
Weather ↢ Other	0.03±0.02	0.21±0.01*	0.04±0.01
Cancer ↢ Other	0.33±0.31	0.23±0.01*	0.08±0.02
Alarm ↢ Other	2.43±0.15	2.59±0.11*	2.27±0.14
Insurance ↢ Other	1.82±0.16	2.28±0.13*	1.82±0.15
Hail.↢ Other	2.85±0.03	3.12±0.03*	2.86±0.03
Average Performance	1.38±0.14	1.46±0.05	1.21±0.06

5. Real Medical Case Studies

The previous section demonstrated the effectiveness of our BNPTL under controlled data and relatedness conditions. In this section we explore its application to learn BN parameters of two medical networks, where the “true” relatedness is unknown, and data volume and relatedness reflect the conditions of real-world medical tasks.

The Indian Liver Patient (ILP) (Bache and Lichman, 2013) has 583 records about liver disease diagnosis based on 10 features. This dataset is publicly available. Because the BN structure for this dataset is not provided. We follow previous work (Friedman et al., 1997) to apply a naive BN structure for this classification problem. To enable transfer learning, this dataset is divided into 4 subsets/domains by grouping patient age, following common procedure in medical literature (Jain et al., 2000). To systematically evaluate transfer, we iteratively take each group in turn as the target, and all the others as potential sources.

The AUC (area under curve) for the target variable of interest is calculated. This is repeated for each of 100 random 2-fold cross-validation splits, and the results averaged (Table 8). Here STL denotes single task learning from target domain data, ALL indicates the baseline of concatenating all the source and target data together before STL. Although we are primarily interested in the case of unknown correspondence, we investigate both the conditions of known and unknown target-source node correspondence (denoted by suffix KC and UC respectively). Note that the ALL baseline needs to know node correspondence, so should be compared with BNPTL (KC) for a fair comparison. The results show that predictive performance can be greatly improved by leveraging the source data. Our BNPTL (UC) outperforms STL and state-of-the-art transfer algorithm CPTAgg in each case. As we can see, ALL also achieves good performance based on the strong assumption of known correspondence. Nevertheless, it is still outperformed by our BNPTL (KC).

Table 8.

Prediction performance (AUC) for medical tasks. The target attributes for ILP and TC datasets are Liver disease and Death respectively. Statistically significant improvements of BNPTL(UC) and BNPTL(KC) over alternatives are marked with symbols * and ∆ respectively.

Dataset	Missing Data	STL	ALL	CPTAgg	BNPTL(UC)	BNPTL(KC)
ILP	YES	0.674*∆	0.709∆	0.674*∆	0.712	0.727
TC	YES	0.771*∆	0.933*∆	0.796*∆	0.967	0.967

Trauma Care (TC) dataset (Yet et al., 2014) has a BN structure designed by trauma care specialists, and relates to procedures in hospital emergency rooms. The full details of the network and datasets are proprietary to the hospitals involved, however it contains 18 discrete variables (of which 3 are hidden) and 11 Gaussian variables. It is important because rapid and accurate identification of hidden risk factors and conditions modeled by the network are important to support doctors’ decision making about treatments which reduce mortality rate (Karaolis et al., 2010). The relevance of this trauma model to our transfer algorithm is that there are two distinct datasets for this model. One dataset is composed primarily of data from a large inner city hospital with extensive data (1022 instances) and the second dataset is composed of data from a smaller hospital and city in another country (30 instances). The smaller hospital would like an effective decision support model. However, using their own data to learn the model would be insufficient, and using the large dataset directly may be sub-optimal due to (i) differences in statistics of injury types in and out of major cities city, (ii) differences in procedural details across the hospitals and (iii) differences in demographic statistics across the cities/countries.

We therefore apply our approach to adapt the TC BN from the inner city hospital to the small hospital. We perform cross-validation in the target domain of the small hospital, using half the instances (15) to train the transfer model, and half to evaluate the model. To evaluate the model we instantiate the evidence variables in the target domain test set, select one of the variables of interest (Death), and query this variable. AUC values are calculated for the query variable, and shown in Table 8. Every method is better than using the scarce target data only (STL). Our BNPTL significantly outperforms the alternatives in each case. BNPTL (UC) also matches the performance of BNPTL (KC) demonstrating the reliability of the fragment correspondence inference.

6. Conclusions

6.1. Summary

When data is scarce, BN learning is inaccurate. Our framework tackles this problem by leveraging a set of source BNs. By making an explicit inference about relatedness per domain and per fragment, we are able to perform robust and effective transfer even with heterogeneous state spaces and piecewise source relevance. Our approach applies with latent variables, and is robust to any degree of source network relevance, automatically adjusting the strength of fusion to take this into account. Moreover, it is able to provide estimated domain and fragment-level relatedness as an output, which is of interest in many applications (e.g., in the medical domain, to diagnose differences in procedures between hospitals). Experiments show that BNPTL consistently outperforms single task STL and former transfer learning algorithms. Finally, experiments with a real-world trauma care network show the practical value of our method, adapting medical decision support from large inner city hospitals with extensive data to smaller provincial hospitals.

6.2. Discussion of Limitations and Future Work

An assumption made by our current framework is that transfer is only performed from the single most relevant source fragment. An alternative would be to transfer from every source fragment estimated to be relevant. This would be a relatively straightforward extension of Eq (6) to sum up multiple potential relevant sources. However, by increasing the number of source fragments used, the risk of negative transfer may be increased. If any irrelevant source is transferred as a ‘false positive’ (i.e., $p(H_{jk1}^s|D_j^t,D_k^s)>0$ for irrelevant source fragment ${\mathbf{𝓓}}_k^s$ then it may negatively affect the target in Eq (6). This eventuality is more likely if many sources can be fused. In contrast, our current framework just needs to rank a irrelevant sources below a relevant source in order to be robust to negative transfer. This is an example of a general tradeoff between flexibility/amount of information possible to transfer, and robustness to negative transfer (Torrey and Shavlik, 2009).

A second limiting assumption is that the underlying relatedness is binary (i.e., sources are relevant or irrelevant). Clearly sources may have more continuous degrees of relatedness to the target. In our framework this is only supported implicitly through the fact that a somewhat related source will have an intermediate probability of relatedness (Eq (2)), and thus be used but with a smaller weight Eq (6). In future continuous degrees of relatedness could be modelled more explicitly.

Finally, in this paper we have addressed relatedness inference in an entirely data-driven way. In future we would like to integrate expert-provided priors and constraints to guide transfer parameter learning, and transfer structure learning.