Cortical Specializations Underlying Fast Computations

Abstract

The time course of behaviorally relevant environmental events sets temporal constraints on neuronal processing. How does the mammalian brain make use of the increasingly complex networks of the neocortex, while making decisions and executing behavioral reactions within a reasonable time? The key parameter determining the speed of computations in neuronal networks is a time interval that neuronal ensembles need to process changes at their input and communicate results of this processing to downstream neurons. Theoretical analysis identified basic requirements for fast processing: use of neuronal populations for encoding, background activity, and fast onset dynamics of action potentials in neurons. Experimental evidence shows that populations of neocortical neurons fulfil these requirements. Indeed, they can change firing rate in response to input perturbations very quickly, within 1 to 3 ms, and encode high-frequency components of the input by phase-locking their spiking to frequencies up to 300 to 1000 Hz. This implies that time unit of computations by cortical ensembles is only few, 1 to 3 ms, which is considerably faster than the membrane time constant of individual neurons. The ability of cortical neuronal ensembles to communicate on a millisecond time scale allows for complex, multiple-step processing and precise coordination of neuronal activity in parallel processing streams, while keeping the speed of behavioral reactions within environmentally set temporal constraints.

Introduction

The size and complexity of the neocortex increase dramatically in the hierarchy of mammals. The number of neocortical neurons increases from about 10 million in mouse to 30 million in rat, 300 million in cat, and more than 20,000 million in the human brain (DeFelipe 2011; Herculano-Houzel 2009; Herculano-Houzel and others 2006). The connectivity becomes richer too. In humans, a prefrontal cortex pyramidal neuron has about four times more spines on the basal dendrites than a pyramidal neuron in a mouse (DeFelipe 2011). The exploding complexity and associated possibilities for processing allow neocortical circuits to mediate increasingly complex behaviors, for example, by expanding the range of factors that can influence decision making.

The expansion of the complexity of cortical structure and function is subject to a number of interrelated constraints. These constraints are imposed by available energy, structural elements and space, but also by functional requirements, such as maintenance of the balances between excitation and inhibition or synaptic potentiation and depression, which are necessary for stable operation of the brain. One further important constraint on processing is time. Decision making processes in large brains must be accomplished within the same time limits as in smaller brains. These time constraints are set externally, by the time course of environmental events relevant for the organisms’ survival. How do mammals make use of the increased number of neurons and connections, mediating their broadened behavioral repertoire, without compromising the speed of decision-making and behavioral reactions? Or, how much of the brain power can be used for a certain task, within a reasonable time? How many ensembles can be involved in processing, and different factors taken into account, while making a decision?

There are two general strategies for making use of the increased number of neurons and connections while keeping up the processing speed: increasing the speed of each iteration, and engaging neuronal ensembles in parallel processing. The speed of one iteration (or one round of processing) is determined by the response time: an interval in which a neuron, or an ensemble of neurons, can accomplish one cycle of information processing, from receiving the input from the upstream neurons to producing the output signal and sending it to downstream neurons. Shortening this time would increase processing speed. Employment of neuronal ensembles in parallel processing necessitates temporal coordination of their activity. To ensure effective integration of results of processing in different neuronal ensembles, they should operate on the same time scale, and be able to generate precisely timed spikes. This latter requirement connects the two strategies for faster processing, because the ability to generate precisely timed spikes is intrinsically related to the response time.

Components of Processing Time in a Neuron

Processing in neuronal networks can be considered as consisting of individual cycles (in this review, cycles, iterations, or rounds of processing are used as synonyms). Stages of a processing cycle can be illustrated by considering a pair of synaptically connected neurons isolated from a multilayer network (Fig. 1). The processing cycle begins with generation of an action potential (AP) in the presynaptic neuron(s) from layer A, and includes the following stages: (1) Propagation of the presynaptic AP down the axon to the presynaptic terminal. (2) Synaptic transmission, generation of postsynaptic current and postsynaptic potential, and dendritic integration, ultimately leading to a postsynaptic potential as recorded in the soma. (3) Change of the membrane potential at the spike initiation zone in the axon initial segment, leading, or not, to (4) generation of a postsynaptic spike. Firing of layer B neurons encodes the ultimate results of computations performed by the neurons of that layer in this processing cycle. This output signal is communicated to the next level neurons thus starting the next round of processing.

Figure 1.

Components of processing time in a neuron. One cycle (or one round) of information processing by a neuron, or by a layer of neurons in multilayer network, starts with the generation of an action potential (AP) in presynaptic neurons. Further stages of this cycle include (1) propagation of presynaptic AP down the axon to presynaptic terminal; (2) synaptic transmission, generation of postsynaptic current and postsynaptic potential (PSP), and dendritic integration, ultimately leading to a PSP as recorded in the soma; and (3) change of the membrane potential at the spike initiation zone of the axon initial segment, leading (or not) to (4) generation of a postsynaptic spike. Generation of an action potential in the postsynaptic neuron concludes the cycle. Note that in the context of present review “layer” has functional rather than morphological meaning, it refers to a population of neurons involved in one iteration, and thus can be applied to processing in networks with both feedforward and feedback connectivity.

Latencies of excitatory postsynaptic potentials (EPSPs) at monosynaptic connections between neocortical neurons measured in slices in vitro are short, in the range of 1 to 2 ms (e.g., Feldmeyer and others 2006; Frick and others 2008; Hardingham and Larkman 1998; Mason and others 1991). Latencies of the similar range (1-2 ms) were measured in cortical neurons in response to electric stimulation of thalamic afferents in vivo (Ferster and Lindstrom 1983). These latencies include time necessary for propagation of action potential down the axon to presynaptic terminals, synaptic transmission, and dendritic integration. Thus, changes in activity of presynaptic neurons are translated into membrane potential changes of the postsynaptic cell (stages 1 and 2 in Fig. 1) within 1 to 2 ms.

How fast can the spike generation mechanism of cortical neurons translate these changes of the membrane potential into changes of postsynaptic firing? A hint that this process is very fast comes from results of cross-correlation analysis of spike trains of simultaneously recorded neurons in vivo. In cortico-cortical connections, spiking of a presynaptic neuron can affect the probability of firing of postsynaptic neuron within few milliseconds: sharp peaks, which are characteristic of direct synaptic connections, are typically shifted by only 2 to 3 ms from the crosscorrelogram origin (e.g., Dickson and Gerstein 1974; Matsumura and others 1996; Michalski and others 1983; Nowak and others 1995). Also in specific thalamocortical pathways transmission is fast. In somatosensory and visual systems, spikes of cortical neurons follow spikes of thalamic neurons with latency of 1.5 to 3 ms (Bereshpolova and others 2011; Reid and Alonso 1995; Swadlow and Gusev 2002; Usrey and others 2000). Thus, latencies of monosynaptic peaks in cross-correlograms, which provide a measure of the duration of the whole cycle (Fig. 1, stages 1-4), are only marginally longer than latencies of monosynaptic EPSPs recorded in the soma (Fig. 1, stages 1 and 2). This suggests that transformation of membrane potential changes into spike responses (Fig. 1, stages 3 and 4) occurs rapidly, on a time scale of milliseconds. Indeed, a unique study employing in vivo intracellular recording of postsynaptic potentials evoked in spinal motoneurons by electric stimulation, demonstrated that spike response of firing neuron (peak in a peristimulus time histogram [PSTH]) begins in less than 0.5 ms (0.48 ms on average) after the EPSP onset (Fetz and Gustafsson 1983). These results from cat motoneurons support the conclusion that neurons can transform changes of the membrane potential into changes of firing rate very quickly, on a millisecond time scale.

How to Make Neuronal Responses Fast?

One intuitive way to make spike responses faster is to increase the input strength. Indeed, there are documented examples of strong synaptic connections in the neocortex, such as some connections between pyramidal neurons (Thomson 1997; Thomson and others 1993), all-or-none connections to layer 2/3 and layer 4 neurons in the visual and auditory cortex (Lee and others 2012; Stratford and others 1996; Volgushev and others 1995), or some of the synapses formed by pyramids on fast-spiking interneurons (e.g., Galarreta and Hestrin 2001). However, strong individual connections that evoke large EPSPs are rare exceptions. EPSP amplitudes at a majority of cortical synapses are well below 1 mV (Feldmeyer and others 2006; Frick and others 2008; Hardingham and Larkman 1998; Mason and others 1991, Song and others 2005; Thomson 1997). With small amplitudes of individual connections, higher input strength could be achieved by increasing the number of activated presynaptic neurons or by more precise synchronization of presynaptic spikes (e.g., Alonso and others 1996; Neuenschwander and Singer 1996; Usrey and others 2000).

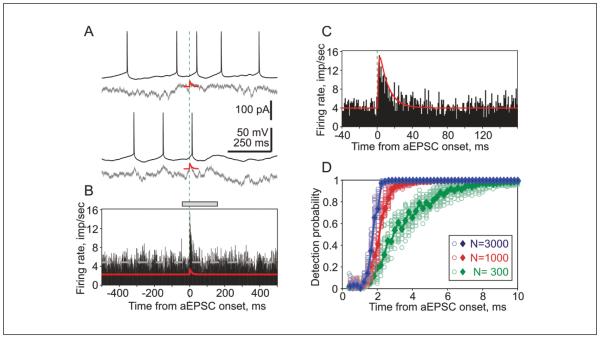
Figure 2A illustrates spike responses of a pyramidal neuron from layer 2/3 in a slice of visual cortex in vitro evoked by somatic injection of an artificial excitatory postsynaptic current (aEPSC) of increasing amplitude. To evoke action potentials by aEPSCs of reasonable amplitude the neuron was kept near threshold, around −55 mV, by injection of depolarizing DC current. At threshold intensity of stimulation (in this cell a 180-pA aEPSC, which produced aEPSPs of 7-8 mV amplitude), latency of detectable spike responses was very long, 17 ms. Spike response latency decreased sharply when amplitude of aEPSCs was increased to 240 pA and then to 300 pA. This strongest tested intensity produced EPSPs of 12-14 mV and evoked spikes with high reliability, in 86% of trials. However, the latency of spike responses did not decrease below ~5 ms (Fig. 2A2 and blue diamond symbols in Fig. 2C). These values are clearly longer than latencies of monosynaptic peaks in the cross-correlograms, discussed above.

Figure 2.

How to make neuronal spike responses fast? (A1) Responses of a neuron to injection of a sequence of excitatory postsynaptic current (EPSC)–shaped depolarizing currents (artificial EPSCs, aEPSCs). The neuron was kept close to the threshold (around −55 mV) using depolarizing direct current. Amplitude of the artificial EPSCs was changed from subthreshold to justthreshold (top) to suprathreshold (bottom). (A2) Peristimulus time histograms (PSTHs) of spike responses superimposed on aEPSCs, with vertical dashed line showing aEPSC onset. Note that even at high suprathreshold intensity, when spikes were evoked with P = .86, spike response starts ~5 ms after the onset of aEPSC. (B1) Responses of the same neuron as in A to aEPSCs immersed in fluctuating noise. Fluctuating current, mimicking background activity in neuronal networks in vivo, induces firing of the neuron at ~5 Hz. Signal-to-noise ratio was modified in these experiments by changing either the amplitude of the fluctuating noise, or the amplitude of aEPSC, as illustrated. (B2) PSTHs of spike responses, data from experiments illustrated in B1. Background firing rate of ~5 Hz was subtracted from PSTHs. The scale for aEPSCs is the same in A and B. Note that changes of the firing rate of spontaneously active neurons in response to small amplitude aEPSCs in B are much faster than spike responses of near-threshold but silent neurons evoked by large aEPSCs in A. (C) Latency of spike response plotted against aEPSC amplitude, data from symbol-coded experiments illustrated in A and B, with more different EPSC amplitudes. Latency was defined as time at which 20 additional spikes relative to pre-stimulus level were generated. Note that a population of spiking neurons responds to aEPSCs of similar amplitudes with shorter latencies than silent neurons (green triangle vs. blue diamond symbols), and that even very small aEPSCs evoke short-latency spike responses in a population of spiking neurons (red square symbols) (Ilin, Stevenson, Volgushev, unpublished data).

Increasing the strength of individual connections as a common strategy for achieving fast spike responses has several further drawbacks. It promotes fixed-route propagation of signals through neuronal networks, thus limiting the flexibility of processing. Presence of a substantial number of very strong connections in networks with plastic synapses might make them prone to runaway dynamics (Miller and MacKay 1994; Oja 1982; von der Malsburg 1973). Finally, experimental evidence from both in vitro and in vivo experiments (Feldmeyer and others 2006; Frick and others 2008; Hardingham and Larkman 1998; Mason and others 1991; Song and others 2005; Thomson 1997) shows that in the neocortex strong synaptic connections are an exception rather than a rule. Thus, simple increase of input amplitude is neither a typical strategy for the neocortex nor is it sufficient for achieving fast spike responses.

Because in individual neuron the transmission of moderate-amplitude PSPs into spikes is not a 1:1 process, spiking needs to be averaged over a number of stimulus presentations to reveal a response, as in Figure 2A. The same effect can be achieved by using the activity of a population of neurons as readout of response to a stimulus (inset in Fig. 2B; see also Box 1). The use of population activity and averaging allows for some “noise.” The effect of noise originating from uncorrelated synaptic activity and producing irregular spiking is effectively reduced by averaging, thus allowing to recover signal-tonoise ratio in the output activity of the neuronal population. Remarkably, addition of background activity enhances the sensitivity of population firing to small inputs and leads to a dramatic increase of the speed of spike responses. The “speeding-up” of spike responses by noise occurs over a broad range of amplitudes of the signal and the noise, and a broad range of signal-to-noise ratios. Figure 2B illustrates example responses of spiking neuronal population to injection of aEPSCs of different amplitudes (varying ~10-fold), immersed in fluctuating background noise with amplitude differed by a factor of 2. Responses of spiking neuronal ensembles are faster than in no-noise conditions both for aEPSCs of comparable amplitudes (Fig. 2C, green triangle vs. blue diamond symbols), as well as for aEPSCs of much smaller amplitudes, which would remain subthreshold for neurons that do not spike spontaneously (Fig. 2C, red square vs. blue diamond symbols).

Box 1. How to study population encoding in slices?

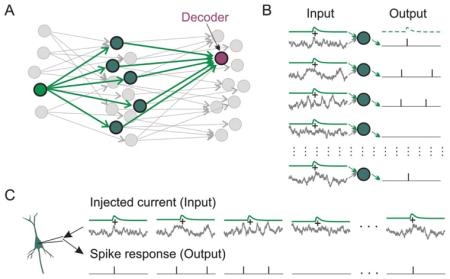
A: A scheme of a three-layer, feed-forward neuronal network, in which one first-layer “source” neuron provides common input to a population of “transmitting” neurons in the second-layer, and transmitting neurons converge on a “decoder” neuron in the third layer. These neurons and connections are shown in green. The rest of the network is shown in gray.

B: Input to each transmitting neuron of the second layer consists of a common signal from the source, in this example an EPSC produced by an action potential in the source neuron, immersed in fluctuating background noise generated by activity of other neurons in the network. Each transmitting neuron has individual background noise, because it is produced by activity of a unique set of presynaptic neurons. Population firing of the transmitting neurons provides input to the decoder of the third layer.

C: Experimentally, population encoding in B can be mimicked by injecting into a neuron fluctuating current consisting of artificial EPSCs immersed in different episodes of fluctuating noise.

Modified from Malyshev and others (2013).

Intuitively, the ability of a population of spiking neurons to rapidly detect even small input perturbations can be understood as following. In the spiking population, at each time point there are some neurons that are very close to the firing threshold. If no stimulus is presented within the next few moments, background noise fluctuations would drive few of these neurons over the threshold to generate an action potential, but will bring other neurons away from the threshold. When stimulus is added, this subpopulation of “super-detectors” responds with spikes that originate from two sources. First, a push toward firing produced by the stimulus leads to action potentials in a portion of neurons that would not fire otherwise, but generate “additional” spikes because of the stimulus. Second, in those neurons that would fire even without stimulation, the additional EPSC may rush-up generation of an action potential, thus shifting the spike closer to the stimulus onset. Total response of the neuronal population to an EPSC immersed in background activity would thus consist of both additionally generated and shifted spikes (Malyshev and others 2013).

In contrast, a silent population does not contain such “super-detectors.” In all silent neurons the membrane potential is well below the threshold, and input signals have to produce substantial depolarization of the membrane before it reaches the threshold range. This process is fundamentally limited by the time constant of cell membrane, hence the latency of spike responses is generally long, and has marked dependence on the strength of stimulation.

Thus, populations of spontaneously firing neurons can respond fast to small-amplitude inputs, while populations of silent neurons respond relatively slow even to high amplitude inputs. Notably, responses of spiking populations are much faster than the membrane time constant of individual neurons. Moreover, firing rate of populations of spiking neurons is influenced by a broader range of signal amplitudes, such that this dynamic range of sensitivity includes small amplitudes, typical for cortical synapses. The ability of spiking populations to respond to stimuli of a broad range of amplitudes with similar, short latencies is advantageous for temporal organization of neuronal activity and parallel processing. It allows integration of signals of different amplitudes on the same temporal scale, and makes processing tolerant to changes of input amplitude, so that plasticity or synchronization would not disrupt temporal coordination of activity. Altogether, the decoupling (at least partial, see below) of changes of firing probability from latency may allow qualitatively different computations to be performed by neuronal networks.

Ultrafast Responses of Cortical Neurons: Experimental Evidence

In the whole brain, in vivo neurons can communicate fast, on millisecond time scale. Sharp peaks, characteristic of direct synaptic connections, are often shifted by only 1.5 to 3 ms in cross-correlograms between pairs of neocortical neurons or in thalamocortical sensory pathways (e.g., Bereshpolova and others 2011; Dickson and Gerstein 1974; Michalski and others 1983; Nowak and others 1995; Reid and Alonso 1995; Swadlow and Gusev 2002; Usrey and others 2000). Di-synaptic transmission from retinal ganglion cells to visual cortex neurons in cats takes only 4.5 to 9 ms (Kara and Reid 2003). In rabbit somatosensory system, peripheral sensory stimuli can evoke spikes in cortical neurons with latency <7.5 ms (Swadlow and Gusev 2002).

Cortical Neurons Can Respond Fast to Small Input Perturbations

In vivo experiments offer advantages of studying encoding in neurons that operate in the natural environment of the whole brain and can be tested using natural sensory stimuli. Disadvantages of in vivo preparation for quantitative analysis of encoding include poor or absent control over essential factors, such as background activity or firing rate of neurons, and unknown number of neurons and connections activated by natural stimulation. In vitro experiments, though lacking the realism of the in vivo brain, offer the advantages of stability of recording and tight control over input stimuli and other experimental conditions. The in vitro approach was initially used for validation of cross-correlation techniques (Moore and others 1970) and then employed to study spike responses evoked by injection of defined input current (Carandini and others 1996; Mainen and Sejnowski 1995; Reyes 2003; Rodriguez-Molina and others 2007; Volgushev and others 1998) or by presynaptic spikes in monosynaptically connected pairs of neurons (Galarreta and Hestrin 2001). This latter study (Galarreta and Hestrin 2001) demonstrated that in fast-spiking inhibitory neurons, the EPSPs evoked by spikes in presynaptic pyramidal neurons, are transformed into firing rate changes reliably and fast, with ~1.7 ms latency from the presynaptic spike to the peak in PSTH.

Extension of these approaches to studies of population encoding in vitro was pioneered by (Silberberg and others 2004). The logic behind the approach of Silberberg and colleagues can be illustrated using an example of a three layer feed-forward neuronal network (Box 1). Consider a population of “transmitting” neurons from the second layer. Each neuron of this population receives a unique pattern of inputs from neurons of the first layer, which results in a unique, different from other neurons pattern of background activity (“noise”). All neurons of the population also receive an input from a common fiber, which introduces a common element to their activity. In experiments, this situation is imitated by injecting into a neuron a mixture of a unique realization of fluctuating noise current, which mimics background activity, and a common signal, such as an artificial EPSC, current step or sinewave modulated signal, which is exactly the same in all neurons and mimics the effect of the shared input (Box 1, panel B). Recording responses to injection of these currents in all neurons of the transmitting population simultaneously is mathematically equivalent to successive recording of responses of several cells to the signal immersed in different realizations of the fluctuating noise (Box 1, panel C). Averaging the spike responses provides an estimate of the population firing, whereby the number of repeated injections is equivalent to the number of neurons in the population (Silberberg et al., 2004).

Figure 3 illustrates results of an experiment on population encoding of small artificial EPSCs. Individual responses to injection of aEPSCs immersed in different realizations of fluctuating current do not show an obvious relation between the aEPSCs and postsynaptic spikes (Fig. 3A). However, the PSTH constructed from N = 2959 responses reveals a clear peak of the population firing at the onset of aEPSC (Fig. 3B). Fast changes of population firing rate in response to injection of aEPSCs are consistent with prior results on rapid spike responses to step-changes of the input (Ilin and others 2013; Silberberg and others 2004; Tchumatchenko and others 2011). Zooming in on the time scale shows that the time-course of the PSTH peak accurately reproduces the shape of the aEPSC (Fig. 3C). This suggests that population firing rate not only can change rapidly in response to input perturbation but also dynamically follow the time-course of input amplitude changes.

Figure 3.

Rapid detection of small excitatory postsynaptic potentials (EPSCs) in changes of population firing. (A) Responses of a neocortical neuron to injection of two episodes of fluctuating noise current (gray traces) with immersed small artificial EPSCs (aEPSCs; red). Traces are aligned by aEPSC onset (vertical dashed line). (B) Firing rate changes of a population of spiking neurons in response to injection of fluctuating current with immersed aEPSCs (red trace). Data from 11 neurons; total of N = 2959 repetitions. Bin 1 ms. Dashed horizontal gray line shows averaged firing rate (4.84 imp/s [impulses per second]). (C) Zoom-in of the response peak, a portion the histogram indicated by gray bar on top of B. Green vertical dashed lines in A-C show aEPSC onset. (D) Probability of EPSC detection by a theoretical decoder (Box 2) receiving inputs from populations of N = 300, 1000, and 3000 transmitting neurons versus time. Results calculated using bootstrapping (circles) and parametrical theoretical estimation (diamonds, solid lines; see Malyshev and others 2013 for details). Modified from Malyshev and others (2013).

A quantitative measure of encoding of input signals into changes of population firing rate—detection probability—can be obtained using a theoretical decoder, which receives inputs from neurons of the transmitting population (Box 2). The decoder reports a change in the input (detects a signal) if the population firing rate exceeds the 95% quantile of the distribution of firing rates before the signal onset (Box 2). Figure 3D shows detection probability calculated using the theoretical decoder on data from Figure 3A-C. The detection probability depends on time and on the number of neurons in the transmitting population. When activity of large number of neurons is available (N = 1000 and N = 3000), aEPSCs can be detected very quickly, within 2 to 2.5 ms from their onset. After decreasing the size of the transmitting population down to N = 300, the time necessary for detection increases, though it still remains within few milliseconds. Thus, small perturbations of the input, such as aEPSCs or steps, lead to rapid changes of population firing rate. Time necessary for detection of these signals decreases with the increasing size of the population.

Box 2. Measuring spike encoding: Detection of changes of firing rate of neuronal population by a theoretical decoder.

A: A theoretical decoder receives inputs from neurons of transmitting population. Histogram shows changes of the population firing rate of the transmitting neurons in response to a depolarizing step immersed in fluctuating current. Bin size 1 ms. Distributions of spike count in 1-ms bins during the periods 120 ms before the step (blue) and 40 ms after the step onset (red) are shown to the right of the histogram. B: Probability of detection of a change in firing rate of a population of N neurons within time interval T was calculated using a theoretical decoder which reports a change in the input if the population firing rate exceeds the 95th quantile of the presignal distribution. Using bootstrapping, we composed 100 trial sets of N randomly selected response sweeps. From these 100 sets we calculated the distributions of the number of spikes during time interval T before the step onset (top), and during time interval T after the step onset (middle). Next, we determined the 95th quantile of the prestep distribution (blue portion of the distribution, dashed vertical line). The portion of the poststep distribution that lies above the 95th quantile of the prestep distribution (red in the middle and bottom plots) provides an estimate of the probability with which the change in firing rate is detected.

C: Probability of step detection versus time (from T=0.4 ms to T=10 ms) for populations of N = 100, 300, 500, 1000, and 3000 neurons. Modified from Malyshev and others (2013) and Tchumatchenko and others (2011).

Cortical Neurons Can Phase-Lock Their Firing to High-Frequency Signals

So far we have considered responses of neuronal populations in the time domain, whereby response speed is assessed by measuring response latency and calculation of detection time. A more general characterization of encoding is provided by measuring the frequency response, or transfer function, which describes how different frequency components of signals are translated into changes of firing rate of neuronal populations. Consider a population of neurons, each receiving individual fluctuating noise and a common sine-wave signal immersed in it. If neurons are able to phase-lock their firing to the signal, information about the signal will be preserved in population firing, and thus the signal will be encoded (Box 3). Measuring the ability of neurons to phase-lock their firing to signals of different frequencies, the transfer function, characterizes the encoding abilities of neuronal population in the frequency domain.

Box 3. Measuring spike encoding: Calculation of frequency transfer function of a population of spiking neurons.

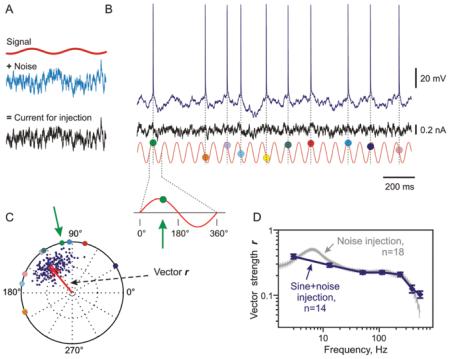
A: Current for injection consisting of a sine-wave signal of frequency f immersed in fluctuating noise.

B: Membrane potential response to current injection recorded in a layer 2/3 pyramidal neuron from rat visual cortex slice. Red trace shows sine wave signal that was present in the injected current, but at greatly expanded Y-scale. Colored circles show timing of each spike and its phase relative to the signal.

C: Calculation of the vector strength r, which characterizes phase-locking of neurons’ firing to sine wave signal of frequency f and thus encoding of that frequency. Each spike is represented by a vector of unit length and a phase between 0 and 2π defined as spike time modulo the stimulus period. Colored circles show phases of all spike-vectors from B. Sum of these vectors, normalized by the number of spikes, gives a vector r. Its length (r = 0.54) characterizes phase-locking of neurons’ firing to the stimulus, and thus encoding of the stimulus frequency f. In the case of ideal phase locking, when all spikes were generated at the same phase of the signal, vector r length would be 1. In the case of no phase locking, when spikes are generated at random phases of the signal, vector r would converge to 0. To assess the variability of the vector length estimate r we used bootstrapping. Each dark blue dot represents a mean vector calculated for random resamplings (N = 200) of 50% of experimentally measured spike times. Note that only 10 action potentials (APs) from a short period of stimulus presentation shown in B were used for these calculations, leading to high variability of bootstrapping results in this example. For calculation of frequency response functions of neurons, such as results presented in panel D, much larger samples of ~300 to ~3000 spikes for each signal frequency per cell were used, thus allowing for reliable statistical analysis.

D: Vector strength r plotted against stimulus frequency provides an estimate of transfer function of neurons (dark blue symbols and line). Data from N = 14 neurons. Note that with this method, phase locking can be estimated only for a set of discrete frequencies (dark blue symbols). A complete characterization of frequency transfer function is possible with a method suggested by Higgs and Spain (Higgs and Spain 2009; Ilin and others 2013) that exploits injection of fluctuating noise containing all encoding-relevant frequencies, and uses frequency-dependent filtering to extract phaselocking of neuronal responses to specific frequencies. Transfer function measured with the noise injection method for N = 18 neurons is shown in gray. Note that the two methods give very similar estimates of the frequency response of cortical neurons.

Modified from Ilin and others (2013).

Transfer functions measured in layer 2/3 and layer 5 pyramidal neurons in slices from rat neocortex are illustrated in Figure 4A. Neurons of both types can phase-lock their firing to high frequencies: layer 2/3 pyramids up to ~300 to 400 Hz, and layer 5 pyramids to even higher frequencies of up to ~600 to 700 Hz. These results agree with a number of reports on experimental measurements of frequency response functions in pyramidal neurons from different areas of the neocortex (Boucsein and others 2009; Broicher and others 2012; Higgs and Spain 2009; 2011; Ilin and others 2013; Kondgen and others 2008; Tchumatchenko and others 2011). In a linear system, characteristics of the response in time domain and frequency domain are related. The response time of a simple low-pass filter is related to the cutoff frequency fc of transfer function as 1/(2πfc). For cutoff frequencies of 200 Hz and above this implies a response time scale <1 ms. Figure 4B illustrates responses to an input step of four idealized systems with different high-frequency cut-off fc of their transfer functions. For transfer functions measured in cortical neurons, with fc values >200 Hz, responses to step changes of the input are fast, but with decreasing fc they become progressively slower.

Figure 4.

Frequency response functions of neuronal populations and response to input steps. (A) Experimentally measured frequency response functions of pyramidal neurons from layer 2/3 (red) and layer 5 (blue) in slices from rat visual cortex. Vertical bars indicate standard error of the mean (SEM). (B) Relation between high-frequency cutoff (fc) of transfer function and dynamics of responses to step-changes of the input. Calculated responses of an idealized system that transfers only frequencies <fc but eliminates frequencies >fc. fc = 1000 Hz, 400 Hz, 200 Hz, and 100 Hz, as indicated. Dashed vertical line indicates the onset of input step (top black trace). Dashed fragmented lines between A and B are for illustration of the relation between measured transfer functions of cortical neurons in A and cutoff frequencies used for calculation of responses in B.

To summarize, measurements made both in the time domain and the frequency domain indicate that ensembles of cortical neurons can communicate on a millisecond time scale and thus support fast processing. Cortical neurons can phase-lock their firing to high-frequency components of the input up to ~300 to 700 Hz, and respond quickly, on a millisecond time-scale, to rapid changes of the input. Considering the theoretical decoder (Box 2) as a “reader” of ensemble activity (Buzsaki 2010), the length of a time unit for neuronal computations is short, only ~1 to 3 ms. The ability of cortical neuronal ensembles to accomplish one iteration of processing within 1 to 3 ms sets the time clock of the “cortical network CPU” at ~300 to 1000 Hz. This time scale is several-fold faster than the membrane time constant of principal cortical neurons (~10-20 ms), which sets a coarse time scale for passive dendritic integration of synaptic inputs—an “integration cycle” (Buzsaki 2010). Fast communication between neuronal ensembles allows cortical networks to perform multiple iterations of processing within the duration of one membrane time constant. This is a useful feature for processing in networks with rich feedback connectivity. It allows feedback signals to influence ongoing dendritic processing: the simplest recurrent scheme includes only two iterations. It is also advantageous for parallel processing. The ability to perform multiple iterations within a single integration cycle facilitates coordination of activity in parallel streams and timing of their outputs for the final integration of results. All in all, fast communication between individual cortical ensembles allows the employment of multiple ensembles in complex, multiple-step processing within a perceptual time-unit, which, depending on sensory modality and complexity of the current task, takes ~50 to 100 ms and upward.

Ultrafast Neuronal Responses: What Are They Good for?

Experimental evidence considered above demonstrated that ensembles of spiking neurons are capable of encoding input perturbations into changes of the firing rate very fast, on the time scale of milliseconds. Does the brain use this high processing speed? And what could these abilities for ultrafast processing be good for?

It is important to note that ability of neuronal populations to change their firing rate in response to very fast changes of the input (on millisecond scale) does not necessarily imply that we can perceive stimuli which change that fast. For instance, even though neurons in the visual cortex can phase-lock their firing rate, and thus encode frequencies of 300 to 700 Hz, this does not mean we can perceive visual stimuli changing at this rate, because any cognitive process involves multiple-stage processing in multilayer neuronal networks. It does mean, however, that cortical neurons can signal changes at their inputs by changing their firing very quickly, and thus are able to support fast computations and temporal coding with precisely timed spikes. This feature is vital for a broad range of phenomena and processes, such as generation of high frequency oscillations, synchrony and precise coordination of activity, or spike-timing dependent plasticity with millisecond-precise windows.

In the cortex, neuronal activity and field potentials express oscillations in high-frequency range, such as high-gamma (>80 Hz) in the visual cortex (Frien and others 2000; Ray and Maunsell 2011), ripples (~200 Hz) in the hippocampus (Bragin and others 1999; Csicsvari and others 1999; Klausberger and others 2003; Ylinen and others 1995) and ultrafast oscillations (>200 Hz) in the barrel cortex (Jones and Barth 1999). For an oscillation at 200 Hz, positive and negative phases of the cycle are only 2.5-ms long. Because these oscillations have synaptic origin, alternating excitatory and inhibitory inputs should fit exactly into this time frame to produce rapidly alternating depolarization and hyperpolarization phases of membrane potential fluctuations. This requires that excitatory and inhibitory neurons generate spikes with millisecond precision. Presence of high-frequency oscillations in brain activity shows that both excitatory and inhibitory neurons can support such precision.

High temporal precision of spike generation is also crucial for spike-timing dependent plasticity, which represents a cellular mechanism of learning and memory. The width of temporal windows for potentiation, though variable for different types of neurons and connections, is often in the range of few milliseconds, for example, ~10 ms in somatosensory and visual cortex (Feldman 2000; Froemke and others 2005), and only ~6 to 7 ms in entorhinal cortex (Haas and others 2006; Zhou and others 2005). Missing this window by just few milliseconds may result in failure to induce potentiation or even in depression.

In perception, hearing has the highest temporal resolution compared to other senses. Leaving aside tonotopically organized “labeled line” representation of kilohertz-range frequencies, neurons of the auditory system can phase lock their firing to frequencies up to ~1 to 2 kHz in subcortical structures and up to ~100 Hz in the primary auditory cortex (Bieser and MullerPreuss 1996; Joris and others 2004; Schreiner and Urbas 1988). Even higher precision, on a sub-millisecond scale, is required for estimation of the azimuth of a sound source from binaural delays that can be as small as 0.1 ms. Although binaural delays are calculated in subcortical structures (e.g., Adachi and others 2014; Golding and Oertel 2012; Kuba and others 2006), this example illustrates that neurons are capable of both, generating signals with this exceptional precision and processing them.

The visual system has a lower temporal resolution of ~20 to 25 ms. For instance, we do not perceive the flickering of a computer screen or TV with a refresh rate of 40 to 60 Hz. Nevertheless, information about higher frequency components of environmental stimuli can be present in activity of visual cortex neurons: visually evoked potentials in some human observers show entrainment to high contrast stimuli up to a 72-Hz refresh rate (Lyskov and others 1998; Williams and others 2004), and significant portion of neurons in primary visual cortex of the macaque phase-lock to high contrast stimuli presented even at a 100 Hz refresh rate (Williams and others 2004). These frequencies are well below the cutoff of the frequency transfer functions of cortical neurons (Fig. 4). In fact, cortical neurons are able to phase-lock their firing, and thus encode, several-fold higher frequencies. This enables neuronal networks of the visual cortex to perform multiple iterations of processing within each time-unit of a slower perceptual scale. Fast communication between neuronal ensembles may thus allow complex, multistage processing of visual information, while achieving the remarkable temporal resolution of visual perception.

Cognitive tasks requiring interactions between multiple brain regions can be performed amazingly quickly. Humans can process complex natural images and relate them to the visual world within 150 to 200 ms (Thorpe and others 1996), and monkeys can make a decision in a color-discrimination task even within 30 ms (Stanford and others 2010). Because such tasks involve multiplestage processing in polysynaptic circuits, the high performance speed implies fast communication between the involved ensembles.

Thus, experimental data provide clear evidence for fast responses in vivo. Moreover, the speed of perception and performance in some specific cognitive tasks shows that abilities of neuronal ensembles to communicate fast are indeed exploited by the brain.

Cellular and Network Mechanisms That Affect the Speed of Neuronal Computations

Ideal Encoders and Spike Onset: Insights from Neuron Models

Theoretical work showed that a population of the most simple model neurons, leaky integrate and fire (LIF) neurons (Tuckwell 1998), can faithfully transfer arbitrary frequencies, which are present in their membrane potential fluctuations, into changes of the firing rate (Brunel and others 2001; Knight 1972a, 1972b; Lindner and Schimansky-Geier 2001; Naundorf and others 2005). In response to a small step-like change of the mean or variance of the input current, populations of such neurons can instantaneously alter their firing rate (Brunel and others 2001). Therefore populations of such neurons have been called “ideal encoders” (Knight 1972a). For faithful encoding of arbitrary input signals by ideal encoders only two requirements have to be fulfilled: signals should be presented on background of correlated (non-white, or filtered) noise, and neurons of the population should fire irregular spontaneous spikes. Considered in isolation, spontaneous firing and background “noise”, unrelated to the stimulus under study consume energy and are thus subject to energy constraint. However, in the whole brain background “noise” activity may originate naturally because of the features of constructing elements (Faisal and others 2008), and/or be a by-product of other ongoing processes, such as parallel processing of multiple factors in the network, and thus come with no or little additional energy costs.

Ideal encoders, such as LIF model neurons, are equipped with an instantaneous spike generation mechanism, while in real neurons action potentials have finite onset dynamics, determined by the activation kinetics of sodium channels (Hodgkin and Huxley 1952a, 1952b; Hodgkin and others 1952). Implementing spike generators with finite onset dynamics, that takes into account the activation kinetics of sodium channels in conductance-based neuron models, fundamentally changes encoding properties of populations of such neuron models. With increasing time scale of spike generation, the time scale of spike responses slows down (Fourcaud-Trocme and others 2003), and the ability of neurons to phase-lock their firing to frequencies f higher than the firing rate of individual neurons is attenuated proportionally to 1/f, thus limiting the reliably encoded range of frequencies (Fourcaud-Trocme and Brunel 2005; Fourcaud-Trocme and others 2003; Naundorf and others 2005).

These theoretical results have two important implications. First, they identify properties of neuronal spike generators, specifically onset dynamics of action potentials, as one of the major determinants of encoding in neuronal networks. Second, because cortical neurons generate APs with finite onset dynamics, they are not ideal encoders, and their transfer function has a finite cut-off. Hence those factors which influence the cutoff frequency of neuron models with finite-scale spike onset, such as their firing rate or spike onset dynamics, might influence the frequency composition of signals encoded by cortical ensembles. This poses a number of questions that are fundamental for understanding encoding and speed of spike responses and neuronal computation. How are APs generated in cortical neurons, and what mechanisms underlie their fast onset, necessary to support encoding of high frequencies and fast spike responses? Which factors determine the frequency composition of signals encoded in spiking of cortical neurons? How does interaction of different factors determine the abilities of neuronal populations for high-frequency encoding, fast responses and high speed of computation?

Distal Initiation of Action Potentials in Cortical Neurons

In neocortical neurons, action potentials are initiated in the axon initial segment, about 30 to 50 µm away from the soma (Baranauskas and others 2013; Fleidervish and others 2010; Kole and Stuart 2012; Palmer and Stuart 2006; Stuart and others 1997; Stuart and Sakmann 1994). Shifting spike initiation into the axon initial segment brings about several advantages, such as a certain degree of isolation of the spike initiation site from the large capacitance of the soma and smaller local capacitance thus allowing a faster time constant; small surface of the initiation zone, which makes maintenance of higher channel density, generation of high-density currents, and restoration of ionic gradients after the spike less energetically expensive; and increasing fidelity of action potential propagation down the axon.

Modeling: Encoding Depends on the Dynamics of the Action Potential at the Initiation Site

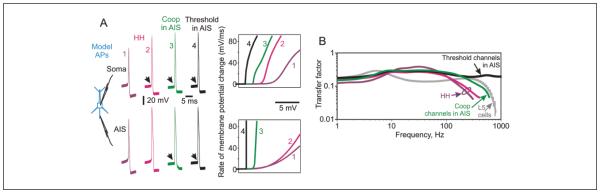
With action potentials initiated in the axon initial segment (AIS), does the transfer function depend on spike onset dynamics, as prior theoretical analysis had shown for single-compartment models? And if yes, is encoding determined by the dynamics of spike initiation in the AIS, or by the onset of somatic spikes? Figure 5A shows action potentials at the initiation site in the AIS and in the soma for four multicompartment neuron models with realistic structure of the initial portion of the axon (see Baranauskas and others 2010; Ilin and others 2013 for model details). In all four models, spike initiation zone was in the distal part of the axon initial segment, 30 to 50 µm from the soma. The four models differed by the composition and kinetics of sodium channels at the spike initiation zone. In the first two models (HH) all sodium channels were Hodgkin-Huxley type. The first model had a moderate density of Hodgkin-Huxley type sodium channels (producing peak sodium current of 2,000 pS/µm²), and the second model had very high density of the same channels (peak current 20,000 pS/µm²) at the spike initiation zone. In addition, the second model had an increased axial resistance in the axon. This combination of extreme parameters was necessary (Baranauskas and others 2010) to achieve fast onset of AP in the soma despite a slow, Hodgkin-Huxley type onset at the initiation zone, as suggested by the “invasion scenario” (Yu and others 2008). The third and fourth models had moderate density of sodium channels at the initiation zone (2,000 pS/µm²). A small portion (10%) of these channels expressed either cooperative activation (Coop in AIS) or threshold activation (Threshold in AIS). Remaining sodium channels in the AIS and all sodium channels in other compartments were Hodgkin-Huxley type. Onset dynamics of spikes in the AIS was clearly different in the four models: slow in the models with moderate or high density of HH channels, fast in the model with a portion of cooperative channels in the AIS, and yet faster, essentially instantaneous, in the model with a portion of threshold channels. Importantly, somatic spikes had slow onset in the first HH model, but expressed fast onset with a characteristic kink at the origin in the remaining three models. Comparison of transfer functions measured in the four models allows us to draw the following conclusions. In models with spike initiation in the AIS, the ability to encode high-frequencies depends on onset dynamics of action potentials (Fig. 5B), similar to the dependence described in point-process simulations. Model neurons with a small portion of threshold channels in the AIS, initiating spikes almost instantaneously, do not express high-frequency cutoff, much like the ideal encoders. In contrast, model neurons with Hodgkin-Huxley channels in the AIS have clear attenuation of encoding of high frequencies. Importantly, encoding of high frequencies was poor in both HH models, despite the fast onset of somatic spikes achieved by extremely high density of sodium channels, as required by the invasion scenario (Yu and others 2008). Thus, onset dynamics of spikes at the site of initiation, but not in the soma, is determining the encoding properties of neurons. These conclusions are further substantiated by encoding properties measured in model neurons with a small portion of cooperative channels in the AIS. In this model, dynamics of spike initiation was intermediate between Hodgkin-Huxley and threshold models, and so was the transfer function: better encoding of high frequencies than in Hodgkin-Huxley models, but with a clear high frequency cutoff unlike the threshold model. Notably, compared with other models, the model with 10% cooperative channels in AIS had transfer function in high frequency range (above ~100 Hz) that resembled most closely the transfer function measured in layer 5 pyramidal cells (Fig. 5B).

Figure 5.

Spike generation and frequency response function of multicompartment neuron models. (A) Action potentials in the soma and at the site of initiation in the axon initial segment (AIS) in four multicompartment models, and phase plots of the initial portions of these action potentials (APs). Black oblique arrows point at the sharp kink at AP onset. Note that in both models with Hodgkin-Huxley channels, AP onset is slow at the initiation site in the AIS, but becomes fast in the soma of the model with high density of sodium channels and increased Rax (magenta traces). In two other models, with a fraction of cooperative or threshold channels in the distal AIS, AP onset is fast both at the initiation site and in the soma. (B) Frequency response functions of the four models from A. Note the difference between the models in the ability to encode high frequencies. For comparison, gray line with error bars shows transfer function of layer 5 pyramidal neurons from Figure 4. All four models had the same morphology, with detailed structure of the axon initial segment and simple morphology of the dendrites (Baranauskas and others 2010), and same passive properties and Hodgkin-Huxley type potassium and sodium channels in the axon, soma and dendrites (Ilin and others 2013). The models differed in the channel composition in the initial segment. In the first two models (HH), the distal portion of the axon initial segment (30-50 µm from the soma) had a moderate (lilac traces, 2,000 pS/µm²) or very high (magenta traces, 20,000 pS/µm²) density of Hodgkin-Huxley type sodium channels. In the second model axial resistance in the axon was increased (Rax = 300 ohm cm compared with Rax = 150 ohm cm in other models). This combination of extreme values was necessary to achieve fast onset of AP in the soma, despite a slow, Hodgkin-Huxley type onset at the initiation zone in the distal initial segment (Baranauskas and others 2010). The distal AIS of the third model (Coop in AIS) had moderate density of sodium channels (2,000 pS/µm²), a small portion of which (10%) expressed cooperative activation (Naundorf and others 2006). Remaining sodium channels in the AIS and in other compartments were Hodgkin-Huxley type. In the distal AIS of the fourth model (Threshold in AIS), 10% of sodium channels expressed threshold activation. Details of model parameters are given in Ilin and others (2013), models 2, 6, 7, and 8 from Figure 3. Modified from Ilin and others (2013).

This analysis identifies onset dynamics of action potentials at the initiation zone, governed by the kinetics of sodium channel activation, as a major factor determining encoding properties of neurons.

Encoding in Neurons Depends on Action Potential Onset Dynamics

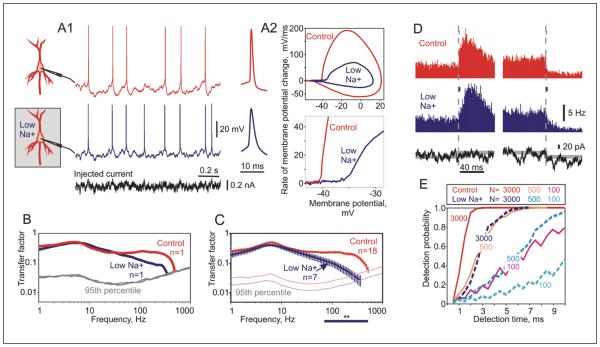
Does the dependence of encoding of high frequencies and response speed on AP onset hold for cortical neurons? Onset dynamics of spikes in cortical neurons can be slowed down by application of low concentration of TTX in the recording chamber (Naundorf and others 2006) or locally to the axon initial segment (Ilin and others 2013; Kole and Stuart 2008), or by lowering extracellular sodium concentration, substituting a portion of sodium ions with choline (Ilin and others 2013). Figure 6 shows that in low extracellular [Na⁺] both the onset of action potentials is slowed down, and encoding of high frequencies is impaired. The impairment of encoding of high frequencies was clear when measured in individual neurons in control conditions and after application of low-sodium solution (Fig. 6A and B), and it was significant for the whole sample: transfer factors for frequencies >65 Hz were significantly lower in low sodium than in control (Fig. 6C). Moreover, slowing down of AP onset dynamics was associated with decreased speed of responses to input steps (Fig. 6D). For a given size of a population of transmitting neurons, detection of the step-induced changes in population firing rate by the theoretical decoder took about twice as long in low sodium solution than in control (Fig. 6E). Because detection time depends on the number of transmitting neurons the effect of slower spike generation could be compensated by increasing the size of the transmitting population. In Figure 6E example, achieving same detection times with neurons with slower spike onset would require a fiveto sixfold increase of the population size as compared to cortical neurons in control, with undisturbed spike onset.

Figure 6.

Artificial slowing down of action potential (AP) onset impairs encoding of high frequencies and decreases the speed of population firing rate response. (A1): Responses of a neocortical neuron to injection of the same fluctuating current (bottom trace, black) in control conditions (red) and in reduced extracellular [Na⁺] (blue). Recordings are from the soma. (A2) AP waveforms, phase-plots, and zoom-in of initial portion of APs in phase plots illustrate slower onset of APs in low extracellular [Na⁺] relative to control. (B) Frequency response functions of the neuron from A recorded in control conditions (red) and then in low [Na⁺] (blue). Transfer functions were cut at intersection with respective 95th percentile of N = 500 transfer functions obtained with shuffled AP timings (gray; see Ilin and others 2013 for details). (C) Averaged frequency response functions measured in control conditions (red; N = 18 neurons) and in low [Na⁺] (blue; N = 7). Transfer functions were cut at respective 95th percentiles (pale color lines). The bar below the plot shows high frequency range in which encoding in low [Na⁺] experiments is significantly impaired (**P < .01) relative to control. (D) Changes of population firing rate in response to the onset and offset of small current steps immersed in fluctuating current (bottom), in control conditions (red) and in the medium with reduced extracellular [Na⁺], which leads to slower AP onset dynamics (blue). Each peristimulus time histogram (PSTH) was calculated using N = 9100 responses. Vertical bars above the onset and offset of steps in histograms show averaged AP duration. (E) Probability of step detection vs. time after step onset, for populations of N = 100, 500, or 3000 neurons. Note that for samesize populations detection time in low [Na⁺] is about twice as long as in control. Modified from Ilin and others (2013).

Thus, the ability of cortical neurons to change their firing rate rapidly in response to input perturbations critically depends on the onset dynamics of action potentials. Slowing down the onset dynamics of spikes by experimental manipulations leads to a decrease of the response speed. These results provide experimental proof for the theoretically predicted dependence of encoding on the dynamics of spike initiation (Fourcaud-Trocme and others 2003; Huang and others 2012; Naundorf and others 2005; Wei and Wolf 2011). Moreover, in combination with results of encoding in multicompartmental models with distal spike initiation these results support the notion that fast onset dynamics is a genuine property of cortical spike generators (Naundorf and others 2006): Encoding depends on action potential onset at the initiation site, and cortical neurons are able to encode higher frequencies than models in which fast onset of somatic spikes is produced solely by invasion of lateral current as suggested by (Yu and others 2008).

Other Factors That Influence Encoding

In addition to onset dynamics of AP initiation, three groups of factors influence encoding in neuronal populations and their response speed.

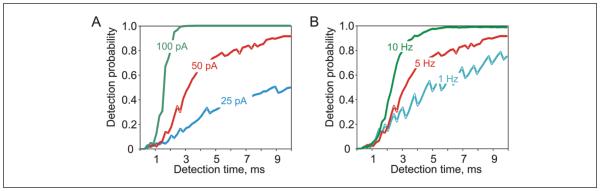
The first group includes properties of the input signal: propagation time along presynaptic axons and input amplitude. Increasing the propagation speed by increasing axon diameter and myelinization is a common strategy in the nervous system, especially for transmission over longer distances. For short-distance communication this factor is subject to strict structural and energy constraints (see Faisal and others 2005 for review). The input amplitude influences response speed too: with other conditions equal, stronger inputs are detected faster (Fig. 7A). As discussed above, the higher amplitude of the input can be due to large amplitude of unitary EPSPs, or result from synchronization of activity in several presynaptic fibers.

Figure 7.

Dependence of detection time and probability on the signal amplitude and the firing rate. (A, B) Probability of detection of artificial excitatory postsynaptic current (EPSC) versus time after the artificial EPSC (aEPSC) onset for population of N = 1000 neurons, for different amplitudes of aEPSCs (A, mean firing rate 5 Hz) and different firing rate of transmitting neurons (B, aEPSC amplitude 50 pA), as indicated. Data from one layer 2/3 pyramidal neuron (Ilin, Stevenson, Volgushev, unpublished).

The second group includes factors that govern integration of inputs, and ultimately determine the input-driven current and membrane potential changes at the site of spike initiation. Although the variety of processes involved in translation of synaptic conductances at the dendrites into changes of the membrane potential at the site of action potential initiation is beyond the scope of this review, few points are worth mentioning. Of clear relevance for encoding is the shortening of the effective time constant, either by decreasing membrane resistance in high conductance state (Destexhe and others 2003), or by decreasing local capacitance at the spike initiation zone by shifting it into the axon, which results in partial isolation of the initiation zone from the large capacitance of the soma (Baranauskas and others 2013; Ma and Huguenard 2013). The isolation from the soma might be especially strong when the axon originates from a dendrite (Hausser and others 1995; Martina and others 2000; Thome and others 2014). An unexpected aspect of crosstalk between properties of the dendritic tree and encoding is reported in a recent computational study: increasing the size of the dendritic tree (and thus its impedance load) leads to faster onset of spikes in the axon initial segment and improved encoding of high frequencies (Eyal and others 2014). Better encoding of high frequencies by layer 5 pyramids than by layer 2/3 pyramids (Figure 4) is consistent with these theoretical results.

The third group includes network factors: the size of the population of transmitting neurons and their firing rate. Increasing the number of neurons that receive a common signal and provide input to the theoretical decoder improves signal detection and makes it faster (Figs. 3D and 6E). Theoretical analysis predicted that increasing the firing rate of neurons in the encoding population shifts the cutoff frequency of the transfer function toward higher frequencies, thus improving the encoding of fast-changing signals (Naundorf and others 2005). Recent experimental results (Ilin and others 2014) confirm this prediction: with averaged firing rate of neurons increasing from 1 to 5 Hz and to 10 Hz, small artificial EPSCs were detected progressively faster (Fig. 7B). Note that the two network factors are directly related to energy expenditure, and thus subject to energy consumption and structural constraints.

To summarize, results of theoretical and experimental analysis of spike encoding have identified the following requirements for high-speed communication between neurons, and factors which affect this speed. Achieving a high speed of the spike responses requires population encoding and background “noise” activity that produces spontaneous firing in the encoding population. A critical factor that determines the response speed is the onset dynamics of action potentials: populations of neurons with fast AP onsets change their firing rate in response to input perturbations faster than neurons generating slowonset spikes. Increasing the size of the population of encoding neurons and their firing rate decreases the time necessary for detecting a change in population firing. Detection time can be also decreased by increasing the signal amplitude, for example by increasing input synchrony. These dependences, initially predicted theoretically (Brunel and others 2001; Fourcaud-Trocme and Brunel 2005; Fourcaud-Trocme and others 2003; Huang and others 2012; Naundorf and others 2005; Wei and Wolf 2011), have now been supported by experimental evidence from neocortical neurons (Boucsein and others 2009; Higgs and Spain 2011; Ilin and others 2013; Ilin and others 2014; Kondgen and others 2008; Tchumatchenko and others 2011).

Outlook: Interplay of Factors Influencing Encoding

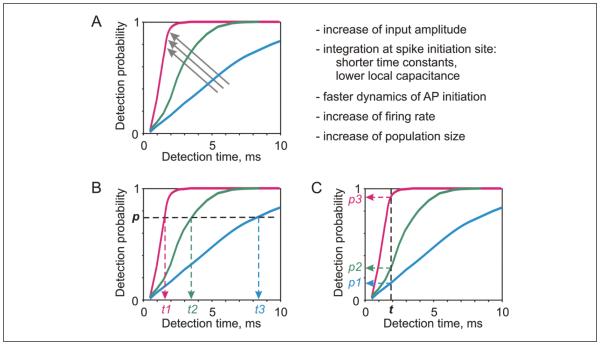
The fact that response speed of neuronal populations depends on multiple factors (Fig. 8A) suggests several strategies for speeding-up neuronal responses and processing in neuronal networks. For example, one way to accelerate processing is to increase signal amplitude. This could be achieved on a short time scale by increasing synchrony of presynaptic activation, but also on the long time scale by long-term potentiation of synaptic transmission. Another way to speed-up processing would be to increase the size of populations involved in encoding, either short term within the limits of existing connectivity, or long term by establishing new connections. Immediate increase of response speed can be achieved also by increasing the firing rate of neurons. With these strategies, processing speed can be increased selectively in neuronal ensembles involved in a specific task or processing of specific types of signals. A drawback of the above strategies is that increase of processing speed comes with an increase of energy consumption and/or additional morphological structures, and thus is subject to respective constraints. A strategy allowing a general increase of processing speed in neuronal networks is acceleration of the onset dynamics of action potential generation. This strategy has several advantages. First, higher processing speed is not associated with additional energy or structural costs. Second, a general increase of processing speed in the whole network does not disturb temporal relations between processing in different parts of the networks, and thus does not disrupt temporal organization of neuronal activity. Rather, the ability of neurons to encode high frequency stimuli and generate high-precision spike patterns expands the possibilities for precise coordination of neuronal activity and for the use of temporal coding. Finally, this strategy preserves the dynamic range of regulation of processing speed with the use of other, energy-expensive strategies, which could be employed in selective fine-tuning of processing.

Figure 8.

Factors influencing response speed of neuronal populations. (A) Schematic representation of the influence of different factors on detection. Multiple factors listed on the right are pushing the detection curve in the same direction, as indicated by the arrows. (B, C) Two perspectives on comparison of detection curves. One perspective (B) is focused on detection time: steeper detection curve means that less time is required to reach a preset probability p of signal detection. Another perspective (C) is focused on detection probability: Steeper detection curve means an increase of the probability with which the signal will influence neuron’s output within a preset time interval t.

The variety of means for increasing processing speed allows for a certain degree of trade-off between them. The use of a cost-neutral speeding-up of processing by accelerating onset dynamics of spike generation may allow to limit the use of other factors, which are associated with increased energy demands, and thus achieve high processing speed without the explosion of energy consumption. An illustrative example from Figure 6E shows that ability of neocortical neurons to generate fast-onset spikes allows neuronal systems to achieve the same processing speed with population sizes ~5-6 times smaller as compared to populations of neurons with a slow spike onset. This does not preclude, however, the use of energy-expensive strategies. For example, increase of the firing rate and/or number of neurons involved allows for a dynamic, “on-demand” speeding-up of processing, such as for in-depth analysis of a specific portion of environment highlighted by attentional spotlight, or in context-dependent processing.

The influence of the above factors on detection probability curves (Figure 8A) can be considered from two perspectives. One is focused on changes of detection time. From this perspective, the outcome of potentiation of synaptic transmission or an increase of the firing rate of neurons is a decrease of time required for detecting a signal with a preset probability p (Fig. 8B). Another perspective is focused on changes of detection probability. From this perspective, potentiation or higher firing rate lead to an increase of the probability with which the signal will be able to influence neurons’ output within a given time interval t (Fig. 8C). Redistribution of synaptic weights as a result of plasticity, or dynamic changes of firing rates of neuronal ensembles will then lead to redistribution of the probabilities with which different inputs influence neurons’ spiking pattern, and thus the message sent by this neuron (or ensemble of neurons) for further processing. The probability-oriented perspective applies for understanding processing in neuronal networks subject to time-constraints, which can be imposed, for example, by rhythmic activity. In this case, the rhythm sets the intervals during which neurons can generate spikes. Inputs communicated via stronger synapses, or by neurons firing at higher rates, will have higher probability to influence the neurons’ output spiking. The resulting spread of activity and the constellation of activated neurons will then reflect most probable, though not the only possible, outcome of processing.

Open Questions

Modern techniques have allowed remarkable advances in mapping neuronal connectivity and revealing morphological and biochemical diversity of neurons. However, understanding how this connectivity is used, and how neuronal networks process information and mediate behavior, is impossible without knowledge of computational properties of neurons and neuronal populations. Recent progress in theoretical and experimental analyses of neuronal encoding has brought about novel insights onto computational abilities of neurons, and their dependence on details of neuronal morphology, electrophysiology, and the state of network in which these neurons are embedded. It also highlighted several groups of unresolved questions that are crucial for further progress.

How are APs initiated in cortical neurons? What are mechanisms of fast onset dynamics of cortical APs? So far, there is no consensus model of AP generation in central neurons which is compatible with all existing pieces of experimental evidence: kinetics of channels and their distribution in the axon initial segment, onset dynamics of APs, and encoding properties of cortical neurons, including the high cutoff frequency of their transfer function.

How different are encoding properties of neurons of different types? What are between-type differences and within-type variability of encoding properties of neurons? Answering these questions will help to understand differential roles played by neurons of different types in cortical computations, and how specific encoding properties allow neurons to serve these roles.

How big are neuronal ensembles mediating behaviors? Can the number of participating neurons be increased to transmit information faster and decrease response time?

For example, are faster responses in a known context mediated by increasing the number of involved neurons and/or their averaged firing rate? Answering these questions will help to understand whether and how abilities of neurons for fast communication are used in the brain and how they are dynamically regulated.