Abstract
The extradiol, aromatic ring-cleaving enzyme homoprotocatechuate 2,3-dioxygenase (HPCD) catalyzes a complex chain of reactions that involve second sphere residues of the active site. The importance of the 2nd-sphere residue His200 was demonstrated in studies of HPCD variants, such as His200Cys (H200C), which revealed significant retardations of certain steps in the catalytic process as a result of the substitution, allowing novel reaction cycle intermediates to be trapped for spectroscopic characterization. As the H200C variant largely retains the wild-type active site structure and produces the correct ring-cleaved product, this variant presents a valuable target for mechanistic HPCD studies. Here the high-spin FeII states of resting H200C and the H200C–homoprotocatechuate enzyme–substrate (ES) complex have been characterized with Mössbauer spectroscopy to assess the electronic structures of the active site in these states. The analysis reveals a high-spin FeII center in a low symmetry environment that is reflected in the values of the zero-field splitting (ZFS) (D ≈ −8 cm−1, E/D ≈ 1/3 in ES) as well as the relative orientations of the principal axes of the 57Fe magnetic hyperfine (A) and electric field gradient (EFG) tensors relative to the ZFS tensor axes. A spin Hamiltonian analysis of the spectra for the ES complex indicates that the magnetization axis of the integer-spin S = 2 FeII system is nearly parallel to the symmetry axis, z, of the doubly occupied dxy ground orbital deduced from the EFG and A-values, an observation which cannot be rationalized by DFT assisted crystal-field theory. In contrast, ORCA/CASSCF calculations for the ZFS tensor in combination with DFT calculations for the EFG- and A-tensors describe the experimental data remarkably well.
TOC image
The H200C variant of homoprotocatechuate-2,3-dioxygenase yields the correct ring-cleaved product of the native substrate. Mössbauer studies of the (S = 2) FeII enzyme–substrate complex indicate a zero-field splitting (ZFS, D = −8 cm−1, E/D ≈ 1/3) with an easy axis of magnetization along the z axis of dxy ground orbital. Neither crystal-field theory nor DFT provide an explanation for this observation. However, CASSCF calculations give a ZFS tensor in excellent agreement with our experimental data.
INTRODUCTION
Mononuclear non-heme FeII centers are present in a myriad of enzyme and protein families throughout biology.1–8 Oxygenase enzymes carrying these centers catalyze a range of reactions which even exceeds that of heme-containing enzymes such as cytochrome P450.1, 3, 5, 9 One way in which the non-heme iron center differs from a heme center is in its ability to simultaneously use up to three ligand sites to directly bind organic substrates and O2.10–16 This ability serves to orient the substrates and to connect them electronically to enhance reactivity and specificity.2, 10, 17–20 The study of the critical substrate binding and subsequent O2 activation reactions in the non-heme ferrous enzyme classes has been hampered by the lack of visible chromophores and the presence of an inherently EPR silent (at X- and Q-band) metal center. However, past studies by our laboratories and many others have successfully employed advanced spectroscopic techniques including Mössbauer spectroscopy, MCD, XAS, parallel mode EPR, and EXAFS to characterize the properties of the resting enzymes and their substrate complexes.4, 21–26 Recent studies, using enzyme active site variants and alternative substrates, have allowed reaction cycle intermediates to be trapped and spectroscopically characterized.4, 16, 26–31
Although considerable progress has been made in understanding substrate binding and O2 activation by ferrous non-heme oxygenases, the complex reactions catalyzed by these enzymes pose ongoing challenges. Homoprotocatechuate 2,3 dioxygenase (HPCD) from Brevibacterium fuscum is the most thoroughly studied enzyme in the class of FeII enzymes that catalyze the extradiol ring cleavage of aromatic catecholic compounds.15, 17, 18, 32 In the past decade, our laboratories have used a variety of techniques to study the wild-type (WT) enzyme as well as active site variants in which important 2nd-sphere residues were mutated.26–30, 33–37 Biochemical studies have shown that His200 serves a variety of critical functions in the activation of dioxygen, among them acid/base catalysis. To further probe the importance of His200, we recently studied a variant, H200C, in which His200 was replaced by cysteine.38 It was shown that H200C is catalytically active, yields the correct ring-cleaved product, and supports a novel long-lived ferric intermediate that was assigned as a (substrate radical)-FeIII-(distal hydroperoxo) species. Like the wild-type enzyme,32 the H200C variant fails to react with O2 to make any oxy intermediate without prior formation of the ES complex.
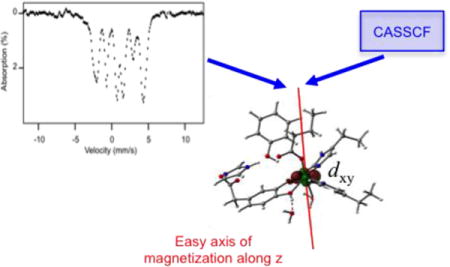
Here we present a detailed Mössbauer study of the resting H200C variant and its complex with the natural substrate homoprotocatechuate (HPCA); a DFT structure of the ES complex is depicted in Figure 1. The spectra of these high-spin FeII species exhibit highly resolved paramagnetic hyperfine structure which allowed us to extract the principal values of the zero-field splitting (ZFS), the 57Fe electric field gradient (EFG), and the 57Fe magnetic hyperfine (A) tensors, and to determine the relative orientations of these tensors’ principal axes, which are not collinear due to the low symmetry (C1) of the ligand environment. These studies, together with the 1.46 Å resolution X-ray structure of H200C–HPCA (PDB 5BWH),38 were combined with quantum chemical calculations to address the relative orientations of the tensor axes.
Figure 1.
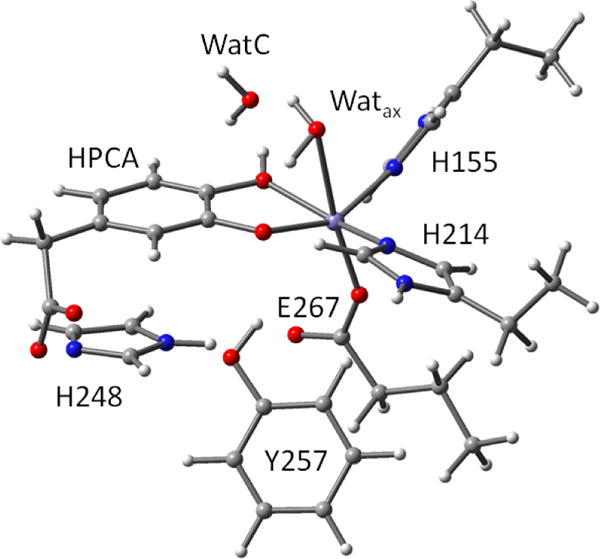
DFT structure of ES complex.
In our studies of the active site variants Y257F29 and the present H200C variant, we observed that resting enzyme as well as the ES complex show a nearly rhombic ZFS tensor oriented such that it produced an ‘easy axis’ of magnetization along a direction, z, that is nearly parallel to the symmetry axis of the doubly occupied dxy orbital. A similar observation was made for the FeII state of the unrelated FeIII intradiol catechol-cleaving protocatechuate 3,4-dioxygenase.39 These observations were puzzling to us because crystal-field theory (CFT) would predict an easy axis in a direction perpendicular to z. Following a suggestion by Neese and coworkers,40 we present here the application of complete active space self consistent field (CASSCF) calculations to address this problem.
METHODS AND MATERIALS
Sample Preparation
Biochemicals and chemicals were purchased from Sigma-Aldrich or Fisher Scientific and 57Fe metal (96.8% enriched) was obtained from Cambridge Isotopes (MA). The H200C variant was produced and Mössbauer samples prepared as previously described.38
Spectroscopic Methods
Mössbauer spectroscopy
Mössbauer spectra were recorded using Janis Research Super-Varitemp dewars that allowed studies in parallel applied magnetic fields up to 8.0 T and temperatures in the range of 4.2 K – 150 K. Mössbauer spectral simulations were performed using the WMOSS software package (SEE Co). Isomer shifts are quoted relative to Fe metal at 298 K.
Quantum Chemical Calculations
The geometry optimization for a structural model of the ES complex (Figure 1) was performed with Gaussian ’09, revision A.02, using functional B3LYP and basis set 6-311G (www.gaussian.com).41 57Fe hyperfine parameters were calculated for the optimized structure, using the same functional/basis set combination, with the PROP keyword. The EFG was also evaluated in a single point calculation for the same structure and functional with basis set TZVP. The G’09 structure was subsequently used for a complete active space self consistent field (CASSCF) calculation using the ORCA program version 3.0 (https://orcaforum.cec.mpg.de/).42 To obtain an initial guess for the CASSCF, a single point BP86 calculation was performed with ORCA, using the triple zeta valence polarized basis set TZVP and auxiliary basis TZVP/J. The ROTATE routine of ORCA was then used to construct the active space orbitals for the 3d6 configurations, CAS(6,5), of the high-spin FeII system described in the text but from which the non-coordinating residues were removed for computational efficiency. The CASSCF calculations used basis set TZVP and auxiliary basis TZVP/C. Calculation of the ZFS tensor, using the Breit–Pauli operator, was activated with the DOSOC keyword and included contributions from S = 2 (5 roots), S = 1 (18 roots), and S = 0 (13 roots).
RESULTS
Mössbauer Studies and Spin Hamiltonian Analysis
Figure 2A shows a Mössbauer spectrum of resting H200C recorded at 4.2 K in zero field (B = 0). The spectrum displays a quadrupole doublet with ΔEQ = 3.28(2) mm/s and δ = 1.22(1) mm/s, parameters typical of high-spin FeII and close to the values reported for the resting states of the WT HPCD and the H200N and Y257F variants.26, 28, 29 Figure 2B shows the B = 0, 4.2 K Mössbauer spectrum of the ES complex, H200C–HPCA. The major species, representing ~80% of total Fe, exhibits a quadrupole doublet with ΔEQ = 3.53(2) mm/s and δ = 1.14(1) mm/s. Figure 2B also reveals the presence of a second high-spin FeII species (≈ 6% of Fe) with δ = 1.20 mm/s and a substantially smaller quadrupole splitting, ΔEQ = 2.33 mm/s, reminiscent of species we have observed, at higher concentrations, in the past for other native and variant HPCD–substrate complexes.26 Figures 3 and 4 show a series of variable temperature/variable field (VTVB) Mössbauer spectra of the H200C–HPCA complex.
Figure 2.
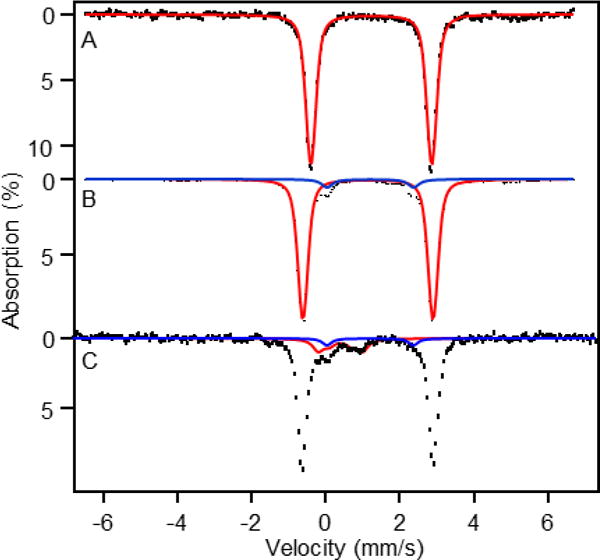
(A) 4.2 K, zero field (B = 0) Mössbauer spectra of resting H200C. The red line is a spectral simulation for a quadrupole doublet with ΔEQ = 3.28 mm/s and δ = 1.22 mm/s (B) 4.2 K spectrum of H200C–HPCA (enzyme substrate complex). The red line is a simulation for the majority species (80 % of Fe). The blue line outlines the minority FeII species (6% of Fe) with ΔEQ = 2.33 mm/s and δ = 1.20 mm/s (C) 150 K spectrum of H200C–HPCA. The blue line indicates the doublet of the 6% FeII contaminant. The red line outlines the contribution of the two quadrupole doublets belonging to FeIII contaminants (15% of Fe). The two FeIII contaminants are difficult to discern in the 4.2 K spectrum of (B) as their absorption is spread over a 16 mm/s velocity range.
Figure 3.
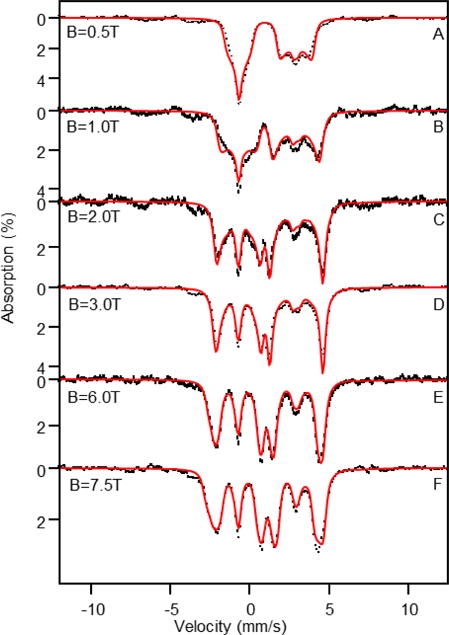
4.2 K Mössbauer spectra of the H200C–HPCA complex recorded in parallel applied fields indicated. Simulated spectra of two unknown FeIII contaminants, shown in Figure S1 and representing ≈ 15% of the Fe, were subtracted from the raw data. The red lines, representing 85% of total Fe, are spectral simulations based on eqs 1 and 2 using the parameters listed in Table 1. Simulations were performed in the slow relaxation limit of the electronic spin.
Figure 4.
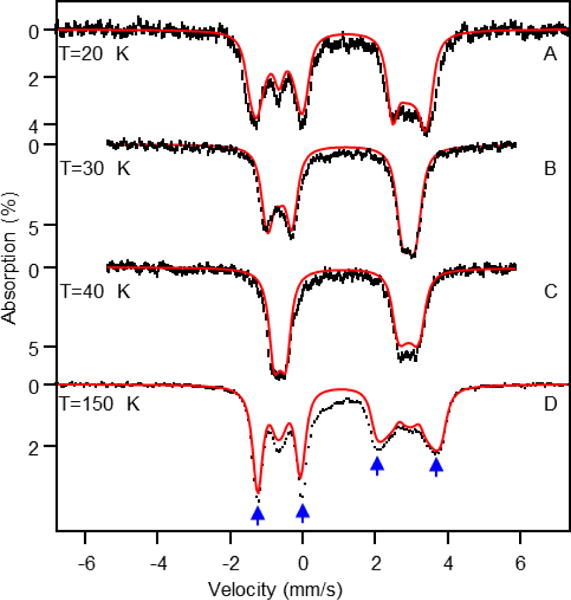
Variable temperature Mössbauer spectra of the H200C–HPCA complex recorded for B = 7.5 T. The high-spin ferric contaminants (≈ 15 %) and the minor (6%) ferrous species have not been removed from the data. At (A) 20 K, (B) 30 K, and (C) 40 K the spins of the FeIII species are relaxing slowly and the FeIII contribution is spread (with small amplitude) over a velocity range of 16 mm/s. At T = 150 K the FeIII species approach the fast relaxation limit (see Figure 2C; part of their contribution is evident in the central portion of the 150 K spectrum. The red lines are simulations of H200C-HPCA using the parameters listed in Table 1, assuming that the electronic spin is in the fast fluctuation limit. In (A–C) the FeIII contaminants are part of the base line, so we scaled the sum of H200C–HPCA and FeII minority species to 100% Fe. The H200C-HPCA simulation of the 150 K spectrum (D) has been plotted to represent 85% of the total absorption. Despite the presence of the FeIII contaminants and the minority FeII species the magnetic splittings of the FeII-H200C–HPCA species (blue arrows) are quite well defined at 150 K.
The absorption of the FeII minority species in the applied-field spectra is difficult to track, and we have thus ignored its presence in the analysis of the applied field data at 20, 30, and 50 K, but have accounted for it in the 150 K spectrum. The sample also contains two high-spin FeIII contaminants (total ≈ 15% of Fe) presumably associated with adventitiously bound iron frequently encountered in non-heme iron enzyme preparations. These contaminants are quite apparent in the 4.2 K applied field spectra of Figure S1. Fortunately, at 4.2 K roughly 60% of the absorption of these species falls outside the range where FeII H200C–HPCA absorbs, and even a rough simulation of its outermost (clearly visible) features constrains the features that overlap with H200C–HPCA sufficiently well so that one can subtract the FeIII species from the 4.2 K spectra with only minor spectral distortion of the spectrum of the species of interest. The black, hash-marked curves shown in Figure 3 are spectra obtained after subtracting 15% of high-spin FeIII from the raw data, according to the simulations shown in Figure S1. In the 20 K, 30 K and 40 K spectra of Figure 4 the two FeIII species disappear in the background noise, for the following reason: At temperatures below 50 K the electronic spin of each FeIII contaminant is nearly in the slow relaxation limit. Under these conditions each of the six sublevels of the spin sextet is associated with a distinct Mössbauer spectrum under the experimental conditions (7.5 T applied field). Thus, for two FeIII species, the ≈ 15% spectral area is distributed among twelve distinct spectra, with the result being that each spectrum has a small signal amplitude. At 150 K, however, the spin relaxation of the FeIII species is sufficiently fast so that two, poorly resolved, quadrupole doublets are observed (shown in Figure 2C, red line). Figure S2 shows the 150 K spectra of Figures 2C and 4D together with simulations for the contaminants. The critical absorption bands (blue arrows in Figure 4D) of the 150 K/7.5 T spectrum, which serve to determine the effective magnetic field at the 57Fe nucleus, are well defined despite the presence of the contaminants.
The VTVB spectra of the majority species were analyzed with the S = 2 spin Hamiltonian,
| (1) |
| (2) |
D and E are the tetragonal and rhombic ZFS parameters, and (x,y,z) label the principal axes of the ZFS tensor. The nuclear quadrupole interactions (eq 2) have been represented in the principal axes frame (x′,y′,z′) of the EFG. For |Vz′z′| ≥ |Vy′y′ | ≥ |Vx′x′|, the order commonly used by Mössbauer spectroscopists, the asymmetry parameter η = (Vx′x′ − Vy′y′)/Vz′z′ is confined to 0 ≤ η ≤ 1. The Euler angles (α,β,γ)EFG rotate the (x′,y′,z′) frame into (x,y,z); here we use the conventions of the WMOSS software. The 57Fe magnetic hyperfine tensor, A, has its own principal axis frame, (x′,y′,z′); (α,β,γ)A rotate this frame into (x,y,z). The A-tensor has two sources of anisotropy, ASD and AL. The spin-dipolar contribution, ASD, is ideally proportional to the valence part of the EFG tensor and reflects the anisotropy of the 3d6 shell of iron. The components of the orbital contribution, AL, are proportional to Δgi = gi − 2 with i = x,y,z. Thus, the EFG- and A-tensors are expected to have different principal axes systems. Although we are only dealing with one iron site, the spectra of H200C–HPCA are exceedingly complex, primarily because of the low symmetry (C1) of the iron active site. The spectra of Figures 3 and 4 depend on as many as 14 fine structure and hyperfine parameters, not counting the unknown g-values (as argued below, the g-values are confined to 2 < gi < 2.15).
In Supporting Information, we discuss a strategy for determining the unknowns of eqs 1 and 2 by considering critical features of particular spectra. With this strategy, we were able to narrow the range of most of the parameters, followed by refinement by simultaneously fitting groups of spectra. From these considerations, the following information was obtained: (i) ΔEQ > 0 and η is confined to 0 ≤ η ≤ 0.5; (ii) the A-tensor has one small and two large components; (iii) the direction of the small component, Az′z′ ≈ −7.5 T, is within 20° (polar angle βA) along z′, the major axis of the EFG tensor; (iv) the components of the A-tensor perpendicular to Az′z′ average to (Ax′x′ + Ay′y′)/gnβn ≈ −23 T; (v) E/D is near the rhombic limit E/D = 1/3; (vi) the two lowest spin levels of the S = 2 multiplet are split by Δ ≈ 3 cm−1, precluding observation of a parallel mode EPR signal at X- or Q-band; (vii) using the results of points (v) and (vi) the relationship Δ ≈ 3|D|(E/D)2 implies that |D| ≈ 9 cm−1.
The magnetic hyperfine splittings of the applied-field Mössbauer spectra of Figure 3 are determined by the internal magnetic fields at the 57Fe nucleus, , where < > is the expectation value of the electronic spin vector operator. For small applied fields, B < 0.5 T, and at 4.2 K the electronic system of H200C–HPCA was found to be uniaxial, with the ‘unique’ axis, z, close to the direction of the smallest A-tensor component. This situation occurs for D < 0 when the MS = −2 ground level produces a spin expectation value (Figure S3) for which |< >| >> |< >|; see Supporting Information. (Note regarding sign of D: the ZFS of H200C-HPCA is near the rhombic limit, E/D = 1/3, for which Dzz = −Dyy and Dxx = 0, where Dxx , Dyy and Dzz are the principal components of a traceless symmetric tensor, ; see also eq 4 below. By convention, the sign of D is taken as the sign of the principal component of with the largest magnitude. However, in the rhombic limit the sign of D is indefinite. In the present case Dzz is negative, with z being approximately collinear to the axes for which the smallest component of the A-tensor and the largest component of the EFG tensor are observed. By choosing D < 0 we retain a coordinate frame that is convenient for describing the A- and EFG tensors.)
From the magnetic hyperfine splitting observed for B ≈ 1–2 T one can readily infer that the smallest component of the A-tensor, Az′′z′′, is nearly (βA = 7°) along the “unique” (magnetization) axis of the ZFS. The simulations were found to be quite sensitive to polar angle βA, preventing us from simply setting βA = 0. Also, the simulations are quite sensitive to βEFG as this angle tilts Bint relative to the largest component of the EFG. In contrast, the simulated spectra are less sensitive to αA, γA, αEFG, and γEFG, primarily because the two lowest spin levels are magnetically uniaxial. Note that αA + γA ≈ 180° in Table 1. Hence the principal axes of the A- and ZFS tensors would be collinear if βA were zero. As we approached the final simulations, we set αA = αEFG and γA = γEFG; allowing these angles to differ improved the fits at best marginally. The splitting of the low energy feature in the 20 K spectrum of Figure 4A depends essentially on Axx< >th as Ayy< >th is much smaller in magnitude (see Figure S4); the thermal average < >th must be used as the electronic relaxation is fast at 20 K. Simulations of the 20 K/7.5 T spectrum yielded the values Axx ≈ −19 T ≈ Ax′′x′′ (as βA is small) from which it follows that Ay′′y′′ ≈ −27 T by using the aforementioned condition (Ax′′x′′ + Ay′′y′′)/2 ≈ −23 T. It is noteworthy that the “unique” axis of the electronic system is along the smallest component, Az′z′ ≈ −7.5 T, of the A-tensor. Since βA ≈ 0 and (x,y,z) ≈ (x′′,y′′,z′′), the A-values suggest that the doubly occupied t2 orbital of iron has dxy character, unless our arguments were severely distorted due to the presence of large orbital contributions. The latter have been estimated as follows.
Table 1.
Parameters for the resting (H200C) and ES (H200C–HPCA) complexes
|
D (cm−1) |
E/D |
gx gy gz |
ΔEQ (mm/s) |
η | (α,β,γ)EFG (°) |
Axx/gnβn Ayy/gnβn Azz/gnβn (T) |
(α,β,γ)A (°) |
δ (mm/s) |
|
|---|---|---|---|---|---|---|---|---|---|
| H200C | −7 | 0.38a | 2.00 2.00 2.10b |
+3.28 | 0.2 | 140 28 42 |
−19.9 −25.7 −8.0 |
135 23 50 |
1.22 |
| H200C–HPCA | −8 | 0.37a | 2.00 2.00 2.10b |
+3.53 | 0.3 | 50 20 130 |
−19.2 −27.5 −7.4 |
50 7 130 |
1.14 |
The E/D values are slightly outside the range for a “proper” coordinate system for which 0 ≤ E/D ≤ 1/3. Choosing a proper coordinate system for E/D = 0.37 yields D = +8.44 cm−1 and E/D = 0.30, with the ‘unique’ axis now being along the y axis of the ZFS tensor (the ‘unique’ axis is along the direction for which Bint, i.e. < >, increases rapidly for small B; see Figure S3). If D > 0 is chosen, the g-, A- and EFG-tensors have to be rotated to preserve the relative orientation of the four tensors. The essence of the result is that the ZFS, within the uncertainties, is in the rhombic limit.
The values of gx and gy were set to 2.00 based on estimates given in the text; gz was estimated from the Mössbauer analysis.
Our data are insensitive to small variations in the electronic g-tensor. The value used for the final simulation, gz = 2.1, can be justified as follows. The magnetic hyperfine tensor depends on contributions from Fermi contact, spin-dipolar, and orbital interactions, A = AFC + ASD + AL. Mössbauer studies of the [FeII(H2O)6]2+ complex in ferrous fluorosilicate43 and the mixed-valent FeII-FeIII state of methane monooxygenase44 suggest the value AFC/gnβn ≈ −21 T. The DFT calculations described below yield for tensor ASD/gnβn the eigenvalues (−5.0, −3.3, +8.3) T. The spin-dipolar contribution along z, ASDzz/gnβn ≈ +8 T, then yields, using the experimentally determined Azz/gnβn = −7.4 T, the value ALzz/gnβn = (gz − 2) P = +5.5 T. The latter value together with P = gegnββn<r−3> ≈ 60 T suggest gz = 2.09.45 The data of Table 1 give Aiso/gnβn = (Ax′′x′′ + Ay′′y′′ + Az′′z′′)/gnβn = −18.0 T. As Aiso/gnβn = AFC/gnβn − ΔgavP, we estimate that Δgav = (gx + gy + gz)/3 − 2 ≈ 0.05, and thus (gx + gy)/2 ≈ 2.03. As the latter value is only marginally different from 2, gx and gy have been set equal 2.00 in the simulations. Finally, as |AFC − Aiso|/gnβn ≈ 3 T the orbital contributions to the A tensor are moderate.
By combining spectral simulations (a few hundred) with group fittings of various sets of up to four spectra (the limit in WMOSS), a parameter set (Table 1) was obtained that describes all spectra quite well. The simulations included variations in the relative orientations of the EFG-, A- and ZFS tensor axes (Table 1).
We have also recorded VTVB spectra of resting H200C (Figure S5 and S6) and analyzed the data in the same spirit as those of H200C–HPCA. The parameter set obtained for this species is also listed in Table 1.
We mentioned above that the observed magnetic hyperfine interactions suggest a (doubly occupied) ground state orbital with dxy character. In standard crystal-field theory a 2nd-order perturbation treatment of the effective spin–orbit coupling operator within the t2 manifold gives for this ground state the value Dzz > 0 (see below), in contrast to what is experimentally observed. This puzzling observation prompted the computational analysis described in the next section.
DFT Calculations for the H200C–HPCA Complex
DFT calculations were performed for a model that included the iron site and its coordinating ligands, His155, His214, Glu267, axial water (Watax) and the bidentate substrate HPCA as well as the 2nd-sphere residues H248 and Y257 and a non-coordinating water molecule (WatC). As the Mössbauer parameters are inherent to the iron–ligands moiety, a small structural model was used that excludes C200 (S···Fe = 5.5 Å) and some of the other second-sphere residues in the vicinity of the metal center (e. g. W192 and N157) for these DFT studies.
Starting from the X-ray structure of the H200C–HPCA complex (PDB: 5BWH)38 the Cα carbons of the coordinating amino acids were replaced by hydrogen atoms that were frozen in space during geometry optimization. All atoms of the 2nd-sphere residues H248 and Y257 were kept fixed to the crystallographic positions in the optimizations. Constraints were imposed on the distance between the iron and the oxygen atom of the axial water ligand (Watax) and on the dihedral angles of the coordinating histidyl residues. The former condition prevents the axial water from dissociating during the geometry optimization and remedies the lack of an axial-water-immobilizing hydrogen bonding network in our computational models. Also included was the non-coordinating crystallographic water, WatC, which occupies the void created by the H200C substitution. The oxygen atom of WatC was fixed to its position in the X-ray structure but its hydrogens were left unconstrained in the optimization. The 2nd-sphere residue H248 was included because it forms an essential hydrogen bond to the distal carboxylate oxygen of E267, stabilizing its position. H248 also limits the allowable motion of the substrate. HPCA binds to iron as a dianion, with protons removed from the carboxylate group and OC2, the oxygen atom that accepts a hydrogen bond from Y257,30 while OC1 remains protonated.15, 35, 38, 46 The mobility of the substrate has been further constrained by fixing the two carboxylate oxygen atoms to their positions in the X-ray structure.
The optimized structure obtained within these constraints, is shown in Figures 1 and 5. As expected, the remaining hydroxyl group of the substrate is hydrogen bonded to WatC, positioning the proton approximately in the substrate plane. The ΔEQ value obtained for the optimized structure with the triple-ζ 6-311G basis, ΔEQ = +4.24 mm/s, is 0.71 mm/s higher than the experimental value. However, the agreement improves significantly, in accord with our previous experience, when ΔEQ is re-evaluated in a single point calculation using a triple-ζ basis set extended with polarization functions (TZVP), ΔEQ = +3.30 mm/s (η = 0.20, δ = 1.02 mm/s), reducing the discrepancy to only 0.23 mm/s. As the electronic state of a high-spin FeII site can be considered as a half-filled 3d5 shell (ΔEQ = 0 in the absence of anisotropic covalency) plus an additional 3d electron, the dominant valence contribution to the quadrupole splitting of this state is essentially determined by the orbital occupied by the added electron. The left panel of Figure 5 shows a contour plot of this orbital. The orbital belongs to the t2 set {dxy, dxz, dyz} as expected for octahedral coordination. For example, the dxy orbital gives rise to a large positive quadrupole splitting, such as the one observed for the majority component, with the largest principal component of the EFG along z (z approximately along Fe-OE267). Orbital dxy is singled out as the lowest t2 orbital by the π system of the substrate. The right panel of Figure 5 shows the HOMO of the substrate, which is a π orbital with significant amplitudes at the coordinating oxygen atoms. The antibonding π interactions of dxz and dyz with the substrate HOMO raise the energies of these two d orbitals above that of dxy, which is less affected by these interactions. The hydroxyl proton reduces the amplitude of the substrate HOMO at the hydroxyl oxygen by lowering the energies of the oxygen-centered atomic orbitals. As a result, the amplitude of the substrate HOMO at the protonated hydroxyl oxygen is smaller than at the deprotonated oxygen such that the dxz level (x || Fe-OH) is pushed up less than the dyz level (y || Fe-O), yielding the energy order E(dxy) < E(dxz) < E(dyz). Removal of the axial water leads to only minor changes in the results (the TZVP value for ΔEQ drops from 3.30 mm/s to 3.11 mm/s); moreover, the contour plot for this case (not shown) indicates that the dxy character of the doubly occupied 3d orbital is retained.
Figure 5.
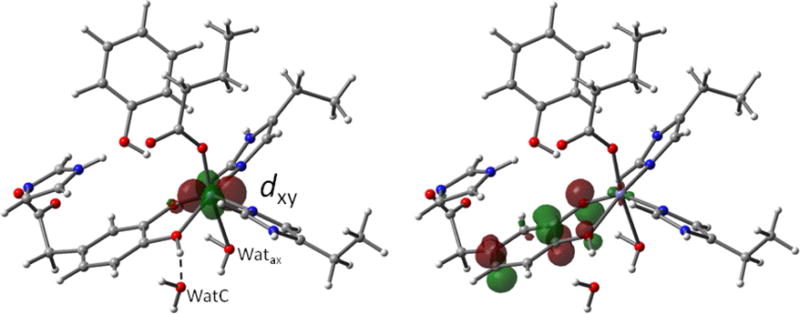
Left: DFT optimized structure showing a contour plot of the doubly occupied 3d orbital of the high-spin FeII site in the model enzyme-substrate complex. The broken line indicates the hydrogen bond formed by the hydroxyl proton of the substrate to WatC. Right: Contour plot of the redox active HOMO of the substrate. This π orbital is the main source of electron density donated by the substrate into the dxz and dyz orbitals (not shown) of the high-spin FeII site. The structure shown here is that of Figure 1 but viewed from a different perspective.
DISCUSSION
Analysis of the ZFS of the ES Complex
The A- and EFG-tensors of both the ES complex and resting H200C are indicative of an orbital ground state with approximate dxy character. Both the X-ray and DFT structures show that the actual symmetry of the ES complex is C1; hence, the character of the ground orbital may deviate from being strictly dxy. The detailed Mössbauer characterization of the ZFS parameters, including Euler angles, for the ES complex makes this system a good benchmark for testing quantum-chemical models that predict the ZFS tensor. It is instructive to start by considering an idealized crystal-field (CF) model that produces orbital splittings as indicated in Figure 6. The model is supported by the orbital contours in Figures S7 and S8 derived from TD-DFT calculations, which show the characteristic features of the standard Cartesian t2g and eg orbitals. Figure 6 illustrates why such a model cannot explain our main experimental result, namely that the “unique” axis associated with the lowest two spin sub levels, z in eq 1, is essentially parallel (βA ≈ 7°) to direction z′′ and close (βEFG ≈ 22°) to the symmetry axis, z′, of the EFG. The spin–orbit coupling (SOC) in high-spin FeII complexes is commonly, but sometimes inappropriately, described with the effective operator
| (3) |
where L = S = 2 and λ ≈ −80 cm−1.47 has non-zero matrix elements between the ground configuration (Figure 6, left) and the dxy→di excitations of the spin-down electron with energies Δi (Figure 6, middle).
Figure 6.

Schematic crystal-field-splitting diagram of high-spin FeII. Orbital mixing by low symmetry components in the crystal field has been ignored. The dashed level does not interact with the ground configuration.
In 2nd-order perturbation theory the effect of these spin–orbit couplings on the relative energies of the sublevels of the S = 2 ground state are obtained by diagonalizing the effective operator
| (4) |
where is a traceless symmetric tensor. The right panel of Figure 6 gives the contributions to the Dii parameters (i = x, y, z) arising from the individual transitions. Each excitation yields a contribution to that is diagonal in the (x,y,z) frame in which the orbitals are defined. The individual contributions are axial but with unique axes that may point along x, y, or z (last column of Figure 6). As is traceless, eq 4 is conventionally written as the first term of eq 1 with D = 3Dzz/2 and E = (Dxx − Dyy)/2. The ratio E/D is confined to 0 ≤ E/D ≤ 1/3 when the standard order |Dxx| ≤ |Dyy| ≤ |Dzz| is adopted. The axiality of the individual dxy→di contributions to implies that the associated rhombicity parameters vanish, Edi = 0. Moreover, since the eigenvalue with the largest magnitude is negative, it follows that all Ddi < 0. Hence, non-zero rhombicity (E/D > 0) and positive D-values can only arise from a combination of two or more excitations.
The ES complex has D ≈ −8 cm−1 and E/D ≈ 0.37 (Table 1), which yields E ≈ −3 cm−1. The tensor in this case has the eigenvalues Dzz ≈ −Dyy < 0 and Dxx ≈ 0. Our DFT analysis revealed a nearly axial EFG with ΔEQ = +3.5 mm/s arising from a doubly occupied dxy orbital (Figure 5) and associated with the eigenvalue Vz′z′ of the EFG. Can a model based on the orbital splittings of Figure 6 yield a ZFS with Dzz = 2D/3 = −5.3 cm−1 and E = −3 cm−1 with z along the symmetry axis of the dxy orbital? As the FeII site is hexacoordinate, the 3d levels appear in two groups, i.e. the eg {dx2-y2, dz2} and at lower energy the t2g {dxy, dxz, dyz}. In the limiting case, Δx2-y2 = ∞ only the excitations dxy→dxz and dxy→dyz contribute to the ZFS. As both these excitations contribute positive terms along z, one obtains Dzz > 0. The only way to obtain Dzz < 0 is by invoking the dxy→dx2-y2 excitation (Figure 6). The viability of this mechanism has been analyzed in section S4 of the Supporting Information. The analysis shows that the condition for Dzz < 0 is that Δx2-y2 ≤ 2,327 cm−1, which is unrealistically small and well below the excitation energies predicted by TD-DFT (Δx2-y2 ≈ 13,000 cm−1), CASSCF (Δx2-y2 ≈ 9,000 cm−1); see Table 3 to be discussed below, and deduced from MCD.48 Furthermore, spin–orbit interactions with S = 1 states, which may also potentially contribute to the ZFS, cannot provide an explanation either, since the lowest S = 1 state is predicted to be 10,000 cm−1 above the ground state and thus contributes too little to the ZFS to explain the Mössbauer result D = −8 cm−1. (N.B. Generating ZFS through the admixture of S = 1 excited states into the S = 2 ground state requires a more general SOC operator, such as the effective operator given in eq S4 of the Supporting Information. The lower bound of 10,000 cm−1 for the vertical excitation energies to the S = 1 states has been estimated from the energy of a single-point DFT solution for the spin triplet at the optimized geometry for S = 2 and from a CASSCF calculation, see below.) Hence, the large negative ZFS along the z-axis in the ES complex remains unexplained within the context of the CF model of Figure 6.
Table 3.
CASSCF analysis of
| Excitation | Energy (cm−1) | Dxx (cm−1) | Dyy (cm−1) | Dzz (cm−1) | Directiond | D d (cm−1) | E/D d |
|---|---|---|---|---|---|---|---|
| xy→xz | 1,038 (2,720)a | 2.14 | 2.68 | −4.82 | z (x) | −7.22 | 0.04 |
| xy→yz | 2,201 (3,496) | −2.98 | 2.03 | 0.95 | x (y) | −4.47 | 0.12 |
| xy→z2 | 6,506 (8,739) | −0.31 | 0.18 | 0.13 | x (none) | −0.47 | 0.06 |
| xy→x2-y2 | 9,275 (13,334) | 1.21 | 0.08 | −1.29 | z (z) | −1.94 | 0.29 |
| Totalb | 0.06 | 4.97 | −5.03 | z | −7.55 | 0.33 | |
| Totalc | 0.53 | 5.13 | −5.66 | z | −8.50 | 0.27 |
In parentheses: TD-DFT excitation energies obtained with B3LYP/6-311G. (Shown in Figure S7.)
Sums of Dii for lowest four transitions, all spin S = 2 conserving, listed in table, and implied D and E/D. The principal axes of the four contributions are assumed to be collinear.
Final totals including all S = 0, 1, 2 contributions.
Rows 1–4 list the D and E/D values associated with levels at Δdi such that E/D is confined to 0 ≤ E/D ≤ 1/3. The direction of the largest component of Dii is given in the 6th column. In parentheses: the direction predicted by the model of Figure 6 with the commonly used spin–orbit coupling operator for the transition indicated.
The first quantum-chemical method for calculating ZFS tested here was the SOC module of ORCA/DFT and yielded the values D = −3.6 cm−1 and E/D = 0.11 for the ES complex, which are both substantially smaller than the corresponding values deduced from the Mössbauer analysis. The Euler angles, listed in Table 2, reveal that the unique axis of the tensor from ORCA/DFT is approximately aligned with the z′ axis of the tensor, in agreement with experiment. It is noteworthy that the ORCA/DFT D value originates predominantly from the spin–orbit couplings of the S = 2 ground state with S = 1 excited states, D(S = 1) = −2.5 cm−1 (cf. Table S1 of the Supporting Information), while the contribution to D from SOC with excited S = 2 states is remarkably small, D(S = 2) = −0.8 cm−1 (cf. Table S1). This result is unexpected as the TD-DFT energy of the lowest S = 2 excitation is much smaller than the lower bound for the energies of the S = 1 excitations and we suspect that the smallness of D(S = 2) may be related to the use of (un-relaxed) orbital energy differences in the denominators of the perturbation theory expression for the tensor.
Table 2.
Euler angles for rotating EFG tensor frame (diagonal in (x,y,z)) into ZFS tensor frame (diagonal in x′y′z′))
EFG tensor, convention |Vx′x′| ≤ |Vy′y′| ≤ |Vz′z′|, 0 ≤ η ≤ 1
ZFS tensor, convention |Dxx| ≤ |Dyy| ≤ |Dzz|, 0 ≤ E/D ≤ 1/3, except for row labeled Exp where |Dyy| is marginally larger than |Dzz| such that E/D = 0.37. This deviation from standard convention was admitted to retain the z-axis.
Both properties were evaluated for identical (B3LYP/6-311G optimized) structures, using G ′09.
Euler angles in zyz convention.
From Mössbauer analysis.
EFG from a single-point B3LYP/TZVP calculation, using G ′09.
ZFS tensor from a single-point BP86 calculation, using ORCA.
Active space: 3d6 configurations, including all S = 2, 1, 0 states, using ORCA.
In the course of the present work, an article by Neese and coworkers caught our attention.40 These authors showed for FeII-azurin that CASSCF calculations yielded D values in remarkably good agreement with the experimental data while DFT-based calculations were substantially off target.40 The FeII-azurin study prompted us to use the CASSCF approach implemented in the program suite ORCA.49 The ORCA results for the multiconfigurational CASSCF calculation of are listed in Table 3. The last row of the table gives the final results for D (−8.5 cm−1) and E/D (0.27), which are in excellent agreement with the experimental values D = −8 cm−1 and E/D = 0.37. Moreover, the eigenvector of associated with the negative eigenvalue (Dz′z′ = 2D/3 ≈ −5.7 cm−1) is approximately collinear with the molecular z-axis (close to the OE267-Fe-WatA direction in Figure 5) and by inference with the z′ axis of the EFG as deduced from experiment. For a quantitative determination of the relative orientation of the principal axes of the EFG ( ) and ZFS ( ) tensors, we considered the possibility of using the CASSCF results for both tensors. However, since the state-averaged potential, required for obtaining reliable solutions for the wide range of CASSCF states contributing to the ZFS, produces nearly vanishing EFG tensors, the tensor from G’09/DFT has been used as a reference for the orientational analysis. The relative orientations of the principal axes of and are presented in Table 2 by listing the Euler angles required for transforming the diagonal tensor into the principal axes frame of (Table 2). The calculated value for βEFG = 29° is in remarkably good agreement with the experimental βEFG = 20°. The differences between theory and experiment for Euler angles αEFG and γEFG are larger than for βEFG, perhaps in part because the Mössbauer spectra are less sensitive to the former parameters (see above). Table 3 also lists the contributions to from the individual dxy→di transitions (3rd, 4th, and 5th column). The CASSCF excitation energies (2nd column) appear in the same sequence as those obtained with the TD-DFT supported CF model (schematically shown in Figure 6) but are smaller in magnitude. The largest ORCA/CASSCF contribution to D comes from the lowest energy S = 2 transition, dxy→d”xz”. Its value of −7.2 cm−1 (Table 3) is about ten times larger than the S = 2 contribution to D obtained with ORCA/DFT; in contrast, the S = 1 contributions obtained with the two methods are about equal (≈−2 cm−1). Like in the model of Figure 6, the Ddi value for each transition is negative (7th column) but, unlike the CF model of Figure 6, the contributions of the individual transitions to are not axial (8th column). The net rhombicity (E/D ≈ 1/3) is largely due to the combination of the first two excitations, each of them being approximately axial but with orthogonal unique axes (6th column), as in the case of the CF model of Figure 6. The contribution to D from the dxy→dz2 excitation is small but not zero as predicted by the CF model (7th column). Just as for the CF model, the dxy→dx2-y2 excitation gives a negative component along z (5th column) which by itself is too small to explain the Mössbauer value for D (see above). A comparison of the last two rows of Table 3 shows that the sum of the contributions to from the four dxy→di transitions constitute the major part of D and E/D, leaving only a minor role for the spin–orbit interactions with S = 1 states, as anticipated from their large excitation energies. Finally and most importantly, the dxy→dxz transition yields a large negative component along z (5th column) and not along x as predicted by the CF model of Figure 6. This prediction of the ORCA/CASSCF approach agrees remarkably well with experiment.
The quantum-chemical calculations reported here used the full Breit–Pauli operator. However, it is shown in section S5 of the Supporting Information that nearly identical results for are obtained with an effective 1-electron SOC operator, using a reduced nuclear charge for iron. The various approximations that were made to attain the wave function of the CF model and which led to the differences in the tensors predicted by CFT and CASSCF are discussed in section S6 of the Supporting Information.
CONCLUSIONS
Analysis of the VTVB Mössbauer spectra of the H200C–HPCA complex has yielded a complete set of fine- and hyperfine-structure parameters, including tensor rotations due to the low symmetry environment. It should be noted that the low symmetry observed for H200C–HPCA is not a particular property of this variant for which water C fills a void created by the absence of H200. Thus, the Y257F–HPCA complex has nearly the same parameters as the complex studied here (these include Euler angles βA ≈ 7° and βEFG ≈ 27°; Table 3 of ref. 29). Similar observations have been reported for the reduced Pseudomonas putida protocatechuate 3,4 dioxygenase.39 From these analyses emerged the puzzling result that the large negative component of the rhombic (E/D ≈ 1/3) ZFS tensor was found to be directed (roughly) along the axis z of the doubly occupied dxy orbital. In order to explain this observation we initially pursued ORCA/DFT calculations. However, since these DFT calculations reproduced the experimental ZFS parameters rather poorly we chose to invoke CASSCF calculations similar to those previously reported by Neese et al. for the tetrahedral FeII-azurin center.40 In spite of a “non-magnetic” orbital ground doublet of eg symmetry, CASSCF predicts for the FeII-azurin center a sizable D value. The calculations presented here for the H200C–HPCA complex are in excellent agreement with our spectroscopic analysis of this system, owing in part to the inherent nature of the CASSCF wave functions for the ground and excited states.
Supplementary Material
Acknowledgments
This work is supported by National Institutes of Health Grant GM024689 (to J.D.L.), by the National Science Foundation Grant CHE-1305111 (to E.M.) and by the Biological Sciences Research Council BB/H001905/1 (to E.G.K). We thank Dr. Marius Retegan for getting us started with the CASSCF calculations and one of the reviewers for suggesting to us that zero-field splittings calculated with an effective 1-electron operator are essentially identical to those obtained with the 2-electron Breit–Pauli operator.
Footnotes
Supporting Information
Figures S1–S8. Figure of the ES variable field raw Mössbauer data with simulations for the high-spin ferric contaminants; figure of the 150 K spectra of H200C-HPCA in zero field and at 7.5 T; plots of the spin expectation value and thermal expectation value for H200C-HPCA; variable field and variable temperature Mössbauer spectra of H200C resting enzyme; TD-DFT orbital diagrams of H200C-HPCA computational model. A discussion of various effective SOC Hamiltonians and their relation to the Breit–Pauli operator has been presented in sections S5 and S6. This material is available free of charge via the Internet at http://pubs.acs.org.
Notes
The authors declare no competing financial interest.
References
- 1.Koehntop KD, Emerson JP, Que L., Jr JBIC, J Biol Inorg Chem. 2005;10:87–93. doi: 10.1007/s00775-005-0624-x. [DOI] [PubMed] [Google Scholar]
- 2.Vaillancourt FH, Bolin JT, Eltis LD. Crit Rev Biochem Mol Biol. 2006;41:241–267. doi: 10.1080/10409230600817422. [DOI] [PubMed] [Google Scholar]
- 3.Kovaleva EG, Lipscomb JD. Nat Chem Biol. 2008;4:186–193. doi: 10.1038/nchembio.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Price JC, Barr EW, Hoffart LM, Krebs C, Bollinger JM., Jr Biochemistry. 2005;44:8138–8147. doi: 10.1021/bi050227c. [DOI] [PubMed] [Google Scholar]
- 5.Hausinger RP. Crit Rev Biochem Mol Biol. 2004;39:21–68. doi: 10.1080/10409230490440541. [DOI] [PubMed] [Google Scholar]
- 6.McDonough MA, Loenarz C, Chowdhury R, Clifton IJ, Schofield CJ. Curr Opin Struct Biol. 2010;20:659–672. doi: 10.1016/j.sbi.2010.08.006. [DOI] [PubMed] [Google Scholar]
- 7.Barry S, Challis GL. ACS Catal. 2013;3:2362–2370. doi: 10.1021/cs400087p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fitzpatrick PF. Adv Enzymol Relat Areas Mol Biol. 2000;74:235–294. doi: 10.1002/9780470123201.ch6. [DOI] [PubMed] [Google Scholar]
- 9.Resnick SM, Lee K, Gibson DT. J Ind Microbiol Biotechnol. 1996;17:438–457. [Google Scholar]
- 10.Arciero DM, Lipscomb JD. J Biol Chem. 1986;261:2170–2178. [PubMed] [Google Scholar]
- 11.Han S, Eltis LD, Timmis KN, Muchmore SW, Bolin JT. Science. 1995;270:976–980. doi: 10.1126/science.270.5238.976. [DOI] [PubMed] [Google Scholar]
- 12.Senda T, Sugiyama K, Narita H, Yamamoto T, Kimbara K, Fukuda M, Sato M, Yano K, Mitsui Y. J Mol Biol. 1996;255:735–752. doi: 10.1006/jmbi.1996.0060. [DOI] [PubMed] [Google Scholar]
- 13.Chen VJ, Orville AM, Harpel MR, Frolik CA, Surerus KK, Münck E, Lipscomb JD. J Biol Chem. 1989;264:21677–21681. [PubMed] [Google Scholar]
- 14.Lipscomb JD, Orville AM. Metal Ions Biol Syst. 1992;28:243–298. [Google Scholar]
- 15.Vetting MW, Wackett LP, Que L, Jr, Lipscomb JD, Ohlendorf DH. J Bacteriol. 2004;186:1945–1958. doi: 10.1128/JB.186.7.1945-1958.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kovaleva EG, Lipscomb JD. Science. 2007;316:453–457. doi: 10.1126/science.1134697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Groce SL, Miller-Rodeberg MA, Lipscomb JD. Biochemistry. 2004;43:15141–15153. doi: 10.1021/bi048690x. [DOI] [PubMed] [Google Scholar]
- 18.Lipscomb JD. Curr Opin Struct Biol. 2008;18:644–649. doi: 10.1016/j.sbi.2008.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Spence EL, Langley GJ, Bugg TDH. J Am Chem Soc. 1996;118:8336–8343. [Google Scholar]
- 20.Bugg TDH, Ramaswamy S. Curr Opin Chem Biol. 2008;12:134–140. doi: 10.1016/j.cbpa.2007.12.007. [DOI] [PubMed] [Google Scholar]
- 21.Arciero DM, Lipscomb JD, Huynh BH, Kent TA, Münck E. J Biol Chem. 1983;258:14981–14991. [PubMed] [Google Scholar]
- 22.Mabrouk PA, Orville AM, Lipscomb JD, Solomon EI. J Am Chem Soc. 1991;113:4053–4061. [Google Scholar]
- 23.Solomon EI, Zhang Y. Acc Chem Res. 1992;25:343–352. [Google Scholar]
- 24.Solomon EI, Light KM, Liu LV, Srnec M, Wong SD. Acc Chem Res. 2013;46:2725–2739. doi: 10.1021/ar400149m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shu L, Chiou YM, Orville AM, Miller MA, Lipscomb JD, Que L., Jr Biochemistry. 1995;34:6649–6659. doi: 10.1021/bi00020a010. [DOI] [PubMed] [Google Scholar]
- 26.Mbughuni MM, Chakrabarti M, Hayden JA, Meier KK, Dalluge JJ, Hendrich MP, Münck E, Lipscomb JD. Biochemistry. 2011;50:10262–10274. doi: 10.1021/bi201436n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Groce SL, Lipscomb JD. Biochemistry. 2005;44:7175–7188. doi: 10.1021/bi050180v. [DOI] [PubMed] [Google Scholar]
- 28.Mbughuni MM, Chakrabarti M, Hayden JA, Bominaar EL, Hendrich MP, Münck E, Lipscomb JD. Proc Natl Acad Sci USA. 2010;107:16788–16793. doi: 10.1073/pnas.1010015107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mbughuni MM, Meier KK, Münck E, Lipscomb JD. Biochemistry. 2012;51:8743–8754. doi: 10.1021/bi301114x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kovaleva EG, Lipscomb JD. Biochemistry. 2012;51:8755–8763. doi: 10.1021/bi301115c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jeoung J-H, Bommer M, Lin T-Y, Dobbek H. Proc Natl Acad Sci USA. 2013;110:12625–12630. doi: 10.1073/pnas.1302144110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miller MA, Lipscomb JD. J Biol Chem. 1996;271:5524–5535. doi: 10.1074/jbc.271.10.5524. [DOI] [PubMed] [Google Scholar]
- 33.Emerson JP, Kovaleva EG, Farquhar ER, Lipscomb JD, Que L., Jr Proc Natl Acad Sci USA. 2008;105:7347–7352. doi: 10.1073/pnas.0711179105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fielding AJ, Kovaleva EG, Farquhar ER, Lipscomb JD, Que L., Jr JBIC, J Biol Inorg Chem. 2011;16:341–355. doi: 10.1007/s00775-010-0732-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kovaleva EG, Rogers MS, Lipscomb JD. Biochemistry. 2015;54:5329–5339. doi: 10.1021/acs.biochem.5b00709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fielding AJ, Lipscomb JD, Que L., Jr J Am Chem Soc. 2012;134:796–799. doi: 10.1021/ja2095365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fielding AJ, Lipscomb JD, Que LJ. JBIC, J Biol Inorg Chem. 2014;19:491–504. doi: 10.1007/s00775-014-1122-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Meier KK, Rogers MS, Kovaleva EG, Mbughuni MM, Bominaar EL, Lipscomb JD, Münck E. Inorg Chem. 2015;54:10269–10280. doi: 10.1021/acs.inorgchem.5b01576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zimmermann R, Huynh BH, Münck E, Lipscomb JD. J Chem Phys. 1978;69:5463–5467. [Google Scholar]
- 40.McLaughlin MP, Retegan M, Bill E, Payne TM, Shafaat HS, Peña S, Sudhamsu J, Ensign AA, Crane BR, Neese F, Holland PL. J Am Chem Soc. 2012;134:19746–19757. doi: 10.1021/ja308346b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Frisch MJ, et al. Gaussian, Inc. Wallingford, CT: 2009. [Google Scholar]
- 42.Neese F. WIREs Comput Mol Sci. 2012;2:73–78. [Google Scholar]
- 43.Johnson CE. Proc Phys Soc. 1967;92:748–757. [Google Scholar]
- 44.Fox BG, Hendrich MP, Surerus KK, Andersson KK, Froland WA, Lipscomb JD, Münck E. J Am Chem Soc. 1993;115:3688–3701. [Google Scholar]
- 45.Kostka KL, Fox BG, Hendrich MP, Collins TJ, Rickard CEF, Wright LJ, Münck E. J Am Chem Soc. 1993;115:6746–6757. [Google Scholar]
- 46.Vaillancourt FH, Barbosa CJ, Spiro TG, Bolin JT, Blades MW, Turner RFB, Eltis LD. J Am Chem Soc. 2002;124:2485–2496. doi: 10.1021/ja0174682. [DOI] [PubMed] [Google Scholar]
- 47.Abragam A, Bleaney B. Electron Paramagnetic Resonance of Transition Metal Ions. Clarendon Press; Oxford: 1970. Chapter 17. [Google Scholar]
- 48.Solomon EI. Inorg Chem. 2001;40:3656–3669. doi: 10.1021/ic010348a. [DOI] [PubMed] [Google Scholar]
- 49.Neese F. J Chem Phys. 2005;122:34107. doi: 10.1063/1.1829047. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


