Mukhtasimova et al. describe experimental modifications of the patch clamp technique that improve temporal resolution of currents through single acetylcholine receptor channels. The study not only distinguishes between the priming and gating steps, but it also reveals how rate and equilibrium constants change as a function of agonist occupancy.
Abstract
The acetylcholine receptor (AChR) from vertebrate skeletal muscle initiates voluntary movement, and its kinetics of activation are crucial for maintaining the safety margin for neuromuscular transmission. Furthermore, the kinetic mechanism of the muscle AChR serves as an archetype for understanding activation mechanisms of related receptors from the Cys-loop superfamily. Here we record currents through single muscle AChR channels with improved temporal resolution approaching half an order of magnitude over our previous best. A range of concentrations of full and partial agonists are used to elicit currents from human wild-type and gain-of-function mutant AChRs. For each agonist–receptor combination, rate constants are estimated from maximum likelihood analysis using a kinetic scheme comprised of agonist binding, priming, and channel gating steps. The kinetic scheme and rate constants are tested by stochastic simulation, followed by incorporation of the experimental step response, sampling rate, background noise, and filter bandwidth. Analyses of the simulated data confirm all rate constants except those for channel gating, which are overestimated because of the established effect of noise on the briefest dwell times. Estimates of the gating rate constants were obtained through iterative simulation followed by kinetic fitting. The results reveal that the agonist association rate constants are independent of agonist occupancy but depend on receptor state, whereas those for agonist dissociation depend on occupancy but not on state. The priming rate and equilibrium constants increase with successive agonist occupancy, and for a full agonist, the forward rate constant increases more than the equilibrium constant; for a partial agonist, the forward rate and equilibrium constants increase equally. The gating rate and equilibrium constants also increase with successive agonist occupancy, but unlike priming, the equilibrium constants increase more than the forward rate constants. As observed for a full and a partial agonist, the gain-of-function mutation affects the relationship between rate and equilibrium constants for priming but not for channel gating. Thus, resolving brief single channel currents distinguishes priming from gating steps and reveals how the corresponding rate and equilibrium constants depend on agonist occupancy.
INTRODUCTION
The essential advance of the patch clamp technique is to reduce background noise below that of the elementary current pulse from a single ion channel (Hamill et al., 1981). The resulting ability to register durations of single channel open and closed dwell times allows the investigation of activation mechanisms. However, the observable dwell times correspond to relatively stable states of the channel protein, whereas short-lived dwell times of potential mechanistic significance remain obscured by background noise. Filtering the signal to reduce background noise necessarily imposes a dead time below which single channel current pulses are not detected. Since the earliest kinetic studies of single acetylcholine (ACh) receptor (AChR) channels, closed dwell times approaching the dead time have been paramount in the quest to decipher the activation mechanism (Dionne and Leibowitz, 1982; Colquhoun and Sakmann, 1985; Sine and Steinbach, 1986; Auerbach and Lingle, 1987). More recently, an increased incidence of the briefest closed dwell times has been associated with the enhanced ability of a full agonist or a gain-of-function mutant to open the AChR channel (Lape et al., 2008; Mukhtasimova et al., 2009). In terms of mechanism, these brief closed dwell times are suggested to originate from a preopen closed state, known as “flipped” or “primed,” in the path toward channel opening.
To better define the activation mechanism of the muscle AChR, the present work implements procedures that reduce the system dead time and markedly increase the number of detected single channel dwell times. The unitary current amplitude is increased through removal of calcium and application of a greater potential driving force, whereas the sampling rate and filter bandwidth are increased to achieve an overall system dead time of 8 µs. In addition, agonist concentrations are maintained below those that reduce the unitary current amplitude via rapid, unresolved channel block, and in contrast to previous studies (Akk and Auerbach, 1996; Lape et al., 2008; Mukhtasimova and Sine, 2013), events within all clusters of channel openings are included in kinetic fitting, rather than editing out apparently aberrant clusters. A minimal kinetic scheme is fitted to the dwell time sequences, and the ability to detect changes in transition rate constants is tested by comparing a full with a partial agonist and the wild-type with a gain-of-function mutant AChR. The kinetic scheme and fitted rate constants are evaluated by simulating stochastic data that incorporate the experimental system step response, sampling rate, background noise, and filter bandwidth, followed by identical procedures in event detection and maximum likelihood fitting. The results shed new light on how agonist occupancy, agonist efficacy, and a gain-of-function mutation affect rate and equilibrium constants for elementary steps within the activation mechanism. The ability to resolve brief single channel currents is expected to allow improved estimates of rate constants in AChRs after pharmacological interventions or mutations of functionally pivotal structures.
MATERIALS AND METHODS
Determining the patch clamp step response
A 1-kHz triangle wave from an 3351A waveform generator (Agilent Technologies) was applied to the “speed test input” of an Axopatch 200B patch clamp amplifier (Molecular Devices) with the gain set at 100 mV/pA and the internal Bessel filter at 100 kHz. The square wave output of the patch clamp was then sampled at intervals of 0.2 µs using a model BNC-2090 A/D converter with a PCI 6111e acquisition card (National Instruments); this sampling interval is the shortest achievable by the A/D converter, yields a smooth, unjointed step response, minimizes aliasing of high frequencies toward lower frequencies, and for consistency, was used in all data acquisition procedures. The step responses were recorded to the hard disk of a PC computer using the program Acquire (Bruxton), and a 20-s continuous stretch of step responses was exported as a .txt file using the program TAC (Bruxton). 10,000 individual step responses were aligned and summed using the program R, and a sigmoid function was fitted to the averaged step response using Prism software (GraphPad Software), yielding the 10–90% rise time for the patch clamp with (a) the 100-kHz internal Bessel filter alone and either an additional (b) 10-kHz or (c) 25-kHz Gaussian digital filter.
Simulating the patch clamp step response
This is required to determine the effective Gaussian filter frequency (Fc) to simulate single channel currents in accord with the experimental data. The Fc depends on the patch clamp step response, the internal 100-kHz Bessel filter, and the subsequent Gaussian digital filter and will differ from the setting of the Gaussian digital filter alone. Using the Yale HMM software included within TAC, a two-state, closed-open model was used to generate square wave current pulses, which were then sampled at intervals of 0.2 µs. Individual pulses were subjected to a range of Fc values, and the 10–90% rise time was determined by fitting a sigmoid function to each pulse. From a plot of the 10–90% rise time against Fc, the exact Fc that matches the rise time of the patch clamp step response was determined by interpolation. The process was repeated for step responses for the patch clamp with (a) the 100-kHz internal Bessel filter alone and either an additional (b) 10-kHz or (c) 25-kHz Gaussian digital filter.
Simulating single channel currents
The first step was to determine parameters describing the baseline and open channel current noise. A sweep from a representative single channel recording was analyzed using the Yale HMM software within TAC, which fits a kinetic scheme and a model of noise to the experimental data. In addition, the patch clamp step response, subjected to only the internal 100-kHz Bessel filter, was required, as described previously (Wang et al., 2000). Noise was modeled as the output of an autoregressive (AR) filter with Gaussian white noise as the input (Venkataramanan and Sigworth, 2002). The analysis yielded coefficients for each of three AR filters, the maximum number available in TAC. The second step was to simulate stochastic dwell time data, again using the Yale HMM software within TAC. Data were simulated given the kinetic scheme, rate constants determined from maximum likelihood analysis of the experimental data, the experimentally determined unitary current amplitude, 0.2-µs sampling interval, effective Fc of the patch clamp and the Gaussian digital filter, AR coefficients determined in the first step, and standard deviations of the baseline and excess open channel noise. To determine the noise standard deviations, simulations were performed first for the baseline and then for the open channel current noise. With everything else constant, the input standard deviation of the baseline noise was varied, initially without excess open channel noise, and the output standard deviation of the baseline noise was measured from the resulting simulated data. The input standard deviation was plotted against the output standard deviation, and the exact input standard deviation that yields an output standard deviation equal to that of the experimental baseline was determined by interpolation. The process was repeated for a range of input excess open channel noise standard deviations, and the exact input standard deviation that yielded an output standard deviation equal to that of the experimental open channel noise was determined by interpolation.
Determining the data acquisition dead time
A 3351A waveform generator was connected to the A/D converter using a 50-Ω resistance load. Rectangular pulses of 200-mV amplitude, 1-kHz frequency, and specified durations were then recorded to the hard disk of a PC computer at a sampling interval of 0.2 µs using the program Acquire. Using the program TAC, a 6-s continuous stretch of pulses was subjected to the effective Fc of the experimental step response determined in simulating the patch clamp step response above, and pulse durations at half the unitary current amplitude were determined. The average pulse duration at the detection threshold was plotted against the original pulse duration, and the process was repeated for rectangular pulses with durations from 1 to 500 µs.
Single channel recordings
Patch clamp recordings from BOSC 23 cells (Pear et al., 1993) transfected with cDNAs encoding adult human wild-type or mutant muscle AChR subunits were obtained in the cell-attached configuration with a membrane potential of −120 mV and a temperature of 21°C. The pipette solution contained (mM) 80 KF, 20 KCl, 40 K-aspartate, 2 MgCl2, 1 EGTA, and 10 HEPES, adjusted to pH 7.4 with KOH; compared with our standard pipette solution (142 KCl, 5.4 NaCl, 1.8 CaCl2, 1.7 MgCl2, 10 HEPES, adjusted to pH 7.4 with NaOH; Mukhtasimova and Sine, 2013), this calcium-free pipette solution not only increased the unitary current amplitude, but also improved seal resistance and patch stability at increased membrane potentials. ACh and carbamylcholine (CCh), at concentrations of 100 mM in pipette solution, were stored at −80°C before each experiment. The external solution contained (mM) 142 KCl, 5.4 NaCl, 0.2 CaCl2, 1.7 MgCl2, and 10 HEPES, adjusted to pH 7.4 with NaOH. Patch pipettes were fabricated from type 7052 nonfilamented glass (King Precision Glass), with inner and outer diameters of 1.15 mm and 1.65 mm, respectively, coated with SYLGARD 184 (Corning) and heat polished to yield resistances from 5 to 8 MΩ. Standard practices for low noise recordings included a short-barrel pipette holder (Molecular Devices), minimizing the solution in contact with the Ag/AgCl wire inside the patch pipette, a thick coating of SYLGARD near the pipette tip and along the shank, avoiding cracking of the SYLGARD by overheating during the curing step, and minimizing immersion of the pipette in the external solution.
Single channel currents from an Axopatch 200B patch clamp amplifier, with the gain set at 100 mV/pA and the internal Bessel filter at 100 kHz, were sampled at intervals of 0.2 µs using a BNC-2090 A/D converter with a PCI 6111e acquisition card and recorded to the hard disk of a PC computer using the program Acquire. Criteria for accepting data for analysis included a patch clamp noise meter reading between 120 and 160 fA (RMSD at 5 kHz bandwidth) and clear temporal separation of clusters of openings arising from a single receptor channel. Single channel openings and closings were detected using the program TAC with the Gaussian digital filter set at 25 kHz and the detection threshold at half the unitary current amplitude. The unitary current amplitude was obtained from an all-points histogram from different segments of each recording and fitted by the sum of Gaussians (see Results, Fig. 4); the difference between the mean of the baseline and open channel currents was taken as the unitary current amplitude. In addition, the analysis yields standard deviations (σn) of the baseline and open channel noise, which together with half the unitary current amplitude (h) and the effective filter frequency Fc determine the rate of threshold crossings (λn) caused by noise alone according to λn = Fc * exp(−h2/2σn2) (Colquhoun and Sigworth, 1983). For a recording in which the patch clamp noise meter reads 160 fA, application of an effective Fc of 23.271 kHz yielded σn = 1.24 pA for the baseline noise, and with h = 6.6 pA, yielded λn = 0.016 s−1, or one threshold crossing every 60 s. In the same recording, the open channel noise σn = 1.385 pA, which yielded λn = 0.27 s−1, or one threshold crossing every 3.6 s.
Figure 4.
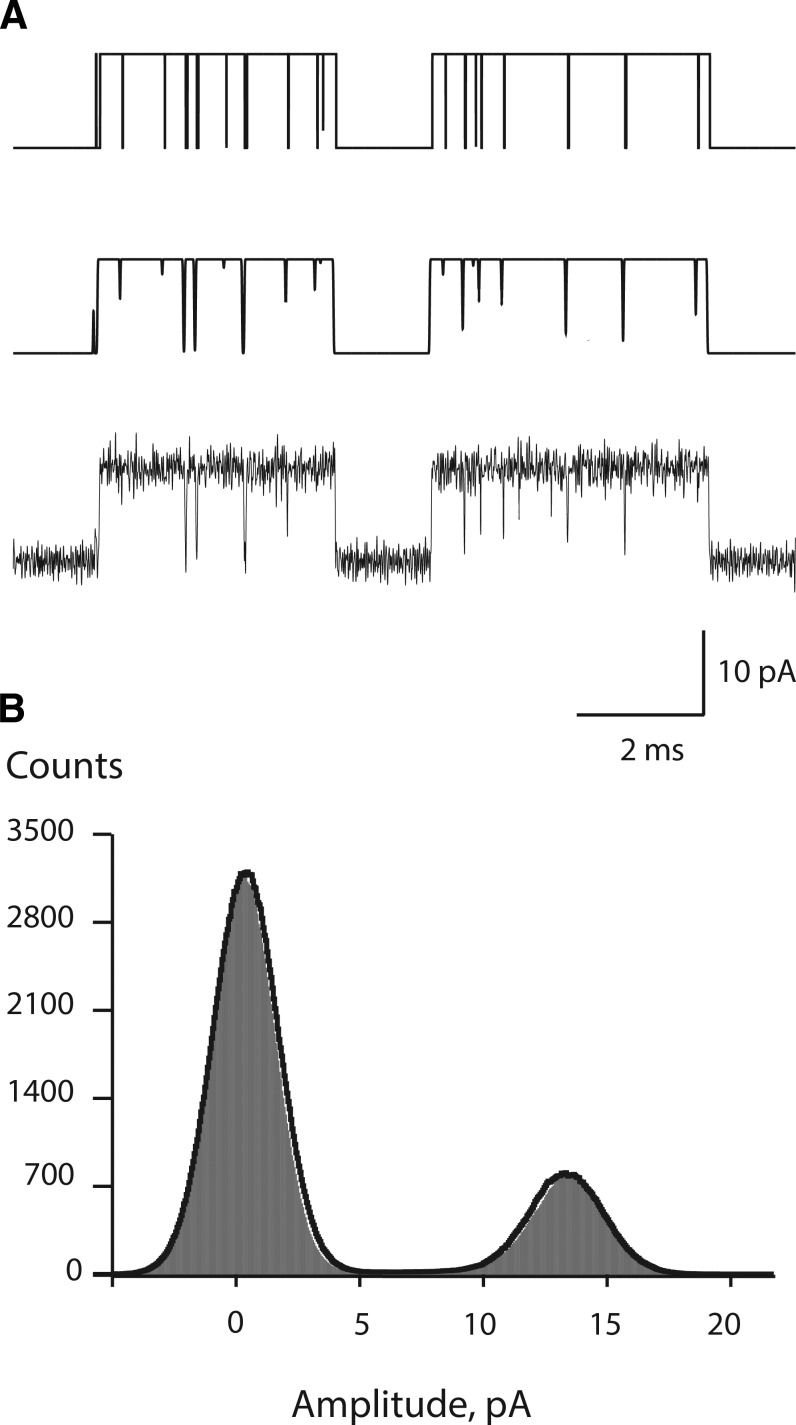
Simulation of single channel currents. (A) Single channel currents are displayed at different stages after stochastic simulation (see Materials and methods), with the top trace digitally sampled at intervals of 0.2 µs, the middle trace after a 25-kHz Gaussian digital filter, and the bottom trace with the addition of baseline and open channel noise. (B) All-points amplitude histogram generated from the bottom trace in A (filled area) overlaid by the Gaussian fit of an all-points histogram from an experimental recording (continuous curve).
Dwell times at the detection threshold were corrected for the effective filter frequency Fc (Colquhoun and Sigworth, 1983) and placed into logarithmic bins (Sigworth and Sine, 1987), and the sum of exponentials was fitted to the open and closed time distributions. The fit of the closed time histogram was used to establish a critical closed time, which distinguishes closings within clusters from those between clusters, as described previously (Sine et al., 1990). Openings and closings within all clusters were included for kinetic analysis, whereas single openings flanked by closings longer than the critical time were excluded. The global dataset comprises event sequences from two to four patches at each agonist concentration, with the concentrations spanning from the lowest concentration that yields clearly defined clusters up to a concentration that minimally reduces the unitary current amplitude caused by rapid, unresolved channel block (Fig. S1). A kinetic scheme was fitted to the global dataset by the maximum likelihood method using MIL software (http://www.qub.buffalo.edu), which corrects for events briefer than the system dead time, uniformly set to 8 µs. For each fitted rate constant, MIL provides an estimate of the error based on the curvature of the likelihood at its maximum (Qin et al., 1996). To further evaluate each fitted rate constant, additional rounds of fitting were performed in which each rate constant was set to a range of trial values, and the remaining rate constants were allowed to vary. Log likelihood values for the constrained and unconstrained fits were then compared using the likelihood ratio test (Horn, 1987). Twice the likelihood ratio was then compared with the χ2 distribution with one degree of freedom. A rate constant was deemed acceptable if a 50% change of the rate constant gave a worse fit with significance of P < 0.01 or better. Nonnested schemes were compared using the Schwarz information criterion (Koehler and Murphree, 1988; Shelley et al., 2010).
Mammalian cell expression
Human α, β, ε, and δ subunit cDNAs, inserted in the cytomegalovirus expression vector pRBG4, were transfected into BOSC 23 cells. The gain-of-function mutation αG153S was generated using the QuikChange site-directed mutagenesis kit (Agilent Technologies), and the presence of the mutation and absence of unwanted mutations were confirmed by sequencing the entire coding region. Cells were maintained in Dulbecco’s modified Eagle’s medium containing 10% (vol/vol) fetal bovine serum at 37°C until they reached 50% confluence. Thereafter, cDNAs encoding wild-type or mutant AChR subunits, plus a cDNA encoding green fluorescent protein, were transfected by calcium-phosphate precipitation. Patch clamp recordings were made 12–48 h after transfection.
Online supplemental material
Fig. S1 shows single channel current amplitude versus ACh concentration. Fig. S2 shows analysis of experimental and simulated single channel currents for the adult human AChR activated by ACh. Fig. S3 shows analysis of simulated single channel currents for the αG153S mutant AChR activated by ACh. Fig. S4 shows analysis of experimental and simulated single channel currents for the adult human AChR activated by CCh. Fig. S5 shows analysis of experimental and simulated single channel currents for the αG153S mutant AChR activated by CCh. Fig. S6 shows predicted macroscopic current as a function of time after a step increase of the ACh concentration for the wild-type AChR. Table S1 shows a comparison of schemes with and without primed states. Table S2 shows a comparison of cyclic and noncyclic schemes. Table S3 shows the effect of noise on event detection in simulated data. Table S4 shows the results from simulation followed by kinetic fitting. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201611584/DC1.
RESULTS
Patch clamp step response
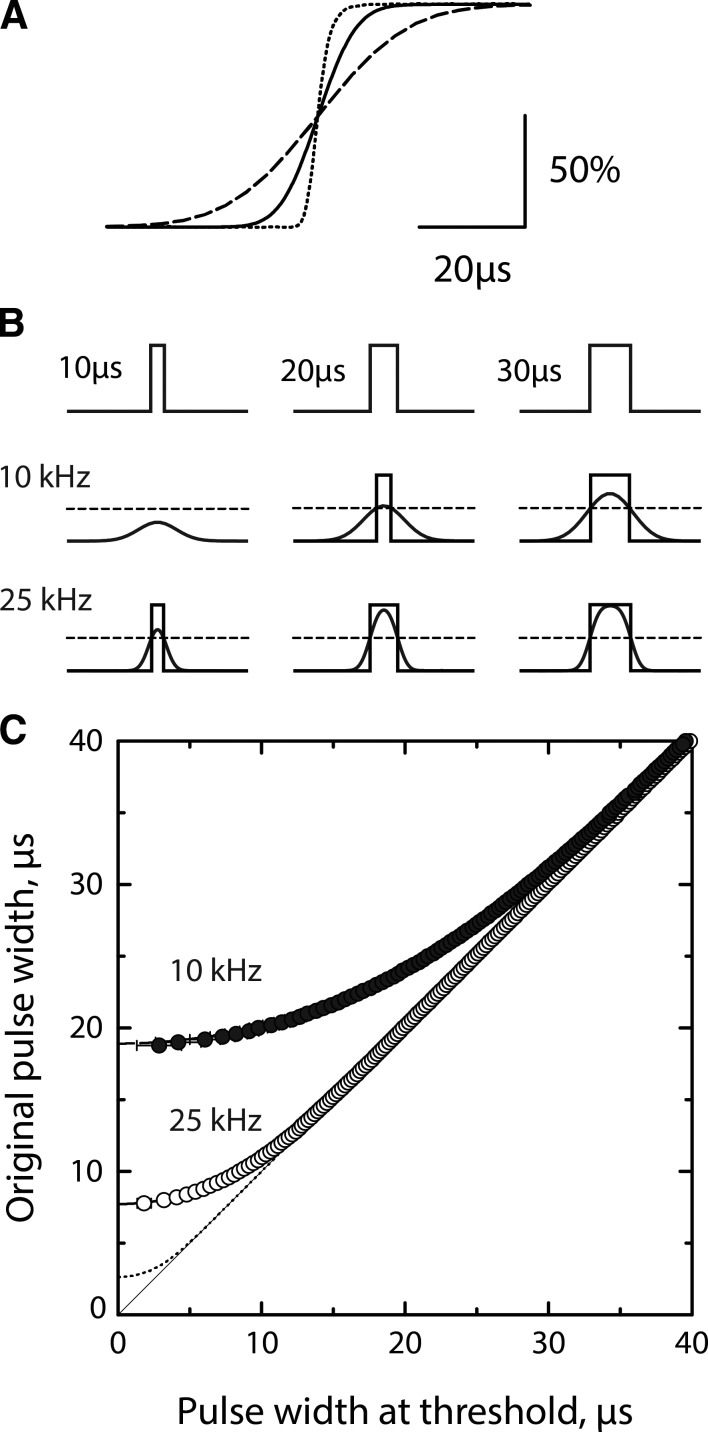
Accurate measurement of brief single channel dwell times requires an assessment of the patch clamp temporal response, data acquisition and signal processing parameters, and event detection procedures. The first step, defining the patch clamp step response, was performed by applying a triangle wave to the patch clamp and then digitally recording the square wave output (Materials and methods). The averaged step response shows slight asymmetry but is approximately sigmoid (Fig. 1 A, dotted curve). Fitting a sigmoid function to the step response for the patch clamp with its internal 100-kHz Bessel filter yields a 10–90% rise time of 4.92 µs. Subsequent filtering with a Gaussian digital filter set to either 10 or 25 kHz yields essentially perfect sigmoid step responses (Fig. 1 A, dashed and continuous curves), with 10–90% rise times of 35.00 and 14.75 µs, respectively. Thus, compared with the patch clamp and its internal 100-kHz Bessel filter, increasing the Gaussian filter frequency from 10 to 25 kHz reduces the rise time by two thirds.
Figure 1.
Patch clamp step response and temporal resolution of current pulses. See Materials and methods. (A) Averaged step response for the patch clamp and internal 100-kHz Bessel filter (dotted curve), sampled at intervals of 0.2 µs, and filtered with a Gaussian digital filter set to 10 kHz (dashed curve) and 25 kHz (continuous curve). The effective Fc for each step response, determined as described in Materials and methods, is 70.086 kHz for the patch clamp with the 100-kHz internal Bessel filter, 23.271 kHz for an additional 25-kHz Gaussian filter, and 9.840 kHz for a 10-kHz Gaussian filter. (B) Current pulses with the indicated durations are sampled at intervals of 0.2 µs and displayed without filtering (top row), with a 10-kHz filter (middle row), and with a 25-kHz filter (bottom row). A detection threshold at half the current amplitude (dashed line) defines the pulse duration at threshold shown by superimposed rectangular pulses. (C) Pulse durations at the detection threshold are plotted against the original pulse durations for the patch clamp with its 100-kHz Bessel filter (dotted curve) and after a Gaussian digital filter of 10 kHz (closed symbols) and 25 kHz (open symbols).
Pulse detection
The effects of a noninstantaneous rise time are illustrated for rectangular pulses of 10, 20, and 30 µs applied directly to the A/D converter and acquired with a sampling interval of 0.2 µs (Fig. 1 B). The rise and fall of each pulse was generated with the Gaussian digital filter set to the effective Fc corresponding to either 10 or 25 kHz. Determination of the effective Fc for each filter frequency is described under simulating the patch clamp step response (Materials and methods). Increasing the filter frequency from 10 to 25 kHz clearly improves detection of brief pulses, as shown by reference to a detection threshold set at half the unitary current amplitude. To assess the ability to quantify pulses of varying durations, test pulses from 1 to 500 µs were acquired using a sampling interval of 0.2 µs and subjected to the effective Fc for three different filter frequencies. Pulse durations above the detection threshold were then plotted against the original pulse duration (Fig. 1 C). For an Fc corresponding to the patch clamp with only the internal 100-kHz Bessel filter, the plot is linear over all but the briefest durations, and the y intercept reveals a dead time of 2.65 µs. With the addition of a 10-kHz Gaussian filter, our previous best bandwidth, the plot is linear over a narrower range of pulse durations, and the dead time is 18.8 µs. With a Gaussian filter of 25 kHz, the bandwidth in this work, the linear range increases and the dead time decreases to 7.9 µs. These limiting dead times, obtained for current pulses with known durations, coincide with those predicted by the equation dead time = 0.538 * [rise time] (Colquhoun and Sigworth, 1983), demonstrating that the measured rise times, dead times, and effective Fc are self-consistent. Thus, compared with the patch clamp and its internal 100-kHz Bessel filter, increasing the Gaussian filter frequency from 10 to 25 kHz reduces the dead time by two thirds.
Resolution of experimental recordings
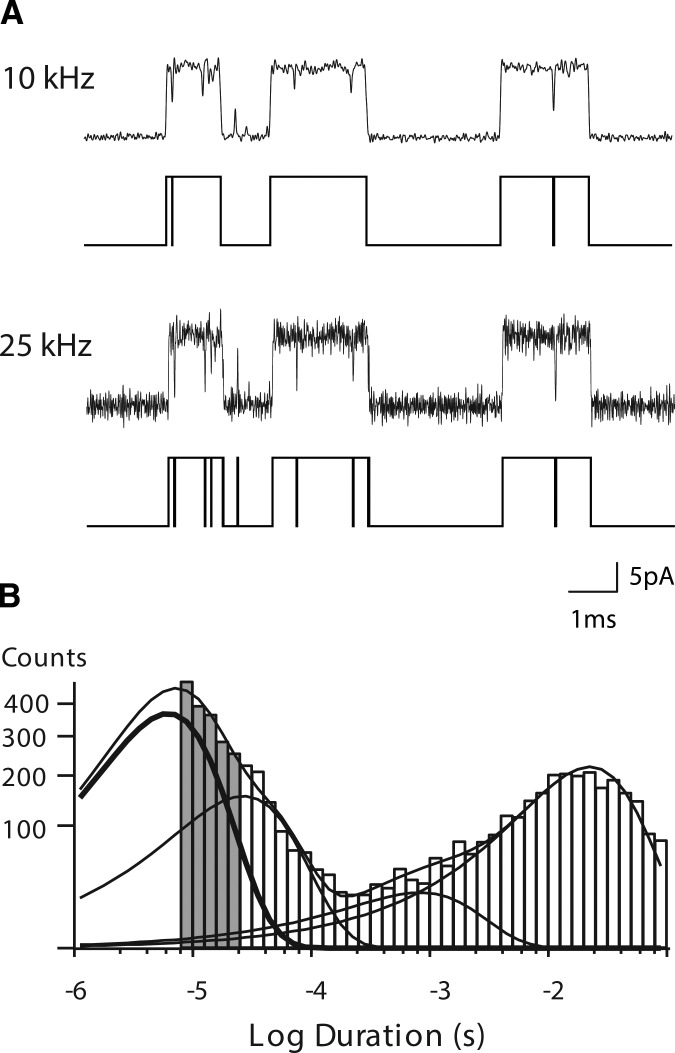
To achieve a signal to noise ratio suitable to a Gaussian filter frequency of 25 kHz (Materials and methods), the membrane potential was increased from our previous standard of −70 to −120 mV, and calcium was omitted from the pipette solution, yielding unitary currents with amplitudes of ∼13.2 pA for the adult human muscle AChR. Single channel currents activated by a low concentration of ACh were acquired with a sampling interval of 0.2 µs and displayed with the Gaussian digital filter set to either 10 or 25 kHz (Fig. 2 A). Idealized current pulses, determined with the detection threshold set at half the unitary current amplitude, are shown below each trace. Increasing the filter frequency markedly increases the number of detected channel opening and closing events. After detecting events from the entire recording and correcting their durations for the effective Fc of the Gaussian filter (Colquhoun and Sigworth, 1983), a histogram of closed dwell times reveals not only a marked increase in the number of brief dwell times, but also the presence of a major exponential component near the dead time (Fig. 2 B). Thus, increasing the Gaussian filter frequency from 10 to 25 kHz increases temporal resolution by approximately half an order of magnitude, which more than doubles the number of closings briefer than 100 µs, as indicated by the shaded bins in the histogram (Fig. 2 B).
Figure 2.
Improved temporal resolution of single channel currents. (A) Currents recorded from adult human muscle AChRs activated by 3 µM ACh with the Gaussian digital filter set to 10 kHz (top trace) and 25 kHz (bottom trace). Channel openings are upward deflections. Below each trace are the detected events using a threshold at half the unitary current amplitude. (B) Histogram of closed dwell times from the entire recording fitted by the sum of four exponential components. The component with shortest mean duration is shown by a thickened curve. The five shaded bins indicate the increase in resolved closed dwell times as the result of the increase in bandwidth from 10 to 25 kHz.
Wild-type adult human AChR activated by ACh
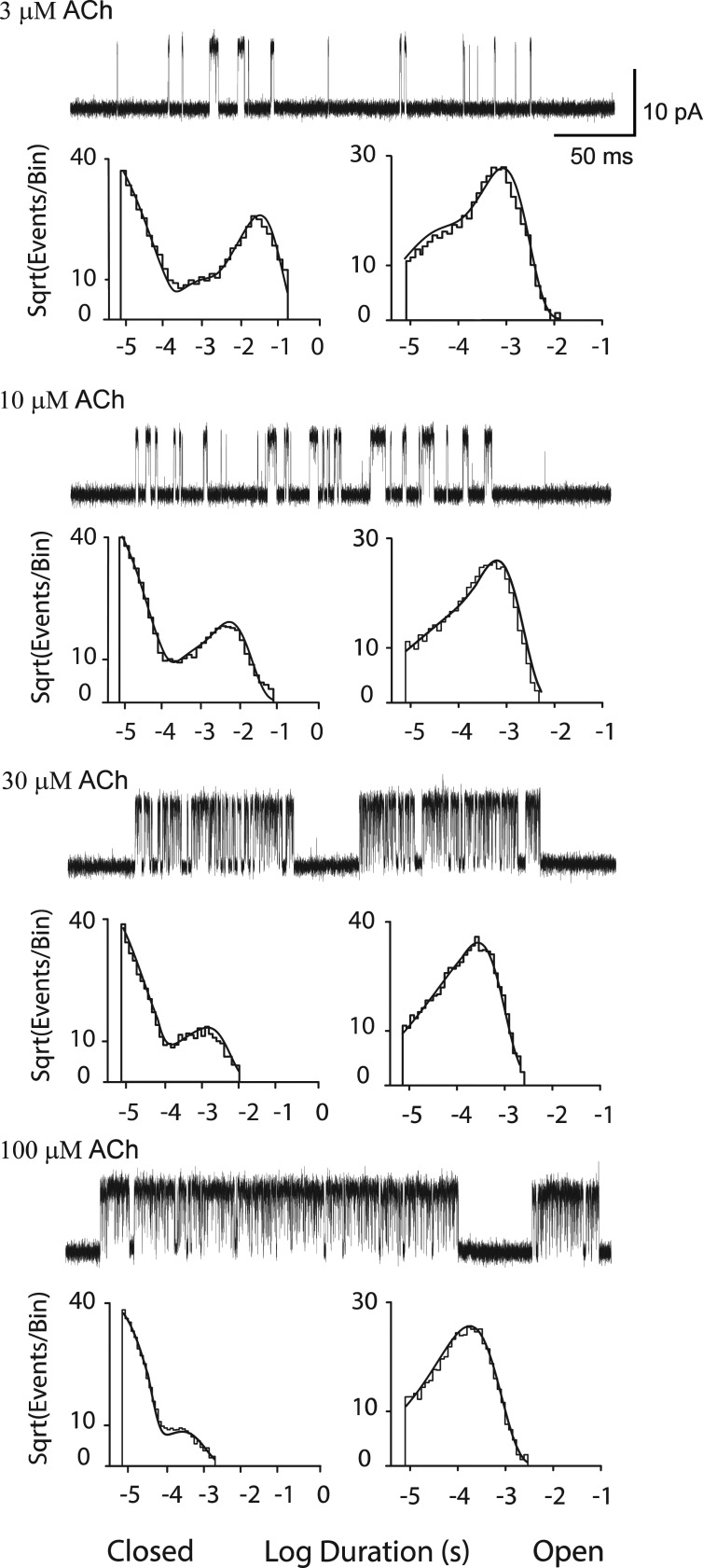
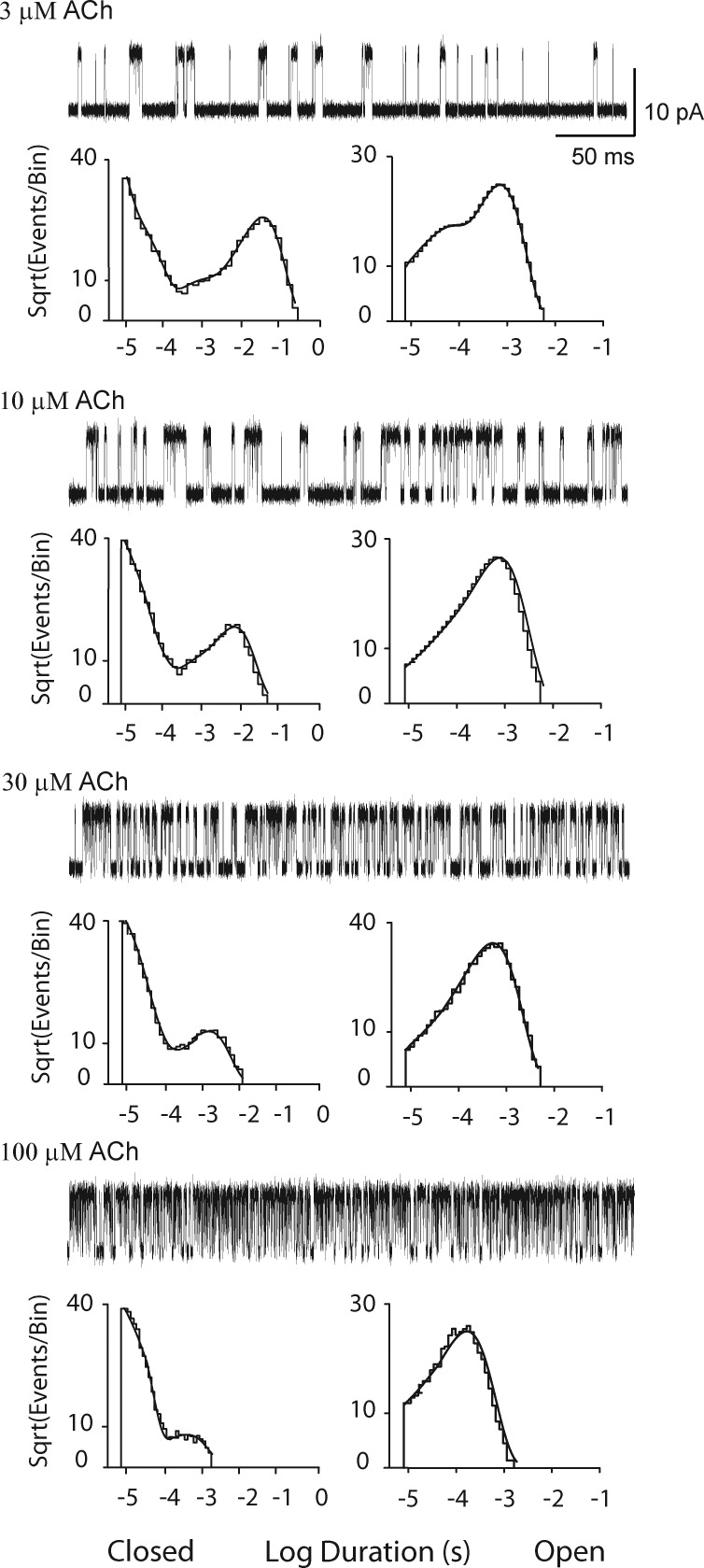
Single channel current traces, obtained using the experimental recording conditions and data acquisition and processing procedures just described, are illustrated for a range of ACh concentrations (Fig. 3). The lowest ACh concentration is the minimum for which channel openings appear in clearly defined clusters; below this concentration, openings appear at a low but steady rate, and thus successive openings may correspond to different AChR channels. The highest ACh concentration was chosen to minimally reduce the unitary current amplitude owing to rapid, unresolved channel block by ACh (Fig. S1; Sine and Steinbach, 1984). Comparison of single channel current traces from low to high ACh concentrations reveals a progressive decrease in the durations of closed dwell times and a commensurate increase in the fraction of time the channel is open, hallmarks of a process driven by agonist concentration. The concentration dependence of closed dwell times is further evident in the closed duration histograms where the exponential component with longest mean duration moves toward briefer durations with increasing ACh concentrations. Open dwell times, comprised of two exponentials at 3 µM ACh, comprise a single exponential at higher concentrations. At a concentration of 100 µM ACh, the mean open duration decreases relative to that at lower concentrations, owing to channel blocking events that exceeded the dead time. Probability density functions generated from the best fit kinetic scheme (Scheme 1) superimposes well on the global set of dwell time histograms (Fig. 3 and Fig. S2).
Figure 3.
Analysis of single channel currents from the adult human wild-type AChR activated by ACh. For each of the indicated ACh concentrations, events from a single channel are displayed at a bandwidth of 25 kHz, and the corresponding closed and open time histograms are displayed with the global fit of Scheme 1 to the data overlaid. Rate constants from the global fit are presented in Table 1.
Choice of kinetic scheme
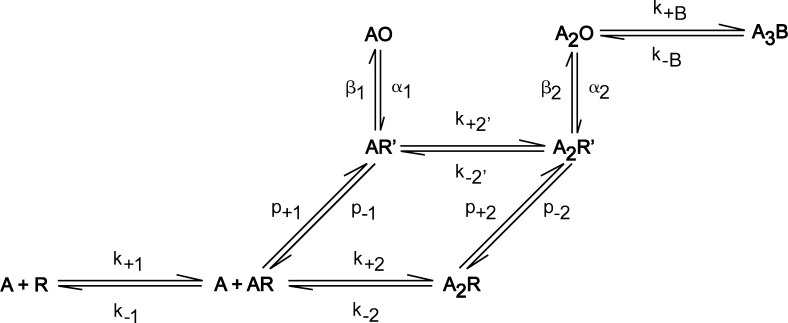
A principal aim of the analysis is to identify a kinetic scheme with a minimum number of states and state transitions that describes dwell time sequences from wild-type and gain-of-function mutant AChRs activated by ACh and the partial agonist CCh. A scheme comprised solely of agonist binding and channel gating steps yields qualitatively poor fits over the global range of agonist concentrations and ranks below a scheme with closed state intermediates in the path toward channel opening (Table S1). In particular, the fitted probability density functions in Fig. 3 were generated from Scheme 1:
(Scheme 1).
The agonist A associates with the resting state R of the receptor with rate constants k+1 and k+2, forming the states AR and A2R, and dissociates with rate constants k−1 and k−2. A statistical factor is not included in either the association or dissociation rate constants because the ligand-binding sites are formed by different pairs of subunits and thus are nonidentical; as a result, the process of agonist binding is effectively sequential, which prevails when the agonist dissociation constants for the two sites diverge sufficiently or if agonist occupancy is negatively cooperative. The primed states, AR′ and A2R′, form with the forward rate constants p+1 and p+2 and return to the resting state with rate constants p−1 and p−2. The agonist associates with the primed state with rate constant k+2′ and dissociates with rate constant k−2′. The open states AO and A2O form with the forward rate constants β1 and β2 and return to the primed states with rate constants α1 and α2. The agonist blocks the open state A2O with the rate constant k+b and unblocks with the rate constant k−b. Agonist block of the AO state is not included because at the high agonist concentrations that produce block, the AO state is negligible. Scheme 1, originally introduced as the Flip model (Lape et al., 2008), is a sub-hypothesis of the subsequent Primed model (Mukhtasimova et al., 2009).
Scheme 1 was fitted to the global set of dwell time sequences for the wild-type AChR activated by ACh with all rate constants free to vary. The only constraint was that of detailed balancing of the rate constants within the cyclic portion of the scheme. Rate constants for ACh association with the resting state (Table 1) are some 10-fold slower than the theoretical rate of free diffusion between a small molecule substrate and an enzyme active site of ∼109 M−1s−1 (Alberty and Hammes, 1958) and are indistinguishable for unoccupied and singly occupied receptors, indicating association with the resting state is independent of occupancy. In contrast, the rate constants for ACh dissociation differ between the two sites, indicating dissociation from the resting state depends on occupancy. Thus, the affinity of ACh for the first binding site is approximately 20-fold greater than that for the second site, solely due to differences in the dissociation rate constants. The rate constant for ACh association with the primed state is some 10-fold greater than that for the resting state and is on par with the rate of diffusion. Thus, although ACh association is independent of occupancy, it depends on receptor state, at least for the resting and primed states.
Table 1. Kinetics of AChR activation by ACh.
| Receptor | k+1 | k−1 | K1 | k+2 | k−2 | K2 | k+2′ | k−2′ | K2′ | p+1 | p−1 | P1 | p+2 | p−2 | P2 | β1 | α1 | Θ1 | β2 | α2 | Θ2 | k+b | k−b | Kb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| µM | µM | µM | mM | |||||||||||||||||||||
| Wild type | ||||||||||||||||||||||||
| Experiment | 135 | 1,410 | 10 | 134 | 25,000 | 187 | 2150 | 17,200 | 8.0 | 325 | 34,100 | 0.01 | 19,200 | 86,400 | 0.2 | 9,200 | 27,300 | 0.3 | 190,000 | 3,140 | 60 | 150 | 93,000 | 0.6 |
| (6) | (90) | (0.8) | (4) | (18,00) | (14) | (270) | (1,450) | (1.2) | (19) | (2,300) | (0.001) | (800) | (2,600) | (0.001) | (230) | (1,225) | (0.02) | (1,100) | (140) | (2.8) | (1.0) | (714) | (0.06) | |
| Simulateda | 137 | 1,470 | 11 | 130 | 23,000 | 170 | 2,050 | 11,700 | 6.0 | 295 | 33,400 | 0.01 | 13,500 | 51,000 | 0.3 | 10,500 | 29,000 | 0.4 | 320,000 | 6,900 | 46 | 160 | 98,000 | 0.6 |
| (9) | (130) | (1.2) | (8) | (1,000) | (13) | (210) | (1,400) | (0.9) | (28) | (2,500) | (0.001) | (880) | (3,500) | (0.003) | (1,300) | (1,750) | (0.05) | (2,400) | (830) | (5.5) | (2) | (1,200) | (0.01) | |
| Simulatedb | 139 | 1,410 | 10 | 115 | 22,200 | 193 | 1,710 | 16,000 | 9.3 | 310 | 34,000 | 0.01 | 13,700 | 72,800 | 0.2 | 9,700 | 27,800 | 0.3 | 200,000 | 3,180 | 62 | 155 | 9,6000 | 0.6 |
| (10) | (137) | (1.2) | (7) | (1800) | (19) | (190) | (1,640) | (1.5) | (26) | (2,330) | (0.001) | (940) | (3,300) | (0.001) | (1,150) | (1,230) | (0.04) | (18,100) | (250) | (7.8) | (2.0) | (1,066) | (0.01) | |
| αG153S | ||||||||||||||||||||||||
| Experiment | 365 | 844 | 2.3 | 300 | 2,450 | 8.0 | 12,100 | 26,000 | 2.1 | 460 | 4,330 | 0.1 | 30,500 | 75,900 | 0.4 | 4,600 | 47,200 | 0.3 | 240,000 | 3,600 | 67 | 176 | 120,000 | 0.7 |
| (27) | (110) | (0.3) | (14) | (190) | (0.7) | (950) | (1,800) | (0.2) | (58) | (390) | (0.001) | (1,600) | (3,000) | (0.03) | (344) | (5,300) | (0.01) | (23,400) | (340) | (6) | (3) | (945) | (0.01) | |
| Simulateda | 357 | 719 | 2.0 | 268 | 2,240 | 8.3 | 10,601 | 11,400 | 1.2 | 450 | 4,540 | 0.1 | 21,700 | 28,200 | 0.7 | 5,550 | 48,000 | 0.1 | 440,000 | 13,500 | 33 | 190 | 120,000 | 0.6 |
| (36) | (117) | (0.1) | (21) | (210) | (1) | (700) | (1,280) | (0.1) | (58) | (360) | (0.01) | (1,000) | (2,900) | (0.09) | (480) | (600) | (0.01) | (2,700) | (2,100) | (2) | (6) | (3,000) | (0.01) | |
| Simulatedb | 374 | 860 | 2.3 | 272 | 2,100 | 7.8 | 9,200 | 24,100 | 2.6 | 560 | 4,410 | 0.13 | 22,000 | 58,200 | 0.4 | 4,900 | 47,700 | 0.1 | 250,000 | 3,700 | 67 | 192 | 110,000 | 0.6 |
| (37) | (150) | (0.5) | (24) | (166) | (0.9) | (630) | (1,616) | (0.2) | (70) | (340) | (0.02) | (1,100) | (2,900) | (0.03) | (360) | (3,400) | (0.01) | (20,600) | (340) | (8.3) | (5) | (2,700) | (0.01) |
Rate constants were estimated from fitting Scheme 1 to global dwell time sequences obtained over a range of ACh concentrations, with errors computed by the MIL program in parenthesis (Materials and methods). Units of the rate constants are µM−1s−1 for association rate constants, and s−1 for all others. The channel gating equilibrium constants (Θn) are βn/αn, and the dissociation constants (K) are k−/k+.
Results from analysis of simulated data with experimental fitted parameters as the input.
Results from analysis of simulated data with the experimental fitted parameters, except with slower channel opening and closing rate constants (wild type: 125,000/2,100; αG153S: 150,000/2,400) as the input.
The affinity of ACh for the singly occupied primed state (Kd ∼8 µM) is higher than that for the singly occupied resting state (Kd ∼190 µM) and drives a commensurate increase in the equilibrium constant for priming the doubly relative to the singly occupied receptor. The cyclic configuration within Scheme 1 is essential, as a scheme without the interconnection between the AR′ and A2R′ states yields a significantly worse fit, as assessed by the likelihood ratio test, with P < 0.001 (Table S2). The forward rate constant for priming is almost 60-fold greater for doubly than singly occupied receptors, whereas the equilibrium constant for priming is only 20-fold greater (Table 1). The change in the log of the forward priming rate constants divided by the change in the log of the priming equilibrium constants is 1.3. According to rate-equilibrium free energy theory (Fersht et al., 1986), after a structural perturbation such as agonist occupancy, the free energy change of the transition state is a linear combination of free energy changes of the flanking ground states, which predicts a log ratio between zero and one. However, a log ratio greater than one indicates agonist occupancy also affects priming at the stage of the transition state, reducing the activation energy barrier independently of free energy changes of the flanking ground states.
Gating of the channel is also greater for doubly than singly occupied receptors and thus, like priming, depends on agonist occupancy. However, unlike priming, the forward gating rate constant is only 14-fold greater for doubly than singly occupied receptors, whereas the gating equilibrium constant is 170-fold greater (Table 1). Thus, the change in the log of the forward gating rate constants divided by the change in the log of the gating equilibrium constants is 0.54, indicating the free energy change of the transition state comprises near equal contributions of the free energy changes of the flanking ground states.
An essential test of the experimental single channel recordings and kinetic analysis is simulation (Materials and methods). Stochastic current pulses were simulated according to Scheme 1, the fitted rate constants, the experimental agonist concentrations, and the experimentally determined unitary current amplitude. The sampling rate, effective filter bandwidth, and noise of the baseline and open channel currents were then applied to the stochastic current pulses. Examples of simulated single channel currents (Fig. 4) are shown after successive application of the experimental sampling interval (top trace), effective filter frequency Fc (middle trace), and baseline and open channel noise (bottom trace). An all-points histogram generated from the simulated data (bottom trace) exhibits peaks corresponding to the baseline and open channel noise (Fig. 4, shaded region), which are very close to the Gaussian fit to an all-points histogram from an experimental recording (Fig. 4, continuous curve). Thus, the simulations recapitulate the signal to noise ratio of the experimental single channel current traces.
The simulated single channel current traces for a range of ACh concentrations (Fig. 5) appear qualitatively similar to those obtained experimentally (Fig. 3 and Fig. S2). Single channel open and closed dwell times were detected using the same half-amplitude threshold crossing method applied to the experimental traces. Histograms of the simulated closed dwell times again show a systematic dependence on agonist concentration in which the closed time component with longest mean duration moves to briefer durations with increasing agonist concentration. Similarly, histograms of open dwell times show two components at the lowest agonist concentration and one component at higher concentrations. Fitting Scheme 1 to the global sequences of simulated dwell times yielded probability density functions that superimpose well on the dwell time histograms (Fig. 5 and Fig. S2). Moreover, the rate constants are very close to those obtained from analysis of the experimental data, with two notable exceptions: the channel opening and closing rate constants for the doubly occupied receptor are roughly twofold greater than those from fitting Scheme 1 to the experimental data (Table 1). A plausible explanation is the previously demonstrated effect of noise on the briefest dwell times (McManus et al., 1987). Owing to the exponential nature of stochastic dwell times, the number of brief events is always greater than the number of longer events, so that the effect of noise is not self-canceling across the range of dwell times. Instead, the number of events in briefer time bins will increase relative to those in longer time bins, leading to an overestimate of the decay rate of the briefest dwell times.
Figure 5.
Analysis of simulated single channel currents for the adult human wild-type AChR activated by ACh. For each of the indicated ACh concentrations, a segment of simulated single channel activity is displayed at a bandwidth of 25 kHz (Materials and methods), and the corresponding closed and open time histograms are displayed with the global fit of Scheme 1 to the data overlaid. Rate constants for simulation are those from the global fit of Scheme 1 to the experimental data (Table 1), but with channel gating rate constants of β2 = 125,000 s−1 and α2 = 2100 s−1 determined by iterative simulations followed by kinetic fitting (see Table S4). Rate constants from fitting Scheme 1 to the simulated data are presented in Table 1.
To test this explanation, single channel dwell times were simulated according to Scheme 1, the fitted rate constants, a range of agonist concentrations, experimental sampling rate, and Fc, but without noise. For each agonist concentration, the number of events that surpassed the detection threshold was determined. After addition of noise to the same events, the number of events that surpassed the detection threshold was compared with that without noise. In all cases, addition of noise increased the number of detected brief events by 6–11% (Table S3), thus contributing to the overestimates of the channel opening and closing rate constants.
To obtain improved estimates of the channel opening and closing rate constants, dwell time sequences were simulated with a series of trial pairs of opening and closing rate constants, whereas the remaining rate constants were set to those from analysis of the experimental data. Scheme 1 was then fitted to the simulated data with all rate constants free to vary, subject to the requirement of detailed balancing of the rate constants in the cyclic portion of the scheme. The process of simulation and kinetic fitting was repeated until the gating rate constants from fitting Scheme 1 to the simulated data concurred with those from fitting Scheme 1 to the experimental data (Table S4). After multiple iterative simulations followed by kinetic fitting, input rate constants of β2 = 125,000 s−1 and α2 = 2,100 s−1 were found to yield output rate constants within 5% or less of those obtained from fitting Scheme 1 to the experimental data (Table 1). In addition, the nongating rate constants were very similar to those obtained from fitting Scheme 1 to the experimental data. Thus, the channel opening and closing rate constants for the doubly occupied receptor are slower than those determined from a direct fit of Scheme 1 to the experimental data, although they still predict rapid and efficient channel gating (β2 = 125,000 s−1; Θ2 = β2/α2 = 59).
The mean burst duration, determined at a low ACh concentration, provides a bandwidth-independent check of the fitted rate constants within the right-hand portion of Scheme 1. A burst is defined as one or more openings in quick succession where the brief intervening closings correspond to sojourns in the states A2R′ and A2R in Scheme 1. From recordings obtained in the presence of the lowest concentration of ACh, 3 µM, the mean burst duration is 1.29 ms. An expression for the mean burst duration, obtained by analogy to Eq. 3.9 in Colquhoun and Hawkes (1981), is given by
| (1) |
where the rate constants are as defined for Scheme 1. Eq. 1 is valid in the limit of low agonist concentration, where bursts terminate by agonist dissociation and reassociation is negligible. The mean burst duration computed from Eq. 1 and the fitted rate constants is 1.42 ms, in good agreement with the value determined experimentally and providing bandwidth-independent support of the rate constants in the right-hand portion of Scheme 1.
αG153S mutant AChR activated by ACh
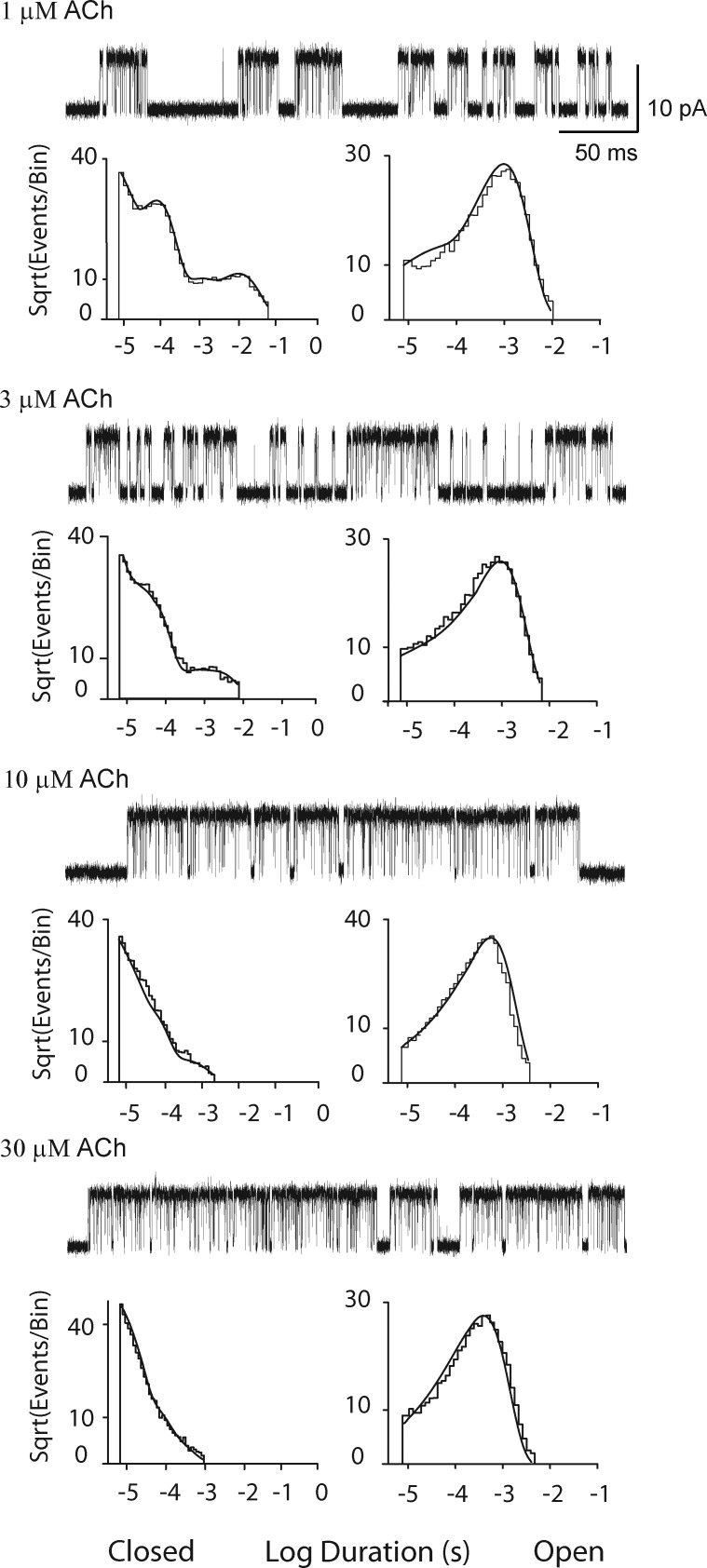
The mutation αG153S, located within each agonist-binding site, markedly prolongs ACh-elicited channel opening episodes. Previous work, based on a scheme with a direct transition between closed and open states, suggested the prolonged channel opening episodes arise from slowing of agonist dissociation from the doubly occupied resting state, which greatly increases channel reopening (Sine et al., 1995a). Thus, single channel currents from the αG153S AChR were examined using the experimental data acquisition and analyses methods just described. The αG153S AChR exhibited well-defined clusters of single channel openings at lower concentrations of ACh than for the wild-type AChR, allowing study of a range of concentrations well below those that reduce the unitary current amplitude caused by rapid, unresolved channel block. Comparison of single channel current traces, from low to high ACh concentrations, again reveals a progressive decrease in the durations of closed dwell times and a commensurate increase in the fraction of time the channel is open (Fig. 6). The closed duration histograms again show a systematic dependence on ACh concentration, but in addition, the αG153S mutation produces a distinct signature: at the lowest ACh concentrations and for durations briefer than 500 µs, two exponential components are clearly distinguished, in contrast to the closely spaced components observed for the wild-type AChR (Figs. 2 B and 3). Open dwell times, comprised of two exponential components at 1 µM ACh, again comprise a single exponential at higher concentrations. However, owing to the lower agonist concentrations, the mean open duration decreased modestly as the result of reduced incidence of channel blockages that exceeded the dead time. Fitting Scheme 1 to the global set of dwell time sequences yields probability density functions that superimpose well on the dwell time histograms (Fig. 6).
Figure 6.
Analysis of single channel currents from the αG153S AChR activated by ACh. For each of the indicated ACh concentrations, events from a single channel are displayed at a bandwidth of 25 kHz, and the corresponding closed and open time histograms are displayed with the global fit of Scheme 1 to the data overlaid. Rate constants from the global fit are presented in Table 1.
Rate constants for ACh association with the resting state are two- to threefold greater for the αG153S compared with the wild-type AChR but remain below the rate of diffusion (Table 1). The association rate constants for unoccupied and singly occupied receptors are similar, in agreement with occupancy independence of the association rate constants observed for the wild-type AChR. Rate constants for ACh dissociation differ between the singly and doubly occupied resting states and thus are occupancy dependent, as observed for the wild-type AChR, but they are slower by 2- and 10-fold, respectively, compared with those for the wild-type AChR. The ratio of dissociation to association rate constants reveals that the αG153S mutation increases ACh affinity by 4- and 20-fold for the first and second occupancy steps, respectively, thus yielding a smaller difference in affinity between the two binding sites compared with the wild-type AChR. The rate constant for ACh association with the primed state is greater than that for the resting state, and thus association depends on receptor state, as observed for the wild-type AChR. However, the rate of association with the primed state exceeds the theoretical rate of diffusion (Table 1), although it is on par with that predicted by diffusion combined with electrostatic, dipolar, and van der Waals attractive forces that increase the local agonist concentration (Zhou and Zhong, 1982). Furthermore, association between the enzyme carbonic anhydrase and its substrate proceeds at a rate greater than that of diffusion (Koenig and Brown, 1972). A scheme without the interconnection between the AR′ and A2R′ states yields a significantly worse fit, as observed for the wild-type AChR, and the likelihood ratio test indicated P < 0.001 (Table S2). Thus, although the association and dissociation rate constants retain their respective dependencies on state and occupancy, the αG153S mutation increases ACh affinity through reciprocal changes in the rate constants for association and dissociation.
The affinity of ACh for the primed state of the αG153S AChR (Kd ∼2 µM) is modestly greater than that for the resting state (Kd ∼8 µM) and drives an only fourfold increase in the equilibrium constant for priming the doubly relative to the singly occupied receptor (Table 1). However, the forward rate constant for priming increases 60-fold for the doubly relative to the singly occupied receptor, indicating successive occupancy by ACh increases the priming rate constant much more than it increases the priming equilibrium constant. The change in the log of the priming rate constants divided by the change in the log of the priming equilibrium constants is 3.1, indicating the αG153S mutation amplifies the contribution of ACh occupancy at the stage of the transition state.
Channel gating of the αG153S AChR increases for singly relative to doubly occupied receptors, with the forward rate constant increasing 33-fold and the equilibrium constant increasing 650-fold (Table 1); the change in the log of the forward rate constants divided by the change in the log of the equilibrium constants is 0.54. Thus, as observed for the wild-type AChR, the free energy change of the gating transition state contains near equal contributions of the free energy changes of the flanking ground states.
The fitted rate constants for the αG153S AChR were tested by simulation, as described for the wild-type AChR. Fitting Scheme 1 to the simulated data yielded rate constants in accord with those from the experimental data, but as observed for the wild-type AChR, the channel opening and closing rate constants for the doubly occupied receptor are too fast (Table 1). Simulation followed by kinetic fitting showed that input rate constants of β2 = 150,000 s−1 and α2 = 2,400 s−1 yield output rate constants within 3% of those obtained from fitting Scheme 1 to the experimental data while the nongating rate constants remain close to their original values (Table 1). Simulated single channel traces, dwell time histograms, and probability density functions obtained from the fit of Scheme 1 to the simulated data are shown in Fig. S3. Thus, simulation confirms the nongating rate constants and provides improved estimates of the channel gating rate constants.
The mean burst duration for the αG153S AChR, determined at a concentration of 300 nM ACh, is 8.9 ms, close to the value of 8.7 ms computed from Eq. 1 and the fitted rate constants and longer than that for the wild-type AChR. By inspection of Eq. 1, the major cause of the prolonged burst duration is a marked slowing of the rate constant for ACh dissociation, k−2. Thus, analysis of burst durations provides bandwidth-independent support of the rate constants in the right-hand portion of Scheme 1.
Wild-type adult human AChR activated by CCh
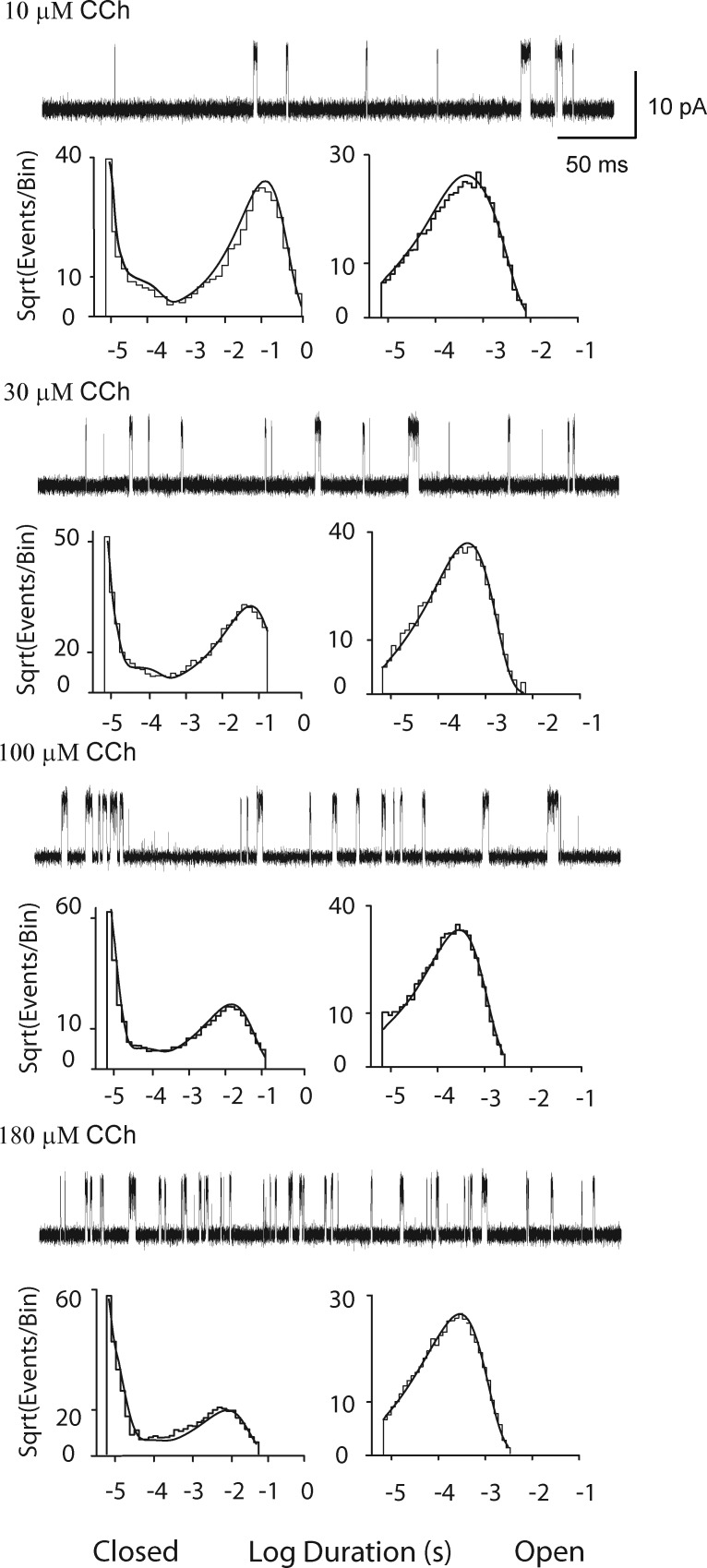
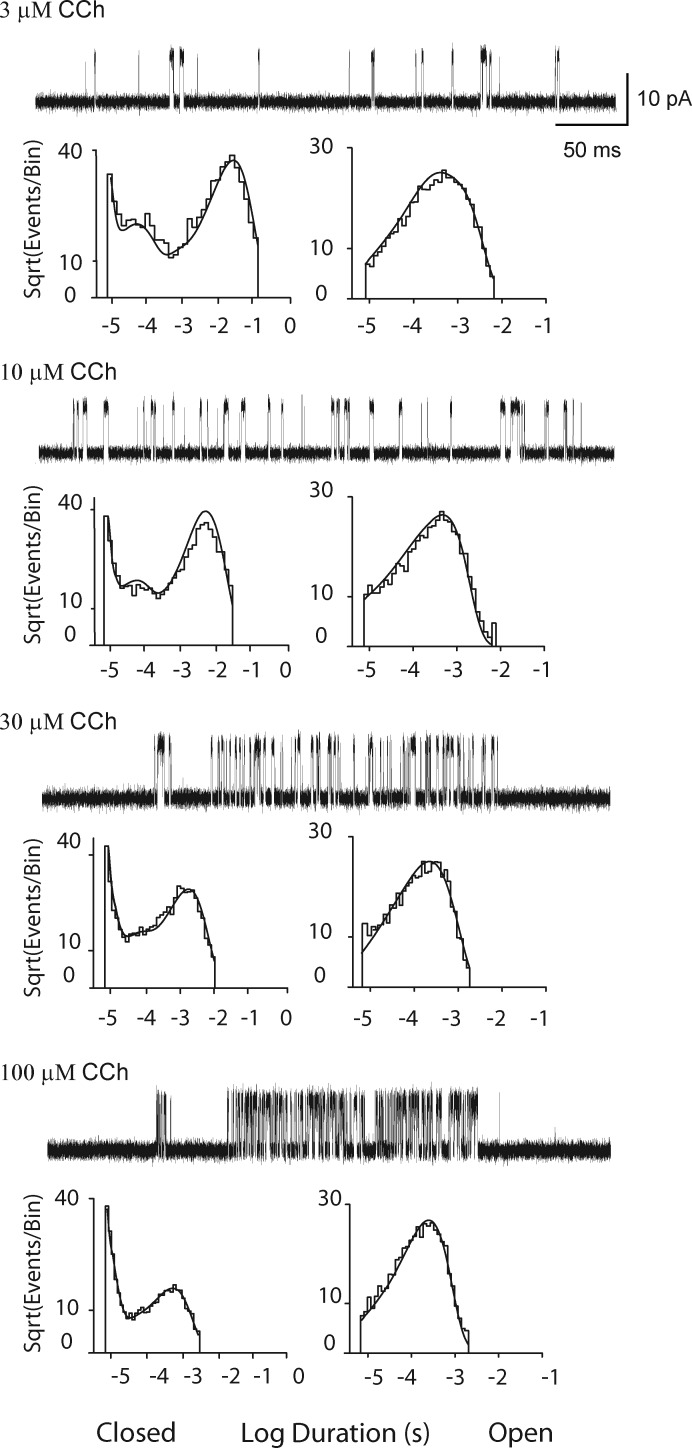
CCh has the same configuration of heavy atoms as ACh, but instead of an acetyl group, it contains an amide group. Moreover, CCh is less potent and less efficacious than ACh (Sine and Steinbach, 1987; Marshall et al., 1991), suggesting binding, priming, gating, or a combination of these steps differ between the two agonists. Thus, single channel currents from the wild-type AChR elicited by CCh were studied using the same experimental, data acquisition, and analyses methods applied to the wild-type and mutant AChRs activated by ACh. Compared with ACh, higher concentrations of CCh are required to elicit well-defined clusters of single channel openings. Comparison of single channel current traces, from low to high CCh concentrations, again reveals a progressive decrease in the durations of closed dwell times, but in contrast to ACh, the fraction of time the channel is open is greatly reduced (Fig. 7). In addition, the closed duration histograms exhibit a signature distinct from that observed for ACh: closings of both brief and long durations are abundant, whereas closings of intermediate durations are relatively sparse. In contrast, the distributions of open dwell times are similar between CCh and ACh. Probability density functions generated from fitting Scheme 1 to the global dwell time sequences superimpose well on the dwell time histograms (Fig. 7 and Fig. S4).
Figure 7.
Analysis of single channel currents from the adult human wild-type AChR activated by CCh. For each of the indicated CCh concentrations, events from a single channel are displayed at a bandwidth of 25 kHz, and the corresponding closed and open time histograms are displayed with the global fit of Scheme 1 to the data overlaid. Rate constants from the global fit are presented in Table 2.
The rate constant for association of CCh with unoccupied, resting state receptors is not well defined, despite error estimates <20% (Table 2). In subsequent rounds of fitting, setting the association rate constant to a range of values, while allowing the remaining rate constants to vary, yielded small but insignificant changes in the log likelihood, as determined by the likelihood ratio test (Materials and methods). However, each trial association rate constant produced a reciprocal change in the dissociation rate constant, so that the ratio of the rate constants was stable over all fitting trials; the resulting dissociation constant was twofold smaller than that for ACh (Table 2). In contrast, the rate constant for association of CCh with singly occupied, resting state receptors is well defined and is more than 10-fold slower than that for ACh. The rate constant for dissociation of CCh from doubly occupied, resting state receptors is twofold slower compared with that for ACh, and the ratio of dissociation to association rate constants reveals nearly a 10-fold reduction in CCh affinity relative to ACh. Thus, the affinity of CCh for the two binding sites differs by 300-fold, indicating CCh is more site-selective than ACh.
Table 2. Kinetics of AChR activation by CCh.
| Receptor | k+1 | k−1 | K1 | k+2 | k−2 | K2 | k+2′ | k−2′ | K2′ | p+1 | p−1 | P1 | p+2 | p−2 | P2 | β1 | α1 | Θ1 | β2 | α2 | Θ2 | k+b | k−b | Kb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| µM | µM | µM | mM | |||||||||||||||||||||
| Wild type | ||||||||||||||||||||||||
| Experiment | 1,280 | 6,520 | 5.1 | 10.5 | 13,000 | 1,240 | 290 | 16,980 | 58 | 75 | 79,800 | 0.001 | 1,500 | 75,300 | 0.02 | 8,200 | 6,370 | 1.3 | 310,000 | 6,200 | 50 | 280 | 360,000 | 1.3 |
| (230) | (1,040) | (0.7) | (0.8) | (2,100) | (286) | (55) | (6900) | (26) | (20) | (12,000) | (0.0001) | (400) | (4,600) | (0.002) | (4,700) | (290) | (0.7) | (1,100) | (530) | (4) | (10) | (5,300) | (0.03) | |
| Simulateda | 1,250 | 5,500 | 4.4 | 8.7 | 11,000 | 1,270 | 345 | 21,000 | 61 | 75 | 75,600 | 0.001 | 1,400 | 69,000 | 0.02 | 8,200 | 6,290 | 1.3 | 330,000 | 10,700 | 31 | 320 | 330,000 | 0.6 |
| (270) | (640) | (1) | (0.9) | (1,300) | (200) | (58) | (3,300) | (14) | (11) | (6,500) | (0.0001) | (190) | (5,200) | (0.002) | (1,560) | (220) | (0.2) | (7,200) | (700) | (2.1) | (9.4) | (3,500) | (0.01) | |
| Simulatedb | 1700 | 7,200 | 4.2 | 10.1 | 14,300 | 1,410 | 270 | 5,210 | 19 | 40 | 96,200 | 0.001 | 1,200 | 39,500 | 0.03 | 22,100 | 6,640 | 3.3 | 310,000 | 6,700 | 46 | 310 | 330,000 | 1.1 |
| (340) | (600) | (0.9) | (0.8) | (1200) | (160) | (31) | (780) | (3.6) | (5) | (70) | (0.0002) | (140) | (4,700) | (0.003) | (4,200) | (320) | (0.7) | (10,400) | (500) | (3.8) | (7) | (3,000) | (0.01) | |
| αG153S | ||||||||||||||||||||||||
| Experiment | 190 | 1,040 | 5.5 | 170 | 17,200 | 100 | 140 | 4,600 | 33 | 370 | 24,000 | 0.015 | 6,100 | 124,000 | 0.05 | 5,100 | 11,400 | 0.45 | 330,000 | 6,400 | 50 | 470 | 440,000 | 0.9 |
| (20) | (140) | (4) | (5) | (2,500) | (10) | (30) | (1,100) | (10) | (30) | (2,300) | (0.0001) | (400) | (11,000) | (0.002) | (650) | (600) | (0.07) | (1,100) | (900) | (8.9) | (3) | (8,700) | (0.01) | |
| Simulateda | 250 | 1,380 | 5.6 | 175 | 14,700 | 84 | 86 | 1,400 | 16 | 345 | 26,600 | 0.01 | 4500 | 66,700 | 0.07 | 5,500 | 11600 | 0.5 | 340,000 | 9,910 | 34 | 490 | 360,000 | 0.7 |
| (12) | (50) | (3.4) | (6) | (500) | (4) | (26) | (46) | (7) | (34) | (2,800) | (0.001) | (940) | (4,600) | (0.01) | (740) | (580) | (0.07) | (7,800) | (2,100) | (1.7) | (11) | (3,000) | (0.01) | |
| Simulatedb | 250 | 1,450 | 5.8 | 170 | 15,000 | 89 | 70 | 1,950 | 28 | 370 | 25,700 | 0.01 | 3,370 | 73,700 | 0.05 | 5,200 | 9,980 | 0.5 | 320,000 | 6,650 | 48 | 490 | 370,000 | 0.7 |
| (13) | (60) | (0.5) | (9) | (1,800) | (6.6) | (23) | (720) | (13) | (38) | (2,800) | (0.02) | (800) | (6,400) | (0.03) | (700) | (450) | (0.01) | (1,400) | (520) | (3.7) | (5) | (2,700) | (0.01) |
Rate constants were estimated from fitting Scheme 1 to global dwell time sequences obtained over a range of CCh concentrations, with errors computed by the MIL program in parenthesis (Materials and methods). Units of the rate constants are µM−1s−1 for association rate constants, and s−1 for all others. The channel gating equilibrium constants (Θn) are βn/αn, and the dissociation constants (K) are k−/k+.
Results from analysis of simulated data with experimental fitted parameters as the input.
Results from analysis of simulated data with the experimental fitted parameters, except with slower channel opening and closing rate constants (wild type: 100,000/1,900; αG153S: 130,000/2,500).
Rate constants for association and dissociation of CCh with the primed state are also not well defined (Table 2). A likely reason is that sojourns in the singly and doubly primed states are rare compared with those in the resting state, and recordings with 10-fold more events would be needed to quantify transitions among primed states. Nevertheless, the log likelihood for Scheme 1 is greater than that for a scheme without the interconnection between the AR′ and A2R′ states, and the likelihood ratio test indicates a significance of P < 0.02 (Table S2). In further rounds of fitting, setting either the priming association or dissociation rate constant to a range of values, while allowing the remaining rate constants to vary, revealed only small and insignificant changes in the log likelihood. The ratio of dissociation to association rate constants remained stable, however, and revealed higher affinity of CCh for the primed (58 µM) than the resting (1,200 µM) state.
The increased affinity of CCh for the primed over the resting state drives a commensurate increase in the priming equilibrium constant for doubly relative to singly occupied receptors (Table 2), as observed for ACh. However, the priming rate and equilibrium constants are much smaller for CCh than ACh, which account for the reduced efficacy of CCh. In further contrast to ACh, successive occupancy by CCh increases the priming rate and equilibrium constants by equal amounts. As a consequence, the change in the log of the priming rate constants divided by the change in the log of the priming equilibrium constants is 0.99, indicating that upon successive occupancy by CCh, nearly all of the free energy change of the priming reaction is realized in the transition state, and unlike a full agonist, occupancy by a partial agonist does not contribute at the stage of the priming transition state. Thus, CCh, an agonist with reduced efficacy, not only reduces the absolute values of the priming rate and equilibrium constants, but it also reduces the occupancy dependence of the priming rate relative to the equilibrium constant.
The channel gating rate and equilibrium constants also increase with successive occupancy by CCh, as observed for ACh. The forward gating rate constant is 12-fold greater for doubly than singly occupied receptors, whereas the equilibrium constant is 40-fold greater. Thus, the change in the log of the forward gating rate constants divided by the change in the log of the gating equilibrium constants is 0.67, again indicating the free energy change of the gating transition state comprises similar contributions of the free energy changes of the flanking ground states.
The fitted rate constants for the wild-type AChR activated by CCh were again evaluated by simulation. Fitting Scheme 1 to the simulated data yielded rate constants in accord with analysis of the experimental data, but as observed for the wild-type and αG153S AChRs activated by ACh, the channel opening and closing rate constants for the doubly occupied receptor are too fast (Table 2). Simulation followed by kinetic fitting shows that input rate constants of β2 = 100,000 s−1 and α2 = 1,900 s−1 yield output rate constants within 8% of those obtained from fitting Scheme 1 to the experimental data (Table 2), whereas the nongating rate constants that are well defined in the fit of Scheme 1 to the experimental data remain close to their original values. Simulated single channel traces, dwell time histograms, and probability density functions obtained from the fit of Scheme 1 to the simulated data are shown in Fig. S4.
The mean burst duration for the wild-type AChR activated by CCh, determined at a CCh concentration of 10 µM, is 1.03 ms, close to the value of 0.93 ms computed from Eq. 1 and the fitted rate constants, again providing bandwidth-independent support for the rate constants in the right-hand portion of Scheme 1.
αG153S AChR activated by CCh
As a final perturbation, single channel currents from the αG153S AChR elicited by CCh were studied using the same experimental, data acquisition, and analyses methods applied to the previous agonist–receptor combinations. The single channel current traces and dwell time histograms exhibit the same systematic dependencies on agonist concentration observed for the other agonist–receptor combinations (Fig. 8 and Fig. S5). The overall data show that the αG153S mutation remains a gain-of-function mutant with CCh as the agonist, whereas CCh remains a partial agonist with αG153S as the receptor (Fig. 8). Both trends, however, differ quantitatively from those for the other three agonist–receptor combinations.
Figure 8.
Analysis of single channel currents from the αG153S AChR activated by CCh. For each of the indicated CCh concentrations, events from a single channel are displayed at a bandwidth of 25 kHz, and the corresponding closed and open time histograms are displayed with the global fit of Scheme 1 to the data overlaid. Rate constants from the global fit are presented in Table 2.
The rate constants for CCh association with the resting state of the αG153S AChR are similar for unoccupied and singly occupied receptors, whereas the dissociation rate constants differ between doubly and singly occupied receptors (Table 2), as observed for the other agonist–receptor combinations (Table 1). The ratio of dissociation to association rate constants indicates the αG153S mutation increases affinity for CCh compared with that for the wild-type AChR, with the greatest increase occurring in the second occupancy step. In contrast, CCh exhibits reduced affinity for the αG153S AChR compared with ACh. Notably, as will be important in determining burst duration, the rate constant for CCh dissociation from the doubly occupied resting state is similar for αG153S and wild-type AChRs. The rate constants for association and dissociation of CCh with the primed state are not well defined; in subsequent rounds of fitting, setting either the association or dissociation rate constant to a range of values, while allowing the remaining rate constants to vary, reveals small and insignificant changes in the log likelihood, but the ratio of dissociation to association rate constants remains stable. Furthermore, the log likelihood for Scheme 1 is greater than that for a scheme without the interconnection between the AR′ and A2R′ states, and the likelihood ratio test indicates a significance of P < 0.02 (Table S2).
The affinity of CCh for the primed state (32 µM) is modestly greater than that for the resting state (102 µM) and drives only a threefold increase in the priming equilibrium constant for doubly relative to singly occupied receptors (Table 2). However, the forward rate constant for priming is 17-fold greater for doubly relative to singly occupied receptors, and the change in the log of the priming rate constants divided by the change in the log of the priming equilibrium constants is 2.4, again indicating CCh occupancy contributes to priming at the stage of the transition state. Thus, as observed for ACh, the αG153S mutation increases agonist efficacy and amplifies the contribution of CCh occupancy at the stage of the priming transition state.
Channel gating of the αG153S AChR increases with successive CCh occupancy, with the forward rate constant increasing 25-fold and the equilibrium constant increasing 110-fold for doubly relative to singly occupied receptors. The change in the log of the gating rate constants divided by the change in the log of the gating equilibrium constants is 0.68, similar to that for the wild-type AChR activated by CCh, again indicating the free energy change of the gating transition state contains similar contributions of the free energy changes of the flanking ground states. Thus, the four agonist–receptor combinations exhibit diverging relationships between rate and equilibrium constants for priming, whereas they exhibit similar relationships between rate and equilibrium constants for channel gating. Furthermore, agonist efficacy and the gain-of-function mutation uniquely affect the priming step, whereas they do not affect the gating step.
The fitted rate constants for the αG153S AChR activated by CCh were again tested by simulation. Fitting Scheme 1 to the simulated data yielded rate constants in accord with those from analysis of the experimental data, but as observed for the other receptor–agonist combinations, the channel opening and closing rate constants for the doubly occupied receptor are too fast (Table 2). Simulation followed by kinetic fitting showed that input rate constants of β2 = 130,000 s−1 and α2 = 2,500 s−1 yield output rate constants within 5% of those obtained from fitting Scheme 1 to the experimental data (Table 2), whereas the nongating rate constants remain close to their original values. Simulated single channel traces, dwell time histograms, and probability density functions obtained from the final fit of Scheme 1 to the data are shown in Fig. S5.
The mean burst duration for the αG153S AChR, at a concentration of 3 µM CCh, is 0.84 ms, close to the value of 0.94 ms computed from Eq. 1 and the fitted rate constants. Surprisingly, however, the mean burst duration is close to that for the wild-type AChR activated by CCh (1.03 ms). Thus, although the αG153S mutation increases burst duration with ACh as the agonist, it does not increase burst duration with CCh as the agonist. From inspection of Eq. 1, the major reason is that the rate constant for CCh dissociation, k−2, is similar between the αG153S and wild-type AChRs, whereas that for ACh dissociation is much slower for the αG153S than the wild-type AChR. Thus, the diverging effects on burst duration suggest ACh, but not CCh, senses the structural change caused by αG153S.
Occupancy dependence of priming and gating steps
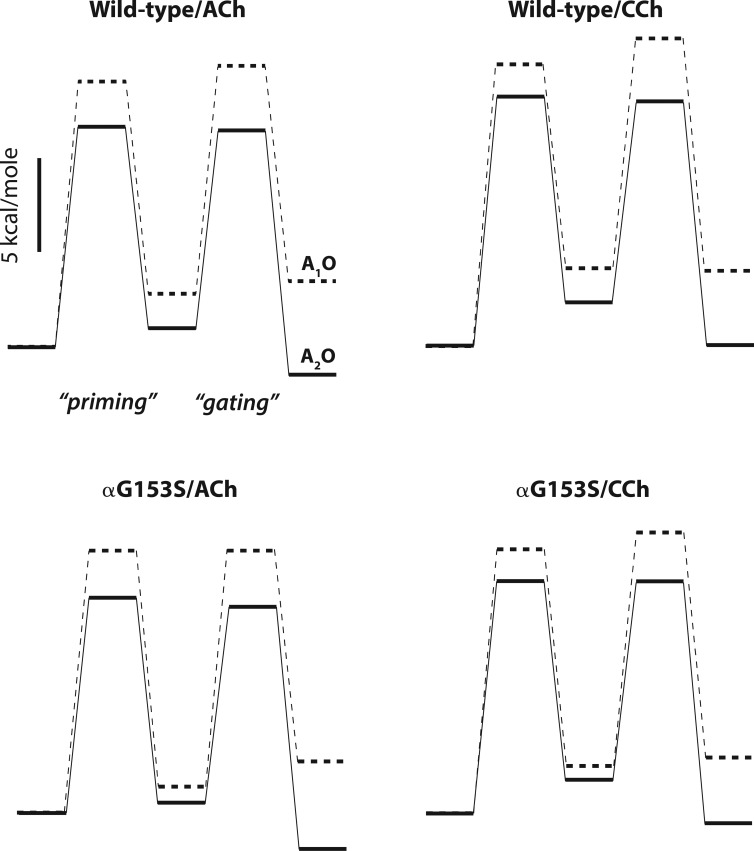
For each agonist–receptor combination, rate constants for priming and gating for singly and doubly occupied receptors are summarized as free energy landscapes (Fig. 9). In all cases, the barriers and wells are higher for singly than doubly occupied receptors, indicating the rate and equilibrium constants for the priming and gating steps depend on agonist occupancy. Wells corresponding to the doubly occupied open state are lower for the full agonist ACh than the partial agonist CCh, owing solely to differences in the priming steps; wells for the singly occupied open state show a similar trend, with the priming step varying more than the gating step. Wells corresponding to either the singly or doubly occupied primed state are lower for the αG153S than the wild-type AChR, and thus enhanced priming rather than gating is the major cause for the increase in channel opening by the αG153S mutation. When expressed in terms of free energy, differences among the four agonist–receptor combinations appear relatively small, but the widely diverging kinetics arise from the exponential dependence of the rate constant on free energy.
Figure 9.
Free energy landscapes for priming and gating of singly and doubly occupied receptors. Free energy for each barrier (ΔG*) was computed from the corresponding rate constant (k) based on transition rate theory and the equation k = κ(kBT/h)exp(−ΔG*/RT), where κ is the transmission coefficient (assumed equal to one), kB is Boltzmann’s constant, h is Planck’s constant, R is the gas constant, and T is the absolute temperature. Rate constants are given in Tables 1 and 2. Rate constants for gating of doubly occupied receptors are those obtained by simulation followed by kinetic fitting to correct for the effects of noise.
DISCUSSION
A major goal of this work is to better define the activation mechanism of the muscle AChR. Although fundamental steps within the mechanism have been identified, the mean durations of single channel events that define those steps approach the system dead time, and only a small fraction of the briefest events is typically detected. Thus, experimental recording conditions, data acquisition, and signal processing are optimized to markedly increase the number of detected brief events. The net result is an increase in temporal resolution approaching half an order of magnitude over our previous best, which improves the ability to fit kinetic schemes to single channel data and increases the accuracy with which rate constants are estimated. A recent study of embryonic muscle AChRs also improved temporal resolution through increases in potential driving force, filter bandwidth, and sampling rate (Stock et al., 2014). Our findings solidify previous conclusions that the rate-limiting step in AChR activation is formation of a primed state intermediate from which channel opening is rapid and efficient. Furthermore, they affirm that changes in the rate and extent of priming, rather than changes in channel gating, underlie differences in agonist efficacy. A second major goal is to better understand the nature of elementary steps within the activation mechanism, including how they depend on state of the receptor, occupancy by agonist, efficacy of the agonist, and a gain-of-function mutation. Association of agonist depends on state of the receptor and type of agonist, but not on the number of bound agonists. In contrast, dissociation of agonist depends on the number of bound agonists, but not on state of the receptor. Priming of the receptor depends on the number of bound agonists and efficacy of the agonist, and the priming rate relative to the priming equilibrium constant also depends on the number of bound agonists and efficacy of the agonist. Gating of the receptor depends on the number of bound agonists but not on efficacy of the agonist, and the gating rate relative to the gating equilibrium constant also depends on the number of bound agonists but not on efficacy of the agonist. The ability to quantify changes in rate and equilibrium constants opens the way toward deeper understanding of the kinetic consequences of pharmacological or structural perturbations.
The kinetic scheme
The major criterion for the choice of kinetic scheme is a minimum number of states and state transitions. For more than 50 years, a scheme comprised of agonist binding and channel gating steps prevailed, as it accounted for macroscopic and single channel measurements of receptor activation in physiological and experimental settings. However, a preopen closed state, initially detected in single channel kinetic studies of the glycine receptor (Burzomato et al., 2004), spurred the search for an analogous state in related Cys-loop receptors. In the muscle AChR, a preopen closed state, called flip, was associated with agonist efficacy (Lape et al., 2008), and an analogous state, called primed, accounted for multiple open and closed states in gain-of-function mutant receptors (Mukhtasimova et al., 2009). In the present study, improved temporal resolution, together with multiple agonist–receptor combinations, provides overwhelming evidence for closed state intermediates between resting closed and open states. Comprised of agonist binding, priming and channel gating steps, Scheme 1 has the minimum number of states and state transitions that describe the global dwell time sequences. A minimal scheme not only enhances the ability to obtain well-defined transition rate constants, but it will also facilitate determination of changes in rate constants caused by pharmacological or structural interventions. An expanded scheme, such as the generalized primed mechanism (Mukhtasimova et al., 2009), remains a possibility and describes more complex activation kinetics from other members of the Cys-loop receptor family (Corradi et al., 2009; Lape et al., 2012; Corradi and Bouzat, 2014; Marabelli et al., 2015). Whereas Scheme 1 contains one primed state, representing a single global conformation, the generalized primed mechanism contains two primed states, each associated with conformational change of one or two ligand-binding sites. However, in the present work, the dwell time distributions contain no missing or supernumerary components, and simulations based on Scheme 1 and the fitted rate constants recapitulate the observed kinetics. The single primed state in Scheme 1 may be a composite of two primed states that are not distinguished, either because the states are tightly coupled in the chosen agonist–receptor combinations or time resolution is still insufficient. Moreover, the utility of Scheme 1 is evident in its ability to associate changes in elementary rate constants with changes in the ability of the AChR channel to open in response to agonist.
The rate constants
The estimation of rate constants depends on quality of the data, which is determined by experimental conditions and data acquisition and data processing procedures. The present work begins with a focus on improving the signal to noise ratio to detect the briefest events under study, which is achieved by removal of calcium from the extracellular solution and increase of the membrane potential; both conditions are expected to affect the observed kinetics and are important in comparing the present with previous studies. Particular attention is given to accurately registering events near the system dead time, including decreasing the sampling interval, determining the effective filter frequency to correct brief event durations, and confirming the procedures by application to events with known durations. The net result is a dead time of 8 µs, which is uniformly applied to all the data. A brief dead time reduces the extent of the missed event correction, which becomes more accurate as more events are resolved. A uniform dead time is required for simultaneous fitting of multiple recordings and is also the reason for choosing a range of agonist concentrations that minimally reduce the unitary current amplitude caused by rapid, unresolved channel block. The range of experimentally accessible agonist concentrations also contributes to data quality and thus the ability to define transition rate constants. For three of the four receptor–agonist combinations, the highest concentration of agonist achieves an open channel probability near the maximum. For example, for the wild-type AChR activated by ACh, the highest ACh concentration achieves an open probability of 0.84, close to the maximum of 0.91 computed from the fitted rate constants (Table 1). However, for the wild-type AChR activated by CCh, the highest CCh concentration achieves an open probability of 0.09, whereas the fitted rate constants predict a maximum of 0.51, potentially contributing to the inability to define rate constants between states with low incidence. A further contributor to data quality is event selection. Previous studies selected clusters of events for analysis based on measures of kinetic uniformity, and apparently aberrant clusters were excluded (Akk and Auerbach, 1996; Lape et al., 2008; Mukhtasimova and Sine, 2013). The present analysis includes all clusters of events, whereas only the infrequent and isolated single openings are excluded.
The estimated rate constants were subjected to both qualitative and quantitative evaluation. A qualitative test is the overlay of the probability density functions computed from the fitted rate constants upon the global set of dwell time histograms, which shows no missing or supernumerary components. Recordings over a range of agonist concentrations maximize the representation of states within the scheme, and global fitting is a powerful means to exclude combinations of rate constants that describe data from a single agonist concentration. The QUB software provides estimates of errors in the fitted rate constants, and each rate constant is further tested by constraining it to a range of values and then repeating the fitting with the remaining rate constants free to vary. Log likelihoods for the unconstrained and constrained fits are then compared using the likelihood ratio test. All but a few rate constants pass the likelihood ratio test, and the noted exceptions correspond to states with low incidence. Finally, Scheme 1 and the data acquisition and signal processing procedures were tested by stochastic simulation combined with the experimental sampling rate, effective filtering frequency, and baseline and open channel noise. The simulations confirm all but the channel gating rate constants, and further rounds of simulation and kinetic fitting yield improved estimates of the gating rate constants that mimic the experimental data. Thus, based on data quality and the ability of a single kinetic scheme to describe data from multiple agonist–receptor combinations, the estimated rate constants were deemed suitable to evaluate their dependence on the number of bound agonists, state of the receptor, agonist efficacy, and a gain-of-function mutation.
Association rate constants
ACh associates with the resting state of the wild-type AChR approximately 10-fold slower than the rate of diffusion, suggesting the binding site is not fully accessible to the surrounding solvent or dynamic conformational changes restrict agonist access. The rate constants are similar to those based on a scheme with a direct transition between closed and open states (Hatton et al., 2003; Lee et al., 2009; Shen et al., 2016), although they are not expected to depend strongly on the presence of closed state intermediates or to require the ultimate in temporal resolution. The association rate constants do not contain a statistical factor, owing to structural nonequivalence of the binding sites, although such a factor would change the rate constants by a factor of two. The rate constant for ACh association does not depend on the number of sites occupied, although that for CCh is defined for association with singly but not unoccupied receptors. The rate constant for CCh association with singly occupied receptors is 10-fold slower than that for ACh and contributes to the potency difference between the two agonists. For ACh, the rate constants for association are more than10-fold faster for the primed than the resting state, and thus association depends on the state of the receptor. The rate constant for ACh association with the primed state is on par with the rate of diffusion (Alberty and Hammes, 1958), suggesting the primed state is more accessible to the solvent than the resting state, is less structurally dynamic, or increases local electrostatic attractive forces. The rate constants for ACh association are increased by the αG153S mutation, yet they remain independent of occupancy but dependent on state of the receptor and type of agonist. Paradoxically, the rate constant for ACh association with the primed state of the αG153S AChR exceeds the rate of diffusion alone, further suggesting that priming increases accessibility to solvent, increases local electrostatic attractive forces (Zhou and Zhong, 1982), or a combination of the two. Thus, the rate constants for agonist association are independent of occupancy but depend on state of the receptor, type of agonist, and a gain-of-function mutation.
Dissociation rate constants
The rate constant for ACh dissociation from the resting state of the wild-type AChR is faster for doubly than singly occupied receptors and thus depends on occupancy. This dependence likely originates from structural differences between the α-δ– and α-ε–binding sites, as established for a variety of ligand types (Sine and Claudio, 1991; Sine et al., 1995b; Osaka et al., 1999; Molles et al., 2002). As a consequence, a statistical factor is not incorporated into the dissociation rate constants, as also noted for the association rate constants. Given that the association rate constants for the two sites are equivalent, the difference in dissociation rate constants is the sole source of agonist site selectivity. In contrast, the dissociation rate constants for the doubly occupied resting state are similar for ACh and CCh, suggesting type of agonist is not a strong determinant of the dissociation rate constant. In addition, the rate constants for ACh dissociation from the doubly occupied primed and resting states are similar, suggesting structural differences between the two states are small compared with those between the α-δ and α-ε sites. The αG153S mutation markedly slows the rate constant for ACh dissociation from the doubly occupied resting state, whereas the corresponding rate constant for CCh dissociation is unaffected; this agonist-selective effect on the dissociation rate constant explains why the mutation increases the mean burst duration for ACh but not for CCh. Thus, the rate constant for agonist dissociation depends on agonist occupancy but depends little on state of the receptor, or for the wild-type AChR, on the type of agonist.
Relationships between rate and equilibrium constants
Seminal work by Fersht et al. (1986) set forth the key conceptual framework in which free energy of the transition state of an enzymatic reaction is a linear combination of the free energies of the flanking ground states. Thus, for a series of structural perturbations, a plot of log rate constant against log equilibrium constant yields a straight line with a slope between zero and one, which indicates the fraction of the free energy change of the overall reaction that is realized in the transition state. However, if the series of perturbations preferentially affects the transition state over the flanking ground states, the slope is greater than one. Edelstein et al. (1996) applied linear free energy relationships to transitions between resting, open channel, and desensitized states of the AChR. In their application, the structure of each functional state was independent of whether the agonist was bound, but each state bound the agonist with different affinity, allowing agonist-driven state transitions. Thus, for the transition between the resting and open channel states, they considered agonist occupancy as a structural perturbation and set forth expectations of how occupancy affects the relationship between the forward gating rate constant and the gating equilibrium constant. In particular, upon successive agonist occupancy, the change in the forward gating rate constant relative to the change in the gating equilibrium constant is determined by the extent to which the free energy change of the gating reaction is realized in the transition state. The following sections apply analogous reasoning to the occupancy dependencies of transitions between the resting and primed states and between the primed and open channel states.
The priming step
We find that the priming rate and equilibrium constants increase with successive agonist occupancy and that the relationship between rate and equilibrium constants depends on the type of agonist and the gain-of-function mutation. For ACh, successive occupancy of the wild-type AChR increases the forward priming rate constant more than it increases the priming equilibrium constant, whereas for CCh, successive occupancy increases the priming rate and equilibrium constants by equal amounts. Thus, for ACh, the ratio of the change in the log rate constant to the change in the log equilibrium constant is greater than one, indicating occupancy has a catalytic effect in which it preferentially stabilizes the priming transition state. In contrast, for CCh, the ratio approaches one, indicating that most, if not all, of the free energy change of the priming reaction is realized in the transition state. The possibility remains, however, that occupancy by either agonist affects the fraction of the free energy change of the reaction that is realized in the transition state, as well as the free energy of the transition state itself. For the αG153S mutation, successive occupancy by either ACh or CCh increases the priming rate constant much more than it increases the priming equilibrium constant. Thus, the mutation amplifies the effect of agonist occupancy at the stage of the priming transition state.
Channel opening and closing rate constants
We find that the rate and equilibrium constants for channel gating increase with successive agonist occupancy, but in contrast to priming, the relationship between rate and equilibrium constants shows little change among the four agonist–receptor combinations. Gating of singly occupied receptors, evident at low agonist concentrations, is faster and more efficient than in previous work based on a scheme with a direct transition between closed and open states (Hatton et al., 2003; Mukhtasimova and Sine, 2013), likely owing to the primed state intermediate between the two states. Gating of singly occupied receptors is also greater than estimates based on the Flip model (Lape et al., 2008), equivalent to Scheme 1, possibly because of differences in experimental conditions or temporal resolution. Gating of doubly occupied receptors is faster and more efficient than that of singly occupied receptors, and both the rate and equilibrium constants exceed previous estimates based on the Flip model. The rate constant for channel closing is much slower than that for channel opening, which contributes to highly efficient channel gating. Successive agonist occupancy increases the forward gating rate constant less than it increases the gating equilibrium constant, in contrast to priming, and the ratio of the change in log rate constant to the change in the log equilibrium constant ranges between 0.54 and 0.68 for the four agonist–receptor combinations. Thus, somewhat more than half of the free energy change of the gating reaction is realized in the transition state, whereas there is no evidence for a catalytic effect of agonist occupancy at the stage of the gating transition state.
Time course of channel opening
A key prediction of Scheme 1 and the fitted rate constants is the time course of channel opening after a step increase of the agonist concentration. If the agonist concentration is saturating and channel block by the agonist is omitted, Scheme 1 becomes Scheme 2:
(Scheme 2).
Accordingly, the time course of the increase in the A2O state is described by the sum of two exponentials with amplitudes and time constants determined by the four rate constants. The absence of a channel blocking step allows comparison of predictions of Scheme 2 with rise times from rapid agonist application at positive membrane potentials that eliminate channel block (Liu and Dilger, 1991; Maconochie and Steinbach, 1998). Given the rate constants determined for the wild-type receptor activated by ACh, the predicted 20–80% rise time is 110 µs (Fig. S6), which approaches the rise time of miniature endplate currents (Stiles et al., 1996) and coincides with the rise time determined by rapid application of ACh to membrane patches containing mouse embryonic type AChRs at a positive membrane potential and a temperature of 11°C (Liu and Dilger, 1991). However, the predicted rise time is longer than that determined by rapid application of ACh to patches containing mouse adult type AChRs at a positive membrane potential and a temperature of 21°C (Maconochie and Steinbach, 1998); in Fig. 7 of that work, multiple determinations yielded 20–80% rise times ranging from ∼15 to 50 µs. The experimental conditions in the present work differ from those in the rapid application experiments and may contribute to the difference between the predicted and the shortest observed rise times. In particular, the present experiments are performed in the absence of extracellular calcium, whereas calcium was present in the rapid application measurements. Evidence that extracellular calcium could affect the activation kinetics comes from determinations of the mean burst duration, which is 1.29 ms in the present work and 3.3 ms in previous work done in the presence of calcium (Shen et al., 2012, 2016). Referring to Eq. 1, six rate constants determine the mean burst duration: β2, α2, p+2, p−2, k−2, and k−2′. Two of these rate constants, α2 and k−2, are similar to those determined from single channel recordings from adult human AChRs in the presence of calcium and analyzed using the flip model (Lape et al., 2008), suggesting they are calcium independent. Of the remaining rate constants, β2, p+2, and p−2 contribute to the rise time, but only p+2 and p−2 vary substantially among the four agonist–receptor combinations (Tables 1 and 2). From Eq. 1, a doubling of p+2 and halving of p−2, with the other rate constants unchanged, yields a mean burst duration of 3.3 ms and, based on Scheme 2, predicts a 20–80% rise time of 50 µs (Fig. S6), approaching that from rapid application of ACh to membrane patches containing mouse adult type AChRs at 21°C. Thus, calcium dependence of the priming and unpriming rate constants may reconcile the difference between the rise time predicted by our rate constants and the shortest rise time determined by rapid agonist application.
Thus, in the present work, increasing the signal to noise ratio and optimizing data acquisition and signal processing improve temporal resolution and deepen mechanistic understanding of AChR activation. Going forward, the methods described herein offer a means to clarify how pharmacological interventions or structural perturbations affect elementary steps in the activation mechanism.
Supplementary Material
ACKNOWLEDGMENTS
We thank Hai-Long Wang, PhD, for contributions to computer programs used in data processing.
This work is supported by National Institutes of Health grant NS031744 to S.M. Sine.
The authors declare no competing financial interests.
Richard W. Aldrich served as editor.
Footnotes
Abbreviations used in this paper:
- ACh
- acetylcholine
- AChR
- ACh receptor
- AR
- autoregressive
- CCh
- carbamylcholine
References
- Akk G., and Auerbach A.. 1996. Inorganic, monovalent cations compete with agonists for the transmitter binding site of nicotinic acetylcholine receptors. Biophys. J. 70:2652–2658. 10.1016/S0006-3495(96)79834-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberty R.A., and Hammes G.G.. 1958. Application of the theory of diffusion-controlled reactions to enzyme kinetics. J. Phys. Chem. 62:154–159. 10.1021/j150560a005 [DOI] [Google Scholar]
- Auerbach A., and Lingle C.J.. 1987. Activation of the primary kinetic modes of large- and small-conductance cholinergic ion channels in Xenopus myocytes. J. Physiol. 393:437–466. 10.1113/jphysiol.1987.sp016832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burzomato V., Beato M., Groot-Kormelink P.J., Colquhoun D., and Sivilotti L.G.. 2004. Single-channel behavior of heteromeric α1β glycine receptors: an attempt to detect a conformational change before the channel opens. J. Neurosci. 24:10924–10940. 10.1523/JNEUROSCI.3424-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D., and Hawkes A.G.. 1981. On the stochastic properties of single ion channels. Proc. R. Soc. Lond. B Biol. Sci. 211:205–235. 10.1098/rspb.1981.0003 [DOI] [PubMed] [Google Scholar]
- Colquhoun D., and Sakmann B.. 1985. Fast events in single-channel currents activated by acetylcholine and its analogues at the frog muscle end-plate. J. Physiol. 369:501–557. 10.1113/jphysiol.1985.sp015912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D., and Sigworth F.J.. 1983. Fitting and statistical analysis of single channel records. In Single Channel Recording. Sakmann B., and Neher E., editors. Plenum Publishing Corp., New York: 191–263. 10.1007/978-1-4615-7858-1_11 [DOI] [Google Scholar]
- Corradi J., and Bouzat C.. 2014. Unraveling mechanisms underlying partial agonism in 5-HT3A receptors. J. Neurosci. 34:16865–16876. 10.1523/JNEUROSCI.1970-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corradi J., Gumilar F., and Bouzat C.. 2009. Single-channel kinetic analysis for activation and desensitization of homomeric 5-HT3A receptors. Biophys. J. 97:1335–1345. 10.1016/j.bpj.2009.06.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dionne V.E., and Leibowitz M.D.. 1982. Acetylcholine receptor kinetics. A description from single-channel currents at snake neuromuscular junctions. Biophys. J. 39:253–261. 10.1016/S0006-3495(82)84515-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelstein S.J., Schaad O., Henry E., Bertrand D., and Changeux J.-P.. 1996. A kinetic mechanism for nicotinic acetylcholine receptors based on multiple allosteric transitions. Biol. Cybern. 75:361–379. 10.1007/s004220050302 [DOI] [PubMed] [Google Scholar]
- Fersht A.R., Leatherbarrow R.J., and Wells T.N.C.. 1986. Quantitative analysis of structure–activity relationships in engineered proteins by linear free-energy relationships. Nature. 322:284–286. 10.1038/322284a0 [DOI] [PubMed] [Google Scholar]
- Hamill O.P., Marty A., Neher E., Sakmann B., and Sigworth F.J.. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. 10.1007/BF00656997 [DOI] [PubMed] [Google Scholar]
- Hatton C.J., Shelley C., Brydson M., Beeson D., and Colquhoun D.. 2003. Properties of the human muscle nicotinic receptor, and of the slow-channel myasthenic syndrome mutant εL221F, inferred from maximum likelihood fits. J. Physiol. 547:729–760. 10.1113/jphysiol.2002.034173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn R. 1987. Statistical methods for model discrimination. Applications to gating kinetics and permeation of the acetylcholine receptor channel. Biophys. J. 51:255–263. 10.1016/S0006-3495(87)83331-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehler A.B., and Murphree E.H.. 1988. A comparison of the Akaike and Schwarz criteria for selecting model order. Appl. Stat. 37:187–195. 10.2307/2347338 [DOI] [Google Scholar]
- Koenig S.H., and Brown R.D. III. 1972. H2CO3 as substrate for carbonic anhydrase in the dehydration of HCO3−. Proc. Natl. Acad. Sci. USA. 69:2422–2425. 10.1073/pnas.69.9.2422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lape R., Colquhoun D., and Sivilotti L.G.. 2008. On the nature of partial agonism in the nicotinic receptor superfamily. Nature. 454:722–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lape R., Plested A.J., Moroni M., Colquhoun D., and Sivilotti L.G.. 2012. The α1K276E startle disease mutation reveals multiple intermediate states in the gating of glycine receptors. J. Neurosci. 32:1336–1352. 10.1523/JNEUROSCI.4346-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee W.Y., Free C.R., and Sine S.M.. 2009. Binding to gating transduction in nicotinic receptors: Cys-loop energetically couples to pre-M1 and M2-M3 regions. J. Neurosci. 29:3189–3199. 10.1523/JNEUROSCI.6185-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., and Dilger J.P.. 1991. Opening rate of acetylcholine receptor channels. Biophys. J. 60:424–432. 10.1016/S0006-3495(91)82068-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maconochie D.J., and Steinbach J.H.. 1998. The channel opening rate of adult- and fetal-type mouse muscle nicotinic receptors activated by acetylcholine. J. Physiol. 506:53–72. 10.1111/j.1469-7793.1998.053bx.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marabelli A., Lape R., and Sivilotti L.. 2015. Mechanism of activation of the prokaryotic channel ELIC by propylamine: a single-channel study. J. Gen. Physiol. 145:23–45. 10.1085/jgp.201411234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall C.G., Ogden D., and Colquhoun D.. 1991. Activation of ion channels in the frog endplate by several analogues of acetylcholine. J. Physiol. 433:73–93. 10.1113/jphysiol.1991.sp018415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McManus O.B., Blatz A.L., and Magleby K.L.. 1987. Sampling, log binning, fitting, and plotting durations of open and shut intervals from single channels and the effects of noise. Pflugers Arch. 410:530–553. 10.1007/BF00586537 [DOI] [PubMed] [Google Scholar]
- Molles B.E., Rezai P., Kline E.F., McArdle J.J., Sine S.M., and Taylor P.. 2002. Identification of residues at the α and ε subunit interfaces mediating species selectivity of Waglerin-1 for nicotinic acetylcholine receptors. J. Biol. Chem. 277:5433–5440. 10.1074/jbc.M109232200 [DOI] [PubMed] [Google Scholar]
- Mukhtasimova N., and Sine S.M.. 2013. Nicotinic receptor transduction zone: invariant arginine couples to multiple electron-rich residues. Biophys. J. 104:355–367. 10.1016/j.bpj.2012.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukhtasimova N., and Sine S.M.. 2013. Nicotinic receptor transduction zone: invariant arginine couples to multiple electron-rich residues. Biophys. J. 104:355–367. 10.1016/j.bpj.2012.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukhtasimova N., Lee W.Y., Wang H.-L., and Sine S.M.. 2009. Detection and trapping of intermediate states priming nicotinic receptor channel opening. Nature. 459:451–454. 10.1038/nature07923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osaka H., Malany S., Kanter J.R., Sine S.M., and Taylor P.. 1999. Subunit interface selectivity of the α-neurotoxins for the nicotinic acetylcholine receptor. J. Biol. Chem. 274:9581–9586. 10.1074/jbc.274.14.9581 [DOI] [PubMed] [Google Scholar]
- Pear W.S., Nolan G.P., Scott M.L., and Baltimore D.. 1993. Production of high-titer helper-free retroviruses by transient transfection. Proc. Natl. Acad. Sci. USA. 90:8392–8396. 10.1073/pnas.90.18.8392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F., Auerbach A., and Sachs F.. 1996. Estimating single-channel kinetic parameters from idealized patch-clamp data containing missed events. Biophys. J. 70:264–280. 10.1016/S0006-3495(96)79568-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelley C., Niu X., Geng Y., and Magleby K.L.. 2010. Coupling and cooperativity in voltage activation of a limited-state BK channel gating in saturating Ca2+. J. Gen. Physiol. 135:461–480. 10.1085/jgp.200910331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X.M., Brengman J.M., Sine S.M., and Engel A.G.. 2012. Myasthenic syndrome AChRα C-loop mutant disrupts initiation of channel gating. J. Clin. Invest. 122:2613–2621. 10.1172/JCI63415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X.M., Brengman J., Neubauer D., Sine S.M., and Engel A.G.. 2016. Investigation of congenital myasthenia reveals functional asymmetry of invariant acetylcholine receptor (AChR) Cys-loop aspartates. J. Biol. Chem. 291:3291–3301. 10.1074/jbc.M115.683995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X.M., Brengman J., Neubauer D., Sine S.M., and Engel A.G.. 2016. Investigation of congenital myasthenia reveals functional asymmetry of invariant acetylcholine receptor (AChR) Cys-loop aspartates. J. Biol. Chem. 291:3291–3301. 10.1074/jbc.M115.683995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth F.J., and Sine S.M.. 1987. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52:1047–1054. 10.1016/S0006-3495(87)83298-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S.M., and Claudio T.. 1991. γ- and Δ-subunits regulate the affinity and the cooperativity of ligand binding to the acetylcholine receptor. J. Biol. Chem. 266:19369–19377. [PubMed] [Google Scholar]
- Sine S.M., and Steinbach J.H.. 1984. Agonists block currents through acetylcholine receptor channels. Biophys. J. 46:277–283. 10.1016/S0006-3495(84)84022-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S.M., and Steinbach J.H.. 1986. Activation of acetylcholine receptors on clonal mammalian BC3H-1 cells by low concentrations of agonist. J. Physiol. 373:129–162. 10.1113/jphysiol.1986.sp016039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S.M., and Steinbach J.H.. 1987. Activation of acetylcholine receptors on clonal mammalian BC3H-1 cells by high concentrations of agonist. J. Physiol. 385:325–359. 10.1113/jphysiol.1987.sp016496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S.M., Claudio T., and Sigworth F.J.. 1990. Activation of Torpedo acetylcholine receptors expressed in mouse fibroblasts. Single channel current kinetics reveal distinct agonist binding affinities. J. Gen. Physiol. 96:395–437. 10.1085/jgp.96.2.395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S.M., Kreienkamp H.J., Bren N., Maeda R., and Taylor P.. 1995a Molecular dissection of subunit interfaces in the acetylcholine receptor: identification of determinants of α-conotoxin M1 selectivity. Neuron. 15:205–211. 10.1016/0896-6273(95)90077-2 [DOI] [PubMed] [Google Scholar]
- Sine S.M., Ohno K., Bouzat C., Auerbach A., Milone M., Pruitt J.N., and Engel A.G.. 1995b Mutation of the acetylcholine receptor α subunit causes a slow-channel myasthenic syndrome by enhancing agonist binding affinity. Neuron. 15:229–239. 10.1016/0896-6273(95)90080-2 [DOI] [PubMed] [Google Scholar]
- Stiles J.R., Van Helden D., Bartol T.M. Jr., Salpeter E.E., and Salpeter M.M.. 1996. Miniature endplate current rise times less than 100 microseconds from improved dual recordings can be modeled with passive acetylcholine diffusion from a synaptic vesicle. Proc. Natl. Acad. Sci. USA. 93:5747–5752. 10.1073/pnas.93.12.5747 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stock P., Ljaschenko D., Heckmann M., and Dudel J.. 2014. Agonists binding nicotinic receptors elicit specific channel-opening patterns at αγ and αδ sites. J. Physiol. 592:2501–2517. 10.1113/jphysiol.2013.267781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkataramanan L., and Sigworth F.J.. 2002. Applying hidden Markov models to the analysis of single ion channel activity. Biophys. J. 82:1930–1942. 10.1016/S0006-3495(02)75542-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.-L., Ohno K., Milone M., Brengman J.M., Evoli A., Batocchi A.P., Middleton L.T., Christodoulou K., Engel A.G., and Sine S.M.. 2000. Fundamental gating mechanism of nicotinic receptor channel revealed by mutation causing a congenital myasthenic syndrome. J. Gen. Physiol. 116:449–462. 10.1085/jgp.116.3.449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou G.-Q., and Zhong W.-Z.. 1982. Diffusion-controlled reactions of enzymes. A comparison between Chou’s model and Alberty-Hammes-Eigen’s model. Eur. J. Biochem. 128:383–387. 10.1111/j.1432-1033.1982.tb06976.x [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.