Abstract
In “Hybrid Search” (Wolfe 2012) observers search through visual space for any of multiple targets held in memory. With photorealistic objects as stimuli, response times (RTs) increase linearly with the visual set size and logarithmically with memory set size even when over 100 items are committed to memory. It is well established that pictures of objects are particularly easy to memorize (Brady, Konkle, Alvarez, & Olivia, 2008). Would hybrid search performance be similar if the targets were words or phrases where word order can be important and where the processes of memorization might be different?
In Experiment One, observers memorized 2, 4, 8, or 16 words in 4 different blocks. After passing a memory test, confirming memorization of the list, observers searched for these words in visual displays containing 2 to 16 words. Replicating Wolfe (2012), RTs increased linearly with the visual set size and logarithmically with the length of the word list. The word lists of Experiment One were random. In Experiment Two, words were drawn from phrases that observers reported knowing by heart (E.G. “London Bridge is falling down”). Observers were asked to provide four phrases ranging in length from 2 words to a phrase of no less than 20 words (range 21–86). Words longer than 2 characters from the phrase constituted the target list. Distractor words were matched for length and frequency. Even with these strongly ordered lists, results again replicated the curvilinear function of memory set size seen in hybrid search. One might expect serial position effects; perhaps reducing RTs for the first (primacy) and/or last (recency) members of a list (Atkinson & Shiffrin 1968; Murdock, 1962). Surprisingly we showed no reliable effects of word order. Thus, in “London Bridge is falling down”, “London” and “down” are found no faster than “falling”.
Introduction
Imagine searching through a list of names, looking for your own name. Assuming that the list is not alphabetical, the nature of this search is quite well understood. With one specific target in mind (your name) most visual search tasks will produce reaction times (RTs) that are a linear function of the number of items – in this case, the length of the list of names. This pattern is seen for many types of simple stimuli (Treisman & Gelade, 1980; Wolfe, 1994, 2007) and the pattern remains the same for visual search of words (Fisk & Schneider, 1983). That is, when observers (Os) are searching for a target word amongst varying numbers of distractor words, search time will increase as a function of the visual set size.
Suppose, instead, you have focused your attention to one name on the list and you are trying to remember if it is the name of one of 20 students in a class. How we perform this search through memory is less clear. Under some conditions, memory search patterns are similar to those found in the visual domain. Sternberg (1966, 1969) showed that the time it takes to decide whether a single item is being held in memory is a linear function of the number of items in memory. Again, this result was replicated using various stimuli types including words (Sternberg, 1969; Cavanagh, 1972; Fisk & Schneider, 1983, Juola & Atkinson, 1971). These studies all used variable mapping paradigms (Schneider & Shiffrin, 1977) in which targets and distractors change on every trial in an unpredictable manner (e.g. a target on one trial could appear as a distractor on the next). In consistent mapping tasks, in contrast, a particular stimulus will always appear as either a target or a distractor over a block of trials. In general, consistent mapping tasks produce much more efficient memory search slopes, in some cases completely eradicating set size effects (Schneider & Shiffrin, 1977; Fisk & Schneider, 1983). Other studies show consistent mapping causes decelerating, curvilinear functions of set size rather than the linear functions of variable mapping (Kristofferson, 1972; Monsell, 1978; McElree & Dosher, 1989; Ratcliff 1978; Donkin & Nosofosky 2012). Simpson (1972) found that mean reaction time was a linear function of the log of the memory set size in a consistent mapping memory recognition task with extended practice for Os. None of the work, mentioned above, used memory set sizes beyond 8 items. Investigating searches through large memory sets, Juola et al. (1971) and Atkinson and Juola (1973, 1974) found linear searches through sets ranging from 10 to 60 words.
Finally, imagine you are searching the entire list for the names of any one of those 20 students. This involves you bringing each of the students’ names into some form of working memory in order to compare it with each word or name in the list. This combination of visual and memory search is known as “hybrid search” (Schneider and Shiffrin, 1977). By combining multiple memory searches into a single trial, and therefore, a single RT, hybrid search can magnify small distinctions between set sizes that may otherwise be lost in a traditional recognition test. Moreover, the hybrid search paradigm allows us to separate out the effects of visual set size from those of memory set size and to look at their interaction. In earlier work with visual objects, Wolfe (2012) found that RT in hybrid search was a linear function of visual set size, as in other visual search tasks. However, Wolfe found that RTs increased with the log of the memory set size. As noted, Wolfe used photorealistic objects as stimuli. Stimuli of this sort have been used to replicate the logarithmic search through memory with a search through time rather than space (Drew & Wolfe, 2013). Moreover, the full hybrid search pattern applies to search through categories of objects, as well as to sets of specific objects (Cunningham & Wolfe, 2014). Leite and Ratcliff (2010) introduced a potentially useful version of a diffusion model to explain the logarithmically increasing response times (diagrammed in Figure 8). In the context of hybrid search, a diffuser is assigned to each member of the memory set. This diffuser accumulates evidence for the presence of its particular memory item as the trial progresses. If and when any of the diffusers cross a decision boundary then a response is given. Noise in the diffusion process might cause an incorrect diffuser to cross the decision bound, generating a false alarm error. More items in memory mean more diffusion processes and, thus a greater chance of such an error. Raising the decision boundary, and therefore requiring more information before committing to a decision, can reduce errors. Higher decision boundaries take longer to reach, increasing the RT. If Os attempt to hold error rates constant, decision boundaries and RTs must rise with memory set size. Leite and Ratcliff (2010) showed that the resulting RT x set size function will be logarithmic.
Figure 8.
Examples of a multiple-accumulator model of hybrid search. (A) With a memory set size of 2, two accumulators collect information. The accumulator corresponding to the target (green) reaches threshold and generates a hit. The other item accumulates noise. (B) Memory set size 3. Here, by chance, the target takes longer to reach threshold, generating a slower hit. (C) Memory set size 6. Here an accumulator reaches threshold by chance, generating a false alarm error. The chance of these errors grows with the number of accumulators so (D) at higher set sizes, the threshold is raised (see text for more details).
In the present paper, we ask if the pattern generalizes beyond objects to words. With small set sizes (1–4), combined memory and visual search through alphanumeric symbols, linear RT x memory set size functions have been reported (Briggs & Blaha, 1969; Burrows & Murdock, 1969; Nickerson, 1966; Schneider & Shiffrin, 1977), but the distinction between linear and logarithmic functions is not easy to detect with small set sizes.
Experiment 1 of the present paper replicates Wolfe’s findings using words rather than photorealistic objects as stimuli. Observers were asked to remember between 2 and 16 words and then to search for those amongst visual set sizes of 2 to 16 items. As in Wolfe (2012), RTs increased linearly with the visual set size and log-linear with the memory set size.
Words provide an opportunity to answer other questions about hybrid search that cannot be readily addressed with object stimuli. For example, up until this point the memorization process for all of the related studies has been the same. Observers are asked to memorize new and arbitrary sets of items at the start of a block of trials. With words it is possible to ask observers to search through previously memorized, familiar texts. These are highly ordered, structured, meaningful sets of stimuli that have long been engrained in the observer’s memory. Again, we can ask if the basic hybrid search results are found and, again, there are good reasons to think that these stimuli might produce a different pattern of results.
For example, it is possible an advantage might exist for targets at the beginning or end of an ordered list, mirroring the well-established primacy and recency effects (Glanzer & Cunitz, 1966). This U-shaped function has been found for lists stored in long-term memory up to a several weeks (Neath & Brown, 2006). Moreover, serial position has been shown as important predictor of recalled targets in coherent passages as well, (Deese & Kaufman, 1957; Rubin, 1977; Rubin 1978; Freebody & Anderson, 1981). Kelly, Neath & Surprenant (2012) found both primacy and recency effects in observers’ memory of cartoon theme song lyrics, the seven Harry Potter books, and two different sets of movies, all of which were thought to be recalled from semantic memory stores. Although, much of the work on serial position effects focuses on recall tasks, both early and late members of a list have shown response time benefits in recognition tasks as well (Monsell, 1978; McElree & Dosher, 1989).
In addition to serial position, the rated importance of a particular section in a passage also proves to be important for recall. Freebody and Anderson (1981) showed that the higher rating of the semantic importance of a particular subsection of a passage, the more likely it was to be recalled. Therefore, in an extension of this finding, we might expect to find RT benefits for words that are rated as more semantically important in a given passage.
To test these possibilities, we asked observers to provide four phrases of varying lengths that they felt confidant were firmly ensconced in their memory. Those words became the memory set in a hybrid search for any member of one of the target phrases amongst distractor words. Again, we replicate the pattern of a linear increase in RT with visual set size and logarithmic increase with memory set size. Interestingly, there was no reliable effect of serial position and almost no effect of the importance of the word in the phrase.
Experiment 1: Arbitrary Memory Sets
Observers
In Experiment 1, 10 observers, ages 18 to 48 were tested (mean age: 29.2, 4 females). Observers gave informed consent and were compensated $10 per hour. All observers had at least 20/25 vision with correction, passed the Ishihara Color Blindness Test, and were fluent speakers of English.
Methods
In Experiment One, observers searched displays of 2, 4, 8, & 16 words for targets drawn from memory sets of 2, 4, 8, or 16 items. Observers were seated so that their eyes were approximately 57.4 cm from a 20″ CRT monitor with an 85 Hz refresh rate. At a 57.4 cm viewing distance, 1 cm is equivalent to a visual angle of 1°. All experiments were written in MATLAB using the Psychophysics Toolbox (Brainard, 1997). Words were displayed in font size 40. Full height, letters were 1.3° tall. Words were presented on a gray background (LUM=51.8 cd/ms2). Words were chosen at random from the Touchstone Applied Science Associates (TASA) database (Zeno, 1995). Target words were chosen at random with the only constraint being they had to be at least 3 letters long. The distractors were chosen to match the targets in word length and frequency.
In each of four blocks, observers memorized 2, 4, 8 or 16 words. During the memorization task, target words were presented one at a time centrally on the screen for 3 seconds at a time. Next, observers were required to pass two recognition tests with 100% accuracy in order to proceed to the search portion of the block. For this learning portion of each block, observers saw a set of words, one at a time, and labeled them as “old” (i.e. part of their memory set) or “new” (distractors). Distractors made up 50% of the recognition test, therefore, in total observers saw twice as many words as the memory set size. If observers failed the test, they reviewed the target words again for 3 seconds each and then attempted the memory test again. Word order was randomized during all portions of the memorization block and distractors were always novel.
After completing the memory portion of the block, observers moved on to a series of 330 search trials: 30 practice trials and 300 experimental trials. During the search task observers saw displays with 2, 4, 8 or 16 printed words and were instructed to localize any one of their targets with a mouse click as quickly and accurately as possible. One random member from the target list was always present among an array of distractor words. The spatial locations of all the words in the display were randomly chosen with the only constraints being that words could not overlap with one another and the entire word fit in the display. After clicking on the target observers received correct/incorrect feedback before moving on to the next trial. Participants completed four blocks with memory set size pseudo-randomized. From start to finish the experiment lasted about 1.5 hours.
Results and Discussion
Results from the memory test showed that observers easily memorized the words (average accuracy of 97% over all possible tests). If observers were perfect in their memorization of their target words they would have to complete exactly two recognition tests before moving onto the search trials. On average, observers complete 3.3 recognition tests in Experiment 1. This strong grasp on the memory sets is further demonstrated by the low error rates (2%), which were not modulated by memory set size nor visual set size. Figure 2a shows the mean RT as a function of visual set size. As is typical in visual search experiments (e.g. Treisman, 1988) and as was seen in the basic Hybrid Search results, RTs increase linearly with visual set size. Larger memory set sizes produce steeper slopes of the RT x Visual Set Size functions (F(1.993,17.94)=11.16, p=.0007; using Greenhouse-Geisser correction), showing that when there are more target words in memory, the cost of adding a distractor to the visual display is higher.
Figure 2.
A) we can see that reaction times increase roughly linearly by visual set size and curvilinear (B) by memory set size. In figure B we can see predictions of memory set size 16 based off of memory set sizes 2–8, the logarithmic model does a noticeably better job of predicting the actual data. Note these graphs represent the same data simply replotted.
Figure 2b shows RTs as a function of memory set size. Note that these are the same data-points as in 2a, simply replotted. The functions appear to be curvilinear. Wolfe (2012) argued that RT was a linear function of log2(memory set size). One way to compare linear and log2 accounts of the data is to use the three smaller memory set sizes to predict the data for Set Size 16. This is shown in Figure 2b with linear predictions shown as Os and log2 predictions shown as Xs. The data and the log2 predictions are quite close (differences: visual set size 2: 31.7 ms, ss4: 77.8 ms, ss8: 87.5 ms, ss16:131.3 ms). The linear predictions overestimate the actual data, especially for the larger visual set sizes (differences: visual set size 2: 85.5 ms, ss4: 43.13 ms, ss8: 481 ms, ss16:691 ms). This illustrates one of the virtues of the hybrid search paradigm in comparison to a standard recognition task. Because Os need to search memory for each attended word, the larger the visual set size, the larger the number of memory searches that will contribute to the RT. This acts to magnify the differences between the predictions of linear and logarithmic processes. That is why the linear prediction is off by hundreds of msec at the largest set size. The absolute errors (the difference between the predicted RT and actual RT) are significantly smaller for logarithmic prediction at visual set sizes 2 and 16 (ts(9)>2.2, ps< .03), and are marginally smaller at set size 8. (t(9)=1.718, p=.0599).
Experiment 1 replicates the work of Wolfe (2012) in the lexical domain showing that the original result is not restricted to specific objects. Furthermore, by using the hybrid search paradigm, we can perhaps shed some light on memory search in a consistent mapping task through words. Since larger visual set sizes require multiple memory searches deviations from a linear model become more evident, this perhaps explains the difference in the present results from earlier work with small set sizes.
In the present experiment, observers had no trouble encoding random words, up to the maximum of 16. In Experiment One, the words in memory had no meaning or grammatical structure. Moreover, they were not presented and tested in any fixed order in the first part of the study. Accordingly, we could not assess the effects of word order including any analysis on serial position. Under normal circumstances, however, word order is important (at least, in English). In Experiment 2, we asked if the basic hybrid search result would change if we switched target sets from arbitrary lists of words, learned for the task, to structured lists of words, derived from well-learned text held in our observers’ long term memory.
Experiment 2: Familiar phrases as memory sets
Methods
In Experiment 2, 12 observers ages 19 to 48 (mean age: 27, 8 Females) were initially asked to select and enter into the computer four phrases that they knew very well. For three of the phrases, they were instructed to think of passages that, as closely as possible, contained 2, 8, and 16 words. For the fourth and final target set, we asked for the longest phrase that the observer had fully committed to memory. These largest set sizes ranged in length from 19 to 86 words with an average of 33.75 words. Participants were told that words less than 3 letters long and repeated words would not count towards their target list. Observers were also given a list of well-known phrases as suggestions (e.g. “Twinkle, Twinkle Little Star”, The US Pledge of Allegiance, etc.) but they were instructed not to simply pick “popular” phrases but rather to choose phrases that they were sure they knew well.
Observers were given a test of their memory for each phrase prior to the search portion of the experiment. Since these target sets were user inputted we expected the memory test not to cause many problems. However, in order to keep the two experiments as close as possible, as in Experiment 1, observers were shown target and distractor words and were asked to make an “old” (part of the phrase) or “new” (distractor) response to each word. Half of the words were target words. We lowered the threshold from Experiment One so the experiment was not delayed due to motor errors, observers had to score 90% or higher twice in a row in order to pass this memory test. In other respects, the methods for Experiment 2 were the same as those for Experiment 1.
Results and Discussion
Unsurprisingly, observers had little difficulty with the memory portion of the experiment, scoring an average of 98.2%. Figure 3 shows the data for all observers with the slope of the RT x visual set size function plotted as function of the memory set size. This slope represents the cost of each additional visual item as a function of how many items are held in memory. The functions would be linear on the log axis of Figure 3 if the results replicated the logarithmic relationship of RT to memory set size seen in Wolfe (2012) and in Experiment 1.
Figure 3.
Slope of the visual set size function as a function of memory set size. Each line represents one observer. The slope represents the cost of each additional visual item as a function of how many items are held in memory. Note that the x-axis is logarithmic scaled.
In fact, because of the variety of memory set sizes and because of variability of individual observer’s data, it is difficult to see the relationship in the individual observer data. Accordingly, in order to pool data for purposes of analysis, the memory set sizes were binned into four distinct groups: short, medium, long, and extra long. All short memory sets were 2 words long. The medium bin consisted of phrases between 4–11 words (average - 7.2 words), the long bin 12–19 words (average - 15.3 words), and the extra long group consisted of phrases of longer than 19 words (average 35.0 words). Using these criteria all but one observer was tested on one phrase per memory group (The longest phrase for that observer was merely “long”, not “extra long”.).
Results are shown in Figure 4.
Figure 4.
RT as a function of visual set size (A) and binned memory set size (B). Error bars, where visible, are +/− 1 s.e.m.
Even though it is a bit problematic to average across multiple set sizes, it is clear that the basic pattern of results in Experiment Two mirrors that from Experiment One; a linear effect of visual set size and a log-linear effect of memory set size. Rather than using the average data from low set sizes to predict the results for the largest set size, as in Figure 2b, in Figure 5a, the three lower set sizes are used to predict the largest set size result for each observer at each visual set size. It is important to note that for Figure 5 we are using observers actual memory set sizes rather than the binned averages from Figure 4. Solid purple symbols show linear predictions, outlined green symbols show log2 predictions. If the prediction matches the data, the datapoint would lie on the diagonal of the graph plotting predicted against real RT. The graph omits 28 data points greater than 4000 msec in order to make the shorter RTs visible. However, the regression lines are based on all data from all participants. It is clear that the linear model (purple) predicts RTs that are longer that the actual RTs while the log2 model (green) predicts RTs that are, on average, closer to the measured RTs for the largest set sizes, though the data are noisy. Figure 5b replots these data as the differences between the predicted and actual RTs. It is evident that the error is much larger for the linear (purple) than for the logarithmic (green) predictions (F(1,11)=9.751, p=.0097), this is especially true for the larger visual set sizes.
Figure 5.
A) Actual RTs for the largest memory set sizes in Exp 2 vs RTs predicted by linear regression from the smaller memory set sizes. Purple points are linear prediction. Green points are Log predictions. The log2 predictions lie closer to the zero-error line (dashed black). The regression lines from the linear and log prediction are in purple and green respectively B) The error data (predicted RT-Actual RT) are plotted for each subject with the linear predictions again in purple and the log predictions in green. Clearly, the log predictions are more accurate.
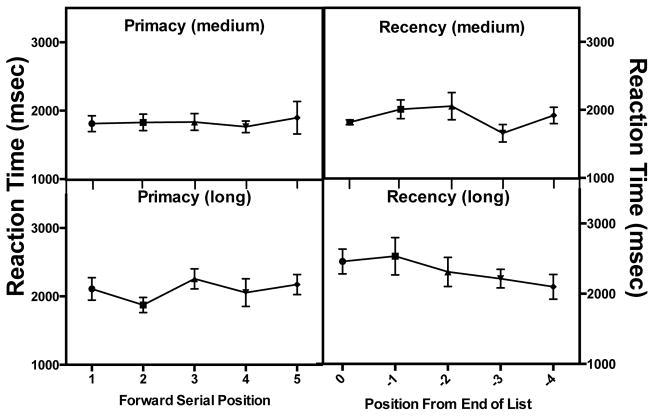
One may suspect the use of highly ordered memorized phrases like “Mary had a little lamb” could produce serial position effects. However, this proves not to be the case. Figure 6 shows average RTs as a function of position relative to the beginning of the phrase (left column) and relative to the end (right column) for the medium and long phrases. Short, 2-item phrases are uninteresting for these purposes. To test for primacy and recency effects, we compared RTs of either the first five words (primacy) or the last 5 words (recency) using a one-way ANOVA in the medium, long, and extra long phrases1. There was no significant difference in RT between the first word and the next four words (medium: F(4,43)=.099, p=.98; long: F(4,45)=.97, p=.43) showing no evidence for a primacy effect, nor was there a difference between the last word and the previous four words (medium: F(4,31)=1.16 p=.345; long: F(4, 36)=.82; p=.51). The results for extra long phrases are noisy and are not plotted but they also do not show effects (primacy: F(4, 33)=1.6, p=.19 recency: F(4, 22)=.74, p=.57. A two-way analysis of variance with phrase length and serial position as factors shows there is no overall effect of serial position (primacy: F(4,120)=2.33, p=.06; recency: F(4,124)=.80, p=.50).
Figure 6.
No evidence for serial position effects in hybrid search for words drawn from well-known phrases. Neither the first nor the last word in a phrase is reported more quickly than neighboring words.
Although serial order does not seem have a significant effect on response times, it might be that some word or words in a phrase are privileged in activated long-term memory (the supposed store for memory set items in hybrid search; Cowan, 1995; Drew & Wolfe, 2013; Cunningham & Wolfe, 2014), in a way that would affect RT. For instance, one may expect words that are more semantically salient to be accessed more quickly (e.g. “America” might be found faster than “under” in the US Pledge of Allegiance). We asked 8 new observers to rate each word of each phrase used in Experiment Two on a semantic salience scale from 1 to 5. Observers were asked how strongly a particular word “contributes to the overall meaning of the phrase” where 1 indicated no contribution and 5 indicates a strong contribution. They were instructed not to consider words that contributed to the grammar or structure of a phrase but rather words that were necessary to understand the feeling of the phrase. With these ratings in mind we looked for a negative correlation between the higher ratings (i.e. more semantically relevant words) and the RT.
Figure 7 shows that the relationship between how important a particular target word is to the meaning of the phrase and the response times are weak (Medium: r=− .002, p=.8819; Long r=.007, p=.6348; Extra-Long: r=−.067 p<.0001). There is no correlation for the shorter phrases though a small but significant relationship does emerge for the Extra-Long Set Sizes. This may indicate that the semantically relevant words only gain an advantage once there is a substantial memory load. It is the weakness of the effect, along with the absence of serial position effects that indicates, for purposes of hybrid search, there is no clear advantage for any member of the target set on the basis of serial position or semantic relevance.
Figure 7.
Individual target words were rated on a scale of 1 to 5 on how strongly they contribute to the overall meaning of the phrase. There are no strong correlations between a word’s rating and the response time, however with the extra long memory set this correlation is significant.
Admittedly, the conditions of the current study are not ideal for finding serial position effects. In a replication of Sternberg (1966), Donkin & Nosofsky (2012) show that serial position curves tend to flatten during recognition tests with enough time for rehearsal. Furthermore, since the phrases used in Experiment 2 are so well known they may be stored as a single unit of information and can therefore be retrieved as such. This would suggest that arbitrary words presented in a specific order (e.g. in a list) are more likely to show primacy and recency effects. However, the goal of this experiment was to investigate the efficiency of memory search in well-known phrases. The lack of serial position effects is in fact consistent with an efficient logarithmic search through the items in the memory with little or no effect of serial position or significance of the words.
General Discussion
The apparently logarithmic increases in memory set size found in both Experiments 1 and 2, accompanied with the failure to find primacy or recency effects in Experiment 2 suggest that hybrid search is not performed by a serial search through the memory set. The added attribute of large visual set sizes, which is not found in the earlier memory search literature, allows us to more easily distinguish logarithmic from linear increases in reaction time as a function of memory set size. It is also clear, that Wolfe 2012’s findings are not restricted to photorealistic objects that are easier to memorize than words (Gehring, Toglia, & Kimble, 1976) and easier to find (Paivio & Begg, 1974) than words.
The memory searches required to complete a hybrid search task may be viewed as multiple-alternative decisions akin to those that produce Hick’s Law behavior in motor RT tasks. In those tasks, the time required to chose between N response keys rises with k(log2(N)) (Hick, 1952; Hyman, 1953). Similarly, the time required to decide if a word in a visual display is one of N words in a list or phrase rises with k(log2(N)). As discussed in the introduction, Leite and Ratcliff (2010) provide one potential model for such a pattern of reaction times. Figure 8 shows a cartooned version of that model in the context of hybrid search. Recognition of each of the potential memory items can be modeled as a diffusion process or accumulator, with a target present response generated when one of those accumulators reaches a decision bound (8a, b). With even small amounts of noise in the system it is intuitively clear that the chance of reaching a boundary by mistake and, thus, generating a false alarm, will increase as the number of items in the memory set grows (8c). Raising the bound to reduce these errors increases the RTs (8d). The bound needed to hold errors roughly constant produces RTs that increase linearly with log2 of the number of diffusors.
Alternatively, Nosofosky et al (2014) propose a model, which also accounts for logarithmic response times in memory search. Similar to Leite & Ratcliff, items are racing to a decision boundary. However, in the Nosofsky version, these memory templates are not affected by the size of the memory set but rather dictated by their “memory strength” or the time in which they were presented last.
The present results show that this pattern of results holds for words, including words in ordered phrases, in a manner that is qualitatively similar to the results seen with specific objects. Hybrid search for words in the present experiments is substantially slower than hybrid search for objects in Wolfe (2012). For instance, in Experiment 1, 3500 msec are required to find the target when memory set size and visual set size are both 16. In the comparable experiment of Wolfe (2012), the RT is 2700 msec. Not too much should be made about differences between experiments. The most obvious source of difference is that word reading probably requires fixation on each item while object recognition does not. What is important is that the pattern of log memory search and linear visual search is a general phenomenon.
Figure 1.
Observers were first asked to memorize between 2 and 16 words. These words were presented centrally one at a time for 3 seconds each. After memorization, observers had to complete an old/new recognition test at 100% accuracy before moving on to the search trials. All words used in this figure are actual words pulled from the experiment.
Footnotes
This analysis was repeated for varying groupings including memory sets between 6 and 9 words long (primacy: F(4,35)=.1249, p=.97, recency: (F(4,36)=1.384, p=.259) as well as memory sets between 18 and 24 (primacy: F(4,23)=.893, p=.48, recency F(4,19)=2.631, p=.07). No reliable effects of primacy or recency were found.
References
- Atkinson RC, Juola JF. Factors influencing speed and accuracy of word recognition. In: Kornblum S, editor. Attention and Performance IV. New York: Academic Press; 1973. [Google Scholar]
- Atkinson RC, Juola JF. Search and decision processes in recognition memory. In: Krantz D, Atkinson R, Luce R, Suppes P, editors. Contemporary Developments in Mathematical Psychology. Vol. 1. San Francisco: W.H. Freeman; 1974. [Google Scholar]
- Brady TF, Konkle T, Alvarez GA, Oliva A. Visual long-term memory has a massive storage capacity for object details. Procedings of the National Academy of Sciences. 2008;105(38):14325–14329. doi: 10.1073/pnas.0803390105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Briggs GE, Blaha J. Memory retrieval and central comparison times in information processing. Journal of Experimental Psychology. 1969;79(3 Pt 1):395–402. [Google Scholar]
- Burrows D, Murdock BB., Jr Effects of extended practice on high-speed scanning. Journal of Experimental Psychology. 1969;82(2):231–237. doi: 10.1037/h0028145. [DOI] [Google Scholar]
- Cavanagh JP. Relation between the immediate memory span and the memory search rate. Psychological Review. 1972;79:525–530. [Google Scholar]
- Cowan N. Attention and memory: An integrated framework. New York: Oxford University Press; 1995. [Google Scholar]
- Cunningham CA, Wolfe JM. The role of object categories in hybrid visual and memory search. Journal of Experimental Psychology: General. 2014 doi: 10.1037/a0036313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deese J, Kaufman RA. Serial effects of unorganized and sequentially organized verbal material. Journal of Experimental Psychology. 1957;54:180–187. doi: 10.1037/h0040536. [DOI] [PubMed] [Google Scholar]
- Donkin C, Nosofsky RM. The structure of short-term memory scanning: an investigation using response time distributions. Psychonomic Bulletin Review. 2012;19:363–394. doi: 10.3758/s13423-012-0236-8. [DOI] [PubMed] [Google Scholar]
- Drew, Wolfe Hybrid search in the temporal domain: Evidence for rapid, serial logarithmic search through memory. Attention, Perception and Psychophysics. 2013;76(2):296–303. doi: 10.3758/s13414-013-0606-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisk AD, Schneider W. Category and word search: generalizing search principles to complex processing. Journal of experimental psychology. Learning, memory, and cognition. 1983;9(2):177–95. doi: 10.1037//0278-7393.9.2.177. [DOI] [PubMed] [Google Scholar]
- Freebody P, Anderson RC. Serial position and rated importance in the recall of text. Champaign, Ill: University of Illinoise at Urbana-Champaign; 1981. [Google Scholar]
- Gehring RE, Toglis MP, Kimble GA. Recognition memory for words and pictures at short and long retention intervals. Memory Cognition. 1976;4(3):256–260. doi: 10.3758/BF03213172. [DOI] [PubMed] [Google Scholar]
- Glanzer M, Cunitz AR. Two storage mechanisms in free recall. Journal of Verbal Learning and Behavior. 1966;5:351–360. [Google Scholar]
- Hick WE. On the rate of gain of information. Quarterly Journal of Experimental Psychology. 1952;4:11–26. [Google Scholar]
- Hyman R. Stimulus information as a determinant of reaction time. Journal of Experimental Psychology. 1953;45(3):188–196. doi: 10.1037/h0056940. [DOI] [PubMed] [Google Scholar]
- Juola JF, Atkinson RC. Memory Scanning for Words Versus Categories. Journal of Verbal Learning and Verbal Behavior. 1971;10:522–527. [Google Scholar]
- Juola JF, Fischler I, Wood CT, Atkinson RC. Recognition time for information stored in long-term memory. Perception & Psychophysics. 1971;10(8) [Google Scholar]
- Kelley MR, Neath I, Surprenant AM. Three more semantic serial position functions and a SIMPLE explanation. Memory Cognition. 2012;41:600–610. doi: 10.3758/s13421-012-0286-1. [DOI] [PubMed] [Google Scholar]
- Kristofferson MW. When item recognition and visual search functions are similar. Perception & Psychophysics. 1972;12(4):379–384. [Google Scholar]
- Leite FP, Ratcliff R. Modeling reaction time and accuracy of multiple-alternative decisions. Attention, Perception, & Psychophysics. 2010;72(1):246–273. doi: 10.3758/APP.72.1.246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElree B, Dosher BA. Serial position and set size in short-term memory: The time course of recognition. Journal of Experimental Psychology: General. 1989;118:346–373. [Google Scholar]
- Monsell S. Recency, immediate recognition memory, and reaction time. Cognitive Psychology. 1978;10:465–501. [Google Scholar]
- Neath I, Brown GDA. SIMPLE: Further applications of a local distinctiveness model of memory. In: Ross BH, editor. The psychology of learning and motivation. 2006. pp. 201–243. [Google Scholar]
- Nickerson RS. Response times with a memory-dependent decision task. Journal of Experimental Psychology. 1966;72(5):761–769. doi: 10.1037/h0023788. [DOI] [PubMed] [Google Scholar]
- Paivio A, Begg I. Pictures and words in visual search. Memory and Cognition. 2:515–521. doi: 10.3758/BF03196914. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85(2):59–108. [Google Scholar]
- Rubin DC. Very long-term memory for prose and verse. Journal of Verbal Learning and Verbal Behavior. 1977;16:611–621. [Google Scholar]
- Rubin DC. A unit analysis of prose memory. Journal of Verbal Learning & Verbal Behavior. 1978;17:599–620. [Google Scholar]
- Schneider W, Shiffrin RM. Controlled and automatic human information processing: 1. Detection, search, and attention. Psychological Review. 1977;84:1–66. [Google Scholar]
- Simpson PJ. High-Speed memory scanning; Stability and generality. Journal of Experimental Psychology. 1972;96(2):240–246. doi: 10.1037/h0033672. [DOI] [PubMed] [Google Scholar]
- Sternberg S. High-speed scanning in human memory. Science. 1966;153:652–654. doi: 10.1126/science.153.3736.652. [DOI] [PubMed] [Google Scholar]
- Sternberg S. Memory-Scanning: Mental processes revealed by reaction-time experiments. American Scientists. 1969;57(4):421–457. [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12(1):97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Wolfe JM. Guided Search 2.0: A Revised Model of Visual Search. Psychonomic Bulletin & Review. 1994;1(2):202–238. doi: 10.3758/BF03200774. [DOI] [PubMed] [Google Scholar]
- Wolfe JM. Guided Search 4.0: Current Progress with a model of visual search. In: Gray W, editor. Integrated Models of Cognitive Systems. New York: Oxford; 2007. pp. 99–119. [Google Scholar]
- Wolfe JM. Saved by a log: how do humans perform hybrid visual and memory search? Psychological Science. 2012;23(7):698–703. doi: 10.1177/0956797612443968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeno SM. The Educator’s Word Frequency Guide. Touchstone Applied Science Associates (T A S A), Incorporated; 1995. [Google Scholar]