Examination of a lumbar spine biomechanical model for assessing axial compression, shear, and bending moment using selected Olympic lifts

Abstract

Background/Aims

Loading during concurrent bending and compression associated with deadlift, hang clean and hang snatch lifts carries the potential for injury to the intervertebral discs, muscles and ligaments. This study examined the capacity of a newly developed spinal model to compute shear and compressive forces, and bending moments in lumbar spine for each lift.

Methods

Five male subjects participated in the study. The spine was modeled as a chain of rigid bodies (vertebrae) connected via the intervertebral discs. Each vertebral reference frame was centered in the center of mass of the vertebral body, and its principal directions were axial, anterior-posterior, and medial-lateral.

Results

The results demonstrated the capacity of this spinal model to assess forces and bending moments at and about the lumbar vertebrae by showing the variations among these variables with different lifting techniques.

Conclusion

These results show the model's potential as a diagnostic tool.

1. Introduction

The hang snatch and hang clean are variations of two Olympic lifts, the snatch and the clean-and-jerk, commonly used as conditioning exercises by strength and conditioning coaches. Similarly, the deadlift, one of three lifts used in powerlifting competitions, is commonly incorporated into athletes' strength training programs. Loads used during the Olympic lifts are usually designed to maximize power development and varied due to training cycle, performance level and training goal.1, 2, 3, 4 Additionally, these lifts are used in varying forms as assessment tools following training interventions,⁵ in descriptive studies2, 6, 7, 8, 9 and as indicators of athletic performance.10, 11

Variations in lifting technique, load, or environment can dramatically change kinematics and muscle utilization patterns during these lifts. For the deadlift exercise differences in form,12, 13 bar utilization,¹⁴ type of contraction,¹⁵ load,¹⁶ base stability,² and lifting experience¹⁷ have been shown to affect power output, as well as kinetic and kinematic variables. This information is more difficult to find for the hang clean and hang snatch, but is available for the power clean, the snatch and their variations. For example, while no differences in peak power, peak vertical force or rate of force development were seen due to variations in the power clean (power clean, hang power clean, midthigh power clean) in a study incorporating young female athletes¹⁸; differences in these variables were detected between these three variations in elite male rugby players.¹⁹ Additionally, load changes have been shown to affect kinematics and kinetics in experienced lifters during the midthigh clean pull.1, 20 The impact of loading has also been established for power output during the power clean.3, 10, 21 Further, kinetic differences have been reported between free weight and machine lifts²² and differences in kinetics, including peak force, peak velocity and power, have been noted among the hang clean, jump shrug and high pull exercise, with these differences varying due to load changes (30%–80% 1RM).²³ Finally, ground reaction forces and segmental forces can be expected to vary among the hang clean, hang snatch and deadlift and within different phases of each lift. For example, in an analysis of ground reaction forces during different phases of the power clean, Souza et al,²⁴ found that greater peak force occurred during the second pull compared to the first pull and unweighted phases of the lift whether performed at 60 or 70%1RM.

For the snatch, kinematic analyses have been performed demonstrating differences in both spatial and temporal variables among competitive lifters in different weight classes²⁵ and of different genders26, 27 and in kinetics due to gender.²⁸ As was the case with the deadlift and power clean, variations in kinematics were also seen with different loading patterns during the snatch²⁹ and for younger, compared to older, competitors.²⁶ Of special interest to the present study was the use of a three-dimensional finite element model by Bao and Meng³⁰ to assess the stresses on the vertebral body, facet joint, pedicle of the vertebral arch and intervertebral disc at L₁–L₂ during performance of the snatch.

To date, information on spine biomechanics during weightlifting is limited.17, 30, 31 Hence, the purpose of this study was to validate a biomechanical model designed to quantify the moments and forces on the lumbar spine during the performance of the deadlift, hang clean, and hang snatch. This was done using comparisons to the limited number of studies that employed spinal models during the performance of these lifts, demonstrating changes in forces and moments among the lifts, and comparing patterns of change to kinematic and kinetic variables reported during the deadlift, hang clean and hang snatch. The model was based solely on standard motion capturing data, and was capable of estimating spinal segments kinematics and loads. The process included two steps. First, the new biomechanical framework was validated by comparing its spine kinematics estimates with data from a continuous spine motion analysis previously reported.32, 33 Next, the model was directly applied for mapping mechanical loads on lumbar spine during the performances of the deadlift, hang clean, and hang snatch.

2. Methods

2.1. Spine biomechanical model

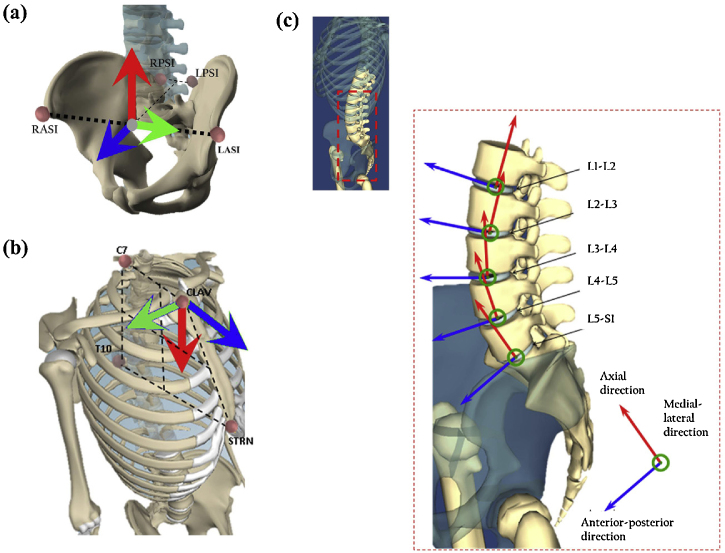
In this model, the lumbar spine was modeled as a chain of rigid bodies (vertebrae) connected to each other via the intervertebral discs. The movement of the spine was driven by the relative motion between the pelvis and thorax, which was computed via a motion capture system. The location and the orientation of the pelvis was computed by tracking four stereotactic markers applied on both anterior (left anterior superior iliac spine, and right anterior superior iliac spine) and posterior (left posterior superior iliac spine, and right posterior superior iliac spine) aspects of the ilium. The pelvic coordinate frame was centered in the midpoint between the two anterior superior iliac spine (ASIS) markers. The principal directions were axial, medial-lateral (line passing through the ASIS), and anterior-posterior (line orthogonal to the medial-lateral and lying on the plane individuated by the ASIS and PSIS; see Fig. 1a). The thorax was discriminated by four other markers located at the midpoint of the two clavicles (CLAV), on the sternum directly above the solar plexus (STRN), on the superior spinal process of the thoracic vertebra T10 (T10), and on the superior spinal process of the cervical vertebra C7 (C7). The origin of its reference frame was at the CLAV. The axes of the reference frame were: a line passing through C7 and CLAV (anterior-posterior direction), orthogonal to the plane defined by C7, CLAV, STRN, and T10 (in the medial-lateral direction), and a line passing through C7 and T10 (in the axial direction) (see Fig. 1b).

Fig. 1.

The static trial and the definition of the lumbar spine.

The spine tract was composed of three-dimensional linked segments representative of the five lumbar vertebrae and the thoracic vertebrae T12, T11, and T10. All vertebrae were treated as rigid bodies. In the neutral configuration (body fully erect with no axial rotation and no loads applied) the spinal vertebrae lay equally spaced on a cubic spline connecting the pelvis with the thorax. The local coordinate frame of each vertebra had its center in the center of mass of that vertebra; the axial direction laid on the sagittal plane, and was tangential to the spine curvature; the anterior-posterior direction also lay in the sagittal plane, but was orthogonal to the tangent of the spine curvature; and, the medial-lateral direction was orthogonal to the axial and anterior-posterior directions (see Fig. 1c). Equivalent intervertebral disc representations with multidimensional translational stiffness connected the lumbar vertebrae to each other, to the pelvis, and to the thorax, providing both translational and rotational freedom in all three axes. Disc stiffness was set to values previously reported.34, 35

Therefore, the criteria for a lumbar model with individual vertebrae having relative movements were the translation and rotation of each individual vertebral body. In addition, it was important to ensure that the curvature of the spine was consistent with the 3rd order spline.

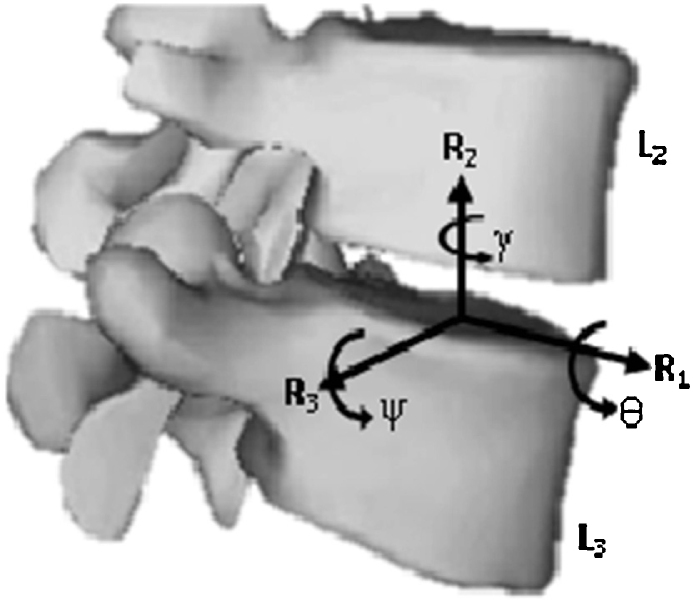
For the lumbar spine, the motion of a vertebra was defined relative to the vertebra below it. This started with the L5 relative to a fixed sacrum (S1), and moved progressively up the spine to L1. The function of each intervertebral disc was to allow 6 degrees of freedom of movement between the vertebrae and to transmit the load from one rigid body to the other. Fig. 2 provides a representation of the axes of transformation and rotation between the L₂ and L₃ vertebrae.

Fig. 2.

The coordinate system for relative motion at L₃/L_4.

To implement the spinal motion within the model, it was necessary to limit the entire system to only 3 coordinates: flexion-extension (ψ about R3), axial rotation (θ about R2), and lateral bending (γ about R1) defined as the angle between the thorax and the sacrum. At each vertebral level, it was necessary to specify the masses and moments of inertia. These values were determined from an extensive examination by Pearsall et al³⁶ using MR imaging.

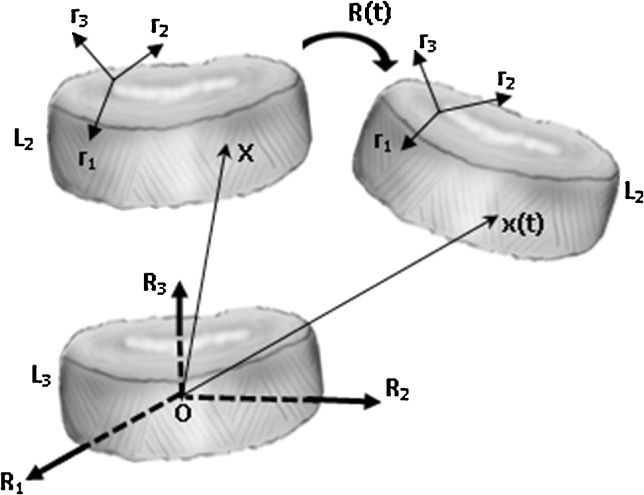
Fig. 3 defines a child body (vertebra) relative to its parent body (vertebra) about which the transformation occurs. As shown in Fig. 3, the child body can also be defined by a vector X in its initial fixed state, and by a vector X on the co-rotational basis in its transformed state. A fixed parent vertebra is located relative to the ground origin O by X. The child vertebra L₂ is able to spatially transform about the axes of rotation. The center of mass and inertia of each body are defined with respect to their body-fixed frames. This figure also displays the co-rotational bases {r1, r2, r3}.

Fig. 3.

Schematic of two rigid bodies: L3, fixed, and L2, moving relative to L3.

The lumbar spine is defined in the static trial (T-Pose) as shown in Fig. 4; Inverse Kinematics is then applied to converting marker data from the motion capture system to actual coordinate values as a function of time. The Inverse Dynamics system is designed to receive a motion file, which fully defines each joint coordinate as a function of time, and uses algorithms to determine the forces and torques needed to create such a motion.37, 38

Fig. 4.

Coordinate frames of the spine biomechanical model. (a) The pelvic segment is defined by the left anterior superior iliac spine (LASI), the right anterior superior iliac spine (RASI), the left posterior superior iliac spine (LPSI), and the right posterior superior iliac spine (RPSI). The principal directions are axial (red arrow), medial-lateral (green arrow), and anterior-posterior (blue arrow). The position and scale of the pelvis is determined by RASI and LASI markers, since they determine the origin of the coronal orientation of the pelvis. The LPSI and RPSI markers determine the anterior tilt of the pelvis. (b) The thoracic segment is defined by C7, CLAV, STRN, and T10 markers. Its origin is in CLAV, and its principal directions are axial (red arrow), anterior-posterior (blue arrow), and medial-lateral (green arrow). (c) The spine model includes thoracic vertebrae (from T10 to T12), all the lumbar vertebrae, and the sacrum. Each vertebral reference frame is centered in the center of mass of the vertebral body, and its principal directions are axial (red arrow), anterior-posterior (blue arrow), and medial-lateral (green arrow).

2.2. Subjects

The procedures and methods used in this study were approved by the Internal Review Board of the University of Miami. All participants in the study were informed of the purpose and experimental procedures and provided written consent prior to beginning the experiment. A total of five healthy male subjects, aged between 21 and 23 years of age, were recruited from students attending a strength and conditioning course at the University of Miami. None of the participants reported any current or prior history of low back pain, or any medical conditions potentially affecting normal physiological spine kinematics. They all had weightlifting experience. Moreover, each participant was instructed on proper performance of each lift before testing, and on the day of testing was coached by experienced strength training personnel regarding the proper technique to be used when executing each lift. Data were not collected until the participant had sufficient practice, felt comfortable performing the exercise, and was able to complete the lift using proper technique.

2.3. Experimental setup and spine kinematics measurements

Spine kinematics and loads were evaluated via a ViconNexus^® Motion Capturing System (Vicon Motion Systems, Inc, Oxford, England) integrating ten MCam cameras (Vicon Motion Systems, Inc, Oxford, England) and four Kistler force plates (Kistler Instrument AG, Winterthur, Switzerland). Thirty-nine reflective markers were placed on subjects according to Vicon's Plug-In Gait Model. Kinematic data and ground reaction forces were collected and processed with Vicon's Plug-In Gait Model algorithms39, 40, 41 and were enhanced by a BodyBuilder^® (Vicon Motion Systems, Inc, Oxford, England) plug-in based on the spine biomechanical model described above. Data post-processing yielded the kinematics of the spine segments, together with the forces and the moments acting on all the vertebrae from S1 to T10.

2.3.1. Model validation

As part of the model validation process, subjects were asked to bend forward and backward (flexion-extension) at a comfortable speed, with no restriction on their pelvic motion; however, they were instructed not to bend their knees, and to keep their feet in full contact with the ground for the entire duration of the task. Although subjects performed flexion-extension over their full range of motion, for the purpose of consistency in the data analysis, the spine range of motion considered in this study varied from 40° (flexion) to −10° (extension). Two trials were used during data analysis for each subject. The spine biomechanical model was designed to yield the relative rotation in the sagittal plane between the L1–L2, L2–L3, L3–L4, L4–L5, and L5–S1 vertebrae. For model validation purposes, the results were compared with those reported in previous studies.32, 33

2.3.2. Spine loads during weightlifting

Subjects were asked to perform the deadlift, hang clean, and hang snatch exercises. More specifically, while performing deadlift, subjects initially positioned their feet flat beneath the bar, and squatted down; subsequently, they lifted the bar by bringing their hips and knees to full extension while keeping their arms fully extended and their back flat. The deadlift cycle was divided into two phases. The first was from the beginning of the lift until the bar reached a position just below the subject's knees (hang position). The second started from the hang position and continued to the completion of the lift. For the hang clean, subjects started from a hang position and jumped upward to completely extend their body (second pull); subsequently, they rotated the elbows around the bar to allow it to rest on their clavicles and deltoids (catch). The hang clean cycle was also divided into two phases. The first stage was from the hang position to the end of the second pull; while the second stage lasted until the end of the catch. In executing the hang snatch, subjects moved from a hang position through the second pull. Subsequently, they positioned their body under the bar, in a partial squat position with their arms extended (catch position). Finally, subjects returned to an erect standing position keeping the bar over the head (recovery). The hang snatch cycle was divided into three phases: the first from the hang position to the end of the second pull, the second phase lasted until the end of the catch, and the third lasted until the end of the recovery. A graphical representation of these tasks, together with their phases, is provided in Fig. 5. For each exercise, subjects lifted weights corresponding to approximately 75% of their 1-repetition maximum (see Table 1). For the purpose of data analysis, two trials were used for each exercise and for each subject. Data were normalized using the sum of each subject's body weight and the weight lifted, and averaged. Parameters evaluated included forces (axial compression and anterior-posterior shear) and moments (bending moment in sagittal plane) acting on the L1, L2, L3, L4, and L5 vertebrae. Data were reported in terms of normative curves over the weightlifting cycles with amplitude equal to ±1 standard deviation.

Fig. 5.

Weightlifting exercise performed in the study. Deadlift: (a) starting position; (b) hang position; (c) recovery. Hang power clean: (d) hang position; (e) second pull; (f) starting catch; (g) end of catch (recovery). Hang power snatch: (h) hang position; (i) second pull; (j) catch; (k) recovery.

Table 1.

Subjects' anthropometric data and weights lifted during tasks. Sample results are mean ± SD.

Subject#	Age	Height (m)	Weight (kg)	Deadlift weight (kg)	Clean weight (kg)	Snatch weight (kg)
1	22	1.84	114	89	47	30
2	23	1.71	76	89	56	38
3	21	1.70	68	59	31	21
4	22	1.96	118	142	86	59
5	22	1.83	91	156	61	46
Sample	22.0 ± 0.7	1.81 ± 0.11	93.4 ± 22.3	107.0 ± 40.6	56.2 ± 20.2	38.8 ± 14.6

3. Results

Results are reported for both the validation of the model and the characterization of spinal loads during lifting. Due to page limitations, spine loads are reported in Table 2 in terms of peak values for all vertebrae, while normative curves are only reported for the L1 and L5 vertebrae.

Table 2.

Peak values of axial compression (AC), shear force (SF), and bending moment (BM) during the lifting cycle. Data are mean ± SD.

AC (N)			SF (N)	BM (Nm)
Deadlift
L1	6488 ± 2494		1341 ± 530	685 ± 352
L2	7057 ± 2584		1220 ± 651	732 ± 398
L3	7447 ± 2620		1439 ± 711	747 ± 388
L4	7724 ± 2696		1656 ± 845	740 ± 356
L5	7963 ± 2784		1903 ± 936	734 ± 331
Clean
L1	8436 ± 3766		1900 ± 1313	1935 ± 1947
L2	8473 ± 3592		1906 ± 1309	1859 ± 1768
L3	8505 ± 3451		2153 ± 1349	1832 ± 1694
L4	8605 ± 3325		2438 ± 1598	1806 ± 1600
L5	8701 ± 3263		2652 ± 1882	1731 ± 1410
Snatch
L1		5085 ± 1278	2810 ± 2409	1439 ± 1189
L2		5433 ± 1415	2590 ± 2137	1382 ± 1080
L3		5706 ± 1516	2317 ± 1809	1304 ± 964
L4		5965 ± 1624	2083 ± 1543	1244 ± 870
L5		6224 ± 1753	1923 ± 1358	1208 ± 809

3.1. Validation

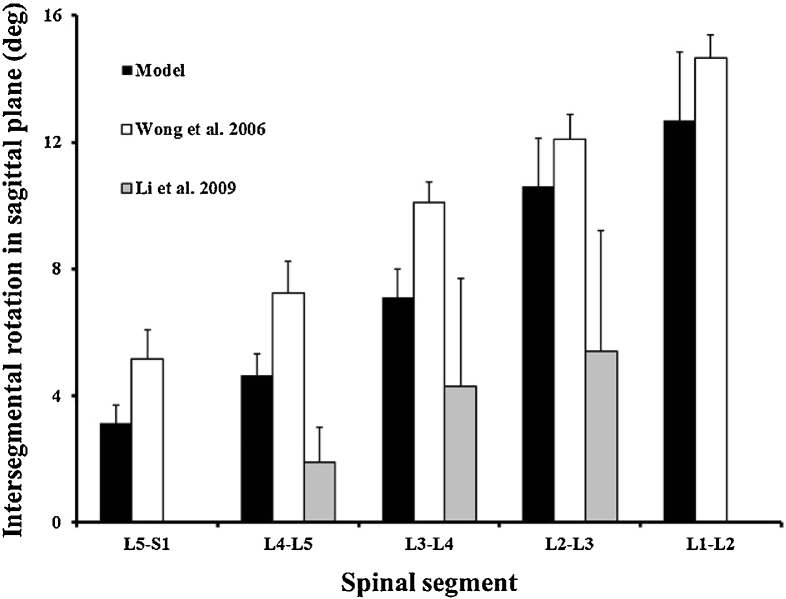
The lumbar spine intersegmental rotations in the sagittal plane during flexion-extension estimated by the biomechanical model are reported in Fig. 6 and compared to previous experimental studies.32, 33 For the studies by Wong et al³² and Li et al³³ our results follow the same pattern across segments, with increased rotation in the sagittal plane from L5–S1 through L1-L2. In contrast, Pearcy et al⁴² reported a parabolic relationship with L1–L2 and L5-S1 showing the lowest flexion and L4-L5 showing the greatest. Results reported by Adams and Hutton⁴³ also differed from ours showing a nearly linear relationship among spinal segments for subjects between 15 and 29 years of age. In a fluoroscopy study by Cholewicki and McGill⁴⁴ the pattern was in direct opposition to our results showing values of 5.3°, 8.9°, and 11.5° for L2–L3, L3–L4 and L4–L5, respectively. For all the spine segments investigated, the model estimated that ranges of motion for sagittal rotations were always smaller than those reported by Wong and co-workers,³² and larger than those found by Li et al.³³ Our model also showed a greater range of values among the L5–S1 through L1–L2 segments than either Pearcy et al⁴² or Adams and Hutton.⁴³

Fig. 6.

Lumbar spine intersegmental rotation in the sagittal plane following unconstrained flexion-extension motion. Model estimates (black) are compared to experimental measurements previously reported by Wong et al³² (white) and Li et al³³ (gray).

3.2. Deadlift

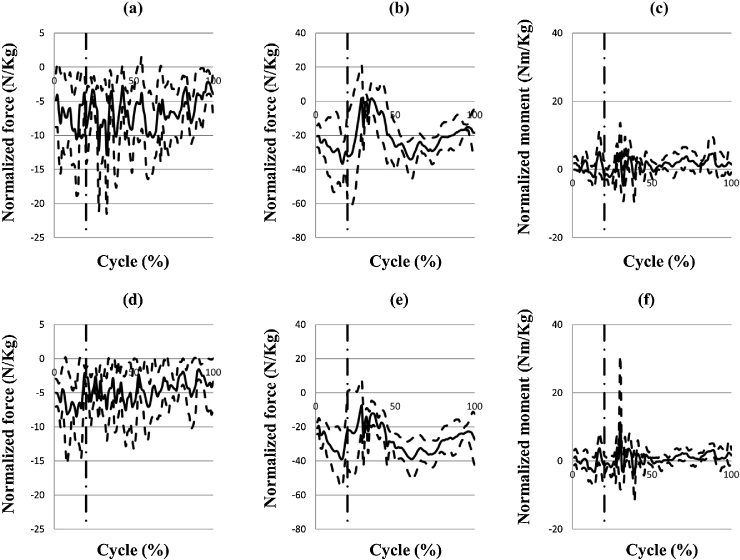
Shear forces were anteriorly oriented and fluctuated during the deadlift cycle (see Fig. 7a and d). Their maximum value of 1903 ± 936 N was observed at L5. As can be seen by the negative slopes of the plots in Fig. 7b and e, axial compressive forces increased throughout the deadlift cycle, reaching a maximum at completion. The magnitudes of the forces progressively increased from L1 to L5, reaching a maximum peak value of 7963 ± 2784 N. A high flexion moment was observed in the very initial part of the lifting cycle, and declined to an almost negligible level as the lifter approached the hang position (see Fig. 7c and f). The magnitudes of the peak values of the flexion moment remained fairly constant from L1 (685 ± 352 Nm) through L5 (734 ± 331 Nm).

Fig. 7.

Loads on lumbar vertebrae during deadlift cycle. (a) Shear force on L1; (b) Axial compression on L1; (c) Bending moment in sagittal plane on L1; (d) Shear force on L5; (e) Axial compression on L5; (f) Bending moment in sagittal plane on L5. For all the data reported, vertical dotted lines indicate reach of the hang position.

3.3. Hang clean

Shear forces during the hang clean cycle are illustrated in Fig. 8a and d. During the entire lifting cycle, shear forces fluctuated in both anterior and posterior direction, with peak values that increased from L1 (1900 ± 1313 N) through L5 (2652 ± 1882 N). For axial compressive forces, the highest values were observed just before reaching the second pull, and at the end of the catch phase (Fig. 8b and e). Force magnitudes did not differ greatly from one vertebra to another ranging from 8436 ± 3766 NN at L1 to 8701 ± 3263 N at L5. The bending moment was prevalently extensive (Fig. 8c and f) for all the vertebrae with peak values oscillating between 1731 ± 1410 Nm and 1935 ± 1947 Nm.

Fig. 8.

Loads on lumbar vertebrae during hang power clean cycle. (a) Shear force on L1; (b) Axial compression on L1; (c) Bending moment in sagittal plane on L1; (d) Shear force on L5; (e) Axial compression on L5; (f) Bending moment in sagittal plane on L5. For all the data reported, vertical dotted lines indicate completion of the second pull.

3.4. Hang snatch

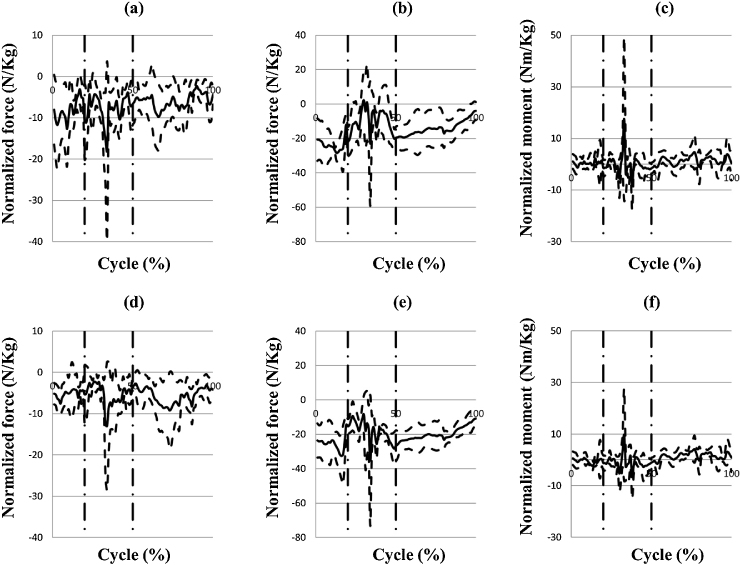
For all vertebrae, shear forces fluctuated around zero. The largest excursions were found in the middle of both catch and recovery phases (see Fig. 9a and d), with the highest peak value of 2810 ± 2409 N reached at L1. The pattern of axial compressive forces is illustrated in Fig. 6b and e. For all the spinal levels investigated, the peak magnitude of the compressive forces was 6224 ± 1753, attained at L5 in the middle of the catch phase. A constant extension moment characterized almost the entire cycle of snatch (see Fig. 6c and f). The highest moment was observed during the catch phase, and its intensity decreased across spinal levels from 1439 ± 1189 Nm at L1 to 1208 ± 809 Nm at L5.

Fig. 9.

Loads on lumbar vertebrae during hang snatch cycle. (a) Shear force on L1; (b) Axial compression on L1; (c) Bending moment in sagittal plane on L1; (d) Shear force on L5; (e) Axial compression on L5; (f) Bending moment in sagittal plane on L5. For each diagram reported, the first vertical dotted line form left to right indicates completion of the second pull, the second at the completion of the catch.

4. Discussion

Since modest information is available on spinal loading conditions during the deadlift, hang clean and hang snatch, this study mapped the distribution of mechanical loads acting on lumbar spine during these exercises. This was accomplished by employing a biomechanical spine model based on motion capturing, which was able to provide kinematics and loads on the lumbar spine during unrestricted body motion. An advantage of the biomechanical model used in this manuscript is that it requires only the use of the standard Vicon Plug-In Gait model.

4.1. Validation

Motion analysis is a widely accepted tool in both clinical and research applications for studying body biomechanics. One of the advantages of this method is that it can be applied for any functional activity of the body with no necessity for motion restrictions. Although most frequently used for performing gait analysis, this approach has also been successfully employed for investigating spine kinematics in both normal and pathological subjects.45, 46, 47, 48 Such studies either considered the trunk as a single rigid body,45, 46 or utilized a multi-segment spine model approach requiring custom configurations of skin-mounted markers.47, 48 The method adopted in this study utilized a standard full-body configuration for skin markers, combined to a mathematical model schematizing the lumbar spine as a kinematic chain of rigid bodies representing the vertebrae. In order to validate this model, its spine kinematic estimates during flexion-extension were compared to experimental data previously reported. The differences seen in sagittal plane rotation across vertebrae were similar to those reported by Wong et al³² and Li et al³³ showing increased angles from the inferior to superior segments. To attain these results Wong et al³² used an in-house image analysis program incorporating three components, a feature learning component to establish texture patterns, a feature detection component to track the movement of the segments using edge landmarks established by the first component, and a tracking component to follow the movement of the established edges across videofluoroscopic images. Our results, in contrast, were derived from using a standard Vicon Plug-In Gait model with no additional hardware or assessment modules. Additionally, the method of Wong et al³² has a number of limitations inherent to the nature of the analysis used. The first is the inability to assess the quality of the images produced using videofluoroscopy. Wong et al³² noted that the images were compromised by the levels of radiation used during the capture process (especially for L5) and that both the learning set and its associated algorithms can be negatively affected by this lack of clarity. Nonetheless, the patterns in both studies were clearly the same. As to the greater rotation values reported by Wong et al,³² clearly, the aforementioned limitations of their technique offers a partial explanation; however, these differences might be expected since Cholewicki and McGill⁴⁴ reported that in their study examining the deadlift, the range of motion of the intervertebral joints was notably greater during unloaded full flexion/extension than during lifting. They suggested that this was due to the necessity to limit range of motion during heavy lifting. The lower range of motion seen in their study may also have been due to the lead skirt, vest and thyroid shields employed during the testing, the static nature of the imaging, the imposed limit of 45° flexion to keep the subjects' lumbar spine within the field of view of the fluoroscopes and finally the differences in age between their subjects (mean age 54.4) and ours (22.0). Our technique also required far less time and cost than that of Li et al³³ who combined MRI scans, two fluoroscopes and an imaging-model technique to produce their results. And finally, the use of a bar and weights to allow assessments during lifting is clearly impossible.

In contrast to our results, Pearcy et al⁴² reported a parabolic relationship with L1–L2 and L5–S1 showing the lowest flexion and L4–L5 showing the greatest. The methods employed in the present study versus that of Pearcy et al⁴² vary considerably. Compared to our analyses, which used unconstrained lifting techniques, they employed x-ray tubes mounted in the sagittal and frontal planes and a complex metal frame which limited the movements of both the pelvis and hips so that the lumbar spine could be maintained within the field of view of the x-ray tubes. Results reported by Adams and Hutton⁴³ also differed from ours showing a nearly linear relationship among spinal segments for subjects between 15 and 29 years of age. The differences seen between our results and those of Adams and Hutton⁴³ are most likely due to the fact that our study used a dynamic model which tracked movements throughout three loaded exercises, while they used lumbar segments from a cadaver to simulate forward bending patterns and compared their data to static x-rays obtained during standing and unloaded forward flexion. Once again neither technique lends itself to dynamic analysis during weightlifting.

The fluoroscopy results reported by Cholewicki and McGill,⁴⁴ showing a pattern in direct opposition to our results, may also be due to differences in collection techniques. Although both studies used the deadlift, the subjects in our study were students perfecting their techniques, while the subjects in their study were Class 1 competitive powerlifters. Second, to reduce exposure to radiation, data were collected during three 6s trials at an exposure rate of 4 mA·s⁻¹ and an intensity of 110 kVp and digitized at 30 Hz during their analyses, while no such limitations were necessary during our analyses. Third, filtering, corrections, comparisons between filtered and non-filtered data, and comparisons with an in vitro vertebral model were used to deal with visual distortion and digitizing errors inherent to their technique; all of which were not required during our analyses. Fourth, Cholewicki and McGill⁴⁴ reported the loss of fluoroscopic images, especially just prior to the upright standing position, while our model was functional throughout the entire lift.

4.1.1. Deadlift

When applying our model to the characterization of mechanical loads on spine during the deadlift, it was found that the axial compressive forces gradually increased during the lifting, starting at about 1 N/kg and reaching 10–15 N/kg at the end of the cycle. In contrast, flexion moments abruptly peaked in the initial part of the lifting, and faded before reaching the hang position (see Fig. 7c and f). These results mirror those of other researchers. For example, in an examination of the kinetics and kinematics of the deadlift performed by adolescent lifters during the Michigan Teenage Powerlifting Championships, Brown and Abani¹⁷ reported that hip intersegmental resultant moment and horizontal bar to the hip moment arm decreased in magnitude throughout the lift. In addition, the moment at L4/L5 reported by Cholewicki et al⁴⁹ for men during the Canadian Powerlifting Championships averaged 714.9 ± 148.4 Nm, which compares favorably to the 734 ± 331 Nm reported in the current study.

The compressive loads at the spine as reported by Cholewicki et al⁴⁹ for men in the 90 kg weight class during the Canadian Powerlifting Championships averaged 14,487 ± 1282 N at L4–L5 for a load of 259.4 ± 16.5 kg; while Granhed et al³¹ reported a compressive load of 21,457 N for males competing in the World Powerlifting Championships while performing an average lift of 284.5 kg. The axial compressive forces computed using our model ranged from 6488 ± 2494 to 7963 ± 2784 N. The loads for the lifts during both comparison studies were nearly twofold greater than the 107.0 ± 40.6 kg average achieved by the subjects in our study; therefore, these differences would be expected. The shear forces were 2958 ± 180 N and 1656 ± 845 N for their lifters and our lifters, respectively. Once again these differences can be attributed to the loads lifted.

4.1.2. Hang clean and hang snatch

The large compressive forces seen in the hang clean and snatch compared to the deadlift (deadlift: 7963 ± 2784 N; hang clean: 8701 ± 3263 N; hang snatch: 6224 ± 1753N) relative to the loads lifted (deadlift: 107.0 ± 40.6 kg; hang clean: 56.2 ± 20.2 kg; hang snatch: 38.8 ± 14.6 kg) can be explained by the greater vertical accelerations of the bar during these lifts compared to the deadlift, which has been shown to be associated with greater vertical forces.¹⁷ Although a number of researchers have examined kinetics and kinematics during various forms of the clean1, 3, 13, 18, 19, 20, 22, 23, 24 and the snatch25, 26, 27, 28, 29; we could find no studies that examined spinal forces or moments during the clean, and only a single case study that examined these variables during the snatch.

There is some evidence supporting the validity of our model by looking at ground reaction forces reported in other studies. For example, using our model peak axial compression and shear forces occurred immediately following an obvious decline in force seen early in the lift. This same pattern was evident in ground reaction forces recorded during both the hang clean³ and mid-shin power clean.⁵⁰

For the snatch, Bao and Meng³⁰ did examine forces at the spine in a case study using a finite element model. These researchers computed an axial compressive force of 1854 N at L1–L2 using a barbell weight of 165 kg. Unfortunately, comparisons between our findings and theirs are not possible because the weight reported by these researchers cannot be correct since it was 275% of the subject's reported body weight of 60 kg. Results of previous studies do support the compressive and shear force and bending moment results seen for our spinal model. Kinematic analyses for barbell vertical velocity²⁵ and angular displacement⁵¹ show the same patterns as our model with declines at the knee and ankle during transition from the first pull to the second pull, a peak at the second pull, and a rapid decline thereafter.

Our study design also allows a comparison between these two modified Olympic style lifts. During both lifts, shear forces fluctuated with excursions averaging from 60 to 85 N/kg (see Fig. 5, Fig. 6d) as would be expected due to the differences in core activation patterns during the hang, pull and catch phases of the hang clean, and the pull, transition and catch phases of the snatch. Additionally, large fluctuations in the extension moments acting on the vertebrae were seen in both lifts at the beginning of the catch phase (see Fig. 5, Fig. 6c, and f). At that stage, the magnitude of the moments' peaks during snatch was nearly 5 times greater than that of the clean at L1 and comparable at L5. The higher value at L1 during the snatch may be attributed to the larger lever arm of the barbell with respect to subject's spine as it is positioned overhead. Large extension moments combined with axial compression may generate unusually high contact forces at facet joints and in turn either acutely, or over an extended training period, affect the health and the integrity of the cartilaginous tissue, and potentially lead to low back pain and spine musculoskeletal diseases.52, 53, 54 Such a scenario is especially true for the snatch, where the peak of the extension moment is attained coincidently with peak compression forces (see Fig. 6).

There are some limitations affecting the interpretation of the results reported in this manuscript. First, the sample size was small (n = 5). This was due to the difficulty in recruiting subjects who already achieved a sufficient level of expertise in weightlifting, allowing them to perform the exercises with an acceptable form. Second, results may have been influenced by factors such as the time of the day at which the testing occurred; subject's nutrition and hydration levels; sleep patterns; and the volume, intensity and nature of any workouts which occurred in the days preceding the testing since these could not be adequately controlled or determined. Finally, subjects participating to the study were amateurs, and their level of fitness and technique were lower than those expected with more proficient lifters. Accordingly, the fluctuations in both forces and moments observed in this study may be substantially reduced when these lifts are performed by more accomplished lifters.

Future studies should employ this model in examining commonly used variations of these lifts. For example, Campos and co-workers reported no kinetic differences among the power clean, hang power clean and midthigh power clean in a sample of 16 collegiate female athletes,²⁵ but this was not the case in elite male rugby players,19, 20 indicating that spinal forces and moments may vary among these lifts. Additionally, Escamilla et al¹³ reported significant biomechanical differences between the conventional and summon deadlifts, supporting the application of this model during these common variations. Second, applying our model in conjunction with kinematic and kinetic analyses during these and other lifts performed by lifters at different skill levels may help to identify biomechanical differences which can potentially increase injury potential in novice lifters and may also be useful as a teaching tool for specific cuing during the learning of these lifts. Third, subjects from different training facilities, training under different coaching staffs, should be evaluated to confirm the reliability of our model. Fourth, the model should be employed at various times during a transitional learning cycle as subjects progress from novice to advanced status so that we may test its sensitivity to change. And finally, the model can be used at specific intervals during periodization cycling so that potential differences in forces and moments related to fatigue or adaptation can be assessed and used to more effectively design training programs.

Funding

There was no funding source for this manuscript.

Conflicts of interest

All authors have none to declare.