Haplotype estimation for biobank scale datasets

Abstract

The UK Biobank (UKB) has recently released genotypes on 152,328 individuals together with extensive phenotypic and lifestyle information. We present a new phasing method SHAPEIT3 that can handle such biobank scale datasets and results in switch error rates as low as ~0.3%. The method exhibits O(NlogN) scaling in sample size (N), enabling fast and accurate phasing of even larger cohorts.

Introduction

Estimation of haplotypes from genotypes, known as phasing, is a central part of the pipeline of many modern genetic analyses. Estimated haplotypes are important for many population genetics analyses^1,2, but also form a central part of imputation algorithms that are routinely used in genome-wide association studies (GWAS) ^3,4. The ability to phase large data sets is especially important in the context of biobanks that comprise hundreds of thousands of genotyped samples. For example, in May 2015 the UK Biobank (UKB) released genotypes from ~152,000 samples, and this will rise to ~500,000 in 2016. Other Biobanks have already collected large scale genetic datasets⁵ or are in the process of doing so⁶. The unprecedented scale of these datasets, and the depth of phenotype information, allows researchers studying many different phenotypes to make novel discoveries⁷. Accurate and efficient statistical methods will play a key role in this research.

In principle, such large samples sizes should lead to more accurately inferred haplotypes. SHAPEIT2⁸ has been shown to be one of the most accurate phasing method currently available. When run on closely related samples it results in haplotypes so accurate that it allows resolution of the handful of recombination events per chromosome^9,10. In other words, the algorithm can capture and utilize long stretches of shared haplotypes between samples when they exist. This is commonly referred to as long-range phasing (LRP) in the literature ¹¹. However, when the number of genotyped samples (N) moves beyond around 10,000 a quadratic O(N²) complexity component of the algorithm begins to have a significant impact on the computational time. HAPI-UR¹² has been applied on datasets of up to ~60,000 samples with sub-quadratic scaling, but has reduced accuracy compared to SHAPEIT2. Other algorithms that compare all individuals to all others, will also have quadratic O(N²) scaling^11,13. Here we present SHAPEIT3, an extension to SHAPEIT2 that exhibits O(NlogN) scaling and results in very low switch error rates on large cohorts. In practice, when run on the ~152,000 UKB samples the method exhibits very good scaling in N (Table 1).

Table 1. Comparison of methods on the UK Biobank dataset.

Sample size	Method	Clustering	New MCMC	Switch Error (%)	Run time (hrs)	Run time scaling	Sample size scaling
1,072	SHAPEIT3	No	Yes	2.6	0.25	1	1
10,072	SHAPEIT2	No	No	1.1	4.2	16.8	9.4
10,072	SHAPEIT3	No	Yes	1.1	3.3	13.2	9.4
10,072	SHAPEIT3	Yes	Yes	1.3	2.5	10.0	9.4
152,112	SHAPEIT3	Yes	Yes	0.4	38.5	154	142

Each row shows the performance on a subset of the full dataset. The clustering column indicates whether the new method for choosing copying states was used or not. The new MCMC column indicates whether the new MCMC routine, which uses completely parallel updates and local algorithm termination, was used or not. Performance is measured as median switch error on the trio children. Run time is given in hours. The Scaling column shows the relative run time compared to the SHAPEIT3 run on a sample size of 1,072. 10 threads were used for all runs.

To describe the context in which we have developed our method, we use the following notation; G_i denotes a vector of genotypes for the i^th of N unphased individuals at L markers; H denotes a set of estimated haplotypes from other individuals at the same set of markers; and H* is a subset of H of size K. SHAPEIT2 estimates haplotypes for an individual iteratively. At each iteration, compatible haplotypes underlying G_i are sampled from a hidden Markov model (HMM) in which they are modeled as an imperfect mosaic of haplotypes in H*. The computational complexity of this step, using the standard forward-backward algorithm for HMMs, is O(LK²)¹⁴. The complexity is quadratic because the model permits the haplotypes that give rise to the genotypes at consecutive sites to switch between any pair from H*. The probability of all such transitions must be computed. One approach to ameliorating this complexity is to ensure that K ≪ 2N. The K haplotypes can be chosen randomly¹⁵ or by similarity to previous haplotype estimates for individual i ¹⁶. Alternatively, a compressed representation of H can be used by considering the region to be phased in small, disjoint windows within which only a few of the haplotypes in H are distinct ^12,17.

SHAPEIT2 introduced a novel strategy that splits G_i into small segments of distinct haplotypes that are consistent with G_i, and results in the HMM component of the method having complexity O(LK). HAPI-UR adopts a similar strategy but in such a way that the scaling with N depends on the diversity of the dataset and is typically super-linear. SHAPEIT2 also gains accuracy by combining linear complexity with the haplotype selection approach of IMPUTE2¹⁶ instead of a compressed representation of H. In this approach, at each iteration, a search is carried out to find a good conditioning set of haplotypes H* that can be used to update each individual. This method can be thought of as a generalization of the LRP¹¹ approach in which a search is carried out for just two other samples that can be used as surrogate parents when phasing each individual. However, these selection approaches used by SHAPEIT2 and LRP involve comparison of all haplotype pairs, which has complexity of O(N²). For N > 10,000 this begins to dominate.

SHAPEIT3 enhances SHAPEIT2 in two ways that enable it to deal with very large datasets, such as the UK Biobank study. The first advance is based on the intuition that larger sample sizes are likely to result in increased local similarity between groups of haplotypes due to the higher probability of more recent shared ancestry. This idea is exploited by using a recursive clustering algorithm to partition the haplotypes into clusters of similar haplotypes of specified size M ≪ 2N. Distances are computed only between haplotypes within a cluster. This reduces the complexity of this step to O(M²) so the complexity of the whole algorithm is dominated by the O(NlogN) scaling of the clustering routine (Online Methods). We set M=4,000 for the experiments in this paper, and this value leads to a reasonable trade-off between run time and accuracy (Supplementary Figure 1). Our clustering method is similar to locality-sensitive hashing and further advances in the SHAPEIT development are likely by pursuing this approach further¹⁸.

The second advance involves changes to the MCMC sampling routine that result in additional gains in speed. As sample size grows it becomes more likely that two individuals will share a long stretch of sequence in common within a window. We modified the algorithm to detect when this occurs as the algorithm proceeds. When a Hamming distance equal to zero is found between a haplotype and at least one of its conditioning haplotypes, we do not perform HMM calculations within that window from that point on. In this way, the method adapts to the local patterns of haplotype sharing, and computation becomes increasingly focused on the challenging parts of the dataset. On the UK BiLEVE dataset of ≈50,000 samples we observed almost 20% of 2Mb windows will have a zero Hamming distances as the algorithm converges (Supplementary Figure 2). We have also updated the MCMC algorithm so that threading is now performed per window rather than per individual as was done in SHAPEIT2. That is, each iteration involves updating N × W haplotype windows (typically around 2Mbp in size), and we now process each window in a separate thread as opposed to entire individuals per thread (Online Methods).

Results

Phasing the UK BiLEVE dataset

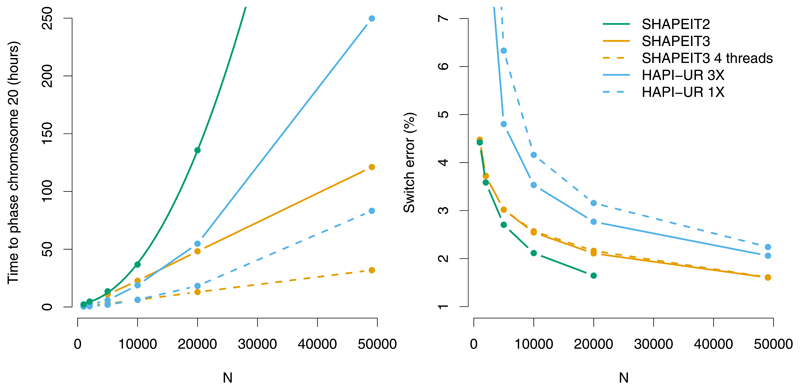
We compared SHAPEIT3 to SHAPEIT2 (r768) and HAPI-UR (v1.01) using a large Biobank scale dataset of N = 49,458 individuals from the UK-BiLEVE study⁷ each of whom were genotyped on an Affymetrix Biobank genotype microarray. We phased chromosome 20, which had 15,795 SNPs after QC filtering, for a range of sample sizes (N =1000,2000,5000,10000,20000,49074) and evaluated computation time and accuracy. We developed a novel method to leverage close relatives within the dataset to assess phasing accuracy. We identified 384 likely sibling pairs, and obtained partially phased, accurate haplotypes for each pair by detecting IBD1 segments using an HMM (Online Methods). After filtering, these individuals had an average of 28.7% of their heterozygous sites phased and a total of 337,634 phased heterozygous sites on which to calculate switch error. One member of each pair was removed from the test dataset and used to provide ‘truth’ haplotypes for the other sibling. Figure 1 shows the variation in computation time and switch error rate (SE) with sample size for each method. SHAPEIT3 was run using both one and four threads, with a cluster size of M = 4,000 (Online Methods). HAPI-UR 3X indicates that haplotypes were averaged across three runs of HAPI-UR, as recommended¹².

Figure 1. Performance on UK-BiLEVE chromosome 20 dataset.

Computation time (left) and switch error rate (right) of different phasing routines. Estimated haplotypes are compared to those derived from the IBD1 segments of the 384 likely sibling pairs. HAPI-UR 1X is the average switch error rate/time across three runs of HAPI-UR. HAPI-UR 3X performs majority voting of haplotypes across three runs (computation is the sum of three runs of HAPI-UR). SHAPEIT3 was run with cluster size M = 4,000, which substantially improves computational complexity, and hence running time compared to SHAPEIT2. Both SHAPEIT runs use K=100 conditioning states.

As expected, accuracy and computation time increase with sample size for all methods. While SHAPEIT2 is consistently the most accurate method for N ≤20,000, its quadratic distance calculations make it more computationally challenging for larger sample sizes (hence it was not run for N >20,000). For the largest sample size (N = 49,074), SHAPEIT3 had an SER of 1.60% and took 121 hours to run (32 hours using four threads). This compares favourably to HAPI-UR-3X (1X), which had a SER of 2.06% (2.24%) and took 250 hours (83 hours) to run. Notably, SHAPEIT3 is consistently more accurate than both HAPI-UR 1X and HAPI-UR 3X and also significantly faster when using four threads.

Supplementary Table 1 reports RAM usage of the different methods. We estimate that phasing chromosome 20 in all 500,000 UKB samples would require ~240GB RAM which is realistic for modern systems. On larger chromosomes a ligation strategy can be used.

Phasing the UK Biobank dataset

As a further validation, we used SHAPEIT3 to phase the first release of the UKB dataset, consisting of 152,256 individuals, and genotyped on a combination of the UK BiLEVE array and the UKB Axiom array (see URLs). The self-reported ethnicity of these individuals is primarily white-British (90.5%) with the remaining 9.5% comprising various ethnic groups. To evaluate performance we used 72 mother-father-child trios that were detected in this dataset. We used these trios to obtain a ground-truth set of haplotypes. We removed the trio parents from the dataset and phased the whole of chromosome 20 (16,265 genotyped sites) for the remaining 152,112 individuals. This run resulted in a median switch error (SE) of 0.4% and took 38.5 hours using 10 threads (Table 1). Supplementary Figures 3-5 show visually the accuracy of each trio child and demonstrates how this error rate corresponds to many long stretches of accurately phased sequence. When SHAPEIT3 is run on the full 152,112 samples, it can be seen that many samples have just a handful of switch errors per chromosome. We find that 68.5% of the inferred haplotypes consist of correctly inferred chunks of length 10Mb or greater (Supplementary Table 2). By increasing the number of conditioning states and the cluster size parameter we have obtained switch error rates as low as 0.3%.

To assess the advantages of phasing such a large dataset we also ran SHAPEIT3 and SHAPEIT2 on a subset of 10,072 samples that included the trio children, and obtained mean switch error rates of 1.3% and 1.1% respectively. These runs took 2.5 hours and 3.3 hours respectively using 10 threads. On a subset of size 1,072 SHAPEIT3 had a switch error rate of 2.6% and took 0.25 hrs. We also ran SHAPEIT3 on the 10,072 subset without using the new clustering routine, resulting in a mean switch error of 1.1% and which took 4.2 hours using 10 threads. These results show that the new MCMC scheme results in no loss in accuracy using ~80% of the run time. The new clustering method results in further reductions in run time, but at a small loss in accuracy. Table 1 also highlight how SHAPEIT3 scales close to linearly with N, with the run on the full 152,112 samples taking 154 times as long as the run on 1072 samples, whereas the sample size scaling was 142. This scaling behavior will be crucial when running SHAPEIT3 on the full 500,000 samples. Supplementary Table 3 shows that SHAPEIT3 also reduces switch error in other ethnicities as sample size increases.

Discussion

Overall, we have demonstrated that SHAPEIT3 provides a highly accurate and scalable solution to phasing biobank scale datasets. The ultra low switch error rates that we have obtained represent strong validation of using SHAPEIT3 to phase the UKB dataset in early 2015. Switch errors that occur megabases apart (see Supplementary Figure 3) will have negligible impact on subsequent downstream imputation¹³. Due to the multi-ethnic nature of the UK population, many thousands of UKB samples will not have European ancestry (~10% of samples in the first release). While many novel loci will be uncovered using predominantly European samples, these non-European samples will be poorly phased (and imputed) using LRP approaches that search for IBD matches of a specific length. Such non-European samples are likely to be invaluable when deciphering the trans-ethnic nature of novel associations. Given SHAPEIT2 was demonstrated to perform well (relative to other methods) on cohorts with heterogeneous ethnicity, we expect SHAPEIT3 to have similar performance⁸. Hence SHAPEIT3 represents a scalable method that can adapt to the multi-ethnic nature of large cohorts due to the custom selection of template haplotypes on a per-subject basis.

Reducing switch errors down to the levels produced by SHAPEIT3 can result in downstream imputation performance at low-frequency SNPs¹⁹. Phasing samples altogether also avoids having to phase in batches, which would be more likely to introduce artifacts to any downstream analysis. In addition, SHAPEIT3 has also been used successfully to re-phase the first release of the Haplotype Reference Consortium (HRC) dataset (see URLs), which consists of genotypes at ~40M SNPs called from low-coverage sequencing of ~33,000 samples²⁰. The boost in imputation performance due directly to this re-phasing, has in effect already led to a boost in power to detect associations at low-frequency variants, since a large number of samples have already been imputed using HRC. Phasing sequence derived genotypes in this many samples could not have been performed using other long-range phasing methods¹³.

In other work²¹, we have shown that large and accurately phased haplotype reference panels can be used to help phase single sequenced samples. This approach uses rare variant sharing between the sequenced sample and the reference panel to efficiently select a set of template haplotypes to use within the HMM model. The Oxford Statistics Phasing Server allows users to phase their samples against the HRC haplotype panel²⁰ (see URLs).

Extending this approach further, we suggest that an accurately long-range phased and imputed version of the UK Biobank dataset, at a union of all SNPs on commonly used genome-wide SNP microarrays, could act as a highly accurate reference panel for phasing newly genotyped samples with predominantly European ancestry. Combining such a panel with the multi-ethnic reference panel planned for the next release of the HRC, and with the planned 100,000 Genomes Project reference panel (see URLs), would likely provide a reference panel useful for phasing samples with a wide range of ancestries.

Online methods

A sub-quadratic method for haplotype distance calculations

At the t^th iteration of SHAPEIT2, a pair of haplotypes, $\left(h_{i1}^t,h_{i2}^t\right)$ for the i^th of N individuals are re-sampled from an HMM. The hidden states of this HMM are a set of K conditioning haplotypes, H*, chosen from the remaining 2(N-1) estimated haplotypes, H, in the cohort. An optimal choice for H* would be the set of conditioning haplotypes that would give rise to $\left(h_{i1}^t,h_{i2}^t\right)$) with highest probability, but this is unknown. As a proxy, we choose haplotypes which are locally similar: the region to be phased is divided into windows of specified size. In each window, H* is formed from the K haplotypes in H that are closest in Hamming distance to the haplotype estimates, $\left(h_{i1}^{t-1},h_{i2}^{t-1}\right)$ from the previous iteration. The intuition is that, in small windows, closeness in Hamming distance is correlated with shared ancestry. In each window, all 2N haplotypes are compared to one another. Consequently, the distance calculation of SHAPEIT2 has O(N²) complexity. When sample sizes become large, say N>10,000, this starts to dominate the computational cost of the algorithm.

In SHAPEIT3, we circumvent the O(N²) distance comparisons by a two step procedure:

1. cluster the 2N haplotypes into clusters of size M;

2. for each individual, form the set H* from the other M-1 haplotypes belonging to the same cluster. An individual’s haplotypes may be in two distinct clusters in which case there are 2(M-1) haplotypes to consider

Step 2 requires distance computations between the M haplotypes within a cluster and so has complexity O(M²), independent of N. We now describe a simple clustering method, divisive k-means clustering, to perform step 1. We show that this has complexity O(NlogN) Consequently, our new algorithm exhibits overall complexity of only O(NlogN).

Divisive K-Means clustering to partition the data

K-Means clustering is a well-known technique for uniquely assigning samples to one of K clusters based on the similarity of some real-valued attribute. Assignments are performed so as to minimize the within-cluster sum of squares, ${\Sigma }_j^{2N}\parallel H_j-{\mu }_{C_j}{\parallel }^2,$, where μ_c is the cluster mean for class c and C_j denotes the cluster membership of haplotype j. This objective function can be minimized by iteratively assigning class labels to each observation based on which cluster mean is closest and then recalculating the cluster means. When the distance measure is Euclidean, convergence is guaranteed²². We implemented this routine, allowing up to ten iterations (or stopping when class labels stabilize). Ten iterations are often not sufficient for convergence but we only require a rough partitioning. We used K-Means with K=2 to partition clusters of haplotypes recursively. Each cluster is split into two smaller clusters. The recursion is terminated when the cluster size is <M. Upon termination, we “top up” the cluster at the leaf of the bifurcating tree with haplotypes from the closest leaf. This last step ensures each haplotype is compared to M-1 other haplotypes.

Formally, we wish to find a vector of labels C = {C₁…C_2N} where C_i tells us the cluster which haplotype H_i belongs to. We refer to C_j as the primary cluster of H_j. We also store a dictionary D of sets, which we call secondary clusters. Every set in D has exactly M<<2N elements. It is possible for a haplotype to be in more than one secondary cluster, but haplotypes will only ever have one primary cluster (determined by C_j). We assume to that we have the functions available; K-Means(H) and euc(H_j, μ_c).The first performs the K-means clustering routine with K=2 on H and returns a vector of class labels, the second which calculates the Euclidean distance between H_j and μ_c. Our algorithm is described using pseudo-code in the Supplementary Note.

On each iteration of the SHAPEIT3 algorithm, we find the primary cluster labels C and build the dictionary of secondary clusters D. For each individual i we choose K conditioning haplotypes from H* = D[C_2i-1] ∪ D[C_2i] based on the minimum Hamming distances but excluding individuals estimated to be IBD2 within the region ⁸. We set the cluster size to M=4,000 for all the experiments described in this paper. We note that the final set of K conditioning haplotypes are chosen based on minimum Hamming distance, whereas the K-means routine uses Euclidean distance. Hamming distance is appropriate for pairs of binary vectors, we use this where possible since such distances can be calculated very rapidly via lookup tables. The K-Means routine needs to use a distance measure appropriate for real numbers, since the means of the clusters are unlikely to be 0 or 1 rather something on the interval [0,1], hence Euclidean distance was used. We suspect that this part of the algorithm can be improved via careful choice of the SNPs used to calculate Euclidean distances between haplotypes. For example, by focusing preferentially on rare SNPs²¹.

We further decrease the computational cost of our routine by thinning the SNPs that K-means is performed on. For each K-means clustering performed (each leaf of the recursion), Euclidean distances are only calculated on SNPs l={8k+o : k ∈ 0… L/8} where o ∈{0,1,2,3,4,5,7} and is sampled randomly within each leaf. In words, we only use every eighth SNP (starting from a random offset) in our clustering routine. So in practice 4NL/8 differences (2 centroids, 2N haplotypes, L/8 SNPs) are calculated per iteration of K-means when clustering N samples, we include this description for completeness but remove the 8 in the denominator henceforth for clarity. The initial iteration of K-Means clustering requires 4NL calculations for calculating the distance between the N haplotypes and two clusters for L SNPs. As a rough approximation, we assume that K-Means divides the data into two clusters of equal size. Consequently, after the d^th recursion, we have 2^d clusters of size N/2^d. The recursion continues until a cluster of size <M is reached. This will take log₂(N/M) recursions. Hence, we can derive the computational complexity of the clustering routine quite simply:

$$\text{Complexity = }{\displaystyle \sum _{d=0}^{{\log }_{2}N/M}{2}^d\frac{4NL}{2^d}=4NL{\log }_2\frac{N}{M}}$$

Since L and M are constants our clustering routine has O(NlogN) complexity.

Modified MCMC sampling routine

We implement two modifications to the MCMC sampling routine of SHAPEIT2. Firstly, when a Hamming distance of zero is found between a haplotype and at least one conditioning haplotype, we do not perform HMM calculations within that window on the current iteration. In such cases, it is unlikely that a different haplotype will be generated in preference to this perfect match. In other words, when there is evidence that locally that the algorithm has converged, then we stop updating that individual. We refer to this as adaptive algorithm termination. Therefore, we simply carry forward the haplotype generated by the previous iteration. As shown in Supplementary Figure 2, this can be expected to happen quite frequently as N increases leading to considerable savings in computation time.

The second modification is an approximation to the MCMC sampling routine, which offers significant additional gains in speed when using multiple threads. In SHAPEIT2, the parallelization scheme updates the phase of T samples in parallel using T threads conditioning on the N-T other samples already processed. The problem with this approach is a given thread becomes idle as soon as it has finished processing its assigned sample before the other threads, and therefore has to wait for the other threads to finish. Because of this synchronization that has to be repeated many times, the parallelization efficiency of this scheme decreases with the number of threads. In SHAPEIT3, we introduce a new parallelization scheme based on another approximation of the MCMC process. This scheme takes advantage of the fact that SHAPEIT updates the phase of samples within windows of usually few Mb: it splits the N samples into W overlapping windows prior to any MCMC iteration and distributes the N × W jobs to be done into T distinct queues, one for each thread. Then, a thread performs the window-sample pairs in its queue independently of the other queue and therefore does not need any particular synchronization, which results in better usage of all CPU cores. Once all the jobs are done, the haplotype for each sample are updated and we move on the next MCMC iteration. Of note, this scheme implicitly assumes a MCMC scheme in which the phase of all samples is updated in parallel at the same time. In other words, we move from a Markov chain state to the next by updating all samples simultaneously which differs to the standard MCMC scheme in which we move from as state to the other by updating only one sample. We refer to this as completely parallel updating. We assessed the performance of this approach by running SHAPEIT3 without the new clustering routine on the 10,072 sample subset of the UK Biobank dataset and compared it to SHAPEIT2 run on the same dataset. The median switch error rate was 1.1% for both methods, indicating little difference in performance when using this new MCMC routine (see Table 1). Performance for increasing numbers of threads is shown in Supplementary Table 4.

Creating a validation data set for assessing accuracy

SHAPEIT3 was initially developed and tested on the UK-BiLEVE dataset, which contained a large number of apparent sibling pairs but no identifiable mother-father-child trios. Regions in which siblings inherit exactly one chromosome from the same parent, (IBD1) can be phased using simple Mendelian rules. So we developed a novel method for inferring the identity by descent (IBD) status of siblings, with the aim of constructing a set of ‘known’ haplotypes against which we could compare accuracy of different methods.

We identified 384 pairs of individuals with a kinship coefficient >0.35, indicating they were likely first order relatives (sibling-pairs or parent-child duos). Parents will share 100% of the chromosomes IBD1 with their children and siblings will share (on average) their genomes 25% IBD0, 50% IBD1 and 25% IBD2. No pairs of individuals had close to 0% IBD0 suggesting these samples were sibling-pairs, not parent-child²³. By detecting IBD1 regions we can accurately phase loci within those regions using simple Mendel rules. This will generate accurate haplotypes for validation purposes, albeit partially phased ones.

We infer regions of IBD1 sharing by a two-stage approach. Firstly, we applied a simple Hidden Markov Model (HMM) to the genotypes of each sib-pair (see Supplementary Note), with three unobserved states indicating IBD status. However, because this model does not account for LD (IBD sharing from more distant ancestors) it is vulnerable to inferring spurious stretches of IBD1. This issue has been noted in previous work on phasing siblings with missing parents²⁴. We circumvent it via simple post-hoc filtering of short (<10cM) IBD1/IBD2 segments. Supplementary Figure 6 shows the consequences of this filtering step for the IBD state for a pair of probable siblings across chromosome 20. The filtering step did indeed reduce the SE for all methods (Supplementary Figure 7) and also flattened the distribution of switch error rates with respect to the percentage of phase resolved sites for the corresponding individual (Supplementary Figure 8).

We note that the switch-error rates when using these validation data were higher than the trio phased validation haplotypes created in the UK Biobank experiments. This suggests our sibling-pair validation haplotypes were not as accurate as those produced via trio phasing. We can think of two likely causes. While we filter short stretches of (likely spurious) IBD1, such a spurious segment may also flank a longer (true) IBD1 segment introducing some errors on the edges of the segment. Secondly, genotyping errors will induce incorrect phase, and there is greater power to detect such errors in the trio setting. Nevertheless, this validation data set provides a reasonable relative comparison of methods and was of great utility when developing SHAPEIT3.

Methods comparison using the UK BiLEVE dataset

For the results presented in Figure 1 of the main paper that compares methods each phasing run was performed on independent Amazon EC2 m2.2xlarge instances to avoid any possibility of diminished performance from other running processes. The elapsed time of each run was measured with the GNU time command. HAPI-UR results were generated with v1.01 of the software, using a window size of 80 as suggested in the HAPI-UR manual for a microarray of this density. SHAPEIT2 results were generated with version r778 of the software using the default parameters.