Abstract
Extracting nuclei is one of the most actively studied topic in the digital pathology researches. Most of the studies directly search the nuclei (or seeds for the nuclei) from the finest resolution available. While the richest information has been utilized by such approaches, it is sometimes difficult to address the heterogeneity of nuclei in different tissues. In this work, we propose a hierarchical approach which starts from the lower resolution level and adaptively adjusts the parameters while progressing into finer and finer resolution. The algorithm is tested on brain and lung cancers images from The Cancer Genome Atlas data set.
Keywords: digital pathology, nucleus segmentation
1. DESCRIPTION OF PURPOSE
Extracting nuclei is one of the most actively studied topic in the digital pathology researches.1, 2 Most of the studies directly search the nuclei (or seeds for the nuclei) from the finest resolution available. While the richest information has been utilized by such approaches, it is sometimes difficult to address the heterogeneity of nuclei in different tissues. In this work, we propose a hierarchical approach which starts from the lower resolution level and adaptively adjusts the parameters while progressing into finer and finer resolution. The algorithm is tested on brain and lung cancer images from The Cancer Genome Atlas (TCGA) data set.
In general, the nuclei detection algorithms from H&E image proceed with the following consecutive steps.3–10 First, the image is pre-processed to normalize the staining and/or illumination conditions. Then, certain scalar is derived from the RGB values of the H&E stained images for the purpose of highlighting the chromatin material. This could be a decomposition process which extracts the hematoxylin component or other possibly non-linear color space transformations. In some learning based algorithms, the scalar may be derived from the learned information and represent nuclear probability measurement. Once such scalar field is computed, prominent locations in the images are picked as seeds or the initial locations of the segmentation contours, which are further refined using contour evolution algorithms, such as graph cut or level set methods. In cases such as multiple nuclei clump in a single region without clear separation in between, clustering based algorithms are adopted to separated them into individual nucleus.
Regardless of the approaches being adopted, there always exist some parameters that affected certain steps in the algorithm. For example, when determining whether certain region is a single nucleus or a clumped area which should be separated, implicitly or explicitly, a parameter indicating the expected nuclear size is necessary. Such parameters are often dictated by the tissue types where the nuclei reside in. As a result, if the digital pathology images contain more than one types of tissues where the nuclear properties differ significantly, a single set of parameter is not sufficient for an optimal nuclear identification task.
In this study, we address such a problem by adopting a top-to-bottom approach. The algorithm starts from the low resolution interpretation of the image, in which an approximated tissue classification is performed. Then, the algorithm proceeds into finer and finer scale, where the identified “tissue type” provides specific estimation for the nuclear features underneath. The algorithm is tested on brain and lung cancer images from (TCGA) data set.
2. METHOD
2.1 Tissue and nuclear context learning
The tissue type and the nuclear features are learned from a set of training images, with the nuclei manually traced out and validated by pathologists. Specifically, denote the training images as
| (1) |
Their corresponding ground truth segmentations are Li : ℝ2 → {0, 1} where 1 indicates the nuclear regions. In order to learn the nuclear features, for the i-th nucleus, a groups of image and morphological features are learned. The feature vector fi ∈ ℝ4 includes: the average of the intensity in the Hematoxylin channel, the area (unit in μm2) of the nucleus, the ratio τ between the square of the nuclear parameter and the area. Denote the total number of nuclei in all the M training images as N, we will then have the feature sets:
| (2) |
The tissue classification is carried out at lower resolution versions of the training images. Image pyramid is constructed to approximate the image appearance at lower resolution of 8μm/pixel. Denote the low resolution version of Ii as Ji, and we collect all the image RGB values in all the M images, that is,
| (3) |
Then, a Gaussian mixture model (GMM) is fit to the data with k clusters. It is noted that the resulting k clusters are related, but not directly mapped, to the different histology tissue types. Indeed, the purpose of clustering is to guide the subsequent nuclear segmentation in a spatially heterogeneous way, not to provide a precise tissue classification. Different clusters may also represent the same tissue type under slightly different staining and imaging condition. Nevertheless, we will call such map as “tissue map” in the subsequent discussion without causing confusion.
After the clustering, each of the feature vector can be assigned a cluster label. More explicitly, depending on the highest image resolution, a pixel in Ji often corresponds to a patch of about 32 × 32 pixels in Ii. A nucleus is labeled according to that of the patch that contains the largest portion (or sometimes entirely) of it. As a result, the N features vectors are grouped into k sub-sets F1 through Fk. For each sub-set, the feature distributions pFi : ℝ3 → ℝ+, i = 1, …, k are learned through a kernel density estimation process. Assuming the independence among the features, the likelihood function for each feature is learned separately so
| (4) |
with the maximum response of each likelihood function being normalized to 1. Such information is used in the subsequent adaptive segmentation.
2.2 Hierarchical adaptive nuclear segmentation
Given a new image I : Ω → ℝ3 from which we want to segment the nuclei, we first identify the “tissue map”. To this end, the image pyramid is constructed to approximate I at lower resolution of 8μm/pixel, denoted as J. Then, the learned GMM is applied to the new image J for a pixel-wise classification, which gives a label image L̃ with the range of {1, …, k}. Note that L̃ does not necessarily have all the k models. After that, L̃ is reconstructed to the original resolution defined on the same discrete grid as I, denoted as
| (5) |
Based on L, the domain Ω is decomposed into k sub-regions with
| (6) |
Apparently we have
| (7) |
With the image domain decomposed, each region is processed with its own set of parameters in the pipeline described below.
First, the hematoxylin channel of the entire image is extracted, denoted as H(x), regardless of the “tissue map”. Then, for each cluster, a set of seeds are extracted based on local and global intensity criteria. Specifically, for the i-th cluster Ωi, the seed set Si := Ai ∪ Bi where Ai contains the local minima of H:
| (8) |
in which 𝒩(x) is the neighborhood of x (within Ωi). Bi is determined by the learned features in pFi as:
| (9) |
In addition, a “rejection region” S̃i is defined as
| (10) |
With the two regions defined, an adaptive geodesic segmentation is performed to extract the region Gi ⊆ Ωi of the nuclei11 in region Ωi. It is possible that multiple nuclei are clumped together in Gi and we need to first identify clumping regions and then decompose them into individual nucleus.
In order to identify the clumping regions, each connected component in Gi, denoted as , is computed. Then, the area (aj) and squared-perimeter-area ratio (τj) for each j are computed. Regions with too large area or too jagged boundary (large τ) will be decomposed. Mathematically, those regions with
| (11) |
are subject to de-clumping. To that end, a set of 5-dimensional feature points are collected:
| (12) |
Then, the meanshift algorithm is used to find clustering in .12, 13 One key parameter in the meanshift algorithm is the kernel size σi, which determines the resulting cluster size. To optimize such parameter, the “most-likely” radius of the learned nuclei in such a “tissue type” is used to determine the kernel size:
| (13) |
where γ is often set to a small positive value, such as 0.2.
3. EXPERIMENTS AND RESULTS
Nuclei in 15 brain images 18 lung images of sizes around 700 × 700 are manually contoured. The images have resolution of 0.25μm/pixel. The number of cluster k is set to 5 empirically. A leave-one-out test is performed for each image.
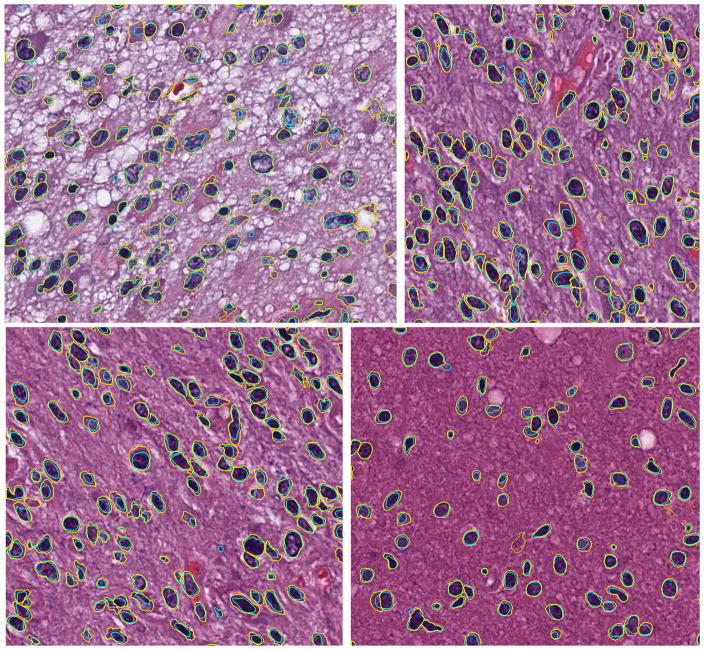
Figure 1 shows 4 examples for brain tissue. The average Dice coefficients for all brain images is 0.71 with standard deviation of 0.048.
Figure 1.
Four example results for brain images. Contour colors: yellow (manual), cyan (algorithm).
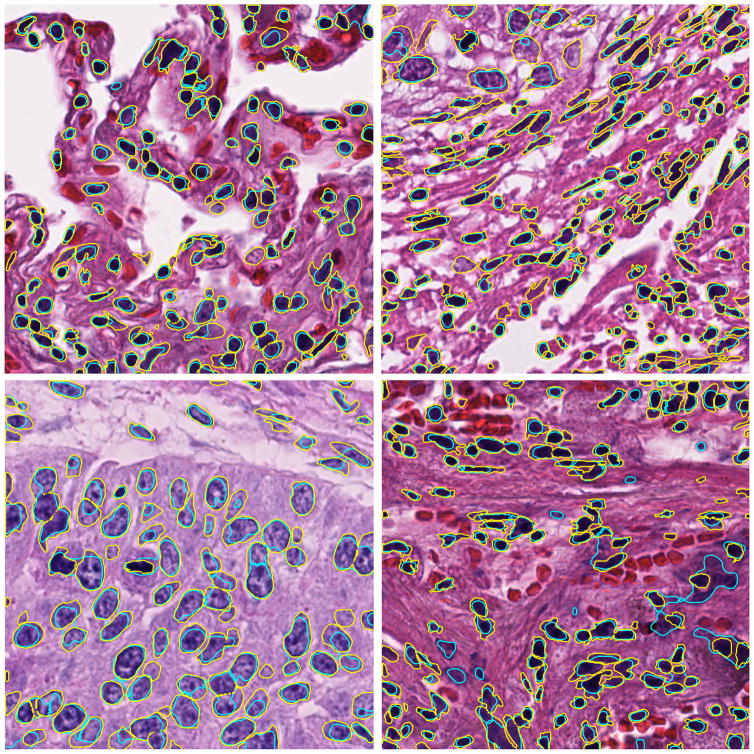
Figure 2 shows 4 examples for lung tissue. The average Dice coefficients for all lung images is 0.70 with standard deviation of 0.045.
Figure 2.
Four example results for lung images. Contour colors: yellow (manual), cyan (algorithm).
4. CONCLUSION AND FUTURE RESEARCH DIRECTIONS
For the purpose of nucleus extraction from digital pathology images, we propose a hierarchical approach which starts from the lower resolution level and adaptively adjusts the parameters while progressing into finer and finer resolution. The algorithm is tested on two types of brain cancers and two types of lung cancers from the The Cancer Genome Atlas data set.
The algorithm is currently implemented for small scale computing using Matlab.14 The ongoing research include scaling the algorithm to larger data set. Furthermore, larger scale evaluation and validation is needed and we are working on a systematic approach to evaluate the segmentation result at WSI level. Moreover, the current Dice coefficient in the 0.7 level should be improved for more accurate morphology studies. Better de-clumping algorithm is also an ongoing research direction.
The work has not been submitted for publication or presentation elsewhere.
References
- 1.Gurcan MN, Boucheron LE, Can A, Madabhushi A, Rajpoot NM, Yener B. Histopathological image analysis: A review. Biomedical Engineering, IEEE Reviews in. 2009;2:147–171. doi: 10.1109/RBME.2009.2034865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Irshad H, Veillard A, Roux L, Racoceanu D. Methods for nuclei detection, segmentation, and classification in digital histopathology: A review—current status and future potential. Biomedical Engineering, IEEE Reviews in. 2014;7:97–114. doi: 10.1109/RBME.2013.2295804. [DOI] [PubMed] [Google Scholar]
- 3.Yang L, Meer P, Foran DJ. Unsupervised segmentation based on robust estimation and color active contour models. Information Technology in Biomedicine, IEEE Transactions on. 2005;9(3):475–486. doi: 10.1109/titb.2005.847515. [DOI] [PubMed] [Google Scholar]
- 4.Naik S, Doyle S, Agner S, Madabhushi A, Feldman M, Tomaszewski J. Automated gland and nuclei segmentation for grading of prostate and breast cancer histopathology. Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium on; IEEE; 2008. pp. 284–287. [Google Scholar]
- 5.Basavanhally AN, Ganesan S, Agner S, Monaco JP, Feldman MD, Tomaszewski JE, Bhanot G, Madabhushi A. Computerized image-based detection and grading of lymphocytic infiltration in her2+ breast cancer histopathology. Biomedical Engineering, IEEE Transactions on. 2010;57(3):642–653. doi: 10.1109/TBME.2009.2035305. [DOI] [PubMed] [Google Scholar]
- 6.Kong H, Gurcan M, Belkacem-Boussaid K. Partitioning histopathological images: an integrated framework for supervised color-texture segmentation and cell splitting. Medical Imaging, IEEE Transactions on. 2011;30(9):1661–1677. doi: 10.1109/TMI.2011.2141674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cooper L, Gutman DA, Long Q, Johnson BA, Cholleti SR, Kurc T, Saltz JH, Brat DJ, Moreno CS. The proneural molecular signature is enriched in oligodendrogliomas and predicts improved survival among diffuse gliomas. PloS one. 2010;5(9):e12548. doi: 10.1371/journal.pone.0012548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kong J, Cooper LA, Wang F, Gao J, Teodoro G, Scarpace L, Mikkelsen T, Schniederjan MJ, Moreno CS, Saltz JH, Brat DJ. Machine-based morphologic analysis of glioblastoma using whole-slide pathology images uncovers clinically relevant molecular correlates. PLoS ONE. 2013;8(11) doi: 10.1371/journal.pone.0081049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Qi X, Xing F, Foran DJ, Yang L. Robust segmentation of overlapping cells in histopathology specimens using parallel seed detection and repulsive level set. Biomedical Engineering, IEEE Transactions on. 2012;59(3):754–765. doi: 10.1109/TBME.2011.2179298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Veta M, van Diest PJ, Kornegoor R, Huisman A, Viergever MA, Pluim JP. Automatic nuclei segmentation in h&e stained breast cancer histopathology images. PLoS ONE. 2013;8:70221. doi: 10.1371/journal.pone.0070221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhu L, Kolesov I, Gao Y, Kikinis R, Tannenbaum A. An effective interactive medical image segmentation method using fast growcut. MICCAI Workshop on Interactive Medical Image Computing; 2014. [Google Scholar]
- 12.Cheng Y. Mean shift, mode seeking, and clustering. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1995;17(8):790–799. [Google Scholar]
- 13.Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2002;24(5):603–619. [Google Scholar]
- 14.Guide MU. The mathworks. Inc Natick, MA. 1998;5:333. [Google Scholar]