Multiple Time Courses of Vestibular Set-Point Adaptation Revealed by Sustained Magnetic Field Stimulation of the Labyrinth

SUMMARY

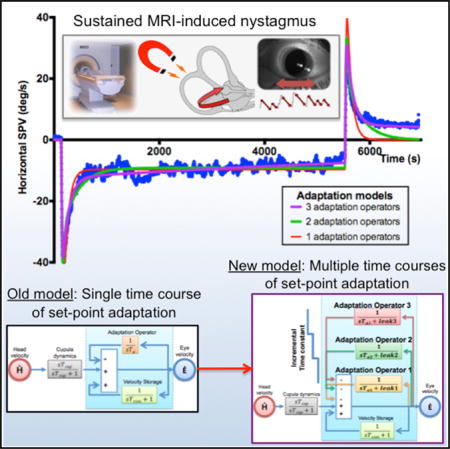
A major focus in neurobiology is how the brain adapts its motor behavior to changes in its internal and external environments [1, 2]. Much is known about adaptively optimizing the amplitude and direction of eye and limb movements, for example, but little is known about another essential form of learning, “set-point” adaptation. Set-point adaptation balances tonic activity so that reciprocally acting, agonist and antagonist muscles have a stable platform from which to launch accurate movements. Here, we use the vestibulo-ocular reflex—a simple behavior that stabilizes the position of the eye while the head is moving—to investigate how tonic activity is adapted toward a new set point to prevent eye drift when the head is still [3, 4]. Set-point adaptation was elicited with magneto-hydrodynamic vestibular stimulation (MVS) by placing normal humans in a 7T MRI for 90 min. MVS is ideal for prolonged labyrinthine activation because it mimics constant head acceleration and induces a sustained nystagmus similar to natural vestibular lesions [5, 6]. The MVS-induced nystagmus diminished slowly but incompletely over multiple timescales. We propose a new adaptation hypothesis, using a cascade of imperfect mathematical integrators, that reproduces the response to MVS (and more natural chair rotations), including the gradual decrease in nystagmus as the set point changes over progressively longer time courses. MVS set-point adaptation is a biological model with applications to basic neurophysiological research into all types of movements [7], functional brain imaging [8], and treatment of vestibular and higher-level attentional disorders by introducing new biases to counteract pathological ones [9].

Graphical abstract

RESULTS

Experimental Rationale and Protocols

To study set-point adaptation, we opted for a vestibular model since the unwanted spontaneous nystagmus that occurs after a unilateral labyrinthine lesion is an archetypical problem for the adaptation networks that adjust set points; they must restore balance centrally to overcome any persistent asymmetrical activity arriving from the periphery [10]. This nystagmus normally dissipates over time through adaptive processes [11, 12]. Using the effects of magnetic fields on the labyrinth of normal humans (magneto-hydrodynamic vestibular stimulation [MVS] due to Lorentz forces that act on fluids within the semicircular canals and push the cupula to a new position [5, 6, 13]), we created a surrogate vestibular lesion to study set-point adaptation. MVS is especially suited to study vestibulo-ocular reflex (VOR) set-point adaptation given current ideas that MVS simulates constant head acceleration and produces a sustained nystagmus. Because of properties of the labyrinth, and a central velocity-storage mechanism [14], the slow-phase velocity (SPV) induced by a constant acceleration should rise to a constant value with a time constant of 10–15 s [15, 16]. During sustained MVS, however, after reaching a maximum value, SPV slowly decays back toward a new but non-zero baseline. An adaptive process, inferring that sustained unchanging nystagmus is unnatural and pathological, supervenes toward eliminating the bias and unwanted eye drift. When the adaptive stimulus is abruptly removed, an aftereffect emerges with oppositely directed slow phases, revealing the prior adaptation.

Adaptation Paradigms

Nine healthy normals (seven males, two females; 21 to 65 years) were studied in a 7T MRI. MRI protocols and video eye movement recordings and analysis were as in earlier papers [6, 17, 18]. After obtaining baseline data, the subject was moved into the MRI bore center and remained there for fixed durations between 5 s and 90 min. Afterward the subject was moved out of the bore to the starting position and remained still while the reversal nystagmus was recorded. Vestibular nystagmus was also elicited with en bloc rotations in a motorized chair. For all recordings, subjects were in total darkness. All experiments were performed in accordance with an approved protocol by The Johns Hopkins University Institutional Research Board. (See Supplemental Experimental Procedures.)

MVS Is Comparable to Constant Acceleration

Seven subjects were exposed to constant acceleration stimuli of the same duration and direction using both MVS and chair rotations (Figures 1A and 1B). The responses were normalized to each subject’s maximum SPV to compare the two stimulus modalities. The normalized responses show that the MVS stimulus is comparable to constant acceleration produced by a rotatory chair (Figure 1B) with a very small root-mean-square difference of 0.429 ± 0.08 degrees/s. The time constant estimates at matched stimulus durations of 45–300 s were not significantly different between chair acceleration and MVS (Figure S1). There were small differences in the post-stimulatory decay in subjects s5 and s6 (see also Figure 1B).

Figure 1. Comparison of Rotatory Chair— Kinetic—and Magnetic Vestibular Stimulation.

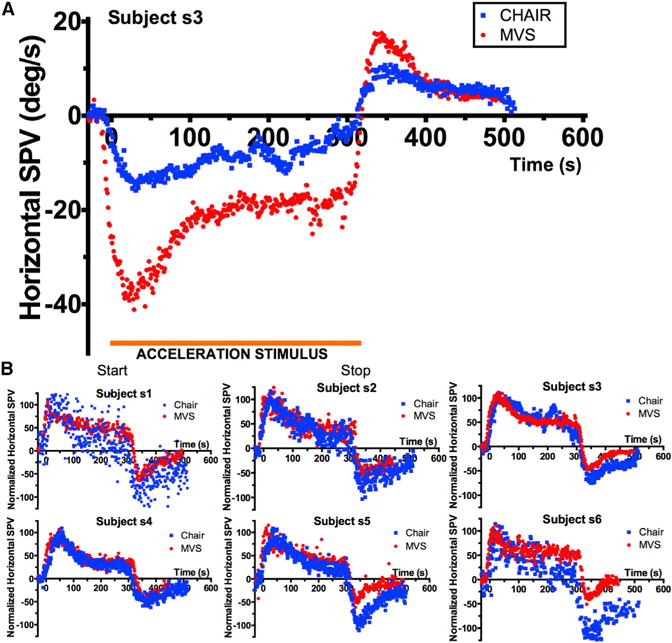
(A) Nystagmus response profile of a subject exposed to a rotation of constant acceleration (blue) and to MVS (red) of 300-s duration. The expected response of the cupula to MVS is a rise to a constant deflection (and a constant SPV), equivalent to the response to a rotation of constant acceleration. Nystagmus during the acceleration stimulus (orange demarcation) represents the perstimulatory response, that is, the response to a constant cupula deflection in both cases. Note that the nystagmus does not remain constant but decays toward a new, above zero, steady-state level. When the constant acceleration stimulus stops, the cupula returns to, but not beyond, its original position, and a post-stimulatory aftereffect emerges.

(B) Comparison of normalized responses to rotational and magnetic-field stimulation in six subjects showing the responses are largely comparable, though some subjects showed more adaptation with the chair stimulus, especially as reflected in the post-stimulation behavior. Responses are normalized to a maximum response of 100 for both rotational and magnetic-field stimulation.

Abbreviations are as follows: SPV, slow-phase velocity; CHAIR, rotatory chair (kinetic) stimulation; MVS, magnetic vestibular stimulation. See also Figures S1 and S2.

In control experiments, we showed that chair acceleration amplitude did not significantly affect the estimated per-stimulatory and post-stimulatory decay time constants (Figure S2). As predicted by the physical model of MVS [6], changing the head orientation in the MRI bore on separate trials altered nystagmus amplitude and direction, but not adaptation dynamics. Likewise, direction of acceleration did not affect the adaptation dynamics. Responses were the same in two individuals who were tested twice with the same stimulus.

Adaptation to Constant Acceleration Is Incomplete and Has More Than One Time Course

MVS allowed us to increase the stimulus duration up to 90 min, considerably beyond that possible with chair accelerations. In all cases, some nystagmus was still present at the end of stimulation. Figures 2A–2C show the responses for three subjects (s3, s8, s9) for 90-min stimulation. VOR adaptation remains incomplete with the residual SPV being between 5 and 10 degrees/s.

Figure 2. A Case for Incomplete Adaptation and Multiple Time Constants.

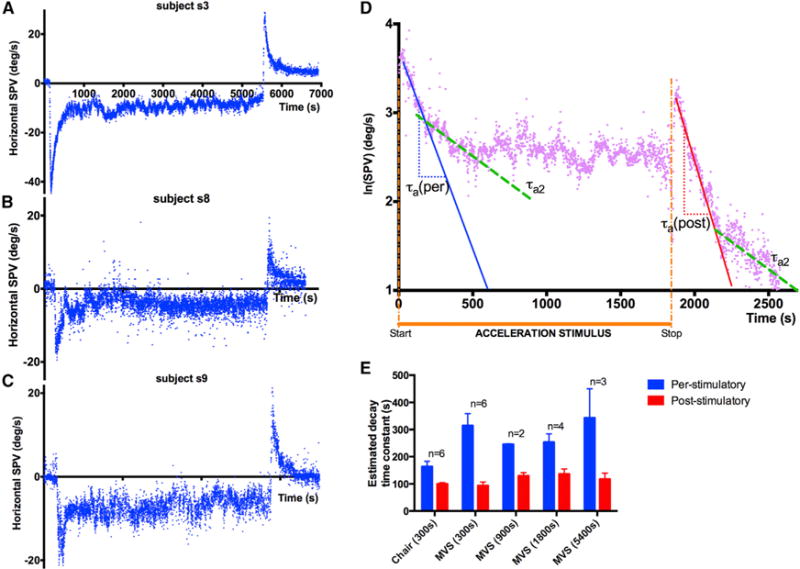
(A–C) Response of subjects s3, s8, and s9 to 90-min MVS (blue). SPV decreases during the per-stimulatory period but never reaches zero. Note the aftereffect in each case.

(D) ln(|SPV|) versus time graph of subject s3 during exposure to 30-min MVS shows two different slopes in both the per- and post-stimulatory responses.

(E) Per- and post-stimulatory responses across all trials are asymmetric as shown by the significant differences in decay time constants estimated from the first linear slopes of the per- (blue) and post-stimulatory (red) phase of the ln(|SPV|) time graph during the first 200 s of each phase. Error bars are SEM. p values using Student’s t test are as follows: Chair (300 s) p = 0.02; MVS (300 s) p < 0.01; MVS (900 s) p = 0.01; MVS (1,800 s) p = 0.02; MVS (5,400 s) p = 0.01. n = number of subject that could be tested at each duration. No significant difference between per-stimulatory time constants (heights of blue bars) between MVS of different durations (p = 0.66, ANOVA). No significant difference between post-stimulatory time constants (heights of red bars) between MVS of different durations (p = 0.27, ANOVA).

Figure 2D shows the SPV data for s3 during 30-min MVS stimulation plotted as a ln(|SPV|) versus time. We see two slopes in both the per- and post-stimulatory phases, suggesting that the adaptive response reflects at least a two time constant process. The other subjects showed a similar pattern of response. The adaptation response during the MVS stimulus and the reversal nystagmus aftereffect were asymmetrical; the latter decayed more rapidly (Figure 2E).

Constructing a New VOR Adaptation Model

Historically, VOR models used engineering control systems “operators” to transform head velocity (H) to eye velocity (EV). Such models allow us to test qualitative hypotheses about neural circuits using a scaffolding of mathematical operators upon which we input our stimuli (in our case MVS) and optimize various parameters (but do not alter the model structure itself) to see whether the output matches the data. Using the same optimized simulation parameters we further validate the model with a different stimulus (in our case head rotations) to see whether its output matches the behavioral response. The first VOR models deduced a high-pass filter (sT_cup/(sT_cup + 1)) to represent semicircular canal-cupular dynamics, explaining the nystagmus response to a constant-velocity step [16]. The human cupula time constant (T_cup) is estimated at 3.5–8 s from models based on rotational [19] and caloric [20] stimuli. Consistent with this, the time constant of primary afferent discharge in monkeys is about 6–7 s [15]. A central “velocity storage” pathway (e.g., a positive feedback loop with a low-pass filter (1/(sT_vsm + 1)) was added to account for the 3-fold larger (12–21 s) behavioral VOR time constant (T_vor) [14].

To explain adaptation to sustained labyrinthine stimulation by constant acceleration, early models used a low-pass filter that integrated the signal from the peripheral vestibular organs and subtracted it from the unadapted output, either in feedback or feedforward manner [21, 22]. Subsequent models incorporated the velocity-storage mechanism with adaptation [23–25]. Here, using our observations from long-duration MVS trials (Figures 2 and 3) and data from previous reports of MVS [5, 6] and caloric stimuli [20, 26], we developed a model to address our finding of incomplete adaptation and test the hypothesis that there are multiple time courses of adaptation to an artificially induced, sustained vestibular imbalance.

Figure 3. VOR Adaptation Models: A Developmental Perspective.

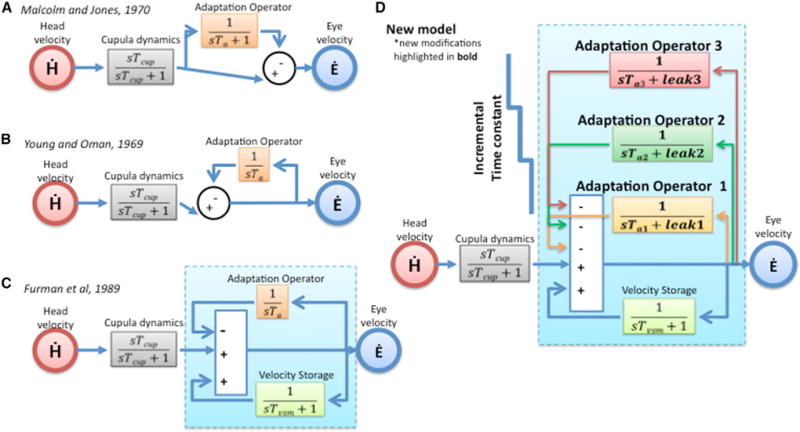
(A and B) Early adaptation models by Malcolm and Jones, 1970 [22] (A) and Young and Oman, 1969 [21] (B) used a single feedforward or feedback adaptation integrator, respectively.

(C) Furman et al., 1989 [23] incorporated the central “velocity storage” mechanism into the model.

(D) Our new model builds on two new ideas: (1) adaptation operators are variably leaky integrators (modifiable leak and time constant parameters), and (2) there are multiple adaptation operators with progressively different dynamics (Ta3 > Ta2 > Ta1).

See also Figures S3 and S4 and Table S1.

Our solution builds on two key ideas:

1. Adaptation operators are imperfect leaky integrators that do not store signals with fidelity. For conceptual simplicity, we adopt a formalism for describing the adaptation operator that emphasizes a leak and an internal time constant parameter. The degree of incomplete adaptation is proportional to a “leak” parameter in the adaptation operator: 1/(sT_a + leak), which is mathematically equivalent to the more commonly used notation:

   $$\mathrm{K}\ast (1/{\text{sT}}_{\mathrm{b}}+1)=(1/{\text{sT}}_{\mathrm{a}}+\text{leak})\text{with}\mathrm{K}=1/\text{leak}\text{and}{\mathrm{T}}_{\mathrm{b}}={\mathrm{T}}_{\mathrm{a}}/\text{leak}.$$

2. More than one adaptation operator exists with different dynamics and in our case three adaptation operators, with progressively slower dynamics and diminishing leak, acting in parallel: adaptation operator 1 [1/(sT_a1 + leak1)], adaptation operator 2 [1/(sT_a2 + leak2)], adaptation operator 3 [1/(sT_a3 + leak3)].

Deriving the New Components of the VOR Model

Starting with the pre-existing VOR models (Figures 3A–3C), we found that complete adaptation was incompatible with our data (Figures 2A–2C). Hence, we used an imperfect integrator (1/sT_a + leak) and by varying the parameter leak, different degrees of incomplete adaptation, leaving different amounts of residual nystagmus, can be achieved (Figure S3A). Next, the model must account for the multiple time constant process as shown in Figure 2D. Our solution was to add additional, slower adaptation operators with longer time constants than the first (Figure 3D). Optimized models with two adaptation operators (opt2) and three adaptation operators (opt3) fit the data better across all paradigms, both qualitatively (Figures 4A–4C) and quantitatively (Figure 4D; p < 0.01 for all comparisons).

Figure 4. Model Fits to MVS and Chair Rotations.

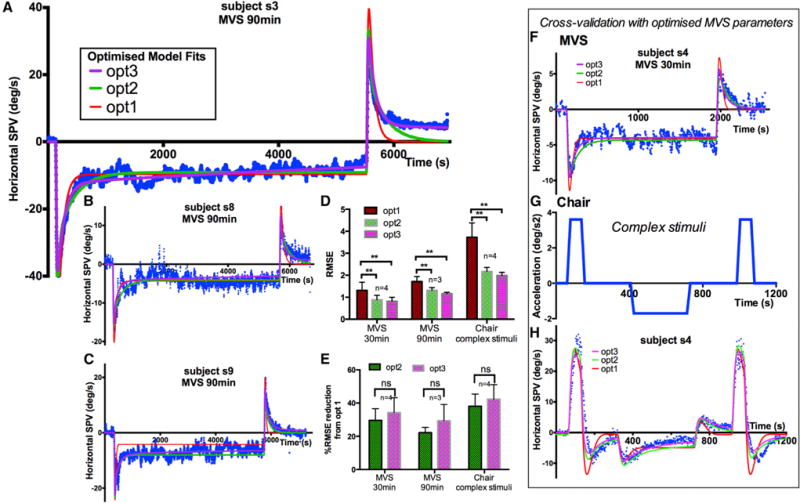
(A–C) 90-min stimulation, subjects 3, 8, and 9. Optimized two-adaptation model (green) and three-adaptation model (purple) better fit the MVS data than a one-adaptation model (red).

(D) Goodness-of-fit comparisons between optimized models for 30 and 90 min of MVS and chair rotation. Statistical significance of p < 0.01 between all comparisons indicated by **.

(E) Improvement of goodness of fit with multiple adaptation models compared to single adaptation model. Qualitatively, the three-adaptation model (purple) best fits the graphs.

(F–H) Cross-validation using MVS parameters with data from complex chair rotations for subject 4. The parameters of simulations for individual subjects are shown in Table S1.

RMSE, root-mean-square-error.

The differences between two and three time course fits were more difficult to determine quantitatively because the third time course is so slow that an extended period of stimulation would be needed to reach statistical significance. In Figure 4E, we quantified the improvement in goodness of fit with a percentage reduction in root-mean-square-error (RMSE) from the optimized single adaptation operator model (opt1) and found no significant difference between two and three adaptation operators. Nevertheless, a three time course explanation is biologically plausible, as nystagmus eventually disappears in most humans who have unilateral labyrinthine loss. Our data show a trend for better fits with three adaptation time courses (Figure 4E), and the nystagmus versus time plots (Figures 4A–4C) show the data is fit better for each subject by three time courses than two in at least some part of the MVS response (e.g., Figures 4A and S3, post). See Table S1 for optimized parameter values for individual subjects.

To validate our approach, we applied the optimized parameters from modeling of MVS to data generated by a complex rotatory chair stimulus with multiple steps of acceleration in both directions (Figures 4F–4H). Models with two and three adaptation operators using optimized parameters from MVS fit the rotational data best (Figures 4D and 4E). The effects of varying adaptation time constants and leaks in isolation and of velocity storage are shown in Figures S3A–S3D.

DISCUSSION

A major function of our motor control systems is to conquer challenges to stability, from gravity, the changing biomechanics of growth and aging, and life’s vicissitudes including exposure to disease and trauma. Here, we have explored a core aspect of this problem, how the brain adjusts set points, the levels of activity that ensure stable postures at rest and allow us to launch movements from solid platforms. We chose a simple model, the VOR, and a novel way of stimulating it, MVS. Our data and modeling provide strong evidence that MVS is comparable to a more natural vestibular stimulus, constant head acceleration. Using the unique characteristics of MVS that make it ideal for studying mechanisms that eliminate unwanted biases in neural activity—set-point adaptation—we show that existing models do not account for timescales of vestibular adaptation of many minutes to hours. Combining data from MVS and vestibular chair rotations, we suggest that (1) adaptation can be interpreted by considering its underlying mathematical operators as variably leaky integrators, and (2) the vestibular system has multiple adaptation operators with different dynamic properties.

What to Infer from Our Results? Comparison with Other Approaches to Learning

From our control engineering perspective, set-point adaptation can be implemented by adaptation operators, representing mathematical integrators of varying fidelity (Figure S4). The greater the integrator time constant, the slower the pace of learning toward the new set point, but the reversal nystagmus (the aftereffect) lasts longer. In our formalism, the leak variable of an adaptation operator represents the degree to which the adapted state approximates the environment; the smaller the leak, the closer the adaptation operator approximates the new set point (Figure S3A). Building on prior work [5, 6, 23, 25–29], we developed a model that accounts for both incomplete and multiple timescales in vestibular set-point adaptation.

One can consider analogies in other theoretical approaches to learning. Interpreted from a Bayesian perspective, one can better infer what enduring behaviors are desired when more information about the environment is collected over longer time periods [2, 30–33] (Figure S4B). A Skinnerian behaviorist would notice an analogy between our adaptation curves and behavioral training and extinction curves [34] (Figure S4C). From this perspective, the more suppression behavior of an unwanted perturbation is reinforced, the longer the extinction curve. Underlying each of these theoretical languages is the concept of adaptation—the process by which one learns to respond optimally to a new environment. What is emphasized here is the concept of multiple time courses of learning with different dynamics that could be integrated with Bayesian and Skinnerian approaches [35].

Set-point adaptation is found in other eye movement systems including eye alignment (phoria adaptation [36]) and the mechanisms that reset the “straight-ahead” or null position, e.g., the rebound phenomenon after holding the eyes eccentrically in the orbit [37] or holding the head eccentrically on the torso [38]. Support for a cascade of progressively longer-term learning processes to sustained environmental change also follows from studies of adaptation of dynamic motor behavior, including VOR amplitude [39] and the accuracy of saccades [40, 41] and reaching [35, 42, 43].

Particularly relevant to VOR set-point adaptation is the podokinetic response (stepping in place) following prolonged marching on a rotating wheel. The afterresponse suggests two adaptation processes with time constants of 15 s and 300 s, and even longer periods of stimulation suggest a third on the order of hour(s) [44]. Since our VOR adaptation timescales are close to those for podokinetic adaptation [45], one can speculate the vestibular and podokinetic systems share similar central adaptation operators within a central balance network that incorporates multiple sensory signals [4, 46, 47].

What Is the Neurophysiology of Set-Point Adaptation?

We know relatively little about vestibular set-point adaptation. Unlike dynamic VOR adaptation, visual error signals do not seem necessary to eliminate a spontaneous nystagmus [48]. Physiological investigations show adaptation processes of various time constants in labyrinthine hair cells and vestibular afferents [15, 49]. The importance of central adaptation mechanisms has been inferred from studies in normal subjects [23, 24] and in cerebellar patients with periodic alternating nystagmus, which occurs without labyrinthine stimulation [25]. Further support comes from studies of perception [50].

Limitations, Caveats, and Future Directions

While our modeling matches our data remarkably well, and our observations were robust and largely consistent within and among subjects, there are still caveats. First, the aftereffects with chair rotations and MVS showed small differences. Perhaps they are from small differences in the patterns of canal and otolith stimulation between chair rotations and MVS. There are also variations in labyrinthine geometry among people, and one’s “adaptation history,” already imprinted in the brain, could influence adaptive responses to new challenges. Second, our model did not reproduce differences between per- (during MVS) and post-stimulation adaptive responses. Forgetting simply may be faster than learning until the need for a more enduring change becomes trusted and the desired response is solidified. Furthermore, when subjects are in the magnetic field, the inputs from the semicircular canals and the otoliths are at odds since the canals signal rotation but the otoliths do not, as head orientation to gravity is unchanging. When out of the magnetic field, however, the otolith and canal inputs quickly become congruent, both signaling the head is still, so forgetting the new set point (or relearning the old set point) could be faster. Third, while our model does not account for the complete absence of nystagmus that occurs over days or weeks, as with naturally occurring, more permanent challenges to the VOR, it can predict the amount of residual nystagmus for stimulus durations beyond 90 min. Fourth, sustained MVS-induced nystagmus differs from pathological loss of labyrinthine function. With MVS, the labyrinths are intact, and one is stimulated and the other inhibited, a pattern close to natural rotation. Nevertheless, MVS still elicits set-point adaptation since the brain assumes the sustained nystagmus derives from a pathology. Finally, we reiterate our data were remarkably consistent considering inherent biological variability, our hypotheses are plausible in view of what is known about motor learning, and our analyses suggest we will find further, even slower adaptation operators that progressively eliminate residual biases as stimulation time increases.

A beauty of MVS is the ability to produce a sustained peripheral vestibular imbalance, similar to a unilateral vestibular lesion, relatively effortlessly, for hours in humans or experimental animals. This cannot be achieved with other vestibular stimuli and allows one to investigate the multiple timescales of adaptation to a sustained, unwanted vestibular imbalance. Combined with MRI imaging, MVS might reveal the anatomical substrate and changes in default networks that underlie vestibular adaptation [8]. Finally, MVS might be used in rehabilitation in set-point adaptation diseases by inducing a new bias to counteract a pathological one. Examples include not only vestibular dysfunction but higher-level behavioral disorders such as unilateral visual neglect, which can be ameliorated in response to other types of vestibular stimuli [9].

Highlights.

• MRI vestibular stimulation acts as head acceleration, producing sustained nystagmus

• After 90-min exposure, the presumed pathological nystagmus is partially removed

• Multiple adaptation time courses are shown, reflecting set-point (bias) adaptation

• We propose a cascade of imperfect integrators of progressively slower dynamics