Electronic Structure of the Ferryl Intermediate in the α-Ketoglutarate Dependent Non-Heme Iron Halogenase SyrB2: Contributions to H Atom Abstraction Reactivity

Abstract

Low temperature magnetic circular dichroism (LT MCD) spectroscopy in combination with quantum-chemical calculations are used to define the electronic structure associated with the geometric structure of the Fe^IV═O intermediate in SyrB2 that was previously determined by nuclear resonance vibrational spectroscopy. These studies elucidate key frontier molecular orbitals (FMOs) and their contribution to H atom abstraction reactivity. The VT MCD spectra of the enzymatic S = 2 Fe^IV═O intermediate with Br⁻ ligation contain information-rich features that largely parallel the corresponding spectra of the S = 2 model complex (TMG₃tren)Fe^IV═O (Srnec, M.; Wong, S. D.; England, J; Que, L; Solomon, E. I. Proc. Natl. Acad. Sci. USA 2012, 109, 14326–14331). However, quantitative differences are observed that correlate with π-anisotropy and oxo donor strength that perturb FMOs and affect reactivity. Due to π-anisotropy, the Fe^IV═O active site exhibits enhanced reactivity in the direction of the substrate cavity that proceeds through a π-channel that is controlled by perpendicular orientation of the substrate C–H bond relative to the halide–Fe^IV═O plane. Also, the increased intrinsic reactivity of the SyrB2 intermediate relative to the ferryl model complex is correlated to a higher oxyl character of the Fe^IV═O at the transition states resulting from the weaker ligand field of the halogenase.

Graphical abstract

1. INTRODUCTION

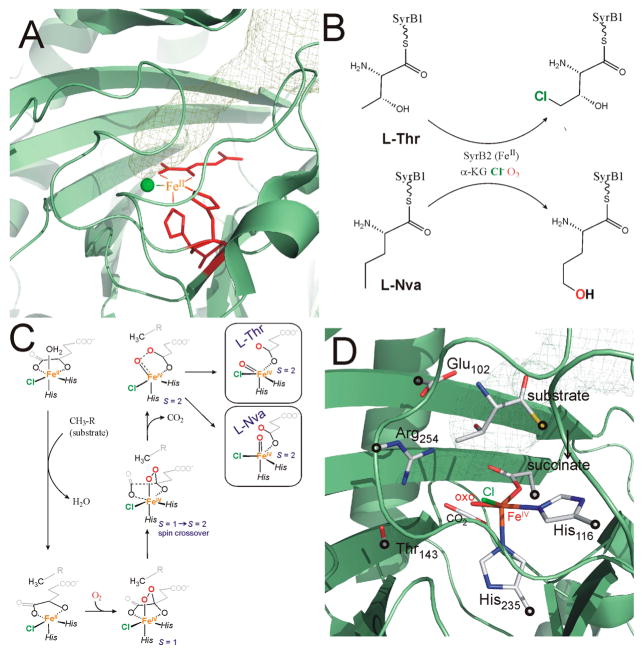
Syringomycin halogenase (SyrB2) is a member of the mononuclear nonheme iron (NHFe) enzymes family that activates ³O₂, through formation of a key high-spin (S = 2) Fe^IV═O intermediate, for H atom abstraction (HAA) from an unreactive C–H bond to perform halogenation or hydroxylation.¹ To date, six NHFe enzymatic Fe^IV═O intermediates have been trapped and spectroscopically characterized mostly by using Mössbauer spectroscopy, five of which are α-ketoglutarate (αKG) dependent (taurine dioxygenase (TauD),^2,3 prolyl-4-hydroxylase (P4H),⁴ cytotrienin halogenase (CytC3),^5,6 syringomicyn halogenase (SyrB2),^1,7 carbapenem synthase (CarC)⁸) and the other two are pterin dependent (tyrosine hydroxylase (TyrH)⁹ and phenylalanine hydroxylase (PheH)¹⁰). In the catalytic cycle of SyrB2, for which the substrate-free crystal structure from ref 11 is displayed in Figure 1A, the halide atom is incorporated into the methyl group of the L-threonine ~ SyrB1 substrate (Figure 1B) in the biosynthesis of the phytotoxin syringomycin E.¹²

Figure 1.

(A) View of the α-ketoglutarate (αKG)-bound Fe^II center in SyrB2 (taken from 2FCT.pdb).¹¹ Green sphere is the halide ligand, whereas red sticks correspond to the αKG and His₁₁₆/His₂₃₅ ligands; the mesh plot indicates the binding cavity for substrate as calculated by the Caver plugin in Pymol.²² (B) Halogenation of the native L-threonine substrate and hydroxylation of the non-native L-norvaline ~ SyrB1 (L-Nva) substrate as defined in ref 1. (C) O₂ activation pathway in SyrB2 in the presence of either L-Thr or L-Nva as calculated in ref 20. (D) The cluster model of the Fe^IV═O intermediate (stick representation) with fixed atoms indicated by ○, overlaid with protein backbone. For clarity, water molecules and hydrogen atoms are not displayed.

NHFe^IV═O enzyme intermediates have stimulated synthetic efforts to prepare Fe^IV═O compounds to elucidate crucial physicochemical factors that contribute to their reactivity in Nature.¹³ While most of the Fe^IV═O model complexes have low-spin (S = 1) ground states,¹⁴ some models have the S = 2 spin state that is present in the enzymatic intermediates.¹⁵ A combined spectroscopic and computational study of one of the S = 2 model complexes, (TMG₃tren)Fe^IV═O,^15a elucidated three reactive channels available for HAA: two are active when the C–H bond is oriented perpendicular to the Fe–oxo bond (π channels leading to S_Fe = 5/2 or S_Fe = 3/2 Fe^III–OH intermediates) and one that is active for C–H bonds oriented along the Fe–oxo bond (σ channel providing an S_Fe^III = 5/2 intermediate).¹⁶ This is strikingly different from the S = 1 Fe^IV═O complexes, which have only one available channel, π(S_Fe^III = 3/2).¹⁷ Thus, S = 2 active sites in NHFe enzymes have both π and σ channels providing flexibility in using different substrate orientations to control selectivity.¹⁸ Note that the σ- and π-channels for HAA reactivity of S = 1 and S = 2 NHFe^IV═O systems are also discussed in ref 19.

Recently nuclear resonance vibrational spectroscopy (NRVS), correlated with density functional theory, allowed elucidation of the structure of the Fe^IV═O intermediate in SyrB2.²⁰ This has a 5C, trigonal bipyramidal (TBP) structure with the Fe–oxo bond oriented along its ~ C₃ axis and perpendicular to the C–H bond of the substrate. This had important implications for π-channel reactivity in controlling halogenation (see also Figure 1C and D).²⁰

For the native L-threonine, L-Thr (and the alternative L-cyclopropylglycine, L-Cpg) substrate, this ferryl intermediate was shown to result from an O₂ activation pathway that involves the two-electron reduction of dioxygen by the αKG-bound Fe^II center to generate an S = 1 peroxy-bridged αKG-bound Fe^IV species that undergoes a subsequent two-electron reduction through an S = 1→ S = 2 oxidative decarboxylation of the αKG cofactor²¹ (summarized in Figure 1C). In the presence of the alternative substrate L-norvaline, L-Nva, the analogous O₂ reaction pathway was proposed to lead to an Fe^IV═O intermediate now with its Fe–oxo bond oriented toward the C–H bond of the substrate. This led to σ-channel reactivity (Figure 1C right) that was suggested to be important in the hydroxylation reaction with this substrate (Figure 1B).²⁰

In the present study we build on this NRVS-defined geometric structure of the Fe^IV═O intermediate in the halogenase. Variable-temperature magnetic circular dichroism (VT MCD) spectroscopy is performed on the Fe^IV═O SyrB2 intermediate with bound Br⁻ and correlated with high-level multireference ab initio and density functional theory (DFT) calculations to define the electronic structure of this Fe^IV═O intermediate. Quantitative comparison to our previous study¹⁶ of (TMG₃tren)-Fe^IV═O elucidates electronic structure contributions to their relative HAA reactivities.

2. EXPERIMENTAL AND COMPUTATIONAL DETAILS

2.1. Sample Preparation

Samples of the SyrB2 Br–Fe^IV═O intermediate with a concentration of ~ 1.8 mM were prepared as described in ref 7 and in the Supporting Information of ref 20 (therein see Figure S9).

2.2. Electronic Absorption (Abs) and Magnetic Circular Dichroism (MCD) Spectroscopy

The Abs spectrum of the enzyme was measured with the Agilent HP8453 diode array spectrophotometer at ~ 285 K. UV/vis VT MCD data (16 000–30 000 cm⁻¹) were collected on a Jasco J810 spectrophotometer with an extended S-20 photomultiplier tube, and near-infrared (NIR) VT MCD data (5000–16000 cm⁻¹) were collected on a Jasco J730 spectrophotometer with a liquid N₂-cooled InSn detector. The sample temperature was measured using a calibrated Cernox resistor (Lakeshore Cryogenics) inserted into the MCD cell. A magnetic field of 7T was applied using an Oxford SM 4000-7T superconducting magnet.

2.3. Vibronic-Structure Analysis

The Franck–Condon (FC) vibronic progressions are simulated in the harmonic approximation as a Poisson distribution:

$$\mathrm{\Delta }\epsilon =\sum _n\mathrm{\Delta }{\epsilon }_{0\to 0}\frac{S^n}{n!}exp\left[-\frac{2.733}{{\mathrm{\Delta }}_{\text{FWHM}}^2}{(E-n\mathrm{\Delta }E-E_{0\to 0})}^2\right]$$ (1)

where S is the Huang–Rhys factor defined by the equation Sⁿ/n! = Δε_0→n/Δε_0→0 reflecting the progression band shape, ΔE is the vibronic spacing corresponding to the frequency of the excited-state Fe–oxo stretching mode (in cm⁻¹), Δ_fwhm is the full width in the half-maximum of each individual peak in the progression (in cm⁻¹), Δε is the intensity distribution over the band, and E_0→0 and Δε_0→0 are the energy (in cm⁻¹) and the intensity maximum (in M⁻¹ cm⁻¹) of the first peak in the progression. E is the variable photon energy (in cm⁻¹). The excited-state distortion (along Fe–oxo bond) with respect to the ground state, ΔQ (in Å), is obtained from

$$\mathrm{\Delta }Q=8.213\sqrt{\frac{S}{\mu \mathrm{\Delta }E}}$$ (2)

with the reduced mass μ of the Fe–oxo stretching mode that is considered in this study to be 15 amu; S and ΔE (in cm⁻¹) are defined above. The parabolic shape of the excited-state potential-energy surface (PES) and its ΔQ and energy (relative to the ground-state PES) along the mode Q is derived from the FC analysis using

$$E_{\text{PES}}=1.4825\times {10}^{-2}\mu {(\mathrm{\Delta }E)}^2{[Q-(Q_0+\mathrm{\Delta }Q)]}^2+E_{min}$$ (3)

where μ (in amu), ΔQ (in Å), and ΔE (in cm⁻¹) are defined above; E_PES is the energy of the PES (in cm⁻¹) along Q that corresponds to the Fe–oxo bond length (in Å) with Q₀ as the ground-state equilibrium geometry (in Å); and E_min is the energy of the excited-state PES minimum (in cm⁻¹), which is determined as E_0→0 + (ΔE_GS−ΔE)/2, where E_0→0 and ΔE are defined above and ΔE_GS is the frequency of the Fe–oxo stretching mode in the ground state.

2.4. Structural Model

If not stated otherwise, the cluster model of the Br⁻/Cl⁻ ligating ferryl intermediate, which was taken from ref 20, consists of one Fe center, one halide, one crystal water molecule, truncated (His_116, His₂₃₅, succinate) ligands, truncated second-shell (Arg₂₅₄, Thr₁₄₃, Glu₁₀₂) residues, and a substrate fragment with its thioester group capped by a H atom (see Figure 1D for the truncated model consisting of 89 atoms). (TMG₃tren)Fe^IV═O was taken from ref 16.

For RASSCF/CASSCF/CASPT2 calculations (section 2.6), the size of the structural model of (SyrB2)Fe^IV═O was reduced to 53 atoms (only the Arg₂₅₄ fragment and one (crystal) water molecule are present in the second shell; see Figure S1), while the truncated model of (TMG₃tren)Fe^IV═O was taken from ref 16.

2.5. Density Functional Theory Calculations

Most of DFT calculations reported in this study were performed using the Turbomole 6.3 program.²³ Unless otherwise mentioned, the hybrid three-parameter Becke’s (B3LYP)²⁴ functional with the empirical correction to dispersion effect (+D2)²⁵ was used throughout. All of the geometry optimizations were carried out using the def2-SVP basis set, whereas the single-point energies were recomputed with the def2-TZVP basis set.

In single-point calculations, to allow for solvation effects, the conductor-like screening model (COSMO) was used with a dielectric constant reflecting the protein environment (ε_r = 4.0).

Reaction and activation Gibbs free energies were evaluated (using the option “frznuclei” for the vibrational analyses of systems with fixed atoms) according to the equation:

$$\mathrm{\Delta }{G}^{(\ne )}=\mathrm{\Delta }{E}_{\text{el},\text{solv}}^{(\ne )}+\mathrm{\Delta }{E}_{\text{ZPE}}^{(\ne )}-RT\mathrm{\Delta }\text{ln}{q}_{\text{vib}}^{(\ne )}{q}_{\text{rot}}^{(\ne )}{q}_{\text{trans}}^{(\ne )}$$ (4)

where $\mathrm{\Delta }{E}_{\text{el},\text{solv}}^{(\ne )}$ is the reaction (or activation) energy of the solvated system (at the B3LYP+D2/def2-TZVP/COSMO_(εr=4.0)//B3LYP+D2/def2-SVP level), $\mathrm{\Delta }{E}_{\text{ZPE}}^{(\ne )}$ is the change in zero-point energy, and $-RT\mathrm{\Delta }\text{ln}{q}_{\text{vib}}^{(\ne )}{q}_{\text{rot}}^{(\ne )}{q}_{\text{trans}}^{(\ne )}$ accounts for the change in the reaction (or activation) entropic terms and the thermal correction to the enthalpy as obtained from a frequency calculation (at 298 K, 1 atm; ideal-gas approximation) using the geometry optimization calculations.

2.6. CASSCF/CASPT2/SO-CASSI Calculations

The state-average complete active space self-consistent field (SA-CASSCF)²⁶ and multistate complete active space second-order perturbation theory (MS-CASPT2)²⁷ calculations were carried out using the MOLCAS 7.4 program.²⁸ For all of the atoms, the ANO-RCC basis set (contracted to [7s6p5d2f1g] for Fe, [6s5p3d] for Br, [4s3p1d] for the ligating O, N atoms, [3s2p] for other N, O, and C atoms, and [2s] for H) was used. The second-order Douglas–Kroll–Hess (DKH2) one-electron spinless Hamiltonian was applied for all of the calculations in order to allow for spin-free relativistic effects.²⁹

The SA-CASSCF/MS-CASPT2 potential energy surfaces along the Fe–O vibration mode of the Br–Fe^IV═O intermediate (obtained from the BP86/def2-SVP frequency analysis using the G09 program package³⁰)²⁰ were calculated with the 16-electrons-in-11-orbitals active space including 5 d_Fe, 3 p_oxo, and 3 ligand-based orbitals (orbitals and further technical details of the CASSCF calculations are in the Supporting Information (SI), Figure S2). The state-average CASSCF and multistate CASPT2 calculations were performed over the three lowest S = 2 and ten lowest S = 1 states.

As an extension of the CASSCF approach, the state-average restricted active space self-consistent field (SA-RASSCF)³¹ calculations were used for simulating electronic spectra (for technical details, see SI on pp S4–S5 and Figure S3). Within these RASSCF calculations, the RAS3 subspace includes Fe 4d orbitals to partially account for the double-shell effect to improve the accuracy of the calculated spectra.³²

Spin–orbit couplings (SOCs) were calculated using the spin–orbit complete active space state interaction (SO-CASSI) method and solving the generalized eigenvalue problem of first-order QDPT [taking the atomic mean-field integral (AMFI) spin–orbit Hamiltonian³³ as the perturbation] to obtain the SOC-corrected quasi-relativistic energies.³⁴ To improve the accuracy of the calculations, the CASPT2 energies were used on the diagonal of the two-component Hamiltonian matrix.

In all of the CASSCF or RASSCF calculations, a level shift of 0.5 au was used in order to improve convergence. In the CASPT2 calculations, none of the orbitals were frozen, and an imaginary level shift of 0.2 au was used to eliminate intruder states.³⁵

3. RESULTS AND ANALYSIS

3.1. Absorption and MCD Spectra of SyrB2 Br–Fe^IV═O Intermediate

3.1.1. Band Assignments and Correlation to Spectra of the (TMG₃tren)Fe^IV═O Model Complex (from Ref 16)

Figure 2A shows the UV–visible Abs and VT MCD spectra of the high-spin (S = 2) SyrB2 Br–Fe^IV═O/L-Cpg intermediate. The abs spectrum shows a weak feature at 12 000 cm⁻¹ and two more intense broad features centered at 19 000 and 26 000 cm⁻¹. These become much more well-resolved and feature-rich in the LT MCD spectrum, which thus allows definitive band assignments for electronic-structure elucidation.

Figure 2.

(A) Absorption (top) and VT MCD spectra (bottom) of SyrB2 Br–Fe^IV═O. The * indicates a minor heme contaminant in the sample. (B) Absorption (top) and VT MCD spectra (bottom) of the (TMG₃tren)Fe^IV═O model complex taken from ref 16. Absorption spectra of both species were fitted by Gaussians through correlation with the MCD data. Three lowest-energy bands in all spectra are labeled I, II, and III. All MCD spectra were measured at a magnetic field of 7T.

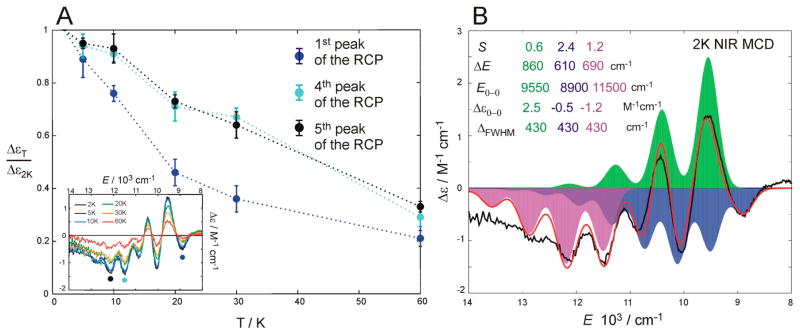
First, within the theory developed in ref 36, fitting the temperature dependence of the MCD bands (data given in Figure 2B varying from T = 2 K through 60 K) allows an estimate of the zero-field splitting (ZFS) parameters that are D = +7 cm⁻¹ and E/D = 0.02 for SyrB2 Br–Fe^IV═O (Figure S4). These parameters are in the range of those determined from magnetic Mössbauer spectra of the Cl–Fe^IV═O intermediate in halogenase CytC3 (D = +7 cm⁻¹ and E/D = 0.02).⁵ Once the ZFS is known, the polarizations of the MCD bands can be determined using the methodology from refs ^{17, 37} (described in the caption to Figure S4). The positive ZFS D parameter gives the splitting of the ±M_s sublevels of an S = 2 species with M_s = 0 lowest in energy. For a z-polarized transition, the lowest-energy sublevel at a magnetic field of 7T is the MCD-active M_s = −1, so the MCD intensity is high at low T and decreases with an increase in T because the population of the M_s = −1 sublevel decreases, and the populations of the MCD-inactive M_s = 0 and the opposite-signed M_s = +1 increase. For x/y- polarized transitions, the magnetic field has a nonvanishing component along the z axis for MCD intensity and the lowest sublevel at 7T is the MCD-inactive M_s = 0 sublevel. This leads to MCD intensity that decreases with increasing temperature at a lower rate than the z-polarized MCD intensity due to populations of the MCD-active M_s = +1 and M_s = −1 sublevels that produce MCD intensities of opposite signs (Figure S4).

In the near-infrared region (NIR), between 6000 and 15000 cm⁻¹, there are distinct positive and negative MCD Franck–Condon (FC) vibronic progressions centered around 11000 cm⁻¹ that form a derivative-shaped pseudo-A term with the negative component at higher energy (feature I in the MCD spectrum in Figure 2A). The temperature-dependent behavior of the pseudo-A term feature indicates that it is x/y-polarized (Figure S4). This transition has a fairly large MCD-to-absorption intensity (C₀/D₀) ratio (0.150) allowing it to be assigned as a ligand-field (LF) transition. The NIR VT MCD spectrum of the SyrB2 Br–Fe^IV═O intermediate is remarkably similar in terms of band energy, derivative band shape, C₀/D₀ ratio, and temperature dependence to the MCD spectrum of the S = 2 (TMG₃tren)Fe^IV═O model complex studied in ref 16 (and included for comparison in Figure 2B and Table 1). It is noteworthy that despite these similarities, the pseudo-A feature in Br–Fe^IV═O is approximately three times weaker than the equivalent MCD feature in (TMG₃tren)Fe^IV═O (its C₀/D₀ for feature I is ~ 0.250). Overall, these results allow assignment of the NIR MCD band I in (SyrB2)Fe^IV═O as the ⁵A → ⁵E LF transition involving electron excitation from the d_xz π* and d_yz π* orbitals into the d_z2 σ* orbital, transitions that are degenerate in the C₃ symmetry of (TMG₃tren)Fe^IV═O.

Table 1.

Spectroscopic Characteristics of SyrB2 Br–Fe^IV═O vs (TMG₃tren)Fe^IV═O Species As Derived from Analyses of MCD/Abs Data in Figure 2, and Band Assignments

	SyrB2-Br			TMG3tren
featurea	type of the MCD feature	C0/D0b	band polarizationc	type of the MCD feature	C0/D0b	band polarizationc	band assignment
I	pseudo-A term	0.150	x/y	pseudo-A term	0.250	x/y	LF
II	negative C term	0.005	z	negative C term	0.040	z	oxo-to-Fe CT
III	positive C term	0.050	z	positive C term	0.002	z	oxo-to-Fe CT

^aMCD and Abs spectral features labeled as I, II, and III in Figure 2.

^bC₀/D₀ = k_BT/μ_BH(Δε/ε)_max.

^cAs shown in Figure S4, polarization directions depend on the signs of the spin-Hamiltonian zero-field splitting (ZFS) parameters (axial D and rhombic E) which were determined from the fit of VT MCD data: (i) (SyrB2)Fe^IV═O: D = +7 cm⁻¹ and E/D = 0.02; (ii) (TMG₃tren)Fe^IV═O D = +5 cm⁻¹ and E/D = 0.02 from ref 15a.

In the 15 000–30 000 cm⁻¹ region of the MCD spectrum, there are four temperature-dependent MCD features located at ~ 17 500, ~ 21 500, ~ 24 000, and ~ 27 000 cm⁻¹. The two lower-energy bands (labeled II and III in Figure 2A) are determined from the temperature-dependence MCD intensity (Figure S4) to be z-polarized C terms that can be assigned to charge-transfer (CT) transitions on the basis of their low C₀/D₀ ratios of 0.005 and 0.050, respectively. The two higher-energy MCD features at ~ 24000 and ~ 27000 cm⁻¹ in Figure 2B cannot be analyzed because of a minor overlapping heme contaminant in the sample (that produces a large MCD contribution). As in the near-infrared region, the UV–vis VT MCD spectra of SyrB2 Br–Fe^IV═O and (TMG₃tren)Fe^IV═O (bands II and III from Figure 2A and B) have very similar spectroscopic characteristics including MCD signs, their polarizations along the molecular z axis, and C₀/D₀ ratios. This comparison is summarized in Table 1 and in parallel to ref 16 bands II and III are assigned as oxo-to-Fe CT transitions. However, note that the bands for SyrB2 are shifted ~ 2000–3000 cm⁻¹ to lower energies as compared to those of the (TMG₃tren)Fe^IV═O model complex. This shows that the oxo group is a better electron donor in SyrB2 Br–Fe^IV═O than in (TMG₃tren)Fe^IV═O indicating that the ligand field strength of the metalloenzyme active site is weaker than that of the model complex. Note, from this correlation to the Fe^IV═O model complex that has no Br⁻ ligand, the Br-to-Fe^IV CT transitions must be higher in energy than band III in the enzyme. This is also consistent with calculations (vide infra).

3.1.2. Band I Pseudo-A Term and Vibronic Structure Analysis

The pseudo-A term of band I has a well-resolved vibronic structure with irregular spacing in both the positive and negative components indicating overlapping progressions of opposite sign. Indeed, the pseudo-A term is reasonably fitted by two Franck–Condon (FC) vibronic progressions (see Figure 3A). These FC progressions differ mostly in band shape, as represented by the Huang–Rhys parameters (S = 0.6 vs 2.6 for the lower-energy positive vs higher-energy negative component) and in the spacing between adjacent peaks that gives the frequency of the Fe–oxo stretching mode in the excited state (ΔE = 860 vs 650 cm⁻¹ for the positive vs negative component; cf., 710 vs 880 cm⁻¹ for the model complex (TMG₃tren)Fe^IV═O from ref 16). Using these FC parameters and the methodology in section 2.3, the two harmonic exited-state potential-energy surfaces (PES) corresponding to the positive (i.e., left circularly polarized, LCP) and the negative (i.e., right circularly polarized, RCP) vibronic progressions were derived (Figure 3B). These parabolas are clearly different: the PES of the RCP state is broad and more distorted from the ground-state minimum and higher in energy at the ground-state equilibrium geometry than the PES for the LCP state. From these PESs, the RCP state becomes lower in energy at the longer Fe–O bond lengths relevant to the TS of the π channel for HAA (vide infra)

Figure 3.

(A) The NIR pseudo-A term (black) fitted according to the eq 1 by two FC vibronic progressions (the LCP component in green, the RCP component in blue and their sum in red). Values of FC progression parameters, defined in section 2.3, are also displayed. The value of 600 cm⁻¹ corresponds to the separation between the zero-phonon energies of the blue vs green FC progression (i.e., separation of the ground vibrational levels of the RCP vs LCP state). The value of 700 cm⁻¹ corresponds to the energy splitting between the most intense vibronic peaks of the green vs blue FC progression, reflecting the LCP vs RCP state splitting at the ground-state equilibrium. Both values are also indicated in Figure 3B. (B) Parabolic PES representations obtained from FC fits as calculated using the eqs 2 and 3. The Fe–oxo stretching frequency (800 cm⁻¹) is assumed for the ground-state parabola. The excited-state distortions, ΔQs, were obtained from eq 2.

There are thus quantitative differences in what was found from the MCD spectrum of the (TMG₃tren)Fe^IV═O species for the ⁵A → ⁵E LF transitions relative to the results for (SyrB2)Fe^IV═O. For (TMG₃tren)Fe^IV═O, the high-energy RCP component of the pseudo-A term in the NIR MCD spectrum had a smaller Huang–Rhys factor and larger vibronic spacing (S = 1.2 and ΔE = 880 cm⁻¹)¹⁶ reflecting a narrower, less distorted PES for the RCP state as compared to the PES of the LCP state (S = 2.8 and ΔE = 710 cm⁻¹). This requires a significant difference in the nature of the interactions among the excited states that shape these ⁵E PESs. In the trigonal bipyramidal (TBP) C₃ model complex (TMG₃tren)Fe^IV═O, the high-energy, narrower, and less distorted RCP-active PES resulted from a strong spin–orbit coupling (SOC) interaction between this component of the in-state SOC split ⁵E (d_xz/yz π*→ d_z² σ* LF) state and a nearby triplet.¹⁶ For SyrB2 Br–Fe^IV═O, it is the low-energy LCP PES that is narrower and less distorted. As explained below this results from a low-symmetry splitting of the d_xz/yz π*→ d_z² σ* LF ⁵E state, due to the presence of the equatorial halide ligand (Figure 4).

Figure 4.

Two different origins of the pseudo-A term in the MCD spectra of S = 2 TBP ferryl species: low-symmetry splitting of LF ⁵E state in Br–Fe^IV═O (right) vs SOC splitting of LF ⁵E in C₃ symmetric (TMG₃tren)Fe^IV═O (left). ΔE_vertical values are derived from the fits of the vibronically resolved pseudo-A term features using two FC progressions.

We finally note that the temperature-dependent MCD data for (SyrB2)Fe^IV═O in the band I region require more than two FC progressions. From the FC analysis presented in Figure 3A, the first, fourth, and the fifth negative peaks do not overlap with the LCP peaks and hence the intensities of these peaks should behave the same with a change of temperature. However, from Figure 5A, the temperature dependence of the first negative peak is different from that of the fourth and fifth negative peaks. This indicates that these peaks, in fact, belong to different RCP vibronic progressions. This is reflected in Figure 5B by a three FC progression fit of the pseudo-A term feature where the first (lower-energy) RCP progression has a distinctly larger S and smaller ΔE than its high-energy RCP cognate. The origin of the two RCP progressions is evaluated in section 3.2.2.

Figure 5.

(A) MCD intensity of the first, fourth and the fifth RCP peak measured at different temperatures T (Δε_T) and normalized to its MCD intensity at 2K (Δε_2K). (B) Fit of the NIR pseudo-A term by three FC vibronic progressions.

3.2. Quantum-Chemical (Multiconfigurational and Multireference) Calculations; Spectroscopy

3.2.1. Calculated Electronic Spectrum and Correlation to MCD Data

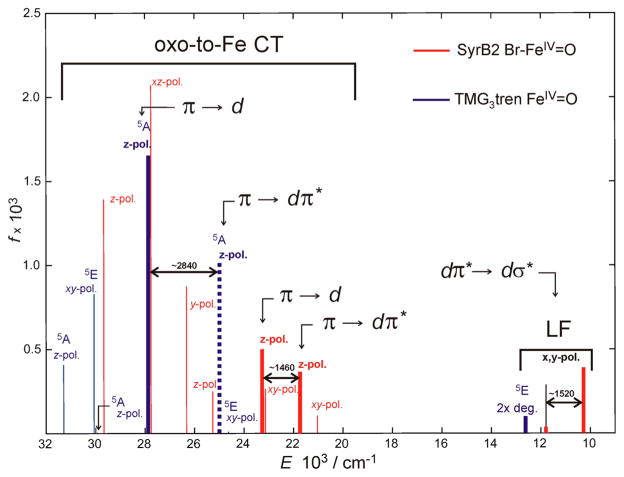
The structural model for the multiconfigurational/multireference calculations was obtained, as described in section 2.4, by truncation of the five-coordinate trigonal-bipyramidal (TBP) Fe^IV═O structure, which was determined in ref 20 from synchrotron-based nuclear resonance vibrational spectroscopy (NRVS) in combination with DFT calculations (for structures see Figure S1). The RASSCF calculated electronic spectrum of this SyrB2 Br–Fe^IV═O structure along with that of (TMG₃tren)Fe^IV═O is shown in Figure 6. Importantly, these calculations correlate well with the experimental spectra in Figure 2:

Figure 6.

RASSCF electronic spectra of the SyrB2 Br–Fe^IV═O (red) and (TMG₃tren)Fe^IV═O species (blue). Heights of solid lines correspond to oscillator strengths of electronic transitions. Dotted line indicates the position of the transition with a near-to-zero oscillator strength. Polarizations and assignments of transitions are also shown. The thick lines are transitions that correspond to experimental bands I, II, and III from Figure 2. For the orbitals, see Figure 8.

We first consider the LF region, band I. For SyrB2 Br–Fe^IV═O, there are two calculated near-infrared x/y-polarized transitions with LF character, the d_xz/yz π* → d_z² σ* transitions that are split by 1520 cm⁻¹ (as shown in Figure 6; cf. experimental 700 cm⁻¹) and have energies that are close to values obtained from the experimental MCD pseudo-A term, band I in Figure 2A (i.e., calculated 10 280 and 11 800 cm⁻¹ vs experimental 9500 and 10200 cm⁻¹). These calculated transition energies are comparable to that of the corresponding 2-fold degenerate transition in the C₃ symmetric (TMG₃tren)Fe^IV═O model complex, which also agrees with the experimental data in Figure 2B.

We next consider the CT spectrum of (TMG₃tren)Fe^IV═O. From group theory for effective C₃ symmetry, three oxo π → d_xz,yz π* CT transitions are predicted: one is 2-fold degenerate (⁵E) and x/y-polarized, while two are nondegenerate (⁵A) and z-polarized. The same is predicted for the oxo π → Fe d_xy/x²−y² CT transitions. According to the nonrelativistic multiconfigurational calculations for (TMG₃tren)Fe^IV═O, the lowest-energy CT state is the oxo π → dπ* ⁵E state at ~ 24 630 cm⁻¹, whereas the two other oxo π → dπ* states (the ⁵A’s) are at ~ 25 040 and ~ 31 290 cm⁻¹ (Figure 6). The three oxo π → Fe d_xy/x²−y² CT states in (TMG₃tren)Fe^IV═O (labeled oxo π → d) are calculated at ~ 27 880, ~ 29 930, and ~ 31 290 cm⁻¹, respectively (Figure 6); the first is z-polarized and has the largest oscillator strength among all of excitations in the 0–32 000 cm⁻¹ region. This lowest oxo π → d CT is attributed to the intense band III in the experimental spectrum of the model complex in Figure 2B. While the lowest-energy experimental CT transition, i.e., band II in the MCD spectrum of the model compound Figure 2B, is z-polarized (Table 1), the lowest calculated oxo-to-Fe CT transition (⁵A_gs → ⁵E CT) in the model in Figure 6 is x/y-polarized. This discrepancy can be reconciled by the fact that the lowest-energy calculated z-polarized nondegenerate oxo π → dπ* CT transition (⁵A_gs → ⁵A CT) is predicted only 500 cm⁻¹ above the ⁵A_gs → ⁵E CT. This z-polarized oxo π → dπ* CT (~ 25 040 cm⁻¹) has ⁵A symmetry and can undergo configuration interaction with the most intense z-polarized oxo π → Fe d CT (band III). Even a few percent CI mixing would produce significant z-polarized intensity and give rise to band II in Abs and MCD spectra of the ferryl model compound (Figure 2B).

Taking advantage of the analysis of the oxo-to-Fe CTs in (TMG₃tren)Fe^IV═O, the eight calculated lowest-energy low-symmetry split CT transitions for the SyrB2 Br–Fe^IV═O active site can be straightforwardly identified. The calculated transitions at ~ 21 040 and ~ 23 140 cm⁻¹ are the low-symmetry split components of the lowest-energy 2-fold degenerate x/y- polarized oxo π → dπ* CT (Figure 6, red). However, these two excitations are masked by the more intense z-polarized transitions, oxo π → dπ* CT calculated at ~ 21 760 cm⁻¹ and oxo π → d at ~ 23 220 cm⁻¹ (bold red lines in Figure 6), that correlate with the first and the second ⁵A_gs → ⁵A CT in the C₃-symmetric (TMG₃tren)Fe^IV═O complex, respectively. Thus, bands II and III in the experimental spectrum of (SyrB2)Fe^IV═O in Figure 2A can be assigned as the oxo π → dπ* and oxo π → d CT transitions, respectively. Importantly, these two z-polarized CT transitions (the lower of which is less intense) are shifted to lower energies and less split as compared to their CT cognates calculated for the model complex. These computational results are in the good agreement with the experimental data (cf. Figures 6 and 2).

3.2.2. Pseudo-A Term (Band I)

Here we address the ⁵A → ⁵E LF transition in SyrB2 Br–Fe^IV═O at ~ 11 000 cm⁻¹ in Figure 6, which is split by the distortion from C₃ symmetry due to the equatorial bromide. In comparing this region between SyrB2 Br–Fe^IV═O and (TMG₃tren)Fe^IV═O, there are several differences. The C₃ degenerate pair of d_xz/yz π* → d_z² σ* LF excited states split in energy in the low-symmetry structure of Br–Fe^IV═O giving rise to the lower-energy LCP and higher-energy RCP transitions. These gain MCD intensities through a C-term mechanism³⁶ that involves SOC between these states to form a derivative-shaped pseudo-A term. The equations that govern C-term intensities related to these SOC-interacting excited states (labeled 2 and 3 below; 1 is the ground state ⁵A) is

$$C_0^{1\to 2}=-\frac{g_z}{6(E_3-E_2)}(D_x^{1\to 3}{D}_y^{1\to 2}-D_y^{1\to 3}{D}_x^{1\to 2})L_z^{3,2}$$ (5)

$$C_0^{1\to 3}=-\frac{g_z}{6(E_2-E_3)}(D_x^{1\to 2}{D}_y^{1\to 3}-D_y^{1\to 2}{D}_x^{1\to 3})L_z^{2,3}$$ (6)

where E₂ and E₃ are energies of states 2 and 3, g_z is the z-component of the Zeeman tensor for the ground state (state 1), $D_x^{1\to 2}$ is the x-component of the transition dipole moment from 1 to 2, and $L_z^{2,3}$ is the z-term of the SOC operator between states 2 and 3, etc. Using CASPT2 calculations, state 2 is determined to arise from the d_yz π* → d_z² σ* LF transition (Fe–oxo and Fe–Br define the z and y axes, respectively) that is calculated to be lower in energy than the d_xz π* → d_z² σ* LF state (state 3). This energy difference is due to the d_yz π* orbital that interacts with the halide and is at higher energy than d_xz π* and thus lowering the energy of the d_yz π* → d_z² σ* state relative to the d_xz π* → d_z² σ* transition. As given in Figure 7, calculations, in agreement with the experiment, identify the LCP-active d_yz π* → d_z² σ* state to be lower in energy (state 2) than its RCP-active d_xz π* → d_z² σ* cognate (state 3). It is noteworthy that calculated SOC interaction between LCP and RCP states is ~ 120 cm⁻¹ in SyrB2 Br–Fe^IV═O, which is smaller than SOC between the corresponding states in (TMG₃tren)Fe^IV═O (~ 220 cm⁻¹);¹⁶ this is in line with the observation of lower pseudo-A term MCD intensity (and lower C₀/D₀ ratio) for the Br–Fe^IV═O species than for (TMG₃tren)Fe^IV═O (cf., Figure 2 and Table 1). This decreased SOC indicates a larger relativistic nephelauxetic effect due to the higher covalency of the Fe–oxo bond relative to the N-based chelating ligation in (TMG₃tren)Fe^IV═O (vide infra).

Figure 7.

MCD transitions to two lowest S = 2 excited states (labeled in this figure as states 2 and 3) give rise to a pair of positively and negatively signed C terms forming a derivative-shaped pseudo-A term with negative component at higher energies. Signs of the C terms ( $C_0^{1\to 2}$ and $C_0^{1\to 3}$) are determined by using eqs 5 and 6. The energies (E), transition dipole moments (D), and SOC matrix elements (L_z) listed in the figure were obtained using CASSCF/CASPT2/SO-CASSI calculations.

To further correlate calculations with the experimental data, the CASPT2 ground-state and two lowest excited-state PESs in the Fe–oxo coordinate were evaluated (Figure 8). Importantly, the excited-state PESs reproduce the main features of the MCD-derived PESs (from Figure 3B): (i) the LCP-active PES is lower in energy at ground-state equilibrium than RCP-active PES (quantitatively the calculations overestimate the experiment by a factor of ~ 2 that corresponds to an error of ~ 1.5 kcal mol⁻¹); (ii) the LCP-state distortion is smaller than that of the RCP state, ΔQ_LCP = 0.095 Å vs ΔQ_RCP = 0.124 Å (cf., experimental values in Figure 3B); (iii) the RCP PES decreases in energy more than the LCP PES in going from the ground-state equilibrium (indicated by a vertical line in Figure 8) to their respective excited-state PES minima; (iv) the frequency of the LCP state Fe–oxo stretching mode (estimated from a third-order Taylor expansion fit of the PES) is higher than that of the RCP state, ΔE_LCP ≈ 870 cm⁻¹ vs ΔE_RCP ≈ 790 cm⁻¹ (cf., experimental values in Figure 3B).

Figure 8.

CASPT2 PESs of three lowest S = 2 states along the Fe–O coordinate (left). Two main configurations contributing to wave function character of each excited state at the ground-state equilibrium are also displayed. The corresponding frontier molecular orbitals are depicted in the right panel.

The different PES curvatures and distortions of the LCP and RCP states in the vicinity of the ground-state equilibrium are attributed to the anisotropy of the π FMOs. Namely, the p orbitals of the Br⁻ ligand interact with d_yz π* (y along Fe–Br, vide supra; orbitals shown in Figure 8) but not with d_xz π*. As a consequence, the d_yz π* has less Fe d character than d_xz π*. Thus, d_yz π* is less antibonding with respect to Fe–oxo. The LCP d_yz π*→ d_z² σ* PES thus has a smaller Hellmann–Feynman distortive force along the Fe–oxo stretching mode than the RCP d_xz π*→ σ* PES. The higher Fe–oxo stretching frequency of the LCP state as compared to RCP is then mostly influenced by the difference in PES curvature at longer Fe–O distances (>1.75 Å) that is caused by the difference in halide admixture into the oxo dπ_yz vs dπ_xz orbitals. This makes Fe^IV ═ O → Fe^III—O^•− polarization in the π_yz orbital at longer Fe–O distances more difficult due to the higher halide donation (see also Figure S5). These findings are reflected in the MCD data by the two (positive and negative) vibronic progressions, with the positive structure associated with the d_yz π*→ d_z² σ* transition having a higher Fe–oxo stretching frequency and smaller Huang–Rhys factor.

From the more detailed analyses of the temperature dependence of the vibronic progressions in Figure 5, there are in fact two negative progressions for SyrB2 Br–Fe^IV═O. The CASPT2/SO-CASSI calculations (Figure S6) indicate that SyrB2 has a strong SOC interaction between the RCP component of the low-symmetry perturbed LF ⁵E state and a close-lying triplet state (SOC matrix element of 480 cm⁻¹; such an interstate SOC was also observed for (TMG₃tren)Fe^IV═O (see ref 16)). This interstate SOC would give rise to two RCP FC progressions, in line with the experimentally observed unequal temperature behavior of the negative vibrational peaks (Figure 5).

3.3. Quantum-Chemical Calculations; Reactivity

According to the NRVS spectroscopy in ref 20, the bromide and chloride ligating (SyrB2)Fe^IV═O structures are structurally equivalent. Ab inito calculations performed in this work (Figure S7) predict that there is no essential difference in their absorption spectra, indicating that electronic structures of the Br–Fe^IV═O and Cl–Fe^IV═O intermediates are equivalent in the region 0–30000 cm⁻¹. In this section, we therefore correlate our results from spectroscopically based electronic-structure analyses for SyrB2 Br–Fe^IV═O with reactivity calculations on the chloride-bound active site for comparison to kinetic results (ref ⁷.).

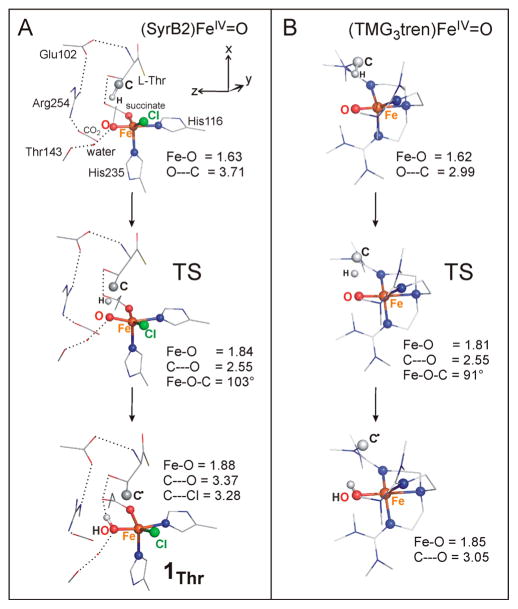
From ref 20, a reaction coordinate was generated for H atom abstraction from the native substrate L-Thr by the chloride-ligating Fe^IV═O intermediate of SyrB2. It was found that this reaction involves the d_xz π* FMO that, due to the perpendicular orientation of the substrate C–H bond relative to the Fe–oxo bond axis (and Fe–Cl axis (y)), interacts with the σ(C–H) bonding orbital. This leads to the formation of a ferric intermediate, halide–Fe^III–OH with five α-electrons on the trigonal bipyramidal Fe^III center and the carbon radical. This parallels the π-mechanism of the HAA reaction in the trigonal bipyramidal model complex (TMG₃tren)Fe^IV═O that undergoes a self-decay process.^15a,16 Both of these calculated HAA reactions are shown in Figure 9. The parallel reactivities of both the synthetic and enzymatic active sites, along with their parallel spectroscopic data, provide a basis for evaluating electronic structure contributions to the protein π-promoted HAA reactivity.

Figure 9.

π Trajectory for H atom abstraction from the native substrate L-Thr in SyrB2 (A) and from the chelate of the S = 2 model complex (B). For the products, the high-spin (S = 5/2) Fe^III center is weakly antiferromagnetically coupled to the C^• of the substrate. Key geometric parameters (in Å) are included. The Cartesian coordinates of all structures are shown in the Supporting Information. For clarity, the H atoms are not visualized. Relative energies, enthapies, and free energies of the structures (calculated as described in section 2.5) are given in Table 2 and Table S2.

3.3.1. Configuration Evolution of FMOs

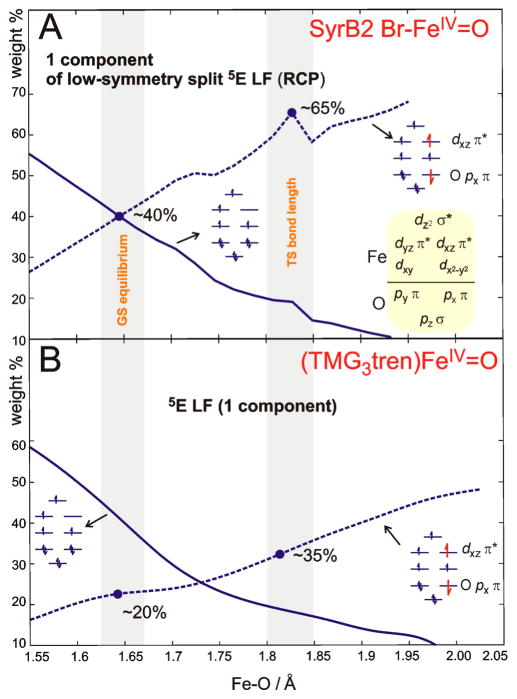
From section 3.2.1, the calculations correlated with spectroscopy show the oxo-to-Fe CT states to be lower in energy in SyrB2 Br–Fe^IV═O than those in (TMG₃tren)Fe^IV═O. This reflects larger CI mixing of the oxo-to-Fe (p_y π → d_yz π* and p_x π → d_xz π*) CT configurations into the d_yz π* → d_z² σ* and d_xz π* → d_z² σ* LF states at the ground-state equilibrium geometry of (SyrB2)-Fe^IV═O as compared to (TMG₃tren)Fe^IV═O (cf., ~ 40% vs ~ 20% CT admixtures into the d_xz π* → d_z² σ* LF state; Figure 10). This is consistent with the more covalent Fe–O bond in SyrB2 than that in TMG₃tren. From Figure 10, in passing from the ground-state equilibrium to the transition-state Fe–O bond lengths, the dashed line representing the oxyl Fe^III character evolves more rapidly for the enzyme than for the model complex (cf. ~ 65% vs ~ 35% of Fe^III—O^•− admixtures into the d_xz π* → d_z² σ* LF state at the TS Fe–O lengths in Figure 10). While both π* FMOs in TMG₃tren remain equivalent along the Fe–O reaction coordinate (i.e., oxyl character in both π directions evolves equally), the π-anisotropy in SyrB2 leads at longer Fe–O distances to the increased oxyl character oriented in the direction of the substrate (cf. 60% of π_yz-oxyl vs 65% of π_xz-oxyl at the TS; Figure S5). This correlates with the difference in halide donation to d_yz π* relative to the d_xz π* orbital; the latter thus undergoes more Fe^IV═O → Fe^III–oxyl polarization at the TS (section 3.2.2).

Figure 10.

Evolution of the dominant electronic configurations contributing to the CASPT2 wave function character of the lowest-energy excited LF state in (SyrB2)Fe^IV═O (A) and (TMG3tren)-Fe^IV═O (B). Only one component of the LF state (associated with the substrate-oriented d_xz π* FMO) is shown in both cases. Orbitals associated with the configurations are displayed in Figure 8 (left panel therein). The GS equilibrium and TS Fe–O lengths are indicated by a gray bars.

In correlating from the spectroscopic analysis to reactivity, only the LF RCP-active state, corresponding to the d_xz π* FMO, is involved in the HAA π pathway, as this is oriented toward the substrate cavity. While this state is higher in energy than the LCP d_yz π* state in ground-state equilibrium geometry, it has a softer PES in the Fe–O bond (Figure 8) and becomes lower in energy at Fe–O lengths (i.e., >1.82 Å) corresponding to the transition state for C–H abstraction.

Finally, in analogy to the MCD study in ref 16, it is noteworthy that for SyrB2 halide–Fe^IV═O there are two additional S = 2 (ground and the lowest-energy oxo-to-Fe CT) states capable of an H atom abstraction. However, in contrast to TMG₃tren, these two states associated with one σ and one π(S_Fe^III = 3/2) HAA channels are not operative in SyrB2. First, the σ-channel that is associated with dσ* FMO is excluded due to the perpendicular orientation of the substrate with respect to the Fe–O vector (Figure 9A). Second, in comparison to TMG₃tren, the PES of the lowest-energy oxo-to-Fe CT state in SyrB2 (Figure S8) is less distorted and steeper at longer Fe–O distances so that it becomes higher in energy for Fe–O lengths of >1.9 Å. This indicates that the π(S_Fe^III = 3/2)-channel for HAA is less accessible in SyrB2 than that in (TMG₃tren)Fe^IV═O. This difference in PES curvature is attributed to a difference in H-bonding to the oxo moiety by its environment (two H-bonds in SyrB2 vs no H-bond in TMG₃tren, Figure S8).

3.3.2. H Atom Abstraction by Fe^IV═O; Correlation of SyrB2 to TMG₃tren

For the comparison of HAA in SyrB2 vs TMG₃tren, the experimental k_cat values (0.071 vs 0.02 s⁻¹)^7,15a indicate that activation free energies in both systems are of similar magnitudes, 19.1 vs 19.9 kcal mol⁻¹, slightly favoring the enzyme. However, there is a large difference in the strengths of the substrate C–H bonds. Experimentally, for methyl groups of small molecules representing threonine (2-propanol) and the chelate ligand (trimethylamine), these are 94⁷ and 86 ± 2³⁸ kcal mol⁻¹, respectively. The calculated difference using the present methodology is 10 kcal mol⁻¹. The fact that (SyrB2)Fe^IV═O is capable of an H atom abstraction from a stronger C–H bond with a lower reaction barrier suggests that the enzyme is more reactive in HAA than its synthetic counterpart.

DFT calculations are consistent with the experimental results (Table 2): the barrier of the π(S_Fe^III = 5/2)-controlled HAA reaction in SyrB2, calculated for the cluster model in the absence of the second-shell Arg residue (see footnote in Table 2), is lower than the corresponding pathway in the model complex (cf., ΔG^≠ 19.8 vs 21.4 kcal mol⁻¹; TSs shown in Figure S9; for π-trajectories in SyrB2 vs TMG₃tren, see Figure 9) despite its larger endergonicity (cf., ΔG° 2.3 vs 0.5 kcal mol⁻¹). The fact that the thermodynamically less favorable reaction is kinetically more feasible indicates an increased intrinsic reactivity of the enzyme system. Indeed, elimination of the effect of the thermodynamic driving force on the reaction barrier through Marcus theory gives an intrinsic barrier ΔG^≠_intr (=[ΔG^≠ − 1/2ΔG° + (ΔG^≠2 − ΔG^≠ΔG°)^1/2]/2)³⁹ of 18.6 (SyrB2) and 21.6 kcal mol⁻¹ (TMG₃tren). The lowered intrinsic barrier for π-controlled HAA in the enzyme correlates well with the increased π-oxyl character of enzymatic Fe^IV═O relative to the model ferryl complex at the TS that was revealed by the spectrocopically supported calculations of the lowest excited state in section 3.3.1.

Table 2.

(Activation/Reaction) Potential Energies, Enthalpies and Free Energies of the π(S_Fe^III = 5/2)-Controlled H-Atom Abstraction from the Native Substrate by the (SyrB2)Fe^IV═O and (TMG₃tren)Fe^IV═O Species; the Intrinsic Reaction Barriers Are Also Given (All Values Are in kcal mol⁻¹)

system	ΔE≠/ΔH≠/ΔG≠	ΔE°/ΔH°/ΔG°	ΔE≠intr/ΔH≠intr/ΔG≠intr
(SyrB2)FeIV═Oa	23.1c/18.9/19.8	3.9/0.6/2.3	21.1/18.6/18.6
(TMG3tren)FeIV═Ob	25.3/21.6/21.4	5.9/3.2/0.5	22.3/20.3/21.6

^aWithin the cluster model from Figure 9, the second-shell residue Arg₂₅₄ appears to sterically destabilize the transition state/product relative to the reactant by ~ 3–4 kcal mol⁻¹. Here, the DFT results are presented for the cluster model in the absence of this Arg residue. For the energetics of the Arg-including cluster model of the active site from Figure 9, see Table S1.

^bCalculated at the same level of theory as SyrB2 (described in Computational Details) but with a dielectric constant of ε = 35.7 mimicking the solvation effect of acetonitrile.

^cThe Fe–O bond length at the TS for HAA is ~ 1.8 Å (Figure S9). For this Fe–O bond distance, the excited d_xzπ* → d_z²σ* state (active in HAA) is calculated at the CASPT2 level of theory to lie ~ 10 000 cm⁻¹ (~ 28 kcal mol⁻¹) above the ground state minimum (Figure 8). This energy difference includes (i) the ground-state Fe–O distortion that is associated with the energy increase by ~ 5000 cm⁻¹ (~ 14 kcal mol⁻¹) and (ii) the excitation from the ground state to the d_xzπ* → d_z2σ* state that requires an additional amount of ~ 14 kcal/mol. The difference of ~ 28 kcal mol⁻¹ taken from Figure 8 relative to the DFT-calculated π-controlled HAA barrier of ~ 23 kcal mol⁻¹ (ΔE^‡ for comparison to PES calculations) reflects the interaction of the Fe^IV═O moiety with the substrate C–H bond.

4. DISCUSSION

This study on SyrB2 has focused on using MCD spectroscopy to determine the electronic structure of the Fe^IV═O intermediate based on its geometric structure from NRVS in ref 20 and quantitative comparisons to studies on TMG₃tren.¹⁶ Importantly, there are strong parallels to the MCD spectra of the (TMG₃tren)Fe^IV═O model complex (i.e., energies and signs of MCD bands, and related spectroscopic characteristics including C₀/D₀ ratios, ground-state ZFS and polarizations of the electronic transitions) that confirm the ~ C₃ TBP arrangement of the Fe^IV═O site in SyrB2 and allow us to define its ground and low-lying excited electronic states that relate to its FMOs. However, the comparison also reveals differences: the oxo π→ dπ* CT transitions are shifted down in energy in SyrB2, the C₀/D₀ ratio for band I is reduced by a factor of ~ 2, and the vibronic structure in the ~ 12 000 cm⁻¹ (pseudo-A) band I, assigned as the pair of dπ* → dσ* LF transitions, is different. These observations reflect quantitative differences in the FMOs. The lower-energy CT reflects a smaller energy gap between oxo p_x/y and d_xz/yz π* orbitals indicating a greater oxo donor interaction reflecting a weaker donor ligand set for the SyrB2 active site. This is also consistent with the lower C₀/D₀ ratio of feature I in Br–Fe^IV═O relative to (TMG₃tren)Fe^IV═O as this increased oxo character lowers the SOC. The change in vibronic structure indicates a π anisotropy in SyrB2 due to the equatorial halide ligand (Scheme 1A and B), i.e., a low-symmetry splitting of the d_xz π* and d_yz π* orbitals with d_xz π* being nonbonding with the Br⁻ (Scheme 1C). This π anisotropy results in different shapes of the PESs along the Fe–oxo stretching coordinate. This leads to a lowest-energy d_xz π* FMO orbital at longer Fe–O distances that is oriented toward the substrate cavity (Scheme 1C).

Scheme 1.

Vibronically Resolved VT MCD Spectra (A) Describe the Electronic Structure of the Halide—Fe^IV═O Active Site at the Equilibrium Geometry As Well As a Difference in the Shape of PESs of the Two Lowest Lf Excited States (B) That Is Associated with Anisotropy of π FMOs; This π-Anisotropy Leads to a Larger Oxyl-Fe^III Character in the Substrate-Oriented Direction at the TS Fe–O Lengths (C) and Results in a Lower-Energy d_xz π* FMO That Is Perpendicular to the Fe–Halide Bond and Well-Oriented for H-Atom Abstraction from the Substrate C–H Bond

Ab initio calculations based on the NRVS-determined geometric structure reproduce these MCD-derived data for SyrB2 and the trends in electronic spectra in going from (TMG₃tren)Fe^IV═O to SyrB2 Br—Fe^IV═O. This allows a correlation of the spectroscopic data with the reactivity of the SyrB2 Fe^IV═O intermediate. The decrease in energy between the oxo-based π and Fe-d_xz/yz π* orbitals results in their larger CI admixture into the dπ* → dσ* LF states. This facilitates spin polarization in the Fe–oxo bond and increases its Fe^III(S_Fe = 5/2)–oxyl character at the TS, compared to (TMG₃tren)-Fe^IV═O. Also, due to the π anisotropy associated with the equatorial halide there are differences in strength and distortion of the Fe–oxo bond between the RCP d_xz π* → d_z² σ* LF and LCP d_yz π* → d_z² σ* LF states (Scheme 1B and C). The RCP d_xz π* → d_z² σ* LF state, active in π-controlled H atom abstraction due to its orientation toward the C–H bond, has a weaker, more distorted Fe–oxo bond. Thus, the d_xz π* state becomes lower in energy at Fe–O lengths relevant to the TS and hence has increased HAA reactivity in the direction of the substrate cavity (Scheme 1B and C).

Indeed, the π-channel for HAA by the SyrB2 Fe^IV═O intermediate (with the substrate C–H bond perpendicular to the Cl–Fe^IV═O plane) involves the RCP d_xz π* state and produces the Cl–Fe^III–OH/L-Thr^• first intermediate. The comparison with the model complex (TMG₃tren)Fe^IV═O reveals that the Fe^IV═O enzymatic intermediate is intrinsically more π-reactive due to its higher oxyl character and lower Fe–oxo stretching frequency as observed by MCD spectroscopy.

5. CONCLUSIONS

This study used low-temperature MCD spectroscopy to define the electronic structure of the S = 2 (SyrB2)Fe^IV═O intermediate, for which the 5C TBP geometric structure was previously determined by NRVS. The VT MCD spectra, obtained for this SyrB2 NHFe^IV═O intermediate, show features that largely parallel those observed for the TBP S = 2 (TMG₃tren)Fe^IV═O model complex and provide significant insight into the low-lying S = 2 excited states and the associated FMOs. The comparison of SyrB2 Fe^IV═O with (TMG₃tren)-Fe^IV═O further allows evaluation of the oxo–Fe bonding and the low-symmetry effects due to a halide on the nature of the FMOs (potential energy surfaces of low-lying S = 2 states). This increased oxo character and π-anisotropy enhance the HAA reactivity along the direction of the substrate. The H atom abstraction pathway occurs through a π channel leading to the TBP halide–Fe^III(S = 5/2)–OH intermediate.