Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jun 30;6:28878. doi: 10.1038/srep28878

The synchronization of neuronal oscillators determined by the directed network structure of the suprachiasmatic nucleus under different photoperiods

Changgui Gu 1,a, Ming Tang 2,3, Huijie Yang 1
PMCID: PMC4928114  PMID: 27358024

Abstract

The main function of the principal clock located in the suprachiasmatic nucleus (SCN) of mammals is synchronizing the body rhythms to the 24 h light-dark cycle. Additionally, the SCN is able to adapt to the photoperiod of the cycle which varies among seasons. Under the long photoperiod (LP), the synchronization degree of the SCN neurons is lower than that under the photoperiod (SP). In the present study, a potential explanation is given for this phenomenon. We propose that the asymmetrical coupling between the light-signal-sensitive part (the ventralateral part, abbreviation: VL) and the light-signal-insensitive part (the dorsalmedial part, abbreviation: DM) of the SCN plays a role in the synchronization degree, which is reflected by the ratio of the number of the directed links from the VL neurons to the DM neurons to the total links of both directions between the VL and the DM. The ratio is assumed to characterize the directed network structure under different photoperiods, which is larger under the SP and smaller under the LP. We found that with the larger ratio in the situation of the SP, the synchronization degree is higher. Our finding may shed new light on the asymmetrical coupling between the VL and the DM, and the network structure of the SCN.

The principal clock situated in the suprachiasmatic nucleus (SCN) which is composed of ten thousands of neurons in mammals, regulates the circadian rhythms of physiological and behavioral activity1,2,3,4. One main function of the SCN is synchronizing the body rhythm to the external 24 h light-dark cycle. The photoperiod of the external 24 h light-dark cycle are altered between seasons especially in the high latitudes, i.e long photoperiod (LP) in the summer and short photoperiod (SP) in the winter. Accordingly, the SCN has evolved to adapt the different photoperiods. Distinct behaviors of the SCN are observed between the LP (e.g. 16 h light: 8 h darkness) and the SP (e.g. 8 h light: 16 h darkness). The neuronal phases are more dispersed under the LP in that the synchronization degree between neurons is smaller compared to the situation of the SP in mice5,6. This smaller synchronization degree results in the lower entrainment ability of the SCN under the LP7. However the mechanism of the altered synchronization degree between different photoperiods has not been clearly discovered so far.

The SCN is a heterogeneous network8. A part of the SCN neurons are capable of self-oscillating with intrinsic periods ranging from 22 h to 28 h9,10,11, which are coupled through neurotransmitters and then constitute a network to output a uniform periodic rhythm12. The SCN neurons can be classified into two groups structurally and functionally, named the ventralateral part (VL) and the dorsalmedial part (DM) which runs faster than the VL13. The VL composed of approximately 25% SCN neurons receives the light information and relays the information to the DM formed by the remaining about 75% SCN neurons in rat14,15,16,17. The neurotransmitters which play a role in the coupling are distinct in different regions. The DM neurons produce vasoactive intestinal polypeptide (VIP), the DM neurons secrete arginine vasopressin (AVP)16,17, and most SCN neurons are sensitive to GABA18.

The coupling between the VL and the DM is found to be asymmetrical. Structurally, the asymmetry is due to the dense projections from the VL to the DM and the sparse projections from the DM to the VL, in that the VL dominates the DM4. Functionally, several experiments suggest the presence of this asymmetry. In slice, after the removal of the VL, the period of the SCN became short, while the period of the SCN was not altered after the removal of the DM13. Another explanation for the asymmetry is that after a jet lag, the VL adapts to the phase (time) of the destination promptly, while the DM requires several days to readjust gradually15.

A lot of theoretical works have been motivated to study the network behaviors such as the synchronization degree between the SCN neurons, the rhythmicity of the SCN, the entrainment ability of the SCN and so on19,20,21,22,23,24,25,26,27,28,29. Most of these works regarded the SCN network as an all-to-all network where each two neuronal nodes are connected. Recently, several works investigated the influence of a small-world network structure of the SCN on the network behaviors30,31,32,33. The small-world network structure such as the Newman-Watts(nw) network30,34 and the Barabási (BA) network31,33,35 improves the synchrony between neurons and strengthens the circadian rhythm of the SCN. The network structure was also taken into account to explain the distinct synchronization degree under different light conditions32,36,37. Refs 32 and 36 suggests that the reduced total number of undirected links between the VL and the DM lead to the smaller synchronization degree under the LP. Nevertheless, no theoretical work has studied the influence of the directed and asymmetrical coupling between the VL and the DM on the network behaviors.

In the present study, an alternative explanation is given for the distinct synchronization degree under different photoperiods by considering the fact of the asymmetrical coupling between the VL and the DM4, which is assumed to be reflected by more directed links from the VL to the DM than vice versa in the present study. In order to measure the asymmetrical degree, we define a key parameter as the ratio of the number of directed links from the VL to the DM to the total number of directed links between the VL and the DM. We assumed that the ratio be associated with the duration of photoperiod, i.e. the ratio is larger (smaller) under short (long) photoperiod.

Description of the Kuramoto Model

Two kinds of models are used to describe the SCN neuronal oscillators, i.e. biochemical models such as Goodwin model19,21,22 and Leloup-Goldbeter model38, and phenomenological models such as Kuramoto model21,39,40 and Poincaré model41,42. One of the simplest biochemical models is the Goodwin model. The Goodwin model takes both the neuronal phase and amplitude into account19,21,22, which is based on the transcription-translation feedback loop in one single neuronal oscillator. The simplest phenomenological mode is the Kuramoto model, which is a generic model and focuses on the phase but not the amplitude21,39,40. Because the amplitude of single neuron does not differ noticeably between the conditions of the LP and SP5, we here use the Kuramoto model. The Kuramoto model composed of N coupled neurons is described as:

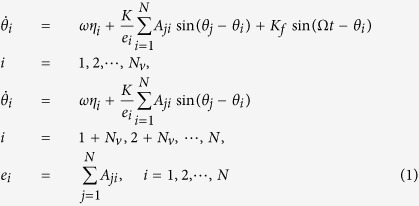graphic file with name srep28878-m1.jpg

where θi, ωηi, K, Kf and Ω represent the neuronal phase, the neuronal intrinsic frequency, the coupling strength, the light intensity and the frequency of the external light-dark cycle. N is the total number of the SCN neuronal oscillators, and Nv and N − Nv are the number of neuronal oscillators in the VL and in the DM respectively. We added the light term Kf sin(Ωt − θi) to the VL neuronal oscillators. The parameters are set as follows: K = 0.05, 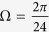Inline graphic, N = 500 and Nv = 125. In order to model the intrinsic periods of the uncoupled neuronal oscillator ranging from 22 h to 28 h, the term ωηi is introduced where ηi satisfies a normal distribution with the mean 1 and the deviation 0.05. Under constant darkness, the period of the SCN network τ (the free running period) varies among species which is around but not exactly equal to 24 h, for example for human 24.5 h, for chipmunk 24.9 h, for deer mouse 22.9 h and for field vole 23.5 h3. 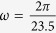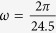For instance we chose Inline graphic and Inline graphic. We here assumed that the duration of photoperiod is related to the value of sin(Ωt). If the value is larger (smaller) than a predefined value L, the time t corresponds to light (dark) time. 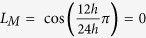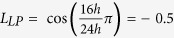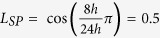For the 24 h cycle of 12 h light: 12 h dark, the predefined value is Inline graphic, for the 24 h cycle of 16 h light: 8 h dark (or 8 h light: 16 h dark), the predefined value is Inline graphic (or Inline graphic. Thus far, it is unclear whether the influence from the light signal is larger than the influence from other neurons to one neuron or not. Consequently, the value of the light intensity Kf is selected as Kf = 0.5 K, K and 2 K.

The network topology is described by a directed adjacent matrix Aji. If there is a directed link from neuronal node j to i, Aji = 1; otherwise Aji = 0. Thus far, the SCN network is suggested to be a small network, yet the details of the SCN network have not been explored. Here, the SCN network is assumed to be a directed Newman-Watts network which is established as follows34: at the first step, if the physical distance between two nodes i and j is smaller than a predefined value d, there are directed links Ai,j = Aj,i = 1 within the VL (DM); at the second step, j is directly linked to i (Aj,i = 1) with possibility p within the VL (i, j = 1, 2, ..., Nv) or DM (i, j = Nv + 1, Nv + 2, ..., N); at the third step, the links are from two directions, i.e. i (i = 1, 2, ..., Nv) in the VL is directly linked to j (j = Nv + 1, Nv + 2, ..., N) in the DM ((Ai,j = 1)) with possibility q1, and j (j = Nv + 1, Nv + 2, ..., N) in the DM is directly linked to i (i = 1, 2, ..., Nv) in the VL (Aj,i = 1) with possibility q2. Note that Ai,j is not necessarily equal to Aj,i in the latter two steps. The parameters are set as: d = 2, p = 0.05 and q1 + q2 = 0.05. The key parameter δ is defined as the ratio 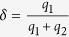Inline graphic, which represents the asymmetrical degree in the number of the directed links from the VL to the DM and that from the DM to the VL. Since the VL dominates the DM and the DM feedbacks to the VL4, the range of δ is from 0.5 to 1. When the ratio is δ = 1, the number of directed links from the DM to the VL is 0; and when the ratio is δ = 0.5, the numbers of directed links are equal for both directions. We assume that the case of δ close to 1 reflect the network topology under the SP, and the case of δ close to 0.5 character the network topology under the LP. A scheme for the SCN network structure is shown in Fig. 1.

Figure 1. The scheme of the SCN network.

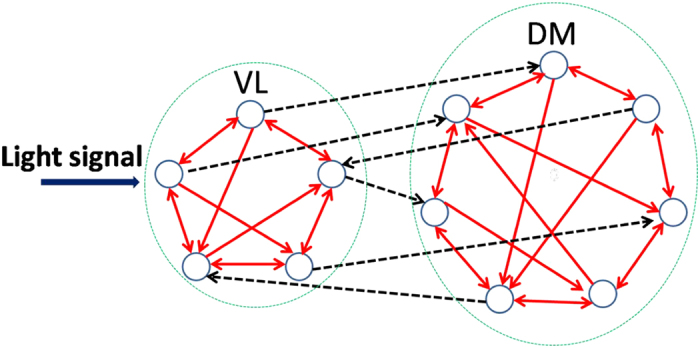
Figure 1

Open in a new tab

The solid arrows represent the directed links within the VL/DM, and the dashed arrows represent the directed links between the VL and DM. Note that, the number of the directed links from the VL to the DM is larger than vice versa.

In order to explain the distinct synchronization degree of the neuronal oscillators between the LP and the SP observed in experiments5, the impact of the asymmetrical degree δ on the synchronization degree between the neuron oscillators is studied. The synchronization degree is defined as:

graphic file with name srep28878-m9.jpg

where 〈...〉 represents average over time. R is 0 for fully unsynchronized oscillators and 1 for perfect synchronization.

The fourth-order Runge-Kutta method is used for the numerical simulation with time increments of 0.01 h. The initial 1,000,000 time steps were neglected in order to avoid the influence of transients. The initial conditions for each variable were selected randomly from a uniform distribution in the range (0–2π) for θ. In the supplemental file, the Goodwin model is also taken into account where the results confirm our findings by the Kuramoto model.

The Effect of the Asymmetrical Degree

The illustrative examples for the effect of the asymmetrical degree δ on the synchronization degree between neuronal oscillators was shown in Fig. 2. We here used the δ = 0.6 (a) and δ = 1.0 (b) to mimic the case of the LP and SP respectively. In both the cases of δ = 0.6 and 1.0, the randomly selected neuronal oscillators are synchronized to the external cycle, i.e. the phase difference between the oscillators and the cycle is stable. However, the neuronal phases are more dispersed (smaller synchronization degree) with δ = 0.6 (LP) than δ = 1.0 (SP).

Figure 2.

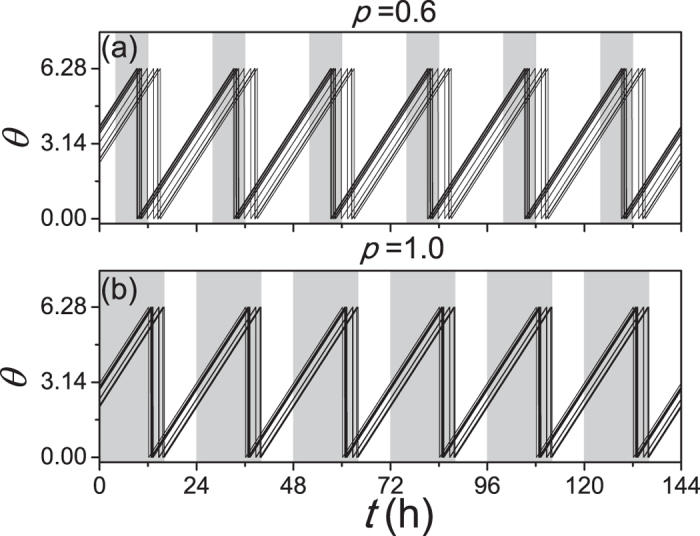
Figure 2

Open in a new tab

The evolutions of randomly selected neuronal oscillators in the LP (a) and the SP (b). The asymmetrical degree p = 0.6 and 1 correspond to the LP (long photoperiod) and the SP (short photoperiod) respectively. The mean of the neuronal intrinsic periods τ is 23.5 h, and the period of the external light-dark cycle is 24 h. The gray (white) area corresponds to the darkness (light).

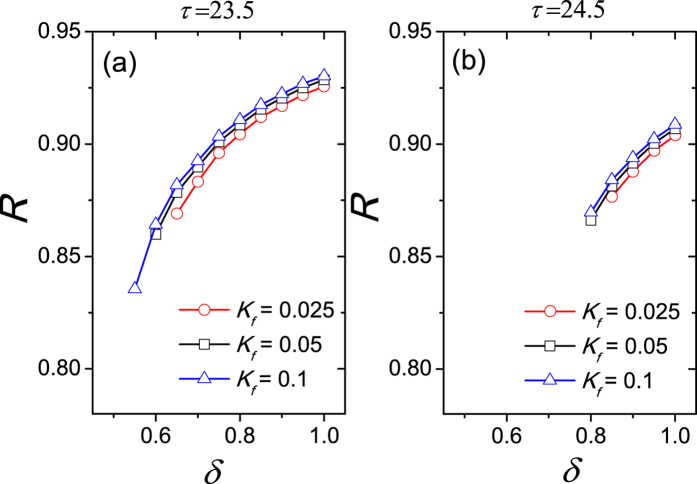
Further the relationship between the synchronization degree R and the asymmetrical degree δ was examined in Fig. 3. Two values of free running periods τ are considered, when τ is smaller than 24 h (a) and τ is larger than 24 h (b). Since the comparison between the influence from light and the influence from the other neurons to one neuron is unknown, we tested three cases of the light intensity, i.e. Kf < K, Kf = K and Kf > K. The synchronization degree R is calculated when the SCN network is entrained to the external SP or LP cycle, i.e. the periods of the neuronal oscillators are equal to 24 h. In both panels, when δ is close to 0.5, the SCN network is not entrained to the external cycle for most light intensity Kf. When δ is close to 1, the SCN network is entrained to the external cycle for each light intensity Kf. With the increase of δ the synchronization degree R increases for each light intensity Kf.

Figure 3.

Figure 3

Open in a new tab

The relationship of the synchronization degree between neuronal oscillators to the asymmetrical degree, when the free running period τ is 23.5 h (a), and when τ is 24.5 h (b). Kf represents the light intensity and the coupling strength is K = 0.05. The synchronization degree R is not calculated when the neurons are not entrained to the external 24 h cycle. The intrinsic periods are not distinct in the VL and the DM.

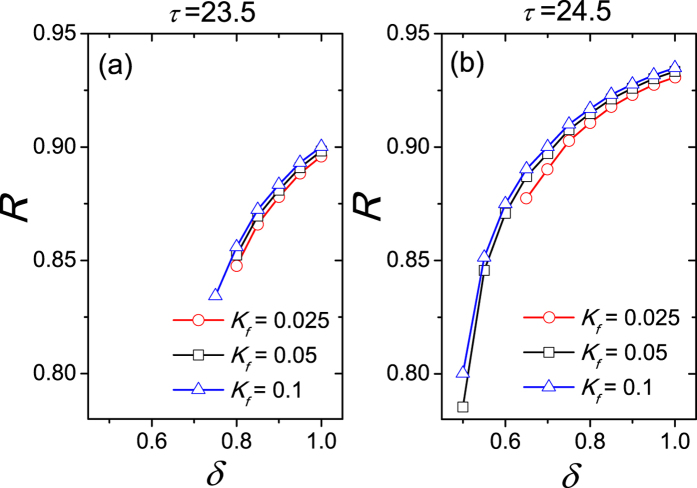
In order to mimic the DM running faster13, let the the mean of ηi, i = 1, 2, ..., Nv, multiply a factor 0.985 and the the mean of ηi, i = 1 + Nv, 2 + Nv, ..., N, multiply a factor 1.005. As a consequent, the mean of ηi, i = 1, 2, ..., N, remains 1 in that the free running period τ of the SCN is not altered, but the intrinsic period of the DM is 0.5 h smaller than it of the VL. The relationship between the synchronization degree R and asymmetrical degree δ was examined in Fig. 4 with the DM neurons running faster than the VL neurons. In Accordance with Fig. 3, we observed that the synchronization degree R increases with the increase of δ in both cases of τ > 24 (a) and τ < 24 (b).

Figure 4.

Figure 4

Open in a new tab

The relationship of the synchronization degree between neuronal oscillators to the asymmetrical degree, when the free running period τ is 23.5 h (a), and when τ is 24.5 h (b). The neurons in the DM run faster than that in the VL. This figure corresponds to Fig. 2.

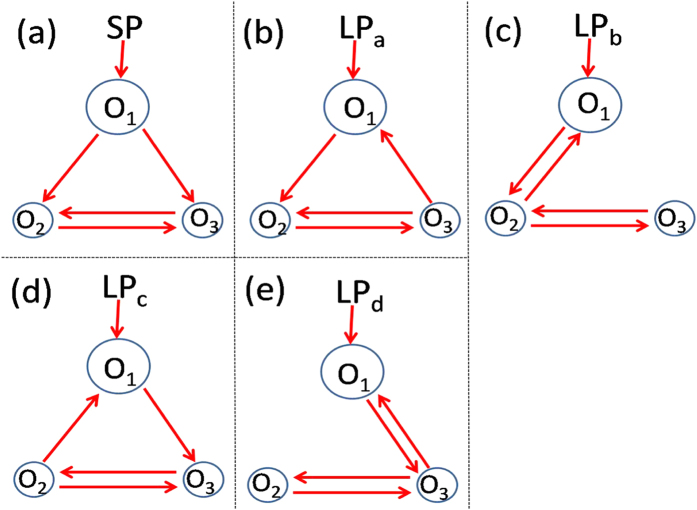
Next to the numerical simulations, we performed the analytical analysis. For simplicity, the number of neuronal oscillators is set as N = 3, where one is in the VL with larger intrinsic period and the other two are in the DM, and two directed links between the VL and the DM (Fig. 5). When both two directed links are from the VL to DM, the asymmetrical degree is δ = 1 which reflects the network topology of the SCN under the SP (a). When there is one link in each direction, the asymmetrical degree is δ = 0.5 which characters the network topology of the SCN under the LP (b-e). Without losing generality, let oscillators ‘2’ and ‘3’ be linked to each other, and their periods be the same (ω3 = ω2). The Kuramoto model, Eq. 1, composed of three oscillators based on the network structure in Penal (a) can be written as:

Figure 5. The network topologies for three neuronal nodes.

Figure 5

Open in a new tab

‘O1’ is located in the VL which receives the light signal, and ‘O2’ and ‘O3’ are situated in the DM, where ‘O’ means oscillator. The SP corresponds to the zero link from the DM to the VL (a), and the LP corresponds to the equal number of links from the DM to the VL and from the VL to the DM (b–e). The size of the cycle represents the length of neuronal intrinsic period.

graphic file with name srep28878-m10.jpg

When the network is entrained to the external cycle, the periods of the neurons are equal to the period of the external cycle (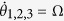Inline graphic). Consequently, the phase difference between each two neuronal oscillators and the phase difference of each oscillator to the external cycle are unchangeable. Thus, we defined ψ = Ωt − θ1, ϕ12 = θ1 − θ2, ϕ32 = θ3 − θ2 and ϕ13 = θ1 − θ3 which determine the synchronization degree. From the first equation of Eq. 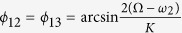3, we obtained Inline graphic. Because the neurons 2 and 3 are identical, ϕ23 = ϕ32 = 0. From the second or third equation of Eq. 3, we obtained Inline graphic.

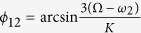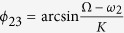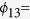
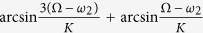Similarly, the phase difference can be found for the network structures of the SCN under the LP described in Fig. 5(b–e). Because oscillators ‘2’ and ‘3’ are identical, (d) and (e) are symmetrical cases for (b) and (c) respectively. Therefore, (b) and (c) are selected for the analysis. Interestingly, we found that the phase differences are not altered between (b) and (c), which are Inline graphic, Inline graphic and Inline graphic Inline graphic. Thus, the absolute values of ϕ12, ϕ23 and ϕ13 are evidently smaller in the SP than in the LP, in that the synchronization degree is smaller in the SP. The theoretical results were confirmed by our numerical simulations (Fig. 6).

Figure 6.

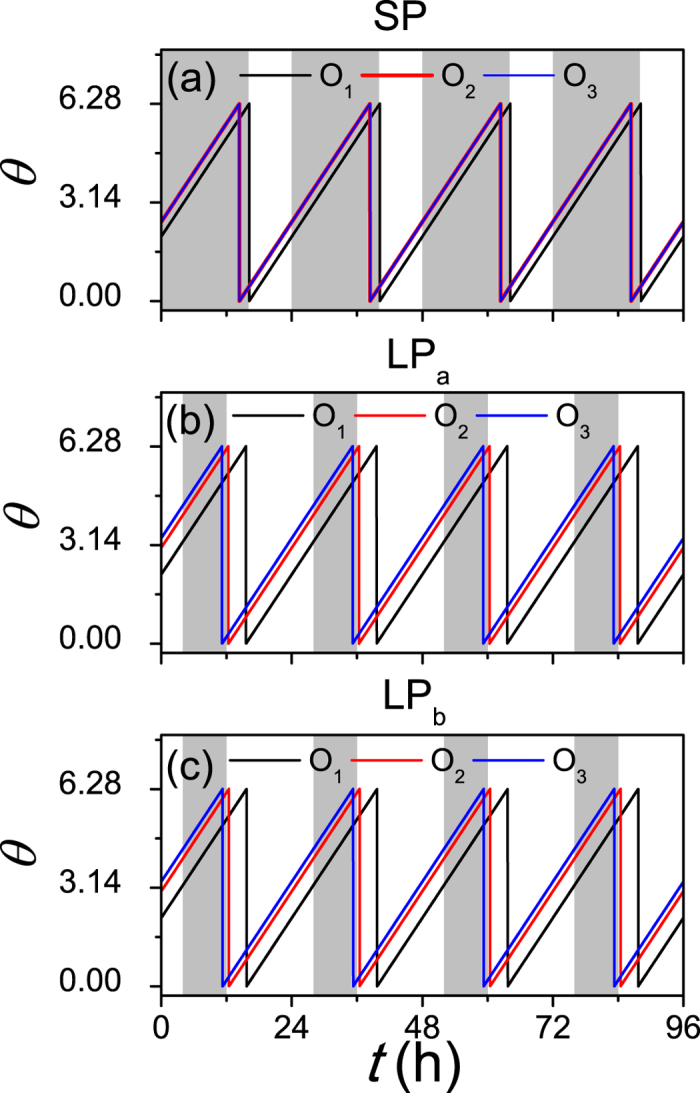
Figure 6

Open in a new tab

The evolutions of neuronal oscillators in the SP (a) and the LP (b,c) with N = 3. The network structures of (a–c) are introduced as in (a–c) of Fig. 5 respectively. ‘O1’ is located in the VL which receives the light signal, and ‘O2’ and ‘O3’ are situated in the DM, where ‘O’ means oscillator. The free running period is τ = 23.5, the coupling strength is K = 0.1 and the light intensity is Kf = 0.1. The gray (white) area corresponds to the darkness (light).

Conclusion and Discussion

In the present study, an alternative explanation was given for the distinct synchronization between the SCN neurons under different photoperiods by considering the asymmetrical coupling between the light-signal-sensitive VL part and the light-signal-insensitive DM part4. This asymmetrical coupling is characterized by the assumption of more directed links from the VL to the DM than from the DM to the VL in the present study. In order to determine the asymmetrical degree, we defined the ratio of the number of the directed links from the VL neurons to the DM neurons to the total links between the VL and the DM. The ratio (asymmetrical degree) is assumed to reflect the directed network structure under different photoperiods, which is larger under the SP and smaller under the LP. We found that with the larger ratio in the situation of the SP, the synchronization degree is higher.

Recently, it has found that not all the SCN neurons are capable of self-oscillating. After the neurons are uncoupled from the SCN network, three oscillatory phenotypes for the SCN neurons are observed: sustained oscillations, damped oscillations, and arrhythmic patterns11,32,43,44. Nevertheless, the Kuramoto model focus on the phase and is in lack of amplitude information. In order to pursue to model the nonrhythmicity, the Goodwin model is studied in the supplemental file, where independent of the oscillatory phenotypes, the synchronization degree is also found to be determined by the asymmetrical degree which reflects the photoperiod.

Most previous theoretical works regarded the SCN as an all-to-all network for simplicity. Very recently, the network structure of the SCN was found to characterize the small-word properties in experiment45, yet the details of the network structure have not been found so far. Several theoretical work investigated the effect of the small-world network structure which was found to improve the synchronization degree and the amplitude of the rhythms30,31,32,33,36,37,44. In refs 32 and 36, the reduction of the synchrony between the SCN neurons under the LP was suggested to be due to the decreased number of undirected links between the VL and DM. However, as best as we know, no work has considered the directed network structure of the SCN, where the directed links from the VL to the DM should be evidently more than vice versa. As a first step, the directed network structure was investigated to explain the distinct synchronization between different photoperiods in the present study, but the directed network structure may also help to understand the other network behaviors of the SCN, such as the ‘dissociation’ phenomenon between the VL and the DM under a 22 h light-dark cycle46 and the ‘split’ phenomenon between the VL and the DM under constant light47. At last, we hope our present study could help understanding the synchronization phenomenon in other neuronal network48,49,50.

Additional Information

How to cite this article: Gu, C. et al. The synchronization of neuronal oscillators determined by the directed network structure of the suprachiasmatic nucleus under different photoperiods. Sci. Rep. 6, 28878; doi: 10.1038/srep28878 (2016).

Supplementary Material

Supplementary Information
srep28878-s1.pdf (334.7KB, pdf)

Acknowledgments

This work was supported by the National Science Foundation of China under Grants Nos 11505114, 10975099 and 11575041, the Program for Professor of Special Appointment (Orientational Scholar) at Shanghai Institutions of Higher Learning under Grants Nos QD2015016 and D-USST02, and the Shanghai project for construction of discipline peaks.

Footnotes

Author Contributions C.G. conceived the research project. C.G. performed research. C.G. and M.T. analyzed the results. All authors wrote the text of the Manuscript and reviewed the Manuscript.

References

  1. Pittendrigh C. S. & Daan S. A functional analysis of circadian pacemakers in nocturnal rodents. I. The stability and lability of spontaneous frequency. J. Comp. Physiol. A 106, 223–252 (1976). [Google Scholar]
  2. Pittendrigh C. S. Temporal organization: reflections of a Darwinian clock-watcher. Annu. Rev. Physiol. 55, 16–54 (1993). [DOI] [PubMed] [Google Scholar]
  3. Refinetti R. Circadian Physiology. (CRC Press, 2006). [Google Scholar]
  4. Welsh D. K., Takahashi J. S. & Kay S. A. Suprachiasmatic nucleus: cell autonomy and network properties. Annu. Rev. Physiol. 72, 551–577 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. VanderLeest H. T. et al. Seasonal encoding by the circadian pacemaker of the SCN. Curr. Biol. 17, 468–473 (2007). [DOI] [PubMed] [Google Scholar]
  6. Meijer J. H., Michel S., Vanderleest H. T. & Rohling J. H. Daily and seasonal adaptation of the circadian clock requires plasticity of the SCN neuronal network. Eur. J. Neurosci. 32, 2143–2151 (2010). [DOI] [PubMed] [Google Scholar]
  7. Ramkisoensing A. et al. Enhanced Phase Resetting in the Synchronized Suprachiasmatic Nucleus Network. J. Biol. Rhythms 1, 4–15 (2014). [DOI] [PubMed] [Google Scholar]
  8. Silver R. & Schwartz W. J. The suprachiasmatic nucleus is a functionally heterogeneous timekeeping organ. Methods Enzymol. 393, 451–465 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Welsh D. K., Logothetis D. E., Meister M. & Reppert S. M. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron 14, 697–706 (1995). [DOI] [PubMed] [Google Scholar]
  10. Honma S., Nakamura W., Shirakawa T. & Honma K. Diversity in the circadian periods of single neurons of the rat suprachiasmatic nucleus depends on nuclear structure and intrinsic period. Neurosci. Lett. 358, 173–176 (2004). [DOI] [PubMed] [Google Scholar]
  11. Webb A. B., Angelo N., Huettnerb J. E. & Herzoga E. D. Intrinsic, nondeterministic circadian rhythm generation in identified mammalian neurons. Proc. Natl. Acad. Sci. USA 106, 16493–16498 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Yamaguchi S. et al. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science 302, 1408–1412 (2003). [DOI] [PubMed] [Google Scholar]
  13. Noguchi T., Watanabe K., Ogura A. & Yamaoka S. The clock in the dorsal suprachiasmatic nucleus runs faster than that in the ventral. Eur. J. Neurosci. 20, 3199–3202 (2004). [DOI] [PubMed] [Google Scholar]
  14. Lee H. S., Nelms J. L., Nguyen M., Silver R. & Lehman M. N. The eye is necessary for a circadian rhythm in the suprachiasmatic nucleus. Nat. Neurosci. 6, 111–112 (2003). [DOI] [PubMed] [Google Scholar]
  15. Rohling J. H. T., vanderLeest H. T., Michel S., Vansteensel M. J. & Meijer J. H. Phase resetting of the mammalian circadian clock relies on a rapid shift of a small population of pacemaker neurons. PLoS ONE 6, e25437 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Aton S. J., Colwell C. S., Harmar A. J., Waschek J. & Herzog E. D. Vasoactive intestinal polypeptide mediates circadian rhythmicity and synchrony in mammalian clock neurons. Nat. Neurosci. 8, 476–483 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Morin L. P. SCN organization reconsidered. J. Biol. Rhythms. 22, 3–13 (2007). [DOI] [PubMed] [Google Scholar]
  18. ALbus H., Vansteensel M. J., Michel S., Block G. D. & Meijer J. H. A GABAergic mechanism is necessary for coupling dissociable ventral and dorsal regional oscillators within the circadian clock. Curr. Biol. 15, 886–893 (2005). [DOI] [PubMed] [Google Scholar]
  19. Gonze D., Bernard S., Waltermann C., Kramer A. & Herzel H. Spontaneous synchronization of coupled circadian oscillators. Biophys. J. 89, 120–129 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Bernard S., Gonze D., Cajavec B., Herzel H. & Kramer A. Synchronization-induced rhythmicity of circadian oscillators in the suprachiasmatic nucleus. PLoS Comput. Biol. 3, e68 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gu C., Wang J. & Liu Z. Free-running period of neurons in the suprachiasmatic nucleus: Its dependence on the distribution of neuronal coupling strengths. Phys. Rev. E 80, 030904 (2009). [DOI] [PubMed] [Google Scholar]
  22. Locke J. C., Westermark P. O., Kramer A. & Herzel H. Global parameter search reveals design principles of the mammalian circadian clock. BMC Syst. Biol. 2, 22 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Gu C., Wang J. & Liu Z. Mechanism of phase splitting in two coupled groups of suprachiasmatic-nucleus neurons. Phys. Rev. E 83, 046224 (2011). [DOI] [PubMed] [Google Scholar]
  24. Gu C., Liu Z., Schwartz W. J. & Indic P. Photic desynchronization of two subgroups of circadian oscillators in a network model of the suprachiasmatic nucleus with dispersed coupling strengths. PLoS ONE 7, e36900 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Xu J., Gu C., Pumir A., Garnier N. & Liu Z. Entrainment of the suprachiasmatic nucleus network by a light-dark cycle. Phys. Rev. E 86, 041903 (2012). [DOI] [PubMed] [Google Scholar]
  26. Gu C., Ramkisoensing A., Liu Z., Meijer J. H. & Rohling J. H. T. The proportion of light-responsive neurons determines the limit cycle properties of the suprachiasmatic nucleus. J. Biol. Rhythms 29, 16–27 (2014). [DOI] [PubMed] [Google Scholar]
  27. Gu C., Xu J., Rohling J., Yang H. & Liu Z. Noise induces oscillation and synchronization of the circadian neurons. PLoS ONE 10, e0145360 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Gu C., Liang X., Yang H. & Rohling J. H. T. Heterogeneity induces rhythms of weakly coupled circadian neurons. Sci. Rep. 6, 21412 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gu C., Rohling J. H. T., Liang X. & Yang H. Impact of dispersed coupling strength on the free running periods of circadian rhythms. Phy. Rev. E 93, 032414 (2016). [DOI] [PubMed] [Google Scholar]
  30. Vasalou C., Herzog E. D. & Henson M. A. Small-world network models of intercellular coupling predict enhanced synchronization in the Suprachiasmatic Nucleus. J. Biol. Rhythms 24, 243 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hafner M., Koeppl H. & Gonz D. Effect of network architecture on synchronization and entrainment properties of the circadian oscillations in the suprachiasmatic nucleus. PLoS Comput. Biol. 8, e1002419 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Bodenstein C., Gosak M., Schuster S., Marhl M. & Perc M. Modeling the seasonal adaptation of circadian clocks by changes in the network structure of the suprachiasmatic nucleus. PLoS Comput. Biol. 8, e1002697 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Gu C. & Yang H. The circadian rhythm induced by the heterogeneous network structure of the suprachiasmatic nucleus. Chaos 26, 053112 (2016). [DOI] [PubMed] [Google Scholar]
  34. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  35. Barabási A. L. & Albert R. Emergence of scaling in random networks. Science 286, 509–512 (1999). [DOI] [PubMed] [Google Scholar]
  36. Šimonka V., Fras M. & Gosaka M. Stochastic simulation of the circadian rhythmicity in the SCN neuronal network. Physica A 424, 1–10 (2015). [Google Scholar]
  37. Henson M. A. Multicellular models of intercellular synchronization in circadian neural networks. Chaos, Solitons & Fractals 50, 48–64 (2013). [Google Scholar]
  38. Leloup J. & Goldbeter A. Modeling the molecular regulatory mechanism of circadian rhythms in Drosophila. BioEssays 22, 84–93 (2000). [DOI] [PubMed] [Google Scholar]
  39. Liu C., Weaver D. R., Strogatz S. H. & Reppert S. M. Cellular construction of a circadian clock: period determination in the suprachiasmatic nuclei. Cell 91, 855C860 (1997). [DOI] [PubMed] [Google Scholar]
  40. Indic P., Schwartz W. J. & Paydarfar D. Design principles for phase-splitting behaviour of coupled cellular oscillators: clues from hamsters with ‘split’ circadian rhythms. J. R. Soc. Interface 5, 873 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Abraham U. et al. Coupling governs entrainment range of circadian clocks. Mol. Syst. Biol. 6, 438 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Gu C., Xu J., Liu Z. & Rohling J. H. T. Entrainment range of nonidentical circadian oscillators by a light-dark cycle. Phy. Rev. E 88, 022702 (2013). [DOI] [PubMed] [Google Scholar]
  43. Westermark P. O., Welsh D. K., Okamura H. & Herzel H. Quantification of circadian rhythms in single cells. PLoS ONE 5, e1000580 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Webb A. B., Taylor S. R., Thoroughman K. A., Doyle F. J. III & Herzog E. D. Weakly circadian cells improve resynchrony. PLoS Comput. Biol. 8, e1002787 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Abel J. H. et al. Functional network inference of the suprachiasmatic nucleus. Proc. Natl. Acad. Sci. USA 113, 4512–4517 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. de la Iglesia H. O., Cambras T., Schwartz W. J. & Diez-Noguera A. Forced desynchronization of dual circadian oscillators within the rat suprachiasmatic nucleus. Curr. Biol. 14, 796–800 (2004). [DOI] [PubMed] [Google Scholar]
  47. Yan L., Foley N. C., Bobula J. M., Kriegsfeld L. J. & Silver R. Two antiphase oscillations occur in each suprachiasmatic nucleus of behaviorally split hamsters. J. Neurosci. 25, 9017–9026 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wang Q., Perc M., Duan Z. & Chen G. Synchronization transitions on scale-free neuronal networks due to finite information transmission delays. Phys. Rev. E 80, 026206 (2009). [DOI] [PubMed] [Google Scholar]
  49. Wang Q., Chen G. & Perc M. Synchronous bursts on scale-free neuronal networks with attractive and repulsive coupling. PLoS ONE 6, e15851 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Fan D., Wang Q. & Perc M. Disinhibition-induced transitions between absence and tonic-clonic epileptic seizures. Sci. Rep. 5, 12618 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep28878-s1.pdf (334.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES