Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 May 13;10(6):5933–5940. doi: 10.1021/acsnano.6b01265

Size-Independent Energy Transfer in Biomimetic Nanoring Complexes

Patrick Parkinson †, Nuntaporn Kamonsutthipaijit ‡, Harry L Anderson ‡,*, Laura M Herz †,*
PMCID: PMC4928140  PMID: 27176553

Abstract

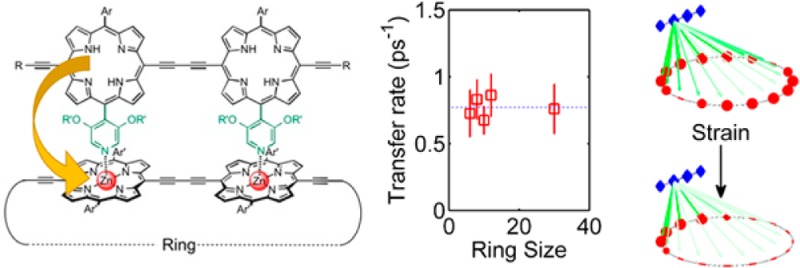
graphic file with name nn-2016-012653_0008.jpg

Supramolecular antenna-ring complexes are of great interest due to their presence in natural light-harvesting complexes. While such systems are known to provide benefits through robust and efficient energy funneling, the relationship between molecular structure, strain (governed by nuclear coordinates and motion), and energy dynamics (arising from electronic behavior) is highly complex. We present a synthetic antenna-nanoring system based on a series of conjugated porphyrin chromophores ideally suited to explore such effects. By systematically varying the size of the acceptor nanoring, we reveal the interplay between antenna-nanoring binding, local strain, and energy dynamics on the picosecond time scale. Binding of the antenna unit creates a local strain in the nanoring, and this strain was measured as a function of the size of the nanoring, by UV–vis-NIR titration, providing information on the conformational flexibility of the system. Strikingly, the energy-transfer rate is independent of nanoring size, indicating the existence of strain-localized acceptor states, spread over about six porphyrin units, arising from the noncovalent antenna-nanoring association.

Keywords: porphyrin nanoring, biomimetics, ultrafast spectroscopy, energy transfer

Supramolecular complexes of chromophores arranged in a cyclic structure are of interest for energy-harvesting applications, due to their occurrence in natural light-harvesting systems such as the LH2 complex of Rhodopseudomonas acidophilia.1 In natural complexes, chromophores with a range of absorption wavelengths are present with the effect of both broadening the spectral absorption of the complex and driving energy migration toward a reaction center.2,3 A cyclic arrangement of chromophores further modifies the energy levels of the component chromophores, altering the interchromophore interaction.4 Much research has been motivated by the desire to elucidate the range of physical processes that lead to robustness and high efficiency of the energy-transfer mechanism, with the twin goals of understanding any potential roles of molecular structure and quantum mechanics in biological systems5−7 and designing synthetic (biomimetic) light-harvesting systems.8−10 In particular, the role of both static (structural) and dynamic (thermal) disorder is of great interest due to the critical importance of symmetry and delocalization in the cyclic systems.

Here, we report fundamental insights into such effects, by unraveling the mechanisms of energy transfer and binding strain in a series of biomimetic antenna-nanoring complexes of varying diameter. While it might be presumed that the size of the natural systems are optimized for solar light harvesting in their specific environments, studies of the relationship between the rate of energy transfer and the size of the acceptor nanoring are extremely challenging. Previous investigations on dendritic synthetic light-harvesting molecules have revealed a decrease in transfer efficiency as molecule size increases,11,12 however until now, systematic study has typically been prohibited by synthetic challenges.

Porphyrin nanorings generally show large exciton delocalization lengths for both singlet and triplet states;13,14 for nanoring acceptors of between 6 and 12 units, we would anticipate that this delocalization would lead to a spatial extent of the acceptor exciton wave function across the whole nanoring.13 The delocalization results in a redshift in absorption with increasing nanoring size,13,15 along with a reduction in radiative rate linked to a symmetry-forbidden ground state.16 In the antenna-nanoring complex, one would expect this to cause a drop in energy-transfer rate within the Förster framework, because of the increased “center-of-mass” distance between the donor and acceptor states. However, we demonstrate here that, surprisingly, the noncovalent binding of an antenna molecule instead leads to strain-induced localization of the exciton state on the nanoring. Strikingly, the emergence of a low-energy localized state on the nanoring results in energy transfer from the dimer antenna to the nanoring being independent of nanoring size. This reveals both challenges and possibilities within supramolecular design, requiring a detailed consideration of strain on energy states in noncovalent complexes as well as showing that such strain can be used as an additional method to tune the local energy landscape.

The sensitive relationship between nuclear disorder and electronic dynamics is both complex and important for light-harvesting molecules17,18 and synthetic nanorings.19,20 In particular, excited-state delocalization and photophysics in cyclic molecules have been widely studied in a number of systems, including cycloparaphenylenes,21 cyclic oligothiophenes,22 and cyclic porphyrin oligomers16,23 as well as from a theoretical standpoint.15 Here, findings can be broadly divided into two categories: those for which static disorder arising from the chemical environment leads to a long-term preferred exciton localization site,24,25 and those for which thermal fluctuations dominate leading to a stochastic emission site,26 often depending on nanoring size.27 While there is clear evidence that nanoring molecules allow for dynamic localization of excited states,20 the impact of this upon antenna-nanoring energy-transfer dynamics is as yet unstudied.

Here we investigate the energy transfer from a porphyrin dimer antenna (P2py2) to nanorings of different sizes (c-P6, c-P8, c-P10, c-P12, and c-P30, Scheme 1).12,28−31 These systems provide a highly controlled synthetic framework with a well-defined supramolecular topology. Use of a dimer antenna provides strong binding and allows for unambiguous control of the lowest-lying dipole transition orientation with respect to that of the nanoring. The binding constants for these complexes, determined by UV–vis-NIR titration, provide a direct experimental measure of the mechanical rigidity of the nanorings and of the strain imposed by binding the antenna unit to each nanoring. By combining stoichiometry, photophysics, binding constant, and strain calculations with modeling of energy-transfer rates, we demonstrate the existence of strain-localized acceptor states that remarkably cause the energy-transfer rate to be independent of nanoring size.

Scheme 1. Formation of Supramolecular Double-Strand Porphyrin Nanoring Complexes from c-PN and P2py2.

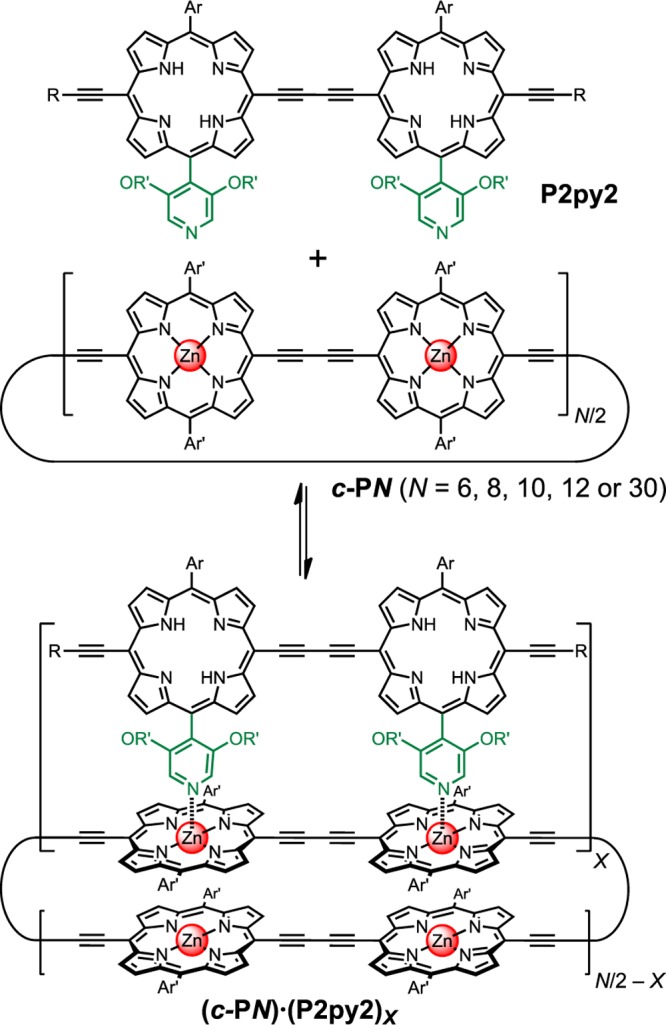
Scheme 1

Open in a new tab

Ar = 3,5-bis(trihexylsilyl)phenyl, Ar′ = 3,5-bis(octyloxy)phenyl, R = trihexylsilyl, R′ = dodecyl.

Results and Discussion

Determination of Stoichiometry

Each free-base P2py2 antenna unit can bind to the zinc-porphyrin nanorings via two Zn–N coordination sites, so that a c-PN nanoring with N zinc centers might be expected to bind to N/2 antenna units to form a complex of the type c-PN·(P2py2)N/2. We started this study by testing whether complexes of this stoichiometry are formed, using the Job plot method of continuous variation,32,33 by means of UV–vis-NIR spectroscopy. In these titrations, the total concentration of all the components was kept constant while varying the molar ratio of host (c-PN) to guest (P2py2). The stoichiometry of each complex was obtained from the abscissa of the maximum of the Job plot, where the x- and y-axes are given by

graphic file with name nn-2016-012653_m001.jpg 1
graphic file with name nn-2016-012653_m002.jpg 2

where [H] and [G] are the total concentrations of host (c-PN) and guest (P2py2) at the initial state, respectively; Aobs is the observed absorbance at a specific wavelength; εH and εG are the molar absorption coefficients of the host and guest at that wavelength, respectively. The x error bars reflect uncertainty in [H] and [G] (originating from uncertainty in εH and εG).

The resulting Job plots and UV–vis-NIR spectra are shown in Figure 1a–e. The changes in the absorption spectra on binding show that the dimers absorb at shorter wavelengths than the nanorings and that complexation results in a slight red-shift of the Q-bands, due to the effects of local planarization on exciton delocalization.

Figure 1.

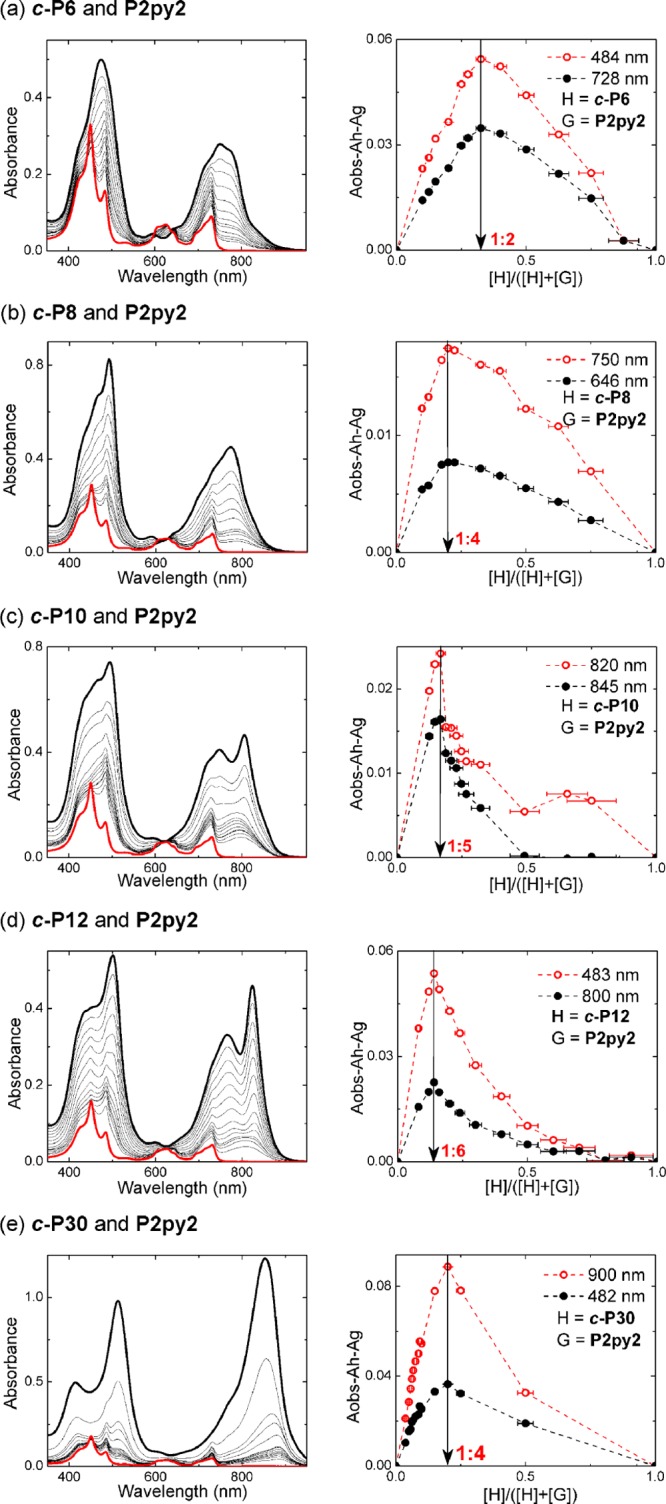
Figure 1

Open in a new tab

Job plots for nanoring-dimer complexes (all in toluene at 298 K). (Left) The UV–vis-NIR spectra upon varying mole fraction of nanoring from 0 (thick red) to 1 (black lines). (Right) Job plots of the complex formations with red and black dots corresponding to the absorbance difference as shown in the legend. Red and black dashed lines are given as a guide to the eye.

The Job plot for c-P6 shows that a 1:2 complex is formed instead of the expected 1:3 complex. This conclusion was confirmed by 1H NMR titration (see Supporting Information). The formation of a 1:2 complex, but not a 1:3 complex, can be explained by the increased strain in the ring upon binding P2py2 to c-P6.

The three medium-sized nanorings c-P8, c-P10, and c-P12 give the expected Job peaks at 0.20, 0.17, and 0.14 (c-P12), respectively, indicating that the stoichiometries of their complexes are 1:4 (c-P8), 1:5 (c-P10), and 1:6 (c-P12). The largest nanoring tested in this study, c-P30, gave a Job peak at 0.20 indicating formation of a 1:4 complex, instead of the expected 1:15 complex. This surprising behavior may be attributed to aggregation of the very large nanoring, either intermolecularly or intramolecularly, to form a hairpin folded conformation.34

Time-Resolved Photoluminescence

Upon photoexcitation of antennae in complexes of both natural3 and synthetic systems,35 energy transfer occurs to the nanoring with almost 100% efficiency, suggesting ultrafast quenching of the antenna emission resulting from energy transfer to the nanoring acceptor.

We experimentally evaluate the energy-transfer dynamics in complexes consisting of one porphyrin dimer (P2py2, fluorescence: E(Qx) = 1.68 eV) bound per porphyrin nanoring (c-PN, fluorescence: E(Qx) = 1.51–1.59 eV), by monitoring the relative photoluminescence decay of the dimers, as described in the Methods section. The complexes were prepared at millimolar concentrations in toluene. The dimer was also displaced from the complex by the addition of an excess of pyridine (>1% v/v) to give a reference sample. Figure 2 shows the photoluminescence ratio of the dimer between the assembled and disassembled states along with monoexponential fits. The energy-transfer rate for each complex is given in Figure 2; strikingly, there is no significant deviation from a (1.3 ps)−1 transfer rate, as the nanoring size is varied between 6 and 30 porphyrin units. A constant energy-transfer rate as a function of acceptor size is unexpected in porphyrin nanoring systems, as the absorbing (initially generated) lowest-lying excited state is thought to be highly delocalized for most of the studied molecules.13 Such delocalization introduces an increasing spatial separation between the donor molecule and the “center-of-mass” of the exciton generated on the acceptor nanoring, reducing the coupling in the Förster resonance energy-transfer framework.

Figure 2.

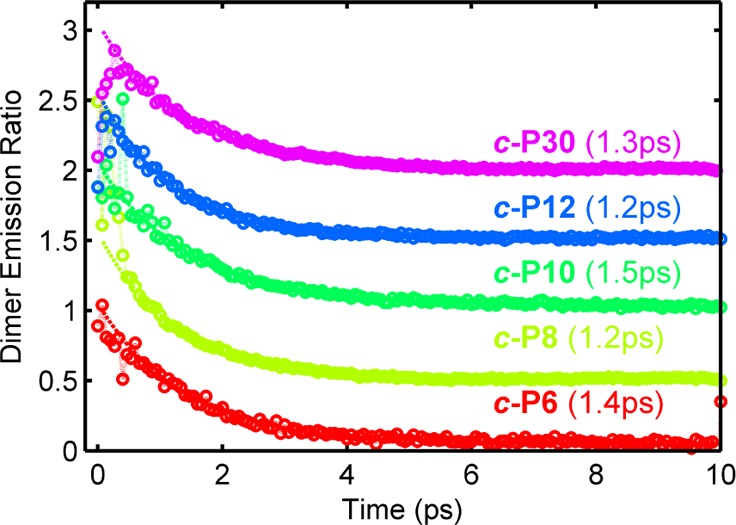
Figure 2

Open in a new tab

Ratio between the time-resolved dimer photoluminescence in the assembled and disassembled state isolating the dimer to nanoring energy-transfer pathway is shown for the five nanoring sizes (circles; vertically offset for clarity). A monoexponential fit (dashed line) is also shown, with the time constant for each complex given. An excitation wavelength of 627 nm was used.

The experimental result suggests that there is a preferred acceptor state that is essentially unchanging with nanoring size. Such constant energy transfer could arise from coupling to a localized absorbing state on the nanoring which would, however, have to be statically correlated with the antenna position. Uncorrelated localization would lead to a reduction in transfer rate with nanoring size, as a randomly placed acceptor site would be further from the antenna (on average) for larger rings. It is therefore proposed that the attachment of an antenna dimer induces a localized acceptor state immediately below the attachment point. The formation of this state is therefore most likely directly related to the binding process itself.

Determination of Binding Strain

We investigated the thermodynamic stabilities of the c-PN·(P2py2)X complexes, as a function of ring-size, to probe the flexibility of the nanorings and to study the role of the noncovalent dimer-nanoring association on the acceptor state. The binding constants of the complexes are too strong to determine by direct formation titrations (Kf > 107 M–1). Thus, denaturation titrations were used to determine Kf indirectly, by quantifying the ability of pyridine to break up the complexes, via the denaturation constant Kdn. At approximately 10–6 M in toluene at 25 °C, a large excess of pyridine was titrated into the complexes of (c-PN)·(P2py2)N/2 (or (c-P6)·(P2py2)2 for N = 6) to displace the bidentate ligand P2py2. The denaturation data were analyzed assuming that each P2py2 binds independently to the nanoring, with no allosteric cooperativity, using a 1:1 binding model, to give the values of Kf listed in Table 1 (see Supporting Information for details).

Table 1. Formation Constants and Binding Strain of Nanoring-Dimer Complexesa.

porphyrin host Kf, M–1 ΔGstrain, kJ mol–1
l-P2 (1.7 ± 0.3) × 108 0
c-P6 (2.6 ± 0.5) × 107 4.60 ± 0.71
c-P8 (7.8 ± 1.6) × 107 1.87 ± 0.72
c-P10 (1.3 ± 0.3) × 108 0.67 ± 0.73
c-P12 (1.5 ± 0.3) × 108 0.30 ± 0.73
Open in a new tab
a

Errors estimated from at least two replicates. See the Supporting Information for calculation of Kf.

Comparison of the binding constants of the various nanorings with P2py2 reveals that Kf increases as the nanoring becomes larger. The binding constant of c-P12 with P2py2 is close to the affinity of the linear zinc porphyrin dimer P2 for P2py2 [(1.7 ± 0.3) × 108 M–1], implying that each segment of c-P12 behaves almost like a linear oligomer. The strain energy, ΔGstrain, of complex formation was estimated by comparing the stability of c-PN·P2py2 with that of the unstrained dimer complex P2·P2py2, using eq 3:

graphic file with name nn-2016-012653_m003.jpg 3

where ΔGbinding = −RT ln Kf. The results, plotted against ring size in Figure 3, show that ΔGstrain decreases with the size of the rings.

Figure 3.

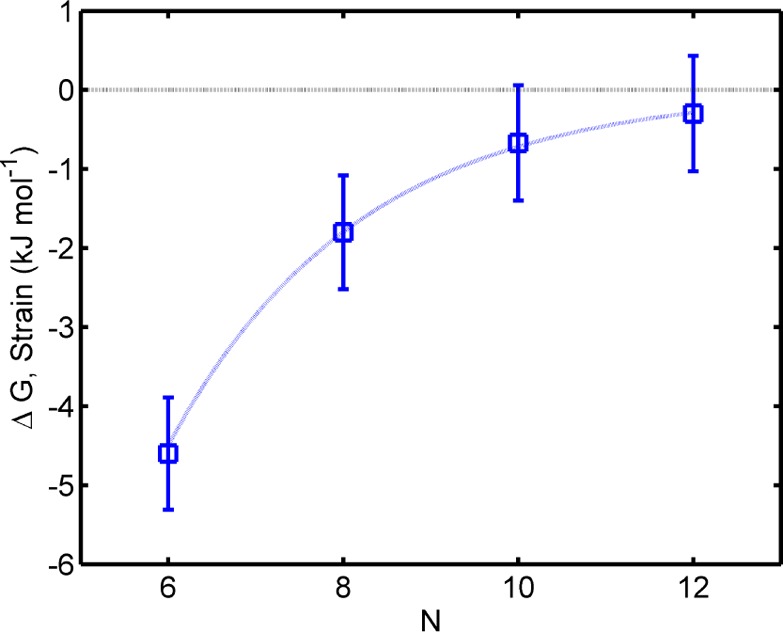
Figure 3

Open in a new tab

Calculated strain energy of ring-dimer complexes from their binding constants as a function of the number of the porphyrin units N. The blue line is a guide to the eye.

The strain in the nanorings, and the increase in strain caused by binding P2py2, was analyzed using molecular mechanics calculations. The geometries of all nanoring structures were calculated using the MM+ force field in HyperChem (see Supporting Information). The decrease in curvature as the rings become larger results in a change in distance between neighboring zinc centers; the Zn–Zn distances are 12.1, 12.2, 12.4, and 12.5 Å for c-P6, c-P8, c-P10, and c-P12, respectively. The structure of c-P12 is the most flexible, and its calculated Zn–Zn distance is close to that of the linear dimer P2 (12.8 Å). The finding that only two P2py2 dimer antenna units bind to the zinc porphyrin sites on c-P6 raises the question of whether the dimers sit close (1,3) or opposite (1,4) to each other on the 6-ring. Models of these complexes from molecular mechanics calculations (Figure 4) indicate that the geometry with the dimers further apart (1,4) is lower in energy.

Figure 4.

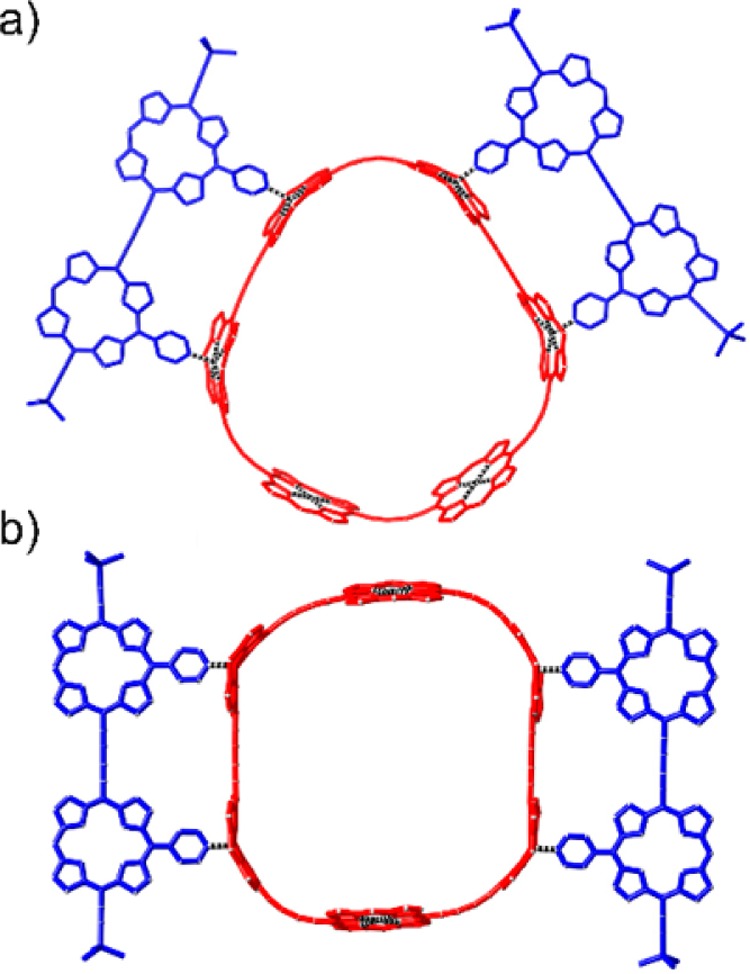
Figure 4

Open in a new tab

Geometries of two possible isomers of the 6-ring-dimer complex from molecular mechanics calculations (MM + force field; HyperChem). (a) Close dimer-ring complex; (b) Opposite dimer-ring complex; the aryl groups and side chains were omitted to simplify the calculations.

Modeling Energy Transfer

While the importance of structural disorder on the energy-transfer dynamics in conjugated molecules is well-known, the specific influence of a small change, such as introducing an antenna molecule, is typically hard to assess. Here we present a sensitive probe of how the exciton state on the nanoring is influenced by associated structural changes that in turn impact on the energy landscape. By combining ultrafast spectroscopy with associated modeling we are able to link the observed energy dynamics with explicit models representing fundamentally different acceptor states.

Any simulation requires a description of both the spatial distribution and transition energies and strengths of the donor and acceptor excitonic states. While the donor emissive state is straightforward to characterize, the acceptor state on the nanoring is more challenging to describe for two key reasons. First, the far-field absorbing state of the smallest nanorings is not expected to be the lowest-lying exciton state (known as the k = 0 state) whose transition dipole is symmetry-forbidden.36 Therefore, electronic coupling is generally assumed to occur through the far-field dipole allowed state (the k = 1 state) as measured using standard single-photon absorption.37 Second, the absorbing states of the free nanoring may not necessarily be energetically identical to those of the bound nanoring in the complex.15 We have previously shown that complete delocalization of the lowest-lying excitonic state can be observed for free nanoring molecules in solution, through both conjugation effects (a redshift in absorption with increasing ring size)13 and symmetry effects: a reduction in radiative rate,16,38 thermally activated emission,27 and emission polarization anisotropy at early times.13 For the complex studied, however, two key observations suggest the existence of a localized absorbing state on the region of the chain directly below the free-base dimer. We have demonstrated that there is no significant change in energy-transfer rate with nanoring size and that coupling to a donor dimer leads to non-negligible strain on the nanoring, with a local planarization and suppression of torsional motion.

To quantitatively assess the influence of localization, strain, and choice of absorbing states, we have calculated the energy-transfer rates in this system as a function of ring size for the three different models shown in Figure 5, as follows:

  • (1)

    Model 1 takes the Förster point-dipole approach, for which we assume an acceptor dipole to be situated at the center of the nanoring and calculate the energy-transfer rate using the traditional point-dipole model39

  • (2)

    Model 2 assumes a fully delocalized (k = 1) absorbing state on the nanoring, with the energy transfer between dimer and nanoring evaluated using the line-dipole model40

  • (3)

    Model 3 assumes an absorbing state of extent Na porphyrin units localized below the dimer. The energy-transfer rate is calculated using the line-dipole approach.

Figure 5.

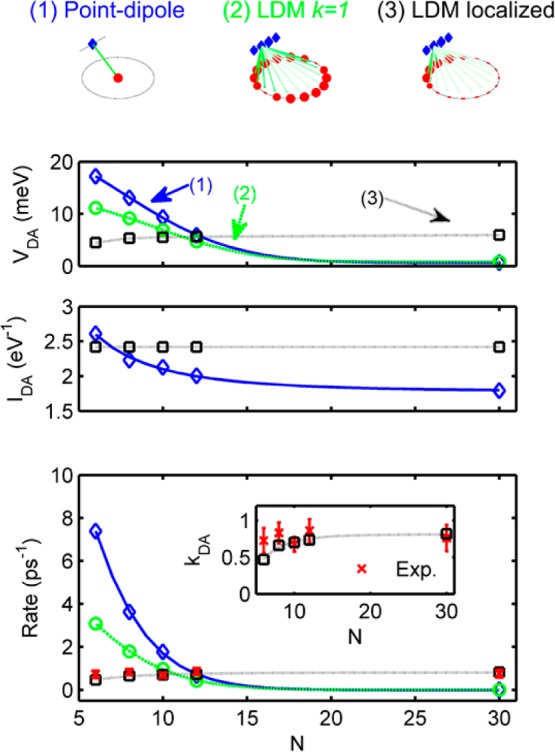
Figure 5

Open in a new tab

(Top) Schematic of three energy-transfer models for the dimer c-P8 system: (left) point-dipole model, (center) line-dipole model with fully delocalized (k = 1) nanoring state, and (right) line-dipole model with partially localized (Na = 6) acceptor state. Arrows indicate subdipole coupling elements. (Lower) Modeled data for (top) coupling strength VDA, (center) spectral overlap IDA, and (bottom) energy-transfer rate kDA. The (1) point-dipole model is shown in blue, (2) line-dipole model (to k = 1) in green, and (3) localized dimer model in black. Experimental data are shown in red (bottom panel only). The inset shows the dimer model and experimental data only. All lines are guides to the eye.

For the line-dipole approach (Models 2 and 3), six subdipoles per porphyrin unit were used, chosen as providing coupling energies within experimental error of the value obtained where the number of subdipoles tends toward infinity.40,41 The models are described fully in the Supporting Information, along with details of input parameters, such as geometry and donor emission and acceptor absorption characteristics.

For Model 3, the specific nature of the localized absorbing state requires particular consideration. The most localizing scenario of a dimer-like absorbing state on the nanoring being formed below the dimer does not appear to be representative of the distribution of strain on the molecule (see Figure 4). In addition, such severe localization would lead to the emergence of a clear dimer-like higher-energy transition in the absorption or photoluminescence spectrum upon binding which is not observed (see Supporting Information). Therefore, a weaker effect of partial localization of the absorbing state over Na units of the ring just below the donor dimer is considered. Here we use absorption spectra for a range of complementary porphyrin oligomers on a suitable template to compute energy-transfer rates that are then contrasted with the experimental data (see Figures S23 and S24 of the Supporting Information). By use of the oligomer as a model, we are thus able to simulate the effect of strain, torsional restriction, and Zn-pyridyl coordination on the electronic state.42 We find that a description of the localized distorted state extending over Na = 6 units offers best match between experimental data and calculations for Model 3, suggesting that strain resulting from dimer attachment weakens the effective conjugation of the absorption state only to a certain extent.

The key outputs from our three models are shown in Figure 5, namely the coupling strength VDA calculated using Models 1–3, the spectral overlap IDA for the full-nanoring (Models 1 and 2), and localized absorbing (Model 3) state, and the predicted energy-transfer rate as a function of nanoring size. It can be seen that Model 3 provides both a qualitative and quantitatively excellent agreement with the experimental data, strongly supporting the emergence of a localized state upon noncovalent binding of an antenna molecule. In particular, Model 3 is the only approach that mirrors the observed striking independence of energy-transfer rates on ring size.

The origin of the emergence of a localized state can be related to two effects: first, the strain applied during binding, and second, the local suppression of torsional motion. Deviation from circularity is known to create localized states,16 while backbone distortion in particular36 creates low-energy sites. Torsional motion has often been implicated as a key driver toward disorder and (de)localization in a number of conjugated systems.43,44 These features are highly relevant, as in the assembled dimer-nanoring complexes, the torsional angle between the two bound porphyrins is locked, which often generates a higher conjugation, lower-energy state,45 as experimentally shown for cyclic oligothiophene molecules with planarizing linkers46 and porphyrin dimers.47,48 In addition to strain-induced localization effects, local coordination with the pyridine groups of the dimer may lower the energetic landscape of the porphyrin sites to which the dimer is coordinated.49 However, our energy-transfer model indicates the existence of an absorbing state longer than two porphyrin units, supporting a spatially extended cause such as strain.

It is logical, therefore, that the noncovalent addition of an antenna molecule onto a nanoring structure induces significant strain, resulting in the distortion of the energetic environment and the emergence of localized states. Such an indirect impact on the exciton states of the nanoring originates from the flexibility of the nanoring systems as well as the sensitivity of the molecule to environmental effects. While environment-driven localization effects have been observed in naturally occurring systems,25,50 the use of strain in the synthetic nanoring systems described provides a tool to control local exciton states in multichromophoric complexes.

Conclusion

In summary, we have revealed the fundamental mechanisms underlying energy transfer in a family of synthetic porphyrin light-harvesting complexes with analogies to the natural LH2 antenna systems. Our ability to vary the ring size 5-fold between 6 and 30 porphyrin units has enabled validity tests of energy-transfer models that are hard to achieve for biological systems. We were able to explore the effect of strain resulting from donor binding to the porphyrin nanorings via a study of binding affinities. Binding constants were shown to increase significantly with the size of the ring, consistent with host distortion and strain effects decreasing from the rigid 6-ring to the more flexible 12-ring. Our subsequent investigation shows that such strain also has significant impact on the energy-transfer rates in the assembled systems. Upon varying the size of the nanoring from 6 to 30 porphyrin units, no change in energy-transfer rate between the attached dimer and the nanoring was observed. These experimental results indicate that the absorbing state is independent of nanoring size, acting as a localized state centered below the antenna molecule. Simulation of energy-transfer rates qualitatively and quantitatively agrees with the existence of a localized acceptor state extending over approximately six porphyrin units. Our findings therefore demonstrate the critical role of both the mechanical and electronic effect of strain in supramolecular systems exhibiting high degrees of exciton delocalization. Our work also highlights an approach to exploit strain in large conjugated materials, to create efficient, size-independent synthetic energy funneling for light-harvesting applications.

Methods

Up-Conversion Spectroscopy

An ultrafast Ti:sapphire laser operating at 820 nm provided 100 fs laser pulses at 80 MHz. A fraction of this was used to pump an optical parametric oscillator operating at 627 nm, to be used as an optical pump pulse. This wavelength was chosen to preferentially excite the dimer in the complex with respect to the nanoring absorption (see Supporting Information). Millimolar solutions with high absorbance were studied to achieve optical excitation within a small volume of sample, to minimize temporal smearing and maximize signal-to-noise ratio. The power of pump pulse incident on the sample was set to be 10 mW (∼0.25 μJ/cm2/pulse), with a vertical polarization, which was focused onto the sample held inside a quartz cuvette. The emitted photoluminescence was collected by a pair of off-axis parabolic mirrors and focused onto a 1 mm thick nonlinear crystal (BBO) along with the remainder of the (vertically polarized) laser pulse. The up-converted signal was spatially and spectrally filtered to remove the gate pulse and residual photoluminescence, before detection using a spectrometer and liquid nitrogen cooled CCD. The system was set to up-convert the photoluminescence signal from the dimer, centered at 735 nm, and had a temporal resolution of approximately 270 fs as measured by cross-correlation. By measuring the ratio of the photoluminescence from the photoexcited dimer as a function of time after excitation for the assembled and disassembled state of the complex (without and with pyridine, respectively), a transfer rate can be determined. Complete photoluminescence decay curves are shown in the Supporting Information.

Acknowledgments

We thank the European Research Council (grant 320969) and the EPSRC for generous financial support and the EPSRC UK Mass Spectrometry Facility at Swansea University for mass spectra. N.K. is supported by a Royal Thai Government Scholarship.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b01265.

  • General chemical methods; synthetic procedures; determination of stoichiometry and binding constants; calculations of the optimum excitation wavelength; photophysical results for complex dissociation; experimentally determined energy-transfer rates and details of the energy-transfer model (PDF)

Author Present Address

School of Physics and Astronomy, Photon Science Institute, University of Manchester, Manchester M13 9PL, United Kingdom.

Author Contributions

§ These authors contributed equally.

The authors declare no competing financial interest.

Supplementary Material

nn6b01265_si_001.pdf (3.9MB, pdf)

References

  1. McDermott G.; Prince S. M.; Freer A. A.; Hawthornthwaite-Lawless A. M.; Papiz M. Z.; Cogdell R. J.; Isaacs N. W. Crystal Structure of an Integral Membrane Light-Harvesting Complex from Photosynthetic Bacteria. Nature 1995, 374, 517–521. 10.1038/374517a0. [DOI] [Google Scholar]
  2. Scholes G. D.; Fleming G. R. On the Mechanism of Light Harvesting in Photosynthetic Purple Bacteria: B800 to B850 Energy Transfer. J. Phys. Chem. B 2000, 104, 1854–1868. 10.1021/jp993435l. [DOI] [Google Scholar]
  3. Cogdell R. J.; Gall A.; Köhler J. The Architecture and Function of the Light-Harvesting Apparatus of Purple Bacteria: From Single Molecules to in Vivo Membranes. Q. Rev. Biophys. 2006, 39, 227–324. 10.1017/S0033583506004434. [DOI] [PubMed] [Google Scholar]
  4. Ketelaars M.; van Oijen A. M.; Matsushita M.; Köhler J.; Schmidt J.; Aartsma T. J. Spectroscopy on the B850 Band of Individual Light-Harvesting 2 Complexes of Rhodopseudomonas Acidophila. I. Experiments and Monte Carlo Simulations. Biophys. J. 2001, 80, 1591–1603. 10.1016/S0006-3495(01)76132-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Engel G. S.; Calhoun T. R.; Read E. L.; Ahn T.-K.; Mancal T.; Cheng Y.-C.; Blankenship R. E.; Fleming G. R. Evidence for Wavelike Energy Transfer through Quantum Coherence in Photosynthetic Systems. Nature 2007, 446, 782–786. 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
  6. Collini E.; Wong C. Y.; Wilk K. E.; Curmi P. M. G.; Brumer P.; Scholes G. D. Coherently Wired Light-Harvesting in Photosynthetic Marine Algae at Ambient Temperature. Nature 2010, 463, 644–647. 10.1038/nature08811. [DOI] [PubMed] [Google Scholar]
  7. Novelli F.; Nazir A.; Richards G. H.; Roozbeh A.; Wilk K. E.; Curmi P. M. G.; Davis J. A. Vibronic Resonances Facilitate Excited State Coherence in Light Harvesting Proteins at Room Temperature. J. Phys. Chem. Lett. 2015, 6, 4573–4580. 10.1021/acs.jpclett.5b02058. [DOI] [PubMed] [Google Scholar]
  8. Wasielewski M. R. Self-Assembly Strategies for Integrating Light Harvesting and Charge Separation in Artificial Photosynthetic Systems. Acc. Chem. Res. 2009, 42, 1910–1921. 10.1021/ar9001735. [DOI] [PubMed] [Google Scholar]
  9. Aratani N.; Kim D.; Osuka A. Discrete Cyclic Porphyrin Arrays as Artificial Light-Harvesting Antenna. Acc. Chem. Res. 2009, 42, 1922–1934. 10.1021/ar9001697. [DOI] [PubMed] [Google Scholar]
  10. Yoneda Y.; Noji T.; Katayama T.; Mizutani N.; Komori D.; Nango M.; Miyasaka H.; Itoh S.; Nagasawa Y.; Dewa T. Extension of Light-Harvesting Ability of Photosynthetic Light-Harvesting Complex 2 (LH2) through Ultrafast Energy Transfer from Covalently Attached Artificial Chromophores. J. Am. Chem. Soc. 2015, 137, 13121–13129. 10.1021/jacs.5b08508. [DOI] [PubMed] [Google Scholar]
  11. Devadoss C.; Bharathi P.; Moore J. S. Energy Transfer in Dendritic Macromolecules: Molecular Size Effects and the Role of an Energy Gradient. J. Am. Chem. Soc. 1996, 118, 9635–9644. 10.1021/ja961418t. [DOI] [Google Scholar]
  12. Choi M.-S.; Yamazaki T.; Yamazaki I.; Aida T. Bioinspired Molecular Design of Light-Harvesting Multiporphyrin Arrays. Angew. Chem., Int. Ed. 2004, 43, 150–158. 10.1002/anie.200301665. [DOI] [PubMed] [Google Scholar]
  13. Parkinson P.; Kondratuk D. V.; Menelaou C.; Gong J. Q.; Anderson H. L.; Herz L. M. Chromophores in Molecular Nanorings: When Is a Ring a Ring?. J. Phys. Chem. Lett. 2014, 5, 4356–4361. 10.1021/jz5022153. [DOI] [PubMed] [Google Scholar]
  14. Tait C. E.; Neuhaus P.; Peeks M. D.; Anderson H. L.; Timmel C. R. Transient EPR Reveals Triplet State Delocalization in a Series of Cyclic and Linear π-Conjugated Porphyrin Oligomers. J. Am. Chem. Soc. 2015, 137, 8284–8293. 10.1021/jacs.5b04511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Chang M.-H.; Hoffmann M.; Anderson H. L.; Herz L. M. Dynamics of Excited-State Conformational Relaxation and Electronic Delocalization in Conjugated Porphyrin Oligomers. J. Am. Chem. Soc. 2008, 130, 10171–10178. 10.1021/ja711222c. [DOI] [PubMed] [Google Scholar]
  16. Gong J. Q.; Favereau L.; Anderson H. L.; Herz L. M. Breaking the Symmetry in Molecular Nanorings. J. Phys. Chem. Lett. 2016, 7, 332–338. 10.1021/acs.jpclett.5b02617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Matsushita M.; Ketelaars M.; van Oijen A. M.; Köhler J.; Aartsma T. J.; Schmidt J. Spectroscopy on the B850 Band of Individual Light-Harvesting 2 Complexes of Rhodopseudomonas Acidophila. II. Exciton States of an Elliptically Deformed Ring Aggregate. Biophys. J. 2001, 80, 1604–1614. 10.1016/S0006-3495(01)76133-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Pajusalu M.; Kunz R.; Rätsep M.; Timpmann K.; Köhler J.; Freiberg A. Unified Analysis of Ensemble and Single-Complex Optical Spectral Data from Light-Harvesting Complex-2 Chromoproteins for Gaining Deeper Insight into Bacterial Photosynthesis. Phys. Rev. E 2015, 92, 052709. 10.1103/PhysRevE.92.052709. [DOI] [PubMed] [Google Scholar]
  19. Adamska L.; Nayyar I.; Chen H.; Swan A. K.; Oldani N.; Fernandez-Alberti S.; Golder M. R.; Jasti R.; Doorn S. K.; Tretiak S. Self-Trapping of Excitons, Violation of Condon Approximation, and Efficient Fluorescence in Conjugated Cycloparaphenylenes. Nano Lett. 2014, 14, 6539–6546. 10.1021/nl503133e. [DOI] [PubMed] [Google Scholar]
  20. Liu J.; Adamska L.; Doorn S. K.; Tretiak S. Singlet and Triplet Excitons and Charge Polarons in Cycloparaphenylenes: A Density Functional Theory Study. Phys. Chem. Chem. Phys. 2015, 17, 14613–14622. 10.1039/C5CP01782C. [DOI] [PubMed] [Google Scholar]
  21. Nishihara T.; Segawa Y.; Itami K.; Kanemitsu Y. Exciton Recombination Dynamics in Nanoring Cycloparaphenylenes. Chem. Sci. 2014, 5, 2293. 10.1039/c3sc53462f. [DOI] [Google Scholar]
  22. Kim P.; Park K. H.; Kim W.; Tamachi T.; Iyoda M.; Kim D. Relationship between Dynamic Planarization Processes and Exciton Delocalization in Cyclic Oligothiophenes. J. Phys. Chem. Lett. 2015, 6, 451–456. 10.1021/jz502395z. [DOI] [PubMed] [Google Scholar]
  23. Ambroise A.; Li J.; Yu L.; Lindsey J. S. A Self-Assembled Light-Harvesting Array of Seven Porphyrins in a Wheel and Spoke Architecture. Org. Lett. 2000, 2, 2563–2566. 10.1021/ol006036d. [DOI] [PubMed] [Google Scholar]
  24. Thiessen A.; Würsch D.; Jester S.-S.; Aggarwal A. V.; Idelson A.; Bange S.; Vogelsang J.; Höger S.; Lupton J. M. Exciton Localization in Extended π-Electron Systems: Comparison of Linear and Cyclic Structures. J. Phys. Chem. B 2015, 119, 9949–9958. 10.1021/acs.jpcb.5b02091. [DOI] [PubMed] [Google Scholar]
  25. Tubasum S.; Camacho R.; Meyer M.; Yadav D.; Cogdell R. J.; Pullerits T.; Scheblykin I. G. Evidence of Excited State Localization and Static Disorder in LH2 Investigated by 2D-Polarization Single-Molecule Imaging at Room Temperature. Phys. Chem. Chem. Phys. 2013, 15, 19862–19869. 10.1039/c3cp52127c. [DOI] [PubMed] [Google Scholar]
  26. Aggarwal A. V.; Thiessen A.; Idelson A.; Kalle D.; Würsch D.; Stangl T.; Steiner F.; Jester S.-S.; Vogelsang J.; Höger S.; Lupton J. M. Fluctuating Exciton Localization in Giant π-Conjugated Spoked-Wheel Macrocycles. Nat. Chem. 2013, 5, 964–970. 10.1038/nchem.1758. [DOI] [PubMed] [Google Scholar]
  27. Yong C.-K.; Parkinson P.; Kondratuk D. V.; Chen W.-H.; Stannard A.; Summerfield A.; Sprafke J. K.; O’Sullivan M. C.; Beton P. H.; Anderson H. L.; Herz L. M. Ultrafast Delocalization of Excitation in Synthetic Light-Harvesting Nanorings. Chem. Sci. 2015, 6, 181–189. 10.1039/C4SC02424A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Scott Wilson G.; Anderson H. L. A Conjugated Triple Strand Porphyrin Array. Chem. Commun. 1999, 1539–1540. 10.1039/a903883c. [DOI] [Google Scholar]
  29. Tsuda A.; Hu H.; Tanaka R.; Aida T. Planar or Perpendicular? Conformational Preferences of Pi-Conjugated Metalloporphyrin Dimers and Trimers in Supramolecular Tubular Arrays. Angew. Chem., Int. Ed. 2005, 44, 4884–4888. 10.1002/anie.200500887. [DOI] [PubMed] [Google Scholar]
  30. Aimi J.; Nagamine Y.; Tsuda A.; Muranaka A.; Uchiyama M.; Aida T. Conformational” solvatochromism: Spatial Discrimination of Nonpolar Solvents by Using a Supramolecular Box of a Pi-Conjugated Zinc Bisporphyrin Rotamer. Angew. Chem., Int. Ed. 2008, 47, 5153–5156. 10.1002/anie.200801332. [DOI] [PubMed] [Google Scholar]
  31. Aimi J.; Oya K.; Tsuda A.; Aida T. Chiroptical Sensing of Asymmetric Hydrocarbons Using a Homochiral Supramolecular Box from a Bismetalloporphyrin Rotamer. Angew. Chem., Int. Ed. 2007, 46, 2031–2035. 10.1002/anie.200604330. [DOI] [PubMed] [Google Scholar]
  32. Job P. Recherches Sur La Formation de Complexes Mineraux En Solution, et Sur Le Stabilite. Ann. Chim. (Paris, Fr.) 1928, 9, 113–203. [Google Scholar]
  33. Hirose K. A Practical Guide for the Determination of Binding Constants. J. Inclusion Phenom. Mol. Recognit. Chem. 2001, 39, 193–209. 10.1023/A:1011117412693. [DOI] [Google Scholar]
  34. Kondratuk D. V.; Perdigão L. M. A.; Esmail A. M. S.; O’Shea J. N.; Beton P. H.; Anderson H. L. Supramolecular Nesting of Cyclic Polymers. Nat. Chem. 2015, 7, 317–322. 10.1038/nchem.2182. [DOI] [PubMed] [Google Scholar]
  35. Parkinson P.; Knappke C. E. I.; Kamonsutthipaijit N.; Sirithip K.; Matichak J. D.; Anderson H. L.; Herz L. M. Ultrafast Energy Transfer in Biomimetic Multistrand Nanorings. J. Am. Chem. Soc. 2014, 136, 8217–8220. 10.1021/ja504730j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sprafke J. K.; Kondratuk D. V.; Wykes M.; Thompson A. L.; Hoffmann M.; Drevinskas R.; Chen W.-H.; Yong C. K.; Kärnbratt J.; Bullock J. E.; Malfois M.; Wasielewski M. R.; Albinsson B.; Herz L. M.; Zigmantas D.; Beljonne D.; Anderson H. L. Belt-Shaped π-Systems: Relating Geometry to Electronic Structure in a Six-Porphyrin Nanoring. J. Am. Chem. Soc. 2011, 133, 17262–17273. 10.1021/ja2045919. [DOI] [PubMed] [Google Scholar]
  37. Nishihara T.; Segawa Y.; Itami K.; Kanemitsu Y. Excited States in Cycloparaphenylenes: Dependence of Optical Properties on Ring Length. J. Phys. Chem. Lett. 2012, 3, 3125–3128. 10.1021/jz3014826. [DOI] [PubMed] [Google Scholar]
  38. Hoffmann M.; Kärnbratt J.; Chang M.-H.; Herz L. M.; Albinsson B.; Anderson H. L. Enhanced Pi Conjugation around a porphyrin[6] Nanoring. Angew. Chem., Int. Ed. 2008, 47, 4993–4996. 10.1002/anie.200801188. [DOI] [PubMed] [Google Scholar]
  39. Förster T. Zwischenmolekulare Energiewanderung Und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. [DOI] [Google Scholar]
  40. Beenken W. J. D.; Pullerits T. Excitonic Coupling in Polythiophenes: Comparison of Different Calculation Methods. J. Chem. Phys. 2004, 120, 2490. 10.1063/1.1636460. [DOI] [PubMed] [Google Scholar]
  41. Schmid S. A.; Abbel R.; Schenning A. P. H. J.; Meijer E. W.; Herz L. M. Impact of Nuclear Lattice Relaxation on the Excitation Energy Transfer along a Chain of π -Conjugated Molecules. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 085438. 10.1103/PhysRevB.81.085438. [DOI] [Google Scholar]
  42. Hestand N. J.; Spano F. C. The Effect of Chain Bending on the Photophysical Properties of Conjugated Polymers. J. Phys. Chem. B 2014, 118, 8352–8363. 10.1021/jp501857n. [DOI] [PubMed] [Google Scholar]
  43. Parkinson P.; Müller C.; Stingelin N.; Johnston M. B.; Herz L. M. Role of Ultrafast Torsional Relaxation in the Emission from Polythiophene Aggregates. J. Phys. Chem. Lett. 2010, 1, 2788–2792. 10.1021/jz101026g. [DOI] [Google Scholar]
  44. Yang J.; Ham S.; Kim T.-W.; Park K. H.; Nakao K.; Shimizu H.; Iyoda M.; Kim D. Inhomogeneity in the Excited-State Torsional Disorder of a Conjugated Macrocycle. J. Phys. Chem. B 2015, 119, 4116–4126. 10.1021/jp5123689. [DOI] [PubMed] [Google Scholar]
  45. Tretiak S.; Saxena A.; Martin R. L.; Bishop A. R. Conformational Dynamics of Photoexcited Conjugated Molecules. Phys. Rev. Lett. 2002, 89, 097402. 10.1103/PhysRevLett.89.097402. [DOI] [PubMed] [Google Scholar]
  46. Kim W.; Sung J.; Park K. H.; Shimizu H.; Imamura M.; Han M.; Sim E.; Iyoda M.; Kim D. The Role of Linkers in the Excited-State Dynamic Planarization Processes of Macrocyclic Oligothiophene 12-Mers. J. Phys. Chem. Lett. 2015, 6, 4444–4450. 10.1021/acs.jpclett.5b02189. [DOI] [PubMed] [Google Scholar]
  47. Camargo F. V. A.; Anderson H. L.; Meech S. R.; Heisler I. A. Time-Resolved Twisting Dynamics in a Porphyrin Dimer Characterized by Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. B 2015, 119, 14660–14667. 10.1021/acs.jpcb.5b09964. [DOI] [PubMed] [Google Scholar]
  48. Gong J. Q.; Parkinson P.; Kondratuk D. V.; Gil-Ramírez G.; Anderson H. L.; Herz L. M. Structure-Directed Exciton Dynamics in Templated Molecular Nanorings. J. Phys. Chem. C 2015, 119, 6414–6420. 10.1021/acs.jpcc.5b00210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Nappa M.; Valentine J. S. The Influence of Axial Ligands on Metalloporphyrin Visible Absorption Spectra. Complexes of Tetraphenylporphinatozinc. J. Am. Chem. Soc. 1978, 100, 5075–5080. 10.1021/ja00484a027. [DOI] [Google Scholar]
  50. van Oijen A. M.; Ketelaars M.; Köhler J.; Aartsma T. J.; Schmidt J. Unraveling the Electronic Structure of Individual Photosynthetic Pigment-Protein Complexes. Science (Washington, DC, U. S.) 1999, 285, 400–402. 10.1126/science.285.5426.400. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn6b01265_si_001.pdf (3.9MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES