Abstract
There are no satisfying tools in tissue microarray (TMA) data analysis up to now to analyze the cooperative behavior of all measured markers in a multifactorial TMA approach. The developed tool TMAinspiration is not only offering an analysis option to close this gap but also offering an ecosystem consisting of quality control concepts and supporting scripts to make this approach a platform for informed practice and further research. The TMAinspiration method is specifically focusing on the demands of the TMA analysis by controlling errors and noise by a generalized regression scheme while at the same time avoiding to introduce a priori too many constraints into the analysis of the data. So, we are testing partitions of a proximity table to find an optimal support for a ranking scheme of molecular dependencies. The idea of combining several partitions to one ensemble, which is balancing the optimization process, is based on the main assumption that all these perspectives on the cellular network need to be self-consistent. Several application examples in breast cancer and one in squamous cell carcinoma demonstrate that this procedure is nicely confirming a priori knowledge on the expression characteristics of protein markers, while also integrating many new results discovered in the treasury of a bigger TMA experiment. The code and software are now freely available at: http://complex-systems.uni-muenster.de/tma_inspiration.html.
Keywords: tissue microarray, protein expression, combinatorial algorithm, systems biology, pathology, cancer
Introduction
Tissue microarrays (TMAs) are the perfect tools in pathology and beyond to analyze the abundance and spatial distribution of proteins in well-defined tissue sections by immunohistochemical means.1–4 The TMA block can include up to many hundred or even more patient samples originating from a certain physiological state, eg, a certain tumor subtype and progression level. Serial ultrathin sections of this TMA block can be stained with different antibodies, and so, many protein expression measurements of many samples at a distinct tissue localization and state can be collected. Therefore, TMA data are perfectly suited for analyzing the cooperative effects in-between the measured proteins.
The theory for such analysis is based on the structure of a biological cell.5 The cell is composed of many different molecule classes where, eg, the proteins are associated with cellular function, phenotype, and physiological state. This state is based on a characteristic pattern of protein expression values, which is altered in a specific way in diseases, such as cancer and also in-between cancer subentities. Because all these molecules are building a discrete and ordered cellular system, they are indirectly or directly connected by an interaction scheme, namely, the biological network.6–8
The major objective in the case of TMAs is to measure relative expression (concentration) values of several proteins in a certain physiological state and tissue compartment to uncover which proteins might work together to form this physiological or pathological state and which might be not specifically involved. One type of approach to conduct such studies are time series experiments9 established for microarray or next-generation sequencing studies. These experiments measure a few different states and deduce network dependencies from the differences in-between these (macro) states. In the case of the TMA data, the high number of patient samples in a certain physiological condition and tissue compartment, but with a microvariance in the sample states, opens an alternative approach, which we follow in this study.
Up to now, the expression values of TMAs were evaluated more or less sophisticated per protein marker,10,11 but every maker with all its measurements was solely seen as a Gaussian distribution of the expected value and not in a sense of slightly different network (micro) states. Some further approaches deal with the modeling of survival probabilities,12 and others try to reconstruct tumor expression characteristics from only a few tissue cores,13 create the prognostic pattern,14 and develop an advanced image analysis algorithm10 or a data mining algorithm for TMA databases,15 but so far no one tried to establish a systematic approach to examine cooperative dependencies in-between many different protein measurements on serial sections of TMAs.
At that point we started from scratch and established a combinatorial procedure16 to unravel consistently, the dependencies between several protein measurements evaluated the power of the procedure with several cancer data sets.17–19 The core of this merely assumption-free and data-driven approach is that we do not only create simply a proximity matrix but also create an order of dependencies by partitioning the proteins and optimizing the interdependency order of the proteins across these partitions by a generalized linear regression approach.
In the following sections, we present an end user suitable message passing interface (MPI)/open multiprocessing (OpenMP)-based implementation of this algorithmic idea together with a small ecosystem in R (https://www.r-project.org/) to evaluate the results.
Despite that the research is ongoing, the real merit of this procedure at its present state is that it extends the scope of TMAs remarkably. We open the perspective for a broader view of TMAs, away from the focus as a validation tool, toward a phenotypic network analysis tool.
Basic Considerations
The combinatorial procedure is introduced already in the study by Buerger et al,16 so we will only highlight the current concept here. The idea behind this approach is to analyze protein expression dependencies measured on TMAs. The observed cooperative effects might be of a direct or indirect nature, so not necessarily showing basic regulatory effects but systemic effects. The basic premise is that we assume that all our single measurements are bound together in a biological network, which is integrating all the observed and expressed proteins in a systemic context. Because we are analyzing the protein expression of a biological cell, this is a well-established assumption as we pointed out in the “Introduction” section. As a consequence, the small, nonerror-based protein signal variance over all patient samples, and over all the different proteins, is systematically reflecting the underlying biological network activity.
The TMA data source used in this context is a histologically and clinically well-defined cohort of patient samples defining a relatively exact physiological state. This state might belong to a normal physiological state or characterizes a disease state. Besides that the pathologists define cell types, morphological features and further clinical aspects according to their classification guidelines, the cohort will still comprise a microvariance in the physiological states of the samples. To discriminate between measurement uncertainty and the specific network variance, a specificity test was established (cf., Buerger et al’s.16 Fig. 6 and Supplementary Fig. 2). The microvariances in the physiological states are only measurable, when the measured proteins exhibit a considerable interaction among each other. This effect is exploited by the presented procedure.
Algorithm
Because we have only a vague idea how biological systems are finally regulating their actions, we try to avoid using the model-based approaches. As a consequence hereof, we chose a combinatorial optimization process that is analyzing the complete space of possible interactions. Due to this brute-force approach, we are limited to a certain number of proteins. In contrast to straighter and computationally more efficient approaches as a cluster procedure, we can efficiently adjust the order by the optimization procedure and additionally are able to analyze the properties of all combinatorial states offering insight into the architecture of the network.
In brief, as many ultrathin serial sections as necessary are cut from the TMA block. The sections, all containing the in vivo situation of interest, are immunohistochemically stained with antibodies directed against the proteins of interest. The imunnohistochemical score values characterizing the cells of interest are generated double blind by two pathologists. So, for every protein and TMA section, a score vector over all samples is generated. At that point, it might be noticed that normally mixing of data sources from different TMA block series is not allowed, due to the different TMA origins.
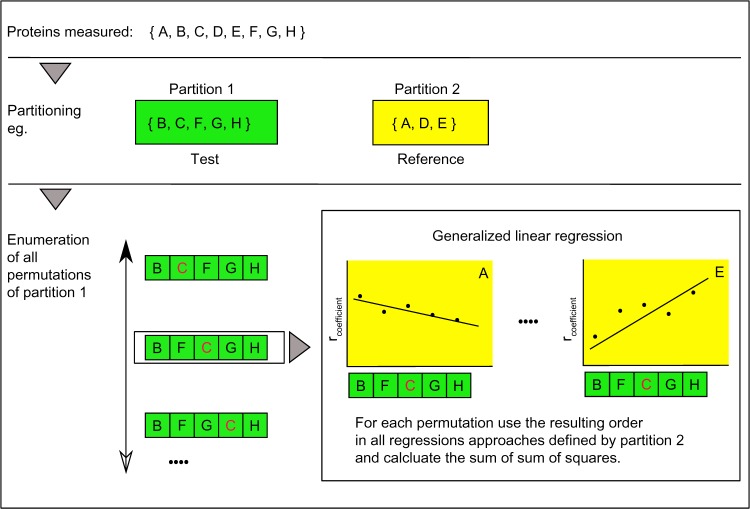
The algorithm utilizes the Pearson correlation as a proximity measure; therefore, a normalization in-between the protein score vectors is not necessary. The group of proteins is divided into two partitions called reference and test partition. Therefore, at least five protein measurements are required (2:3), but optimal is 12–16. The test group contains proteins that are finally ranked toward their interdependency with each reference group member. The proximity values between the two groups are calculated. Now for every member of the reference partition, all tests to reference correlation coefficients will be calculated. With these correlation coefficients, the respective number of regression approaches is performed together for each order of the test partition. The order of the test configuration will be drawn from a complete enumeration of all possible and unique test group orders. The sum of squares will be summed up over all regressions per order. This will be done on all enumerated orders, and the minimum will be selected (Fig. 1).
Figure 1.
Algorithm – searching for the optimal order explaining best all connected reference situations. The graph describes the core functionality of the algorithm. Top panel: as an example, a set of eight proteins named A–H was measured. Middle panel: the set of proteins is partitioned in two sets also called test and reference. The two groups can be interchanged, but normally the test group will collect less well-characterized proteins, while the reference groups might comprise well-characterized proteins, marking different equilibrium states of a biological system, eg, contrasting differentiation end points, such as CK 5/6 and CK 8/18, in basal and luminal cells in the mammalian gland. Bottom panel: The space of a complete enumeration of all test string permutations of partition 1 is searched for a minimal sum of squares resulting from the generalized regression. The regression is based on the Pearson correlation coefficients of, eg, A–B to A–H.
Note: The red character C should be a visual marker to recognize different orders in the string.
So, the process exhaustively analyzes systematically all possible permutations of the test partition concerning the optimization measure (sum of sum of squares). This measure does mark an optimal ranking of the strength of the dependencies of all proteins. Additionally, the measure controls (a) the errors resulting from imprecise measurements and even more importantly improves (b) the accuracy by comparing different situations of dependencies (for each reference member).
The result can be visualized in a panel of connected regression plots and will show an optimal rank order of dependencies of one partition of proteins against a reference partition. One feature of this rank order is that some few proteins added to the ranking partition do not destroy the overall ranking structure instead insert in the ranking due to their interdependency strength.
The algorithm is not limited to TMA data, but application to other types of expression data or even more generalized to any data describing systemic changes has to be carefully examined.
Implementation of the Algorithm
The software is available for download in an OpenMP variant and a MPI variant, therefore nicely scaling by CPU core and computer number. Both program types are also functional on single core machines.
The command line binaries are compiled for Linux. Additionally, the Fortran sources are available and can be compiled by either the GNU compiler collection (4.6.3) or the Intel Fortan compiler (Intel parallel studio XE 2013 update 1) for Linux and newer versions thereof. The code does not include any specific dependencies except that for the MPI packages. The MPI versions for 2 and more cores are therefore dependent on the MPI framework (MPICH 3.0.2–3.1.4 are tested). For the binaries, we utilized the compiler option -static to pack all the essential libraries into the executables to make them largely independent.
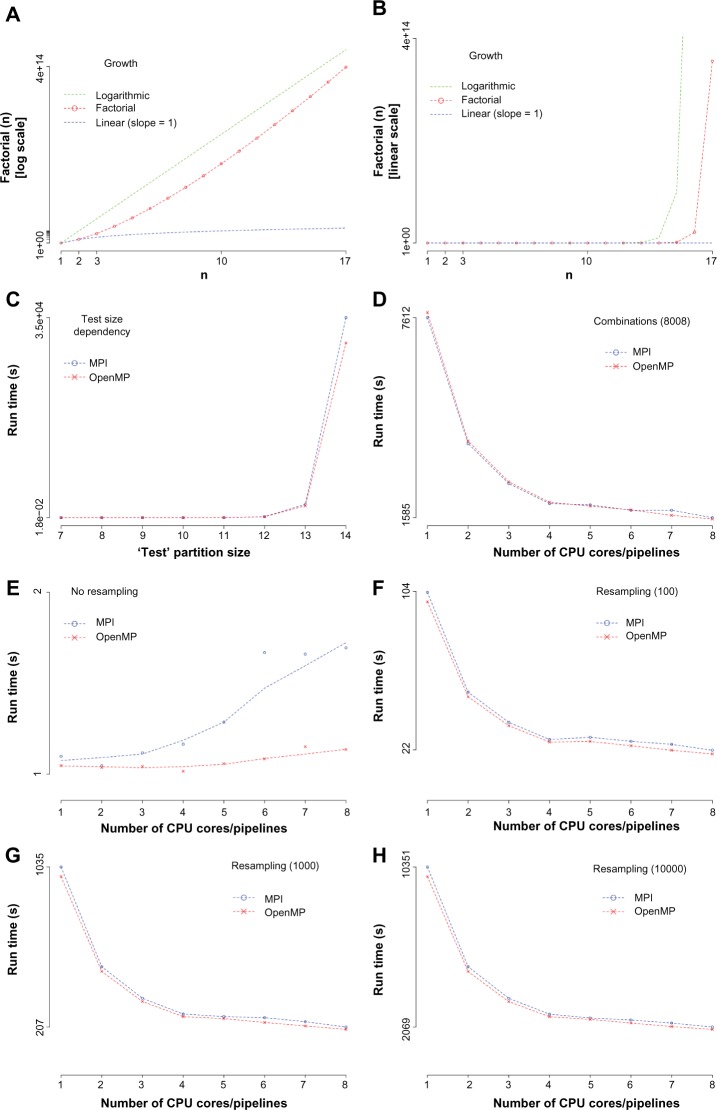
The procedure takes relative score values of proteins immunohistologically measured on a TMA generated according to established scoring schemes. These score values should be positive or scaled to be positive due to the used proximity measure (Pearson correlation). In the rare cases where the return values of the correlation measure are indetermined, the smallest nonzero values will be taken. Normally, these cases are rare and might only happen if constant integer vectors are used or if the numerical limits of the program are touched (4 byte; decimal fraction of 10 digits). Nevertheless, these cases are reported in the report file (.log) to raise attention. Overall, the impact of this issue on the results is low, until the variance in all of the data is as low. So the preanalytical procedures should include some testing of the (statistical) data properties to exclude such situations. After the run, the log file will contain all run-specific details and the used amount of time. The result file will host the minimum sum of squares (ssqg) value and the corresponding ranking (a vector representing the new order of the test proteins). If the number of protein measurements in the test partition exceeds 14, the computational time to calculate all permutations explodes (Fig. 2A and B). At the moment, the workaround to deal with such a situation is to divide the analysis into multiple approaches. This can be realized by analyzing overlapping chunks of the test partition versus a constant reference partition.
Figure 2.
Software performance. (A–C) The run time determining step for larger calculations, the computation of the permutations of the test partition is illustrated. The results of the factorial function used to calculate the number of permutations are given for the test partition size from 1 to 17. (A and B) It can be clearly seen that for larger partition sizes, the combinatorial space grows dramatically. (A) A logarithmic scale while (B) shows the linear situation. For the purposes of comparison, a logarithmic growth (green) and a linear growth (blue) are also given. (C) The computational run time as a consequence thereof for the parallelization technology MPI and OpenMP. (D) The computational cost for the tool tins_mpi/omp (all combinations) in dependency from CPU core or pipeline number and parallelization technology. (E–H) The performance values of the tool tins_s_mpi/omp (best order) are presented in dependency from CPU core or pipeline number, resampling number and parallelization technology.
A detailed description on input and output data formats and further information is given in a tutorial file at the download location. Additionally, some R scripts are provided to import this data format into the R platform for statistical computing (https://www.r-project.org/) for further analysis and visualization.
Performance Aspects of the Software
The most time consuming step of the algorithm is the analysis of all permutations of the test partition. To get some insight into the behavior and time dependency of the tools under certain load conditions, we run several performance checks. The test computer was a typical workstation with a 4 core CPU (Intel Xeon E3–1200 “Ivy-Bridge” CPU up to 3.6 GHz), each owning two pipelines (eight CPU threads in total) and 32 GB ECC-RAM. The main memory was no limiting factor. The used random data set was based on 20 proteins with each having 600 observations.
Figure 2A and B illustrates how fast the number of computations is growing when the test partition size increases. The computational time for this process is shown in Figure 2C. It can be easily seen that PCs and workstations are limited to a test partition size of 15, while super computers might go until a size of 19. Therefore, this direct approach is limited to a small size of the test partition and different approaches or approximate solutions needed to be established to reach bigger sizes. Nevertheless, many interesting experimental situations can be perfectly addressed.
In Figure 2D, the performance behavior of the software tool calculating all combinations is given (the reference partition size of 6 and the test partition size of 10). Only a very weak dependency from the parallelization technology can be seen, and the software is scaling well across the cores. Additionally, it can be noted that using the second CPU core thread does not really improve the overall performance. This result might be compared with Supplementary Figure 3 in the study by Buerger et al.16
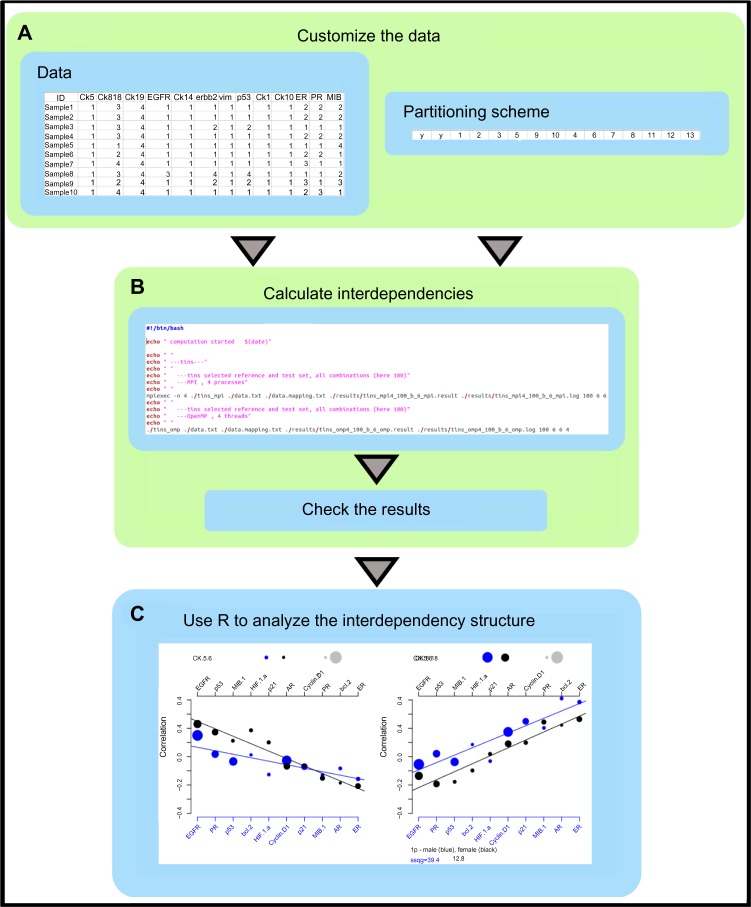
Figure 3.
Software workflow. The workflow highlights the major process steps. (A) Generating or adopting a multivariate data set, which is based on one and the same TMA block (series), and being discrete or continuous measurements. Selecting the data partitions. (B) Performing the calculations and verifying that the results are reliable, and no warnings were reported in the output files. (C) Importing the results via the provided scripts into the mathematical platform R and analyzing or visualizing the results. A complete test environment for this workflow is provided via the software link.
Figure 2E–H presents results of the main software tool calculating the best dependency order of a selected pair of partitions while also be able to estimate the stability of the result by a resampling approach. We see that without any resampling, the use of multiple cores is counterproductive (Fig. 2E, using again a partition size of 6 and 10, respectively). In the resampling situation (Fig. 2F–H), we see the same savings of computing time as in Figure 2D.
The parallelization technology does not differ much on one workstation but indeed this will change on a computing cluster.
Example of Use
The core elements of the workflow are illustrated in Figure 3. The algorithm was already applied on several different cancer TMAs with a varying number of samples. Several examples of use are already published.16–19
A step-by-step tutorial including a fully functional test example is available in the download section. Some important aspects are also exemplified in the following paragraphs.
If the number of samples is low or only molecules with the same regulatory behavior will be analyzed, the algorithm might not show remarkable results. The latter one is a constitutive problem and can only be solved by introducing antagonistic molecular player in the reference partition. In a noisy environment, it might be helpful to increase the number of samples beyond the guiding value of approximately 150–200 samples. The appropriate values should be estimated according to the quality plots given in the study by Buerger et al.16 (cf., Fig. 6 and Supplementary Fig. 2 in that publication). The impact of these limits has to be evaluated for each specific situation.
According to Figure 3, the data have to be a tab separated text format (end of line marker: Linux style). The data are organized in columns per protein measurement. The rows depict samples. A header and sample identifier column is advised. Names should be simple and without blanks. The partitioning scheme is a single line with tab-separated entries. The order and length count. The first block consists of two characters, followed by a reference block and a test block. Every number in the second and third blocks is a pointer to the column position in the data matrix. The length of the reference block is defined by a command line parameter.
There are two different command line tools. The primary one tins_s_mpi/omp is searching for an optimal interdependency solution for the selected partitions. This tool is also able to test in the same run the quality of the solution by creating shuffling or bootstrap controls. In our context, shuffling means that the whole order of the raw data matrix is randomized, while bootstrap refers to the bootstrap algorithm,20 and samples will be drawn with replacement on each raw protein measurement vector separately. So, both resampling approaches address different levels of randomization.
The second tool tins_mpi/omp explores all partitions of a certain size. At this point, we get insight in the distribution of minimal sum of squares values. This tool is of interest if properties of the combinatorial space should be analyzed. Both tools are available in the MPI (mpi) and OpenMP (omp) technology.
Conclusion
The established procedure analyzes protein dependencies in TMA data and fills a gap in this field. Beyond that, it is a combinatorial procedure that tries to decipher system states in a noisy environment. The already published results document the gain for the TMA-based research in pathology and molecular pathology. The now published tool allows a broader scientific audience to utilize this approach autonomously for their own research.
Availability and Requirements
Project name: TMAinspiration
Project home page: http://complex-systems.uni-muenster.de/tma_inspiration.html
Operating system(s): Binaries: Linux, source code: any Programming language: Fortran 95 (and up), R scripts Other requirements: none
License: GNU GPL
Acknowledgments
The authors thank John Burkardt from the Department of Scientific Computing at Florida State University for ingenious code elements.
Footnotes
ACADEMIC EDITOR: J. T. Efird, Editor in Chief
PEER REVIEW: Four peer reviewers contributed to the peer review report. Reviewers’ reports totaled 520 words, excluding any confidential comments to the academic editor.
FUNDING: This study has been supported in part by the Federal Ministry of Education and Research BMBF grant 01GM0869 TranSaRNet and in part by grant 01KT1310 European Transcan I – Prospective Validation of Biomarkers in Ewing Sarcoma (PROVABES). Support was also received from the Open Access Publication Fund of the University of Münster. The authors confirm that the funder had no influence over the study design, content of the article, or selection of this journal.
COMPETING INTERESTS: Authors disclose no potential conflicts of interest.
Paper subject to independent expert blind peer review. All editorial decisions made by independent academic editor. Upon submission manuscript was subject to anti-plagiarism scanning. Prior to publication all authors have given signed confirmation of agreement to article publication and compliance with all applicable ethical and legal requirements, including the accuracy of author and contributor information, disclosure of competing interests and funding sources, compliance with ethical requirements relating to human and animal study participants, and compliance with any copyright requirements of third parties. This journal is a member of the Committee on Publication Ethics (COPE).
Author Contributions
Implemented the parallel versions of the algorithm: FB. Performed the tests and experiments: FB, HB, NVM, EK. Verified the results of the algorithm: FB, EK. All the authors wrote and approved the article.
REFERENCES
- 1.Kononen J, Bubendorf L, Kallioniemi A, et al. Tissue microarrays for high-throughput molecular profiling of tumor specimens. Nat Med. 1998;4(7):844–7. doi: 10.1038/nm0798-844. [DOI] [PubMed] [Google Scholar]
- 2.Bubendorf L, Nocito A, Moch H, Sauter G. Tissue microarray (TMA) technology: miniaturized pathology archives for high-throughput in situ studies. J Pathol. 2001;195(1):72–9. doi: 10.1002/path.893. [DOI] [PubMed] [Google Scholar]
- 3.Kallioniemi OP, Wagner U, Kononen J, Sauter G. Tissue microarray technology for high-throughput molecular profiling of cancer. Hum Mol Genet. 2001;10(7):657–62. doi: 10.1093/hmg/10.7.657. [DOI] [PubMed] [Google Scholar]
- 4.Camp R, Neumeister V, Rimm D. A decade of tissue microarrays: progress in the discovery and validation of cancer biomarkers. J Clin Oncol. 2008;26(34):5630–7. doi: 10.1200/JCO.2008.17.3567. [DOI] [PubMed] [Google Scholar]
- 5.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. New York: Garland Science; 2014. [Google Scholar]
- 6.Alm E, Arkin A. Biological networks. Curr Opin Struct Biol. 2003;13(2):193–202. doi: 10.1016/s0959-440x(03)00031-9. [DOI] [PubMed] [Google Scholar]
- 7.Zhu X, Gerstein M, Snyder M. Getting connected: analysis and principles of biological networks. Genes Dev. 2007;21(9):1010–24. doi: 10.1101/gad.1528707. [DOI] [PubMed] [Google Scholar]
- 8.Friedman J, Alm E. Inferring correlation networks from genomic survey data. PLoS Comput Biol. 2012;8(9):e1002687. doi: 10.1371/journal.pcbi.1002687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dzeroski S, Todorovski L. Equation discovery for systems biology: finding the structure and dynamics of biological networks from time course data. Curr Opin Biotechnol. 2008;19(4):360–8. doi: 10.1016/j.copbio.2008.07.002. [DOI] [PubMed] [Google Scholar]
- 10.Idikio H. Quantitative analysis of p53 expression in human normal and cancer tissue microarray with global normalization method. Int J Clin Exp Pathol. 2011;4(5):505–12. [PMC free article] [PubMed] [Google Scholar]
- 11.Meyer S, Fuchs T, Bosserhoff A, et al. A seven-marker signature and clinical outcome in malignant melanoma: a large-scale tissue-microarray study with two independent patient cohorts. PLoS One. 2012;7(6):e38222. doi: 10.1371/journal.pone.0038222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu X, Minin V, Huang Y, Seligson DB, Horvath S. Statistical methods for analyzing tissue microarray data. J Biopharm Stat. 2004;14(3):671–85. doi: 10.1081/BIP-200025657. [DOI] [PubMed] [Google Scholar]
- 13.Shen R, Taylor J, Ghosh D. Reconstructing tumor-wise protein expression in tissue microarray studies using a Bayesian cell mixture model. Bioinformatics. 2008;24(24):2880–6. doi: 10.1093/bioinformatics/btn536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gould Rothberg B, Berger A, Molinaro A, et al. Melanoma prognostic model using tissue microarrays and genetic algorithms. J Clin Oncol. 2009;27(34):5772–80. doi: 10.1200/JCO.2009.22.8239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Song YS, Park CH, Chung HJ, Shin H, Kim J, Kim JH. Semantically enabled and statistically supported biological hypothesis testing with tissue microarray databases. BMC Bioinformatics. 2011;12(suppl 1):S51. doi: 10.1186/1471-2105-12-S1-S51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Buerger H, Boecker F, Packeisen J, et al. Analyzing the basic principles of tissue microarray data measuring the cooperative phenomena of marker proteins in invasive breast cancer. Open Access Bioinform. 2013;5(1):1–21. [Google Scholar]
- 17.Schymik B, Buerger H, Krämer A, et al. Is there ‘progression through grade’ in ductal invasive breast cancer? Breast Cancer Res Treat. 2012;135(3):693–703. doi: 10.1007/s10549-012-2195-1. [DOI] [PubMed] [Google Scholar]
- 18.Kornegoor R, van Diest PJ, Buerger H, Korsching E. Tracing differences between male and female breast cancer: both diseases own a different biology. Histopathology. 2015;67(6):888–97. doi: 10.1111/his.12727. [DOI] [PubMed] [Google Scholar]
- 19.Frohwitter G, Buerger H, van Diest PJ, Korsching E, Kleinheinz J, Fillies T. Cytokeratin and protein expression patterns in squamous cell carcinoma of the oral cavity provide evidence for two distinct pathogenetic pathways. Oncol Lett. 2016 doi: 10.3892/ol.2016.4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Efron B, Tibshirani R. An Introduction to the Bootstrap. 1st ed. London, New York: Chapman & Hall/CRC; 1993. [Google Scholar]