Simulations on the Influence of Myelin Water in Diffusion-Weighted Imaging

Abstract

While myelinated axons present an important barrier to water diffusion, many models used to interpret DWI signal neglect other potential influences of myelin. In this work, Monte Carlo simulations were used to test the sensitivity of DWI results to the diffusive properties of water within myelin. Within these simulations, the apparent diffusion coefficient (D_app) varied slowly over several orders of magnitude of the coefficient of myelin water diffusion (D_m), but exhibited important differences compared to D_app values simulated that neglect D_m (=0). Compared to D_app, the apparent diffusion kurtosis (K_app) was generally more sensitive to D_m. Simulations also tested the sensitivity of D_app and K_app to the amount of myelin present. Unique variations in D_app and K_app caused by differences in the myelin volume fraction were diminished when myelin water diffusion was included. Also, expected trends in D_app and K_app with experimental echo time were reduced or inverted when accounting for myelin water diffusion, and these reduced/inverted trends were seen experimentally in ex vivo rat brain DWI experiments. In general, myelin water has the potential to subtly influence DWI results and bias models of DWI that neglect these components of white matter.

INTRODUCTION

Axons, and especially the myelin sheaths that surround them, present an significant barrier to water diffusion in white matter—a phenomena that has been measured with diffusion-weighted magnetic resonance imaging (DWI) to identify the structure of white matter (Basser et al 1994, Basser and Jones 2002) and identify white matter pathologies (Rose et al 2000, Horsfield et al 1996, Horsfield and Jones 2002). Because water density in myelin is low (Knaap and Valk 2005) and myelin water exhibits a short transverse relaxation (T₂) time-constant (MacKay et al 1994, Menon et al 1992, Vasilescu et al 1978), it is often assumed that myelin has no direct signal contribution to DWI signal. Still, it is unclear if DWI is sensitive to the amount of myelin present within white matter or to the movement of water between myelin and surrounding tissues—water in myelin may be mixing with surrounding water compartments on a time scale relevant for DWI, allowing it to contribute to the measured signal.

Analytic and computational models of DWI signal used to quantitatively assess white matter generally use one of three approximations related to myelin. First, many models considered myelin to be an impermeable boundary, restricting the extent that water can diffuse. This approximation is inherent in ActiveAx (Alexander et al 2010, Alexander 2008), AxCaliber (Assaf et al 2008), NODDI (Zhang et al 2012), DBSI (Wang et al 2011), and the WMTI model (Fieremans et al 2011), all of which treated the white matter DWI signal as the sum of signals from a number of non-exchanging tissue compartments—primarily intra- and extra-axonal spaces.

Second, some models include water exchange directly between intra- and extra-axonal spaces. This approach has been used both in Monte Carlo models (Ford et al 1998, Fieremans et al 2010, Nilsson et al 2010a), and models of coupled differential equations (Stanisz et al 1997, Vestergaard-Poulsen et al 2007). Although some work has suggested that the nodes of Ranvier provide a source of exchange (Nilsson et al 2010b), these approaches still neglect the potential impact of myelin as well as the potential for myelin as an intermediate region regulating water exchange between intra- and extra-axonal spaces.

Finally, a few models incorporate both the presence of myelin and water diffusion through myelin (Baxter and Frank 2013, Chin et al 2004, Sen and Basser 2005, Peled 2007). Within these studies, there is some debate on the coefficient of water diffusion within myelin (Sen and Basser 2005, Baxter and Frank 2013, Harkins et al 2012), and only one of these models consider T₂ differences between water compartments (Peled 2007). Further, myelin is a radially anisotropic structure, consisting of successive wrappings of lipid membrane. No model has tested the sensitivity of DWI to myelin as a radially anisotropic structure, with water able to diffuse more freely in the circumferential path (between individual lipid bilayers) and less freely in the radial direction (across lipid bilayers).

In this study, we report a series of simulations used to assess the role of myelin content and myelin water diffusion on clinical DWI. We present a new Monte Carlo model of DWI signal within myelinated axons that includes myelin sheaths as well as water diffusion within the anisotropic structure of myelin. This model is used to test the influence of these properties on the apparent diffusion coefficient (D_app) and kurtosis (K_app) measured transverse to the white matter tract orientation. These theoretical findings were then tested with a follow up DWI study in ex vivo rat brain.

METHODS

DWI Simulations in White Matter

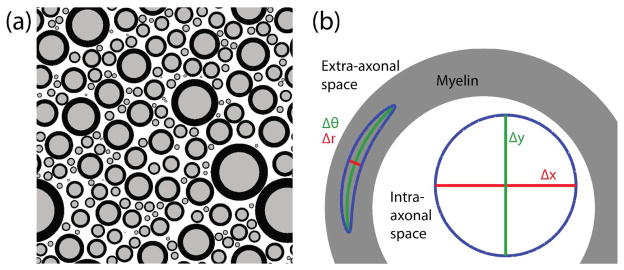
Pulsed gradient spin echo (PGSE) experiments (Stejskal and Tanner 1965) were simulated using the Monte Carlo method. For each simulated experiment, individual sources of MR signal (i.e. “water molecules”) were tracked through an arrangement of 200 myelinated axons, represented by two concentric circles. Geometries were generated as previously outlined (Hall and Alexander 2009) based upon specified values for the mean inner axon radius (R̄), g-ratio (g, defined as the inner axon radius divided by outer axon radius), and intra-axonal volume fraction (v_i). Axon sizes were drawn from a gamma distribution (k=2.331, θ= R̄/k) (Panagiotaki et al 2012). An example geometry is shown in Fig 1a for v_i = 0.35 and g = 0.70.

Fig 1.

(a) An example geometry showing a distribution of axon sizes with R̄ = 1 μm, v_e = 0.35, and g = 0.7. (b) Zoom in view of a myelinated axon, showing isotropic diffusion in intra- and extra-axonal space, as well as diffusion that is radially anisotropic within myelin.

Dynamics of Water Diffusion

The biophysical properties of water in white matter were characterized by 6 parameters—the unhindered diffusion coefficient of water in intra- and extra-axonal spaces (D₀), the apparent diffusion coefficient of myelin water across lipid bilayers (i.e. through myelin in the radial direction, D_mr), the apparent diffusion coefficient of myelin water circumferential to the lipid bilayer surface (i.e. staying between lipid bilayers, D_mc), the transverse time-constants of water in the intra- and extra-axonal spaces (T_2ie) and in myelin (T_2m), and the relative density of water in myelin compared to the intra- and extra-axonal spaces (p_m).

Water molecules were individually seeded through an iterative procedure to account for the difference in water density between myelin and non-myelin tissue compartments—if a potential seed was located within myelin, the location was rejected with probability 1-p_m and iteratively re-seeded.

Prior to each time-step, using a combined multiple recursive algorithm (available in MATLAB as the default random number generator), two random numbers were generated for each water molecule corresponding to the random jump angle (given below as φ) and the random number used to evaluate elastic reflections (given below as P). Within each time-step, a new random number was generated for any subsequent reflections using a linear congruential algorithm.

Within intra- and extra-axonal spaces, individual molecules jumped a fixed distance at a random angle, given by

$$\begin{array}{l}\mathrm{\Delta }x=\sqrt{4·D_0·\mathrm{\Delta }t}·cos(\phi )\hfill \\ \mathrm{\Delta }y=\sqrt{4·D_0·\mathrm{\Delta }t}·sin(\phi )\hfill \end{array},$$ [1]

where Δx, Δy is the change in location of the molecule at each time-step, Δt is the time-step, and φ is angular direction of the step, randomly chosen with uniform likelihood between 0 to 2π. A blue circle shown in Fig 1b depicts the potential set of jumps in Δx and Δy.

Within myelin, diffusion was considered to be radially anisotropic by breaking diffusion into circumferential and radial components

$$\begin{array}{l}\mathrm{\Delta }\theta =\sqrt{4·D_{mc}·\mathrm{\Delta }t}·cos(\phi )/r\hfill \\ \mathrm{\Delta }r=\sqrt{4·D_{mr}·\mathrm{\Delta }t}·sin(\phi )\hfill \end{array},$$ [2]

where Δθ and Δr represent the change in angle and radius relative to the center of the axon, while r is the current distance from the center of the axon. In this case, φ was drawn from a non-uniform distribution

$$p(\phi )=\frac{r-\sqrt{4·D_{mr}·\mathrm{\Delta }t}sin(\phi )/2}{2\pi r},$$ [3]

where φ = π/2 points away from center of the axon. This distribution is necessary to prevent a net flux of molecules towards the center of the axon caused by breaking diffusion into circumferential and radial directions. Practically, this was implemented by taking a uniform distribution of φ, then adding π to φ with probability P = 1 − 2·π· p(φ) (or 0 when P is negative). An illustration of radially anisotropic diffusion is shown as a bent ellipse-like shape in the myelin region of Fig 1b.

For each molecule, a change in the signal phase was proportional to the applied diffusion gradient strength at each time-step

$$\mathrm{\Delta }\varphi =x_i·\gamma ·G_{\mathit{diff}}·\mathrm{\Delta }t,$$ [4]

where x_i is the location of the i-th molecule at the end of the present time-step, G_diff is the applied diffusion gradient, and γ is the gyromagnetic ratio. To incorporate T₂ relaxation, the signal amplitude of each water molecule (s_n) decayed at each time-step as exp[−Δt/T₂], where T₂ is T_2ie or T_2m corresponding to the location of the molecule.

In intra- or extra-axonal spaces, a molecule interacting with a myelin boundary crossed into myelin with a probability

$$P=\sqrt{\frac{D_{mr}}{D_0}}·p_m,$$ [5]

and otherwise was elastically reflected. A molecule leaving myelin experienced no boundary. Because of the change in diffusion coefficient and density of water between these compartments, this asymmetric boundary condition was required to maintain equilibrium concentrations of water molecules in each compartment (Baxter and Frank 2013).

At the experimental echo time (TE), signal was summed from the total number (N) of simulated water molecules

$$S=\frac{1}{N}\left(\sum _{n=1}^N{s}_n·cos\left({\varphi }_n\right)\right)/\sum _{n=1}^N{s}_n.$$ [6]

Simulations were implemented in CUDA, wrapped into MATLAB with the Parallel Computing Toolbox, and run on a Linux computer with a GeForce GTX TITAN GPU. For each simulated experiment, D_app and K_app were estimated from DWI signal using the equation (Jensen et al 2005)

$$\frac{S(b)}{S_0}=exp\left[-b·D_{\mathit{app}}+{\left(b·D_{\mathit{app}}\right)}^2·K_{\mathit{app}}/6\right].$$ [7]

The following parameters were held constant for all simulations: N=200,000, Δt=0.02 ms, D₀ = 3.0 μm²/ms, T_2ie = 80 ms, T_2m = 15 ms (MacKay et al 1994, Stewart et al 1993, Vavasour et al 1998), p_m = 0.5 (Knaap and Valk 2005). With these parameters, an example simulation with 200 axons, R̄ =1 μm and TE = 100 ms completes in about 100 s.

Validation

The specific implementation of the simulation was validated to ensure that boundary conditions were being properly enforced, and that simulated signal agreed in conditions with known analytic solutions:

• Validation #1: In the case of free diffusion (i.e. no axons), diffusion-weighted raw signals were unbiased compared to the analytic solution (i.e. S₀•exp[−bD₀]), and signal errors had an upper bound of $S_0/\sqrt{N}$.

• Validation #2: In geometries with impermeable boundaries, molecules were not able to pass between compartments.

• Validation #3: In geometries with impermeable boundaries, intra-axonal signal decay was in good agreement with low b-value approximated analytic solutions to diffusion within cylinders (Callaghan 1995).

• Validation #4: In geometries with completely permeable boundaries (p_m = 1, D₀ = D_mc = D_mr), diffusion-weighted signal decayed with the analytic solution (S₀•exp[−bD₀]).

• Validation #5: In geometries that included water exchange between compartments (p_m = 0.5, D₀ = 3.0 μm²/ms, D_mc = D_mr = 10⁻³ μm²/ms), equilibrium concentrations of water within each compartment were stable throughout the simulation.

Simulation Set #1: Myelin water diffusion

Simulations were performed to test the sensitivity of DWI to myelin water diffusion. A PGSE experiment was simulated (Δ = 40 ms, δ = 20 ms, and TE = 100 ms, G_max = 0–60 mT/m in steps of 5 mT/m) in a white matter geometry with g = 0.7, v_i = 0.35 and R̄ = 0.25, 1, and 4 μm. This set of parameters was selected as an example of physiologically relevant tissue. Myelin water diffusion was varied in the radial direction, D_mr = 0, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹ μm²/ms, while the myelin water diffusion coefficient in the circumferential direction was tested in the cases of isotropic (D_mc = D_mr) and anisotropic myelin water diffusion (D_mc = D₀). For each combination of tissue geometry, D_mc and D_mr, the simulated signal decay at G_max values 0, 30, and 45 mT/m (corresponding to b-values of 0, 0.85 and 1.93 ms/μm²) was used to calculate D_app and K_app. These b-values are lower than typically used for DKI (Jensen and Helpern 2010), but are suitable for simulated data without added noise.

Simulation Set #2: Myelin content

Using the same PGSE experiment in Set #1, simulations were also performed to test if v_m uniquely impacts the set of D_app and K_app values, or if geometries with different v_m could be generated that have the same values for both D_app and K_app. To test this hypothesis, geometries were created at two different values of v_m. A single geometry was generated with v_m = 0.36: v_i = 0.35, g = 0.7, R̄ =1 μm, and this geometry was used to compare values of D_app and K_app simulated with several geometries generated with v_m = 0.10. Since a change in v_m requires a corresponding change in the set of v_i and v_e, geometries were generated with 6 different values in the relevant range of v_i between 0.50 and 0.60. To keep v_m constant, g was calculated with g = (1/(v_m/v_i+1))^1/2 for each geometry. Simulations were performed with four instances of myelin water diffusion: no myelin water (p_m=0), water present in myelin with no myelin water diffusion (p_m=0.5, D_mr=D_mc=0 μm²/ms), isotropic myelin water diffusion (p_m=0.5, D_mr=D_mc=10⁻³ μm²/ms), and anisotropic myelin water diffusion (p_m=0.5, D_mr=10⁻³ μm²/ms, D_mc=3.0 μm²/ms).

Simulation Set #3: Myelin Water Weighting with Short Echo times

Simulations were also used to test how D_app and K_app were affected by TE-dependent contributions of myelin water signal—at low values of TE, reduced decay of myelin water will increase its contribution to the measured signal. Stimulated echo diffusion experiments (Tanner 1970) (δ = 5 ms, Δ = 60 ms, mixing time = 50 ms) were used to permit TE < Δ and were run with TE = 25, 50, 75 and 100 ms. The T₁ relaxation time-constants of myelin and intra-/extra-axonal water were defined at 350 ms and 850 ms, respectively (Lancaster et al 2003). Simulations were performed in a white matter geometry with R̄ = 1 μm, g = 0.7, and v_i = 0.35. Simulations were performed on same four sets of myelin water diffusion characteristics used in Simulation Set #2.

DWI in Ex Vivo Rat Brain

This set of simulations was followed by an experimental imaging study to test the dependence of D_app and K_app on TE. With approval by Vanderbilt University Institutional Animal Care and Use Committee, two female Sprague Dawley rats were anesthetized with isoflurane, perfusion fixed with 4% paraformaldehyde, and brains were dissected for ex vivo evaluation by MRI. Brains were imaged at bore temperature using a 15.2 T Bruker Biospec scanner (Bruker Biospin, Billerica, MA, USA). Within a 1 mm slice thickness, a field of view of 25.6 mm × 12.8 mm was encoded with 0.2 mm × 0.2 mm in-plane resolution. Stimulated echo PGSE experiments were carried out (δ = 5 ms, Δ = 60 ms, and b = 0, 4, 8, 12 & 16 μm²/ms) at TE = 23, 35, 45 and 55 ms. The receiver bandwidth was set at 20 kHz, and TR was 2 s. For this data set, a single diffusion direction was collected perpendicular to the orientation of axons through the corpus callosum. Regions of interest were drawn in the cerebral cortex and the corpus callosum, and the raw signal vs b-value was fit to Eqn 7 to estimate D_app and K_app.

RESULTS

Simulation Set #1

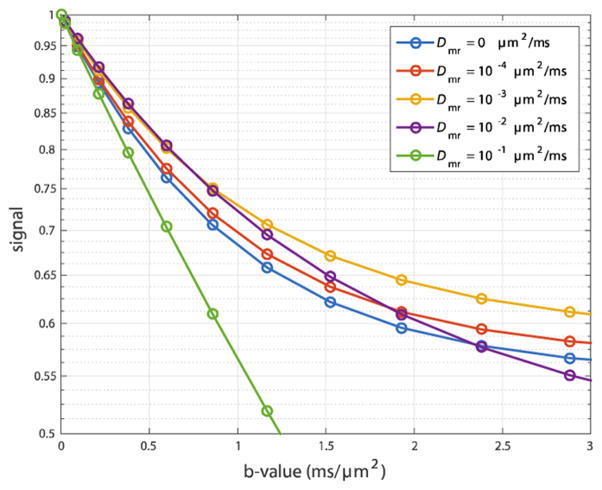
Simulations were first used to test the sensitivity of DWI to myelin water diffusion. Signal vs. b-value is shown in Fig 2 at R̄ = 1 μm and D_mr, D_mc = 0, 10⁻⁴, 10⁻³, 10⁻², and 10⁻¹ μm²/ms. As D_mr increases from 0 to 10⁻³ μm²/ms the overall rate of signal decay with b-value decreases. This is due an increased amount of signal from water that has resided in the slowly diffusing myelin water compartment at some point during the diffusion weighting, reflecting that while water is still greatly restricted, it has become sufficiently mobile that it can enter and leave myelin before its signal is lost by transverse relaxation. As D_mr increases further, the effect on signal decay reverses, meaning that myelin has become less restrictive to water diffusion. In the case of D_mr = 10⁻¹ μm²/ms, myelin provide little barrier to diffusion resulting in a near mono-exponential signal decay with b-value.

Fig 2.

The diffusion-weighted signal (log scale) vs b-value for a five values of the myelin water diffusion coefficient. The simulations used a geometry with R̄ = 1 μm, v_i = 0.35, and g = 0.7.

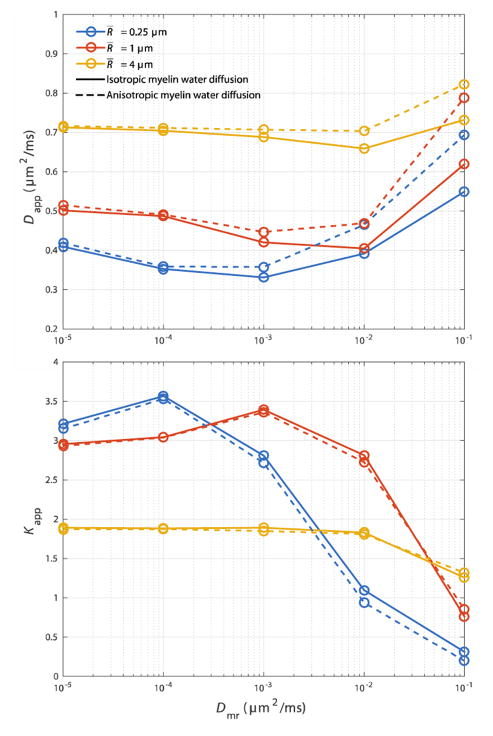
D_app and K_app from this set of simulations are given in Fig 3. In general, an increase in R̄ causes an increase in D_app, and a decrease in K_app. D_app varies slowly over several orders of magnitude in D_mr. However as D_mr increases from 0, there is an initial slight decrease in D_app present in most curves, followed by an increase. In cases of anisotropic myelin water diffusion (dashed lines), D_app deviates from its isotropic values (solid lines) primarily where D_mr ≥ 10⁻³ μm²/ms.

Fig 3.

The influence of the myelin water diffusion coefficient (D_mr) on D_app and K_app at R̄ = 0.25, 1 & 4 μm, g = 0.7 and v_i = 0.35. Solid lines show values where myelin water diffusion is isotropic (D_mc = D_mr), while dashed lines show values where myelin water diffusion is anisotropic (D_mc = D₀).

Overall, K_app is more sensitive to myelin water diffusion. K_app is decreased in regions where water can easily diffuse through myelin. Plots show an intermediate increase in K_app with an increase in D_mr, caused by an increase in the apparent contribution of water from the slow-diffusing myelin compartment. Throughout this range in D_mr, K_app within tissues with anisotropic myelin water diffusion did not greatly differ from the values simulation within geometries with isotropic myelin water diffusion.

Simulation Set #2

A second set of simulations were performed to test if myelin content can uniquely inform basic DWI measurements. To illustrate the effect of myelin content, relative differences in D_app and K_app calculated as

$$\mathrm{\Delta }{D}_{\mathit{app}}=\frac{D_{\mathit{app}}\left(v_m=0.1\right)-D_{\mathit{app}}\left(v_m=0.36,v_i=0.35\right)}{D_{\mathit{app}}\left(v_m=0.36,v_i=0.35\right)}·100\%$$ [8]

$$\mathrm{\Delta }{K}_{\mathit{app}}=\frac{K_{\mathit{app}}\left(v_m=0.1\right)-K_{\mathit{app}}\left(v_m=0.36,v_i=0.35\right)}{K_{\mathit{app}}\left(v_m=0.36,v_i=0.35\right)}·100\%$$ [9]

are plotted in Fig 4. Since this change in v_m also requires a change in v_i and/or v_e, ΔD_app and ΔK_app are plotted vs. v_i, representing the range in v_i (and v_e) that provide similar values for D_app and K_app. Solid lines connect ΔD_app (blue) and ΔK_app (red) in the case of no water diffusion, while dashed lines represent simulated values with isotropic myelin water diffusion. Values of ΔD_app and ΔK_app from simulations with no myelin water and anistropic myelin water diffusion are not shown, as those curves depict similar characteristics to those with no myelin water diffusion and isotropic myelin water diffusion, respectively. As predicted in other models, a simple increase in v_i caused a decrease in D_app and an increase in K_app due to an increase in the fraction of restricted intra-axonal water (Szafer et al 1995, Fieremans et al 2011).

Fig 4.

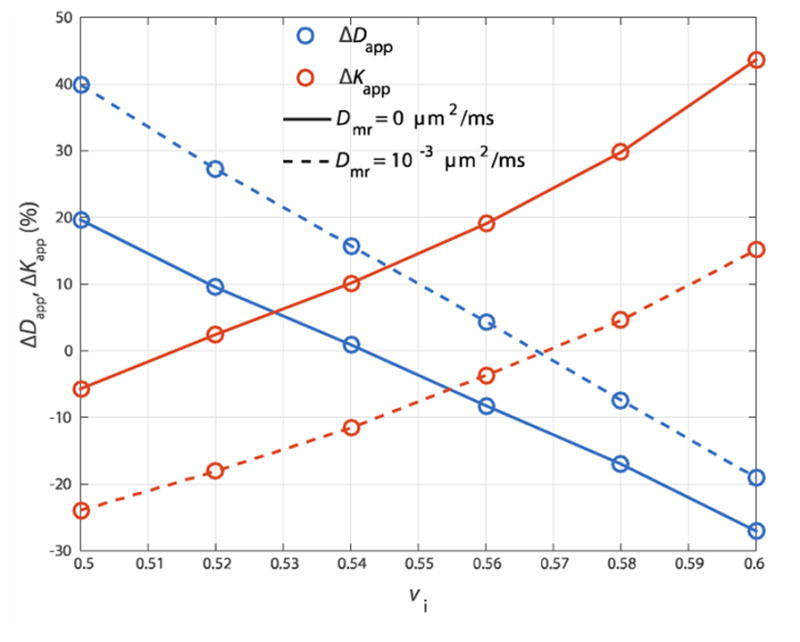
Change in D_app (blue) and K_app (red) caused by a decrease in v_m from 0.36 to 0.10, calculated over a range in relevant v_i in the absence (solid lines) or presence (dashed line) of myelin water diffusion.

When myelin water diffusion was neglected, these simulations indicate that a difference in v_m caused a change in the values of either D_app or K_app or changed both values depending on the selected value of v_i. It was impossible to generate a geometry with v_m = 0.1 where both D_app and K_app values were unchanged relative to a geometry with v_m = 0.36. For example, the relative value of K_app was unchanged at v_i ≈ 0.515m, but D_app was increased by ≈10–15%. While this seems to imply that a set of D_app and K_app values could be used determine myelin content, the introduction of myelin water diffusion reduced the differences in these values—when D_mr = 10⁻³ μm²/ms, ΔD_app and ΔK_app are unchanged (=0) at v_i ≈ 0.57.

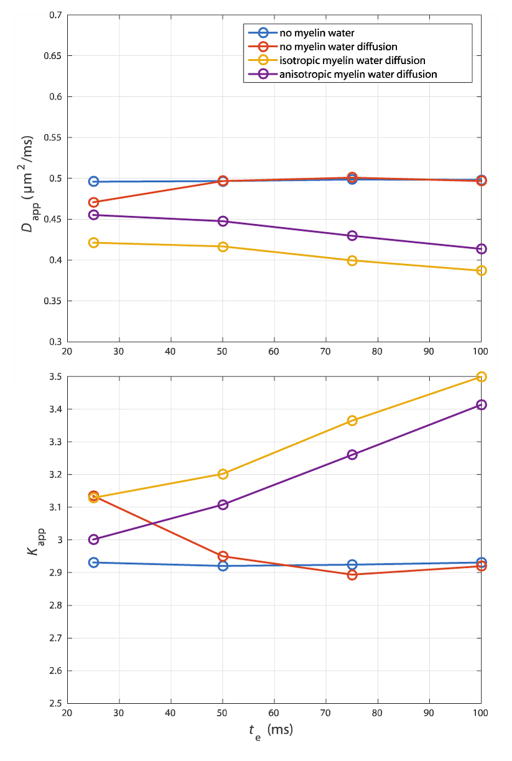
Simulation Set #3

A third set of simulations were performed to test how modeling of myelin water and myelin water diffusion affected the TE dependent nature of D_app and K_app, as shown in Fig 5. In theory, shorter echo times could be used to increase the contribution of the slowly diffusing myelin water to measured DWI signal. This was obviously not seen in the simulations that included no myelin water. D_app decreased and K_app increased at lower values of TE when myelin water was included, with D_mr = 0. However, when myelin water diffusion was included in the simulation, this trend was reversed.

Fig 5.

When myelin water diffusion is neglected, D_app decreases and K_app increases with an increase in myelin water weighting (i.e. a decrease in TE) shown at R̄ = 1 μm, v_i = 0.35. However, modeling of myelin water diffusion reverses trends in D_app and K_app with TE.

DWI in Ex Vivo Rat Brain

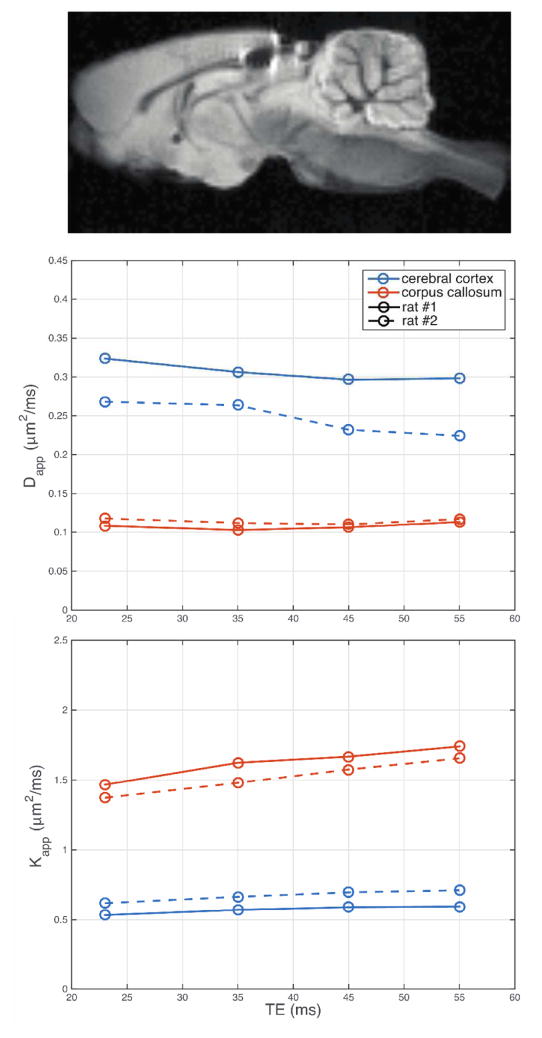
An example ex vivo rat brain image is given in Fig 6, along with corresponding plots showing the dependence of D_app and K_app on TE in two rat brains (represented as solid and dashed lines) within regions of interest in the cerebral cortex and corpus callosum. For both rats imaged, D_app in the corpus callosum was largely independent of TE, while K_app increased in the same range. In cerebral cortex, D_app decreased and K_app increased with TE.

Fig 6.

D_app and K_app measured in the cerebral cortex and corpus callosum from two ex vivo rat brains.

DISCUSSION

While myelin serves as an important source of restriction measured by DWI, this study indicates that myelin water diffusion has the potential to make subtle but important influences on DWI measurements.

Myelin Water Diffusion

Recent interest in the role of myelin water diffusion on DWI signal has been motivated in part by multi-component T₂ relaxation studies investigating signal from myelin water. While the myelin water fraction (f_my) has been used as an estimate of myelin content (MacKay et al 1994, Menon et al 1992, Vasilescu et al 1978, Laule et al 2002), recent studies have suggested that f_my underestimates myelin content in regions with thin myelin (Dula et al 2010). To explain the discrepancy between f_my and histologic myelin volume fraction, a computational model estimated a myelin water diffusion coefficient of D_mr ≈ 10⁻³ μm²/ms (Harkins et al 2012). While this value of D_mr generally agrees with measurements of water diffusion through synthetic myelin (Khakimova et al 2008), a couple studies have indirectly estimated that water exchange through myelin is much slower than this value would suggest (Laule et al 2004, Kalantari et al 2011). Within the context of these previous studies, the physiologic value of D_mr is estimated to be between 0 and 10⁻³ μm²/ms.

Within these bounds, our data suggest that myelin water diffusion has the potential to influence DWI experiments and bias analysis that does not take into account water movement between compartments. While D_app varied slowly over several orders of magnitude of D_mr, there were important differences compared to its value in the no-diffusion limit (D_mr → 0). Specifically, D_app values decreased as D_mr increased from 0. While this trend may be somewhat counterintuitive, the decrease in D_app with an increase in D_mr is caused by an increased contribution of signal from the slow diffusing (and short T₂) myelin compartment, aided by movement of water between compartments. Relative to D_app, K_app was somewhat more sensitivity to the rate of myelin water diffusion. Similar to the bimodal nature of D_app, K_app initially increased with an increase in D_mr, caused by an increased contribution from slowly-diffusion myelin water.

While the present study neglects the potential for exchange directly between intra- and extra-axonal compartments, some work has suggested that exchange can happen directly between these compartments at Nodes of Ranvier (Nilsson et al 2010b). While it is unclear how direct exchange of water between these compartments would impact the current results, the bi-modal features of Fig 3 with D_mr will be absent from models that ignore T₂ variations between myelin and non-myelin components of tissue (Harkins et al 2009).

Anisotropic Myelin Water Diffusion

Anisotropic diffusion within myelin is supported both by the structure of myelin mentioned earlier and diffusion experiments that have estimated diffusion in myelin. Experiments in synthetic myelin have measured very slow diffusion orthogonal to the lipid bilayer surface (represented as D_mr in the present work) and faster diffusion along the lipid bilayer surface (i.e. D_mc) (Khakimov et al 2008). In other experiments, combined multi-exponential T₂ and diffusion experiments have been used to measure D_app of the myelin water T₂ component, which was estimated to be > 0.1 μm²/ms (Andrews et al 2006, Stanisz and Henkelman 1998). This value represents a mixture of D_mr and D_mc, as water is able to diffuse around axons as well as through myelin within those experiments. Further, those estimates of myelin water diffusion may be sensitive to any movement of water between compartments.

As part of this work, we tested the sensitivity of DWI measurements to the anisotropic structure of myelin. While D_app was higher in some geometries containing anisotropic myelin water diffusion, this was primarily at the edge of what is considered the physiologic range in D_mr.

Sensitivity of DWI to Myelin Content

Another question posed by this work is whether the amount of myelin present in tissue can affect DWI signal in a unique way, or if it is possible to generate geometries with different amounts of myelin that produce effectively identical D_app and K_app. Previous work has hypothesized that myelin content could affect D_app and K_app (Fieremans et al 2011), while even a simple analytic model of DWI generally supports the role of myelin content to uniquely influence DWI measurements. Consider a three-compartment model with intra- (i.e. slowly diffusing) and extra-axonal (i.e. faster diffusing) compartments, where myelin (the third compartment) does not contribute to the measured signal. The extra-axonal signal fraction (f_e) would be characterized by

$$f_e=\frac{v_e}{v_i+v_e}=\frac{v_e}{1-v_m}.$$ [10]

Meanwhile the rate of extra-axonal diffusion (D_e) is primarily a function of v_e. In the long diffusion-time limit,

$$D_e=v_e{D}_0$$ [11]

(Latour et al 1994, Lam et al 2014). In theory, these two measures could be used to quantify myelin content,

$$v_m=1-\frac{D_e}{D_0{f}_e}.$$ [11]

Since the simulations contained in the present work are not in the long diffusion-time limit for extracellular space, Eqn [11] represents a simplified model of extra-axonal water diffusion. It is beyond the scope of this work to fully characterize D_e/D₀ in terms of v_e and the cellular spacing relative to the probed diffusion time. However in the case that myelin water diffusion can be neglected, the present simulation study implies that this type of estimation for myelin content is possible—in the solid lines of Fig 4 where myelin water diffusion is neglected, there is no value of v_i over which both ΔD_app and ΔK_app are negated.

Still, these simulations suggest that myelin water exchange further complicates these relationships—the influence of myelin content on DWI is reduced when myelin water diffusion is included. Within the dashed lines in Fig 4, which includes myelin water diffusion, ΔD_app and ΔK_app both cross zero near v_i ≈ 0.57.

Myelin Water Weighting

Similar to its effect on myelin content dependent diffusion changes, myelin water diffusion also changes the influence of TE on D_app and K_app. In the present work, when excluding myelin water diffusion, D_app increases and K_app decreases with increasing TE, indicating a decreased weighting of myelin water within the acquired signal. To our knowledge, there are no studies of DWI in white matter that report such an increase in D_app with echo time. One previous study in white matter found no difference between spin-echo and stimulated-echo DWI measurements at different echo times (Avram et al 2010), while another study in white matter showed a decrease in the radial diffusion eigenvalues with echo time at 1.5 and 3T (Qin et al 2009). A slight trend in D_app with TE was observed in ex vivo rat corpus callosum in the present work, shown in Fig 6.

While this generally agrees with trends in D_app and K_app under the influence of myelin water diffusion predicted by simulation in Fig 5, a decrease in D_app and/or an increase in K_app with TE could also occur if the restricted intra-axonal space had a longer intrinsic T₂ relaxation time-constant than extra-axonal space. There is direct evidence for such an assignment of intra- and extra-axonal T₂ components in peripheral nerve (Peled et al 1999, Wachowicz and Snyder 2002, Dortch et al 2010, Does and Gore 2000), which is known to contain three T₂ components (Vasilescu et al 1978). For instance, in frog sciatic nerve it has been shown that a long T₂ component (≈300 ms) exhibited a generally lower rate of water diffusion than the intermediate T₂ component (Peled et al 1999). In contrast to peripheral nerve, only two T₂ components are generally observed in white matter (Menon et al 1992, MacKay et al 1994); however, a couple studies have suggested that distinct intra- and extra-axonal T₂ components were required to explain findings on myelin water exchange in spinal cord and optic nerve (Dortch et al 2013, Harkins et al 2012). Thus, the trends in D_app and K_app observed in Fig 6 with echo time could indicate either myelin water diffusion or T₂ differences between intra- and extra-axonal compartments. Future work is aimed at investigating the influence of distinct intra- and extra-axonal T₂ relaxation time-constants in DWI and the potential to experimentally separate these influences to evaluate the influence of myelin water diffusion directly.

It should be noted that the decrease in D_app with TE measured in cerebral cortex is in disagreement with several previous studies that investigated echo time dependent effects in gray matter (Does and Gore 2000, Vestergaard-Poulsen et al 2007, Buckley and Blackband 1999), and may reflect changes in tissue associated with fixation.

Limitations of the Present Study

There are several methodological limitations to the current work. Previous work has suggested that intra- and extra-axonal T₂ may not be equivalent (Harkins et al 2009, 2012, Vestergaard-Poulsen et al 2007). Further, within this work, D₀ is taken as the diffusion of free water at body temperature; however, the value of D₀ in tissue may be reduced by macromolecular components in intra- and extra-axonal compartments, and may even differ between these compartments. Also within this work, g is independent of R̄, which is not generally true (Berthold et al 1983, Chatzopoulou et al 2008, Crawford et al 2010). The shape of the distribution of axon sizes may not be constant with mean axon size, and may even be log-linear instead of gamma distributed (Buzsaki and Mizuseki 2014). Still, this work contains the most microstructrually complex model of axons published so far, as it considers the structure of myelin sheaths.

CONCLUSIONS

D_app and K_app measured by DWI represent a complicated set of interactions between water and its local environment that are not completely understood. The results presented in this manuscript indicate that myelin water could present subtle but important contributions to DWI results. For instance, D_app and K_app simulated with physiologic values of myelin water diffusion were biased by up to and around 10% compared to simulations that neglected myelin water. It is also shown that myelin water diffusion can change the TE-dependence of D_app and K_app, although other mechanisms could also cause TE-dependent variations in D_app and K_app observed in white matter. Given the limited sensitivity of the simulated data to the diffusion characteristics of myelin water, it remains unclear whether the reported trends will be useful in clinical imaging. Still, as complex models of DWI signal are increasingly applied to experimental and clinical MRI, it is important to understand the full range of biophysical properties that could affect DWI results.