A new spin on perovskites untwined: Ultrafast optical switching and tuning of spin-energy states in layered halide perovskites.
Keywords: Non-linear, light-matter interactions, Ultrafast, Spin-selective, Optical Stark Effect, Solution Processed, Layered Halide Perovskites, room temperature, opto-spin-logic, Rabi-splitting
Abstract
Ultrafast spin manipulation for opto–spin logic applications requires material systems that have strong spin-selective light-matter interaction. Conventional inorganic semiconductor nanostructures [for example, epitaxial II to VI quantum dots and III to V multiple quantum wells (MQWs)] are considered forerunners but encounter challenges such as lattice matching and cryogenic cooling requirements. Two-dimensional halide perovskite semiconductors, combining intrinsic tunable MQW structures and large oscillator strengths with facile solution processability, can offer breakthroughs in this area. We demonstrate novel room-temperature, strong ultrafast spin-selective optical Stark effect in solution-processed (C6H4FC2H4NH3)2PbI4 perovskite thin films. Exciton spin states are selectively tuned by ~6.3 meV using circularly polarized optical pulses without any external photonic cavity (that is, corresponding to a Rabi energy of ~55 meV and equivalent to applying a 70 T magnetic field), which is much larger than any conventional system. The facile halide and organic replacement in these perovskites affords control of the dielectric confinement and thus presents a straightforward strategy for tuning light-matter coupling strength.
INTRODUCTION
Optical Stark effect (OSE) is a coherent, nonlinear light-matter interaction arising from the hybridization between photons and electronic states (also known as the photon-dressed state). Spin-selective OSE, with the additional spin degree of freedom, offers exciting new prospects to realizing opto–spin logic (1–5) and spin-Floquet topological phases (6) for ultrafast optical implementations of quantum information applications. Apart from the fundamental criterion of strong light-matter coupling, spin-switching applications using OSE also imposes additional material selection demands requiring (i) strong spin-orbit coupling (SOC) for spin selectivity, (ii) high-charge mobility for electronic integration, and (iii) room-temperature operation for practical applications. Material systems that could simultaneously fulfill all these requirements are few and far between. Substrate-insensitive organics (for example, J aggregates) would be excluded because of criterion (i) (7). Conventional III-V or II-VI inorganic nanostructures grown under stringent lattice-matched conditions while fulfilling criteria (i) and (ii) are severely limited to cryogenic temperature operations for the clear resolution of the spin states. Tuning the OSE (or, consequently, the Rabi energy, that is, splitting for the case of zero detuning) in these conventional systems without the aid of external photonic cavities is an extremely arduous endeavor. The two-dimensional (2D) organic-inorganic halide perovskite family of materials can meet all the abovementioned demands while offering facile tunability and strong spin selectivity.
Recently, halide perovskites (for example, CH3NH3PbI3) with outstanding optoelectronic properties are in the limelight because of their record solar cell efficiencies exceeding 20% (8). CH3NH3PbI3 is a 3D analog that belongs to the broad halide perovskite family, which is characterized by their large SOC originating from the heavy Pb and I atoms in their structure. Novel spin and magnetic field phenomena in CH3NH3PbI3 have recently been discovered (9–13), highlighting their potential for spin-based applications. Unlike 3D perovskites where the organic and inorganic constituents are uniformly distributed, the 2D analog [for example, (C6H5C2H4NH3)2PbI4] comprises alternating organic (C6H5C2H4NH3+) and inorganic ([PbI6]4− octahedron) layers that form naturally self-assembled multiple quantum well (MQW) structures (Fig. 1A), with thicknesses (gaps) of ~1 nm (~4.2 eV) and ~0.6 nm (2.39 eV), respectively (14). These repeating organic and inorganic layers, bound together by van der Waals interaction, form the barrier and the well, respectively (15). Likewise, 2D perovskites also have relatively outstanding optoelectronic properties and relatively high in-plane carrier mobilities (~2.6 cm2 V−1 s−1), on the basis of which transistors and light-emitting devices have previously been demonstrated (16–19). The large dielectric contrast between the barrier and the well gives rise to strong dielectric confinement that enhances its exciton binding energy (hundreds of millielectron volts) (20–22) and oscillator strength (22–24). These unique properties of 2D perovskites point to a highly promising system for realizing intrinsic spin-selective OSE, even in the absence of any photonic cavity.
Fig. 1. OSE in PEPI.
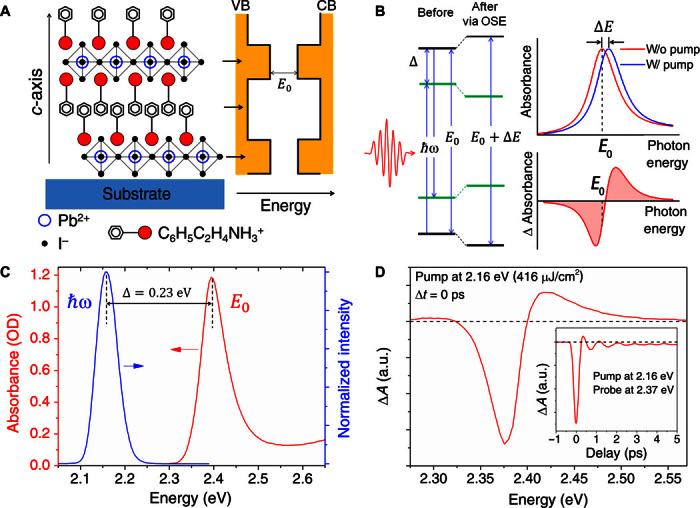
(A) Structure of PEPI with alternating organic and inorganic layers, forming multiple natural type I QW structures, with the barrier (well) being the organic (inorganic) layer (18). CB, conduction band; VB, valence band. (B) Illustration of OSE in a two-level system represented by the equilibrium states (black line) and the pump-induced Floquet quasi-states (green line) and the corresponding linear absorption and TA spectra. (C) The energy separation Δ between the excitonic absorption peak E0 of PEPI (red) and the excitation pump ħω (blue). OD, optical density. (D) TA spectrum of PEPI following a linearly polarized pump-probe at Δt = 0 ps. Inset: Ultrafast kinetics of OSE showing a fast process comparable to the pulse duration. a.u., arbitrary units.
Here, we report on the study of ultrafast spin-selective OSE in low-temperature solution-processed 2D perovskite thin films using transient absorption (TA) optical spectroscopy. Spin degeneracy lifting via OSE (Rabi energy, ħΩR) is observed by as much as 1.2 ± 0.3 meV (33 ± 3 meV), 4.5 ± 0.3 meV (47 ± 2 meV), and 6.3 ± 0.3 meV (55 ± 2 meV) for (C6H5C2H4NH3)2PbBr4 (or PEPB), (C6H5C2H4NH3)2PbI4 (or PEPI), and (C6H4FC2H4NH3)2PbI4 (or FPEPI), respectively. Equivalently, this magnitude of energy separation through the Zeeman effect (for FPEPI) will require an applied B field >70 T. Furthermore, we identify the dielectric contrast of the barrier and well layer as the direct criterion of tuning the Rabi energy in this material system.
RESULTS
Spectral signature of OSE
Figure 1B illustrates the key spectral signatures of OSE: (i) a nonresonant photoexcitation (ħω)–induced transient blue shift (ΔE) of the excitonic absorption peak (E0) (that is, E0 – ħω = Δ > 0) and (ii) a near-symmetrical derivative-like feature in the TA spectrum as a result of the shift of the energy levels (25). This phenomenon could also be understood from the Floquet picture as a repulsion between the equilibrium states (black) and Floquet quasi-states (green) (see Fig. 1B and the Supplementary Materials for detailed discussion) (6). Figure 1C shows the excitonic absorption peak of PEPI at E0 ~ 2.39 eV and the pump pulse of ~2.16 eV (that is, detuned by Δ ≈ 0.23 eV) as our excitation source. Figure 1D shows the characteristic OSE spectral signature in the TA spectrum of the PEPI film (at a probe delay Δt = 0 ps) following a linearly polarized pump-probe photoexcitation at 2.16 eV with a fluence of 416 μJ/cm2. Here, a less symmetrical derivative-like feature in the experimental TA spectrum is observed, which comprises the OSE signal, superimposed on a photobleaching peak (that is, negative ΔA peak) arising from the state filling of excitons by two-photon excitation (see Fig. 3, A and C). The kinetic trace of the probe at 2.37 eV (Fig. 1D, inset) shows that the ultrafast OSE process is comparable to the pulse duration. The much weaker oscillatory photobleaching signal arises from coherent two-photon–excited exciton dynamics (fig. S8).
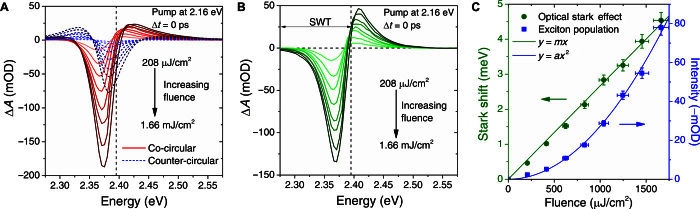
Fig. 3. Fluence dependence of OSE.
(A) Pump fluence–dependent TA spectra for co-circular (red) and counter-circular (blue) polarization pump-probe at Δt = 0 ps. (B) Resultant spectra from the difference between the co-circular TA spectra and the counter-circular TA spectra at the same pump fluence at a probe delay of 0 ps. The vertical black dashed line indicates the position of the exciton absorption peak. SWT, spectral weight transfer. (C) Estimated Stark shift as a function of pump fluence (green, left axis) and two-photon–excited exciton population (blue, right axis) and as a function of pump fluence (blue, right axis). The Stark shift exhibits a linear relation, whereas the two-photon-excited process exhibits a quadratic relation with the pump fluence.
Spin-selective OSE
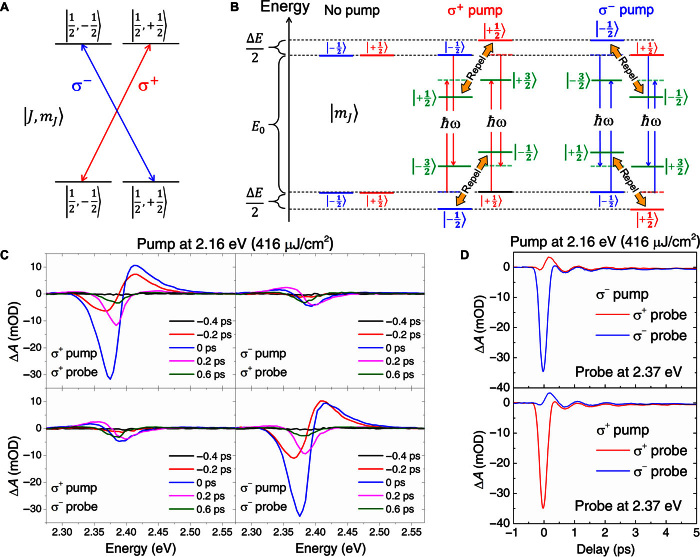
We first examined the origins and the mechanism of spin selectivity and established the spin selection rules for OSE in the generic PEPI system. In this 2D perovskite system, the conduction band, which is strongly affected by the crystal field and large SOC, arises mainly from the Pb-6p orbital, whereas the valence band arises mainly from the Pb-6s and I-5p orbitals (20–22). The organic component does not play any significant role in determining the electronic structure (22). Taking into account the crystal field and SOC, the electronic structures of both the valence band maximum and the conduction band minimum are described by the angular momentum quantum number J = ½ and the magnetic quantum number mJ = ±½, which is preserved for the case of excitons (20). Figure 2A shows the optical selection rules for the photon with wave vector k parallel to the c axis (that is, k∥c or k perpendicular to the substrate). Conservation of angular momentum dictates that the absorption of left/right (σ+/σ−) circularly polarized light will raise/lower mJ by 1. Analogous to our earlier work (9) for the 3D CH3NH3PbI3, absorption of σ+/σ− will create J-polarized (or spin-polarized) carriers, which are spin-polarized excitons in this case.
Fig. 2. Spin-selective OSE.
(A) Optical selection rule for the lowest singlet exciton in PEPI. Both the electron and the hole have a total angular momentum quantum number and a magnetic quantum number . (B) Schematic of the spin-selective OSE mechanism in PEPI, showing only the mJ in ket notation. The red (blue) arrow illustrates the interaction between the σ+ (σ−) photon that forms the Floquet quasi-states (green line). The hybridization of the equilibrium states (red or blue lines) with the Floquet quasi-states results in the shift in energy levels. The dashed (solid) lines represent the energy levels before (after) the repulsion. Repulsion only occurs between the equilibrium states and the Floquet states with the same mJ. (C) Co-circularly and counter-circularly polarized pump and probe TA spectra at various Δt. (D) The corresponding kinetics at the negative ΔA peak (2.37 eV). mOD, milli-optical density.
On the basis of these selection rules, Fig. 2B illustrates the spin-selective OSE mechanism in PEPI. From the quantum mechanical description (see the Supplementary Materials), only the Floquet quasi-states (green lines) with the same mJ as the equilibrium states (blue or red lines) will undergo a repulsion (that is, for but not for ; Fig. 2B) in the presence of the σ± pump. This gives rise to the spin-selective OSE, whose coupling strength is parameterized by the Rabi energy. Figure 2C shows the co-circular and counter-circular pump-probe TA spectra. The corresponding kinetic traces of the probe at the negative ΔA peak (~2.37 eV) are given in Fig. 2D. The circularly polarized probe is used to probe specific exciton spin states. The figures show a large photoinduced signal (that is, ΔA arising from OSE and state filling) when both pump and probe beams are co-circular. The signal is greatly reduced for the counter-circular case. The large ΔA signal present only for the co-circular case indicates OSE with a specific spin orientation. This validates the spin selectivity of the OSE signal in PEPI. The small ΔA signal present in the counter-circular case arises from the state filling due to two-photon photoexcitation (see Fig. 3, A and C). This spin-selective OSE can be further controlled through the ellipticity of pump polarization (see fig. S9).
Figure 3A shows the fluence-dependent TA spectra for both co-circular and counter-circular pump-probe configurations from 0.208 to 1.66 mJ/cm2. The spectral signature increases with increasing pump fluence for both configurations. On the basis of the excitonic peak in the linear absorption spectrum (Fig. 1C and fig. S8B), we attribute the −ΔA peak (2.39 eV) in the counter-circular TA spectrum (blue traces) to arise from the state filling of the excitons. This exciton bleaching signal exhibits fluence-dependent quadratic behavior consistent for a two-photon excitation process (Fig. 3C). To elucidate the OSE contribution and eliminate the excitonic contribution from the signal, we subtract the co-circular TA signal from the counter-circular TA signal at the same pump fluence (Fig. 3B). We estimate the energy shift ΔE from OSE using the spectral weight transfer of the subtracted signal (see the Supplementary Materials). Figure 3C shows the linear dependence of the OSE on the pump fluence, which yields excellent agreement with theoretical predictions (Eq. 1)
| (1) |
In Eq. 1, ħΩR is the Rabi energy (which parameterized the light-matter coupling strength of the material) and Δ is the detuning energy. The approximation holds for the case of Δ ≫ ħΩR. A large ΔE of 4.5 ± 0.2 meV at room temperature can be tuned with a pump fluence of 1.66 mJ/cm2 without any external magnetic field (Fig. 3C). At a given fluence of 1.66 mJ/cm2, Δ = 0.23 eV and ΔE = 4.5 ± 0.2 meV, and the corresponding ħΩR = 47 ± 2 meV, calculated by using Eq. 1. Similarly, for PEPB, our measurement yields ħΩR = 33 ± 3 meV (fig. S6). From these values and the oscillator strengths, we determine the exciton reduced mass to be 0.11 ± 0.01 m0 or 0.18 ± 0.02 m0 and the transition dipole moment (TDM) to be (5.26 ± 0.20) × 10−29 C m or (5.16 ± 0.50) × 10−29 C m, for PEPI and PEPB, respectively, where m0 is the free electron rest mass (see the Supplementary Materials). These results are consistent with previous reports for both I-based (14) and Br-based (20) 2D perovskite systems. Furthermore, as a self-consistency check, we determine the radiative lifetime to be 190 ± 10 ps from the TDM value, which corresponds well with the experimental data (fig. S7), thereby further validating our measurements.
Tuning of the Rabi energy
Tuning the coupling strength or the Rabi energy in 2D perovskite is not as trivial as merely modulating the exciton oscillator strength of the material. Although a large oscillator strength is important for obtaining a large Rabi energy, other contributions (such as effective mass and band gap) play crucial roles as well (eq. S29). Our observation suggests that the more deterministic criterion is the dielectric contrast between the barrier and the well layer. Figure 4 shows a plot of Rabi energy per square root of fluence () for various solution-processed 2D perovskite systems as a function of oscillator strength and the dielectric contrast. Herein, we performed the tuning of the dielectric contrast between the well and the barrier layer by substituting the organic and halide components of the perovskites. The dielectric constant of the barrier layer can be further reduced by fluorination of the organic layer (that is, C6H5C2H4NH3+ to C6H4FC2H4NH3+, hence PEPI to FPEPI; fig. S6A) as a result of the increase in free volume fraction and large electronegativity of the C–F bond (26), thus enhancing the dielectric contrast. Such simple substitution of organic components enhances ΔE from 4.5 ± 0.2 meV (that is, ħΩR = 47 ± 2 meV) to 6.3 ± 0.3 meV (that is, ħΩR = 55 ± 3 meV) (fig. S6). Meanwhile, the dielectric constant of the well layer can be reduced by substituting the halide component from iodide (~6.1) (14, 22) to bromide (~4.8) (20), thus reducing the dielectric contrast, together with the Rabi energy (ħΩR = 33 ± 3 meV for PEPB). We demonstrated that although does not exhibit any clear trend with the oscillator strength, there is direct increasing correspondence with the dielectric contrast. This latter parameter would therefore provide a clear criterion for the straightforward tuning of the coupling strength in 2D perovskite. Further theoretical studies are needed to establish the quantitative relationship between the Rabi energy and the dielectric contrast.
Fig. 4. Correlation between the Rabi energy and the oscillator strength or dielectric contrast.
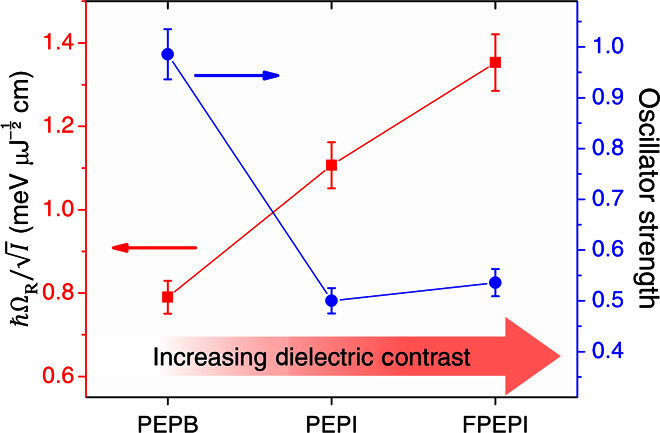
Measurement of Rabi energy via OSE on various lead-based 2D perovskite systems (that is, PEPB, PEPI, and FPEPI). There is a clear increasing relation between (red) and the dielectric contrast. Meanwhile, no clear correlation is observed between the oscillator strength (blue) and .
DISCUSSION
Our observation of spin-selective OSE in 2D perovskite systems demonstrates the viability of this material class for opto-spintronic applications. The spin degeneracy lifting by light via OSE of 6.3 ± 0.3 meV for FPEPI (or 4.5 ± 0.2 meV for PEPI) is estimated to be equivalent to the spin degeneracy lifting by >70 T of magnetic field (or >50 T for PEPI) via the Zeeman effect (see the Supplementary Materials). Therefore, our results also demonstrate a novel method for spin-state manipulation in 2D perovskite systems by light rather than by high magnetic field, which is much more practical and relevant for optoelectronic applications. Comparing 2D perovskite systems with other systems without any external photonic cavity, this room-temperature ħΩR value is larger than that for Mn-doped CdTe quantum dots (at 5 K) (3) or approximately four times larger than the largest value reported for GaAs/AlGaAs QWs (at 15 K) (27) photoexcited by a femtosecond pump with similar fluence (table S1). Although a recent publication on valley-selective OSE in monolayer WS2 reported an energy splitting of 18 meV (6), these 2D transition-metal dichalcogenides face stringent monolayer constraints that are essential for valley selectivity.
In summary, our findings show that the facile solution-processed natural MQW 2D perovskites have highly desirable characteristics for ultrafast spin-selective OSE. The PbI6 layer lends inorganic character to 2D perovskites, whereas the organic constituent bestows their solution processability. Their low-temperature solution processing is highly feasible for a broad range of substrates. In the absence of any external photonic cavity or hybrid metal nanostructures, an OSE-induced ultrafast optical spin-selective energy level splitting (ΔE) of 4.5 ± 0.2 meV (ΔE = 6.3 ± 0.3 meV) and a corresponding Rabi energy (ħΩR) of 47 ± 2 meV (ħΩR = 55 ± 3 meV) at room temperature are demonstrated in PEPI (FPEPI). In principle, a larger energy shift ΔE is possible if the pump pulse with a smaller detuning Δ is used. Here, we are limited by the spectral bandwidth of our femtosecond laser system with full width at half maximum at ~30 nm. Tuning of the energy level splitting and the Rabi energy is also feasible through halide or organic cation replacement (dielectric contrast tuning) and with the use of optical microcavities (23, 24). A high-quality external photonic microcavity will greatly enhance the strength of light-matter interaction through strong photon modal confinement (eq. S8), where a Rabi energy of ~190 meV from PEPI under lamp excitation (24) was previously demonstrated. Our work aptly demonstrates the untapped potential of halide perovskites for new applications beyond photovoltaics and light emission. The facile processability of these systems, together with the strategy of tuning the dielectric contrast in this family of materials, would open up new avenues for ultrafast opto–spin logic applications.
MATERIALS AND METHODS
Sample preparation
All the 2D perovskite samples were fabricated by mixing R-NH3X (where R is C6H5C2H4 or C6H4FC2H4 and X is Br or I) and PbX2 (in a 2:1 ratio) in N,N-dimethylformamide to make (R-NH3)2PbX4 solutions with a concentration of 12.5 weight percent. The solutions were then spin-coated on a cleaned quartz substrate at 4000 rpm and 30 s and were subsequently annealed at 100°C for 30 min. The thin films obtained had a thickness of 45 ± 5 nm, measured by a step profiler. All the chemicals were purchased from Sigma-Aldrich.
Optical spectroscopy measurement
Optical spectroscopy measurement was performed using a home-built chirp-corrected TA system with monochromator + photomultiplier tube + lock-in amplifier detection. It was powered by an 800 nm Libra Ti:sapphire laser (Coherent Inc.) with a pulse width of ~50 fs at a repetition rate of 1 kHz. The output was split into two beams: one beam was directed to the optical parametric amplifier (Coherent OPerA SOLO) to generate tunable photon energy (pump) and was mechanically chopped at 83 Hz, whereas the weaker beam was steered to a delay stage for white light generation (1.4 to 2.8 eV) on a sapphire crystal (probe). The measurement was performed in transmission mode. Linear polarizers together with a Soleil-Babinet Compensator and an achromatic quarter–wave plate (λ/4) were used to generate circular polarization for the pump and probe beams, respectively (fig. S1).
Supplementary Material
Acknowledgments
Funding: We acknowledge financial support from Nanyang Technological University (NTU) start-up grants M4080514 and M4081293, the Ministry of Education Academic Research Funding Tier 1 grants RG184/14 and RG101/15 and Tier 2 grants MOE2013-T2-1-081 and MOE2014-T2-1-044, the NTU–A*STAR (Agency for Science, Technology and Research) Silicon Technologies Center of Excellence Program Grant 11235100003, and the Singapore National Research Foundation through the Singapore-Berkeley Research Initiative for Sustainable Energy CREATE (Campus for Research Excellence and Technological Enterprise) Program and the Competitive Research Program grant NRF-CRP14-2014-03. D.G., N.M., and T.C.S. acknowledge the financial support from Johnson Matthey PLC. We also acknowledge E. J. Sie for the fruitful discussions and J. R. Abraham’s assistance in some optical measurements. Author contributions: D.G., T.C.S., and N.M. conceived the idea for the manuscript and designed the experiments. D.G. and W.K.C. developed the basic concepts and conducted the spectroscopic characterization. H.A.D., K.T., and I.N. fabricated and characterized the samples. W.K.C. contributed to the data analysis. T.C.S., N.M., D.G., R.R., and S.M. analyzed the data and wrote the paper. T.C.S. and N.M. led the project. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/6/e1600477/DC1
Experimental setup
Estimation of energy shift ΔE
Quantum mechanical description of the OSE
Estimation of the Rabi energy
Comparison of the Rabi energy
Estimation of the equivalent B field for Zeeman splitting of energy levels
Estimation of the TDM of PEPI
Estimation of ħΩR and oscillator strength in various organic-inorganic halide perovskite systems
Estimation of the exciton reduced mass
Estimation of the radiative lifetime
Oscillatory signal in PEPI
Effect of pump polarization ellipticity
fig. S1. TA spectroscopy setup.
fig. S2. Calculation of transient change due to a positive x shift.
fig. S3. Quantum description of OSE.
fig. S4. OSE with different pump detuning.
fig. S5. Pump properties in the energy and time domains.
fig. S6. Comparison of various halide perovskites with different dielectric contrasts.
fig. S7. Photoluminescence kinetics of PEPI.
fig. S8. Exciton dynamics in PEPI.
fig. S9. Polarization ellipticity control experiment of OSE in PEPI.
table S1. Comparison of OSE and Rabi energy in various inorganic semiconductors.
REFERENCES AND NOTES
- 1.Amo A., Liew T. C. H., Adrados C., Houdré R., Giacobino E., Kavokin A. V., Bramati A., Exciton–polariton spin switches. Nat. Photonics 4, 361–366 (2010). [Google Scholar]
- 2.Žutić I., Fabian J., Das Sarma S., Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
- 3.Le Gall C., Brunetti A., Boukari H., Besombes L., Optical Stark effect and dressed exciton states in a Mn-doped CdTe quantum dot. Phys. Rev. Lett. 107, 057401 (2011). [DOI] [PubMed] [Google Scholar]
- 4.Reiter D. E., Axt V. M., Kuhn T., Optical signals of spin switching using the optical Stark effect in a Mn-doped quantum dot. Phys. Rev. B 87, 115430 (2013). [Google Scholar]
- 5.Unold T., Mueller K., Lienau C., Elsaesser T., Wieck A. D., Optical Stark effect in a quantum dot: Ultrafast control of single exciton polarizations. Phys. Rev. Lett. 92, 157401 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Sie E. J., McIver J. W., Lee Y.-H., Fu L., Kong J., Gedik N., Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 14, 290–294 (2015). [DOI] [PubMed] [Google Scholar]
- 7.Sun D., Ehrenfreund E., Vardeny Z. V., The first decade of organic spintronics research. Chem. Commun. 50, 1781–1793 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Yang W. S., Noh J. H., Jeon N. J., Kim Y. C., Ryu S., Seo J., Seok S. I., High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 348, 1234–1237 (2015). [DOI] [PubMed] [Google Scholar]
- 9.Giovanni D., Ma H., Chua J., Grätzel M., Ramesh R., Mhaisalkar S., Mathews N., Sum T. C., Highly spin-polarized carrier dynamics and ultralarge photoinduced magnetization in CH3NH3PbI3 perovskite thin films. Nano Lett. 15, 1553–1558 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Miyata A., Mitioglu A., Plochocka P., Portugall O., Wang J. T.-W., Stranks S. D., Snaith H. J., Nicholas R. J., Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites. Nat. Phys. 11, 582–587 (2015). [Google Scholar]
- 11.Zhang C., Sun D., Sheng C. X., Zhai Y. X., Mielczarek K., Zakhidov A., Vardeny Z. V., Magnetic field effects in hybrid perovskite devices. Nat. Phys. 11, 427–434 (2015). [Google Scholar]
- 12.Hsiao Y.-C., Wu T., Li M., Hu B., Magneto-optical studies on spin-dependent charge recombination and dissociation in perovskite solar cells. Adv. Mater. 27, 2899–2906 (2015). [DOI] [PubMed] [Google Scholar]
- 13.Kepenekian M., Robles R., Katan C., Sapori D., Pedesseau L., Even J., Rashba and Dresselhaus effects in hybrid organic–inorganic perovskites: From basics to devices. ACS Nano 9, 11557–11567 (2015). [DOI] [PubMed] [Google Scholar]
- 14.Hong X., Ishihara T., Nurmikko A. V., Dielectric confinement effect on excitons in PbI4-based layered semiconductors. Phys. Rev. B 45, 6961–6964 (1992). [DOI] [PubMed] [Google Scholar]
- 15.Mitzi D. B., Chondroudis K., Kagan C. R., Organic–inorganic electronics. IBM J. Res. Dev. 45, 29–45 (2001). [Google Scholar]
- 16.Kagan C. R., Mitzi D. B., Dimitrakopoulos C. D., Organic–inorganic hybrid materials as semiconducting channels in thin-film field-effect transistors. Science 286, 945–947 (1999). [DOI] [PubMed] [Google Scholar]
- 17.Mitzi D. B., Dimitrakopoulos C. D., Kosbar L. L., Structurally tailored organic–inorganic perovskites: Optical properties and solution-processed channel materials for thin-film transistors. Chem. Mater. 13, 3728–3740 (2001). [Google Scholar]
- 18.Mitzi D. B., Dimitrakopoulos C. D., Rosner J., Medeiros D. R., Xu Z., Noyan C., Hybrid field-effect transistor based on a low-temperature melt-processed channel layer. Adv. Mater. 14, 1772–1776 (2002). [Google Scholar]
- 19.Matsushima T., Fujita K., Tsutsui T., Electroluminescence enhancement in dry-processed organic–inorganic layered perovskite films. Jpn. J. Appl. Phys. 44, 1457 (2005). [Google Scholar]
- 20.Tanaka K., Takahashi T., Kondo T., Umeda K., Ema K., Umebayashi T., Asai K., Uchida K., Miura N., Electronic and excitonic structures of inorganic–organic perovskite-type quantum-well crystal (C4H9NH3)2PbBr4. Jpn. J. Appl. Phys. 44, 5923 (2005). [Google Scholar]
- 21.Even J., Pedesseau L., Dupertuis M.-A., Jancu J.-M., Katan C., Electronic model for self-assembled hybrid organic/perovskite semiconductors: Reverse band edge electronic states ordering and spin-orbit coupling. Phys. Rev. B 86, 205301 (2012). [Google Scholar]
- 22.Ishihara T., Takahashi J., Goto T., Optical properties due to electronic transitions in two-dimensional semiconductors (CnH2n+1NH3)2PbI4. Phys. Rev. B 42, 11099–11107 (1990). [DOI] [PubMed] [Google Scholar]
- 23.Brehier A., Parashkov R., Lauret J. S., Deleporte E., Strong exciton-photon coupling in a microcavity containing layered perovskite semiconductors. Appl. Phys. Lett. 89, 171110 (2006). [Google Scholar]
- 24.Lanty G., Bréhier A., Parashkov R., Lauret J. S., Deleporte E., Strong exciton–photon coupling at room temperature in microcavities containing two-dimensional layered perovskite compounds. New J. Phys. 10, 065007 (2008). [Google Scholar]
- 25.Autler S. H., Townes C. H., Stark effect in rapidly varying fields. Phys. Rev. 100, 703–722 (1955). [Google Scholar]
- 26.Simpson J. O., St. Clair A. K., Fundamental insight on developing low dielectric constant polyimides. Thin Solid Films 308–309, 480–485 (1997). [Google Scholar]
- 27.Mysyrowicz A., Hulin D., Antonetti A., Migus A., Masselink W. T., Morkoç H., “Dressed excitons” in a multiple-quantum-well structure: Evidence for an optical Stark effect with femtosecond response time. Phys. Rev. Lett. 56, 2748–2751 (1986). [DOI] [PubMed] [Google Scholar]
- 28.Uemoto M., Ajiki H., Large and well-defined Rabi splitting in a semiconductor nanogap cavity. Opt. Express 22, 22470–22478 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Khitrova G., Gibbs H. M., Kira M., Koch S. W., Scherer A., Vacuum Rabi splitting in semiconductors. Nat. Phys. 2, 81–90 (2006). [Google Scholar]
- 30.Von Lehmen A., Chemla D. S., Heritage J. P., Zucker J. E., Optical Stark effect on excitons in GaAs quantum wells. Opt. Lett. 11, 609–611 (1986). [DOI] [PubMed] [Google Scholar]
- 31.Bose R., Sridharan D., Solomon G. S., Waks E., Large optical Stark shifts in semiconductor quantum dots coupled to photonic crystal cavities. Appl. Phys. Lett. 98, 121109 (2011). [Google Scholar]
- 32.Xu C.-q., Sakakura H., Kondo T., Takeyama S., Miura N., Takahashi Y., Kumata K., Ito R., Magneto-optical effects of excitons in (C10H21NH3)2PbI4 under high magnetic fields up to 40 T. Solid State Commun. 79, 249–253 (1991). [Google Scholar]
- 33.Hirasawa M., Ishihara T., Goto T., Sasaki S., Uchida K., Miura N., Magnetoreflection of the lowest exciton in a layered perovskite-type compound (C10H21NH3)2PbI4. Solid State Commun. 86, 479–483 (1993). [Google Scholar]
- 34.Zhang S., Audebert P., Wei Y., Al Choueiry A., Lanty G., Bréhier A., Galmiche L., Clavier G., Boissiére C., Lauret J.-S, Deleporte E., Preparations and characterizations of luminescent two dimensional organic-inorganic perovskite semiconductor. Materials 3, 3385 (2010). [Google Scholar]
- 35.Hilborn R. C., Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 50, 982–986 (1982). [Google Scholar]
- 36.Kenichiro T., Takashi K., Bandgap and exciton binding energies in lead-iodide-based natural quantum-well crystals. Sci. Technol. Adv. Mater. 4, 599 (2003). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/6/e1600477/DC1
Experimental setup
Estimation of energy shift ΔE
Quantum mechanical description of the OSE
Estimation of the Rabi energy
Comparison of the Rabi energy
Estimation of the equivalent B field for Zeeman splitting of energy levels
Estimation of the TDM of PEPI
Estimation of ħΩR and oscillator strength in various organic-inorganic halide perovskite systems
Estimation of the exciton reduced mass
Estimation of the radiative lifetime
Oscillatory signal in PEPI
Effect of pump polarization ellipticity
fig. S1. TA spectroscopy setup.
fig. S2. Calculation of transient change due to a positive x shift.
fig. S3. Quantum description of OSE.
fig. S4. OSE with different pump detuning.
fig. S5. Pump properties in the energy and time domains.
fig. S6. Comparison of various halide perovskites with different dielectric contrasts.
fig. S7. Photoluminescence kinetics of PEPI.
fig. S8. Exciton dynamics in PEPI.
fig. S9. Polarization ellipticity control experiment of OSE in PEPI.
table S1. Comparison of OSE and Rabi energy in various inorganic semiconductors.