Biophysical Characterization of Fluorotyrosine Probes Site-Specifically Incorporated into Enzymes: E. coli Ribonucleotide Reductase As an Example

Abstract

Fluorinated tyrosines (F_nY’s, n = 2 and 3) have been site-specifically incorporated into E. coli class Ia ribonucleotide reductase (RNR) using the recently evolved M. jannaschii Y-tRNA synthetase/tRNA pair. Class Ia RNRs require four redox active Y’s, a stable Y radical (Y·) in the β subunit (position 122 in E. coli), and three transiently oxidized Y’s (356 in β and 731 and 730 in α) to initiate the radical-dependent nucleotide reduction process. F_nY (3,5; 2,3; 2,3,5; and 2,3,6) incorporation in place of Y₁₂₂-β and the X-ray structures of each resulting β with a diferric cluster are reported and compared with wt-β2 crystallized under the same conditions. The essential diferric-F_nY· cofactor is self-assembled from apo F_nY-β2, Fe²⁺, and O₂ to produce ∼1 Y·/β2 and ∼3 Fe³⁺/β2. The F_nY· are stable and active in nucleotide reduction with activities that vary from 5% to 85% that of wt-β2. Each F_nY·-β2 has been characterized by 9 and 130 GHz electron paramagnetic resonance and high-field electron nuclear double resonance spectroscopies. The hyperfine interactions associated with the ¹⁹F nucleus provide unique signatures of each F_nY· that are readily distinguishable from unlabeled Y·’s. The variability of the abiotic F_nY pK_a’s (6.4 to 7.8) and reduction potentials (−30 to +130 mV relative to Y at pH 7.5) provide probes of enzymatic reactions proposed to involve Y·’s in catalysis and to investigate the importance and identity of hopping Y·’s within redox active proteins proposed to protect them from uncoupled radical chemistry.

Introduction

F_nY’s (Figure 1) have long been used to probe enzyme reaction mechanisms, protein environmental perturbation of pK_a’s, and protein structures in biology.¹⁻³ Prime examples of the former can be found in recent studies on ketosteroid isomerase, which has three Y’s and conserved waters in its active site environment with one Y with a pK_a of 6.3,^4,5 and protein Y kinases in which the Y pK_a within a polypeptide substrate is perturbed and the rate of its phosphorylation is examined.⁶ 3-Fluorotyrosine (3-FY) has been incorporated into the oxygen evolving core complex of photosystem II to probe the mechanism of proton-coupled electron transfer (PCET) operative in Y_Z oxidation to Y_Z· over a broad pH range.⁷ The high sensitivity of NMR analysis to the ¹⁹F nucleus, in conjunction with its large window and sensitivity to environment,⁸ have been used extensively to study conformational changes in proteins and the interaction of proteins with other biological molecules.⁹ Recent technology has allowed site-specific incorporation of F_nY (n = 2 or 3, Figure 1) into any protein of interest.¹⁰⁻¹² In our case, an evolved polyspecific tRNA synthetase (RS) was used.¹⁰ These F_nY’s have played an important role in studying the mechanism of the 35 Å radical transfer in the E. coli ribonucleotide reductase (RNR), a process which involves one stable and three transient Y·’s (Figure S1).¹³⁻¹⁷ In this manuscript we report the general method of F_nY insertion into proteins using the small β2 subunit of RNR as an example and the characterization of each F_nY-β2 by X-ray crystallography and of each oxidized F_nY· by multifrequency electron paramagnetic resonance (EPR) and electron nuclear double resonance (ENDOR) spectroscopy methods. This work provides the foundation for others to use these tools to investigate enzyme mechanisms proposed to involve stable or transient Y·’s in their catalytic mechanism¹⁸⁻²³ or to determine if hole hopping through Y and W chains protect redox active proteins from oxidative damage.²⁴⁻²⁶

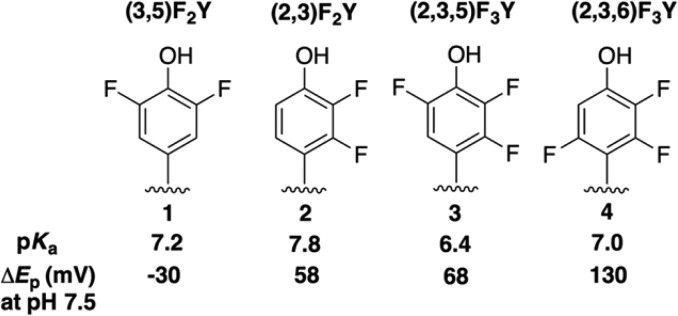
Figure 1.

Unnatural amino acids (UAAs) utilized in this study. ΔE_p represents the potential difference vs the Y·/Y couple at pH 7.5 as determined by differential pulse voltammetry (DPV) studies performed on the N-acetyl fluoro-l-tyrosinamides.⁸

RNRs catalyze the conversion of nucleotides to deoxynucleotides in all organisms (Scheme 1).²⁷⁻²⁹ Although the mechanism of nucleotide reduction is conserved, the mechanism by which the complex radical reaction is initiated is dependent on the metallo-cofactor.³⁰ The class I RNRs are composed of two subunits, α and β, which in E. coli form an active α2β2 complex. A Y· in the β subunit is used to oxidize the active site cysteine to a thiyl radical in the α subunit. This oxidation occurs over a very long distance and involves a specific pathway (Figure S1).^13,16,31 Since in the best studied E. coli RNR, the rate-limiting step is a conformational change that masks all the chemistry,³² altering this step by a variety of methods has been crucial to our current understanding of this process. The most successful approach has been to use the suppressor tRNA/RS methodology to incorporate Y analogs in place of four Y’s in the pathway.^{10,17,33−36} Recently we evolved an RS to incorporate (2,3,5)F₃Y and found that it was polyspecific; i.e., it was able to incorporate a variety of F_nY’s (Figure 1).¹⁰ These F_nY’s have been shown to have peak potentials (E_p’s) that range from 30 mV easier to oxidize than Y to 130 mV harder to oxidize at pH 7.5 in addition to having altered pK_a’s. These perturbations are ideal for investigating the multistep redox chemistry that involves a number of PCET steps, required to initiate nucleotide reduction. In the original paper, we also demonstrated that when the stable Y₁₂₂· in β2 is replaced with (2,3,5)F₃Y, it could be oxidized to the (2,3,5)F₃Y·.¹⁰ The electron paramagnetic resonance (EPR) spectrum of this radical exhibited hyperfine features at the low-field and high-field sides of the spectrum associated with the ¹⁹F (I = 1/2) nucleus that allowed detection of this radical even in the presence of overlapping unlabeled Y· signals. From these early studies and the chemical properties of the F_nY’s themselves,⁸ it was clear that these compounds (Figure 1) might provide a useful tool to study enzymatic mechanisms involving stable and transient Y·’s.

Scheme 1. Reaction Catalyzed by RNR.

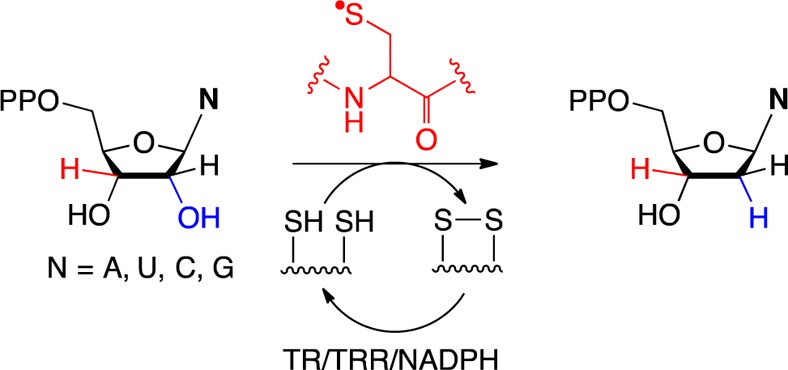
A pair of cysteines in the active site of α2 are oxidized to a disulfide on each turnover. Multiple turnovers require re-reduction of the disulfide by the thioredoxin (TR), thioredoxin reductase (TRR), NADPH system.

In this paper we report the general optimized methodology for incorporation of these F_nY’s in place of Y₁₂₂ in β2. We also report the methodology used to generate each F_nY· at this position, taking advantage of self-assembly of the essential diferric-Y· cofactor subsequent to the addition of Fe²⁺, O₂ and reductant to apo-β2 or its assembly during recombinant expression. A potential issue with the asymmetric F_nY’s (2, 3, 4, Figure 1) is whether they adopt multiple conformations in β2 either during the folding process or due to rotation around the Cβ-Cγ bond. The structures of F_nY-β2 and F_nY· have been determined by X-ray crystallography and multifrequency EPR and ENDOR methods, respectively. The results support a model where the fluorine substitution minimally perturbs the overall protein conformation of β2, although in several cases, multiple conformers of the F_nY itself are observed by both paramagnetic and crystallographic methods. The EPR spectra of each of the radicals, the simulation of these spectra, and the calculated spin density are reported and reveal the detailed ¹⁹F hyperfine parameters. In conjunction with the range of reduction potentials spanned by these analogs (Figure 1),^8,37 this information will be generally useful to investigate redox active Y’s reported in a number of metabolically important enzymes.

Materials and Methods

Materials

(His)₆ wt-α2 (specific activity −2600 nmol/min/mg) was expressed from pET28a-nrdA and purified using the standard laboratory protocol.³⁴ Tyrosine phenol lyase³⁸ and F_nY’s³⁹ were isolated as previously described. E. coli thioredoxin (TR, 40 U/mg) and thioredoxin reductase (TRR, 1400 U/mg) were purified following previously published methods.^40,41 [³H] CDP was obtained from ViTrax (Placentia, CA). Roche provided the calf alkaline phosphatase (20 U).

General Method for Incorporation of F_nY’s into β2 of E. coli RNR

Expression and Purification of F_nY-β2

E. coli TOP10 chemically competent cells were transformed with pBAD-nrdB_122TAG and pEVOL-F_nYRS-E3¹⁰ and grown at 37 °C on LB-agar plates containing 100 μg/mL ampicillin (Amp) and 35 μg/mL chloramphenicol (Cm). A single colony was used to inoculate a starter culture (5 mL) that was grown until saturation (37 °C, 12–16 h). This culture was diluted 100-fold into fresh 2xYT medium supplemented with Amp and Cm. After 16 h at 37 °C, the culture was diluted 100-fold into 4 × 2 L of 2xYT containing the antibiotics and variable concentrations of F_nY (0.5 mM (3,5)F₂Y, 0.7 mM (2,3,5)F₃Y, 1.5 mM (2,3)F₂Y, or 1.5 mM (2,3,6)F₃Y). F_nYRS and nrdB were both induced at an OD₆₀₀ of 0.6 with 0.05% (w/v) l-arabinose. In the case of (2,3,5)F₃Y-β2 and (2,3,6)F₃Y-β2, 100 μM o-phenanthroline was added to chelate the iron 30 min prior to induction with l-arabinose. In all cases, growth was continued for an additional 5 h and the cells were harvested by centrifugation (3500g, 15 min). Apo (2,3,5)F₃Y-β2 and (2,3,6)F₃Y-β2 and holo (3,5)F₂Y-β2 and (2,3)F₂Y-β2 constructs were isolated by anion-exchange chromatography as previously described.⁴²

General Methods To Assemble the Diferric-F_nY· Cofactor in β2

Chelation of Iron from Holo (3,5)F₂Y-β2 and (2,3)F₂Y-β2

As-isolated (3,5)F₂Y-β2 and (2,3)F₂Y-β2 were deoxygenated and taken into an anaerobic chamber (4 °C). Solid sodium dithionite (Na₂S₂O₄) and methyl viologen (MV) were also taken into the chamber where stock solutions of each (400 mM and 11 mM respectively) were prepared in 50 mM N-2-hydroxyethylpiperazine-N′-ethanesulfonic acid (HEPES) pH 7.6, 5% glycerol. Na₂S₂O₄ and MV were added to the protein at final concentrations of 20 mM and 110 μM, respectively. The resulting blue solution was stirred in the anaerobic chamber for 1 h prior to addition of ferrozine (final concentration 20 mM). The purple mixture was taken out of the chamber, and the (ferrozine)₃Fe complex was removed by Sephadex G-25 chromatography to obtain apo (3,5)F₂Y-β2 and (2,3)F₂Y-β2.

Reconstitution of the Diferric-F_nY· Cofactors

Apo F_nY-β2s (either isolated or generated using the protocol described above) were reconstituted as previously described.^17,35 After a 15 min incubation period with 5 equiv of ferrous ammonium sulfate, the iron-loaded proteins were treated with 3.5 equiv of O₂ in the form of O₂ saturated 50 mM HEPES pH 7.6, 5% glycerol. The reconstituted proteins (F_nY·-β2s) were analyzed by X-band EPR spectroscopy to quantitate the radical yield.

Kinetics of Diferric-(2,3,6)F₃Y· Cluster Assembly Measured by Rapid Freeze–Quench (RFQ) EPR Spectroscopy

The methods followed previous protocols^43,44 to study Y₁₂₂· formation with wt-β2 and are described in more detail in the Supporting Information (SI).

Steady-State Activity Assays of F_nY·-β2s

The specific activities of F_nY·-β2s were determined by the spectrophotometric and radioactive assays utilized for wt RNR.^45,46 For the spectrophotometric assay, 0.5 μM F_nY·-β2, 2.5 μM wt-α2, 1 mM CDP, 3 mM ATP, 30 μM TR, 0.5 μM TRR, and 0.2 mM NADPH in 50 mM HEPES pH 7.6, 15 mM MgSO₄, and 1 mM EDTA were combined in a total volume of 300 μL. In the case of (3,5)F₂Y·-β2, the concentrations of β2 and α2 were 0.15 μM and 0.75 μM respectively. The reaction was monitored for 1 min at 340 nm for consumption of NADPH. For the radioactive assays, [³H]-CDP was utilized (0.5 mM, 2000–4000 cpm/nmol) and the amount of NADPH was increased to 1 mM. The reactions were performed in a total volume of 170 μL, aliquots were quenched at different time points by heat denaturation, and the samples were worked up as previously described.⁴⁶

Crystallization of F_nY-β2

All β2s were prepared at 250 μM (∼21 mg/mL) in assay buffer (50 mM HEPES pH 7.6, 15 mM MgCl₂, 1 mM EDTA) for crystallization. Wt-β2 was reduced with hydroxyurea⁴⁷ in order to ensure all of the protein was in the met state (Y·-reduced diferric state). Initial crystallization conditions were identified for wt-β2 in 96-well, sitting drop, sparse matrix screens (Hampton Research, Qiagen) dispensed by a Phoenix pipetting robot (Art Robbins) at room temperature (∼23 °C). Optimization of the initial conditions was carried out in 24-well, hanging or sitting drop, vapor diffusion trays at room temperature. All crystallization reagents were from Hampton Research. The final, optimized conditions contained 1.1 M (NH₄)₂SO₄, 0.9–1.2 M KCl, and 0.1 M Tris pH 8.0. Protein and precipitant were mixed in a 1:1 ratio with a final drop volume of 2 μL. Crystals of each of the F_nY-β2 variants grew in the same conditions as identified for wt-β2 and typically appeared after 24–48 h and grew to maximum size over 1–2 weeks. Most crystals appeared as pale green hexagons or pyramids, but crystal size and morphology did not greatly influence the quality of the resulting data set. All crystals were transferred to a cryoprotection solution containing 60% saturated Li₂SO₄, 0.4 M KCl, 0.1 M bicine pH 8.5–9.5 for 1–3 h prior to cryocooling by plunging in liquid N₂. The length of the soak did not alter the quality of the data set.

Data sets for F_nY-β2 variants were collected at the Advanced Photon Source beamline 24ID-C on a Pilatus 6 M detector (Dectris) or 24ID-E on a Q315 CCD detector (ASDC). The raw diffraction images for each data set have been deposited in the SBGrid Data Bank. Data were indexed in space group P6₁22, integrated, and scaled in HKL2000⁴⁸ with cell dimensions of a = b = 91 Å, c = 206 Å. A similar crystal form has been reported for the dimanganese(II)-containing E. coli β2 (PDB ID 2ALX);⁴⁹ the structure was solved by molecular replacement in the Phenix implementation of Phaser⁵⁰ using this structure as the search model. A single β monomer is found in the asymmetric unit of this crystal form with the physiological dimer generated by crystallographic symmetry. The highest resolution structure, (3,5)F₂Y-β2, was rebuilt and refined first using reciprocal- and real-space positional refinement in phenix.refine.⁵¹ Atomic displacement parameters (B factors) were optimized for each chain with translation/libration/screw refinement. Water molecules were added automatically in Coot⁵² and checked manually against composite omit electron density maps. The entire model was checked for geometry and fit to the density in Coot. This completed model was used as the basis for refining the other F_nY- and wt-β2 structures after removal of the UAA.

Restraints for each F_nY residue were generated in Phenix eLBOW, and the residues were placed in F_o – F_c omit density. For (3,5)F₂Y-β2, this residue was placed into unambiguous omit density in a single conformation. The (2,3), (2,3,6), and (2,3,5)F₃Y models contain some fraction of a second orientation of the F_nY, as described below. For angle measurements, hydrogen atoms were added in PyMOL, and the dihedral angle to the ring plane (H_β–C_β–C₁–C_2/6) was measured. θ was calculated by subtracting the dihedral to the ring plane from 90°.

The final structures for all of the models were verified with composite omit electron density maps. In each case the final model contains residues 2–349 out of 375 and residue 1, the N-terminal methionine, is not visible in any structure. The final models have been deposited in the Protein Data Bank (5CI0, 5CI1, 5CI2, 5CI3, and 5CI4). All software used for crystallographic data processing and refinement was compiled and maintained by the SBGrid consortium.⁵³ Structural figures were created in PyMol (Schrödinger).

CW EPR Spectroscopy

All reconstituted F_nY·-β2s were transferred to the appropriate EPR tubes and frozen in liquid N₂ prior to EPR spectroscopy at a specific observation temperature. In the case of (2,3,6)F₃Y·-β2 only, the sample was aged for 2 min following addition of O₂ during reconstitution of the active cofactor and then frozen in liquid N₂. The reason for this aging procedure is detailed in the Results. All 9 GHz (X-band) continuous-wave (CW) EPR spectra were collected at a temperature of 80 K under slow-passage, nonsaturating conditions using a Bruker (Billerica, MA) ELEXSYS E500 X-band spectrometer equipped with an Oxford Instruments ESR900 cryostat and an ITC-503 temperature controller.

High-Field EPR Spectroscopy

All pulsed EPR and ENDOR spectroscopic studies were performed at a temperature of 30 K using a recently redesigned home-built 130 GHz EPR spectrometer (vide infra) equipped with an Oxford-CF935 liquid helium cryostat and an ITC-503 temperature controller. The spectrometer is also equipped with an 8 T cryogen-free magnet (Cryogenic Limited, UK), and all data were acquired using a TE₀₁₁ mode cylindrical resonant cavity designed and manufactured by HF EPR Instruments, Inc. (V. Krymov, New York) equipped with radio frequency (RF) coils for ENDOR.⁵⁴ Spectrometer control is achieved using the SpecMan software.⁵⁵ Magnetic field-swept echo-detected EPR spectra were acquired using the Hahn echo pulse sequence: π/2−τ–π–echo. The magnetic field axis for each field-swept spectrum was calibrated using MgO with an Mn²⁺ impurity (95+% fused MgO, Aldrich) with a g-value of 2.00100(5) and a ⁵⁵Mn hyperfine coupling constant of −243.6(5) MHz, as determined previously.^56,57 Each field swept echo-detected EPR absorption spectrum was modified using a pseudomodulation function (modulation amplitude = 0.3 G) to approximate the effect of field modulation and produce the CW-like first derivative spectrum.⁵⁸ RFs for Davies ENDOR experiments were generated by an HP 8656B signal generator under GPIB control, and pulses were formed by a TTL-driven Mini-Circuits (Brooklyn, NY) ZASWA-2-50DR+ RF switch. The RF pulses were then amplified by either a 300 W Bruker Blax300 RF amplifier (6–250 MHz dynamic range) or a 500 W Kalmus RF amplifier (200–330 MHz dynamic range). ENDOR spectra were acquired using the pulse sequence π–t_RF–π_RF–t_RF–π/2−τ–π–echo, where π_RF is the optimized RF pulse length and t_RF is a fixed delay separating MW and RF pulses. ENDOR spectra spanning 80 to 250 MHz were acquired using the Blax300 amplifier with π_RF = 24 μs, and those spanning from 200 to 330 MHz were acquired using the Kalmus amplifier with π_RF = 18 μs. The resultant spectra were stitched together by first normalizing each to the most intense β-¹H signal near 220 MHz and then splicing them together at 212.5 MHz to give the resultant ENDOR spectrum shown in each figure. The specific parameters for field positions, microwave frequencies, and pulse and delay lengths are given in the captions of each figure.

The transmitter section of the microwave bridge (HF EPR Instruments, Inc., V. Krymov, New York) of our laboratory-built 130 GHz spectrometer⁵⁹ was heavily modified in order to increase microwave pulse power and operational stability (Figures S2 and S3). The topology of our upgraded 130 GHz microwave transmitter is very similar to that described in Smith et al.⁶⁰ As in the original bridge, a single phase-locked dielectric resonator oscillator at 7.647 GHz (output power = 20 dBm, Nexyn, Inc.) serves as the base frequency, preserving the CW EPR functionality. This base frequency is then mixed and multiplied up to 32.5 GHz and provides 0 dBm (1 mW) input power to the high-power side of the transmitter arm. The dual-channel IMPATT diode (cascaded) amplifiers of the original bridge were replaced with a single channel amplifier–multiplier chain (AMC) fabricated by Virginia Diodes, Inc., (VDI) of Charlottesville, VA. The AMC consists of a set of cascaded varactor multipliers, in our case an x2 × 2 design, with a Spacek Laboratories input preamplifier and a separate power supply module. The AMC pulse output power is 23.2 dBm (210 mW) as measured by VDI at 130 GHz. A synthesizer channel (Herley-CTI XS-7314) was added so that two-frequency experiments such as DEER and EDNMR could also be conducted. Further details on these modifications to the bridge can be found in the SI (Figure S2 and Table S1).

Dealing with the Hole in the ENDOR Spectrum: Simulations and the Importance of the Suppression Effect

All spectral simulations were performed in the MATLAB 8.1.0 (R2013a) software package (The Mathworks Inc., Natick, MA) using the EasySpin 5.0.0 toolbox.^61,62 A nucleus exhibiting a large anisotropic hyperfine interaction (A) will have an orientation relative to the static B₀-field at which the isotropic and anisotropic contributions to the hyperfine tensor are of equal magnitude and opposite sign. This condition leads to a cancellation of the hyperfine field for this nucleus, i.e., A = 0 for this orientation. The theoretical ENDOR spectrum of such a nucleus would possess spectral intensity at the corresponding Larmor frequency. In practice, however, the Davies ENDOR spectrum suffers from a lack of ENDOR response as the hyperfine interaction approaches zero, A → 0. Fortunately, this behavior is easily modeled by convolving simulated ENDOR spectra by the detectability function:⁶³

1

where A is the hyperfine coupling in MHz and t_p is the duration of the initial microwave π-pulse in the Davies sequence in μs. The breadth of this blind spot is inversely proportional to the length of the initial preparation pulse.

In the case of each of the F_nY· species investigated here, this suppression effect must be taken into account in order to accurately simulate the ENDOR intensities arising from all hyperfine-coupled ¹⁹F nuclei whose A-tensors are highly anisotropic owing to the unpaired spin populating the fluorine 2p_z orbital (vide infra).

Electronic Structure Calculations

All DFT calculations were performed on a desktop computer using the ORCA 2.9.1 suite of software.⁶⁴ Y and F_nY derivatives were approximated as the corresponding phenol (i.e., a methyl group replaced the β-methine and amino acid). The atomic positions were optimized for each Y· model using the unrestricted Kohn–Sham method with Becke’s three-parameter hybrid functional for exchange^65,66 combined with the Lee–Yang–Parr correlation functional⁶⁷ (B3LYP/G) using the default 20% Hartree–Fock exchange. All atoms were treated with the 6-31G*(d,p) basis set,⁶⁸ and all computations were completed using a polarizable solvent dielectric field (ε = 10 D).^69,70 The size of the integration grid used in all cases was 5.

Single-point calculations on the converged geometries were performed with the hybrid functional B3LYP using Barone’s EPRII basis set⁷¹ on all atoms. EPR properties were computed using coupled-perturbed self-consistent field (CP-SCF) theory with the origin of the gauge dependence set at the center of electronic charge.⁷²

Results

Expression and Purification of F_nY-β2

F_nY-β2s were expressed from the pBAD-nrdB_122TAG and pEVOL-F_nYRS-E3 plasmids.¹⁰ The effect of the concentration of F_nY and media pH to optimize F_nY uptake into cells, and the induction time for protein production were examined in an effort to maximize the yield of each full length F_nY-β2. The optimized yields for (3,5) and (2,3,5)F₃Y-β2 were obtained with 0.5–0.7 mM F_nY, whereas for (2,3) and (2,3,6)F₃Y-β2, the concentrations were 1.5 mM. The pH had minimal effect in all cases and induction of F_nY-β2 at an OD₆₀₀ of 0.6 followed by 4–5 h of growth, proved optimal for protein expression.

Isolation of F_nY·-β2 with high yields of F_nY· required extensive experimentation and the results are summarized in Table S2. In the case of (2,3,5) and (2,3,6)F₃Y-β2 expression was carried out in the presence of 100 μM o-phenanthroline in the growth media prior to protein induction¹⁷ as well as inclusion of o-phenanthroline in the lysis buffer prior to purification of the apo protein. On the other hand, (3,5) and (2,3)F₂Y-β2 were expressed and purified in the holo form, with addition of ferrous ammonium sulfate to crude cell extracts. By this protocol, the concentrations of the (3,5) and (2,3)-F₂Y· were low and consequently, subsequent to purification, the iron was removed from these proteins with dithionite, MV and ferrozine.^73,74 In each case, the resulting apo protein was then reconstituted with 5 equiv of Fe^II and 3.5 equiv. O₂ (at 4 °C), the standard protocol for wt-β2.⁴⁴ Although the basis for the requirement for distinct optimization procedures remains unclear, in all cases the F_nY·-β2 had ∼3 Fe/β2 and ∼1 F_nY·/β2 (Table S2).

Stability of F_nY·’s and Evidence for Multiple Conformations of (2,3,6)F₃Y·

The stability of Y₁₂₂· in wt-β2 is ∼4 days at 25 °C,⁷⁵ whereas that of the nitrotyrosyl radical (NO₂Y·), a much stronger oxidant, was recently found to be only 40 s.³⁵ X-band EPR spectroscopy was used to assess the stability of F_nY· in each β2 at 20 s, 2.5 min, and 20 min subsequent to cluster assembly. No changes in the total spin or the spectrum appearance were observed for any of the F_nY·-β2s except for (2,3,6)F₃Y·-β2. In this case, 40% spin loss was observed by 2 min (0.7 F_nY·/β2).

To investigate the basis for this observation with one possibility being that the asymmetric fluorine distribution on the aromatic ring results in multiple (2,3,6)F₃Y· conformations during the protein folding process, the assembly of the diferric (2,3,6)F₃Y· was studied in more detail by RFQ-EPR spectroscopy (Figure S4). The spectra between 23 and 256 ms (Figure S4A–C) reveal that intermediate X, the Fe³⁺/Fe⁴⁺ core responsible for the oxidation of Y to Y·, is completely formed within 23 ms and that it had disappeared within 256 ms. The 256 ms time point showed 1.2 F₃Y·/β2 (Figure S4C), which decayed to 0.7 F₃Y·/β2 over the subsequent 60 s and then remained unchanged (Figure S4D). Our current model to explain this observation is that (2,3,6)F₃Y· exists in at least two distinct conformations generated during β2 folding. One gives rise to a rapidly decaying radical, whereas the other results in a radical that is substantially stabilized. All EPR data discussed subsequently were collected on the “stable” (2,3,6)F₃Y·. Although, we have not investigated the reconstitution of the other F_nY·-β2s by RFQ-EPR spectroscopy, no spin loss was observed with any of them up until 2–3 h after reconstitution or with multiple freeze–thaw cycles.

Steady-State Activity of F_nY·-β2s

Subsequent to optimization of [F_nY·] to 1 F_nY·/β2 for all F_nY·-β2, their activities were measured and the results are summarized in Table S2. All F_nY·-β2s are active with activities that vary between 5% to 85% of wt-β2 and that scale with radical concentration. The turnover number for (2,3,6)F₃Y·-β2 is measured for the “stable” radical, and even for this species, activity is lost as a function of time (50% loss within 2 min).⁷⁶ Thus, this β2 variant which has the largest reduction potential is, perhaps not surprisingly, the least stable, a result that parallels our observations with NO₂Y·-β2 (NO₂Y at position 122 in β2).³⁵

Structures of met-F_nY-β2 by X-ray Crystallography

All of the met-F_nY-β2s and met-wt-β2 proteins were crystallized under similar conditions at pH 8.0 at room temperature (∼23 °C). The overall structures show minimal perturbations relative to wt-β2 (Figure 2). The details of the refinement are described in the methods, and the results are summarized in Table S3. The resolutions of the structures vary from 2.0 to 2.5 Å. An important issue in the refinement process was that in three of the four F_nY’s, the fluorines are asymmetrical with respect to the aromatic ring and can thus potentially have multiple conformations resulting from a 180° rotation around the Cβ–Cγ bond of the aromatic ring. Our previous structural studies on NO₂Y-β2³⁵ showed a single conformation in which the NO₂ group resided on the side away from D84 and was embedded within the hydrophobic pocket composed of L₇₇, Q₈₀, I₁₂₅, N₂₂₇, I₂₃₁, and I₂₃₄ (Figure S5). In the case of all the F_nY-β2 structures, these residues adjacent to Fe1 are identical to wt-β2 and refined to an all-atom RMSD of ∼0.1 Å (Figure S5).

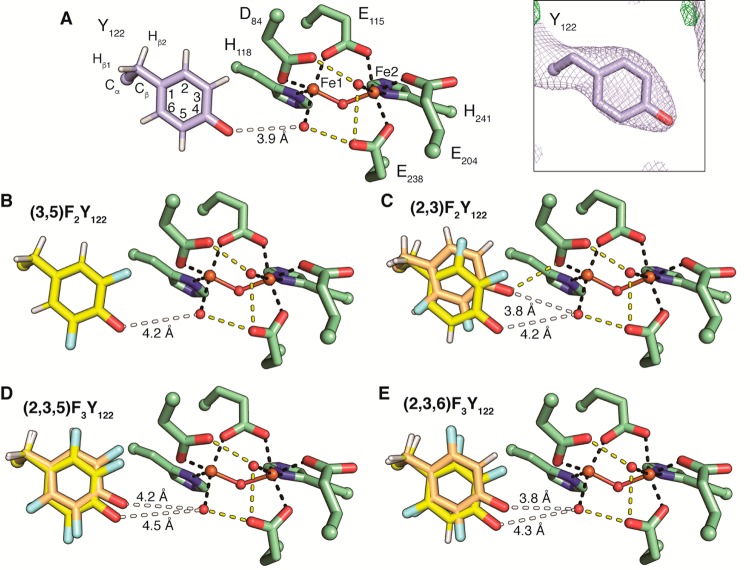
Figure 2.

Cofactor arrangement in F_nY-β2. (A) The structure of wild-type met-β2 contains a diferric cluster (Fe1 and Fe2, ball and stick) that coordinates two water molecules (red spheres). Iron ligation by protein residues (green) or water is represented by black dashes. Putative hydrogen bonds are shown as yellow dashes. Y₁₂₂ (light blue) is positioned adjacent to Fe₁, but not within hydrogen bonding distance (white dash). The electron density for Y₁₂₂ is shown inset (2F_o – F_c at 1 σ; green: F_o – F_c at 3 σ; red: F_o – F_c at −3 σ). (B–E) Each F_nY-β2 is shown as in (A). For (2,3)F₂Y, (2,3,5)F₃Y, and (2,3,6)F₃Y two conformations are present. The IN conformation (yellow) in each structure places the fluorine atoms on carbons 2 and 3 adjacent to D₈₄. The OUT conformation (orange) is flipped 180°. Analysis of the occupancy of these conformations (Figure S6) suggests the IN conformation is typically dominant.

Several additional features of the Fe1 in the cluster are thought to play an important role in active cofactor assembly and in initiation of radical transfer (RT) between the α and β subunits. Both D₈₄ and the water ligand to Fe1 may be involved in the redox chemistry of Y₁₂₂. In all the structures, D₈₄ in F_nY-β2 is almost identical to that in wt-β2 and is always monodentate; the distances for its two oxygens to the Fe1 are ∼2.0 and 2.8 Å. All structures also have one water molecule bound to Fe1. With wt-β2, this water has been shown to play a role in RT initiation.⁷⁷ The distance between the phenolic oxygen of Y₁₂₂ and the water in wt-β2 is 3.9 Å (Figure 2A). This distance is comparable to the 3.95/3.88 Å distance in PDB 1MXR,⁷⁸ a previously reported 1.42 Å resolution structure. In the initial structure (PDB 1R1B(79)) distances of 4.12/4.21 Å are reported. However, these structures contained Hg atoms in a number of positions that could alter the cofactor environment. As observed in Figure 2C–E, two conformations of the phenol ring in (2,3)-, (2,3,5)-, and (2,3,6)F₃Y-β2 are modeled to interact with the water with distances between 3.8 and 4.5 Å. Finally the iron occupancy in each site of the cluster appears complete, despite the fact that there are only 3–3.5 Fe/β2 measured biochemically.

The presence of different fluorine substitution patterns in each of the F_nY at position 122 as noted has given rise to multiple conformations of the aromatic ring relative to the Fe1 site. As will be discussed subsequently, published structures with 3-FY and 2-FY globally incorporated into different proteins show that the fluorine conformation(s) are protein environment-dependent and, in most cases, not predictable.⁸⁰ Multiple conformations of F_nY’s can arise either from complete flipping of the aromatic rings (a 180° rotation around the Cβ–Cγ bond of Y) or from a subtle shift in their positions. In the case of (2,3)-, (2,3,5)-, and (2,3,6)F₃Y-β2, the electron density cannot be modeled well by a single conformation of the aromatic ring but instead is more consistent with two conformations that differ by a 180° rotation around the Cβ–Cγ bond and a slight shift within the hydrophobic pocket (Figure S6). The precise ratio of these two conformations is uncertain due to the modest resolution of these structures, but refinement of a single conformation or complete omission of F_nY yields difference density clearly indicating a second conformation is present (Figure S6). In all cases, the favored conformation has two fluorine atoms packed against D₈₄, which we will now call the “IN” conformer. The alternate conformation, in which C₂ and C₃ fluorines are away from D₈₄, is accordingly denoted “OUT”.

Finally, the C-terminal tail (residues 340–375) of β2, which provides the interaction site between the α and β subunits, is disordered in all published β2 structures. Here all of the F_nY-β2 structures have an additional 9 residues (341–349) that are observed although they are moderately disordered (average B factors of ∼100–150 Ų) and have no specific, stabilizing contacts with the exterior of the protein. Residues 360–375 have been previously visualized in structures of the inactive α4β4 complex⁸¹ and in structures of α2 in complex with a 20-mer peptide corresponding to residues 355–375 of β2;³¹ these residues, however, are completely absent in wt-β2 and all F_nY-β2 structures.^79,82 Although observation of residues 341–349 is unprecedented, these residues are highly flexible in our current model and are likely to adopt a different conformation in the proposed α2β2 active conformation, as they would bridge the intersubunit interface.

Characterization of F_nY· by Multifrequency EPR and ENDOR Spectroscopies

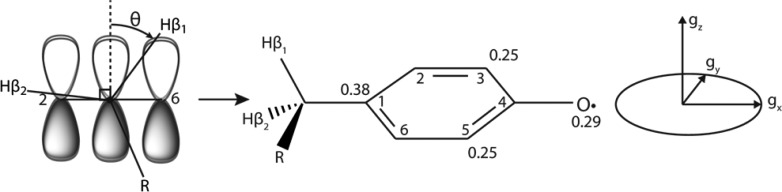
The magnetic properties of natural Y· have been shown to be sensitive reporters of the surrounding protein environment. For example, the magnitude of the g_x-shift (Figure 3, right) is correlated to the strength and number of hydrogen bonds to the phenoxy oxygen.^69,83 The hyperfine couplings of the ring protons report on the spin distribution about the π-system and the magnitude of the hyperfine couplings to the two β-methylene protons, which arise from their interaction with the π-electrons (Figure 3, left), can be interpreted to give the degree to which the Y ring is rotated relative to the peptide backbone.

Figure 3.

From left to right: Depiction of interaction between π-electrons and β protons as a function of angle θ (see discussion on McConnell relations); the numbering of tyrosine ring atoms and typical approximate spin densities at selected atoms in Y·, and the alignment of the g-tensor relative to the molecular frame for Y· and FY·.

Although EPR spectroscopy has previously been used to examine F_nY’s installed in both photosystem II⁷ and class Ia RNR,^8,10,17 a spectroscopically validated electronic structure description of these non-natural amino acid radicals has not yet been developed. To this end, we have produced RNRs with one of four different F_nY’s installed at position 122 of β2 and characterized the oxidized F_nY (F_nY·) using multifrequency EPR and orientation-selected pulsed ENDOR spectroscopies at high field (Figures 4, 6, 7, and S7–S10). We hope that the detailed analysis of these spectra will encourage the use of F_nY· as a redox-tunable radical probe for the local protein environment. In what follows, we will illustrate the process of interpreting these multiple data sets using the EPR and ENDOR spectra of (3,5)F₂Y·-β2 as an example.

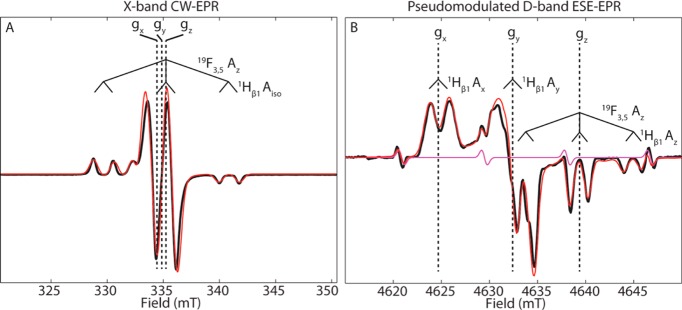
Figure 4.

X-band CW EPR (Panel A) and D-band Pseudomodulated ESE-EPR spectra (Panel B) and simulations of (3,5)F₂Y· in RNR β2. Field positions of g-tensor principle components are shown with vertical dotted lines. Resolved hyperfine splittings from ¹⁹F and ¹H are denoted with the solid angled brackets. Acquisition parameters: X-band CW EPR: Temperature = 80 K; MW Frequency = 9.395 GHz; MW Power = 317 μW; Modulation amplitude = 1.5 G; Modulation Frequency = 100 kHz; Conversion time = 50 ms. D-band ESE-EPR: Temperature = 30 K; MW Frequency = 129.996 GHz; π/2_MW = 37.5 ns; τ = 200 ns; shot rep time (srt) = 10 ms.

Figure 6.

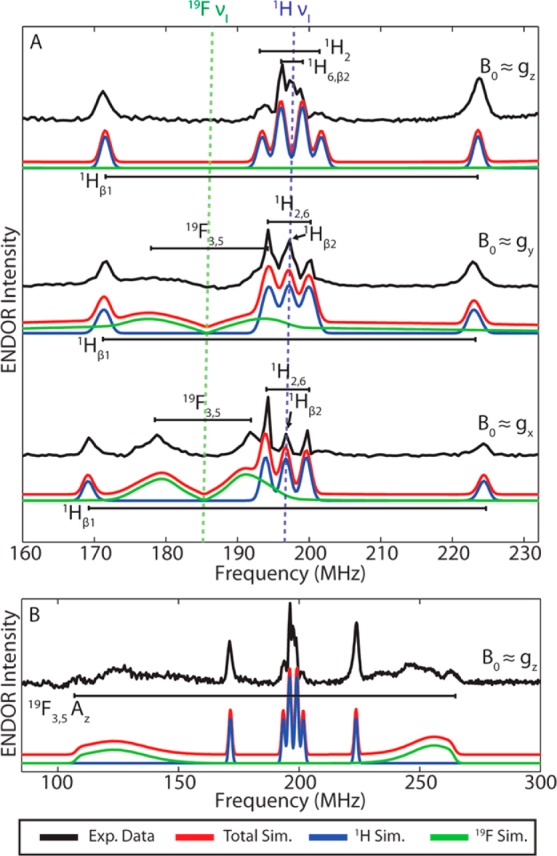
(A) Field-dependent D-band Davies ENDOR of (3,5)F₂Y· in RNR β2 in the frequency range from 160–233 MHz. Experimental data are shown in black, the total simulated spectrum is in red, and isolated contributions from ¹H and ¹⁹F nuclei are in blue and green, respectively. Resolved peaks and assigned nuclei are denoted with black brackets. (B) Full ENDOR spectrum acquired at B₀ ≈ g_z (4643 mT). Broad signal associated with the ¹⁹F_3,5A_z component is denoted with the black bracket below the experimental spectrum. Acquisition parameters: Temperature = 30 K; MW Frequency = 129.996 GHz; π/2_MW = 37.5 ns; π_RF = 24 μs; τ = 300 ns; shot rep time (srt) = 10 ms.

Figure 7.

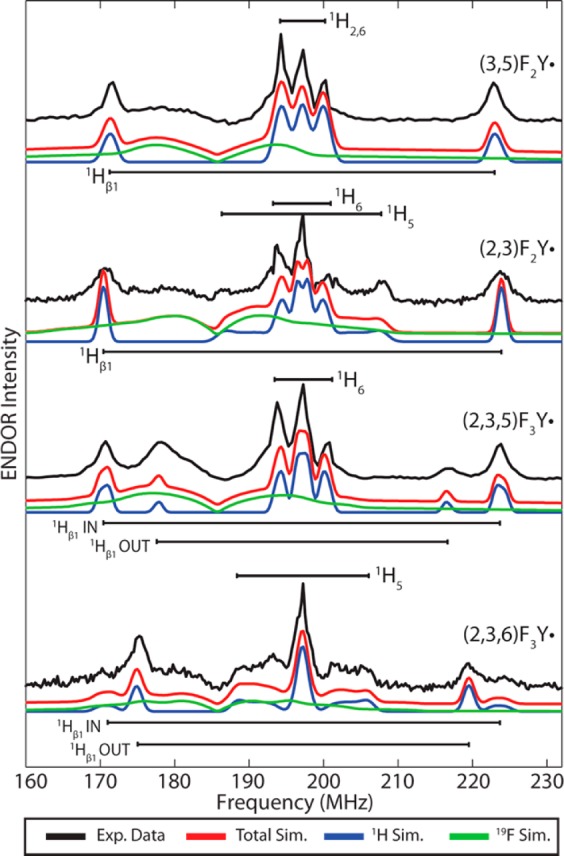
Comparison of D-band Davies ENDOR acquired at the spectral center (B₀ ≈ g_y) of each F_nY· in RNR β2. Experimental data are shown in black, total simulated spectrum is in red, and isolated contributions from ¹H and ¹⁹F nuclei are in blue and green, respectively. Resolved peaks and assigned nuclei are denoted with black brackets. Acquisition parameters: Temperature = 30 K; MW Frequency = 129.996 GHz; π/2_MW = 37.5 ns; π_RF = 24 μs; τ = 300 ns; shot rep time (srt) = 10 ms.

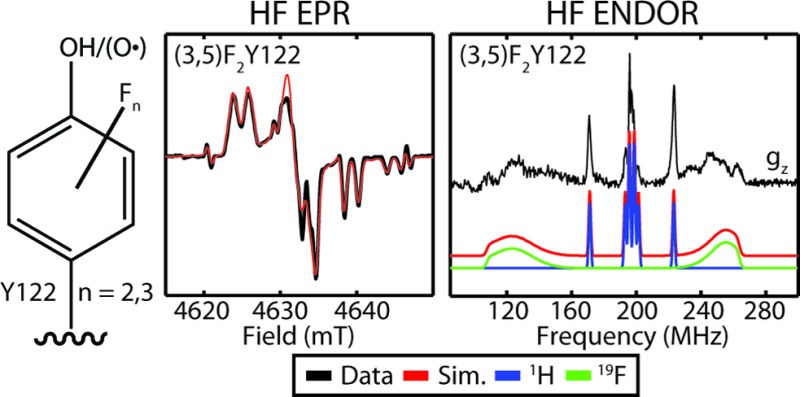
The EPR spectrum of (3,5)F₂Y·-β2 was acquired at both X-band (9.4 GHz) and D-band (130 GHz) excitation frequencies (Figures 4A and 4B, respectively). The multifrequency EPR spectra for all four F_nY·-β2s are presented in the SI (Figures S7–10). At the relatively low magnitude of the applied magnetic field (B₀ = 330 mT) at X-band, the g-anisotropy of (3,5)F₂Y·-β2 is not well resolved (see vertical dashed lines, Figure 4A). Instead, the spectral line shape is determined by the largest ¹H and ¹⁹F hyperfine interactions (Figure 5 and Table 1). In the case of (3,5)F₂Y·-β2, a splitting pattern composed of a triplet of doublets is observed (Figure 4). These doublets are caused by a ¹H hyperfine interaction that is relatively large and isotropic (A ≈ 53 MHz)—properties that preclude the signals from being assigned to the ring protons and point instead to a strongly coupled β-methylene proton, ¹H_β1, as the source (Figure 3 and Table 1). The triplet pattern results from the hyperfine interaction of the two nearly equivalently coupled ¹⁹F nuclei at the 3 and 5 positions. If the intensity pattern of the triplet were simply 1:2:1, this ratio would indicate that these hyperfine interactions are nearly isotropic. That the observed intensity pattern is closer to 1:6:1 is instead indicative of an axial hyperfine interaction in which the largest component (A_z) is approximately 157 MHz and the splittings along g_x and g_y are not resolved.

Figure 5.

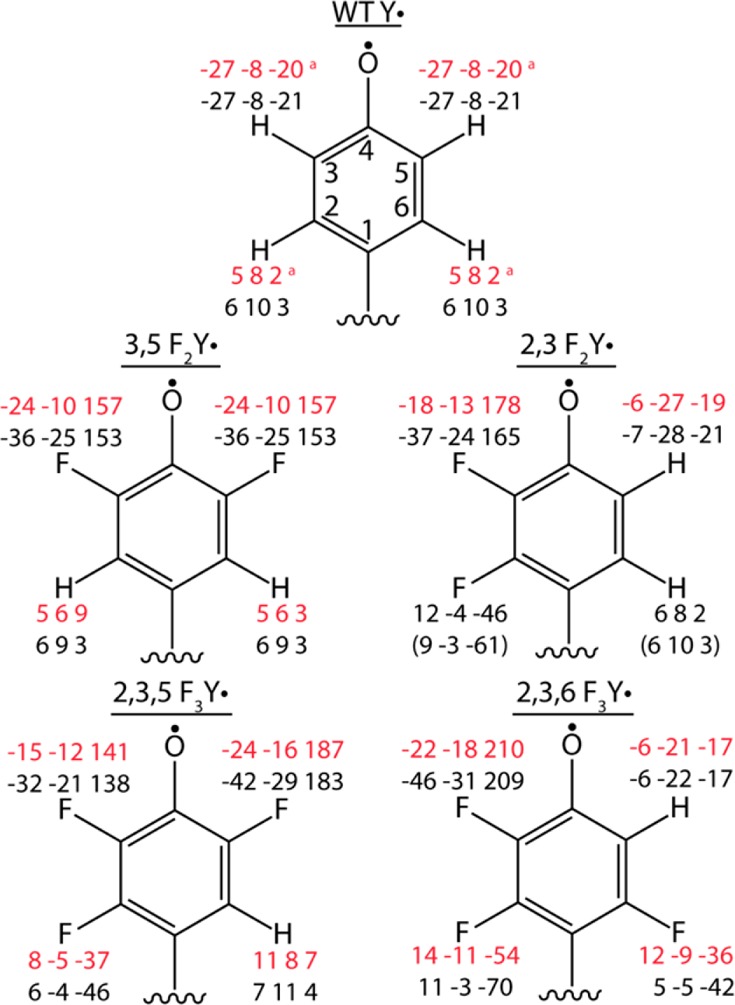
Hyperfine values (MHz) for ring atoms of Y₁₂₂· and F_nY₁₂₂·s. Values of each component of the hyperfine tensor are presented in order as A_x, A_y, A_z. Parameters determined from simulations of the combined EPR and ENDOR data for each position are presented on top in red, and the parameters from DFT calculations are presented on the bottom in black. Experimental values for WT Y· are from an ENDOR study by Hoganson et al.⁸⁴

Table 1. β-¹H Hyperfine Coupling and Geometric Parameters.

	A (MHz)
RNR β2 variant	Ax	Ay	Az	Aiso (MHz)	Relative abundance	ρC1c	1Hβ1 θ° from EPRc,e	1Hβ1 θ° from XRDd,e
wild type Y122 1Hβ1a	+59	+52	+55	56	1.00	0.387	19.0	15.8f
wild type Y122 1Hβ2b	+2.1	–5.0	–4.0	2.3
wild type Y122 1Hβ1 (this work)								11.9
(3,5)F2Y122 1Hβ1	+56	+50	+52	53	1.00	0.370	20.3	19.7
(3,5)F2Y122 1Hβ2	–0.5	–0.5	+3	1.7
(2,3)F2Y122 1Hβ1 INg	+56	+53	+53	54.3	1.00g	0.388	21.7	17.2
(2,3)F2Y122 1Hβ2 IN	+1	+1	+2	1.3
(2,3,5)F3Y122 1Hβ1 IN	+57	+51	+54	54	0.80	0.386	21.7	14.0
(2,3,5)F3Y122 1Hβ2 IN	+0.5	+0.5	+3	1.3
(2,3,5)F3Y122 1Hβ1 OUT	+43	+38	+38	39.7	0.20	0.357	34.1	29.9
(2,3,5)F3Y122 1Hβ2 OUT	–0.5	–0.5	+2	0.3
(2,3,6)F3Y122 1Hβ1 IN	+52	+50	+56	53	0.25	0.372	20.3	20.1
(2,3,6)F3Y122 1Hβ2 IN	+1	+1	+3	1.7
(2,3,6)F3Y122 1Hβ1 OUT	+48	+44	+44	45.3	0.75	0.360	28.2	21.6
(2,3,6)F3Y122 1Hβ2 OUT	–0.5	+0.5	+0.3	0.1

^aHFI parameters from Hogbom et al.⁷⁸

^bHFI parameters from Hoganson et al.⁸⁴

^cComputed using TRSSA with B″ = 162 MHz (Svistunenko et al.).⁸⁵

^dX-ray diffraction (XRD) angles measured manually in PyMOL after addition of hydrogen atoms.

^eThe IN and OUT conformations differ by an approximate 180° rotation of the tyrosine ring about C_β–C_α; here we report the reduced angles (e.g., for θ > 180°, subtract 180°).

^fFrom PDB 1MXR.⁷⁸

^gNo signal attributable to the OUT conformation was observed.

By going to a much higher applied field using our 130 GHz spectrometer (ca. 4630 mT), the g-anisotropy becomes apparent (see vertical dashed lines in Figure 4B and g-values in Table 2). The strong nuclear hyperfine interactions of ¹H_β1, 3-¹⁹F, and 5-¹⁹F still contribute to the spectrum, and we observe that the largest component of the two ¹⁹F hyperfine tensors is aligned along g_z (ca. 4639 mT), where the familiar triplet of doublets splitting pattern from the two equivalent ¹⁹F nuclei and ¹H_β1 is centered. Again, along g_x (ca. 4625 mT), only a single splitting arising from the isotropically coupled ¹H_β1 is resolved.

Table 2. g-Values for Y₁₂₂•.

RNR β2 or DFT phenoxyl variant	gx	gy	gz
wild typea	2.00912	2.00454	2.00219
DFT Phen	2.00864	2.00465	2.00221
(3,5)F2Y	2.00828	2.00500	2.00196
DFT (3,5)F2-Phen	2.00803	2.00538	2.00212
(2,3)F2Y	2.00850	2.00465	2.00205
DFT (2,3)F2-Phen	2.00817	2.00494	2.00218
(2,3,5)F3Y	2.00820	2.00510	2.00205
DFT (2,3,5)F3-Phen	2.00788	2.00534	2.00213
(2,3,6)F3Y	2.00844	2.00470	2.00210
DFT (2,3,6)F3-Phen	2.00810	2.00489	2.00218

^aFrom Hoganson et al.⁸⁴

Thus, far, with just these two multifrequency EPR spectra, the molecular g-values can be determined from the high-field D-band spectrum and the largest components of ¹⁹F and ¹H hyperfine tensors can be estimated, first by inspection of both spectra in Figure 4, then refined by performing least-squares optimization of simulations of the X and D-band EPR data. However, ENDOR spectroscopy is necessary to determine the smaller hyperfine couplings of the ¹⁹F tensors and those from the ring protons at the 2 and 6 positions as the corresponding hyperfine splittings are lost in the inhomogeneously broadened lines of the field-swept EPR spectrum. High-field ENDOR at 130 GHz is particularly helpful in identifying the smaller couplings arising from ¹H vs ¹⁹F because their respective nuclear Larmor frequencies, and thus the center of their respective ENDOR spectra, are separated by a much greater extent (¹H ν_I = 197 MHz, ¹⁹F ν_I = 186 MHz) than at X-band (¹H ν_I = 14.3 MHz, ¹⁹F ν_I = 13.4 MHz) or Q-band (¹H ν_I = 51.6 MHz, ¹⁹F ν_I = 48.6 MHz).

Again returning to our exemplar data for the symmetrically fluorinated (3,5)F₂Y·-β2 sample, we show in Figure 6A the central region (i.e., within ±40 MHz of the ¹H Larmor frequency) of the ENDOR spectra collected at three field positions across the EPR envelope. At 130 GHz/4630 mT, all hyperfine interactions for these radicals fall within the weak coupling limit (|ν_I| > |A|/2), meaning that each individual nuclear coupling can be expected to produce an ENDOR spectrum that consists of a pair of peaks centered about |ν_I| and split by |A|. Because the individual g-values are resolved at these high fields (Figure 4B), changing the field at which the ENDOR experiment is performed allows us to select only a subset of possible orientations of the F₂Y·, allowing for unambiguous determination of the principal components (e.g., A_x, A_y, A_z) of each hyperfine tensor. From these data, the smaller couplings from ¹H’s at the 2 and 6 positions as well as the second, more weakly coupled β-methylene proton (¹H_β2) can be determined (Figure 6A), with assignments guided by comparison to DFT-predicted values for a simplified (3,5)F₂-phenoxy radical model (Figure 5). A modest asymmetry in the intensity of the ¹H ENDOR patterns likely arises from a combination of hyperfine enhancement^86,87 (for the more strongly coupled protons) and a small amount of saturation of the ENDOR transitions.⁸⁸ The complete ENDOR spectrum (100–300 MHz) for the g_z component is shown in Figure 6B. This spectrum reveals that the ¹⁹F hyperfine interactions from the fluorines at positions 3 and 5 are extremely large (157 MHz) and broad. Thus, by combining analysis of the multifrequency EPR spectra, high-field (HF), orientation-selected ENDOR, and insights from DFT calculations, all relevant magnetic couplings and g-tensor elements can be rigorously assigned. This same methodology was used for evaluating the other three asymmetric F_nY·-β2 radicals and the combined X-band, D-band and D-band ENDOR data sets with simulations can be found in the SI in Figures S7–S10.

The parameters obtained from the simulations of the multifrequency EPR data reveal a great deal of information on the electronic structure of each F_nY·-β2 variant through changes in the g-tensor and hyperfine couplings at each ring position, as well as yielding structural information regarding the rotational orientation of the Y side chain through the hyperfine coupling from the protons on the β carbon. Each of these matters will be discussed in turn.

g-Tensor Analysis

Analysis of the g-tensors for each radical (Table 2) reveals that the g_x values of all of the F_nY·-β2s are very similar to each other (2.0082–2.0085) though rather different from the g_x value of the wt-β2 (2.00912) previously determined by Hoganson et al.⁸⁴ In the case of wt-β2, the g_x element of the g-tensor is aligned along the C–O bond of Y· (Figure 3) and its value is often invoked as a measure of the strength of hydrogen bonding or a sensor of the electrostatic environment of the O of the phenoxy group.⁸³ All of the F_nY·-β2s exhibit smaller g_x values than wt-β2 that could be indicative of differences in their electrostatic environments. However, the DFT-predicted magnetic parameters using fluorinated phenoxyl radicals indicate that O4 has moderately reduced spin populations compared to those for the nonfluorinated Y (Table 3), which would also affect g_x.⁶⁹ In contrast to g_x and g_z, the addition of fluorines appears to have a larger effect on the value of g_y, a trend also predicted by DFT (Table 2). Importantly, the orientation of the predicted g-tensor relative to the molecular frame is conserved in all cases, even with the asymmetrical F_nY’s. Despite the strong electronegativity of fluorine, the changes in the spin density distribution remain roughly symmetrical about the C2 rotational axis of the phenoxyl ring; thus, g_x remains aligned along the C–O bond and g_z is oriented orthogonal to the plane of the ring (Figure 3).

Table 3. Computed Total Mulliken Spin Populations for Fluorotyrosine Models.

model	C1	C2	H/F2	C3	H/F3	O4	C5	H/F5	C6	H/F6
Phen	0.374	–0.119	0.005	0.262	–0.013	0.362	0.261	–0.013	–0.119	0.005
(3,5)F2-Phen	0.338	–0.109	0.004	0.231	0.019	0.357	0.230	0.019	–0.109	0.004
(2,3)F2-Phen	0.362	–0.114	–0.004	0.244	0.021	0.359	0.258	–0.013	–0.117	0.005
(2,3,5)F3-Phen	0.346	–0.089	–0.003	0.201	0.017	0.354	0.268	0.023	–0.131	0.005
(2,3,6)F3-Phen	0.368	–0.135	–0.005	0.299	0.027	0.351	0.200	–0.010	–0.085	–0.002

Ring Atom Hyperfine Tensors

For each F_nY·-β2, the hyperfine tensors for each of the ring protons and fluorine nuclei (Figure 5) were determined primarily by fitting the field-dependent D-band ENDOR spectra (Figure 7). The exceptions were the A_z components of the ¹⁹F hyperfine tensors of positions 3 and 5 which were constrained by large splittings observed in the X- and D-band EPR (Figure 4). The fit was of particular importance for determination of the magnitude of the smaller ¹H and ¹⁹F couplings at the 2 and 6 positions, which have only minor effects on the appearance of the field-swept EPR spectra. In addition, results from the orientation-selected ENDOR experiments allowed the small elements of the hyperfine tensors for the strongly coupled but highly anisotropic nuclei to also be determined. Comparison of the ENDOR spectra of each radical acquired at the center of each spectrum reveals substantial differences (Figure 7). Though the magnitude of the largest element of the most strongly coupled ¹⁹F nucleus was not as well resolved in the ENDOR spectrum for all of the F_nY·’s examined due to the considerable breadth of this ENDOR feature, this parameter is constrained by the span of the X-band CW spectrum for each variant (Panel A of Figures S7–S10). The ¹⁹F hyperfine tensors, particularly in the 3 and 5 positions, show strong, axial anisotropy due to the unpaired spin contained in the fluorine 2p_z orbital. This value is estimated by DFT to be up to 2% to 3% for fluorine in the 3 or 5 position and 0.3% to 0.8% for fluorine in the 2 or 6 position.

In the case of (3,5)F₂Y·-β2, the only symmetric F_nY we studied, the two ¹⁹F hyperfine tensors are essentially identical (Figure 5). This result suggests that any differences in the protein environment near F3 and F5 are either small or do not influence the magnetic properties. However, to best fit the weaker ¹H couplings required slightly different tensors for H2 and H6. These differences in this symmetric F_nY may be due to the rotation of the side chain about the β-carbon, as this rotation has been shown to have modest effects on the hyperfine couplings of ring protons in Y models in a previous DFT study.⁶⁹

When the symmetric (3,5)F₂Y·-β2 is compared to the asymmetric F_nY·’s, the A_z of the most strongly coupled ¹⁹F displays an upward trend in magnitude between variants, with (3,5)F₂Y· < (2,3)F₂Y· < (2,3,5)F₃Y· < (2,3,6)F₃Y· (Figure 5). For (2,3)F₂Y· and (2,3,6)F₃Y·, the ¹⁹F at the 3 position is predicted to exhibit the largest coupling, while in (2,3,5)F₃Y· the largest ¹⁹F coupling is predicted to occur at the 5 position. This trend in the magnitude of the ¹⁹F HFI for each variant is matched by estimations of the Mulliken spin populations for F atoms at these positions, as well as for the adjacent spin-carrying C3 and C5 atoms by DFT (Table 3). The changes in spin localization about the tyrosine ring that are reflected in the experimentally observed ¹⁹F and ¹H couplings and calculated spin populations on the ring atoms are primarily caused by inductive effects of the electron-withdrawing, highly electronegative fluorine atoms.

The sign and magnitude of the ring atom hyperfine tensors for each F_nY· are qualitatively predicted by DFT calculations (Figure 5), although the anisotropy of all ¹⁹F tensors appear to be slightly overestimated, thus precluding quantitative accuracy compared to the experimental results. DFT calculations predict that A_x and A_y for ¹⁹F at the 3 and 5 position are negative, but A_z is positive, which is consistent with the simulations of the D-band EPR and ENDOR when the Davies suppression hole is included as A → 0.⁶³

For each ring ¹⁹F or ¹H atom, the relative orientation of the coordinate system of the nuclear hyperfine tensor A to the molecular g-tensor must also be considered, as related by the Euler rotation angles α, β, and γ. DFT calculations predict that the A tensors for each ring atom for all F_nY· variants are rotated by angle α about the ring plane normal (corresponding to g_z) such that A_x is aligned approximately along the chemical bond vector, with minor deviations not exceeding 15° (Table 4), with no appreciable rotations about g_x or g_y. The α angles predicted by DFT were used in our simulations of the multifrequency EPR and HF ENDOR for each variant and appear to be in excellent agreement with the experimental data.

Table 4. Estimated Euler Angles (α,β,γ)° between A Tensors and g Tensor for Ring Atoms of RNR F_nY-β2 Radicals.

RNR β2	2	3	5	6
(3,5)F2Y	(−130, 0, 0)	(−55, 0, 0)	(55, 0, 0)	(130, 0, 0)
(2,3)F2Y	(−120, 0, 0)	(−58, 0, 0)	(65, 0, 0)	(135, 0, 0)
(2,3,5)F3Y	(−120, 0, 0)	(−58, 0, 0)	(58, 0, 0)	(125, 0, 0)
(2,3,6)F3Y	(−120, 0, 0)	(−58, 0, 0)	(65, 0, 0)	(120, 0, 0)

β-Proton Hyperfine Couplings

In addition to hyperfine couplings arising from the ring ¹H and ¹⁹F nuclei, we also observe relatively large isotropic proton couplings of approximately 45–55 MHz (Table 1), as well as very small isotropic couplings of less than 3 MHz which reside near the ¹H Larmor frequency (ν_n ≈ 197 MHz at 4634 mT, Figures 6–7). These isotropic proton couplings arise from the two unequivalent protons of C_β (Figure 3). The magnitude of these couplings is dependent on the degree of hyperconjugation of the C_β–H bonding orbital with the π-system of the aromatic ring (see Figure 3) as a function of the dihedral angle θ between the C_β–H bond and the normal vector of the Y ring plane. This interaction is maximized when the C_β–H bond is aligned perpendicular to the Y ring plane such that the dihedral angle θ = 0 and is minimized when this bond is parallel to the ring plane. The observed A_iso for each β proton can be mathematically correlated to the dihedral angle between the C_β–H bond and the vector normal to the ring plane using the McConnell relations:⁸⁹

2

Here A_β1 and A_β2 are the isotropic hyperfine couplings of the two respective β ¹H nuclei, ρ_C1 is the spin density on the C1 atom, and B″ is a constant (B″ = 162 MHz).^85,90 This relationship allows for facile estimation of both the spin density on ρ_C1 and θ through the use of the Tyrosyl Radical Spectral Simulation Algorithm (TRSSA) developed by Svistunenko and Cooper.⁸⁵ This analysis has been utilized to estimate these parameters for each of the F_nY· variants examined here (Table 1), with comparison to the θ calculated for each F_nY· refined in the XRD data.

For the symmetric (3,5)F₂Y·, only a single large β¹H coupling with A_iso = 53 MHz is clearly resolved. This value is near the maximum of the theoretical limit for a ¹H_β1 coupling where ρ_C1 is in the range 0.35–0.42 that is typically observed for Y·;⁸⁵ thus we assign the very small isotropic coupling observed with A_iso = 1.7 to the other β proton, ¹H_β2. Using these values, TRSSA analysis indicates a dihedral angle for ¹H_β1 of 20.3°, which is in excellent agreement with the modeled orientation from the XRD of 19.7° (Table 1). The presence of only a single strong β ¹H coupling is indicative of the presence of a single, conserved rotational orientation of the Y side chain within all proteins in the sample, which is also consistent with the refined position of (3,5)F₂Y in the X-ray structure presented here. Though the ρ_C1 value of 0.387 obtained from this analysis is higher than the Mulliken spin population estimate of 0.338 from DFT (Table 3), it should be noted that the DFT models are simplified phenoxy radicals with only protons on C_β and, thus, would not exhibit effects from the rotation of the carbon relative to the ring plane that may affect ρ_C1.⁶⁹

For each of the asymmetric F_nY·’s, there is also at least one clearly resolved large isotropic ¹H coupling assigned to a β-¹H. For the (2,3)F₂Y·, there appears to be only a single large β-¹H coupling with an A_iso of 54.3 MHz, with a paired weakly coupled β-¹H with A_iso = 1.7 MHz, indicating a θ of 21.7° for ¹H_β1, which is very similar to the (3,5)F₂Y·. This result is consistent with the X-ray refinement of (2,3)F₂Y, in which the IN conformer, with the fluorines of C₂ and C₃ packed against the side chain of D₈₄, predominates (Figure S6).

Interestingly, for (2,3,5)F₃Y· and (2,3,6)F₃Y·, two distinct large isotropic couplings are clearly resolved with different relative spectral intensities (Figure 7, Figures S9C and S10C). Here, the high-field ENDOR is invaluable in identifying these distinct couplings, as in the X-band CW and D-band EPR spectra the inhomogeneous line broadening largely obscures these subtleties. In both cases, these two values are too large to represent the two β protons of a single orientation of F₃Y· due to the constraints imposed from the McConnell relations described above. Rather, these couplings must arise from two distinct, conserved populations of rotational conformers of F₃Y· with different ¹H_β1 dihedral angles, each with their own associated weakly coupled ¹H_β2 (Table 1). By using weighted multicomponent simulations of these two subpopulations, where all g-values and nuclear couplings were held fixed except the ¹H_β1 values, a rough estimate of the relative abundance of each conformer was achieved by comparison to the observed spectral intensity of these strongly coupled β-¹H peaks in the D-band ENDOR (Figures S9C and S10C). The weighting of the two individual components was optimized to fit the experimental data and yielded the estimates of the relative abundance of each conformation presented in Table 1. As the IN conformation observed by XRD displayed a smaller ¹H_β1 θ, we assigned this conformation to the larger ¹H_β1 coupling according to the McConnell relation described above. Likewise, the smaller ¹H_β1 coupling is produced by the OUT conformation. Interestingly, the proportions of these rotational conformers seem to be reversed between these two F₃Y· variants, with the IN conformation exhibiting the larger ¹H_β1 coupling being dominant (0.80) in (2,3,5)F₃Y·, whereas the OUT conformation exhibiting the smaller ¹H_β1 coupling is more abundant in (2,3,6)F₃Y· (0.75). While the crystal structures also indicate the presence of two conformations for both (2,3,5) and (2,3,6)F₃Y side chains, the favored one in both cases has the fluorines at positions 2 and 3 pointing toward D₈₄ (the “IN” position). These differences may be due to the fast-decaying component observed for (2,3,6)F₃Y· by RFQ-EPR during cluster assembly (Figure S4). As described in the Materials and Methods, the (2,3,6)F₃Y·-β2 samples used for the EPR analysis in this paper were aged for 2 min to represent the “stable” (2,3,6)F₃Y·. The apparent change in the relative abundance of the IN and OUT conformations of (2,3,6)F₃Y· relative to that of the reduced (2,3,6)F₃Y present in the crystal structure may indicate that the IN conformation corresponds to this rapidly decaying population observed by RFQ-EPR.

Discussion

F_nY’s have long been used to study protein structure and function, as they perturb the electronic properties of Y, while minimally perturbing its size (van der Waals radius of F is 1.42 Å compared to 1.27 Å for H). Global incorporation of FY and site-specific incorporation of F_nY by expressed protein ligation (EPL) have been the most widely used methods.⁹¹ In the former case, a Y auxotroph is grown with 2- or 3-FY in medium that is depleted of Y. Thus, all Y’s in the protein of interest are replaced by the Y analog. Efforts to incorporate F_nY with n > 1 by this method, however, typically result in lower incorporation efficiency.⁹² In the case of EPL, site-specific incorporation of F_nY involves ligation of a chemically synthesized peptide containing F_nY with a recombinantly expressed protein to generate the intact mutant protein. In this case, only a designated Y is replaced with F_nY (n = 2, 3, or 4). The EPL method is limited, as the residue of interest must be synthetically accessible and, hence, localized to either the C- or N-terminus of the protein.^93,94 However, EPL can be mechanistically informative when the F_nY properties are compared to each other, as the pK_a of F_nY’s range from 5.6 to 10.0⁹⁵ and their reduction potentials cover a range of 300 mV.⁸ The incorporation of these analogs has provided investigators with the tools to study the mechanisms of phosphorylation of Y in a peptide and of proteins by tyrosine kinases,^6,95 the importance of H-bonding networks, and pK_a perturbation within these networks in ketosteroid isomerase⁵ and to study PCET in the oxygen evolving complex as a function of pH.⁷

Recently, Li et al.¹¹ and Minnihan et al.¹⁰ have used a third method to site-specifically incorporate F_nY analogs, the amber suppressor method developed by Peter Schultz that utilizes an evolved, orthogonal tRNA/RS pair.⁹⁶ In the former case, the method has been used to study the oxidase activity of an engineered myoglobin model of cytochrome oxidase proposed to involve a transient Y· intermediate.^97,98 In the latter case, the unique properties of the E. coli RNR system to self-assemble the active diferric-F_nY· cofactor from diferrous-F_nY, O₂, and reducing equivalents⁹⁹ have allowed investigation of Y· equilibration and assessment of the thermodynamic landscape of the RT pathway (Figure S1).³⁶ The crystallographic and multifrequency EPR and HF ENDOR spectroscopic studies reported in this paper have allowed characterization of the ground state and oxidized state of F_nY within the protein environment providing a benchmark for other protein systems.

We have successfully incorporated F_nY in place of all four Y’s in the RT pathway (Figure S1).⁷⁶ The unique positioning of Y₁₂₂, adjacent to the diiron cluster in β2, allows generation of F_nY₁₂₂· and investigation of their spectroscopic properties (Figures 4, 6, 7, and S7–S10). The ¹⁹F nucleus provides distinct features in the low- and high-field regions of the EPR spectra relative to Y·. Simulation of these EPR spectra is critical to the deconvolution of spectra involving multiple Y·’s, as the features of most Y·’s are narrow and superimposable. Our ability to site-specifically incorporate (3,5)F₂Y in place of Y₇₃₁ or Y₇₃₀ of α2 has allowed detection of radical equilibration between the three transient Y·’s in the RT pathway between the two RNR subunits.³⁶ When NO₂Y·-β2 is incubated with α2, CDP, and ATP (effector), the Y₃₅₆· is generated concomitant with reduction of NO₂Y· to NO₂Y phenolate (NO₂Y¯). The inability of Y₃₅₆· to reoxidize NO₂Y¯ to NO₂Y· allows Y₃₅₆· to equilibrate with the pathway Y’s in α2. Unfortunately, this equilibration cannot be observed due to substantial overlap in the EPR spectra of Y₃₅₆·, Y₇₃₁·, and Y₇₃₀·. When the experiment was repeated with (3,5)F₂Y₇₃₁- or (3,5)F₂Y₇₃₀-α2, the unique ¹⁹F hyperfine features allowed observation and quantitation of Y₃₅₆· and (3,5)F₂Y· demonstrating, for the first time, the equilibration between the pathway Y’s. Although the majority of the spin was localized to either Y₃₅₆· or NO₂Y· (>85%), we were able to detect (3,5)F₂Y· at each position.

A second example of the usefulness of the method was recently demonstrated with the myoglobin system engineered to model cytochrome c oxidase. In studies of O₂ reduction, an EPR active species was observed, postulated to be a Y·.¹⁰⁰ Site-specific incorporation of (3,5)F₂Y in place of Y allowed unambiguous assignment of the new radical based on the observation of the ¹⁹F hyperfine interactions.⁹⁸ Furthermore, site-specific incorporation of several Y analogs with altered pK_a’s and reduction potentials provided insight into the mechanism of the model oxidase. Interpretation of these results, however, requires an understanding of the perturbation of the pK_a’s and reduction potential of each UAA within the protein environment as well as an understanding of the rate-limiting steps in the overall reaction.⁹⁸

Recently, Liu et al. reported the design of a genetically encoded photoinduced electron transfer (PET) sensor starting with a flavoprotein iLovU optimized for its fluorescence properties by engineering of a Y adjacent to the FMN binding site.¹² F_nY and Cl_nY were incorporated in place of Y as their lowered pK_a’s allowed them to function as excellent PET quenchers relative to Y. The charge neutral (i.e protonated) F_nY and Cl_nY are not efficient PET donors, and the sensor iLovU is in the fluorescence ON state. The deprotonated F_nY and Cl_nY are much more rapidly oxidized than the neutral phenols and are better PET donors. Similar to protonation, the Y· state results in a reduction in the PET rate, turning on fluorescence. Liu et al. successfully evolved tRNA/RS pairs to each of the Y analogs. PET from Cl₂Y to the FMN of iLovU was supported by detection of Cl₂Y·. The authors also described several interesting examples for the use of this PET sensor.

In addition to covering a range of reduction potentials, F_nY’s also offer a range of pK_a’s that can be mechanistically informative. By replacing each of the pathway Y’s in RNR with NO₂Y and by taking advantage of the visible properties of the NO₂Y¯, we have previously shown that the pK_a is minimally perturbed at Y₃₅₆, Y₇₃₁, and Y₇₃₀, whereas it is shifted >3 units at Y₁₂₂ (Figure S1).⁴² Given that Y oxidation requires loss of a proton and an electron, the protein environment plays a very important role in this process. If reversible redox chemistry is occurring at a specific Y, it is not clear with the F_nY analogs what the fate of the proton will be subsequent to oxidation. In the case of NO₂Y·-β2 the phenol in the resting state is protonated. The cofactor assembly process generates the NO₂Y· that then initiates RT into the active site. Initiation of RT with NO₂Y·, however, generates the phenolate and not the phenol,³⁵ in contrast with Y₁₂₂.⁷⁷ During reverse RT, Y₃₅₆· cannot reoxidize the phenolate, and thus, NO₂Y·-β2 only catalyzes one turnover. Radical initiation with (2,3,5)F₃Y·-β2 catalyzes multiple turnovers;^10,17 however, it is not known if this radical gets transiently reduced to the phenolate or the phenol. A method to measure the pK_a’s of the F_nY’s in the different environments and linking this information to the mechanism is thus important. This conclusion will definitely be protein environment dependent, and one cannot assume that the pK_a of the analog is not perturbed.^7,98

From our studies, a number of issues may be encountered when using this site-specific incorporation methodology especially if 100 mg quantities of homogeneous protein are required for mechanistic studies. We have had experience with F_nY incorporation at positions 122 and 356 within β2 of RNR and at positions 731 and 730 within α2.^16,76 We have also incorporated F_nY into a small three helix bundle protein (α3X, 65 amino acid) containing a single buried Y that we have used to measure the reduction potentials of F_nY·’s.³⁷ In general, incorporation of the same Y analog into a different position and into distinct proteins requires optimization. The vectors used, the timing of induction of the tRNA and RS expression relative to the expression of the protein of interest, and the growth conditions, all need careful study. The timing of addition of F_nY to the growth media and uptake into the cell also need optimization. In our hands, the purification of the proteins can also be challenging. In all cases one obtains truncated and full-length proteins that must be separated, the relative amounts of which depend on the level of suppression. In addition, in the case of proteins that are multimeric, β2 in our case, full length and truncated hetero- and homodimers are obtained. Their separation depends on charge and size and may require considerable effort or, in the worst-case scenario, may not be successful. Finally, in the case of F_nY-β2s, assembly of the active cofactor also required optimization with different protocols for each β2.

Our evolved F_nY tRNR/RS is polyspecific, and thus a single tRNA/RS pair could be used to incorporate all of the F_nY’s. We note that F₄Y is missing from the incorporated analogs (Figure 1). In our hands the suppression levels were poor, we think as a consequence of the inability of the predominant anionic form (pK_a 5.6) to cross the membrane, resulting in low concentrations inside the cell and consequently poor suppression efficiency. Although an engineered myoglobin containing F₄Y was presented in the recent paper of Liu et al.,¹² SDS-PAGE gels in the SI show poor expression of the full-length protein (i.e., low suppression efficiency).

A second issue that requires comment is that both our crystallographic analyses and the EPR simulations require that some of the F_nY analogs exist in multiple conformations at position 122 in β2. An examination of 28 crystallographically distinct glutathione S-transferase structures containing globally incorporated 3-FY⁸⁰ reveal that, even with this minimal perturbation, multiple conformations are observed in distinct sites. From these studies, no generalizations about conformational expectations were possible.⁸⁰ Since multiple F_nY conformations can give rise to mechanistic complexity, this possibility is important to consider in any kinetic analyses.

An additional possibility that we considered is that the aromatic ring of the F_nY’s can flip within the protein environment. Our structures, however, reveal that F_nY’s at position 122 fit snugly in a very hydrophobic cavity. Flipping would require a sizable activation volume as well as coordinated movement of these hydrophobic residues, which seems unlikely given the structures shown in Figure S5. Only recently have rate constants for aromatic ring dynamics within different environments been measured using ¹³C relaxation dispersion measurements.^101,102 Thus, we cannot say whether the two conformations that we observe of these side chains were established during protein folding or if they represent a slow flipping process that occurs after protein folding is complete.

Conclusions

This paper provides new tools to investigate the mechanistic role of proposed Y·’s in catalysis. A growing list of proteins including photosystem II,¹⁹ cytochrome oxidase²² that catalyzes the reduction of O₂ to water, prostaglandin synthase,⁵⁴ the target of nonsteroidal anti-inflammatory agents, DNA repair photolyases,¹⁸ and fatty acid oxidases¹⁰³ utilize Y·’s in their mechanisms. In addition, Y·’s have been proposed to be involved in the repair of off pathway oxidations with oxidoreductases having increased levels of Y’s and W’s adjacent to the metallo-cofactor site.^{25,26,104,105} The tools described in this paper may be useful in unraveling the mechanisms of these systems and other enzymes that have yet to be discovered.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b03605.

• Reconstitution of the diferric-(2,3,6)F₃Y· cofactor at 25 °C monitored by RFQ-EPR spectroscopy; components of the modified bridge transmitter (Table S1); specific activity of F_nY·-β2 as determined by spectrophotometric and radioactive assays for nucleotide reduction (Table S2); data collection and model statistics for wt and F_nY-β2 variants (Table S3); Cartesian coordinates (Å) for geometry optimized Model of phenoxyl radical (Table S4); Cartesian coordinates (Å) for geometry optimized model of (2,3)F₂Y· (Table S5); Cartesian coordinates (Å) for geometry optimized model of (3,5)F₂Y· (Table S6); Cartesian coordinates (Å) for geometry optimized model of (2,3,5)F₃Y· (Table S7); Cartesian coordinates (Å) for geometry optimized model of (2,3,6)F₃Y· (Table S8); Hyperfine values (MHz) for ring atoms of Y₁₂₂· (Table S9); PCET pathway in E. coli class Ia RNR (Figure S1); block diagram of the modified and upgraded 130 GHz transmitter section of the original Krymov microwave bridge (Figure S2); photographs detailing the upgraded 130 GHz microwave bridge (Figure S3); reconstitution of the diferric-(2,3,6)F₃Y· monitored by RFQ-EPR spectroscopy (Figure S4); uniformity of residues surrounding Y₁₂₂ or F_nY₁₂₂ variants (Figure S5); evaluation of multiple conformations of F_nY₁₂₂ variants (Figure S6); combined X-band CW, D-band Pulse EPR and ENDOR data sets of (3,5)F₂Y·-β2 (Figure S7); combined X-band CW, D-band Pulse EPR and ENDOR data sets of (2,3)F₂Y·-β2 (Figure S8); combined X-band CW, D-band Pulse EPR and ENDOR data sets of (2,3,5)F₃Y·-β2 (Figure S9); combined X-band CW, D-band Pulse EPR and ENDOR data sets of (2,3,6)F₃Y·-β2 (Figure S10) (PDF)

The authors declare no competing financial interest.