Temporal binning of time-correlated single photon counting data improves exponential decay fits and imaging speed

Abstract

Time-correlated single photon counting (TCSPC) enables acquisition of fluorescence lifetime decays with high temporal resolution within the fluorescence decay. However, many thousands of photons per pixel are required for accurate lifetime decay curve representation, instrument response deconvolution, and lifetime estimation, particularly for two-component lifetimes. TCSPC imaging speed is inherently limited due to the single photon per laser pulse nature and low fluorescence event efficiencies (<10%) required to reduce bias towards short lifetimes. Here, simulated fluorescence lifetime decays are analyzed by SPCImage and SLIM Curve software to determine the limiting lifetime parameters and photon requirements of fluorescence lifetime decays that can be accurately fit. Data analysis techniques to improve fitting accuracy for low photon count data were evaluated. Temporal binning of the decays from 256 time bins to 42 time bins significantly (p<0.0001) improved fit accuracy in SPCImage and enabled accurate fits with low photon counts (as low as 700 photons/decay), a 6-fold reduction in required photons and therefore improvement in imaging speed. Additionally, reducing the number of free parameters in the fitting algorithm by fixing the lifetimes to known values significantly reduced the lifetime component error from 27.3% to 3.2% in SPCImage (p<0.0001) and from 50.6% to 4.2% in SLIM Curve (p<0.0001). Analysis of nicotinamide adenine dinucleotide–lactate dehydrogenase (NADH-LDH) solutions confirmed temporal binning of TCSPC data and a reduced number of free parameters improves exponential decay fit accuracy in SPCImage. Altogether, temporal binning (in SPCImage) and reduced free parameters are data analysis techniques that enable accurate lifetime estimation from low photon count data and enable TCSPC imaging speeds up to 6x and 300x faster, respectively, than traditional TCSPC analysis.

1. Introduction

Fluorescence lifetime is the time a fluorophore remains in the excited state upon absorption of an incident photon, before emission of a subsequent photon and return to ground state. Fluorescence lifetimes range from several hundred picoseconds to several nanoseconds, and are dependent on the microenvironment of the molecule, such as temperature, pH, and proximity to quenchers [1]. Additionally, the fluorescence lifetime is dependent upon molecule conformation and binding, with short and long lifetimes depending on quenched or unquenched fluorophore configuration [1,2]. In this way, fluorescence lifetime can be used to evaluate protein interactions.

The fluorescence lifetime can provide information about fluorophore behavior and environment and has been used to detect intracellular pH and ion concentration [3–5], differentiate cancerous tissue from normal tissue [6–8], and detect early response to cancer treatment [8,9]. However, fluorescence lifetime decays are difficult to measure due to the required sub-nanosecond temporal resolution. Fluorescence lifetime imaging (FLIM) can be performed in the time domain by directly detecting the fluorescence decay following an excitation pulse. Several methods have been developed for detecting fluorescence lifetime, including the use of gated cameras [10–12], fast oscilloscopes [13], and time-correlated single photon counting [14]. While gated cameras and fast oscilloscopes are advantageous for fast imaging of bright samples, both methods are limited in decay sampling (temporal resolution) to ~0.5-1 ns which does not provide sufficient sampling of the decay curve to accurately resolve multiexponential decays.

Time correlated single photon counting (TCSPC) provides the highest temporal resolution within a decay curve for accurate analysis of multi-exponential fluorescence decays. In TCSPC, a fast, ultra-sensitive detector detects individual photons. Electronics time the arrival of the photon with respect to the laser pulse and build a histogram of fluorescence events across time. With repeated observations of fluorescence events, a fluorescence decay curve is assembled. TCSPC systems typically use a very short excitatory laser pulse, <200 fs, which approximates an impulse function. TCSPC electronics can detect the arrival photons with approximately 50 ps time resolution (12.5 ns/256 time bins) [14].

For all time domain approaches, the fluorescence decay can be described by an exponential decay function Eq. (1) with multiple components corresponding to the fractional lifetimes present in the sample [1,15],

$$F(t)={\displaystyle \sum _{i=1}^x{\alpha }_i{e}^{\frac{-t}{{\tau }_i}}}+C$$ (1)

where F(t) is the fluorescence intensity at time t after an excitation pulse, x is the number of exponential components, τ_i is the lifetime of the ith component, α_i is the weight of the ith lifetime, and C accounts for background signal. When F(t) is normalized to a peak value of 1, the sum of the lifetime component weights, Σα_i = 1. However, the measured fluorescence decay signal I(t) Eq. (2) includes the fluorescence decay convolved with the instrument response function, IRF(t).

$$I(t)=IRF(t)\ast F(t)$$ (2)

In TCSPC data, I(t) is the histogram of detected photons. F(t) contains the lifetime endpoints, τ and α. The IRF(t) is the response of the system to a laser pulse. The shape of the IRF(t) is dependent on the laser excitation pulse, cable length, and TCSPC electronics. While the IRF(t) can be measured experimentally, either by direct detection of a laser pulse or detection of an instantaneous event such as second-harmonic generation, subsequent data deconvolution lacks an analytical solution. Therefore, deconvolution to extract fluorescence lifetime parameters is achieved though iterative reconvolution of a predicted model function (1, 2 or 3 component exponential decay) with the measured IRF until least squares residuals are minimized [14].

The fluorescence decay of a fluorophore which can exist in quenched and unquenched states is described by two lifetimes Eq. (3),

$$F(t)={\alpha }_1{e}^{\frac{-t}{{\tau }_1}}+{\alpha }_2{e}^{\frac{-t}{{\tau }_2}}+C$$ (3)

where F(t) is the fluorescence intensity at time t after an excitation pulse, τ₁ and τ₂ are the short (quenched) and long (unquenched) lifetimes, respectively, α₁ and α₂ are the weights of the short and long lifetimes (α₁ + α₂ = 1 when F(t) is normalized to a peak value of 1), respectively, and C accounts for background signal. This two component exponential decay is appropriate for describing the fluorescence decay of endogenous fluorophores, NADH and FAD [2,16], ion concentration fluorescence dyes [4], and Förster Resonance Energy Transfer (FRET) donors [17].

While TCSPC provides the highest temporal resolution of fluorescence lifetime decays, TCSPC image acquisition and data analysis are inherently slow. TCSPC FLIM images typically require seconds to minutes to acquire for adequate SNR in each pixel. Shot noise in TCSPC data follows a Poisson distribution, where the SNR is proportional to the number of photons detected [14]. Detector dark current and after pulsing can also contribute to TCSPC noise; however, these noise sources are effectively reduced to negligible levels with the use of hybrid GaAsP detectors [18]. Thousands to tens of thousands of photons per pixel are required for accurate deconvolution and exponential decay fitting of multi-exponential decays. Furthermore, TCSPC can only resolve one photon per laser pulse, yet photon yield must be much less, around 10%, in order to avoid bias towards early arrival photons [14]. Therefore, approximately 82 seconds are required for a 256x256 pixel image, with an average of 10,000 photons per pixel, imaged on a typical TCSPC FLIM system with an 80 MHz laser source and one detector. Unfortunately, this imaging speed is too slow to allow investigation of dynamic physiological processes, such as calcium fluxes in neurons, which occur much faster, within ~100ms. Multifocal mulitphoton fluorescence lifetime systems have been shown to reduce image acquisition times with multiple detectors operating in parallel [19,20]; however, these systems still rely on typical TCSPC data analysis.

The purpose of this study is to investigate the inherent limitations of photon count/SNR for accurate TCSPC data analysis and identify strategies to reduce the number of required photons and image acquisition times. Simulated fluorescence lifetime decays were generated with varying lifetime parameters and SNR. These lifetime decays were convoluted with a system response and analyzed to determine the accuracy of the extracted fluorescence decay parameters. Two techniques were investigated to increase the accuracy of fits for low photon count/SNR, binning the data temporally and reducing the unknown fit parameters. Simulated decay curves were analyzed by two software packages, SPCImage and SLIM Curve. SPCImage is a commercial fluorescence lifetime analysis program, which uses a least squares method with iterative re-convolution to determine the fluorescence decay parameters [14]. SLIM Curve is an open-source software for analyzing fluorescence lifetime data, which uses a triple integral to estimate the single exponential lifetime value and then applies a Levenberg-Marquardt algorithm with a least squares minimization approach to compute double or triple exponential decays. These simulation experiments define the minimum number of photons required, and therefore the imaging speed, for a given fluorescence decay. Finally, the analysis techniques were tested on fluorescence lifetime data of fluorescent cofactor molecule and cofactor receptor protein, nicotinamide adenine dinucleotide – lactate dehydrogenase (NADH-LDH) solutions.

2. Methods

2.1 One-component exponential decay simulations

One-component exponential decay simulation experiments were performed to evaluate the accuracy of fluorescence lifetime deconvolution and parameter fitting in SPCImage (Becker &Hickl) and SLIM Curve (http://fiji.sc/SLIM_Curve). Simulated 256-time channel TCSPC fluorescence decay curves (256 per input conditions) were generated in MATLAB^® with Poisson noise and lifetime values from 0.1 ns to 6 ns and total photons per curve from 100 to 10000. These decay curves were convoluted with an IRF measured from the SHG of a urea crystal on a TCSPC system, as previously described [8,21]. The resulting I(t) decay was analyzed by SPCImage and SLIM Curve to extract the lifetime value. The percent errors of the extracted lifetime values were computed, error = [|true-computed|/true]*100, and analyzed.

2.2 Two-component exponential decay simulations

Two-component TCSPC exponential decays (Eq. (4)) with Poisson noise and 256-time channels were simulated in MATLAB.

$$F(t)={\alpha }_1{e}^{\frac{-t}{{\tau }_1}}+{\alpha }_2{e}^{\frac{-t}{{\tau }_2}}$$ (4)

τ₁ varied from 0.1 to 3.5 ns in 0.1 ns steps, τ₂ varied from 0.1 to 4 ns in 0.1 ns steps, α₁ = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9, and the number of photons per curve varied from 50 to 100,000. 256 decay curves were simulated for each parameter set. These simulated decay curves were convolved with the urea IRF, and the resulting I(t) decays were analyzed in SPCImage and SLIM Curve to extract τ₁, τ₂, α₁, and α₂ values. A multiexponential model was evaluated with the offset and scatter values set to 0 due to the lack of background and SHG/instantaneous light leakage, respectively. The shift value was set to a median value obtained by randomly sampling points in a representative image. The shift value was uniform across all simulated data. The errors of the lifetime parameters were analyzed. α₁, and α₂ are reported as the normalized weights found when F(t) is normalized to a peak value of 1 (α₁ + α₂ = 1).

2.3 Temporal binning

The temporal resolution of the simulated decay curves created in 2.2 was reduced from 256 time bins to 128, 85, 64, 51, 42, 36, and 25 by summing the number of photons in 2, 3, 4, 5, 6, 7, and 10 consecutive time bins, respectively. These new fluorescence decay curves were analyzed by SPCImage and SLIM Curve to extract τ₁, τ₂, α₁, and α₂ values and the errors of the lifetime parameters analyzed. The shift value of the multiexponential decay (in SPCImage) was set to a median value obtained by randomly sampling points in a representative image and was uniform across a data set with the same number of time bins.

2.4 Reduced parameters

The decay curves simulated in 2.2 and 2.3 were analyzed in SPCImage and SLIM Curve with the τ₁ and τ₂ parameters fixed to the appropriate value. The error in the resulting α₁ value was analyzed.

2.5 NADH-LDH experiments

Tris-buffered saline at pH 7.6 was used as the solvent for all solutions. Varying concentrations of lactate dehydrogenase (LDH) from porcine heart (Sigma) were mixed with 100 μM NADH (Sigma) in order to generate solutions with desired free-to-bound ratios of NADH (Table 1). Required concentrations were calculated based on a published value for the dissociation constant of NADH to LDH (4.6 μM), and the fact that each LDH molecule has four identical binding sites [22].

Table 1. Concentrations of NADH and LDH for solutions with certain α₁ values.

NADH α1	[LDH] (μM)	[NADH] (μM)
0.3	20	100
0.5	13.5	100
1	0	100

Following mixing, a 100 μl droplet of each solution was placed in a separate 35 mm glass-bottom imaging dish (MatTek Corp.), and a coverslip was placed over each droplet to reduce evaporation.

Fluorescence lifetime images were acquired using a custom-built multiphoton fluorescence microscope system (Bruker) using a 40x oil-immersion objective (1.3 NA) and an inverted microscope (Nikon). A titanium:sapphire laser (Chameleon Ultra II, Coherent) was tuned to 750 nm for excitation of NADH, and a 440/80 nm bandpass filter was used to collect fluorescence emission. A pixel dwell time of 4.8 μs was used to collect images that were 256x256 pixels, and a GaAsP PMT (H7422P-40, Hamamatsu) detected emitted photons. Imaging was performed in the solutions at a depth of 30 μm. Time-correlated single photon counting electronics (SPC-150, Becker and Hickl) were used to acquire fluorescence decay curves. Laser power and integration time were varied in order to generate fluorescence decay curves with an average of 50, 100, 200, 400, 600, 800, 1000, 2500, 5000, 7000, and 10000 photons per pixel. A single image with 256x256 pixels was obtained for each evaluation yielding 65,536 decay curves. The second harmonic generated signal from urea crystals at 900 nm excitation was used to measure the instrument response function, which was found to have a full width at half maximum of 220 ps.

NADH-LDH experimental data was analyzed in SPCImage. The scatter value was set to 0 as there was no evidence of SHG or laser light being detected. The offset and shift values were set to a median value obtained by randomly sampling points within an image, but kept uniform among data with consistent photon counts (offset) and time bins (shift). Data were first analyzed as collected with 256 time bins with unknown lifetimes. Next, data were binned temporally as described in 2.3 and the resulting decays analyzed in SPCImage. Finally, repeat analysis was performed with the τ₁ and τ₂ parameters fixed to 0.52 ns and 1.25 ns, respectively. These values for free and bound NADH were determined experimentally and agree with published values of free and protein-bound NADH [2,8,21].

3. Results

3.1 Accuracy for single exponential decays

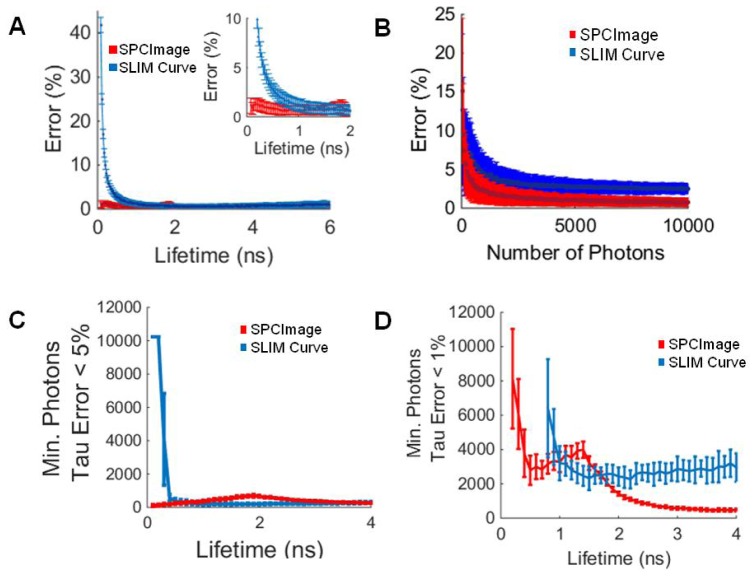
The SPCImage and SLIM Curve calculated fluorescence lifetimes closely match the true values of the single exponential decays. The mean lifetime error for SPCImage is less than 5% for lifetime values between 0.1 and 6 ns (Fig. 1(a)). The error for lifetimes fit by SLIM Curve was less than 5% for lifetimes above 0.5 ns (Fig. 1(a)). Below 0.5 ns, the error for lifetimes computed by SLIM Curve increased exponentially (Fig. 1(a)). The error of the estimated lifetime for decays with τ = 0.6 ns, increased as the number of photons/SNR decreased (Fig. 1(b)). If a lifetime error of 5% is tolerated, fewer than 500 photons per pixel are required to resolve lifetimes greater than 0.5 ns in SLIM Curve (Fig. 1(c)). If a 1% τ error is tolerated, additional photons are required, ~3000 for SLIM Curve to resolve lifetimes greater than 1 ns (Fig. 1(d)).

Fig. 1.

(A) Percent error of the SPCImage and SLIM Curve calculated lifetime values for a single-exponential decay, insert shows errors for lifetimes less than 2 ns. (B) Error in calculated lifetime of SPCImage and SLIM Curve for single component lifetime decays where τ = 0.6 ns. (C) Minimum number of photons for SPCImage and SLIM Curve to calculate the lifetime of a single-exponential decay within 5%. (D) Minimum number of photons for SPCImage and SLIM Curve to calculate the lifetime of a single-exponential decay within 1%. Mean +/− SD (256 simulations).

3.2 Lifetime analysis accuracy for double exponential decays

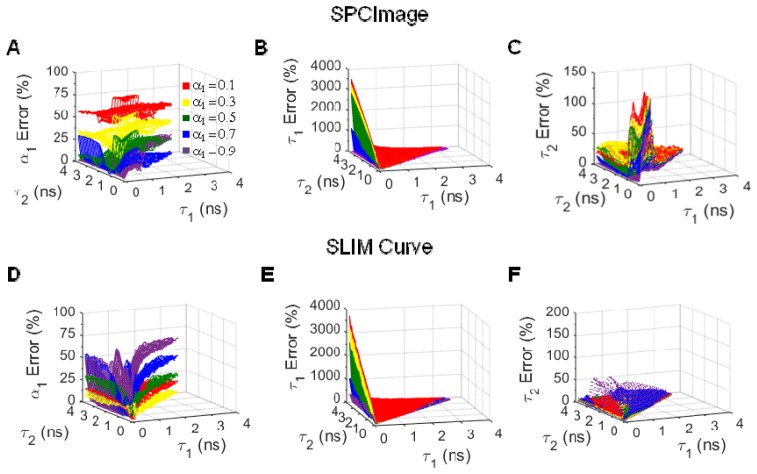
Both SPCImage and SLIM Curve fail to accurately fit some two component fluorescence lifetimes. At 10,000 photons per decay curve (SNR = 100), SPCImage fails to accurately fit (component error > 20%) fluorescence lifetimes with α₁ values < 0.5 (Fig. 2(a)), τ₁ values < 0.3 ns (Fig. 2(b)), and τ₂ values < 1 ns (Fig. 2(c)). Likewise, SLIM Curve fails to accurately fit fluorescence lifetimes with α₁ values > 0.5 (Fig. 2(d)) and τ₁ values < 0.3 ns (Fig. 2(e)). SLIM Curve accurately fits all τ₂ values, provided that α₁ is < 0.8 (Fig. 2(f)).

Fig. 2.

α₁ (A), τ₁ (B), and τ₂ (C) error for simulated two-component fluorescence decay curves analyzed in SPCImage. α₁ (D), τ₁ (E), and τ₂ (F) error for simulated two-component fluorescence decay curves analyzed in SLIM Curve. Average of 256 simulations, 10,000 photons/curve (SNR = 100).

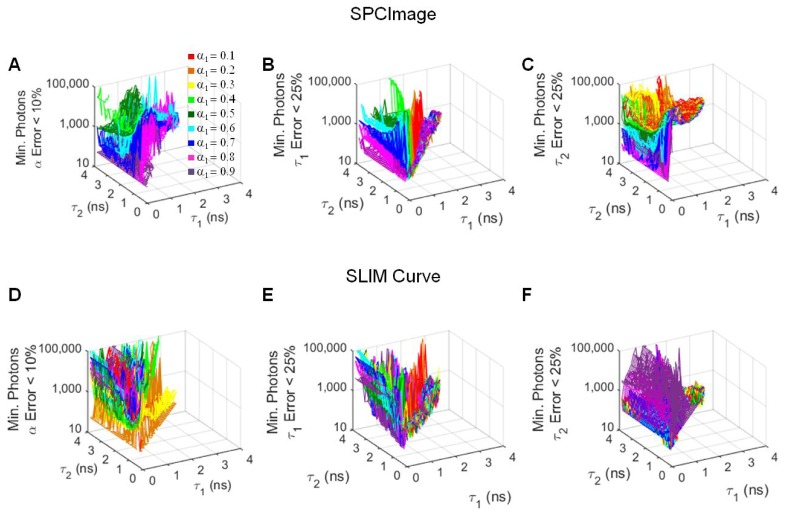
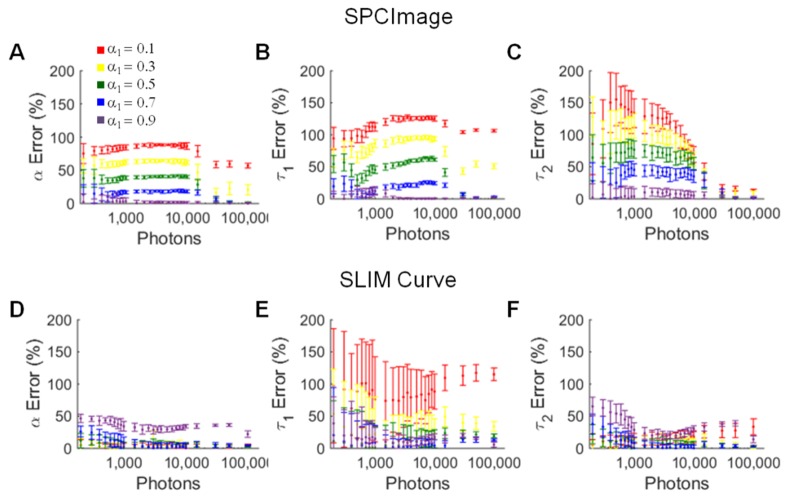
For the two component lifetimes that can be accurately fit, the minimum number of photons required for certain error thresholds, α₁ error < 10%, τ₁ error < 25%, and τ₂ error < 25%, was determined (Fig. 3). For SPCImage, the fewest photons are required for decay curves of high α₁ values (Fig. 3(a)-3(c)) and (τ₂ - τ₁)> ~2 ns (Fig. 3(c)). For SLIM Curve, the number of photons required for good fits is minimized for α₁ values = 0.2 (Fig. 3(d)) and τ₂~ = τ₁ (Fig. 3(d), 3(f)). For the fluorescence lifetimes of free and bound NADH, τ₁ = 0.5 ns and τ₂ = 1.2 ns, respectively, lifetime component error is minimized with increasing photons, when analyzed with both SPCImage and SLIM Curve (Fig. 4).

Fig. 3.

Minimum number of photons required in a decay curve for α₁ error < 10% (A), τ₁ error < 25% (B), and τ₂ error < 25% (C) when simulated decays are analyzed in SPCImage. Minimum number of photons required in a decay curve for α₁ error < 10% (D), τ₁ error < 25% (E), and τ₂ error < 25% (F) when simulated decays are analyzed in SLIM Curve. Average of 256 simulations.

Fig. 4.

α₁ (A), τ₁ (B), and τ₂ (C) error for simulated lifetime decays where τ₁ = 0.5 ns and τ₂ = 1.2 ns analyzed in SPCImage. α₁ (D), τ₁ (E), and τ₂ (F) error for simulated lifetime decays where τ₁ = 0.5 ns and τ₂ = 1.2 ns analyzed in SLIM Curve. Average +/− SD of 256 simulations.

3.3 Improved accuracy with temporal binning

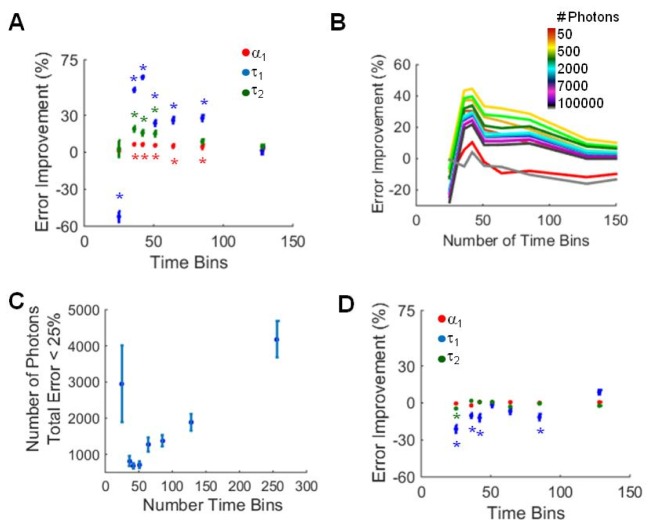
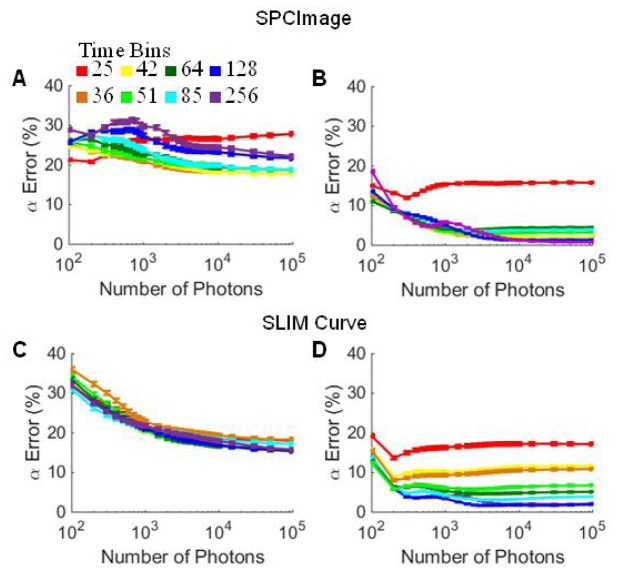
Temporal binning of fluorescence decay curves was evaluated as a method to improve fitting accuracy. Typical TCSPC decay curves contain 256 time bins over 12.5 ns. Here, sequential time bins were summed to reduce the total number of time bins to 128, 85, 64, 51, 42, 36, and 25. A significant improvement in α₁ error (red, Fig. 5(a)) and τ₁ error (blue, Fig. 5(a)) was observed for decays with 85, 64, 51, 42, and 36 time bins analyzed in SPCImage. Likewise, τ₂ error (green, Fig. 5(a)) improved for decays with 51, 42, and 36 time bins. This improvement in fitting accuracy was dependent on the number of photons per curve, with the greatest improvement observed for curves with 400-1000 photons (Fig. 5(b)). For fluorescence lifetimes which can be resolved with a cumulative error in all endpoints < 25% (decay curves with high α₁ values and τ₁ and τ₂ separations > 2 ns), the average minimum number of photons required decreased from 4185 photons to a minimum average of 681 photons at 42 time bins (Fig. 5(c)). Additionally, the number of simulated decay curves that could be accurately fit increased with temporal binning to 42 bins (Table 2). Temporally binned fluorescence decay curves were evaluated in SLIM Curve; however, no improvement in fitting accuracy was observed (Fig. 5(d), Table 2).

Fig. 5.

(A) Component error improvement (mean +/− SD) for all simulated data sets analyzed in SPCImage as a function of time bins. * p<0.05 versus 256 time bins (error improvement = 0%). (B) Error improvement of the extracted lifetime components analyzed in SPCImage as a function of the number of photons in the curve. (C) Minimum number of photons required (mean +/− SD) for decay curves with total error less than 25% (SPCImage). (D) Component error improvement (mean +/− SD) for all simulated data sets analyzed in SLIM Curve as a function of time bins. * p<0.05 versus 256 time bins (error improvement = 0%).

Table 2. Percent Simulations with Total Error < 25%.

Time Bins	SPCImage	SLIM Curve
256	40.4	50.2
128	68.1	47.8
85	75.4	48.5
64	77.7	40.7
51	77.8	47.4
42	89.0	56.4
36	78.3	53.0
25	8.9	46.6

3.4 Improved accuracy with fixed lifetime components

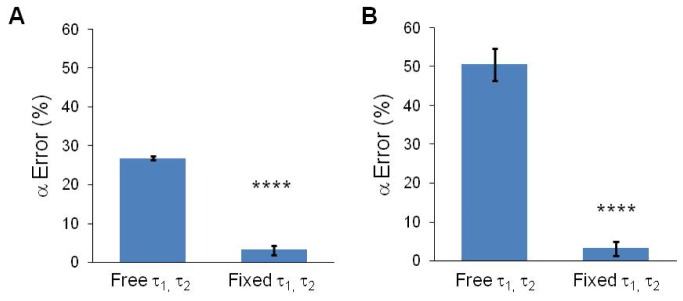
The values of the short and long lifetime components may be known in many cases, or determined experimentally, as is the case for FLIM dyes and FRET pairs. If the fluorescence lifetimes are known values, the values can be fixed in the decay models of SPCImage and SLIM Curve to improve the accuracy of the estimated α parameters. To evaluate the α parameter estimation, the same two-component simulated decay curves evaluated in 3.2 and 3.3 were analyzed with the lifetimes fixed in the analysis. The accuracy of the calculated α₁ parameter increased when the τ₁ and τ₂ values were fixed in the analysis model. For SPCImage, the average α₁ error decreased from 26.7% to 3.2% (p<0.0001; Fig. 6(a)). For SLIM Curve, the average α₁ error decreased from 50.6% to 4.2% (p<0.0001; Fig. 6(b)). While the α₁ error can be improved by temporal binning of data analyzed by SPCImage with free τ₁ and τ₂ values (Fig. 7(a)), no significant improvement in α₁ error is achieved by fixed-parameter analysis of temporally binned data (Fig. 7(b)). However, an overall more accurate calculation of α₁ can be achieved and at a fewer required number of photons when the lifetime parameters are fixed in SPCImage (Fig. 7(a)-7(b)). Likewise, for SLIM Curve, an overall more accurate estimate of α₁ at a fewer required number of photons is achieved when the lifetime parameters are fixed, and there is no improvement with temporal binning (Fig. 7(c)-7(d)).

Fig. 6.

α₁ error (mean +/− SD) when τ₁ and τ₂ are free or fixed in SPCImage (A) or SLIM Curve (B). Average for all simulated curves generated in Methods 2.2. **** p< 0.0001.

Fig. 7.

α error (average +/− SD) for all simulated decay curves analyzed in SPCImage with free (A) and fixed (B) τ₁ and τ₂ values. α error (average +/− SD) for all simulated decay curves analyzed in SLIM Curve with free (C) and fixed (D) τ₁ and τ₂ values.

3.5 Improvement in photon requirement and imaging speed

As shown in Sections 3.3 and 3.4, temporal binning and fixed lifetime parameters in decay analysis reduces the required number of photons for an accurate decay fit. The minimum photons required for total error (τ₁ error + τ₂ error + α error) to be less than 10% was evaluated using the simulated NADH fluorescence decays where τ₁ = 0.5, τ₂ = 1.2 and α₁ = 0.8, for the original data and the data with processing techniques (Table 3). With no SNR improvement techniques, 30,000 photons are required for accurate fitting (total error < 10%; Fig. 4), which would take approximately 246 s to acquire a 256x256 pixel image. With temporal binning in SPCImage, the required number of photons is reduced to 4000 (data not shown), and the image capture time reduced to 32.8 s. By fixing the lifetime values, the required number of photons is reduced to 100 (Fig. 7(b)), and imaging time reduced to 0.819 s. By combining fixed parameter analysis and spatially binning 9 pixels, accurate fits can be achieved with as few as 11 photons/pixel (108 total for the binned area), and an imaging time of 90 ms.

Table 3. Photons and time (s) required for a 256x256 pixel image of a two-component fluorescence decay where τ₁ = 0.5, τ₂ = 1.2 and α₁ = 0.8, with and without noise reduction techniques. Calculations assume a 80MHz laser source and 10% photon efficiency. Minimum photons required for total error < 10%.

Analysis Technique	Minimum Photons Required	Imaging Time for 256x256 Image (s)
None	30000	246
Temporal^ Binning	4000	32.8
Spatial* Binning	3333	27.3
Temporal and Spatial* Binning	444	3.64
Fixed τ1 & τ2	100	0.819
Fixed τ1 & τ2 with Spatial* Binning	11	0.090

^ Binning to 42 time bins.

* 9 pixel moving spatial bin.

3.6 Validation in NADH-LDH solution experiments

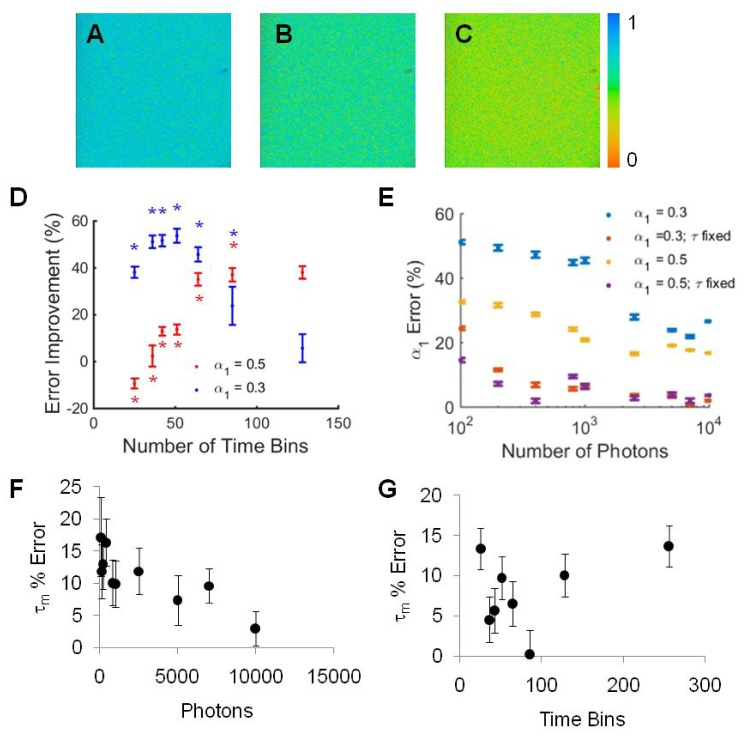
The simulated fluorescence decay curve experiments demonstrate improvement in SPCImage analysis of fluorescence lifetime decays with temporal binning and fixed lifetime parameters. To ensure these analysis techniques improve SPCImage fitting of real data, fluorescence lifetime images of solutions of NADH-LDH with α₁ values of 0.3 and 0.5 were acquired and analyzed. Representative images demonstrate the improvement in α₁ values between the orginal data (α₁ = 0.5) with 800 photons and 256 time bins evaluated with free components (Fig. 8(a)), fixed components (Fig. 8(b)), and temporally binned to 64 time bins (Fig. 8(c)). As a representative example, temporal binning from 256 to 51 time bins of fluorescence decay curves with 800 photons improved the total error from 108% to 55% (p<0.0001) for α₁ = 0.3 (Fig. 8(d)). Likewise, temporal binning from 256 time bins to 64 time bins of fluorescence decay curves with 800 photons improved the total error from 76% to 44.0% (p<0.0001) for α₁ = 0.5 (Fig. 8(d)). This reduction in error is comparable to that obtained by spatially binning 9 pixels of the original 256 time-bin image, 44.0% vs. 44.3%, respectively. In addition to improving the lifetime fitting by temporal binning, fixing the lifetime values in SPCImage greatly improves the estimation of α₁ (Fig. 8(e)) and allows accurate estimations of α₁ at reduced photon numbers. For NADH, error in the mean lifetime is reduced with large photon counts (Fig. 8(f)) and a reduction in error with temporal binning in SPCImage is observed (Fig. 8(g)).

Fig. 8.

(A) Representative α₁ image of the α₁ = 0.5 NADH-LDH solution with 800 photons, evaluated with 256 time bins. (B) Representative α₁ image of the α₁ = 0.5 NADH-LDH solution with 800 photons, evaluated in SPCImage with lifetime values fixed to τ₁ = 0.52 ns and τ₂ = 1.25 ns, (C) Representative α₁ image of the α₁ = 0.5 NADH-LDH solution with 800 photons, evaluated with 64 time bins. (D) Total error (τ₁ error + τ₂ error + α error) improvement for SPCImage analysis of NADH-LDH solutions with 800 photons per curve with temporal binning versus no temporal binning. * p< 0.05 vs. 256 time bins (error improvement = 0%). (E) α error as a function of number of photons per decay curve for NADH-LDH solutions analyzed in SPCImage with short and long lifetimes either free or fixed to τ₁ = 0.52 ns and τ₂ = 1.25 ns. For α₁ = 0.3 and 0.5, the p-value between the α₁ errors from free and fixed lifetime estimation is less than 0.0001 at each photon count. (F) Mean lifetime (τ_m) error for NADH decreases with increased photons collected (α₁ = 0.5). (G) Mean lifetime (τ_m) error for images with 800 photons per pixel is reduced with temporal binning (NADH α₁ = 0.5).

With a 90% error threshold tolerance, temporal binning improves the required number of photons to fit NADH decays with α₁ = 0.3 from 10,000 photons to 800 photons, which corresponds to an imaging time improvement of a 256x256 pixel image from 82s to 6.55s (Table 3). Likewise, temporal binning reduces the number of photons and imaging time required from 7000 photons, 58s, to 400 photons, 3.3s, for NADH decays with α₁ = 0.5. With the lifetimes fixed in SPCImage analysis, α₁ errors less than 10% are achieved with as few as 400 photons for α₁ = 0.3 and 200 photons for α₁ = 0.5 (Table 3, Fig. 8(e)), equating to imaging times of 3.3 s and 1.64 s. When combined with a 9-pixel moving spatial bin, further reductions in imaging time can be achieved, down to 0.37 s for α₁ = 0.3 and 0.188 s for α₁ = 0.5, although with reduction in spatial resolution.

4. Discussion

TCSPC remains the optimal method to obtain fluorescence lifetime decay data with high temporal resolution within a decay curve. However, conventional imaging and analysis protocols require a large number of photons per pixel, 10,000 photons or more, for accurate deconvolution of the instrument response function and lifetime parameter estimation. This high photon count number for image resolution requires lengthy image acquisition times (>1 min) that are not conducive to imaging fast biological phenomena. Therefore, this study applied simulation experiments to define the limitations of conventional FLIM analysis algorithms and determine the photon count requirements for accurate analysis of fluorescence decay curves. Additionally, two methods to improve fitting accuracy are demonstrated on simulated fluorescence decay curves and NADH-LDH experimental data.

The deconvolution of the measured signal into the system response and the fluorescence decay curve does not have an analytical solution. Therefore, the fluorescence decay parameters are approximated by iterative analysis of the convolution of the instrument response with a 'best guess' fluorescence decay curve. This method assumes an exponential shape of the fluorescence decay with a set number of components. Commercial software, SPCImage uses a least squares method with iterative re-convolution to determine the fluorescence decay parameters [14]. An open-source alternative, SLIM Curve, uses a triple integral to estimate the single exponential lifetime value and then applies a Levenberg-Marquardt algorithm with a least squares minimization approach.

Simulation experiments demonstrate the fluorescence decays which can accurately be evaluated by TCSPC and conventional analysis. The single-component exponential decay simulation results show that both SPCImage and SLIM Curve can accurately evaluate single-component fluorescence decays for lifetimes greater than 0.5 ns (Fig. 1). Furthermore, both SPCImage and SLIM Curve accurately describe fluorescence decays of two components with large lifetime separation and either high or low α₁ values, respectively (Fig. 2). However, even at high photon counts, both analysis programs fail to accurately fit certain decay curves (Fig. 3). SPCImage fails to fit fluorescence lifetimes with α₁ values < 0.4, τ₁ values < 0.3 ns, and τ₂ values < 1 ns. SLIM Curve fails to accurately fit fluorescence lifetimes with α₁ values > 0.5 and τ₁ values < 0.3 ns. Fortunately, the short and long lifetimes of most two-component fluorescence decay systems are less than 0.4 ns and greater than 1 ns, respectively, and have a separation greater than 0.5 ns [2,21].

TCSPC noise follows a Poisson distribution where $SNR=\sqrt{N}$, where N is the number of photons [14]. Therefore, the SNR of fluorescence decays is improved by increasing the number of photons. Post-imaging, this can be achieved by binning spatial pixels. However, spatial binning degrades the resolution of the image and assumes congruent fluorophore states within the binned area. As an alternative to spatial binning, temporal binning was evaluated to increase SNR. Temporal binning was achieved by reducing the number of decay time bins from 256 to 128, 85, 64, 51, 42, 36, and 25 time bins by summing sequential time bins of the original 256 bin decay curve. By combining the photons in consecutive time bins within a pixel, the error due to shot noise in the time bin is reduced by the averaging effect of the multiple bins combined. Temporal binning greatly improved the fitting by SPCImage with the greatest improvements in fluorescence parameters observed for the curves with 42 time bins (Fig. 4). Evaluated by SPCImage, temporal binning resulted in a greater number of fluorescence decays that could be accurately resolved and reduced the average number of photons required for accurate fitting from 4500 photons for decay curves with 256 time bins to about 500 photons for decay curves with 42 time bins, a 9x reduction in the required number of photons (Fig. 4). The improved results for SPCImage evaluation of temporally binned data suggests that for many two-component exponential decay curves, the time axis is oversampled, at the expense of added noise into the decay curve. Temporal binning reduces the noise in each time bin and yields a more accurate decay approximation. Temporal binning also improved SPCImage fitting of NADH-LDH data (Fig. 7(a)). While temporal binning to 42 bins improved fits in SPCImage, further binning to 36 or 25 bins increased error, indicating that with too low temporal resolution, the shape of the decay is degraded and the two-component fit accuracy is reduced.

SLIM Curve did not show improvements with temporal binning, which suggests SLIM Curve is less influenced by noise in the decay curveor the improvement in noise is offset by the degradation of temporal resolution. SPCImage uses a least squares method with iterative re-convolutionwhile SLIM curve uses a triple integral to estimate the single exponential lifetime value and then applies a Levenberg-Marquardt algorithm with a least squares minimization approach to determine the multi-component lifetime parameters. These subtle differences in algorithms lead to different lifetime approximations, lifetime parameter accuracies, and behaviors when data is binned temporally to improve SNR.

Additional instrumentation configurations exist for fast FLIM and fast data processing. Camera-gated methods can be used to image whole-field fluorescence; however, these are typically limited to 2-20 gates/time bins [10–12] which, as shown in Fig. 5(a), is insufficient for accurate analysis of two component lifetime decays. Rapid lifetime determination (RLD) [23] and Laguerre estimation methods [24–26] exist for improved speed of lifetime approximation, yet linear least squares remains the most accurate for lifetime determination. Additionally, single-photon avalanche diode (SPAD) arrays can be used to rapidly resolve fluorescence lifetime decays in a sensitive manner not limited by the single photon aspect of TCSPC [27–29]. SPAD acquisition can be combined with center-of-mass method processors for hardware-based temporal binning for single-component lifetime estimation [27]. Furthermore, hardware-based temporal binning to 4 (16 time bins) enables faster transfer of data to the computer, demonstrating improved imaging speeds with in-pixel histogramming to fewer time bins [30]. This method supports the advantages of temporal binning for improved FLIM imaging. For TCSPC, the data analysis method of temporal bining described here improves exponential decay fits in SPCImage analysis and may enable robust results with fewer collected photons.

In addition to increasing SNR, lifetime fitting can be improved by reducing the number of unknown parameters. By fixing the lifetime values in SPCImage and SLIM Curve, the average α₁ error decreased significantly from 26.7% to 3.2% and from 50.6% to 4.2%, respectively. While the fluorescence lifetime of the sample may not always be known or may be influenced by the environment, there are many experiments where the lifetime components are known. For example, the fluorescence lifetime of dyes designed to report ion concentrations exist in one state when unquenched by the ion and a second when quenched [4,5]. These lifetime values can be measured independently and then these values used to evaluate mixed samples. Furthermore, often the fluorescence lifetime of a FRET donor is known to be a certain value determined by the quenched or unquenched state of the molecule [17]. As demonstrated by the NADH-LDH experimental data (Fig. 7), fixing the lifetime parameters improves the estimation of α₁, and the substantial improvement suggests lifetime values should be fixed when known. However, for in vivo experiments, fluorescence lifetimes may exist in a continuum of values due to local changes in temperature, pH, viscosity, proximity to quenchers. In this case, when fluorophore lifetime is largely variant, fixing the lifetimes to set values may introduce error.

Improvements in image acquisition time and fluorescence lifetime decay estimation benefit all TCSPC FLIM studies. In particular, more accurate estimation of the lifetime weight components, α, will improve FRET experiments and yield more accurate approximations of FRET donor and acceptor concentrations. Additionally, clinical and in vivo FLIM studies have been limited by the lengthy image acquisition times which introduce motion error and other artifacts into the images. Faster image acquisition may enable additional clinical FLIM studies, previously hindered by image acquisition time. Furthermore, increasing evidence supports characteristic changes in intrinsic fluorophore lifetimes with diseases such as cancer and precancers [7,8,31]. Therefore, increased accuracy in lifetime estimation will increase the sensitivity and specificity of FLIM-based screens.

Altogether, these simulation and NADH-LDH experiments demonstrate that fluorescence lifetime fitting accuracy is highly dependent on the lifetime parameters and number of photons/SNR. Temporal binning in SPCImageand fixed lifetime parameters can achieve high fidelity fits of noisy or low photon count data, enabling accurate lifetime component estimation with reduced number of photons and faster imaging. Combining analysis techniques amplifies the effect with theoretical improvements in imaging speed from 246 s for a 256x256 pixel image to 0.82 s, a 300X improvement. Image acquisition times can be reduced further, to as low as 90 ms with a 9-pixel moving spatial bin; however, this approach reduces spatial resolution. These improvements in photon count and imaging time will allow improved imaging of weakly fluorescent signals, such as autofluorescence, or fast phenomena.