Automated volumetric segmentation of retinal fluid on optical coherence tomography

Abstract

We propose a novel automated volumetric segmentation method to detect and quantify retinal fluid on optical coherence tomography (OCT). The fuzzy level set method was introduced for identifying the boundaries of fluid filled regions on B-scans (x and y-axes) and C-scans (z-axis). The boundaries identified from three types of scans were combined to generate a comprehensive volumetric segmentation of retinal fluid. Then, artefactual fluid regions were removed using morphological characteristics and by identifying vascular shadowing with OCT angiography obtained from the same scan. The accuracy of retinal fluid detection and quantification was evaluated on 10 eyes with diabetic macular edema. Automated segmentation had good agreement with manual segmentation qualitatively and quantitatively. The fluid map can be integrated with OCT angiogram for intuitive clinical evaluation.

1. Introduction

Diabetic retinopathy (DR) is a microvascular disease characterized by hyperpermeability, capillary occlusion, and neovascularization [1]. These pathophysiologic changes can lead to macular edema and proliferative diabetic retinopathy, which are responsible for most of the vision loss associated with this disease [2]. Therefore early detection and monitoring of these complications is important in preventing permanent visual impairment.

Optical coherence tomography (OCT) [3] is commonly used in clinical ophthalmology to detect diabetic macular edema (DME) and assess treatment response by mapping the total retinal thickness [4–10]. The retinal thickness correlates with vascular leakage, but can also paradoxically decrease due to ischemic atrophy, which happens not infrequently in the setting of DME. Retinal fluid volume, not retinal thickness, would be a more accurate indication of vascular permeability in DME.

Direct detection of retinal fluid has been performed qualitatively through laborious visual inspection of sequential OCT cross sections. Thus, an automated image processing algorithm that detects and quantifies retinal fluid would be necessary to make this practical in clinical settings. A few state-of-the-art algorithms [11–18] provided fluid segmentation methods on clinical two dimensional (2D) OCT images. These have been used to classify the fluid associated abnormalities based on extraordinary retinal layer texture and structure gradient in DME. To the best of our knowledge, no fully-automated algorithm capable of a generalized and robust application has been validated to identify fluid-filled regions in a three dimensional (3D) fashion.

In this paper, we present and validate an automated volumetric segmentation algorithm based on fuzzy level-set method [19] to identify and quantify retinal fluid, including intraretinal fluid (IRF) and subretinal fluid (SRF), on OCT structural images. Our proposed method uses OCT angiography volume scans [20–22], where structural OCT is simultaneously acquired. Finally, by registering the structural (fluid accumulation) and functional (blood flow) information into a single 3D volume, clinicians can intuitively evaluate pathological structures and microvascular dysfunction simultaneously.

2. Materials and method

2.1 Patient selection and data acquisition

Participants diagnosed with DME and varied levels of retinopathy severity were recruited from the Casey Eye Institute. An informed consent was obtained and the protocol was approved by the Institutional Review Board at the Oregon Health & Science University. The study was conducted in compliance with the Declaration of Helsinki.

Two volumetric data sets were collected from single eyes of participants with DME within a visit. All of the data was acquired using a commercial spectral domain OCT system (RTVue-XR; Optovue, Fremont, CA) with a center wavelength 840 nm, a full-width half-maximum bandwidth of 45 nm, and an axial scan rate of 70 kHz [23]. A single volumetric data set contained two volumetric raster scans covering a 3 × 3 mm area with a 2 mm depth. In the fast transverse scanning direction, 304 axial scans were sampled to obtain a single 3 mm B-scan. Two repeated B-scans were captured at a fixed position before proceeding to the next location. A total of 304 locations along a 3 mm distance in the slow transverse direction were sampled to form a 3D data cube. All 608 B-scans in each data cube were acquired in 2.9 seconds. Blood flow information was acquired using the split-spectrum amplitude-decorrelation (SSADA) between consecutive B-scans [23, 24]. The SSADA algorithm detected blood flow by calculating the signal amplitude-decorrelation between consecutive B-scans. OCT structural images were obtained by averaging two repeated B-scans. The structural and angiography data were generated simultaneously on each scan. For each volumetric data set, two volumetric raster scans, including one x-fast scan and one y-fast scan were registered and merged through an orthogonal registration algorithm [25]. The digital resolution is 10 × 10 × 3.0μm³/pixel.

One eye of sixteen DME participants was scanned. Ten eyes had retinal fluid in the macular scans based on clinician grading. These were used to test the automated algorithm.

2.2 Algorithm overview

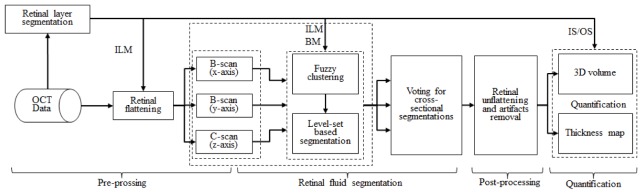
Figure 1 summarizes the algorithm. A pre-processing step was first performed to prepare the tissue region for segmentation. Fluid segmentation using fuzzy level-set method followed. Finally, post-processing steps were applied to remove artifacts. The following three sections will describe the process in detail. The algorithm was implemented with custom software written in Matlab 2011a (Mathworks, Natick, MA) installed on a workstation with Intel(R) Xeon(R) CPU E3-1226 v3 @ 3.30GHz and 16.0 GB RAM.

Fig. 1.

Overview of the automated volumetric retinal fluid detection algorithm. ILM: inner limiting membrane, BM: Bruch’s membrane, IS/OS: junction of inner and outer photoreceptor segments.

2.3 Pre-processing

The retina was defined as the region between inner limiting membrane (ILM) and Bruch’s membrane (BM). Three dimensional structural OCT data (Fig. 2(A)) was flattened using ILM plane (Fig. 2(B)). The junction of inner and outer photoreceptor segments (IS/OS) defined the boundary between IRF and SRF.

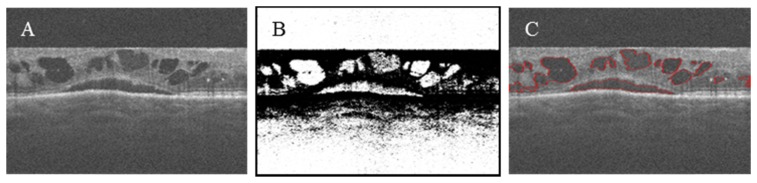
Fig. 2.

(A) Original OCT structural volume. (B) OCT structural volume flattened according to the inner limiting membrane (ILM) boundary. B-scans (x and y-axes) and C-scans (z-axis) were indicated with red, green and blue, respectively.

All aforementioned layer boundaries were segmented by the directional graph search method (Fig. 3), published in [26]. Because of the tissue damage inherent to DME, automatic layer segmentation is likely to fail even with robust algorithms. By using the graph search based segmentation method, ILM and BM can be automatically detected with a high degree of precision (Fig. 3(A)), while IS/OS requires some manual intervention in the data with SRF (Fig. 3(B)).

Fig. 3.

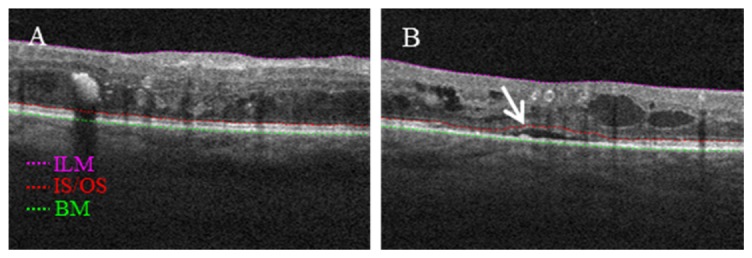
(A) An example B-frame showing inner limiting membrane (ILM), Bruch’s membrane (BM) and junction of inner and outer photoreceptor segments (IS/OS) boundaries used in this study can be automatically segmented. (B) An example B-frame with subretinal fluid showing IS/OS needs be manually corrected in the position pointed by a white arrow.

2.4 Retinal fluid segmentation

In this stage, a fuzzy level-set method, (combination of fuzzy C-means (FCM) and level set method) is implemented. Briefly, the intensity of retinal fluid is lower than retinal tissues, so fluid region can be clustered using FCM scored by probability. Then, the boundary of the retinal fluid can be detected by level-set method. Fuzzy level-set method is applied frame by frame on C-scans (z-axis) and B-scans (x and y-axes) to identify fluid filled regions (Fig. 2(B)). Therefore, three separate volumetric segmentation results are obtained. The synthetic candidates are combined by voting the three volumetric segmentation results for each voxel.

2.4.1 Fuzzy level-set method

Level-set methods are widely used in image segmentation [27–29], and has recently been applied to detect abnormality in OCT en face images [30]. Level-set method represents the boundary of interest in image I as contour ϕ = 0 (i.e. level-set curve), where the level-set function ϕ, is a function of time and spatial coordinates in I. ϕ was initialized with an estimate of the segmentation and evolves to get the accurate boundary. For example, in our implementation the evolution of ϕ was described by [19] and [31].

$$\frac{\partial \varphi }{\partial \text{t}}\text{=}\mu \left[\Delta \varphi -div\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)\right]+\lambda \delta (\varphi )div\left(g\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)+g(1-2R_b)\delta (\varphi )$$ (1)

where δ is the Dirac function, div is the divergence operator, μ, λ, R_b are estimated based the FCM result.

The first term has two purposes. It smooths the level-set when ϕ is too steep (|Δϕ|>1) and also makes the level-set steeper when ϕ is too smooth (|Δϕ|<1). The second and the third term on the right hand side of Eq. (1) are responsible for driving the zero level curves towards the boundary of interest.

Typically, a Gaussian smoothing operator is used to calculate the boundary weight g [19, 31]. However, considering that the dominate noise in OCT images is the speckle noise [32], we used median operator M instead

$$g=1/\left[1+{\left|\nabla M(I)\right|}^2\right]$$ (2)

The median operator suppresses the noise while maintaining the edge sharpness in OCT images.

A drawback of the traditional level-set method is that its performance is subject to optimal configuration of the controlling parameters (μ, λ and R_b) and appropriate initialization of ϕ (an estimate of the segmentation). This requires substantial manual intervention [19]. The fuzzy level-set based method achieves full automation by first obtaining a probabilistic clustering result using the FCM. This clustering information is then used to determine the initialization and controlling parameters.

On OCT structural images, retinal fluid has a low intensity value compared to the high intensity of surrounding retinal tissue. Based on this intensity contrast, FCM assigns every pixel a probability of belonging to both the fluid and tissue cluster, by minimizing a cost function

$$E={\displaystyle \sum _{i=1}^K{\displaystyle \sum _{j=1}^N{p}_{i,j}^m{\Vert I(j)-C(i)\Vert }^2}},\text{with}{\displaystyle \sum _i^K{p}_{i,j}}=1,\forall j=1,2,\cdots ,N$$ (3)

where K is a predetermined number of clusters, N is the number of pixels, p_i,j is the probability of I(j) belong to the i-th cluster, m is a initialized parameter (m>1) (in this study, m = 2). C(i) is the center of mass of the i-th cluster, and the C of the low intensity cluster is initialized using the mean intensity of vitreous region (above the ILM, top dark area in Fig. 3(A)). The p_i,j and C(i) was updated by Eq. (4) during the iteration of the segmentation process.

$$\{\begin{array}{c}{p}_{i,j}={\left({\displaystyle \sum _{k=1}^K{\left(\frac{\Vert I(j)-C(i)\Vert }{\Vert I(j)-C(k)\Vert }\right)}^{2/(m-1)}}\right)}^{-1}\\ C(i)=\frac{{\displaystyle \sum _{j=1}^N{p}_{i,j}^{m}I(j)}}{{\displaystyle \sum _{j=1}^N{p}_{i,j}^m}}\end{array}$$ (4)

The probability map p_i,j of the lowest intensity cluster (Fig. 4(B)) contains retinal fluid, vitreous, shadows of vessels, and other low intensity regions in or below retina. FCM results were used to initialize ϕ and calculate controlling parameters (μ, λ, R_b in Eq. (1)) for level-set evolution. (detailed implementation can be found in [19]).

Fig. 4.

(A) OCT structural B-scan (y-axis) image of a participant with severe macular edema. (B) Lowest intensity cluster generated by applying fuzzy C-means (FCM) on image (A). (C) Retinal fluid delineated by applying fuzzy level-set method on image (A).

The fuzzy level-set based segmentation method is fully-automated and self-adaptive for images with quality variation. In these DME cases, it detected retinal fluid boundaries (shown in red on the B-scan (y-axis) Fig. 4(C)) with few remaining artifacts, which were filtered out in the following steps.

2.4.2 Voting of cross-sectional segmentations

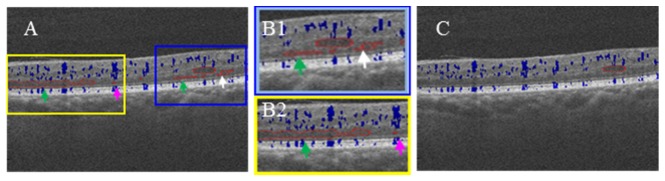
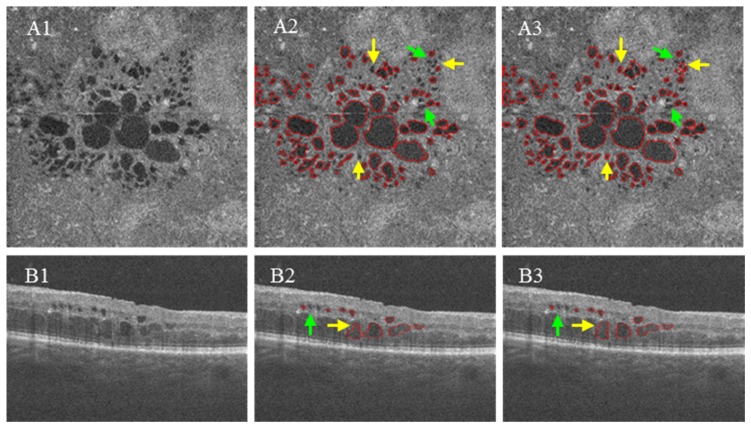
Each voxel at location ω = (x, y, z) has a segmentation result for each of the three cross-sectional orientations (S_YZ, S_XZ and S_YZ). These segmentations vary among the orientations due to differences in image contrast and bulk motion artifacts (Fig. 5, the regions outlined by yellow). In order to improve segmentation accuracy, a voting rule was used to automatically determine the segmentation results for each voxel. If a voxel was identified as belonging to retinal fluid in at least two of the cross-sectional orientations, it was considered to be “true” retinal fluid; otherwise, it was considered as retinal tissue. An example shown in Fig. 5 indicates the segmentation errors are dramatically reduced in the integrated results.

Fig. 5.

Illustration of improving retinal fluid segmentation accuracy by voting of cross-sectional segmentations. (A1) (B1) and (C1) are the segmentation results obtained by applying the fuzzy level-set method on C-scan and two B-scans, respectively. (A2) (B2) and (C2) are the segmentation results represented on a C-scan extracted from (A1) (B1) and (C1). (A3) (B3) and (C3) show a zoomed in perspective of the yellow square region in (A2) (B2) and (C2). (D1) is the segmentation result after voting. (D2) shows a zoomed in perspective of the yellow square region in D1. It can be seen that D2 has much less error than (A3) (B3) and (C3).

2.5 Post-processing

Voting of the results on three cross-sectional orientations improved the accuracy of segmentation. However, some segmentation artifacts still remain (Fig. 5(D1)). Areas of retinal thickening or areas under vascular shadow have low intensity on OCT and can be misclassified as retinal fluid.

Morphological characteristics can distinguish retinal thickening from retinal fluid. Generally, retinal fluid appears as a near-round region with smooth boundaries on OCT cross sections, while retinal thickening has boundaries that change sharply (Fig. 6(A) and 6(B1), marked with white arrows). The smoothness of the boundary quantified by both the shape descriptor [33] and polar coordinates, in addition to the aspect ratio of the region, are all used to remove retinal thickening segmentation errors (Fig. 6(A), 6(B1) and 6(B2), marked with green arrows).

Fig. 6.

Structural OCT B-scan images overlaid with SSADA (blue) and retinal fluid segmentation results (outlined by red). (A) Before post-processing results where segmentation artifacts due to retinal thickening (white arrow, green arrow) and vascular shadow (purple arrow) can be seen in the square regions. (B1) and (B2) showed the zoomed in perspective of the yellow and blue square regions in A. (C) After post-processing image where artifacts contained in the square regions have been removed.

Shape descriptors were reflected by the contour inflexion points of the detected regions [31]. The contour C of the detected region was expressed using two parametric functions x(l) and y(l): C = (x(l), y(l)). where l is a normalized parameter ranging from [0, 1], which represents the length variable. Curvature in variation levels were computed using Eq. (5).

$$\tau \left(l,{\sigma }_1\right)=\frac{X^{\prime }\left(l,{\sigma }_1\right)Y^{″}\left(l,{\sigma }_1\right)-Y^{\prime }\left(l,{\sigma }_1\right)X^{″}\left(l,{\sigma }_1\right)}{{\left\{{\left[X^{\prime }\left(l,{\sigma }_1\right)\right]}^2+{\left[Y^{\prime }\left(l,{\sigma }_1\right)\right]}^2\right\}}^{3/2}}$$ (5)

where, X(l, σ₁) and Y(l, σ₁) are smoothed curves using Gaussian filter g(l, σ₁), X'(·) and X”(·) are first and second derivatives of length l, respectively, and similarly for Y'(·) and Y”(·). The zero-crossing of τ(l,σ₁) indicates the curvature inflexion.

Since we express the curve in polar coordinates, the curve variation can also be reflected in a one-dimensional sequence, following

$$R(l,{\sigma }_2)=\left(\sqrt{{\left[x\left(l\right)-X_o\right]}^2+{\left[y\left(l\right)-Y_o\right]}^2}\right)\ast g\left(l,{\sigma }_2\right)$$ (6)

where (X_o, Y_o) is the center of detected region. The inflexion of R(l,σ₂) is another parameter to evaluate smoothness.

In our study, σ₁ = 12, σ₂ = 6 were used in Eqs. (5) and (6). Zero-crossings of τ(l,σ₁) and inflexions of R(l,σ₂) above the preset thresholds are identified as artifacts. Furthermore, the aspect ratio of the region, the ratio(r) between major axis and minor axis of the minimum enclosing ellipse, was also assessed.

Hemoglobin in perfused vessels absorbs and scatters the incident light of OCT and creates a vascular shadow. The SSADA angiogram, computed using the same OCT scan, can identify these blood vessels. By targeting the low intensity area associated with the vessels from the angiogram, we removed segmentation errors caused by vascular shadowing. Figure 6(A) and 6(B2) provide an example of how we removed the detected regions (indicated by purple arrows). This region can be differentiated as a segmentation error because the far left and far right points both fall within the vascular shadowing.

In the final step, the boundaries of volumetric detected regions were smoothed. We rejected the clutters with dimension smaller than 3 pixels on each axis. Therefore, the smallest fluid volume we can resolve is 30 × 30 × 9.0µm³.

2.6 Quantification and visualization

The fluid volumes were calculated as the product of the number of detected voxels and the voxels dimension (10 × 10 × 3.0μm³) in each scan. Fluid thickness maps were generated by calculating the product of the number of detected voxels and voxel size in each axial position. This was then projected on 2D en face maps. Fluid voxels above the IS/OS reference plane were classified as IRF and those below as SRF. This allowed separate volume calculations and thickness maps of IRF and SRF to be made.

Three-dimensional rendering of retinal fluid were constructed by 3D visualization module of ImageJ (1.49, http://imagej.nih.gov/ij/). This 3D rendering showing the retinal fluid (blue) and OCT angiogram (sepia) can be combined to visualize the retinal fluid in relation to vasculature. Here, en face OCT angiogram was created by projecting the maximum SSADA flow signals internal to BM boundary [20].

2.7 Verification of results

To evaluate the accuracy of the proposed method, we compared our segmentation results with ground truth which is the manually corrected segmentation results. An expert human grader manually corrected the boundaries detected by automated algorithm through the whole volumetric data set. The correction was done on the OCT orientation with the clearest fluid boundaries for contouring. During correction, the grader compared the structural OCT frames at all three orientations to make a grading decision, and use an editing tool incorporated in the same software interface to delineate the correct fluid boundary. The smallest fluid region that the editing tool could resolve was 9 pixels. In order not to introduce too much error during contouring, the regions smaller than this were neglected.

Jaccard similarity metric (J) [34] was used for comparison, which is defined as

$$J=\frac{\left|S\cap G\right|}{\left|S\cup G\right|}$$ (7)

where S is our automated segmentation results, G is the ground truth that is the manually corrected results based on S. The Jaccard coefficient ranges from 0 to 1, where 1 denotes the two were identical and 0 if they were completely different. Errors rates were also computed by comparison to ground truth. False positive error was the ratio of the total number of automatically segmented pixels that were not included in the manual segmentation result to the total number of ground truth pixels. False negative error was the ratio of the total number of manually segmented pixels that were not included in the automated segmentation result to the total number of ground truth pixels. Difference between the automated segmentation results and ground truth is described as the total number of false positive and false negative errors.

We also conducted the same evaluations described above on the fuzzy level-set algorithm using the fast-axis orientation. Paired Wilcoxon rank-sum tests were performed to compare the performance between our proposed algorithm using three different orientations and the simple 2D processing using one orientation only.

We assessed intra-visit repeatability of the proposed method using and intra-class correlation (ICC).

3. Results

The results from automated fuzzy level-set algorithm were compared with the results from manual correction (ground truth). Data from a single eye of 10 participants with DME were analyzed. The results from two representative cases were shown in Fig. 7 and Fig. 8. The first case (Fig. 7) has IRF only and shows the high image contrast between IRF and surrounding tissues. The second case carries both IRF and SRF, and also diffused retinal thickening. It represents a challenging case with low contrast between retinal fluid and thickening. The fuzzy level-set algorithm automatically outlined the boundary of fluid space. The algorithm required about 26 minutes of processing time on an Intel Xeon CPU (E3-1226, 3.3 GHz), of which 73% of the time was spent on the iteration of fuzzy level-set segmentation. Segmentation of each orientation required 6 minutes of processing time.

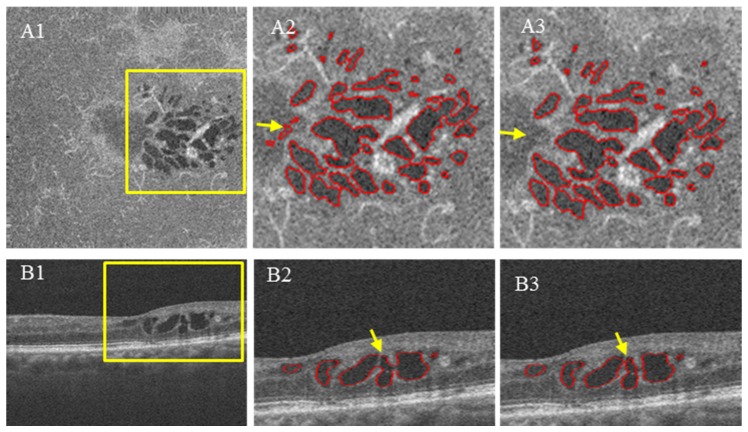
Fig. 7.

Segmentation results compared to ground truth. (A1) and (B1) are original images on C-scan and B-scan. (A2) and (B2) are segmentation results of our proposed method. (A3) and (B3) are ground truth delineated by human expert. Yellow arrows identify the false positive segmentation results corrected by an expert human grader.

Fig. 8.

Segmentation results compared ground truth in a case with both IRF and SRF. (A1) and (B1) are original images on C-scan and B-scan. (A2) and (B2) are segmentation results of our proposed method. (A3) and (B3) are ground truth delineated by human expert. Yellow arrows identify the false negative segmentation results corrected by an expert human grader. Green arrows identify the rejected regions by both automated algorithm and manual correction.

A qualitative comparison between both B-scans and C-scans shows a very small difference between the fuzzy level-set algorithm and expert grading. This difference is due to false positive segmentation where the boundaries between IRF spaces are indistinct (Fig. 7(B2)) and the retinal thickening cause extremely low intensity (Fig. 7(A2)). Some difference was due to false negative segmentation (Fig. 8(A2) and 8(B2)) where the real fluid detected region may be excluded in the step of removing clutters (see 2.5 post-processing). Fluid regions appearing as black holes on C-scans were infrequently missed by the manual grading. This is due to the indistinct size and boundary of small fluid regions (indicated by green arrows in Fig. 8).

Quantitatively, the proposed method agreed well with manual grading, which is significantly higher than the same processing using one orientation only (Tables 1 and 2). Repeatability of retinal fluid measurement was computed from the 2 sets of OCT scans obtained from each eye. The automated method has excellent repeatability as measured by ICC (0.976).

Table 1. The retinal fluid volumes detected by our proposed algorithm and ground truth.

Case		1	2	3	4	5	6	7	8	9	10
Fluid Volume (mm3)	Ground truth	0.286	0.290	0.051	0.022	0.020	0.027	0.059	0.232	0.139	0.052
	Fuzzy level-set	0.297	0.336	0.048	0.024	0.019	0.020	0.065	0.246	0.132	0.051
	Differencea	0.037	0.068	0.009	0.005	0.005	0.007	0.021	0.044	0.023	0.006

^a Difference is the total number of false positive and false negative errors

Table 2. Agreement between automated segmentation and ground truth.

	Our proposed method	Fuzzy level-set on fast-axis	P-valuea
Jaccard similarity metric	0.811 ± 0.052	0.724 ± 0.049	0.005
False positive error	0.092 ± 0.036	0.136 ± 0.461	0.005
False negative error	0.121 ± 0.061	0.232 ± 0.077	0.008

^a P-values were based on paired Wilcoxon rank-sum test.

To visualize the segmented fluid spaces better, the thicknesses of IRF and SRF were projected separately on 2D map (Fig. 9(A) and 9(B)), and 3D volumetric fluid were rendered separately (Fig. 9(D) and 9(E)). The detected IRF in the case shown stays together in the same region, appearing in petaloid pattern. The detected SRF are shown as a large dome shape, which corresponds to the classical pattern. An en face composite map combining fluid volume map and angiogram presents the vasculature and the fluid cysts in an intuitive fashion and highlights the relationship between the vascular and anatomic changes in DR (Fig. 9(C) and 9(F)).

Fig. 9.

Quantification of volumetric spaces of retinal fluid. (A) Thickness maps of intraretinal fluid (IRF). (B) Thickness maps of subretinal fluid (SRF). (C) En face retinal OCT angiogram. (D) 3D rending of IRF volume. (E) 3D rending of SRF volume. (F) OCT angiogram overlaid with retinal fluid thickness map.

4. Discussion and conclusion

We developed an automated volumetric segmentation method to quantify retinal fluid (IRF and SRF) on OCT which involves three main steps: (1) segment and flatten retinal layers; (2) identify retinal fluid space using a fully automated and self-adaptive model (fuzzy level-set method) on OCT cross-sections from three orthogonal directions (two types of B-scans and C-scans); (3) remove remaining artifacts by identifying morphological characteristics and vascular shadowing. We showed that the proposed algorithm can detect and quantify the retinal fluid in DME eyes with a varied image contrasts. The fuzzy level-set algorithm agreed with expert human grading very well. Our technique offers a major advance in providing clinically valuable quantitative measurements of IRF and SRF.

The clinical relevance of IRF and SRF on OCT is well established. Resolution or stabilization of IRF and SRF was a main indicator of disease activity for the studies of DME, neovascular aged-related macular degeneration (AMD) and retinal vein occlusion [35–40]. Current OCT platforms provide retinal thickness and volume measurements, but the retinal fluid volume may be a more robust and accurate biomarker of disease activity compared to retinal thickness and volume. Numerous factors such as atrophy and fibrosis, in addition to vascular permeability, influence retinal volume. An automated segmentation technique that provides a quantitative measurement of retinal fluid could offer a more precise tool in the management of macular diseases with hyperpermeability.

Despite its clear applicability, automated detection of volumetric retinal fluid has been a poorly explored area. No commercial system offers this function, leaving the identification of fluid space to subjective assessment or manual delineation. Carera Fernandez [17] applied active contours (a gradient vector flow snake model) to extract fluid regions in retinal structure of AMD patients. This method is slow and requires substantial grader input, including initial boundary location estimation. Wilkins [41] described an approach for automated segmentation of retinal fluid on Cirrus OCT of cystoid macular edema. This method applies an empirical thresholding cutoff on the contrast enhance images by bilateral filtering, sparse details were presented on the assessment of the segmentation reliability. Chiu [16] recently presented a fully automated algorithm based on a kernel regression classification method to identify fluid-filled region in real world spectral domain OCT images of eyes with severe DME. However, this algorithm did not yet distinguish between intraretinal from subretinal fluid or focal from diffuse retinal thickening. All aforementioned algorithms were developed for 2D OCT images only. Quellec [13] and Chen [14] introduced an approach working on volumetric data set using prior information to classify the fluid associated abnormalities based on feature- and layer-specific properties in comparison with the normal appearance of macula. Unfortunately this method did not provide a clean measurement of fluid-filled space.

Compared to the previously reported methods using 2D images, our method makes full use of the volumetric information by operating detection on three directions. The voting process increases the accuracy of detecting true fluid voxels. The remaining false positives are rejected using morphological characteristics and OCT angiography.

There are several reasons leading to the use of level-set segmentation on 2D instead of 3D. First, the time cost of segmentation step using 2D algorithm is lower than 3D algorithm. This is because the complexity of 2D algorithm [O(n²)] is lower than 3D algorithm [O(n³)]. Second, the segmentation of each frame is independent; therefore, parallel computing could further shorten the processing time. Furthermore, the 2D algorithm can easily incorporate manual grading results, making the trouble-shooting easier compared to 3D approach.

In our proposed method, we removed the dependence on parameter tuning and the needs for initialization by using a rigorous classification algorithm. This classification assumes that the retinal fluid filled regions have similar reflectance to the vitreous region. The classification initialized by the intensity of vitreous avoids the process of data training for searching optimal parameters, so that it has a strong self-adaptive capacity. This is critical in applying the method to real world clinical situations where a wide variability of image quality and pathology exists. Due to its self-adaptive capability, this classification method would enable utilizing data sets acquired from multiple different clinical OCT systems. Although our method was developed on the OCT angiography scan pattern from a commercial spectral domain OCT (Optovue RTV-ue XR Avanti) it can be applied easily to other OCT devices that generates volumetric scans. The removal of vascular shadowing artifact can be modified by use of other criterion as described in [41].

In summary, this novel algorithm can automatically detect and quantify retinal fluid space accurately, offering an alternative and possibly more meaningful way to evaluate diabetic macular edema than total retinal thickness and volume.