A spatiotemporal theory for MRI T₂ relaxation time and apparent diffusion coefficient in the brain during acute ischaemia: Application and validation in a rat acute stroke model

Abstract

The objective of this study is to present a mathematical model which can describe the spatiotemporal progression of cerebral ischaemia and predict magnetic resonance observables including the apparent diffusion coefficient (ADC) of water and transverse relaxation time T₂. This is motivated by the sensitivity of the ADC to the location of cerebral ischaemia and T₂ to its time-course, and that it has thus far proven challenging to relate observations of changes in these MR parameters to stroke timing, which is of considerable importance in making treatment choices in clinics. Our mathematical model, called the cytotoxic oedema/dissociation (CED) model, is based on the transit of water from the extra- to the intra-cellular environment (cytotoxic oedema) and concomitant degradation of supramacromolecular and macromolecular structures (such as microtubules and the cytoskeleton). It explains experimental observations of ADC and T₂, as well as identifying the rate of spread of effects of ischaemia through a tissue as a dominant system parameter. The model brings the direct extraction of the timing of ischaemic stroke from quantitative MRI closer to reality, as well as providing insight on ischaemia pathology by imaging in general. We anticipate that this may improve patient access to thrombolytic treatment as a future application.

Introduction

MRI has the potential to make highly detailed and objective assessments of the brain in patients suffering ischaemic stroke.^1,2 However, there yet exists no widely accepted method for the inversion of MRI observations to parameters describing ischaemia in a clinical sense, including the time of onset. It is therefore desirable to have a framework for modelling ischaemia that can be fitted to MRI data, as well as predict the spatio-temporal progress of ischaemia, in the time window for which patients are eligible for current drug protocols.¹ For acute stroke, the time of onset is one of the key factors in decision-making for potentially beneficial and safe administration of thrombolytic therapy.^3,4 However, as many as 30% of acute stroke patients lack the data allowing exact onset time to be determined at the time of admission to emergency medicine,⁵ thus prompting need for an objective means for timing of stroke. It is well established that absolute relaxation times of brain water change in a time dependent manner in focal brain ischaemia.^6–9

Apparent diffusion coefficient (ADC) mapping (the voxel-wise fitting of ADC values from a set of diffusion-weighted images) has for some time been used as the gold standard for locating lesions caused by ischaemia. The ADC for water is highly sensitive to the location of ischaemia, reducing rapidly after onset, ^10–13 but carries little information on the time of onset, stabilising rather quickly after onset. In hyperacute ischaemia, a shortened T₂ is detected for up to 60 min after vascular insult,¹⁴ followed by an increase for the first 5–6 h of insult. Recent preclinical^15,16 and clinical¹⁷ studies have demonstrated that the time course of T₂ relaxation times in diffusion-positive stroke lesions can be described heuristically by linear¹⁵ or quadratic¹⁷ functions. Indeed, the potential of the T₂ MRI signal to aid in clinical decision-making for thrombolytic therapy has been clinically trialled using T₂-FLAIR/ADC mismatch as a proxy of stroke duration.¹⁸ While this approach has acceptable specificity for stroke timing, it suffers from rather low sensitivity for patient stratification.¹⁹ The reason for the low sensitivity is currently researched; however, our rodent study suggested that absolute relaxation times, but not weighted signal intensities, are able to provide accurate timing for ischaemia.¹⁶

A major difficulty in using MRI to assess ischaemia is relating its many observables to parameters of direct clinical utility. The complex relationships between MR acquisition parameters and ischaemia “system” parameters are not understood, yet at the very least the dominant system parameters should be identified before realistic attempts to make objective assessments of ischaemia from quantitative MRI data.⁹ There currently exists no combined mathematical model capable of explaining spatio-temporal changes in both ADC and T₂ of the type observable in MRI experiments, though there has been useful progress. In particular, a model based upon oxygen metabolism has been able to explain reductions in T₂²⁰ but was not spatio-temporal, whilst a recent approach used diffeomorphic mapping to explain spatiotemporal changes in diffusion/perfusion mismatch lesion morphology but not ADC or T₂ values.²¹ An approach to determine the distinct penumbra and lesion, based on integrating various physiological processes, has also been proposed, which, although not constructed for the prediction of MRI parameters, is quite comprehensive and is able to model cytotoxic oedema.²²

Part of the difficulty is that the biophysical mechanisms for the changes in ADC and T₂ remain ambiguous from experimental findings.^10,23,24 Early work identified a redistribution of water between intra- and extracellular spaces as a determinant of ADC in ischaemia.^25–29 Theoretical and experimental models for ADC have considered changes in cell membrane permeability and intra/extracellular water distribution,^24,30,31 restricted diffusion,^32–34 and extracellular tortuosity.^30,32,35 An emerging picture is that a redistribution of water from the extra- to intracellular space, although insufficient to account for the ADC changes in the acute phase of ischaemia alone, may do so, if concomitant changes in either the intracellular or extracellular environment are accounted for.²⁹ However, to reiterate, no such model has yet carried its assumptions across to the simultaneous prediction of T₂ from the same principles.

The objectives of this study were three-fold: (i) to develop a spatiotemporal model for ischaemia which simultaneously predicts T₂ and ADC changes; (ii) to compare its predictions with measurements made in a rat model of ischaemia, and (iii) to establish an automated procedure to delineate volumes with abnormal T₂ values inside the ischaemic lesion for an unambiguous assessment from combined diffusion and absolute T₂ data. To the latter end, we have used quantitative diffusion and T₂ MRI data from rat stroke model. Clinical applicability of the approach is discussed.

Materials and methods

Animal model for stroke and MRI data acquisition

Male Wistar rats (n = 5, weight 200–300 g) were exposed to permanent middle cerebral artery occlusion (MCAo) according to Longa et al.³⁶ The occluding thread was left in place for the duration of the MRI scanning and the animal was sacrificed thereafter by decapitation in deep isoflurane anaesthesia. All animal procedures were approved by the Committee for the Welfare of Laboratory Animals of the University of Eastern Finland and the Provincial Government of Kuopio, Finland, and conducted in accordance with the guidelines set by the European Community Council Directives 86/609/EEC.

Scans were conducted using a horizontal 9.4 T Agilent MRI scanner (Agilent, Palo Alto, CA, USA) equipped with an actively decoupled linear volume transmitter and quadrature receiver coil pair (RAPID Biomedical GmbH, Rimpar, Germany). Each “measurement” comprised a three-plane (orthogonal) diffusion-weighted sequence (b-values = 0, 400, 1040 mm² s⁻¹; TE = 36 ms, TR = 2000 ms) and a multi-echo spin-echo sequence (12 echoes 10 ms inter-echo spacing, starting at 10 ms, TR = 2000 ms). Twelve slices were imaged with the following parameters: 0.5 mm gap, slice thickness = 1 mm, FOV = 2.56 cm × 2.56 cm was covered by 128 × 256 points. Such measurements, each taking ∼20 min, were made at times commencing 60, 120, 180, and 240 min after MCAo.

Image processing for rat data

To increase the confidence of parameter estimates, all data prior to fitting were filtered with a squared Hamming window function in the phase and frequency encoded dimensions in k-space. T₂ fitting was performed by a mono-exponential fit in a logarithmic space, in which the system was solved on a voxel-wise basis using linear least squares by the Moore-Penrose pseudo-inverse. A bi-exponential function was also fitted, but f-tests at each voxel revealed virtually no voxels within the image for which the additional parameters could be justified (see Supplementary material). An image of p-values for these f-tests is provided in the SI.

Trace of diffusion tensor (ADC) maps were calculated from diffusion-weighted data by the analytical solution to the diffusion equation.

In order to define an ADC lesion, it was found to be easier to use reciprocal ADC values, such that the lesion is bright with high values akin to T₂ maps later on during MCAo. Such an ADC map is proportional to the translational correlation time (and its cube the rotational correlation time). Lesion detection proceeds by selecting voxels which have values significantly higher than average in the reciprocal-ADC map, as well as fulfilling any additional filters in use (such as excluding unrealistic T₂ values likely to be CSF, for instance). By “higher than average”, we found that 1 standard deviation above the median, when using reciprocal ADC values, was very effective. However, with such large datasets, equally stable results were obtainable using the mean or mode to define the “average”.

The “lesion” is then stored as a binary mask. This will typically contain several distinct clusters of non-zero voxels, and even single voxels due to noise in the data. It is therefore filtered to remove clusters of voxels smaller than a prescribed cluster size, in order that clusters too small to realistically be ischaemic lesions are removed. The smallest acceptable lesion is a user-supplied parameter.

To complement average T₂ in the ADC lesion, we introduce the parameter f₂, given by

$$f_2=\frac{N^{\mathrm{High}}-N^{\mathrm{Low}}}{N^{\mathrm{Lesion}}}$$ (1)

where N^High is the number of high T₂ voxels in the lesion, N^Low is the number of low T₂ voxels in the lesion, and N^Lesion is the total number of voxels in the ADC lesion. A T₂ observation is counted as “high” if its value is more than one half-width at half-maximum higher than the modal T₂, and “low” if less than one half-width at half-maximum below the modal T₂ (this definition being numerically stable). Numbers of voxels can of course be replaced with volumes and the result is unchanged. The parameter f₂ offers advantage over average T₂ for lesion assessment being relatively insensitive to the B₀ field variation. In addition, the subtraction of the N^Low term allows for decreases in relaxation times due to ischaemia or other pathology. Its values are between −1 and 1.

All image pre-processing, computation of parametric maps, as well as lesion detection were conducted by software written in-house using the Matlab programming environment (Mathworks, Natick, MA, USA) unless otherwise specified.

Model for MRI parameters in ischaemic brain parenchyma

Our spatio-temporal model may be qualitatively summarised as follows: upon ischaemia with collapse in energy state, water moves from the extra- to the intracellular environment. However, as mentioned already, this is insufficient to explain either ADC or T₂ changes. We therefore invoke, in the intracellular environment, a two-state model for water in which it exists in exchange between a “free” state and one in which it is bound to macromolecules and supra-macromolecular structures (such as microtubules and other cytoskeletal structures). The ADC of the latter state is assumed to increase with time after insult due to dissociation and/or proteolysis.²⁹ The transit of water from the extra- to intracellular space may be interpreted as cytotoxic edema, whilst the concomitant disassembly of supra-macromolecular structures, collectively a dissociative process, gives rise to the name “cytotoxic oedema/dissociation” (CED) model. This is summarised in Figure 1, along with the terms that are used in its mathematical formulation. We do not consider vasogenic oedema, involving disruption of the blood-brain-barrier, in our model.

Figure 1.

The “Cytotoxic oEdema Dissociation” (CED) model for ischemia. Water is represented by red dots, the entire system by the black line, partitioned into the intra- and extra-cellular spaces. Macromolecules and supra-macromolecular structures are represented by blue objects. The various symbols of the model are indicated; K_F(t) is the partition coefficient for water across the cell membrane with time dependence encoded by δ. K_I is the (time-independent) equilibrium constant between bound and free intracellular water. D_EF and D_IF are the time-independent diffusion coefficients for the free extra- and free intracellular states, respectively, whilst D_IB(t) is the time-dependent diffusion coefficient for the bound intracellular state with time dependence encoded by ɛ.

More rigorously, we consider three “pools” of water; the free extracellular (“EF”) water, the free intracellular (“IF”) water and the bound intracellular (“IB”) water. The EF and IF states exchange across in plasma membrane with time-dependent equilibrium constants K_F, whilst the IF and IB states are in exchange with equilibrium constant K_I. To obtain an MR parameter, we model magnetic moments using the Bloch–McConnell–Torrey equation for transverse magnetisation, given by

$$\frac{\partial }{\partial t}{\overrightarrow{M}}^{+}(t,\overrightarrow{X})=(-i\Omega \mathbf{\Omega }-i\gamma \overrightarrow{G}.\overrightarrow{X}-{\mathbf{R}}_2(t)+\mathbf{D}(t){\nabla }^2+\mathbf{K}(t)){\overrightarrow{M}}^{+}(t,\overrightarrow{X})$$ (2)

Here, Ω is a diagonal matrix of chemical shifts, R₂ a diagonal matrix of transverse relaxation rate constants, D a diagonal matrix of (isotropic) diffusion coefficients, K the kinetic matrix, i the imaginary unit, γ the gyromagnetic ratio for the relevant nucleus (in this case ¹H), G the magnetic field gradient, X a Cartesian coordinate vector, and ${\overrightarrow{M}}^{+}(t,\overrightarrow{X})$ the complex-valued transverse magnetisation at time t and position X. The field gradient and diffusion term is relevant only for ADC modelling. If there is no field gradient applied, then we can ignore the effect of translational diffusion. For numerical simulations, the time-evolution can be evaluated by means of

$${\overrightarrow{M}}^{+}(t_k)=\exp ((\mathbf{L}(t_{k-1})+\mathbf{L}(t_k))\Delta t/2){\overrightarrow{M}}^{+}(t_{k-1})=\mathbf{U}\exp (\mathbf{V}(t_k,t_{k-1})\Delta t/2){\mathbf{U}}^{-1}{\overrightarrow{M}}^{+}(t_{k-1})$$ (3)

where L represents the time-evolution operator appropriate for the simulation, $\Delta t=t_k-t_{k-1}$, and in the second line U and V are the eigenvector and eigenvalue matrices of the time evolution operator, respectively, such that U diagonalises $\mathbf{L}(t_{k-1})+\mathbf{L}(t_k)$. The time-zero magnetisation is given by the equilibrium water fraction vector $\overrightarrow{f}(0,\overrightarrow{X})$. The T₂ or ADC, as appropriate, is then the least-squares fit to the observable signal

$$S(t_k)=\sum _j|{\overrightarrow{M}}_j^{+}(t_k)|$$ (4)

In the case of ADC, typically we used only two b-values in the simulations, rather than the entire time-domain signal, in which case the ADC has the simple and well known form

$$\mathrm{ADC}=-\frac{\ln (S(b_0))-\ln (S(b_1))}{b_1-b_0}$$ (5)

where the b-value has the usual definition

$$b={\gamma }^2{G}^2{t}^3$$ (6)

The exchanging system is governed by the set of differential equations

$$\frac{\partial }{\partial t}\overrightarrow{f}(t,\overrightarrow{X})=\mathbf{K}(t,\overrightarrow{X})\overrightarrow{f}(t,\overrightarrow{X})$$ (7)

where K is the kinetic matrix describing the system and $\overrightarrow{f}(t,\overrightarrow{X})$ is the vector-valued fractional concentration, ordered f_IB, f_IF, f_EF. They satisfy the identity

$$f_{\mathrm{IB}}+f_{\mathrm{IF}}+f_{\mathrm{EF}}=1$$ (8)

The EF and IF states exchange across the plasma membrane, whilst the IF and IB states exchange intracellularly. Defining k_mn as the reaction rate constant between states m and n, we can then write the rate matrix K as

$$\mathbf{K}=(-k_{\mathrm{BF}}^I{k}_{\mathrm{FB}}^{I}0k_{\mathrm{BF}}^I-k_{\mathrm{FB}}^I-k_{\mathrm{IE}}^F{k}_{\mathrm{EI}}^{F}0k_{\mathrm{IE}}^F-k_{\mathrm{EI}}^F)$$ (9)

For example, $k_{\mathrm{BF}}^I$ is the first-order rate constant for the exchange from the IB state to the IF state. We define the following equilibrium constants

$$K_I=\frac{f_{\mathrm{IF}}}{f_{\mathrm{IB}}}=\frac{k_{\mathrm{BF}}^I}{k_{\mathrm{FB}}^I}$$ (10)

$$K_F=\frac{f_{\mathrm{EF}}}{f_{\mathrm{IF}}}=\frac{k_{\mathrm{IE}}^F}{k_{\mathrm{EI}}^F}$$ (11)

We model cytotoxic oedema by making the parameter K_F, the equilibrium constant for partition of water between the intra- and extracellular spaces, a function of time. We use the heuristic expression

$$\frac{1}{K_F(t)}=\exp (-\frac{t}{\delta })(\frac{1}{K_F(0)}-\frac{1}{K_F(\infty )})+\frac{1}{K_F(\infty )}$$ (12)

where δ is the time constant for water uptake by cells, and $K_F(0)$ and $K_F(\infty )$ refer to the values of K_F in the non-ischaemic state and at the end of the acute phase, respectively.

Changes in the intracellular ADC for the bound state, D_IB, are modelled by a similar heuristic function

$$D_{\mathrm{IB}}(t)=\exp (-\frac{t}{\varepsilon })(D_{\mathrm{IB}}(0)-D_{\mathrm{IB}}(\infty ))+D_{\mathrm{IB}}(\infty )$$ (13)

where ɛ is the time constant for the changes in intracellular diffusion coefficient due to reduced averaged macromolecular size or other processes, again with its values in the non-ischaemic state and at the end of the acute phase required. The value of $R_2^{\mathrm{IB}}(t)$ is then calculated from $D_{\mathrm{IB}}(t)$ using the expression for dipolar relaxation

$$R_2^{\mathrm{IB}}(t)=\frac{3}{40}{d}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\times (6{\tau }_{\mathrm{IB}}(t)+\frac{10{\tau }_{\mathrm{IB}}(t)}{1+({\omega }_H{\tau }_{\mathrm{IB}}(t){)}^2}+\frac{4{\tau }_{\mathrm{IB}}(t)}{1+(2{\omega }_H{\tau }_{\mathrm{IB}}(t){)}^2})$$ (14)

where d is the intramolecular dipolar coupling constant for the water protons and the term ${\tau }_{\mathrm{IB}}(t)$ is related to $D_{\mathrm{IB}}(t)$ through the Stokes–Einstein relations and can be written as

$${\tau }_{\mathrm{IB}}(t)=\frac{(k_{B}T{)}^2}{162{\pi }^2{\eta }^2{D}_{\mathrm{IB}}(t{)}^2}$$ (15)

Here, k_B is Botlzmann constant, T is the absolute temperature, and η is the solvent viscosity.

Finally, as a model of the spread of ischaemia through tissue, we assume the lesion to be spherical, spreading with kinetics described by

$$L(t)=\alpha (1-\exp (-\frac{t}{\beta }))$$ (16)

where L(t) is the radius of the lesion at time t, α is the final radius of the lesion, and β is the time constant for the spread of ischaemia. The total volume of a spherical lesion can then be expressed as

$$V(t)=\frac{4\pi }{3}{\alpha }^3(1-\exp (-\frac{t}{\beta }){)}^3=v_{\mathrm{Lesion}}(1-3\exp (-\frac{t}{\beta })+3\exp (-\frac{2t}{\beta })-\exp (-\frac{3t}{\beta }))$$ (17)

The simulations were designed and conducted using software written in-house in the Matlab programming environment. Further details can be found in the Supplementary material (equations (S1)-(S27)).

Results

MRI changes in rat MCAo

The ADC lesion, with T₂ segmentation, along with the other images acquired at several time points for a typical rat brain which has undergone MCAo is shown in Figure 2. The ADC lesion detected by the current method is a realistic and well-defined volume. The ADC lesion expands with time, as does the fraction of elevated T₂ voxels (shown in red in Figure 2(a), (f), (k), and (p)). It is clear that a considerable amount of tissue within the lesion retains a T₂ relaxation signature characteristic of healthy tissue. Growth of high-T₂ area within the ADC lesion has a time dependence associated with it, which may reflect a transition to irreversible ischaemic damage.^6,8,9 Inspection of the T₂-weighted images shows that the T₂ segmentation is not merely a separation of tissue types (such as gray and white matter), though this may come into play to some extent in other species.

Figure 2.

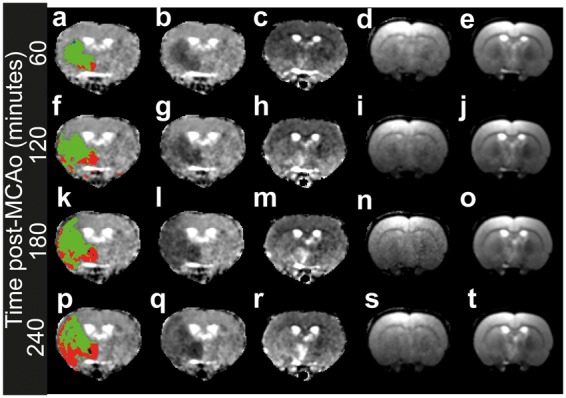
Example of lesion detection and T₂ segmentation over time in rat brain. The MRI data in rows were recorded at different time points, whilst columns are different image types. Row 1 (a–e), 60 min post-MCAO, row 2 (f–j), 120 min post-MCAO, row 3 (k–o) 180 min post-MCAO, row 4 (p–t) 240 min post-MCAO. The first column shows the ADC map with the lesion shown. Green denotes regions with “normal” T₂, red with elevated T₂, blue (apparent only in a) reduced T₂ (see text). Column 2 shows the ADC map alone, column 3 shows the T₂ map, column 4 the I(0) map from T₂ fitting, and column 5 the T₂-weighted images.

The T₂ kinetics of ischaemia are summarised for several different animals (Figure 3). It is striking that lesions expand into healthy-appearing regions at very different rates, and that this is apparently manifested in the T₂ absolute percentage difference (APD) between voxels in the ADC lesion and those outside, and likewise f₂ (additional figures are provided in the Supplementary material). The lesion volume, despite the aspherical nature of the lesions, could be described by equation (17), enabling extraction of effective ischaemic spread time constants and radii (which are later compared to theoretical predictions of the CED model).

Figure 3.

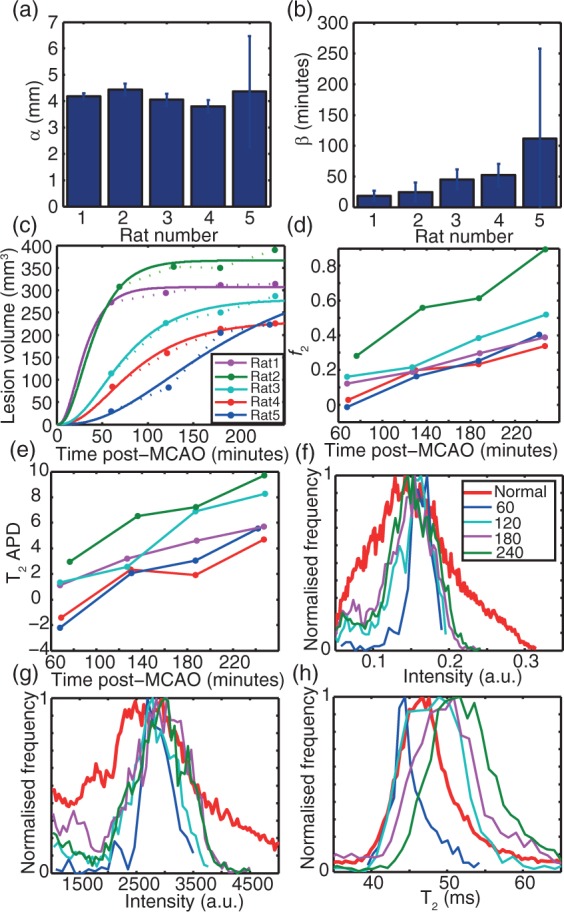
Time dependence of MRI parameters relating to ischaemia in rat MCAo. (a–e) findings for all animals; (f–h) detailed findings for a typical animal (Rat 3, f–h all use the legend as in f). (a,b) Fitted effective lesion radii and time constants, respectively, using equation (16), showing 95% confidence intervals on fitted parameters; (c) lesion volume by automated detection including the fit using the parameters in (a and b) and equation (16). Solid lines indicate the fit, dotted lines connect points for visual guidance; (d) f₂ for all animals plotted separately; (e) absolute percentage difference (APD) for T₂ between lesion and non-lesion for all animals. Panels (c) to (e) share the legend shown in (c). (f) In a typical animal, the distribution of I(0) derived from T₂ fitting as a function of time; (g) Echo-summed T₂-weighted signal intensities obtained by summing all 12 echoes with TEs ranging from 10 ms to 120 ms; (h) absolute T₂ distribution. In (f) to (h), the “normal” reference histogram (red) is derived from all non-lesion voxels for the 60-min post-MCAO scan.

The f₂ parameter is very stable across all animals (Figure 3d). Comparison to APD between average lesion and non-lesion T₂ (Figure 3e) shows that f₂ kinetics were better separated between animals. We therefore surmise that f₂ is a potentially sensitive marker of the time dependence of ischaemia, more numerically stable than T₂ APD.

The change in T₂ distribution shows a progression towards higher values as time elapses, with approximately normal distributions but with increasing widths. T₂ distribution therefore becomes wider as time progresses, a manifestation of the differential kinetics of ischaemia at different spatial coordinates (Figure 3h). Such clear time dependence is not apparent in the I(0) (Figure 3f) or T₂-weighted intensities (Figure 3g).

Simulations of MRI parameter changes in ischaemia using the CED model

The predictions of the three-state CED model for brain tissue within ischaemic ADC lesion, where T₂ changes take place within minutes of insult, are shown during the first 30 min after onset (Figure 4). In all the simulations we present, a lesion radius (α) of 3.5 mm is used, motivated by the experimental data (Figure 3a), with the ischaemic spread time constant (β) having values from 10 to 180 min, again in the range of our experimental findings (Figure 3b). Further details of values of simulation parameters can be found in the Discussion section. In the Supplementary material, video simulations are also provided. At an individual voxel, for argument’s sake the site of onset, the time course of the ADC is predicted to comprise a rapid drop initially stabilising at the low level. By contrast, the T₂ first drops, then increases monotonically, eventually rising well above the baseline value. The timescale on which cells increase permeability to water, described by the parameter δ, was influential only in the first 30 min after onset of ischaemia (Figure 4). Thereafter, over at least an order of magnitude, the model was stable to the value of δ.

Figure 4.

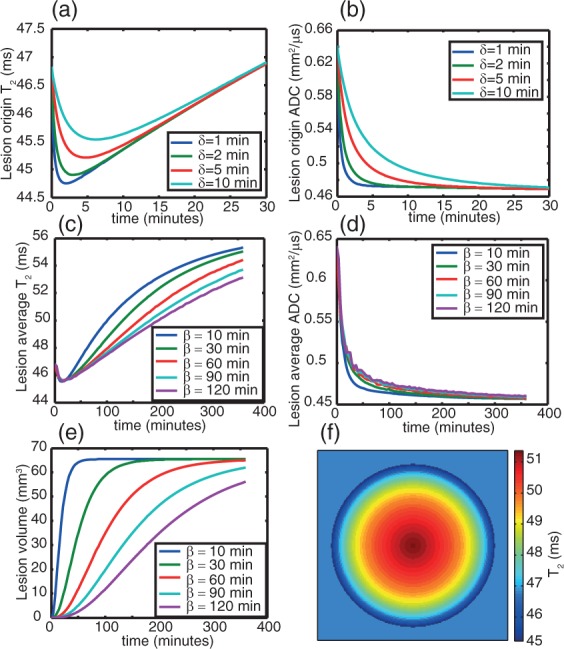
Simulation of the time-course of T₂ and ADC using the CED model. Panels (a) and (b) show the early time dependence of T₂ (a) and ADC (b) respectively, demonstrating different behaviour for different oedema timescales (given by δ). Panels (c) and (d) shows T₂ (c) and ADC (d) kinetics over a longer timescale, for a fixed value of δ = 2 min but different values of β (the lesion growth coefficient), which is the main determinant of T₂ and ADC kinetics after 30 min. Panel (e) shows the lesion volume kinetics for different β values; panel (f) shows the heterogeneity of T₂ within a simulated circular lesion 2 h after onset at β = 60 min.

It is common practice to report the average ADC or T₂ (or any other parameter) over a lesion, rather than values recorded at any particular voxel. For this reason, we have also simulated the time-course of the average (i.e. over an entire lesion) ADC, T₂, I(0), sum-of-echoes intensities and I(TE_optimal), where I(0) is the signal intensity before any T₂ decay and TE_optimal denotes the TE calculated to give optimal contrast between healthy and ischaemic tissue (this TE lies between that of the healthy and ischemic tissue and is ∼50 ms at 9.4T). These results are shown in Figure 4c-f, where the heterogeneity of T₂ within the lesion is also simulated (Figure 4f). From Figure 4(f), we can see that an average parameter over a lesion is a complex term, dependent on the entire history of the lesion, discussed further in the Supplementary material (equations (S26) to (S27), Figures S1–S2).

The “average” ADC kinetics are, unsurprisingly, similar to those at a single coordinate and in agreement with the experimental findings here and by others.^8,9 The predictions for the T₂ kinetics both at a single coordinate and across an entire lesion are also consistent with experiment; initially, the T₂ drops, then increases again monotonically after the minimum has been passed. The shape of this function, under the assumption of a spherical, cylindrical or circular model for the lesion morphology, depended most strongly upon the parameter β, describing the rate of lesion growth. The prediction is in good agreement with the experimental finding that the T₂ increases can be heuristically described with a linear or quadratic function, though rigorously it is neither. Interestingly, the T₂ kinetics at different β values, when sampled at times longer than 60 min, are approximately parallel lines, very similar to the experimental findings (Figure 3 d and e), such that the rate of lesion growth, that is, the rate at which effects of ischaemia extends throughout a tissue, may be able to explain the different time courses of T₂ in the different test animals. In the case of ADC, however, this parameter made almost no difference. These simulations are shown in Figure 4.

Combining the CED model with the lesion detection method

We next used a set of T₂-weighted and diffusion-weighted scans measured for a control rat to simulate an ischaemic stroke with the CED model, including a realistic noise level measured experimentally (the SD of signal intensity in an ROI placed in a single tissue). Using these detailed simulations, we sought to detect the simulated lesion with the approach described in the Methods section as a means of both validating the detection approach and examining the validity of the model under the most realistic circumstances. The simulated lesion was spherical with known size and position, so that the accuracy of its “experimental” determination could be assessed.

Figures 5 and 6 show the results from these simulations, which should be compared to Figures 2 and 3. The lesion masks in Figure 5 are very close to the simulated lesions, with only a few voxels spuriously missed or erroneously included, a finding expected in the presence of noise. This is an encouraging sign that the approach to automated detection of lesions is robust. Figure 6 demonstrates simultaneously the robustness of the detection method and accuracy of the model; the changes in f₂ and APD as a function of lesion growth are very similar to that seen experimentally. The distributions of T₂ with time are also similar to the experimental observations; one hour after onset of ischaemia, the T₂ distribution of the lesion is rather narrow, before becoming broader but longer on average, then contracting in width again. The α and β input parameters are reproduced well by the automated lesion detection when equation (17) is fitted to the resulting lesion volume data, as seen in Figure 6(b) to (d).

Figure 5.

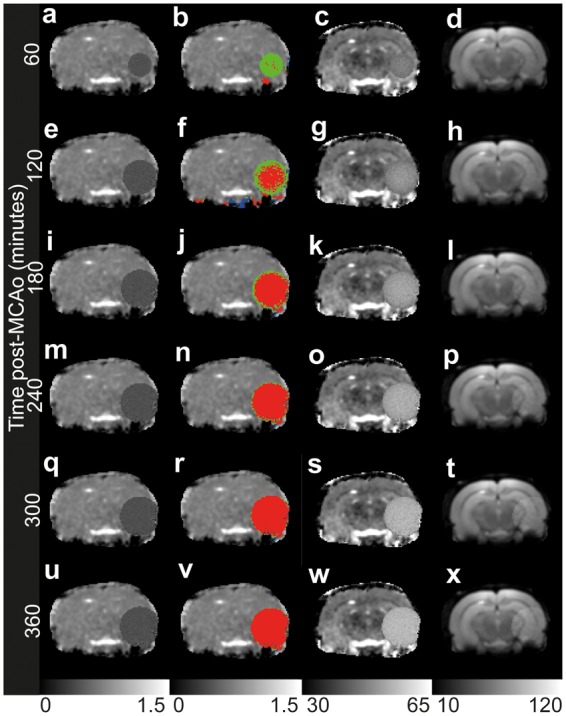
Lesions simulated in diffusion-weighted and T₂-weighted data from a control rat and detected using the automated procedure given in the Methods section at different times post-onset. Panels (a, e, i, m, q, u): ADC maps with scale bar in mm²/µs. Panels (b, f, j, n, r, v): ADC maps with automatically detected lesions, coloured by proximity of T₂ to healthy values (for details see Figure 1 legend) with scale bar in mm²/µs. Panels (c, g, l, o, s, w): T₂ maps with scale bar in ms. Panels (d, h, k, p, t, x): T₂-weighted maps at a TE of 50 ms, calculated as the optimum TE, with scale bar in arbitrary units.

Figure 6.

Time-dependence of MR parameters in lesions simulated in otherwise experimental data detected automatically using the criteria given in the Methods section, as a function of post-MCAO time and the lesion progression time coefficient β. (a): f₂. (b) Lesion volume including the fit using equation (16) shown in solid lines. Dotted lines connect points as a visual guide. (c) and (d) α and β parameters, respectively, fitted to the extracted lesions from the simulated data using the automated procedure. (e) APD between the detected lesion and non-lesion T₂. (f) Using β = 60 min, T₂ histograms are plotted as a function of post-MCAO (onset) time. (g) and (h) APD between the detected lesion and non-lesion T₂-weighted intensity at the optimum TE of 50 ms and T₂-weighted intensity histograms for β = 60 min, respectively. (i) and (j) APD between the detected lesion and non-lesion echo-summed T₂-weighted signal intensities and histograms of echo-summed T₂-weighted signal intensities for β = 60 min, respectively. Panels (k) and (l) show the APD between the detected lesion and non-lesion I(0) (as determined from T₂ fitting) and I(0) histograms for β = 60 min, respectively. Panels (a, b, c, e, g, i, k) share the legend shown in panel (a). Panels (f, h, j, l) share the legend shown in panel (f).

We also simulated T₂-weighted images for a TE of 50 ms, which was calculated to be the optimal TE at 9.4 T for contrasting healthy and infarcted tissue (a TE of 50 ms is close to the T₂ of the healthy brain parenchyma at 9.4 T). The resulting intensity distributions gave no clear separation of ischemic from non-ischemic tissue (Figure 6(g) and (h)). T₂-weighted image intensity, even when optimised, is thus a far less robust experimental parameter to describe the ischaemic lesion than quantitative T₂ (Figure 6). In these simulations, it was also observed that the use of an optimal TE gave near-identical results to using the sum of all echoes in a multi-contrast experiment, whereas the I(0) fitted during the computation of a T₂ map (a proxy of proton density) gave different, and also rather uninformative, results.

Discussion

Predictions of the CED model and qualitative agreement with experiment

We have introduced a simple automated method for the rapid detection of cerebral ischaemia using quantitative ADC and T₂ maps, as well a theoretical framework which explains many MRI observations and has enabled the validation of our lesion detection method. In particular, the CED model is able to provide a rational basis for the previously observed quasi-linear increase in T₂ with time during the hyper-acute phase of ischaemia, the slower changes in T₂ as compared to ADC, and identifies the rate of spread of ischaemia through rat brain parenchyma, encoded by the model parameter β, as the critical system parameter that directs the different form of the T₂ time dependence in different areas of ischaemia. In addition, temporal changes in the spatial T₂ distribution are accounted for, as well as the initial drop in T₂, along with the basis for improved sensitivity of T₂ to T₂-weighted intensities to the time after onset.

The dependence of the T₂ kinetics upon the rate of progression of ischaemia was also observed experimentally, and is now explicable with a single, measurable parameter. An easily accessible experimental parameter when assessing ischaemia is the width of the T₂ distribution. In this regard, the CED model is broadly in agreement with experiment: the width of the lesion T₂ distribution contracts relative to non-infarcted tissue around 1-h post-MCAo, before broadening around 2 h and contracting again (at β = 1 h). This time dependence in itself could in future be used as a restraint in determining parameters of clinical importance, being more informative than simply the average T₂ over the lesion.¹⁷

An important finding of the simulations is that the T₂-weighted signal intensity, even at optimal TE, is less sensitive to ischaemia, and apparently more so to tissue type, than T₂. The latter can therefore be expected to be a more sensitive marker of ischaemia provided it can be experimentally determined with sufficient confidence.¹⁶ This may well be due to the broader dynamic range of T₂-weighted intensity as a function of tissue type, such that ischaemia is a “second-order” perturbation, whilst the narrow dynamic range of absolute T₂ as a function of tissue type make ischaemia the dominant “first-order” perturbation to its average value.

Rationalising the predictions of the CED model

The basis for the CED model’s predictions may be rationalised as follows: the fast drop in ADC and initial fast drop in T₂ is driven by the shift of water from the extracellular space into the intracellular environment (i.e. cytotoxic oedema), before the slower dissociative terms take effect. However, the increased intracellular water content slowly shifts the equilibrium for supra-macromolecular structures, favouring states with fewer subunits. At the same time, associated with the ischaemic cascade is the activation of proteases.²⁹ These two effects therefore decrease the average supra-macromolecular and macromolecular size intracellularly, so that bound intracellular T₂ is substantially increased, and exchange with intracellular macromolecules no longer relaxes nuclear spins to such a degree. Nonetheless, ADC remains stable since the bound intracellular state contributes very little to its observed value; it is so very much slower than diffusion in either the free intra- or extracellular states, even with some dissociation.

The inclusion of a third state in our model, the bound intracellular state, was largely to overcome the fact that two-state models of intra- and extracellular water fail to account fully for ADC kinetics^23,24 and in our own pilot simulations fail comprehensively to explain T₂ kinetics. However, we have not explored the possibility of a two-state model incorporating the effects of changes in tortuosity (either extra- or intracellular) to calculate T₂. Models based on changes in extracellular tortuosity have been successfully applied to explain ADC changes when in conjunction with changes in water distribution (as mentioned in the Introduction), but the incorporation into a model for T₂, no matter how interesting the prospect, lies beyond the scope of the current work. It is worth considering, however, that our approach to modelling the increase in intracellular ADC may be reformulated as a tortuosity model (commensurate with cytoskeletal remodelling in response to oedema), but in that case the calculation of T₂ from the rotational correlation time from the ADC is not physically reasonable.

Shortcomings of the CED model

The proposed CED model is certainly incomplete, like any other three pool model is when trying to describe complex hydrodynamics in complex biological systems. First, it has been formulated only to model lesions with spherical, cylindrical or circular geometry. This can be extended, for example by modelling the lesion morphology using a polynomial expansion in three dimensions, such as a spherical harmonic series, but would require additional parameters (this is described in the Supplementary material). Second, we also have taken no account of blood oxygenation, which is likely to influence T₂ at least very in early ischemia,²⁰ through the BOLD effect. Vasogenic oedema also lies outside the scope of the model in its current incarnation, though again it could be incorporated into a more comprehensive formalism.

Our model includes a considerable number of parameters, not all of which yet have known values. Those that remain outstanding provide potential means to validate the model experimentally, and in principle could be made free parameters in the eventual case that the model is extended to such an extent as to be fitted to data. Our choice of the “healthy tissue” intracellular water fraction of 0.8 and “infarcted” intracellular water fraction rising to 0.95 were based on literature values.³⁷ Likewise, we used water exchange timescales across the plasma membrane in the 0.1–1 s range (a lifetime of 550 ms has been measured³⁸), but the model was not at all sensitive to this parameter, provided the lifetime was shorter than ∼1 s. Due to the total stability of the model in this case, we do not present simulations as a function of exchange rate constants. T₂ for the “free” water in intra- and extracellular compartments have also to be chosen, both set at 65 ms in our simulations which was found to reproduce observed values at 9.4 T reasonably well.

When fitting to equation (4) to determine the model-dependent effective T₂, deviations from mono-exponential behaviour can be expected, if there are slow-exchange terms in the kinetic matrix with large populations. Multi-exponential relaxation is therefore permitted within the CED model, as well as the model being arbitrarily extensible to any number of non-interacting (or slowly interacting) subspaces not currently accounted for, which may result in deviations from mono-exponential signal attenuation behaviour. However, as explained above, the exchange lifetimes of the components modelled argue for the CED model pertaining to a fast-exchange subspace of the total system. If there is a deviation from mono-exponential behaviour detectable in the experimental data (which in our data there was not, as shown in the Supplementary material, but in other systems may be the case), then one or more of the T₂ “components” detected in experimental data belongs to a subspace not relevant to the CED model.

An explicit assumption of the model, and one that was necessary to describe the data, is that the ADC for extracellular water is higher than that for intracellular. These were set at in our simulations at 1.8 × 10⁻⁹ m² s⁻¹ and 0.45 × 10⁻⁹ m² s⁻¹ respectively, which placed the simulations in reasonable agreement with experiment, albeit without rigorous optimisation. These theoretical (essentially predicted) values are also in good agreement with experimental MRI observations for water ADC in the rat brain made using contrast agents to separate intra- and extracellular compartments.³⁹

Summary and outlook

A major advantage of having a model that explains multiple MRI observations in ischemia is that the model can be applied to the design of future experiments or studies to maximise their impact and efficiency. Likewise, computerised means for the detection of ischemia and other applications in noisy data can be extensively tested using simulated data in advance of application to experimental data, reducing cost and animal burden, and ultimately with a potential translation into clinics. The purpose of our model was to understand the processes driving the time dependence of ischaemic stroke and serve as a means of testing the robustness of lesion detection approaches. Whilst we have not conducted a rigorous “system identification” analysis, it is clear that the rate of progression of ischemia is a parameter which drives the system. Realistically, in acute ischaemic stroke patients, symptoms will not allow comprehensive time-dependent data sets of the type possible in animal experimentation. Therefore, identification of parameters which facilitate estimation of system parameters from measurements at a single (and perhaps unknown) time after onset of symptoms is necessary. In that regard, our identification of the rate of lesion progression as a key system parameter as well as the width of the lesion T₂ distribution having a characteristic time distribution may facilitate the formulation of an analytical or numerical model which does not require multiple time-point measurements. It is, however, certain that further theoretical and experimental work is required here.

In summary, we have introduced a simple empirical parameter to describe T₂ kinetics in ischemia which is numerically stable and obtained experimental data in a rat MCAo model. We have introduced a mathematical model based on hydrodynamics to explain ADC and T₂ from unified biophysics and used it to explain many of our findings, as well as others in the literature. Although the excellent agreement between the model’s predictions is necessary, but not sufficient to validate its hypotheses, we believe that such a model is of great value in understanding ischaemia and designing MRI experiments for its detection. With an understanding of the parameters which drive ADC and T₂ kinetics in ischaemia, a simplified model may be derived which could be used to extract the most relevant parameters describing ischemia from MRI data, such as time of onset,^15,17,18 which would be of great value in clinical MRI.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: MJK is funded by grants from ARUK and BRACE Charity. BLM and HJR received a travel grant to University of Eastern Finland from the School of Experimental Psychology, University of Bristol. OG and KJ are funded by Academy of Finland, UEF-Brain strategic funding from University of Eastern Finland and by Biocenter Finland

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Authors’ contributions

MJK created the model, performed the simulations, fitted the experimental data into the model and wrote the first draft of the paper; BLM and HJR performed the MRI scans and initial analyses of experimental data; KJ and OHJG designed the MRI protocol, supervised animal experiments and MRI scans; RAK initiated and supervised the study, contributed to the creation of the model and finalised the paper. All authors reviewed the paper and approved it for submission.

Supplementary material

Supplementary material for this paper can be found at http://jcbfm.sagepub.com/content/by/supplemental-data