MRI-based methods for quantification of the cerebral metabolic rate of oxygen

Abstract

The brain depends almost entirely on oxidative metabolism to meet its significant energy requirements. As such, the cerebral metabolic rate of oxygen (CMRO₂) represents a key measure of brain function. Quantification of CMRO₂ has helped elucidate brain functional physiology and holds potential as a clinical tool for evaluating neurological disorders including stroke, brain tumors, Alzheimer’s disease, and obstructive sleep apnea. In recent years, a variety of magnetic resonance imaging (MRI)-based CMRO₂ quantification methods have emerged. Unlike positron emission tomography – the current “gold standard” for measurement and mapping of CMRO₂ – MRI is non-invasive, relatively inexpensive, and ubiquitously available in modern medical centers. All MRI-based CMRO₂ methods are based on modeling the effect of paramagnetic deoxyhemoglobin on the magnetic resonance signal. The various methods can be classified in terms of the MRI contrast mechanism used to quantify CMRO₂: T₂*, T₂′, T₂, or magnetic susceptibility. This review article provides an overview of MRI-based CMRO₂ quantification techniques. After a brief historical discussion motivating the need for improved CMRO₂ methodology, current state-of-the-art MRI-based methods are critically appraised in terms of their respective tradeoffs between spatial resolution, temporal resolution, and robustness, all of critical importance given the spatially heterogeneous and temporally dynamic nature of brain energy requirements.

Introduction

Brain energy requirements

Although comprising only 2% of total body mass, the brain accounts for approximately 20% of the body’s total oxygen consumption.¹ The brain is almost entirely dependent on oxidative metabolism of glucose to meet its significant energy requirements and is therefore especially susceptible to hypoxia and ischemia. If circulation to the brain is stopped, such as following cardiac arrest, loss of consciousness occurs in seconds, and brain tissue is irreversibly damaged in as little as three minutes.² Because of the brain’s dependence on oxygen to meet its energy needs, the cerebral metabolic rate of oxygen (CMRO₂) provides a direct, quantitative measure of the brain’s energy utilization and represents an important marker of brain tissue viability and function.

The linkage between regional brain activity and changes in cerebral blood flow (CBF), cerebral glucose metabolism (CMRGlu), and CMRO₂ was initially studied using evoked activity, which tends to cause highly localized changes in metabolism. While this provides insight into the structural and functional organization of the brain, measurement of such local metabolic changes is challenging, requiring spatial imaging rather than whole-organ measurement. However, the majority of brain blood-flow and metabolism is not associated with dynamic responses to the environment, but rather represents more sustained “state” or “trait” effects. This so-called “resting-state” brain function is organized into distinct distributed networks of brain regions such as the “default mode” network,³ which was originally identified by its elevated brain metabolism at rest compared to task-activated conditions. While the precise cellular mechanisms relating neuronal signaling and cerebral metabolism are still an area of active investigation, it is known that approximately 80% of resting CMRO₂ is devoted to active signaling processes, i.e. the propagation of action potentials and the restoration of those potentials after neurotransmission.⁴

Because CMRO₂ is remarkably well conserved in normal physiology, there is much interest in understanding physiologic and pathologic states in which CMRO₂ is affected. Although alterations in CMRO₂ have been suggested in several common neurologic disorders, these changes appear to be relatively small given the critical importance of oxygen in maintaining tissue viability. Pathological changes in CMRO₂ have been studied most intensively in patients with cerebrovascular disease in whom declining CMRO₂ despite increased oxygen extraction in the brain is thought to represent the final stage of autoregulatory decompensation.⁵

Measuring brain activity: A historical perspective

Developing methods for quantification and imaging of brain activity and metabolism has long been a major goal of basic and clinical neuroscience research. One of the major challenges in studying brain function is that the brain is relatively inaccessible to direct measurement. The electrical signals produced by the discharge of neuronal action potentials provide perhaps the most direct measure of brain activity. These signals were first observed by Richard Caton in 1875,⁶ using galvanometric measurements in animals during chewing and visual stimulation. This work was expanded to humans with the invention of electroencephalography (EEG) by Hans Berger in 1929,⁷ which allowed non-invasive measurement of brain electrical activity through the scalp. Unfortunately, EEG and magnetoencephalography⁸ – a complementary technique based on measurement of magnetic fields – have limited spatial resolution and depth penetration.

Despite producing relatively small changes in brain oxygen metabolism, motor and mental processes are associated with larger changes in CBF. In fact, these CBF changes are large enough to be observed by the naked eye, as demonstrated in 1881 by Italian physiologist Angelo Mosso,⁹ who observed increased regional pulsations in the brains of patients performing mental tasks while undergoing neurosurgery. In 1890, Charles Roy and Charles Sherrington hypothesized that such CBF responses were related to increases in metabolic demand.¹⁰ However, quantitative methods for testing such hypotheses did not yet exist.

A major breakthrough came in 1945, when Seymour Kety and Carl Schmidt introduced the first method for quantifying CBF and CMRO₂ in humans based on the Fick Principle.^11–13 In the 1950s through 1970s, Kety and his student, Louis Sokoloff, led the development of autoradiographic methods to create quantitative images of CBF and CMRO₂ in animals.¹⁴ The advent of positron emission tomography (PET) allowed extension of this autoradiographic work to humans, where it was used to detect regional activations associated with specific mental functions, for example, language processing.¹⁵ Seminal work by Peter Fox and Marcus Raichle^16,17 demonstrated that in response to mental and motor tasks, local CBF increases in excess of CMRO₂ (Figure 1).

Figure 1.

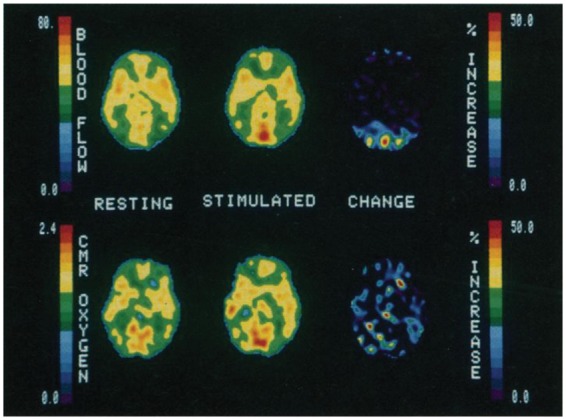
Early demonstration of uncoupling between blood flow and CMRO₂ during visual stimulation using multimodal PET. Despite a large increase in occipital blood flow, corresponding CMRO₂ changes are below the level of detection. This mismatch between flow and metabolism provides the basis for the BOLD fMRI technique. Reproduced from Fox et al.,¹⁶ with permission.

This mismatch between changes in blood flow and oxygen metabolism during task activation provides the physiological foundation for the blood-oxygen-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) method, which allows observation of brain activity based on MRI-measured changes in local blood oxygenation. The BOLD fMRI effect was first observed by Seiji Ogawa in hypoxic rats in 1990¹⁸ and subsequently demonstrated in humans by Ogawa¹⁹ (Figure 2) and several other groups.^20–22 Increased BOLD contrast with task activation reflects a regional net decrease in venous deoxyhemoglobin due to the proportionally larger changes in CBF as compared to CMRO₂ during regional brain activation.

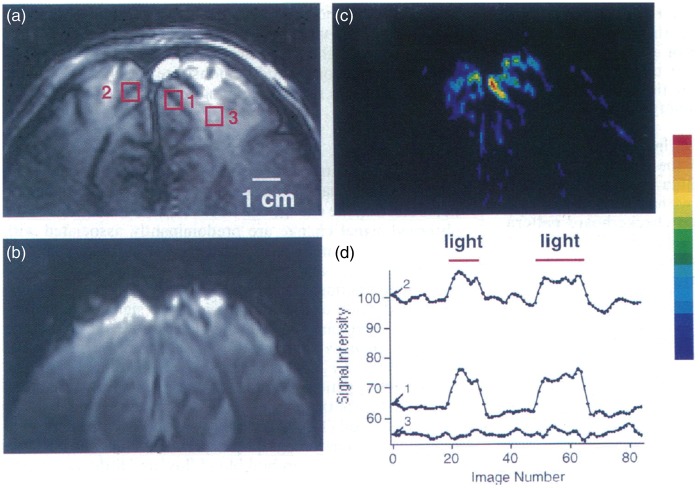
Figure 2.

Early demonstration of the BOLD effect in humans. (a) T₁-weighted axial image with several regions of interest (ROIs) indicated by square boxes; (b) T₂*-weighted BOLD image at the same slice location; (c) Pseudo-color map of BOLD image intensity changes in response to visual stimulation and (d) corresponding time-course plots of signal intensities from ROIs in (a), indicating restriction of BOLD effect to ROIs (1 and 2) in the visual cortex. Reproduced from Ogawa et al.,¹⁹ with permission.

Unlike PET-based metabolic imaging, BOLD fMRI does not require injection of radioactive tracers, can be performed on standard clinical imaging systems, and provides higher spatial and temporal resolution. In the past 20 years, use of BOLD fMRI has grown exponentially and provided enormous insights into the spatiotemporal functional or organization of the brain.

Why quantify CMRO₂?

Though the contribution of BOLD fMRI to basic neuroscience cannot be overstated, the technique has fundamental limitations. The method’s relative simplicity belies the enormous complexity of interpreting the underlying physiologic meaning of BOLD data.

BOLD signal changes are predominantly vascular in origin, driven by changes in CBF and cerebral blood volume (CBV) more so than metabolism. The relationship between the BOLD signal and its vascular and metabolic determinants is a complex one, modified by a number of physiologic and external factors. Therefore, the BOLD signal must always be quantified in terms of changes relative to a baseline state, and it cannot be used to quantify baseline cerebral metabolism. These relative BOLD signal changes can vary significantly within²³ and across²⁴ subjects, reducing statistical power in studies aimed at detecting group differences. Group comparisons can also be confounded by vascular effects unrelated to metabolism, for instance, in studies of aging.^25,26 Although simultaneous fMRI and intracortical EEG in animals have shown that BOLD signal change correlates with underlying electrical activity,²⁷ BOLD signal onset latency is an order of magnitude greater compared to electrophysiological changes.²⁸ Furthermore, the BOLD signal primarily originates from the post-capillary venous vasculature, which may be far from the site of activation.²⁹

In contrast to BOLD signal, CMRO₂ is a direct gauge of brain activity, and can be measured in absolute physiologic units. It is hypothesized that CMRO₂ may therefore provide a more sensitive measure of the brain’s neurometabolic state, and improve sensitivity to detect group differences and longitudinal changes. Animal studies have suggested that the CMRO₂ response to stimuli exhibits closer spatiotemporal correlation with neuronal activation compared to BOLD signal.²⁸ Accordingly, CMRO₂ imaging could provide a more precise and accurate tool for studying the temporal dynamics of neurologic function and spatial organization of brain functional systems. Developing improved methods for the quantification and mapping of CMRO₂ is of great interest to both basic scientists and clinicians. Pre-clinical applications of brain oxygen consumption imaging have been demonstrated in several of the most common neuropathologies, including stroke,^30,31 brain tumors,³² and Alzheimer’s disease (AD).³³

CMRO₂ quantification theory

Brain oxygen delivery and consumption

In aerobic metabolism, oxygen acts as the final electron acceptor of the electron transport chain, driving the formation of adenosine triphosphate (ATP), the main energy substrate in the body

$$6\text{O}2+\text{C}6\text{H}12\text{O}6+36\text{ADP}+36\text{P}\text{i}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\to 6\text{CO}2+6\text{H}2\text{O}+36\text{ATP}$$ (1)

Oxidative phosphorylation of glucose (and additionally ketone bodies during starvation) is the principal mechanism through which the brain can produce ATP for any appreciable amount of time. While non-oxidative glucose consumption (glycolysis) plays an important role in providing rapid energy during functional activation,^16,34 it is considerably less efficient than aerobic metabolism, producing only 2 moles of ATP per mole of glucose compared to 36 moles of ATP. Thus, there is significant evidence that increased energy demand even during transient brain activation is met largely through oxidative metabolism.³⁵

Oxygen is not produced endogenously and must be continuously transported to the brain via the blood. This transport is achieved by passive diffusion of oxygen across the alveolar and capillary membranes of the lungs, where it binds to hemoglobin in erythrocytes, and, to a much lesser extent, is dissolved in blood plasma. The degree of binding of oxygen to hemoglobin is governed by the partial pressure of oxygen, represented by the hemoglobin dissociation curve (Figure 3).

Figure 3.

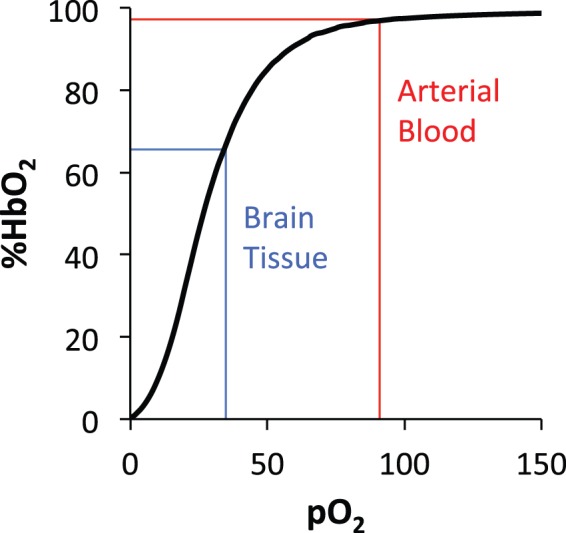
Hemoglobin (Hb) dissociation curve illustrating the relationship between oxygen partial pressure (pO₂) and percent hemoglobin oxygen saturation (%HbO₂). Normal values for arterial blood and brain tissue are indicated. The sigmoidal shape of the curve results from cooperative binding of oxygen at the four heme sites of the Hb tetramer, and facilitates unloading of oxygen from blood to brain tissue along the pO₂ gradient.

In normal physiologic and atmospheric conditions, the oxygen partial pressure (pO₂) in the arterial blood is 80–100 mmHg, resulting in an arterial oxygen saturation (Y_a) of approximately 98% hemoglobin oxygen saturation (%HbO₂). Because pO₂ in the brain (and other end-organs) is much lower, oxygen is released in these tissues from hemoglobin and diffuses along a decreasing pO₂ gradient: across the capillary membrane, through the cellular membrane of neurons and glial brain cells, and finally into the mitochondria where aerobic metabolism takes place. The oxygen depleted venous blood, with about 1/3 of its hemoglobin desaturated, is returned to the heart and lungs. The different magnetic properties of oxygenated and deoxygenated hemoglobin provide the foundation for MR-based quantification of blood oxygen saturation and CMRO₂.

Fick principle for CMRO₂ quantification

Assuming all oxygen extracted from the blood is used for ATP production, CMRO₂ can be quantified via the Fick principle^11–13

$$\text{CMRO}2=Ca·\text{CBF}·(Y\text{a}-Y\text{v})$$ (2)

where Y_a and Y_v are the arterial and venous oxygen saturation in %HbO₂, CBF is the CBF in µmol per minute per 100 g of brain tissue, C_a is the arterial oxygen content of fully saturated arterial blood (i.e. blood with Y_a=100 %HbO₂) in µmol of O₂ per mL blood, giving CMRO₂ in µmol per minute per 100 g of brain tissue. C_a is a Hb-dependent constant

$$Ca=0.620559·\text{Hb}$$ (3)

where Hb is in g/dL and the scaling factor is calculated based on a hemoglobin molar mass of 64,458 g/mol.³⁶ Y_a can be measured continuously with a digital pulse oximeter, leaving Y_v and CBF to be quantified from the MR imaging experiment. Y_a−Y_v is often called the arteriovenous oxygen difference (AVO₂D), and brain oxygen extraction is frequently reported in terms of the OEF, which is equal to AVO₂D/Y_a. OEF and AVO₂D values are very similar for Y_a in the normal physiologic range and are sometimes used interchangeably.

Kety and Schmidt^12,13 were the first to quantify CMRO₂ in humans using the Fick Principle. Y_a and Y_v were measured directly via co-oximetry of arterial and venous blood. To quantify CBF, they integrated the differential concentration of nitrous oxide (N₂O) in the arterial and venous blood during continuous inhalation of N₂O gas. Though accurate and well validated, the technique is highly invasive, requiring catheterization of the femoral artery and jugular vein. It also provides only a single steady-state global measurement of Y_v, CBF, and CMRO₂. However, this landmark work laid the foundation for the vast array of CBF, oxygenation, and metabolism measurement and mapping techniques introduced in the subsequent 60 years.

Non-MRI-based CMRO₂ quantification methods

Optical methods

Several optical methods exist for quantification of CBF and oxygen saturation. These methods take advantage of the different wavelengths at which oxyhemoglobin (oHb) and deoxyhemoglobin (dHb) absorb light.

Jugular bulb oximetry involves intravenous insertion of a fiber optic probe and determination of Y_v from the absorption spectrum of different wavelengths of light. The method can be combined with transcranial Doppler³⁷ measurement of CBF for quantification of CMRO₂. While the approach has the advantage of allowing continuous bedside monitoring, the catheter insertion is invasive and prone to possible serious complications such as carotid artery puncture,³⁸ and the technique is prone to errors due to poor catheter tip placement and calibration.³⁹

Optical methods can also be applied to regional measurement of blood flow and oxygenation. Near-infrared spectroscopy (NIRS)⁴⁰ involves application of light with wavelength 650–1100 nm, which can penetrate the scalp, skull, and brain to a depth of a few centimeters. The measured absorption spectra are used to estimate relative concentrations of oHb and dHb, which are then used to derive Y_v. A complementary optical technique for CBF measurement, diffuse correlation spectroscopy (DCS),⁴¹ measures the scattering of near-infrared light in tissue. NIRS and DCS can be combined to quantify local CMRO₂⁴²; however, the low penetration depth of light inherently limits the approach to measurement of cortical regions near the skull surface. Thus, the technique is best suited to studies involving neonates,⁴³ whose skulls are thinner, or in animals, where smaller brain sizes and use of cranial windows improve light penetration.

PET

PET involves the injection or inhalation of exogenous, positron-emitting radioactive tracers with specific chemical properties. The emitted positrons annihilate with surrounding electrons to produce equal energy 511 keV photons that are emitted in opposite directions and detected by the PET scanner. The position of these detection events can be used to tomographically compute the spatial distribution of annihilation events, and, thus, the spatial distribution of the tracer.

PET-based quantification of CMRO₂^44–46 uses intravenous injection of H₂¹⁵O water to quantify CBF and separate inhalation of radioactive ¹⁵O₂ gas to quantify OEF, which together can be used to quantify CMRO₂. Although the method is considered the gold standard for CMRO₂ mapping, it has a number of significant limitations. It is invasive, requiring both arterial and venous punctures as well as significant exposure to radiation. Due to the complexity and cost of the protocol, and the need for an on-site cyclotron to produce the ¹⁵O tracers, only a handful of sites around the world are equipped to conduct PET-based CMRO₂ studies. While the generated CMRO₂ maps are of good quality, the spatial resolution is somewhat coarse (≈5 mm³). Finally, the acquisition time for PET-based CMRO₂ is on the order of minutes, requiring that measurements be made in steady-state and thus limiting its ability to resolve time-course responses to dynamic stimuli.

MRI-based CMRO₂ quantification methods

MRI contrast and CMRO₂

Unlike PET, MRI is inherently non-invasive and relatively ubiquitous in modern medical centers. In MRI imaging, radiofrequency (RF) pulses are applied to induce precession of nuclear spin magnetic moments in the tissue or object of interest. Electromagnetic induction produces a signal, which decays with a time constant called the effective transverse relaxation rate (R₂*). The portion of the signal decay due to static magnetic field inhomogeneity can be removed by spin-echo refocusing, thus isolating the transverse relaxation rate (R₂). These two quantities define a third relaxation rate, R₂′ = R₂* − R₂, which represents the rate of signal decay due to static magnetic field inhomogeneities. Of note, R₂′ is only an exponential decay constant when the distribution of the inhomogeneous field is Lorentzian. These relaxation rates are often defined in terms of relaxation times: T₂* = 1/R₂*, T₂ = 1/R₂, and T₂′ = 1/R₂′. The varying chemical and structural properties of tissues have characteristic effects on the time evolution of the MR signal, allowing generation of images with widely varying contrast. The tunability and variability of MRI contrast have made the modality an enormously powerful tool for clinical diagnosis and scientific discovery.

A fundamental limitation of MRI is that the degree of polarization of nuclear magnetic moments is quite small, only a few parts per million, and the exponential time constant for repolarization (the T₁) is quite long, on the order of seconds for water protons in many tissues of interest. For this reason, tradeoffs between signal-to-noise-ratio (SNR), spatial resolution, and temporal resolution must be considered in almost all MRI applications, including CMRO₂ measurement.

In principle, MRI is possible with any nuclei possessing non-zero spin magnetic moment. Direct detection of oxygen with ¹⁷O MRI is one possible approach to MR-based CMRO₂ quantification. However, enriched ¹⁷O is enormously expensive, and the detection sensitivity is low. Because the human body is mostly composed of hydrogen-containing water molecules, ¹H, the principal isotope of hydrogen (≫99% abundance), is the nucleus of choice for most human MRI imaging, including CMRO₂ techniques.

The various ¹H-MRI CMRO₂ quantification methods are all based on application of the Fick Principle. CBF is typically measured non-invasively using either phase-contrast MRI (PC-MRI)⁴⁷ in large cerebral vessels or mapped on a voxel-wise basis with arterial spin labeling (ASL).^48,49 Y_a can be measured with pulse oximetry or assumed to be near 98 %HbO₂ in normal conditions. This leaves quantification of Y_v, the crux of most MR-based CMRO₂ quantification techniques. Y_v is itself of interest in certain applications, for instance, in stroke, where it may provide a marker for potentially salvageable tissue in the ischemic penumbra region.^30,31

MR-based Y_v quantification takes advantage of the unique magnetic properties of the metalloprotein hemoglobin, first demonstrated by magnetic mass balance experiments conducted by Pauling and Coryell in 1936.⁵⁰ In the deoxygenated state, the Fe²⁺ heme iron’s six electrons in the five 3d orbitals are distributed across the e_g and t_2g orbitals, resulting in four unpaired electrons and a spin S = 2. When the heme iron becomes oxygenated, the ligand field separating the t_2g and e_g orbitals is increased, making the configuration in which all electrons occupy the three t_2g orbitals more energetically favorable, and resulting in spin pairing with a net electron spin S = 0. Thus, only dHb is paramagnetic, whereas oHb is diamagnetic. dHb paramagnetism causes the magnetic susceptibility of blood to scale linearly with dHb concentration, and also has various effects on the relaxation rates of blood and surrounding tissue.

The paramagnetism of dHb is exploited in a variety of MR-based techniques to quantify Y_v and CMRO₂, as summarized in Table 1. These methods can be categorized based on the tissue compartment in which the effects of dHb are modeled (extravascular vs. intravascular) and the MR contrast method used to quantify these effects (T₂*, T₂′, T₂, or susceptibility), as outlined in the sections that follow. Furthermore, the methods are distinguished by whether the measurements are made on a global, regional, or voxel-wise basis, and the resultant tradeoff between their spatial and temporal resolutions.

Table 1.

Summary of MR-based Y_v/CMRO₂ quantification methods and their respective features.

Signal Origin	Contrast	Spatial Res.	Method	Yv Temp. Res.	Simul. CBF?
Extravascular	T2*	Voxel-wise	Calibrated BOLD51	0:03	YES
	T2′	Voxel-wise	qBOLD52	8:30	NO
Intravascular	T2	Global	TRUST53	0:24	NO
		Regional	TRU-PC54	2:50	NO
			Projection-based T255	0:15	NO
		Voxel-wise	QUIXOTIC56	27:30	NO
			VSEAN57	6:18	NO
	Susceptibility	Global	OxFlow58	0:28	YES
		Regional	Quantitative Venography131	15:42	NO
		Voxel-wise	Zhang et al.59	60:00	NO

Note: “Signal origin” is the tissue compartment in which signal used for Y_v quantification is modeled. “Contrast” is the MRI contrast mechanism used in the Y_v quantification model. “Spatial Res.” is the spatial resolution for Y_v quantification in minutes:seconds. “Method” is the name/acronym or authors associated with the published method and the most relevant citation. “Y_v Temp. Res.” is the reported approximate temporal resolution for a single Y_v measurement (ignoring any requisite planning or calibration scans). “Simul. CBF?” denotes whether the method/pulse sequence measures CBF simultaneously with Y_v. Of note, all of the above techniques allow quantification of absolute Y_v and CMRO₂, whereas calibrated BOLD techniques provide only relative changes in CMRO₂ in response to a stimulus. This limitation is removed by some recent BOLD calibration techniques employing multiple gas-mixture breathing calibration,^60,61 as discussed in the text.

Extravascular T₂*-based methods (Calibrated BOLD)

Because CMRO₂ measurement provides greater physiological insights compared to BOLD contrast alone, the development and application of BOLD fMRI have been paralleled by attempts to resolve CMRO₂ from the BOLD signal. This requires modeling the various physiologic factors that contribute to the BOLD signal, schematically illustrated in Figure 4. During neural activation, there is a local increase in both CMRO₂ and CBF; however, the increase in CBF is several times greater than what is required to meet the additional CMRO₂ demand,¹⁷ resulting in a counterintuitive decrease in the OEF and thus [dHb], the local concentration of deoxyhemoglobin in a voxel. CBF also independently increases the venous cerebral blood volume (CBV_v) fraction, which acting alone would increase [dHb]. Overall, the CBF washout effect dominates, resulting in a reduction in [dHb] and the characteristic increase in signal intensity in R₂*-weighted BOLD fMRI images.

Figure 4.

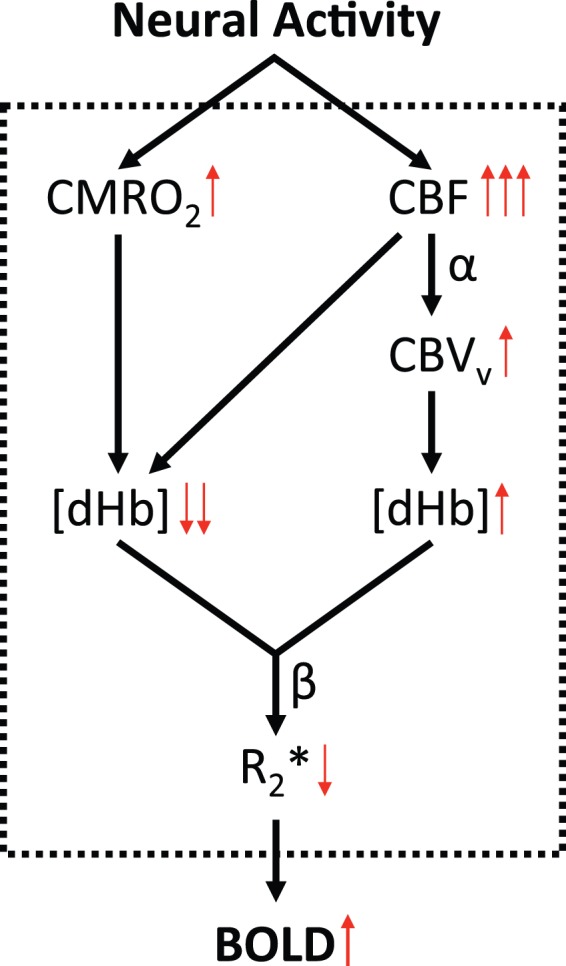
Schematic diagram illustrating the various physiologic contributions relating neural activity to BOLD signal: During neural activation, both CMRO₂ and CBF increase; however, the latter far exceeds the additional CMRO₂ requirements, thereby resulting in a decrease in OEF (and thus local dHb concentration). Further, CBF independently increases the venous cerebral blood volume (CBV_v) fraction, which acting alone would increase [dHb]. Overall, the CBF effect dominates, causing a reduction in [dHb] and concomitant increase in BOLD signal intensity.

The BOLD signal is a simple exponential function of R₂* and echo time (TE). Because fractional BOLD signal changes are only a few percent, the exponential function can be linearized

$$\frac{\Delta \text{BOLD}}{\text{BOLD}0\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}}\cong -\mathrm{TE}·\Delta R_2^{*}$$ (4)

where the subscript 0 denotes the baseline state and Δ denotes the change from baseline to activation. ΔR₂^* can be expressed as

$$\Delta R_2^{*}=A·(\text{CBV}v·[\text{dHb}]v\beta -\text{CBV}v0·[\text{dHb}]v0\beta )$$ (5)

where the subscript v denotes the venous blood compartment, and A is a scaling factor that incorporates effects due to vessel geometry, magnetic field strength, and the susceptibility difference between blood and tissue.^62,63

The supralinear (i.e. β > 1) effect of [dHb] in equation (5) results from the combined effects of: (1) the linear exponential decay of the signal for spins in the vicinity of large venous vessels as predicted by the static dephasing model of Yablonskiy and Haacke⁶⁴ and (2) the quadratic exponential decay of the signal for spins in the vicinity of small vessels (capillaries) due to diffusion of water molecules in large local field gradients, somewhat analogous to exchange between two chemical shift sites as predicted by the Luz and Meiboom⁶⁵ model for fast exchange. Monte Carlo simulations based on the distribution of vessel sizes in the brain have suggested a β value of 1.5 at 1.5 T.⁶³ However, the majority of functional imaging studies in recent years have been conducted at 3.0 T field strength, where β is predicted to be closer to 1.3.⁶⁶

The traditional physical interpretation of β is somewhat oversimplified. For example, it does not account for intravascular BOLD signal, which is especially significant at lower field strengths. However, at very high field, the intravascular contribution to the BOLD signal is negligible. Recently, Shu et al.⁶⁷ determined β experimentally in the rat brain at 9.4 T field strength by systematically varying the blood magnetic susceptibility via administration of a superparamagnetic contrast agent. The authors reported values on the order of 0.8 in the neocortex of rat brains, significantly lower than values used at 3.0 T. Furthermore, while β was found to be quite uniform across different neocortical regions, lower values were measured in sub-cortical regions. This suggests caution must be exercised in treating β as a spatially uniform constant across the entire brain.

Equation (5) requires mapping of venous CBV. Although non-invasive techniques for direct quantification of CBV exist, most notably vascular-space-occupancy (VASO) MRI,⁶⁸ they suffer from low sensitivity, and cannot easily distinguish between arterial and venous CBV. Furthermore, the VASO method requires imaging at a specific blood inversion null point, making whole-brain coverage difficult. Thus, CBV is generally derived from ASL-measured CBF using the Grub power relationship⁶⁹

$$\frac{\text{CBV}}{\text{CBV}0}=(\frac{\text{CBF}}{\text{CBF}0})\alpha$$ (6)

where α is the Grubb constant. While the original Grubb constant value (0.38) accounts for total CBV changes, because only dHb-containing CBV_v, rather than total CBV, determines the BOLD signal, recent work has suggested a lower value for α of 0.18⁷⁰ or 0.23.⁷¹ Like β, α is typically treated as a constant, but may in fact vary between subjects and brain regions.^72–74

Combining equations (4) to (6) and invoking the Fick Principle (with Y_a approximated to equal 100 %HbO₂) gives an expression – known as the Davis model⁵¹ – relating BOLD signal changes to CMRO₂ and CBF

$$\frac{\Delta \text{BOLD}}{\text{BOLD}0}=M·(1-(\frac{\text{CMRO}2}{\text{CMRO}2|0})\beta (\frac{\text{CBF}}{\text{CBF}0})\alpha -\beta )$$ (7)

Here M is the BOLD calibration constant, defined as

$$M=\mathrm{TE}·A·\text{CBV}vo·[\text{dHB}]vo\beta$$ (8)

Appraisal of equation (8) demonstrates that M is the maximum possible BOLD signal change that would result from total washout of all dHb from a voxel.^51,75 This can be appreciated by assuming that in such a maximal BOLD response, the increase in CBF would dominate any changes in CMRO₂, thus reducing the entire term in parentheses in equation (7) to unity.

Despite the aforementioned limitations of treating α and β as constants, simulations based on a more complete BOLD signal model suggest that the general form of equation (7) is remarkably valid if the traditional physical interpretations of α and β are relaxed and they are instead treated as fitting constants.⁷⁶ This heuristic approach suggests lower values for α (0.14) and β (0.91) are optimal.

With knowledge of M, subsequent measurement of CBF and BOLD during a functional paradigm allows quantification of fractional changes in CMRO₂ by solving equation (7). However, M varies both across subjects and brain regions,^77,78 and must therefore be “calibrated”.

Davis et al. first demonstrated an approach to BOLD calibration via hypercapnic gas-mixture breathing.⁵¹ Assuming that hypercapnia does not result in changes in CMRO₂ allows further simplification of equation (7)

$$\frac{\Delta \text{BOLD}}{\text{BOLD}0}=M·(1-(\frac{\text{CBF}}{\text{CBF}0})\alpha -\beta )$$ (9)

M can be solved from equation (9) via simultaneous measurement of BOLD and CBF signal during both baseline and hypercapnic states.

Application of hypercapnia calibrated BOLD to functional tasks may provide improved intra- and inter-subject reproducibility compared to traditional BOLD signal methods.⁷⁹ However, the method has several limitations. Breathing hypercapnic gas can induce breathlessness, which may be especially problematic in patients who are distressed or infirm. Furthermore, the assumption of isometabolism to hypercapnia has been challenged in several recent papers employing direct CMRO₂ quantification based on T₂.^80,81 Finally, due to the large exponent on the relative CBF changes in equation (9), the technique is highly sensitive to noisy ASL-derived CBF data.

Recently, an alternative approach to BOLD calibration based on hyperoxic gas-mixture breathing was proposed.⁸² Hyperoxia is assumed to cause minimal changes in blood flow.⁸³ Following the derivation of the deoxyhemoglobin dilution model⁷⁵ and assuming minimal hyperoxic CBF changes results in an alternative calibration equation

$$\frac{\Delta \text{BOLD}}{\text{BOLD}0}=M·(1-(\frac{[\text{dHb}]v}{[\text{dHb}]v0})\beta )$$ (10)

where [dHb]_v is assumed to vary uniformly across the brain and is quantified via capnographic measurement of end-tidal O₂ (EtO₂) before and during hyperoxia. This approach avoids the patient discomfort associated with hypercapnia as well as the sensitivity of the model to errors in ASL-derived CBF (as CBF is assumed to remain constant). Unlike hypercapnia calibration (equation (9)), equation (10) can be derived from equation (5) without invoking the Fick Principle, and therefore does not require assuming a particular value for Y_a. However, it has the major disadvantage of requiring an assumed baseline Y_v value in order to derive [dHb]_v from EtO₂ measurements. While Y_v is relatively uniform across the brain,¹⁷ it varies considerably even between healthy subjects.^53,58 Finally, hyperoxia may induce a modest reduction in CBF.⁸³ Although this can be incorporated into the model, it is difficult to measure for individual subjects due to the low sensitivity of ASL to small hyperoxic flow changes. ASL-based CBF measurement during hyperoxia is further complicated by the T₁ shortening of blood due to dissolved O₂.

Recently, several groups^60,61 have proposed combining multiple gas-mixture breathing paradigms in order to improve the precision of calibrated BOLD, as well as to allow extension of calibrated BOLD to the quantification of not just fractional CMRO₂ changes but also resting-state CMRO₂ in absolute physiologic units. Example images obtained from such a dual gas approach (hypercapnia and hyperoxia) are shown in Figure 5. In addition to providing M maps for calibration of subsequent task-based fMRI studies, these dual gas methods can also provide resting-state OEF, CBF, and CMRO₂ maps. Of course, the need for multiple gas manipulations adds significant complexity to the experimental protocol, and also increases the physiologic assumptions inherent in the calibration process.

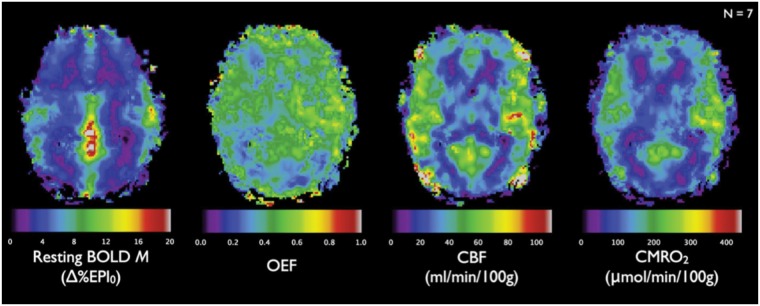
Figure 5.

Group average (N = 7) maps of resting-state parameters obtained from dual gas (hyperoxia and hypercapnia) calibrated BOLD. Unlike traditional BOLD calibration using a single gas-mixture challenge, dual gas mixture paradigms allow generation of absolute resting-state CBF, OEF, and CMRO₂ maps in addition to M maps. Images of M, OEF, CBF, and CMRO₂ exhibit plausible patterns of anatomic contrast. Gray–white matter contrast is absent in the map of resting OEF, consistent with previous PET studies. Reproduced from Gauthier and Hoge ⁸⁴ with permission.

As pointed out earlier, the calibration constant M essentially represents the maximal BOLD effect achievable by replacement of all dHb by oHb. Recently, Blockley et al.⁸⁵ suggested an alternative calibration experiment not relying on gas mixture breathing. Since the majority of the BOLD effect results from R₂′-based signal attenuation, the idea is to capture this portion of the signal modulation by voxel-wise measurement of R₂′, for instance, by using an asymmetric spin-echo sequence. However, since a small portion of the BOLD signal is due to irreversible spin dephasing, a scaling parameter is required to correct the calibration constants derived in this manner. Furthermore, since R₂′ is also affected by magnetic field perturbations unrelated to dHb, the accuracy of the method will hinge on how well such extraneous field inhomogeneities can be eliminated.

While the calibration constant M has been shown to depend on the anatomic location in the brain, recent work suggests that it may also depend on the resting brain state. Using an R₂′-based approach to M mapping in anesthetized rats, Shu et al.⁸⁶ found M to depend on both the level and method of anesthesia.

Calibrated BOLD is the single current CMRO₂ quantification technique with both voxel-wise spatial resolution and sufficient temporal resolution for application to functional experiments. However, it has numerous challenges, including a complex experimental setup and the many physiologic assumptions inherent in the signal model and calibration procedures. Thus, significant spatial averaging is often required to reduce noise and recover physiologically plausible CMRO₂ values. BOLD calibration techniques will benefit from higher SNR BOLD/ASL acquisition strategies. Improved results may also be achieved by replacing physiologic assumptions (i.e. isometabolism to hypercapnia) with additional direct measurements of these physiologic parameters. Advances in BOLD calibration techniques are discussed extensively in a recent review.⁸⁷

Extravascular T₂′-based methods

Like T₂*-based calibrated BOLD, T₂′-based methods involve modeling the effects of intravascular dHb on the temporal evolution of extravascular signal. Rather than invoking the semi-empirical model of equation (5), which requires calibration and corresponding physiologic assumptions, the MRI signal behavior is modeled explicitly in terms of known or measurable physical quantities by invoking the so-called static dephasing regime (SDR). In the presence of magnetic field inhomogeneities, spins accumulate phase at different rates determined by the local magnetic field strength, causing phase incoherence and signal decay. Diffusion of spins between sites of different field strengths can also cause signal decay. In the SDR, it is assumed that static dephasing leads to complete signal decay before diffusion dephasing has an appreciable effect.

The time behavior of extravascular MR signal in the SDR was first described by Yablonskiy and Haacke.⁶⁴ By modeling small blood vessels as a network of randomly oriented cylinders, Y_v can be expressed in terms of the spin-echo reversible decay rate, R₂′

$$R2\text{'}=\text{CBV}v·\gamma ·\frac{4}{3}·\pi ·\Delta \chi \mathrm{do}·\text{HCT}·(1-Yv)·B0$$ (11)

where Δχ_do is the susceptibility difference between fully oxygenated and fully deoxygenated erythrocytes, Hct is the blood hematocrit, and B₀ is the main magnetic field strength. It is noted that equation (11) has the same functional form as equation (5); however, the SDR does not consider diffusion effects and thus β = 1.

The SDR model also predicts that in a free induction decay (FID) experiment, the time-dependent MR signal, S(t), exhibits different behavior in the short and long time scales related to the characteristic time, t_c

$$S(t)=S(0)·\text{exp}[-\frac{4}{3}·\text{CBV}v·(\frac{t}{tc})2-R2·\text{t}]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\text{for}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}t<1.5·tc$$ (12)

$$S(t)=S(0)·\text{exp}[\text{CBV}\text{v}]·\exp [-R_2^{*}·t]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\text{for}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}t>1.5·tc$$ (13)

CBV_v can be solved by fitting the FID MR signal to equations (12) and (13), leaving measurement of R₂′ to determine Y_v via equation (11). Several spin-echo-based pulse sequences exist for R₂′ mapping,^88–90 all of which involve measuring the MR signal evolution in the vicinity of a spin echo. The method was first applied to human studies by An and Lin,⁹¹ and later improved upon by He and Yablonskiy,⁵² who additionally considered the effects of static field inhomogeneities and signal contributions from cerebrospinal fluid (CSF) and intravascular blood, dubbing the method ‘quantitative BOLD’ (qBOLD). qBOLD-derived resting-state OEF maps are displayed in Figure 6. In subsequent studies, the qBOLD technique was validated relative to pulse oximetry in rats⁹² and has shown promise in defining the ischemic penumbra region in acute stroke and post-stroke recovery in humans.⁹³ A recent iteration of the method⁹⁴ suggests that a simulation-based “fingerprinting” approach⁹⁵ may allow better fitting of acquired data to the qBOLD model. For more detailed discussion, the reader is directed to a recent review.⁹⁶

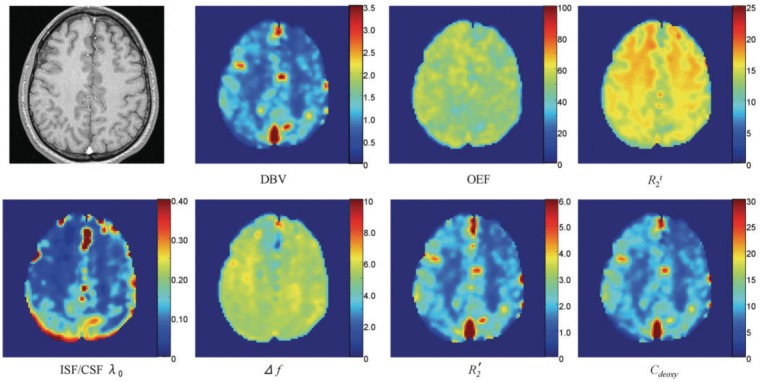
Figure 6.

Representative maps of estimated brain parameters obtained with a high-resolution GESSE (gradient-echo sampling of spin echo)⁸⁸ pulse sequence. The top leftmost image is a high-resolution anatomic image. The rest of the maps are deoxygenated blood fraction (%), OEF (%), R₂ of brain tissue (R₂^t, s⁻¹), interstitial fluid and cerebrospinal fluid (ISF/CSF) volume fraction, ISF/CSF frequency shift (Hz), R₂′ of brain tissue (s⁻¹), and brain deoxyhemoglobin concentration (μM). Reproduced from He et al.,⁵² with permission.

Although qBOLD achieves quantitative mapping of Y_v without gas calibration, successful implementation is challenged by the need to fit data to a multi-parameter model with many underlying assumptions. While the original signal model defined by equations (11) to (13) does not account for contributions from diffusion, inclusion of diffusive processes as signal modulators has been addressed in more recent work.⁹⁷ In addition to theoretically improving the accuracy of qBOLD-derived Y_v, diffusive BOLD models can also provide information on mean vessel size. This approach has shown potential for imaging of tumors,⁹⁸ which in addition to affecting local metabolism, also tend to be highly vascularized relative to surrounding tissue. It is important to note that because R₂′ mapping techniques are based on spin-echo sampling, they have relatively long acquisition times compared to echo-planar imaging (EPI)-based T₂* mapping (calibrated BOLD). Thus, unlike calibrated BOLD, qBOLD is inherently limited to measurement of steady-state Y_v and CMRO₂. However, it has the advantage of not requiring gas-mixture breathing calibration.

Intravascular T₂-based methods

T₂-based CMRO₂ quantification methods are based on isolation of venous blood T₂, which can be related to Y_v through theoretical and empirical models. As blood water protons diffuse through the magnetic field inhomogeneities created by dHb-containing erythrocytes, spin-echo irreversible (T₂) dephasing occurs in the intravascular space. This decay can be estimated by a multi-spin-echo Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence, containing 180-degree pulses with spacing t_CPMG. The Luz and Meiboom⁶⁵ model for two-site fast exchange can be modified and applied for diffusion of spins between intra- and extra- erythrocyte compartments^99–101 to quantify R₂ of venous blood

$$R2,\mathrm{blood}=R2,\mathrm{plasma}+\mathrm{Hct}·\{\Delta R2,v+(1-\mathrm{Hct})·(\Delta \omega v)2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}·\tau ·[1-\frac{2\tau }{t\mathrm{CPMG}}·\tanh (\frac{t\mathrm{CPMG}}{2\tau })]\}$$ (14)

where R_2,plasma is the relaxation rate of blood plasma, ΔR_2,v and Δω_v are the relaxation rate and susceptibility-shift differences, respectively, between the erythrocytes and plasma for exchanging water in the blood, τ is the exchange time between frequency-shifted sites, and t_CPMG is the time spacing between consecutive 180-degree pulses in the CPMG echo train. This complex model can be simplified by combining multiple physical quantities into calibration constants, resulting in a second-order polynomial relating R₂ of blood and Y_v¹⁰²

$$R2,\mathrm{blood}=A+B·(1-Yv)+C·(1-Yv)2$$ (15)

where A, B, and C are Hct- and CPMG spacing (t_CPMG)-dependent constants which can be determined empirically from blood samples. Such an approach to Y_v quantification was first demonstrated by Wright et al.¹⁰¹ in the major thoracic vessels and later demonstrated in cerebral veins in response to visual stimulation.^99,103 Figure 7 shows an example calibration curve obtained from ex vivo blood samples.

Figure 7.

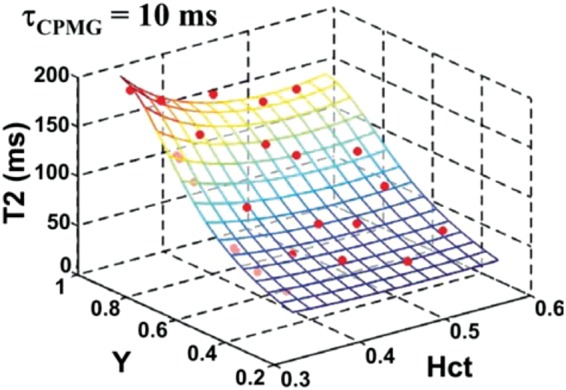
Calibration curve relating blood T₂ to Y_v and Hct for t_CPMG = 10 ms. Each red symbol represents a blood sample with known Hct and Y_v obtained from gold-standard blood co-oximetry, with blood T₂ measured from MR. The data are used to derive the fitting constants in equation (15), allowing subsequent determination of Y_v via measurement of blood T₂. Reproduced from Lu et al.,¹⁰² with permission.

Determining the values of the calibration constants in equation (15) is a major challenge in implementing these T₂-based methods. The constants lack specific physical meaning and must be determined empirically from measurements in blood samples using a range of precisely controlled oxygenation and Hct levels. Furthermore, the constants must be derived separately for different field strengths and t_CPMG times, ideally using a sequence with a CPMG echo train identical to that used for in vivo T₂ mapping. Care must be taken in the calibration experiment to maintain normal blood chemistry (e.g. temperature and pH) and prevent blood settling.

Another challenge for T₂-based methods is the need to isolate pure blood signal, as partial volume mixing of tissue or CSF will significantly bias measured T₂ and Y_v. Even in the largest vessels, such as the superior sagittal sinus (SSS), blood signal isolation is non-trivial due to the relatively large voxel sizes required by the fast imaging readouts used in CPMG-based T₂-mapping sequences. Several different approaches have been proposed, as discussed below.

Spin-tagging venous blood isolation (TRUST)

T₂-Relaxation-Under-Spin-Tagging (TRUST)⁵³ isolates venous blood signal via application of spin tagging, similar in principle to ASL-based CBF quantification. Subtraction of images acquired with and without venous blood inversion isolates pure blood signal. Application of various amounts of CPMG T₂ weighting prior to imaging allows for quantification of blood T₂. This method has been applied in both the SSS and internal jugular veins, with very comparable values obtained,¹⁰⁴ suggesting that the SSS can be used as a surrogate for global Y_v. Combining TRUST with PC-MRI CBF quantification allows determination of CMRO₂.¹⁰⁴ Figure 8 provides a schematic illustration of the TRUST method.

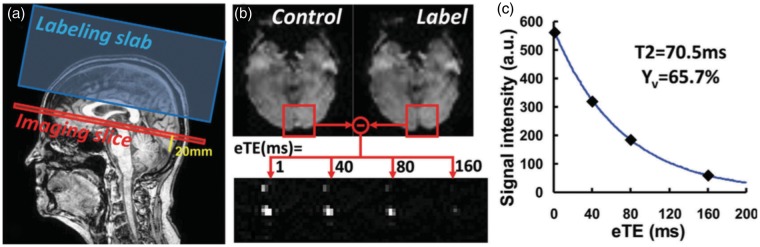
Figure 8.

Illustration of the positioning of T₂-relaxation-under-spin-tagging (TRUST) MRI and representative results. (a) Imaging slice (red) and labeling slab (blue) of TRUST MRI scan. Imaging slice was positioned to be parallel to anterior-commissure–posterior-commissure line and 20 mm above sinus confluence. (b) Typical data of TRUST MRI. Subtraction of control and label images yields pure venous blood signal, which is subject to increasing T₂ weightings. (c) Monoexponential fitting of blood signal in superior sagittal sinus as a function of effective echo time (eTE) results in T₂ estimation. T₂ value can then be converted to venous oxygenation (Y_v) via a calibration plot.¹⁰² Reproduced from Liu et al.,¹⁰⁵ with permission.

Since its introduction, TRUST has been improved in terms of speed and reliability¹⁰⁶ and extensively validated.^102,105,107 It has been applied widely in physiologic investigations of the effects of hypercapnia,⁸¹ hypoxia and hyperoxia,¹⁰⁸ caffeine,¹⁰⁹ exercise,¹¹⁰ and cognitive training,¹¹¹ in studies of neonatal development¹¹² and normal aging,¹¹³ and in diseases including multiple sclerosis¹¹⁴ and mild cognitive impairment.¹¹⁵ Although providing a robust and reliable approach to global Y_v quantification, TRUST temporal resolution for CMRO₂ quantification is on the order of minutes, due to the temporally inefficient nature of CPMG-based T₂-mapping and the need for a separate measurement of CBF with PC-MRI. This limits the method’s application to steady-state measurement of CMRO₂.

Phase-contrast venous blood isolation (TRU-PC, projection-based T₂)

As an alternative to spin tagging, blood signal can also be isolated through complex difference subtraction of images acquired with different first gradient moments,^54,55 in a similar manner to PC-MRI blood flow quantification. An advantage of this approach over TRUST is that it does not require spin tagging in a drainage territory corresponding to a particular vein and can thus be applied to smaller cortical vessels with arbitrary vessel geometry, as demonstrated using the T₂-Relaxation-Under-Phase-Contrast (TRU-PC) method.⁵⁴

A similar technique using a projection-readout was demonstrated to quantify Y_v in as little as 15 s.⁵⁵ However, because the complex difference signal is also dependent on blood flow, multiple averages are required to ensure blood flow effects are removed, limiting application of these phase-contrast-based techniques to situations of steady-state blood flow, and partially negating the advantage of high temporal resolution.

While these techniques can provide Y_v in regional vessels, the utility of regional Y_v quantification based on intravascular (as opposed to voxel-wise) measurement is fundamentally limited. Unlike arterial perfusion territories, venous drainage territories corresponding to particular vessels are poorly defined. Thus, determining the Y_v of a given tissue region from the Y_v measured within nearby veins is a major challenge. A recently proposed method for quantitative imaging of venous drainage territories aims to address this challenge.¹¹⁶ However, the method’s spatial and temporal resolution are significantly limited by the need to separately spatially encode both the venous drainage vessels as well as their corresponding upstream tissue regions.

Velocity selective excitation venous blood isolation (QUIXOTIC, VSEAN)

Clever application of velocity selective excitation pulses¹¹⁷ in combination with blood tagging and T₂-preparation similar to TRUST can be used to specifically isolate signal from venous blood in the post-capillary venous compartment. Two similar techniques, QUantitative Imaging of eXtraction of Oxygen and TIssue Consumption (QUIXOTIC)⁵⁶ and Velocity Selective Excitation with Arterial Nulling (VSEAN),⁵⁷ use this approach to obtain voxel-wise quantification of Y_v. However, because post-capillary blood comprises only a few percent of total parenchymal volume, these techniques suffer from low sensitivity and SNR. As such, they require multiple averages and thus have long acquisition times even when being limited to a single acquisition slice. CSF signal contamination is also a concern, and may result in overestimation of Y_v values.⁵⁶

Intravascular susceptibility-based methods

While the aforementioned techniques are based on modeling the effect of paramagnetic dHb on transverse relaxation rates, Y_v can also be more directly quantified by measurement of blood susceptibility itself. This technique exploits the relative paramagnetism of dHb versus oHb, which causes the susceptibility of whole blood relative to surrounding tissue, Δχ, to be linearly related to Y_v¹¹⁸

$$\Delta \chi =\mathrm{Hct}(\Delta \chi \mathrm{do}(1-Yv)+\Delta \chi \mathrm{oxy})$$ (16)

where Hct is venipuncture-derived hematocrit, and Δχ_do and Δχ_oxy are the experimentally determined volume susceptibility differences between fully oxygenated and deoxygenated erythrocytes and fully oxygenated erythrocytes and water, respectively. Values of 4π × 0.273 p.p.m and 4π × 0.008 p.p.m. (SI units) are used for Δχ_do and Δχ_oxy, respectively, based on theoretical calculations^119,120 as well as ex vivo calibration experiments.^119,121 Of note, the model in equation (16) assumes that the susceptibilities of water, plasma, and tissue are the same to within experimental noise, and also assumes a single value for the mean corpuscular hemoglobin content (MCHC), the concentration of hemoglobin per volume of packed red blood cells. MCHC is known to vary in certain diseases, particularly anemia. Thus, a more complete model is obtained by substituting MCHC_norm/Hb in place of Hct in equation (16), where Hb is the individual subject’s measured Hb, and MCHC_norm is the MCHC value assumed in the derivation of the Δχ_do and Δχ_oxy constants. A MCHC_norm value of 33.3 g/dL was used in deriving the above values of Δχ_do and Δχ_oxy.¹²¹

Although blood susceptibility cannot be measured directly, it induces a local field offset, ΔB, which can be measured with an MRI multi-echo gradient-recalled echo (GRE) field mapping sequence as

$$\Delta B=\Delta \phi /\gamma \Delta \mathrm{TE}$$ (17)

where Δφ is the difference in phase accrual between echoes spaced apart by ΔTE in the blood versus surrounding reference tissue, and γ is the proton gyromagnetic ratio.

Thus, solving for Y_v hinges on determining Δχ from the measured ΔB. The relationship between the two quantities can be described in terms of a convolution in the image domain

$$\Delta B=d\otimes \chi$$ (18)

where d = cos²θ_r/4πr³ is the dipole kernel. Equation (18) can also be expressed as a point-wise multiplication in the Fourier domain

$$F(\Delta B)=D·X$$ (19)

where D = 1/3 – k_z²/k² is the dipole kernel in the Fourier domain.

Because D contains zeros on a pair of conical surfaces at 54.6 degrees relative to the z-direction, inversion of the dipole kernel is ill-posed.¹²² Regularization or conditioning is necessary in order to find a unique solution for Δχ given ΔB. This inversion problem is a major focus of the growing field of quantitative susceptibility mapping (QSM) (reviewed in Wang et al.¹²³).

Although inversion of equation (18) is ill-posed in the general case, it can be solved for certain simple susceptibility distributions, including ellipsoids and specifically cylinders, as the latter approximate the geometry of blood vessels. By modeling a vein of interest as a pseudo-infinite cylinder (i.e., with length ≫ diameter) and accounting for field cancellation due to the Lorentz sphere contribution, the relationship between ΔB and Δχ is given by equation (20)^124,125

$$\Delta B=\frac{1}{6}\Delta \chi B0(3\cos 2\theta -1)$$ (20)

where θ is the vessel angle with respect to B₀, and the reference region outside the vessel is chosen to be sufficiently far from the vessel axis such that the induced field is negligible. Combining equations (16), (17), and (20) allows for determination of Y_v by measurement of Δφ

$$Yv=1-\frac{6(\Delta \phi /\Delta \mathrm{TE})}{\gamma B0\Delta \chi \mathrm{do}\mathrm{Hct}(3\cos 2\theta -1)}+\frac{\Delta \chi \mathrm{oxy}}{\Delta \chi \mathrm{do}}$$ (21)

Study of equation (21) reveals that for a given Y_v, larger vessel angles will result in increasingly smaller phase shifts between the intra and extravascular compartments, thus reducing the precision of Y_v quantification. In fact, approaching the magic angle (54.6 degrees), equation (21) becomes indeterminate. For this reason, the model is ideally suited for smaller vessel angles, and theoretical modeling suggests it is quite precise for vessels with angles less than 30 degrees.¹²⁶ The model is schematically illustrated in Figure 9.

Figure 9.

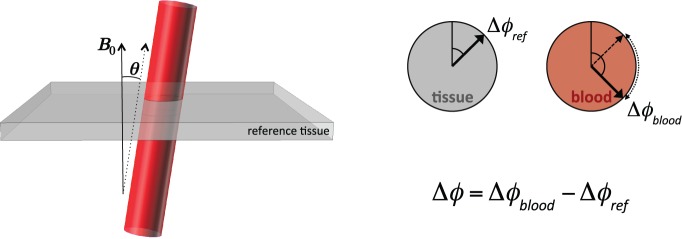
Schematic illustration of a blood vessel approximated by the infinite cylinder model. Due to paramagnetic dHb, MR signal in the blood has additional phase (Δφ_blood) compared to surrounding reference tissue (Δφ_ref). The phase difference (Δφ) and vessel angle (θ) are the two imaging-derived parameters used to compute Y_v in equation (21).

In addition to providing a surrogate for global Y_v,^55,104 the SSS is long (in terms of length:diameter ratio), relatively straight, and nearly parallel to the B₀ field when the subject is lying supine in an MRI scanner, making it an excellent candidate for application of the infinite cylinder model. Application of this susceptometry-based oximetry (SBO) approach to Y_v quantification in the SSS has been validated both theoretically¹²⁶ and with anatomical phantom models.⁵⁸

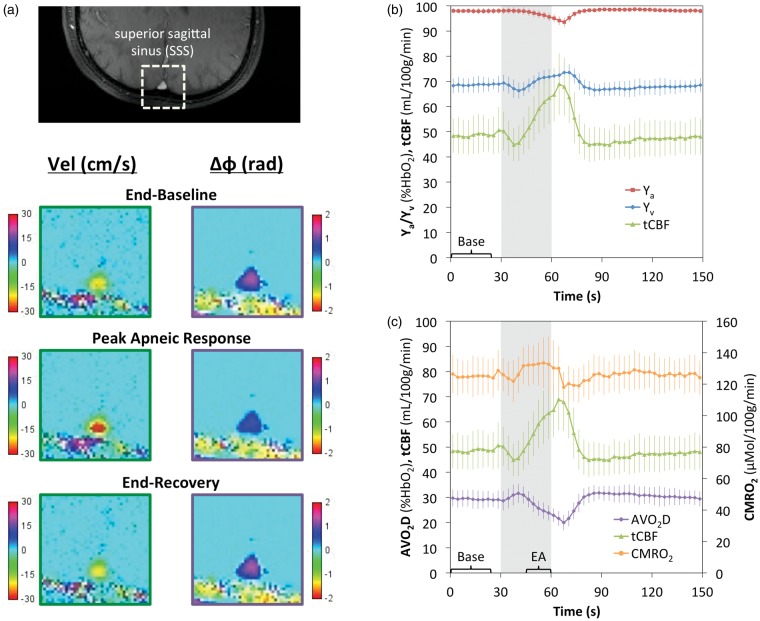
Because the method is based on a simple 2D GRE phase mapping sequence, SBO is very fast compared to T₂-based methods such as TRUST. Furthermore, it can be naturally interleaved with GRE-based PC-MRI for additional simultaneous quantification of CBF and, therefore, CMRO₂. This combined blood Oxygenation and Flow (dubbed ‘OxFlow’) pulse sequence has been used to quantify CMRO₂ with 30-s temporal resolution.⁵⁸ The method was later applied to study the CMRO₂ response to hypercapnia, both in healthy subjects¹²⁷ and neonates with congenital heart disease.¹²⁸ More recent iterations of the OxFlow method have achieved temporal resolutions as low as two seconds with the aid of view sharing.¹²⁹ This accelerated OxFlow sequence was applied to study the CMRO₂ response to breath-hold apnea in healthy subjects (Figure 10),¹²⁹ as well as in patients with obstructive sleep apnea (OSA).¹³⁰ Compared to control subjects, OSA patients were found to have both reduced baseline CMRO₂, as well as a reduced ability to maintain CMRO₂ during volitional breath holds. Such blunting of the normal CMRO₂ response to apnea may in part explain the significant neurologic comorbidities associated with OSA.¹³¹

Figure 10.

High temporal resolution CMRO₂ quantification applied to breath-hold apnea in 10 young healthy subjects. (a) Magnitude image with a superior sagittal sinus (SSS) ROI outlined and corresponding velocity and phase-difference (Δφ) maps illustrating an increase in blood flow velocity and decrease in blood−tissue phase difference in response to apnea. Time-course plot of cohort-averaged Y_a, Y_v, and tCBF (b) and AVO₂D, tCBF, and CMRO₂ (c) absolute parameter values in response to apnea, with the 30 second apneic period illustrated by the grey bar. Error bars indicate ±1 s.d. Across subjects, a small but statistically significant (6.0 ± 3.6%, P = 0.00044) increase in CMRO₂ in response to apnea was observed between the baseline (“Base”) and the end-apnea (“EA”) periods. Reproduced from Rodgers et al.,¹²⁹ with permission.

Compared to TRUST and other T₂-based Y_v techniques, SBO provides a simplified model relating measured signal parameters to Y_v and does not require sequence-specific calibration. As mentioned, a major limitation of the technique is the requirement for vessels with appropriate geometry, such as the SSS. Another limitation is that static magnetic field inhomogeneity from non-dHb sources (e.g. air–tissue interfaces) must be removed. This can be accomplished with polynomial fitting,¹³² but this approach will perform poorly in situations of severe background field variation (e.g. near metal orthodontics).

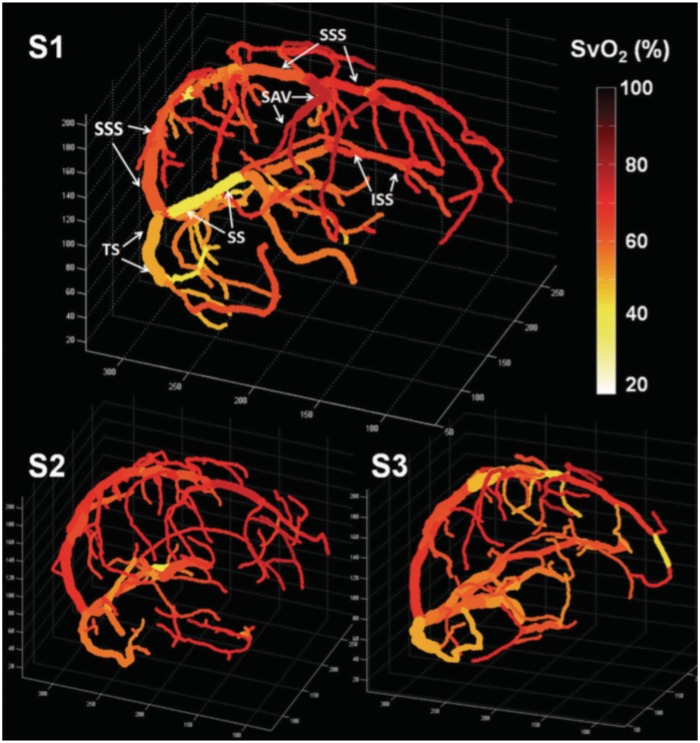
The second subset of susceptibility-based Y_v quantification techniques involves 3D phase mapping of the brain and dipole inversion by means of QSM techniques. This has been approached by: (1) focusing on only the intravascular signal to determine Y_v of large and medium sized (MRI-resolvable) veins,^133,134 and (2) modeling the susceptibility effects of the small venous blood compartment of tissue to determine voxel-wise Y_v.⁵⁹ The first approach has been used to produce venograms of Y_v values in the venous vascular tree (Figure 11),¹³³ whereas the second gives voxel-wise Y_v maps similar to the qBOLD technique. In both methods, ASL can be used to measure CBF. Acquisition times for the 3D field maps are several minutes, thus, both techniques are limited to measurement of baseline physiology or steady-state stimuli.

Figure 11.

Quantitative oxygenation venograms produced from whole-brain 3D phase mapping and QSM. Color bar indicates intravascular Y_v. Venograms are shown from three healthy volunteers. In the first subject, major veins in the brain are labeled, including the superior sagittal sinus (SSS), inferior sagittal sinus (ISS), straight sinus (SS), transverse sinus (TS), and superior anastomic vein (SAV). Reproduced from Fan et al.,¹³³ with permission.

As with T₂-based techniques for small vessel Y_v quantification, the venogram approach to Y_v-determination requires relating vessel-specific Y_v values to surrounding voxels, for which there is currently no feasible approach. As with SBO, vessel angles near the magic angle will have an increasingly small effect on the induced blood-tissue phase difference, which may explain the pronounced correlation between vessel angle and Y_v observed with the technique.¹³³ Although the voxel-wise QSM approach avoids these problems by focusing on the microvascular component of tissue, due to the small blood volume fraction of the microvessels, the induced changes in susceptibility for a given Y_v are approximately two orders of magnitude smaller than the corresponding intravascular susceptibility shifts. In fact, the intravascular blood susceptibility model (equation (16)) ignores the effects of such shifts in tissue susceptibility entirely. Furthermore, the voxel-wise method requires imaging during both baseline and an assumed isometabolic stimulus (with caffeine used in Zhang et al.⁵⁹) in order to separate blood and non-blood susceptibility effects.

Conclusions

CMRO₂ is a key physiological parameter with the potential to yield important insights into both normal brain function and brain pathophysiology in disease states. Pathophysiological alterations in CMRO₂ have been studied in cerebrovascular disease, where reductions in CBF limit the delivery of sufficient oxygen to meet metabolic needs, ultimately leading to cerebral infarction. Alterations in CMRO₂ may also occur due to mitochondrial dysfunction, which has been associated with numerous neurodegenerative disorders,¹³⁵ or may be due to alterations in energy regulation such as in the Warburg effect¹³⁶ described in cancer.

A number of magnetic resonance techniques for measurement and mapping of CMRO₂ have emerged during the past two decades. Whole-brain CMRO₂ quantification techniques, in particular TRUST and SBO, have been successfully applied in a variety of studies of normal human physiology and disease, suggesting the potential of global CMRO₂ as a clinical biomarker. However, even in physiologic and pathologic states, alterations in CMRO₂ are small, demanding that techniques have high levels of precision, accuracy, and reproducibility. This is illustrated, for instance, by the disparate results obtained regarding the CMRO₂ response to hypercapnia with TRUST⁸¹ and SBO.¹²⁷ As CMRO₂ becomes more widely adopted as a clinical biomarker, clinicians need to understand the potential biases and relative robustness of the various approaches, and recent work has begun to explore the relative agreement between methods.^80,137,138

In contrast to global CMRO₂ methods, voxel-wise mapping techniques – both T₂*- and T₂′-based – are at an earlier stage of technical development, and there is much space for improvement in terms of both acquisition strategies and theoretical models. Because they do not rely on gas breathing calibration, T₂′-based methods may ultimately emerge as the preferred approach to steady-state CMRO₂ mapping in clinical populations, for instance, in patients presenting with ischemic stroke. In contrast, T₂*-based BOLD calibration methods – though complicated by the need for gas calibration – are unique among all MR-based CMRO₂ quantification techniques in that they can achieve both high temporal resolution and voxel-wise spatial resolution. Calibrated BOLD could greatly improve the power of fMRI in longitudinal and group comparison studies by removing confounding by vascular effects unrelated to metabolic differences.

Significant progress continues to be made in developing and refining MR-based methods for CMRO₂ quantification. Much work remains in addressing critical challenges and defining new avenues of discovery.

Funding

This work was supported by the following grants from the National Institutes of Health: R21 HD069390, R01 HL109545, R01 HL122754.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Authors’ contribution

Dr. Rodgers drafted this work, Dr. Wehrli advised Dr. Rodgers and edited this work, Dr. Detre reviewed this work.