Evaluation of the Effect of Transcytolemmal Water Exchange Analysis for Therapeutic Response Assessment using DCE-MRI: A Comparison Study

Abstract

This study compares the Shutter-Speed (SS) and the Tofts models as used in assessing therapeutic response in a longitudinal DCE-MRI experiment. Sixteen nu/nu mice with implanted colorectal adenocarcinoma cell line (LS-174T) were randomly assigned into treatment/control groups (n=8/group) and received bevacizumab/saline twice weekly (Day1/Day4/Day8). All mice were scanned at one pre- (Day0) and two post-treatment (Day2/Day9) time points using a high spatiotemporal resolution DCE-MRI pulse sequence. The CA extravasation rate constant $K_T^{\mathit{trans}}/K_S^{\mathit{trans}}$ from the Tofts/SS model and the mean intracellular water residence time τ_i from the SS model were analyzed. A biological subvolume (BV) within the tumor was identified based on the τ_i intensity distribution, and the SS model parameters within the BV ( $K_{S,BV}^{\mathit{trans}}$ and τ_i,BV) were analyzed. It is found that $K_S^{\mathit{trans}}$ and $K_T^{\mathit{trans}}$ have a similar spatial distribution in the tumor volume. The Bayesian information criterion (BIC) results show that the SS model was a better fit for all scans. At Day9, the treatment group had significantly higher tumor mean $K_T^{\mathit{trans}}$ (p=0.021), $K_S^{\mathit{trans}}$ (p=0.021) and τ_i (p=0.045). When BV from transcytolemmal water exchange analysis was adopted, the treatment group had higher mean $K_{S,BV}^{\mathit{trans}}$ at both Day2 (p=0.038) and Day9 (p=0.007). Additionally, at Day9, the treatment group had higher mean τ_i,BV (p=0.045) and higher $K_{S,BV}^{\mathit{trans}}$ spatial heterogeneity indices (Rényi dimensions) d₁ (p=0.010) and d₂ (p=0.021). When mean $K_{S,BV}^{\mathit{trans}}$ and its coefficient of variation (CV) were used to separate treatment/control group samples using supporting vector machine (SVM), the accuracy of treatment/control classification was 68.8% at Day2 and 87.5% at Day9; in contrast, the Day2/Day9 accuracy were 62.5%/87.5% using tumor mean $K_S^{\mathit{trans}}$ and its CV and were 50.0%/87.5% using tumor mean $K_T^{\mathit{trans}}$ and its CV, respectively. These results suggest that the SS model parameters outperformed the Tofts model parameters in terms of capturing bevacizumab therapeutic effect in this longitudinal experiment.

1. Introduction

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is an imaging technique used for functional non-invasive measurements of microvascular properties. Based on the fast acquisition of a series of images before, during, and after the intravenous administration of a low molecular weight contrast agent (CA), DCE-MRI can measure differences in microvessel physiology associated with tumor angiogenesis (Hylton, 2006). Quantitative pharmacokinetic (PK) and heuristic model-based parameters have been established to characterize in-vivo microvascular features including blood volume, blood flow and vascular permeability (O’Connor et al., 2007). Compared to CT in characterizing microvascular function, DCE-MRI involves no use of ionizing radiation (Kershaw and Buckley, 2006) and has the additional merit of combining morphological and functional information in a single imaging session without sacrificing spatial resolution (Choyke et al., 2003). Because of these advantages, DCE-MRI is considered as a promising imaging technique for tumor staging (Delongchamps et al., 2011) and treatment planning (van der Heide et al., 2012). In the area of treatment response assessment, DCE-MRI is also capable of monitoring the therapeutic effect of radiotherapy (Cabrera et al., 2013; Wang et al., 2015), chemotherapy (Abramson et al., 2013; Yankeelov et al., 2007) and anti-vascular drugs (O’Connor et al., 2012).

Therapeutic response is commonly quantified by morphological descriptors of tumor volume (Jaffe, 2006) and first order statistics (mean/median/variance) of the PK parameters over the entire tumor volume or within manually selected regions of interest (ROIs) (O’Connor et al., 2011). However, human solid tumors are reported to be heterogeneous in terms of CA kinetic characteristics (Parker et al., 1997), and the current statistics for treatment response assessment cannot fully quantify tumor heterogeneity. For the purpose of automated extraction of image features with great throughput potentials for computer-aided diagnosis and outcome prediction (which recently can be referred as Radiomics) (Aerts et al., 2014), the tumor heterogeneity extracted from the texture analysis of PK parametric maps have been incorporated as a key component for DCE-MRI characterization (Lambin et al., 2012; Jiang et al., 1999). Pilot studies have demonstrated the use of tumor heterogeneity as a biomarker for treatment assessment (Alic et al., 2011; Goh et al., 2011; Rose et al., 2009; Yang and Knopp, 2011). To ensure the prompt capture of treatment induced functional changes, the derivation of PK parameters needs to be accurate and precise (Chang and Wang, 2015). So far, the most widely used PK model is the one proposed by Tofts and Kermode (Tofts and Kermode, 1991) in which the CA kinetics in the microvessel environment is described by the CA bidirectional transendothelium exchange between two compartments, blood plasma and extravascular-extracellular space (EES). Prior to model fitting, the CA concentration maps at each post-injection time point need to be determined. The conversion of MR signal to CA concentration is frequently reported as a linear relationship between the CA concentration and the change of longitudinal relaxation rate R₁ = (1/T₁). Such linear relationship relies on the assumption that the extravascular space is a single well-mixed medium and thus the interstitium can be treated as a homogeneous solution. Hence, it is required that water exchange from the intracellular space to EES (also known as transcytolemmal water exchange) must be sufficiently fast. However, biological tissue could be highly compartmentalized on a histological scale (Landis et al., 1999) and the assumption of fast transcytolemmal water exchange (Fast-Exchange Limit FXL) may not always be satisfied. If the transcytolemmal water exchange is not fast enough to equilibrate the effects of CA in EES, the aforementioned linear relationship between the CA concentration and the change of longitudinal relaxation would be violated (Labadie et al., 1994). In practice, the Bloch equations should incorporate the effects of the limited transcytolemmal water exchange rate with a bi-exponential decay term of longitudinal relaxation (Landis et al., 2000). The main result of this modification is known as the shutter-speed (SS) model (Yankeelov et al., 2003). In this model, the transcytolemmal water exchange rate is modelled as the inverse of the mean residence time of water molecules in the intracellular space, and the relationship between the CA concentration and longitudinal relaxation rate change is expressed as a nonlinear equation with the presence of limited transcytolemmal water exchange rate.

The SS model has been applied for the PK characterization of head and neck cancer (Kim et al., 2010; Kim et al., 2007), breast cancer (Huang et al., 2008) and prostate cancer (Li et al., 2013). For treatment response assessment, this model has been investigated in a limited number of clinical studies (Huang et al., 2014; Yankeelov et al., 2007). However, to our best knowledge, a comprehensive comparison of the SS model and the classic Tofts model in capturing therapeutic response effect has not been fully explored, especially with the comparison of randomized treatment/control groups in a longitudinal experiment setup with multiple post-treatment evaluation. The present work was conducted to evaluate the performance of the SS model with transcytolemmal water exchange analysis in a small animal therapeutic response assessment experiment with high spatiotemporal resolution DCE-MRI. The potential use of first order statistics, histogram descriptors and spatial heterogeneity indices of the PK parametric maps from both models were investigated at multiple time points.

2. Materials and methods

Small Animal Experiment

All animal studies were approved by the Institutional Animal Care and Use Committee. In this longitudinal experiment, a total of 16 female nu/nu mice with a colorectal adenocarcinoma cell line LS-174T (Charles River Laboratories, Wilmington, MA) implanted in the mammary fat pad were followed for four weeks. The mice were randomly assigned into the equally-sized treatment group or the control group (n = 8/group) when tumor volume was approximately 100μL. A pre-treatment DCE-MRI scan was acquired at Day0 as the baseline. The treatment/control group received bevacizumab (Avastin^®, Genentech, South San Francisco, CA) or normal saline via an intraperitoneal injection at a dose of 5 mg/kg or 5 mL/kg twice weekly. Two post-treatment DCE-MRI scans were performed weekly. The first two post-treatment scans at Day2 and Day9 were evaluated since the therapeutic effects of the treatment group were prominent after the first two weeks’ experiment.

DCE-MRI Protocol

All DCE-MRI scans were performed in a 7T small animal MRI scanner (Bruker BioSpin MRI GmbH, Ettlingen, Germany) equipped with self-shielded gradient coils with a maximum strength of 450 mT/m and a rise time of 110 μs. An actively detuned volume RF coil (linear transmit, ID = 72 mm) was used in conjunction with a four-element coil (2×2 linear array, 10×10 mm loops) for surface receive. An interleaved ultra-short-echo radial sampling sequence was adopted for 4D reconstruction using a sliding-window keyhole approach as described in previous work (Subashi et al., 2013). The acquisition parameters were listed as follows: FOV = 20×20×20 mm³, matrix = 128×128×128, TR/TE = 5/0.02 ms, NEX = 1, flip angle α = 10°, temporal resolution = 9.9s, spatial resolution = 156μm. Using this pulse sequence, the selection of TE=0.02 ms allows for the application of the SPGR equation without T2* corrections (Kleppestø et al., 2014), and the calculated CA concentrations have been shown to be within the theoretically predicted uncertainty (Subashi et al., 2014). Prior to the CA injection, two calibration scans with α = {2°, 10°} were acquired to calculate the native longitudinal relaxation rate with dual flip angle calculate method (Fram et al., 1987). An automatic syringe pump (KD Scientific Inc., Holliston, MA) was used to administer Gd-DTPA (Magnevist, Schering AG, Berlin, Germany) via a 27-gauge tail vein catheter at a dose of 0.5 mmol/kg and a flow rate of 2.4mL/min. The dynamic acquisition was initiated two minutes prior to the CA injection and lasted for approximately 20 minutes after the CA injection. For a well-controlled setup for dynamic imaging, animals were positioned in a custom-made MR-cradle and were maintained under anesthesia by isoflurane delivery via a nose cone. The body temperature was controlled between 36°C and 37°C by circulating warm water. Breathing was monitored through a pneumatic pillow and was maintained at a rate of 50–60 breaths/min via adjusting isoflurane delivery.

Image Analysis

For each DCE-MRI scan, the tumor volume V was measured on one of the contrast-enhanced volumes. The tumor growth rate at each post-treatment scan day was defined as the volume ratio to the pre-treatment baseline value and was selected as the primary tumor morphological descriptor. In the PK analysis using the Tofts model, the CA concentration C(t) at each post-injection time point was estimated using the following linear equation:

$$C(t)=(R_1(t)-R_{10})/r_1$$ (1)

where r₁ is the longitudinal relaxivity ( = 3.275 mM⁻¹s⁻¹ at 7T) of the CA (Noebauer-Huhmann et al., 2010), R₁₀ is the native longitudinal relaxation rate prior to CA injection and R₁(t) is the post-injection longitudinal relaxation rate (= 1/T₁) determined by using a published method (Schabel and Parker, 2008). The two-compartment Tofts model is expressed as below with Kety rate law employed (Kety, 1960):

$$C(t)=K^{\mathit{trans}}{\int }_0^t{C}_p(u)·e^{-(K^{\mathit{trans}}/v_e)·(t-u)}du$$ (2)

where K^trans is the rate constant of CA extravasation from blood plasma to EES, and v_e is the volume fraction of EES. The parameter k_ep = K^trans / v_e is the rate constant describing the CA transport from EES back to blood plasma. The arterial input function (AIF) C_p(t) in this study was approximated by a reported population measurement (Loveless et al., 2012). Eq. (2) was then solved on a voxel-by-voxel basis using a linear least-squares method (Murase, 2004).

The SS model with transcytolemmal water exchange is expressed as:

$$R_1(t)=\frac{1}{2}\left[R_{1i}+R_{1e}+r_1<CA,t>+\frac{1}{{\tau }_i}+\frac{1-v_e/f_w}{{\tau }_i{v}_e/f_w}\right]-\frac{1}{2}{\{{\left[R_{1i}-R_{1e}-r_1<CA,t>+\frac{1}{{\tau }_i}+\frac{1-v_e/f_w}{{\tau }_i{v}_e/f_w}\right]}^2+\frac{4(1-v_e/f_w)}{{\tau }_i^2{v}_e/f_w}\}}^{1/2}$$ (3)

where R_1i and R_1e represent the native longitudinal relaxation rate of intracellular space and EES water molecules, respectively. τ_i denotes the mean residence time of water molecules in the intracellular space whose inverse represents the transcytolemmal water exchange rate constant. f_w is the fraction of water molecules in EES that are accessible to mobile CA particles, and a constant of 0.8 was chosen as previously reported (Landis et al., 2000; Yankeelov et al., 2007). In Eq. (3), the notation <CA> represents the indirect CA concentration result at a post-injection time point, which is still related to the CA extravasation constant K^trans with Kety rate law:

$$<CA,t>=K^{\mathit{trans}}{\int }_0^t{C}_p(u)·e^{-(K^{\mathit{trans}}/v_e)·(t-u)}du$$ (4)

A substitution of Eq. (4) into Eq. (3) yields the operable equation of the SS model for three PK parameters: K^trans, v_e (or k_ep = K^trans/ v_e) and τ_i. R_1i and R_1e can be approximated as R₁₀ in Eq. (1) (Landis et al., 2000). The SS model was solved by the nonlinear least-squares fitting Levenberg-Marquardt method on a voxel-by-voxel base (Ahearn et al., 2005). To avoid the potential fitting error due to the local minimum, the Levenberg-Marquardt iteration was repeated with 25 groups of randomly-selected initial points within the reported range: K^trans: 0–2 min⁻¹; τ_i: 0–2 s; and v_e: 0–1 ml/ml, and the result with the best fitting quality with the least χ² value was reported (Kim et al., 2007):

$${\chi }^2=\frac{1}{N}\sum _{i=1}^N\frac{{(S_i-P_i)}^2}{P_i}$$ (5)

where N is the length of measurement data series, S_i is the measured data (C(t) for Tofts model and R₁(t) for SS model), and P_i is the fitted data by the model.

The CA extravasation rate constant from the Tofts model ( $K_T^{\mathit{trans}}$) and the SS model ( $K_S^{\mathit{trans}}$) were reported as the primary PK parameters. The mean of K^trans within a ROI has been frequently reported as an important DCE-MRI biomarker and has been selected as the primary clinical DCE-MRI biomarker by the Quantitative Imaging Biomarker Alliance (QIBA) of Radiological Society of North America (RSNA) (Padhani and Leach, 2005; DCE-MRI-Technical-Committee, 2012). For the SS model, τ_i was also selected as an additional PK parameter. For each recorded parametric map, the tumor mean value was calculated. The coefficient of variation (CV) defined as the ratio of the standard deviation to the mean value was also reported as a measure of the parameter’s probability distribution dispersion (Sokal and Rohlf, 1981). The histogram descriptors, kurtosis (measurement of ‘peakedness’ of the probability distribution) and skewness (measurement of asymmetry of probability distribution) were recorded to describe the shape of the intensity distribution. Inspired by initial promising work (Collins et al., 2003), the classic fractal dimensions d₁ and d₂ defined by the generalized Rényi dimensions were analyzed for spatial heterogeneity measurement (Allen et al., 1995). As the heterogeneity information measurement, Rényi dimensions d₁ and d₂ measure the Rényi entropy at different scales:

$$\begin{array}{c}{d}_q=\underset{\epsilon \to 0}{lim}\frac{\mathit{log}{\sum }_i{p}_i^q}{(1-q)\mathit{log}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\epsilon $}\right.}\\ d_1=\underset{q\to 1}{lim}{d}_q\end{array}$$ (6)

where ε is the scale resolution (ranging from a single voxel dimension to the size of field of view) and p_i is the normalized intensity value of i-th voxel such that Σ_ip_i = 1 ∀i. Two heterogeneity indices of intensity object, d₁ information dimension and d₂ correlation, were adopted in this work. For objects with pre-defined shape, d₁ and d₂ values were reported for objects with larger intensity variations (Bartholdi et al., 2003). Previous studies have reported that d₁ and d₂ of K^trans map might reflect the tumor heterogeneity differences between low and high-grade glioma (Rose et al., 2009). In one of our recent works, the d₁ and d₂ of K^trans map were found to be useful in determining the bevacizumab therapeutic effect (Wang et al., 2016).

As a further utilization of transcytolemmal water exchange analysis, for each scan, a biological subvolume (BV) within the tumor was identified based on τ_i intensity distribution. Specifically, the τ_i histogram was generated, and an intensity threshold was automatically determined based on the leftmost peak position. The BV was then identified as the voxels with τ_i intensity higher than the threshold. Within the BV, the CA extravasation rate constant ( $K_{S,BV}^{\mathit{trans}}$) and intracellular water molecule residence time (τ_i,BV) were analyzed. The aforementioned PK parameter metrics (mean, CV, kurtosis, skewness, d₁ and d₂) of $K_{S,BV}^{\mathit{trans}}$ and τ_i,BV were recorded.

The performance of the two models with respect to data fitting quality was estimated with the Bayesian information criterion as a commonly used statistical criteria for model selection (Schwarz, 1978):

$$\mathit{BIC}=log({\chi }^2)+(\mathit{k}logN)/N$$ (7)

where N is the length of measurement data series, χ² is the median value of the χ² map from one model and k is the model freedom degree (2 for Tofts model and 3 for SS model). A smaller BIC value can be interpreted as better data fitting quality.

Statistical Analysis

Each recorded metric was compared longitudinally, and at each post-treatment scan day, the Mann-Whitney U-test was used to assess the difference of the recorded metric between treatment and control groups. Significance was determined based on a p-level less than 0.05 with multi-comparison correction if applicable (Chen et al., 2007). To determine the model fitting quality, the BIC values of the Tofts model and the SS model of all examined scans were compared using Wilcoxon signed-rank test with significance level p < 0.05. Of all 48 scans, 2 were excluded for analysis as the CA injection was unsuccessful. To validate the potential use of the recorded metrics from PK parameter analysis for treatment/control group separation, classification experiments using support vector machine (SVM) in a leave-one-out approach were performed at each post-treatment scan day with single/multiple metric(s) as input.

3. Results

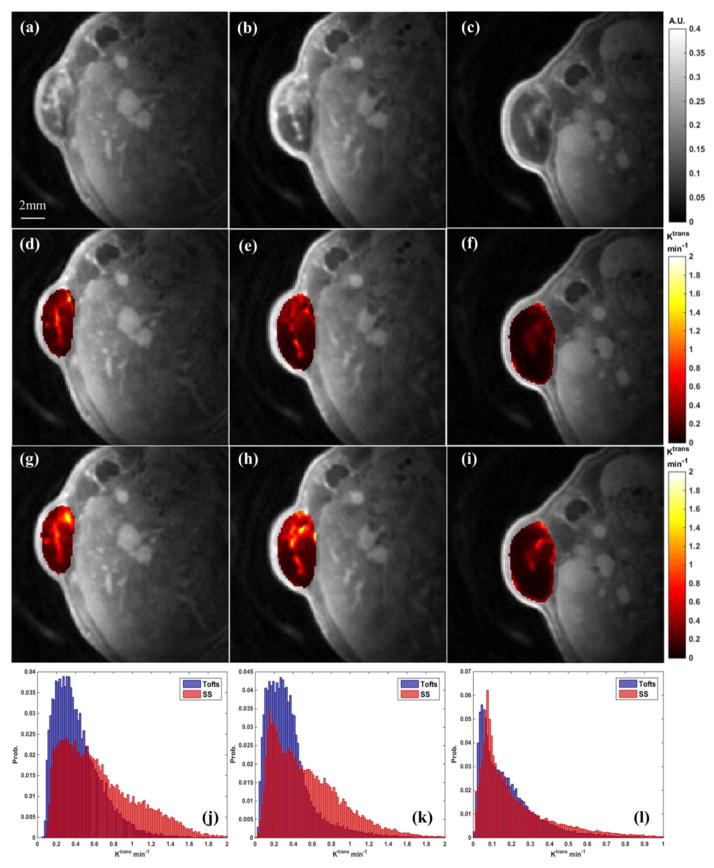
Figure 1 shows the analysis of a representative animal from the treatment group at three DCE-MRI scan days (left column: Day0; middle column: Day2; right column: Day9). The spatial heterogeneity of intensity distribution within the defined tumor can be readily appreciated in the DCE volumes about 60 seconds after the CA injection (Figure 1 (a)–(c)). The $K_T^{\mathit{trans}}$ maps (Figure 1 (d)–(f)) and the $K_S^{\mathit{trans}}$ maps (Figure 1 (g)–(i)) at each scan day were morphologically similar with comparable shape patterns. Compared to the $K_T^{\mathit{trans}}$ maps, the $K_S^{\mathit{trans}}$ maps had higher intensity values across the tumor. K^trans hotspots were identified at the same locations on both sets of maps, and the hotspots on $K_S^{\mathit{trans}}$ maps had relatively larger sizes and higher intensities. The K^trans histograms (Figure 1 (j)–(l)) from both models had peak positions towards the low intensity region (i.e., positive skewness), and the $K_S^{\mathit{trans}}$ were likely to exhibit higher probability towards the high intensity region. This observation is consistent with the high K^trans values of $K_S^{\mathit{trans}}$ maps. The bevacizumab treatment effect was obvious on (f) and (i) after three doses, as the K^trans intensities across the tumor decreased in reference to the pre-treatment maps.

Figure 1.

A demonstration of K^trans from a selected animal at three scan days. Left column: Day0; middle column: Day2; right column: Day9. First row: post-injection T1w DCE image; 2^nd row: $K_T^{\mathit{trans}}$ maps from the Tofts model; 3^rd row: $K_S^{\mathit{trans}}$ maps from the SS model; 4^th row: joint histogram of $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$. The tumor mean values of this animal are: Day0: $K_T^{\mathit{trans}}=0.429{min}^{-1},K_S^{\mathit{trans}}=0.661{min}^{-1}$; Day2: $K_T^{\mathit{trans}}=0.361{min}^{-1},K_S^{\mathit{trans}}=0.559{min}^{-1}$; Day9: $K_T^{\mathit{trans}}=0.153{min}^{-1},K_S^{\mathit{trans}}=0.229{min}^{-1}$

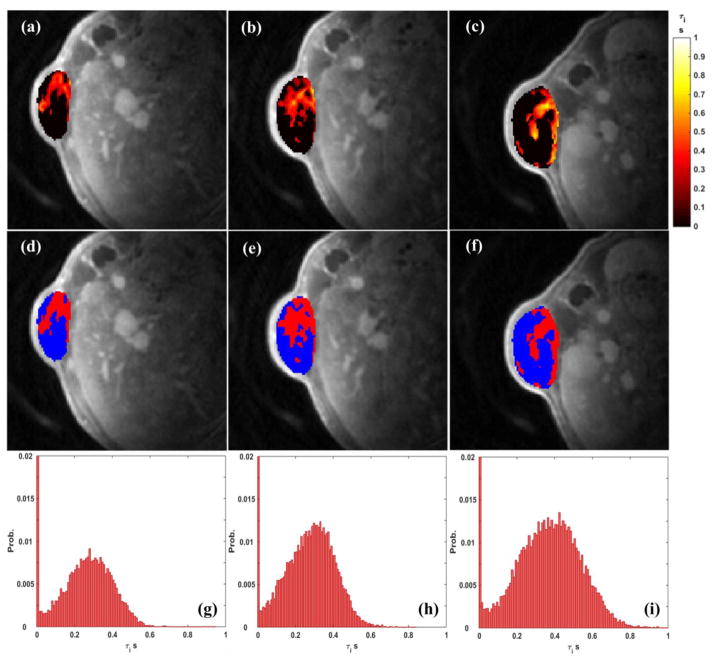
Figure 2 shows the τ_i results of the same animal in Figure 1 from the transcytolemmal water exchange analysis (left column: Day0; middle column: Day2; right column: Day9). As can be observed in Figure 2 (a)–(c), at each scan day, τ_i had an intensity-elevated region with very clear and sharp boundary. Accordingly, the identified BV regions are presented in the 2^nd row as red areas. Within these BVs, the transcytolemmal water exchange rate ( = 1/τ_i) was relatively limited with higher τ_i values. At each scan day, the τ_i histogram Figure 3 (g)–(i) had its first peak at the leftmost bin. Based on the aforementioned BV identification method, the τ_i intensity threshold for BV was about 10ms in these three scans. The increase of probability sum of all non-zero bins was consistent with the increase of mean τ_i value along the experiment (Day0: 0.159 s; Day2: 0.170 s; Day9: 0.193 s). Such increase is also supported by the observable intensity elevation from Figure 2(d) to (f).

Figure 2.

A demonstration of τ_i from a selected animal at three scan days. Left column: Day0; middle column: Day2; right column: Day9. First row: the τ_i maps across the tumor; 2^nd row: the identified BV (red area) within the tumor; 3^rd row: the τ_i histograms. The tumor mean values of this animal are: Day0: τ_i = 0.159 s; Day2: τ_i = 0.170 s; Day9: τ_i = 0.193 s

Figure 3.

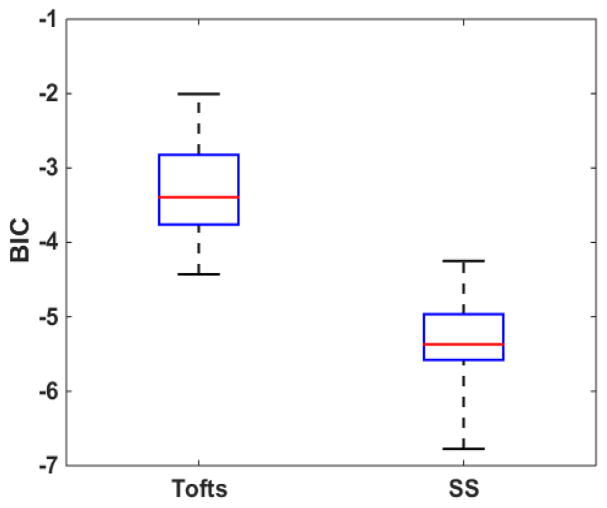
The BIC statistics of the Tofts model and the SS models of all analyzed scans. The red horizontal line indicates the median value and the whiskers indicate ± 1.5 interquartile range (IQR)

Figure 3 reports BIC results for the comparison of data fitting quality using the two investigated models. The median BIC value (indicated by red line) of the SS model was lower than the corresponding value of the Tofts model. Wilcoxon signed-rank test showed that the SS model’s BIC values were significantly lower than the Tofts model’ values (p<.0001), indicating that the SS model has generally improved data fitting qualities than the Tofts model.

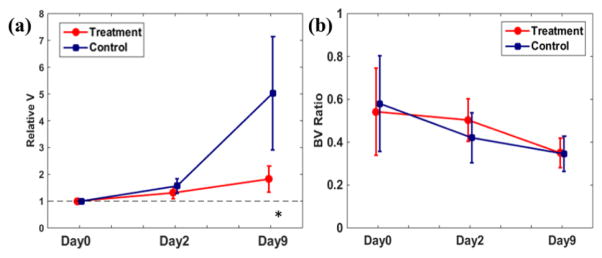
Figure 4 demonstrates the therapeutic response assessment using tumor morphological descriptors. The error bar represents the group standard deviation. At Day0, the initial tumor volumes of the treatment and control group were 115 ± 41 μL and 91 ± 37 μL, respectively. As reflected by the tumor growth rate (Figure 4 (a)), during the treatment course, the tumors in the treatment group grew slower than the tumors in the control. At the end of the experiment at Day9, the tumor growth rates of the treatment group were significantly lower than the control group rate (p = 0.002). Figure 4(b) shows the evolution of the ratio of identified BV using τ_i to the tumor volume from transcytolemmal water exchange analysis. The ratio decreased in both treatment and control groups during the experiment with no statistically significant difference.

Figure 4.

Comparisons of tumor growth rate (a) and the ratio of identified BV to tumor volume (b). The error bar represents the group standard deviation. * indicates statistical significance

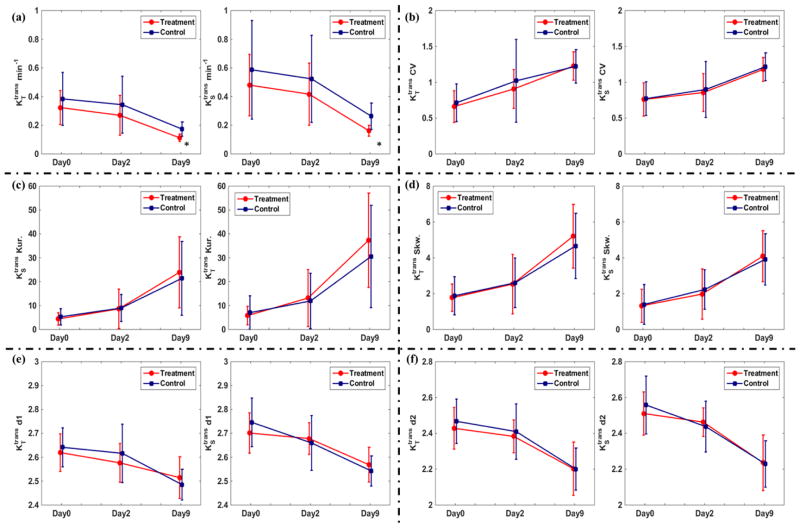
Figure 5 summarizes the therapeutic response assessments using $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ metrics. Regarding tumor mean $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ values (Figure 5 (a)), at Day0, there was no significant difference between the treatment/control groups $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ value. At end of follow-up, both treatment and control groups showed a decreasing trend of K^trans. The CV of $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ of both groups (Figure 5 (b)) increased in the experiment, suggesting the increased K^trans probability distribution dispersion. The evaluation of K^trans kurtosis and skewness in (c) and (d) suggest that in both models, the peak of K^trans probability distribution moved towards the zero-value direction with increased peak height. The decreases of the spatial heterogeneity indices d₁ and d₂ of both groups in (e) and (f) suggest the tumor heterogeneity reduction along the experiment. At Day9, the treatment group had significantly lower $K_T^{\mathit{trans}}$ (p = 0.021) and $K_S^{\mathit{trans}}$ (p = 0.021) values than the control group. The other statistics including CV, kurtosis, skewness, d₁ and d₂ did not show significant difference between the treatment/control groups.

Figure 5.

Comparisons of $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ at three treatment days in terms of tumor mean value (a), CV (b), kurtosis (b), skewness (b), d₁ (e) and d₂ (f) at three treatment days. The error bar represents the group standard deviation. At Day9, the treatment group had significantly lower (indicated by *) $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$.

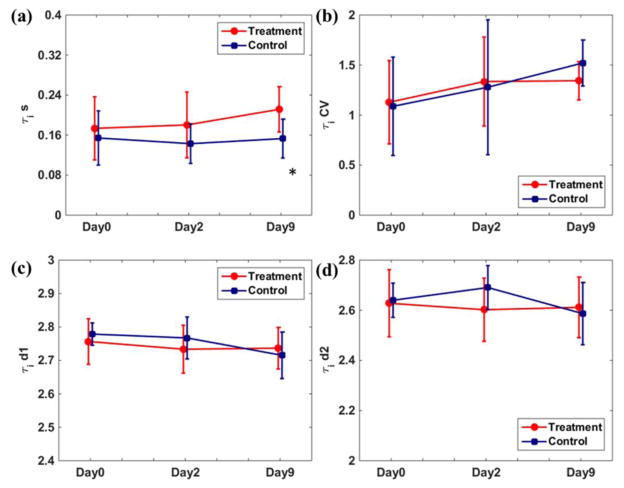
Figure 6 shows the therapeutic response assessment using τ_i from transcytolemmal water exchange analysis. As shown in (a), the tumor mean τ_i of the treatment group increased during the experiment, while the control group values were relatively stable. At Day9, the treatment group had significantly higher mean τ_i values (p = 0.045). While the control group τ_i CVs kept increasing in (b), the treatment group τ_i CV increased from Day0 to Day2 but was relatively stable from Day2 to Day9. The τ_i CV difference between treatment/control groups was not statistically significant. Unlike the decreasing trend of $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$ spatial heterogeneity indices, the d₁ and d₂ values of τ_i were relatively stable in both treatment/control groups with no significant difference, though the d₂ differences at Day2 showed a trend towards significance (p = 0.083). The evaluations of kurtosis and skewness were not reported since all τ_i histograms had their first peak at the first bin and thus the histogram descriptors comparison became trivial.

Figure 6.

Comparisons of τ_i mean value (a), CV (b), d₁ (c) and d₂ (d) at three treatment days. The error bar represents the group standard deviation. At Day9, the treatment group had significantly higher (indicated by *) τ_i.

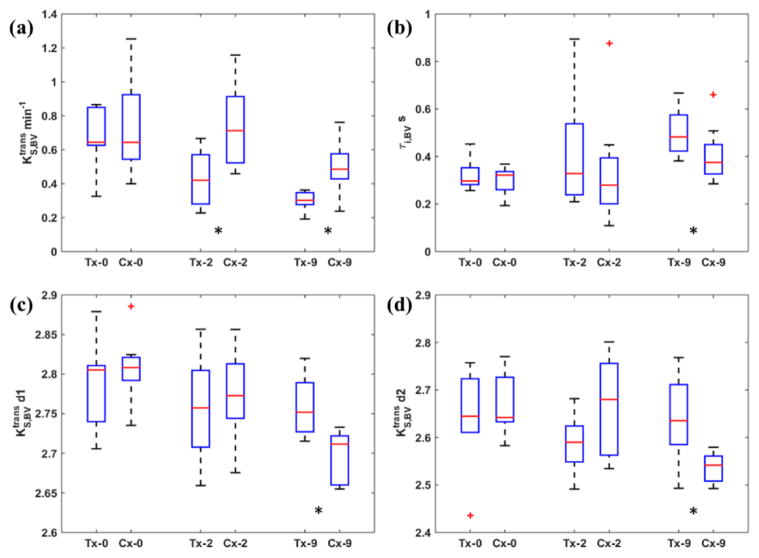
Figure 7 shows the results using $K_{S,BV}^{\mathit{trans}}$ and τ_i,BV within the identified BVs with boxplot comparisons as the identified BV at different days were not necessarily overlapped. As shown in (a), the mean $K_{S,BV}^{\mathit{trans}}$ across the BV had higher intensities in comparison with Figure 5(a), and the decreasing trend in both treatment/control groups was observed. It is important to point out that the treatment group had significantly lower mean $K_{S,BV}^{\mathit{trans}}$ values at both Day2 (p = 0.038) and Day9 (p = 0.007), while the treatment group had significantly lower mean $K_{S,}^{\mathit{trans}}$ values only at Day9 (p = 0.021) in Figure 5(a). This suggests a potential value of $K_{S,BV}^{\mathit{trans}}$ for early capture of bevacizumab therapeutic effect. Similarly to τ_i results in Figure 6(b), the treatment group had significantly higher τ_i,BV values at Day9 (p = 0.045). Additionally, the spatial heterogeneity indices in (c) and (d) show that the treatment group had significantly higher $K_{S,BV}^{\mathit{trans}}$ d₁ (p = 0.010) and d₂ (p = 0.021) values after the experiment at Day9. The other comparisons of $K_{S,BV}^{\mathit{trans}}$ and τ_i,BV metrics did not show significant difference between treatment/control groups. These results in Figure 7 suggest that the identified BV could provide additional benefits for early treatment response assessment using K^trans and τ_i statistics.

Figure 7.

Comparisons of mean $K_{S,BV}^{\mathit{trans}}$ (a), mean τ_i,BV (b), $K_{S,BV}^{\mathit{trans}}$ d₁ (c) and d₂ (d) at three treatment days. Tx = treatment group; Cx = control group. The red horizontal line indicates the median value and the whiskers indicate ± 1.5 interquartile range (IQR). At Day2, the treatment group had significantly lower (indicated by *) $K_{S,BV}^{\mathit{trans}}$; At Day9 the treatment group had significantly lower (indicated by *) $K_{S,BV}^{\mathit{trans}}$, τ_i,BV and $K_{S,BV}^{\mathit{trans}}$ d₁ and d₂ values

Table 1 summarizes the results of treatment/control groups’ classification experiments using SVM. When the tumor mean value of $K_T^{\mathit{trans}}$ or $K_S^{\mathit{trans}}$ was selected as the sole parameter for SVM, the classification accuracy at Day9 was 68.8%. In contrast, the accuracy at Day9 using mean $K_{S,BV}^{\mathit{trans}}$ as the input was as high as 87.5%. When CV was used along with tumor mean $K_T^{\mathit{trans}}$ and tumor mean $K_S^{\mathit{trans}}$, the classification accuracy at Day9 were improved to 87.5% and 87.5%, respectively. With BV information, the Day2 classification accuracy using mean $K_{S,BV}^{\mathit{trans}}$ and its CV were improved from 62.5% to 68.8%, while the Day9 accuracy remained 87.5% without improvement. The classifications tests using τ_i/τ_i,BV metrics were suboptimal than the tests using K^trans metrics from both models, as the highest achievable accuracy at Day9 were 62.5% using mean τ_i,BV and its CV. As a general summary of Table 1, the treatment/control group classification using K^trans across the whole tumor from the Tofts model and the SS model were comparable at Day9; when using K^trans statistics the identified BV, the classification accuracies at Day2 were further improved.

Table 1.

The results of treatment/control group classification using SVM

		SVM Input	Classification Accuracy
			Day2	Day9
Tofts Model	Whole tumor	Mean $K_T^{\mathit{trans}}$	43.8%	68.8%
		(Mean $K_T^{\mathit{trans}}$, CV)	50.0%	87.5%
		(Mean $K_T^{\mathit{trans}}$, Kurtosis, Skewness)	31.3%	56.3%
		(Mean $K_T^{\mathit{trans}}$, d1, d2)	43.8%	75.0%
SS Model	Whole tumor	Mean $K_S^{\mathit{trans}}$	50.0%	68.8%
		(Mean $K_S^{\mathit{trans}}$, CV)	62.5%	87.5%
		(Mean $K_S^{\mathit{trans}}$, Kurtosis, Skewness)	43.8%	62.5%
		(Mean $K_S^{\mathit{trans}}$, d1, d2)	50.0%	56.3%
		Mean τi	56.3%	56.3%
		(Mean τi, CV)	37.5%	68.8%
		(Mean τi, d1, d2)	50.0%	56.3%
	BV	Mean $K_{S,BV}^{\mathit{trans}}$	50.0%	87.5%
		(Mean $K_{S,BV}^{\mathit{trans}}$, CV)	68.8%	87.5%
		(Mean $K_{S,BV}^{\mathit{trans}}$, Kurtosis, Skewness)	68.8%	75.0%
		(Mean $K_{S,BV}^{\mathit{trans}}$, d1, d2)	68.8%	75.0%
		Mean τi,BV	43.8%	56.3%
		(Mean τi,BV, CV)	43.8%	62.5%
		(Mean τi,BV, Kurtosis, Skewness)	37.5%	56.3%
		(Mean τi,BV, d1, d2)	56.3%	56.3%

4. Discussion

In this work, the therapeutic response assessment using the classic Tofts model and the SS model with transcytolemmal water exchange analysis were compared in a longitudinal small animal study. This study used bevacizumab as a recombinant humanized monoclonal IgG₁ antibody that selectively binds to and neutralizes the functional activity of vascular endothelial growth factor (VEGF) (Jain et al., 2006). Such neutralization can lead to the reduction of tumor vascularization and the decrease of lesion volume, which reflects an effective response and would be the desirable treatment outcome function (Cohen et al., 2007). In this study, the application of bevacizumab caused a decrease of tumor growth rate, though complete tumor regression was not achieved. This may explain the observation that some of the investigated metrics of the treatment and the control groups showed similar evolution trends during the experiment.

As the primary functional imaging biomarker from the quantitative PK analysis, the parameter K^trans describes the combined information of capillary wall surface, capillary permeability, and blood flow. As shown in Figure 1 and Figure 5(a), the tumor mean values of $K_S^{\mathit{trans}}$ from the SS model were higher than the tumor mean values $K_T^{\mathit{trans}}$ from the classic Tofts model. This result was consistent with the previously reported results about larger $K_S^{\mathit{trans}}$ (Huang et al., 2014; Kim et al., 2007). As another potential parameter-of-interest, the tumor mean CA rate constant k_ep (=K^trans/ v_e) results from both models were summarized as Figure S1 in the supplementary document. For a short conclusion, in both treatment and control group, k_ep from both models showed a decreasing trend during the experiment, and no statistically significant difference were found between treatment/control groups’ values at Day2/Day9. The inclusion of limited transcytolemmal water exchange rate has been argued to consider the CA particles that cannot be immediately distributed in EES. Thus, the SS model yielded higher CA concentrations and thus higher CA extravasation rate values in comparison with the classic Tofts model. When the injected CA dose is high (0.5 mmol/kg body weight in this work), the adoption of SS model becomes necessary to correct the CA concentration underestimation (Yankeelov et al., 2005). The K^trans maps identified by the two models were morphologically comparable in Figure 1, and the SS model was found to be a better fit for all scans in terms of BIC comparison in Figure 3. These results may serve as the evidence that SS model could describe the microvessel environment more accurately than the classic Tofts model. The histology report would be valuable as the gold standard for the correlation study with PK parametric maps. The histology report after the 2^nd post-treatment imaging was not included in this experiment. For our ongoing and future experiments, the histology report will be included as an essential component for direct evaluation of PK model validity.

Many studies have reported a decreased tumor mean K^trans value after bevacizumab application or its combination with other treatment regimens (Cabrera et al., 2013; De Bruyne et al., 2012; Levin et al., 2011). In this work, when using both models, the treatment group had significantly lower tumor mean $K_T^{\mathit{trans}}$ and $K_S^{\mathit{trans}}$, suggesting the effective treatment effect of bevacizumab. In addition, the K^trans kurtosis of both the treatment and the control group increased along with the experiment, which indicated that K^trans distribution evolved towards leptokurtosis. This observation is not consistent with a previous study in which the increase of kurtosis was correlated with the tumor chemotherapy response (Chang et al., 2004). The skewness statistics in this work were all positive, and this means that the observed K^trans distributions’ peaks were with low intensity region with a longer tail at the high intensity region. Consistent with the decreasing K^trans statistics in Figure 5(a), the increase of skewness reflects the shift of K^trans peak value towards the lower intensities. Few studies regarding the longitudinal change of K^trans histogram descriptors after therapy have been reported. This renders the use of kurtosis and skewness preliminary and challenging in DCE-MRI therapeutic response assessment.

The value of the additional PK parameter τ_i from the transcytolemmal water exchange analysis for therapeutic response assessment was demonstrated. Previously, τ_i has been shown to be potentially valuable for diagnostic assistance (Li et al., 2005). In terms of treatment assessment, however, some studies concluded that τ_i may not be able to offer extra information for monitoring treatment response (Yankeelov et al., 2007). In this work, the tumor mean τ_i of the treatment group increased in the experiment and was significantly higher than the corresponding values of the control group. As is presented in the theory (Landis et al., 1999), τ_i =V/(P · A) where P is the diffusional permeability of the cell membrane, A is the cell surface area and V is the volume of the cell. As a result, the increased τ_i of the treatment group could be a result of the increased cell size and/or decreased diffusional cell permeability. The diffusional cell membrane permeability may be reflected by the apparent diffusion coefficient (ADC) from diffusion-weighted imaging (DW-MRI). Future work with the inclusion of DW-MRI technique may improve the understanding of τ_i in therapeutic response assessment.

The introduction of biological subvolume (BV) based on τ_i distribution has been proved valuable for DCE-MRI therapeutic response assessment. Previous work has predicted that FXL holds when τ_i⁻¹/p₀ ≫ |R_1o0 − R_1i|, where p₀ is the fractions of water molecules in EES, R_1o0 is the native longitudinal relaxation rate of EES water molecules, and R_1i is the longitudinal relaxation rate of intracellular water molecules (Landis et al., 1999). For the Day0 scan presented in Figure 2, the τ_i in BV ranged from about 10ms to 1s. If R_1o0 was approximated by R₁₀ and R_1i could be roughly estimated as R₁, then the observed mean |R₁ − R₁₀| at the maximum enhancement time point was about 0.233s⁻¹, and its maximum value was around 0.952 s⁻¹. Given the range of p₀ as [0.13, 0.95] (Donahue et al., 1995), it is possible that FXL could be invalid in some BV voxels with higher τ_i values. Without further knowledge of p₀, it is infeasible to do further quantitative evaluation of FXL condition distribution in BV. The BV volume ratio of both treatment/control groups decreased during the experiment. Although the treatment group was inclined to have higher BV volume ratio, no significant difference was observed. Future studies with histology report may validate the potential physiological meaning of BV.

The $K_{S,BV}^{\mathit{trans}}$ analysis within the BV was proved to be superior to the analysis in whole tumor. In Figure 7(a), the treatment group had a significantly lower mean $K_{S,BV}^{\mathit{trans}}$ value as early as after the first treatment delivery at Day2, while in Figure 5(a), the mean $K_S^{\mathit{trans}}$ and $K_T^{\mathit{trans}}$ across the tumor did not show significant differences between treatment/control groups until Day9. When using mean $K_{S,BV}^{\mathit{trans}}$ and its CV as the biomarkers for treatment/control separation, the achieved accuracy was 68.8%, which was higher than the accuracy 62.5% using tumor mean $K_S^{\mathit{trans}}$ and its CV and 50.0% using tumor mean $K_T^{\mathit{trans}}$ and its CV, respectively. Furthermore, the spatial heterogeneity indices d₁ and d₂ of $K_{S,BV}^{\mathit{trans}}$ demonstrated significant difference between treatment/control groups at Day9. These results suggest that the SS model should be adopted in small animal DCE-MRI experiment for monitoring the early bevacizumab therapeutic response.

One of the contributions of our work is the longitudinal study of d₁ and d₂ change using in vivo small animal data. Although the theory of fractal dimensions were developed primarily for abstract mathematical objects, it can be applied to the real objects that may not come from fractal process. Biologically, the branching nature of the tumor vascularity is likely to be a fractal process, but it cannot be directly observed on current diagnostic MR images with the current imaging resolution (~1mm). In this work, the improved spatial resolution (156μm) makes the fractal dimension analysis appealing. As the tumor evolves, the periphery and the core of the tumor may have different enhancing rates during the CA uptake with a heterogeneous K^trans distribution (Su et al., 2003). The inclusion of spatial heterogeneity information could provide supplementary information for capturing treatment response. As quantitative metrics describing the object complexity, high d₁ and d₂ values were associated with high degree of heterogeneity. Previous studies reported increased K^trans d₁ and d₂ values after the simulated treatment using digital tumor phantom (Rose et al., 2009). In this work, however, both treatment/control groups had a decreasing trend of K^trans d₁ and d₂ when evaluating the whole tumor and the BV, and the treatment group had significantly higher $K_{S,BV}^{\mathit{trans}}$ d₁ and d₂ values at Day9. This inconsistency could be explained by the incomplete tumor regression. Nevertheless, the therapeutic response evaluation using d₁ and d₂ is far from straightforward and needs to be exploited with future studies with larger small animal population.

5. Conclusion

This study compares the use of SS model with transcytolemmal water exchange analysis versus the classic Tofts model for longitudinal therapeutic response assessment in a small animal anti-angiogenesis drug experiment. Results show that when using the K^trans information across the tumor, the performances of the two models in treatment/control differentiation were comparable. When the biological subvolume from the SS model was adopted, the PK parameters’ metrics were capable of capturing the therapeutic effects as early as after the first treatment delivery, while the Tofts model analysis can only demonstrate the therapeutic effects after three treatment deliveries. Our results suggest a great potential of the SS model for DCE-MRI early therapeutic response assessment.