Quantifying the Balance Between Total Bone Formation and Total Bone Resorption: An Index of Net Bone Formation

Abstract

Context:

Bone gain vs loss across the skeleton loss depends on the balance between total bone formation and total bone resorption.

Objective:

The objective of the study was to determine whether resorption and formation markers can be combined to gauge net bone formation across the skeleton.

Design:

The study included a cohort followed up across menopause transition (Study of Women's Health Across the Nation).

Setting and Participants:

Community-dwelling women, 42–52 years old, premenopausal or early perimenopausal at baseline, participated in the study.

Outcome:

The study included the following measures: 1) bone balance index (BBI) created by estimating the relationship between resorption (urinary N-telopeptide) and formation (osteocalcin) markers when the total formation equals the total resorption in 685 women with stable bone mineral density (BMD) (>5 y before the final menstrual period [FMP]) and applying this relationship to measured bone turnover markers in 216 women beginning to lose bone (≤2 y from FMP); and 2) annualized percentage declines over the following 3–4 years in the lumbar spine (LS) and femoral neck (FN) BMD.

Results:

Adjusted for covariates, the BBI was greater (more favorable) in women with a greater body mass index (P = .03) and lower (less favorable) in women closer to the FMP (P = .007). Each SD decrement in BBI was associated with 0.27%/y faster LS BMD decline (P 0.04) and a 38% higher odds of faster-than-average loss of LS bone mass (P = .008, c-statistic 0.76). BBI was not associated with decline in FN BMD. Urinary N-telopeptide alone was not associated with either LS or FN BMD decline.

Conclusions:

An index that quantifies net bone formation vs resorption can be created from bone turnover markers and may help identify individuals at high risk for LS bone loss.

We created a bone balance index from bone turnover markers that gauges net bone formation, and predicts longitudinal change in vertebral bone mineral density across the final menstrual period.

Biochemical markers of bone resorption and formation (bone turnover markers [BTMs]) have been available for clinical and research purposes for many years (1–8). In postmenopausal women, BTMs are correlated with histomorphometric indices of bone turnover, especially at sites of high remodeling (8–10). Elevated BTM levels are also associated with faster rates of bone loss and increased fracture risk (1–7). However, one reason that interpreting individual BTM values remains challenging is that bone resorption and formation are coupled. As such, markers of both bone resorption and formation increase in states of increased bone turnover, regardless of whether there is net bone gain (eg, after initiating regular exercise or teriparatide therapy) or loss (eg, during the menopause transition) (6, 7, 11). This implies that to accurately assess bone balance across the entire skeleton, bone resorption and formation markers cannot be examined in isolation but ideally should be combined to gauge the direction and magnitude of total bone gain or loss (6, 11–16).

Net bone gain or loss across the entire skeleton is determined by the total amounts of bone removed and deposited at all sites of bone remodeling and modeling. When total bone formation and resorption are equal, bone mineral density (BMD) is stable. When total bone formation is less than resorption (as in postmenopause), BMD decreases; when total formation exceeds resorption (as in adolescence), BMD increases. In this proof-of-concept study, we aimed to develop and test a novel methodology for combining an individual's measured BTMs (which reflect total bone formation and resorption across the skeleton) to gauge net bone balance. The term balance in this context refers not to the balance between formation and resorption within a single basic multicellular unit but rather the balance between total bone formation and total resorption at the level of the whole skeleton (17–20). We hypothesized the following: 1) the quantitative relationship between bone resorption and formation markers in a state of whole-skeleton bone balance (ie, when total formation equals total resorption) can be estimated from a sample of healthy adults with stable BMD; and 2) this estimate of the in-balance relationship can be combined with an individual's measured BTMs at a time when total formation may or may not equal total resorption to create a bone balance index (BBI) that reflects the individual's net bone formation relative to resorption. Under this paradigm, a more positive BBI value indicates more favorable bone balance, and a more negative BBI value indicates less favorable bone balance.

Using data from the Study of Women's Health Across the Nation (SWAN), we used the above paradigm to create a BBI and tested its ability to predict the rate of BMD loss. All participants in SWAN were premenopausal or early perimenopausal at the baseline visit. Since baseline, almost the entire cohort has transitioned to postmenopause. For participants with a dated final menstrual period (FMP), we knew how many years prior to their FMP they were at SWAN baseline. This allowed us to estimate the in-balance relationship between resorption and formation markers from baseline BTM data in women who were more than 5 years from their FMP (and therefore likely to be in stable whole skeleton bone balance, ie, stable BMD). We then used this in-balance estimate to calculate BBI values in women who were 2 or fewer years from the FMP (and therefore had begun to lose BMD). Menopause transition (MT)-related bone loss generally starts approximately 2 years before the FMP and BMD declines in a linear fashion (at a constant rate) until approximately 1 year after the FMP (21). In these women, we assessed the ability of the BBI to predict longitudinal decline in BMD (21). We hypothesized that more positive BBI values (reflecting more favorable bone balance) would be associated with slower declines in BMD.

Materials and Methods

Study samples

SWAN is a multicenter, longitudinal study of the MT in a community-based cohort. Participants at baseline were aged 42–52 years, were premenopausal (menstruating 3 mo prior to screening without a change in menstrual regularity in the past year) or early perimenopausal (menstruating 3 mo prior to screening with a decreased regularity in the past year), had an intact uterus with one or two ovaries, were not pregnant, were not lactating, and were not taking exogenous sex steroid hormones or bone-active medications. Five of the seven SWAN study sites (Boston, Massachusetts, Detroit, Michigan, Los Angeles, California, Oakland, California, and Pittsburgh, Pennsylvania) measured BTMs and BMD. BTMs were measured at baseline; BMD was measured at baseline and on annual follow-up. Participants gave written informed consent, and sites obtained institutional review board approval. Detailed recruitment and participant information has been previously reported (21).

Since SWAN baseline, almost the entire cohort has transitioned to postmenopause, and for many, we have determined the date of the FMP. Of 2413 SWAN bone cohort participants, the FMP date was known for 1331 women. Major reasons for not being able to identify an FMP date were hysterectomy before the FMP and use of menopausal hormone therapy. Of these 1331 women, 703 were more than 5 years before their FMP at the baseline visit. After excluding 18 women with missing BTM data, we were left with an in-balance sample (of women more than 5 y before the FMP) size of 685 for estimating the in-balance relationship between formation and resorption markers. Of the 1331 women with a known FMP date, 223 were 2 or fewer years before their FMP at the baseline visit; after excluding seven women with missing BTM data, we had a test sample (of women no more than 2 y prior to their FMP) size of 216 to create and test the BBI.

Measurements: bone turnover markers

The bone formation marker, serum osteocalcin (OC), was measured from fasting blood collected before 10:00 am. The bone resorption marker, urinary N-telopeptide (U-NTX), was measured from a nonfirst voided urine collected before 10:00 am. If a woman could not provide a urine sample before 10:00 am, the time of collection was recorded. Because BTMs show diurnal variation, we adjusted for time of urine collection in sensitivity analyses described below (see Statistical analyses). Specimens were stored at −20 to −80°C until centralized analysis (Medical Research Laboratories). OC was measured using the ELSA-OSTEO immunoradiometric assay (nanograms per milliliter; CisBio International; interassay coefficient of variation [CV] < 6%; intraassay CV < 6%). U-NTX was measured using the Osteomark competitive inhibition enzyme immunoassay (nanomoles bone collagen equivalent [BCE]; Osteomark; Ostex International Inc; interassay CV < 12%; intraassay CV < 8%). Urinary creatinine was measured using the Cobas Mira autoanalyzer (millimoles; Horiba ABX; interassay CV 4.1%; intraassay CV 0.6%). U-NTX was normalized to urinary creatinine and expressed in nanomoles BCE per millimole of creatinine. U-NTX and OC measured at the SWAN baseline visit were used in this study to create the BBI at the SWAN baseline.

Measurements: BMD

Lumbar spine (LS) and femoral neck (FN) BMDs were assessed by dual-energy x-ray absorptiometry (Hologic QDR 2000 at Pittsburgh and Oakland sites; Hologic QDR 4500A at Boston, Los Angeles, and Michigan sites). At the SWAN baseline, cross-site calibration was accomplished by circulating an anthropomorphic spine phantom. To ensure that drift did not occur over the course of the SWAN study (thus undermining the calibration), daily manufacturer's phantom measurements were completed before each BMD measurement session and shipped to quality control centers at Synarc Inc. If any drift was observed, correction factors were applied to maintain cross-site comparability.

Rates of ongoing change in BMD

BMD was measured at baseline and annually thereafter. In the test sample group, we used BMD (grams per square centimeter) measured at baseline (within 2 y of the FMP) and at a follow up visit 3–4 years later to calculate the annualized percent change in BMD as the difference between BMD at the two visits divided by the starting BMD and the number of years between visits and converted to a percentage. MT-related bone loss generally begins at approximately 2 years before the FMP, with the rate of bone loss remaining constant until approximately 2 years after the FMP (21). The period over which we calculated the annualized rate of BMD change corresponds to a period when the rate of BMD is thought to be fairly constant.

Measurements: covariates

Body mass index (BMI) was calculated from weight and height measurements (BMI = weight in kilograms/[height in meters]²). The FMP date for those who underwent natural menopause was defined as the last menstrual bleeding date reported during the visit immediately preceding the first visit at which participants were classified as postmenopausal (12 mo of amenorrhea). Physical activity level was summarized by a score combining intensity with frequency of active living, home, and recreational physical activity from a modified Baecke interview (22).

Statistical analysis

Creating the BBI

We first confirmed that U-NTX and OC were normally distributed in the in-balance sample. A BBI that quantifies the net excess of bone formation over resorption was created in the following four steps. In step 1, the bone resorption marker (U-NTX normalized to urinary creatinine [nanomoles BCE per millimole of creatinine]) was regressed on the formation marker (OC [nanograms per milliliter]) in the in-balance sample. This provided a quantitative estimate of the in-balance relationship between resorption and formation markers to use in constructing BBI in the test sample group in the following three steps. In step 2, regression coefficients from step 1 were combined with each individual's measured bone formation marker level(s) to create participant-specific predictions (P_NTX) of the NTX level that would be expected when bone resorption equals formation. In step 3, a raw BBI value was generated for each participant as P_NTX − NTX, the difference between the expected and measured values of the bone resorption marker. In step 4, BBI was standardized by dividing raw BBI values by the SD of the raw BBI.

Testing the BBI

In the test sample group, we conducted three different types of construct validation. First, we examined the association between BBI and factors known to impact whole-skeleton bone balance, namely physical activity, BMI, and time from FMP. Second, we assessed the ability of BBI to predict longitudinal decline in LS and FN BMD. Third, we assessed the ability of BBI to identify women who lost bone at a greater-than-average rate.

To examine the association of BBI with expected determinants of whole-skeleton bone balance, we used multivariable linear regression to regress BBI on BMI, years from the FMP, concurrently measured physical activity and relevant covariates (study site, race/ethnicity, and age).

We examined the ability of BBI to predict longitudinal bone loss and identify those who lost bone at a faster-than-average rate in a subset of 157 individuals from the test sample group after excluding 59 participants who initiated bone-active medications between baseline and follow-up BMD measurements. Bone-active medications included osteoporosis medications (bisphosphonates, calcitonin, teriparatide), selective estrogen receptor modulators, aromatase inhibitors, sex steroid hormones, GnRH agonists, glucocorticoids, antiepileptics, and chemotherapeutic agents.

To examine the ability of BBI to predict the rate of bone loss, we used multivariable linear regression to regress annualized percentage change in BMD on BBI and relevant covariates (study site, race/ethnicity, BMI, age, and years from FMP). Rates of decline in LS and FN BMD were the dependent variables in separate analyses. We did not include the starting BMD as a covariate to avoid bias due to measurement noise and regression to the mean (23).

To examine the ability of BBI to identify women whose bone loss was faster than average, we used multivariable logistic regression to regress faster-than-average bone loss (defined as annualized percentage BMD decline rate exceeding the median value) on BBI and relevant covariates (study site, race/ethnicity, BMI, age, and years from FMP).

Sensitivity analyses

Because not all women were able to provide urine samples before 10:00 am, and BTMs have diurnal variation, we created an alternate BBI formula in which we adjusted for time of urine collection. In addition, because the race/ethnic distributions of the in-balance and test samples were different, we created a third BBI formula in which we adjusted for race/ethnicity. We then conducted construct validation for each alternate BBI.

Results

Study samples

Mean age in the in-balance sample (those for whom the FMP was more than 5 y away) was 44.6 years, and the mean time before the FMP was 8.1 years. Nearly half of the in-balance sample were Caucasian, 28.6% were African American, 11.4% were Chinese, and 13.8% were Japanese (Table 1). The test sample group (those who were within 2 y of their FMP) was older and closer to the FMP on average than the in-balance sample. Mean age here was 48.0 years and the mean time before FMP was only 0.9 years. The test sample also had more African Americans and fewer Caucasians than the in-balance sample: 36.6% were African American and 37.0% were Caucasian (Table 1). The mean annualized percentage change in BMD from baseline to 3–4 years later was −1.7% per year and −1.2% per year at the LS and FN, respectively, but there was a significant variability between women in the rate of change (Table 1).

Table 1.

Descriptive Statistics for Analytic Samples: SWAN^a

	In-Balance Sampleb (n = 683)	Test Samplec (n = 216)
Age, y	44.6 (2.1)	48.0 (2.6)
Time before or after FMP, yd	−8.1 (2.1)	−0.9 (0.8)
Race/ethnicity
Caucasian	316 (46.3)	80 (37.0)
African American	195 (28.6)	79 (36.6)
Chinese	78 (11.4)	28 (13.0)
Japanese	94 (13.8)	29 (13.4)
BMI, kg/m2	27.8 (7.2)	28.5 (8.1)
Physical activity score	7.8 (1.8)	7.7 (1.9)
BTMs
U-NTX, nM BCE/mM creatinine	32.6 (13.4)	38.1 (15.7)
OC, ng/mL	15.1 (5.1)	18.1 (6.6)
BBI	0.0 (1.0)	−0.2 (1.1)
Annualized percentage change in BMDe
FN, %/y	N/A	−1.2 (1.8)
LS, %/y	N/A	−1.7 (1.8)

^aCount (percentage) for categorical variables; mean (SD) for continuous variables. All variables (other than rate of change) were measured at the baseline visit.

^bSample of women who were more than 5 years from their FMP at study baseline, in whom we estimated the in-balance relationship between bone resorption and formation to create the formula for calculating individual-specific bone balance index values.

^cSample of women who were less than 2 years from their final menstrual period at baseline, in whom we calculated individual-specific bone balance index values and tested their ability to predict longitudinal change in BMD.

^dNegative values indicate time prior to FMP (the zero reference) and positive values indicate time after the FMP.

^eBased on measurements of BMD from the baseline visit and a follow-up visit 3–4 years after the baseline visit.

BBI creation

The quantitative estimate of the in-balance relationship between the bone formation marker (OC) and bone resorption marker (U-NTX) was determined using measurements at the SWAN baseline visit from the in-balance sample. This was used to estimate P_NTX, the participant-specific prediction of the NTX level expected if bone resorption equals formation. The BBI at the SWAN baseline was created for each participant in the test sample group as P_NTX − NTX and standardized to SD units. The resulting formula for the BBI was: (16.3 + 1.1OC − NTX)/12.2, where 16.3 is a constant term; 1.1OC represents the predicted U-NTX value corresponding to the measured OC level (in nanograms per milliliter); NTX represents the measured U-NTX value (in nanomoles BCE per millimole of creatinine); and 12.2 represents the SD of the raw (unstandardized) BBI.

Determinants of BBI

After adjusting for age, race/ethnicity, and study site, the time from the FMP and BMI were both independently associated with BBI, but physical activity was not. As expected, the closer proximity to the FMP was associated with more negative (less favorable) BBI, such that every year closer to the FMP was associated with a 0.3 U decrease in a standardized BBI (P = .007). Also as expected, a higher BMI was associated with a more positive (more favorable) BBI, such that every 5 kg/m² increment in the BMI was associated with a 0.1 U increase in the standardized BBI (P = .03) (Table 2).

Table 2.

Adjusted Associations Between Characteristics Known to Affect Bone Balance and BBI^a

	β-Coefficient (95% Confidence Interval)	P Value
Time from FMP (per year)	−0.29 (−0.50, −0.08)	.007
BMI (per 5 kg/m2)	0.11 (0.01, 0.22)	.04
Physical activity score (per unit score)	0.03 (−0.05, 0.11)	.50

^aAdjusted associations for study site, race/ethnicity, and age.

BBI as predictor of longitudinal change in BMD

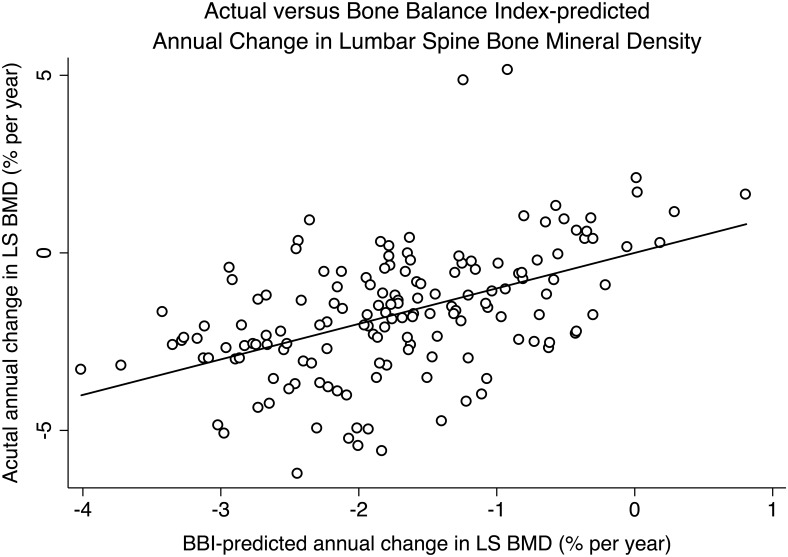
After adjusting for age, the time from the FMP, race/ethnicity, BMI, and study site, a higher (more favorable) BBI was significantly associated with slower decline in LS BMD (P = .03) but was not associated with rate of decline in FN BMD (P = .5). Each unit decrement in standardized BBI was associated with 0.27% faster annual decline in LS BMD change (P = .03). In contrast to BBI, U-NTX was not significantly associated with rate of decline in either LS (P = .1) or FN (P = .5) BMD (Figure 1 and Table 3).

Figure 1.

Scatter plot of actual vs BBI-predicted annual change in lumbar spine BMD.

Table 3.

Adjusted Associations Between BBI vs U-NTX and Rate of Bone Loss^a

		P Value
Annualized percentage decline in BMD (95% confidence interval) per unit decrement in standardized BBI
LS	0.27 (0.02, 0.51)	.03
FN	−0.10 (−0.38, 0.17)	.50
Annualized percentage decline in BMD (95% confidence interval) per SD increment in U-NTX
LS	−0.18 (−0.42, 0.03)	.10
FN	0.08 (−0.17, 0.32)	.50

^aAdjusted associations for study site, race/race/race/ethnicity, BMI, age, and years from the FMP.

BBI as predictor of faster-than-average bone loss

The median rate of decline in BMD was 1.8% and 1.2% per year in the LS and FN, respectively. After adjusting for age, time from FMP, race/ethnicity, BMI, and study site, a higher (more favorable) BBI was associated with a lower odds of faster-than-median BMD decline at the LS (P = .008) but not at the FN (P = .9). Each unit increment in BBI was associated with a 38% lower odds of LS BMD loss at a faster-than-median rate (P = .008). The ability of BBI (in combination with the covariates listed) to identify the faster losers of LS BMD, as measured by the area under the receiver-operating characteristic (ROC) curve, was 0.76. Recognizing that the time from the FMP cannot be readily discerned in real time by pre- and early perimenopausal women before the FMP and that the study site is not relevant to clinical practice, we also tested the ability of BBI (in combination with age, race/ethnicity, and BMI) to identify faster losers of LS BMD. The area under the ROC curve for this model was 0.74.

Sensitivity analyses

Associations of the alternate BBIs (adjusted for time of urine collection or race/ethnicity) with factors known to influence whole-skeleton bone balance, BMD decline rates, and faster-than-average bone loss were essentially the same (data not shown).

Discussion

This proof-of-concept study was designed to show that the balance between total bone formation and total resorption at the level of the skeleton can be quantified by referencing currently measured BTMs against an estimate of the relationship between resorption and formation markers when total formation equals total resorption. Previous attempts to quantify whole-skeleton bone balance used the difference between Z-scores of bone formation and resorption markers. These were developed and tested in study samples of fewer than 100 participants and were based on the assumption that in a state of whole-skeleton bone balance, each SD increment in bone resorption markers corresponds to a SD increment in bone formation markers (6, 11–13, 15, 16). More recently, another group mathematically transformed BTM levels to generate graphic plots that provided visual indices of changes in the balance of resorption vs formation and in the rate of bone turnover of individual patients in relation to reference individuals (14). In contrast, our approach was to estimate the in-balance relationship between resorption and formation markers when total formation equals total resorption from a sample of healthy women with stable BMD and to combine this with BTMs from individuals potentially losing or gaining BMD to create an index of total formation relative to resorption.

As a first step in construct validation of the new BBI, we confirmed that BBI did indeed increase (become more positive, indicating greater total formation relative to resorption) as BMI increased, consistent with our understanding that increased mechanical loading secondary to higher body weight stimulates bone formation (24, 25). As hypothesized, BBI decreased (became more negative) as women approached the FMP, concordant with increasing total resorption relative to formation as the MT progresses (4, 26–28).

For further construct validation of the BBI, we examined the ability of BBI to predict longitudinal change in BMD during the rapid phase of MT-related bone loss (21). Because bone remodeling is dynamic, it is important to note that we assessed the association between BBI and rate of BMD loss over a period when the rate of BMD loss is relatively constant (21). As hypothesized, greater (more positive) BBI was associated with a slower decline in BMD at the LS, but no association was evident with BMD decline at the FN. This is consistent with prior reports that bone resorption related to early menopause occurs primarily on trabecular surfaces, of which there are more in the LS than the FN (29–31). It has also been reported previously that early in the MT, bone loss is greater at the spine than at the femoral neck (21). BBI was also robust at identifying faster-than-average BMD loss, with an area under the ROC of 0.76, which exceeds the discrimination ability of some clinical prediction tools (32, 33).

Importantly, it should be noted that U-NTX by itself did not predict rate of either LS or FN BMD loss. This contrasts with prior studies demonstrating an association between individual resorption markers and rate of BMD loss (2, 5–7). One potential explanation for this discrepancy is that our test sample group consisted entirely of early perimenopausal women, whereas prior studies included or were restricted to postmenopausal women (2, 5–7). Even more importantly, net bone gain vs loss across the skeleton is determined by the balance between total formation and total resorption. As such, resorption or formation markers alone may not predict change in BMD because markers of both resorption and formation increase in states of increased bone turnover, regardless of whether there is net bone gain (eg, after initiating regular exercise or teriparatide therapy) or loss (eg, during the menopause transition) (6, 7, 11). The ability of resorption or formation markers alone to predict change in BMD is likely to be particularly poor when the magnitude of change is small, as in premenopausal and early perimenopausal women. In contrast to U-NTX, BBI was able to predict longitudinal rate of BMD loss and faster-than-average bone loss in women within 2 years of the FMP.

Our study has limitations that should be noted. First, we created the BBI using U-NTX and OC, BTMs that were measured in SWAN when it was initiated in 1996. The International Osteoporosis Foundation and the International Federation of Clinical Chemistry and Laboratory Medicine now recommend serum C-terminal cross-linking telopeptide of type I collagen and serum procollagen type I N-terminal propeptide as the bone resorption and formation markers of choice, respectively (34). Urinary measures of NTX are more variable than serum measures (35). In addition, storing frozen specimens for BTM measurement at −20°C may also lead to analyte deterioration, especially for OC (36). These sources of variability, however, would have biased our findings toward null. Future studies should recreate and test the BBI using referent BTMs, which may further improve the ability of BBI to identify faster-than-average bone loss. Second, we were unable to test the ability of BBI to predict fracture risk because of the small size of the test sample group, despite the nearly 20 years of follow-up in SWAN. Further studies are needed to assess the ability of the BBI to predict fracture risk. Finally, although we adjusted for race/ethnicity, the test sample group was too small to permit assessing whether BBI predicts longitudinal BMD change differently in different race/ethnicity groups. This also requires further study.

Despite these limitations, this proof-of-concept study demonstrated that a potentially useful index of whole-skeleton bone balance can be created by referencing currently measured BTMs against an estimate of the relationship between resorption and formation markers in a state of whole-skeleton balance (when total formation equals total resorption). An index, such as this, that reliably predicts future change in BMD could be used to identify individuals at the greatest risk for large declines in bone strength, making it possible to test the efficacy of interventions to prevent bone loss and maintain bone strength.